在密集图的应用分析中,研究顶点之间的关系是图分析的热点,而对三角形关系的研究又是重要的研究方向。
在图论的研究中,三角形关系是复杂社会网络分析中常见的结构[1]。如在社交网络关系中,通过分析三角性关系可以确定节点之间的联系程度;在角色行为识别中,通过分析三角形关系可以判断角色之间的地位。三角关系的一个重要应用是在枚举图的极大团(Maximal Clique)过程中[2],即将一跳(one-top,即与被选点直接相邻的点构成的集合)数据转换为三角形结构。
研究者已提出很多算法[3-5]实现一跳数据集向三角形数据集的转换,但伴随着数据量的增大,传统的单机算法已无法快速地处理大规模图数据。随着MapReduce并行计算框架的普及,很多研究已开始使用MapReduce框架进行图数据的处理[6-7],并且已有研究者实现了MapReduce框架下将一跳数据集向三角形数据集转换的GT(Graph Twiddling)算法[8]。GT算法通过两轮MapReduce任务来完成数据结构的转换,该算法可以很高效地将整个原图的一跳形式处理成三角形结构,但却无法直接生产部分点的三角形结构。同时,该算法是图上迭代计算,在MapReduce计算框架下,由于需要将中间结果写回磁盘,将造成很大的读写瓶颈。
基于以上两个问题,本文首先提出可直接枚举部分点三角形结构的改进GT算法,该算法经过两轮MapReduce任务:第一轮为查询点的筛选,第二轮为查询点三角形结构的生成;同时,将改进算法在Spark系统上实现,以实现该算法高效迭代的特性。本文的主要工作如下:
1) 改进GT算法,使该算法可以直接生产部分点的三角形结构;同时,在三角形的筛选过程中,提出按照最小度数点进行切分的优化思想,以提高枚举效率。
2) 将改进算法在Spark系统实现,避免因MapReduce框架下需要将中间结果写回磁盘的瓶颈,以提高迭代计算效率。
3) 通过合成数据集和真实数据集验证该算法的高效性,与改进前相比,具有至少3倍的运行效率提升。
1 相关技术本章介绍与本文研究密切相关的两个概念:三角形结构和MapReduce计算框架。
1.1 三角形结构设无向图G=(V, E),其中:V是顶点的集合,|V|是顶点的总数;E是边的集合,|E|是边的总数。
定义1 三角形结构。给定一个无向图G=(V, E),{u, v, w}∈V,若三个顶点满足以下关系{u, v},{w, v},{u, w}∈E,则称三个顶点构成了一个三角形结构,记为△uvw。
1.2 MapReduce计算框架MapReduce计算模型是将计算分为Map和Reduce两个阶段。在Map阶段,由用户定义的map函数将输入的每条元组转换为〈key, value〉形式,然后按照partition函数对key进行分区,并将各分区Shuffle到Reduce端,且严格保证分区和Reducer是一一对应的关系。当各Reducer获取分配给各自分区的全部数据后开始执行用户定义的reduce函数,并输出结果。
影响Reducer执行效率的关键是partition函数的定义,合理的partition函数可以实现各Reducer运行过程中的均衡性,反之会出现数据倾斜,严重影响执行效率。对于数据的分配均衡问题,文献[9]已进行了探讨并提出了相应的策略。该问题的避免可以通过定义partition函数或定义map函数等方法优化,因此,在设计MapReduce算法时应该考虑该数据倾斜的问题。
MapReduce在处理迭代计算时,有两处磁盘操作,map函数后和reduce函数的结果输出,因此MapReduce在处理图的迭代计算时存在数据传输的瓶颈问题。针对该问题,已有i2MapReduce[10]方法可进行高效的迭代计算,同时Spark系统更是被广泛应用的图处理平台。
2 GT算法本章介绍基于MapReduce编程模型的GT算法。
GT算法将三角形的枚举过程分为两个MapReduce任务:第一,合并公共点;第二,判断合并后的公共点集合中是否存在三角形结构。
第一轮MapReduce任务:map函数将同一节点的所有邻接点进行汇总,并传到一个Reducer上处理。reduce函数将与该点相连,且编号大于该点的所有顶点进行笛卡尔积运算,并将结果输出。
第二轮MapReduce任务:map函数将原图和第一轮Reduce端的输出结果合并,即边作为key值输出。reduce函数判断第一轮笛卡尔积所构成的边集合中,是否存在原图中的边。若在原图中存在该边,则说明该边的两个顶点与生成该边的点,即第一轮中reduce函数key所表示的顶点,构成了一个三角形结构。
根据对GT算法的描述可知,在第一轮Reduce阶段,需要进行笛卡尔积操作,度数较大的点会产生大量的中间结果。GT算法在处理时,将原图以一跳的形式表示,并满足第一个顶点编号的值小于第二个顶点编号的值,同时,将度数小的顶点作为key值,然后再进行分区,从而达到减少中间结果的目的。
GT算法不能直接枚举出部分点所构成的三角形结构。由于第一轮map函数是按照度数或者顶点编号进行划分的,因此在枚举部分点构成的三角形结构时,当被选点出现在value中,就无法获得被选点的完整邻接点集合,从而导致查询的结果不完整。因此,若使用GT算法来枚举部分点的三角形结构,首先需要枚举出原图的所有三角形,然后从全图的三角形集合中筛选出包含被选点的结构。由此可见,这样将造成大量的不相关计算。
3 PGT算法本章介绍可直接枚举部分顶点构成三角形结构的改进GT算法,本文称为PGT(Parts-of-vertex for GT)算法。
3.1 算法描述要解决GT算法直接枚举部分点构成三角形结构的问题,就需要解决如何在划分过程中保持数据的完整性问题,因此首先需要统计出被选点划分后的分布情况。由于MapReduce模型采用〈key, value〉对处理数据的特点,在数据划分后被选点只会现在两个集合中:第一是在key中,如图 1(a)所示的第一层顶点编号为A的顶点(被选点);第二个是在value中,如图 1(b)所示的第二层顶点编号为B的顶点(被选点)。因此,要保证数据的完整性需要同时将两种情况进行分析。

|
图 1 被选点的分布 Figure 1 Distribution of candidate vertexes |
如图 1(a)所示,被选点在key集合中。在该结构中,value集合中的顶点是key的邻接点集合,如图中实线所示。在该结构中若存在三角形,一定是value中的某两个顶点存在一条边,即如图中虚线所示。因此,对于这种情况,需要将value集合中的所有顶点进行笛卡尔积运算,即构建出一条新边,并通过下一轮MapReduce任务判断该边是否在原图中存在,若存在,则该点(key)与相连的两点(value中的顶点)构成了三角形结构。
如图 1(b)所示,被选点出现在value中。出现这种情况的原因是:为了减少笛卡尔积集合的大小,在划分时是以两个点的度数为标准,即度数小的点为key,因此导致被选点会出现在value中的现象。在此种结构中,同样value集合中的点是key点的邻接点,然而只需要枚举包含有被选点的集合。因此,此时只需要将被选点从value中取出,然后将该点和value中的其他点进行笛卡尔积运算,构建出一条新边,如图 1(b)中虚线所示。同样,通过下一轮MapReduce任务判断该边是否在原图中存在,若存在,则该点(value中的被选点)和相连的两个点(key顶点和在value中与被选点相连的顶点)构成了三角形结构。
3.2 算法实现算法1 PGT算法的MapReduce实现。
输入 集合key, 集合value, 被选点构成的集合Cand;
输出 候选边集Edge。
1) if key in Cand //被选点在key集合中
2) for v to value //遍历value集合,求笛卡尔积
3) Edge←v×{value-v}
4) Write(Edge, key) //输出,并标注是在key集合中
5) endfor
6) endif
7) else
8) for n to value //被选点在value集合中
9) if n in Cand
10) Edge←n×{value-n }
11) Write(Edge, n) //输出,并标注是在value集合中
12) endif
13) endfor
14) endelse
算法1可分为两部分:第一部分从1)~6)行,是对被选点在key中情况的处理,第二部分从7)~14)行,是对被选点在value中的处理。由于在第二轮MapReduce任务中,需要将被选点进行聚合,所以在输出时,需要标明被选点的编号,即如算法1第4)行和第11)行所示。由算法1描述可知,该算法的复杂度为O(n)。
算法2 PGT算法的Spark实现。
输入 集合key,集合value,被选点构成的集合Cand;
输出 三角形边集edges。
1) def PGT(key: Int, value: Set[Int], Cand: Set[Int])={
2) if (Cand.contains(key)) {
3) for (v←value){ //遍历value集合
4) val notV=value-v
5) val edges=notV.map(v2 => {
6) (v, v2) //对value中的点求笛卡尔积
7) })
8) (edges, key) //第一种情况的输出
9) } //end for
10) } //end if
11) else {
12) for (n← value) {
13) if (Cand.contains(n)){ //被选点在value中
14) val notN=value-n //除去本点后求笛卡尔积
15) val edges=notN.map(n2=> {
16) (n, n2) //第二种情况的输出
17) }
18) (edges, n)
19) } //end if
20) } //end for
21) } //end else
22) } //end function
算法2由两部分组成:第一部分从1)~10)行,是对被选点在key中情况的处理,第二部分从11)~22)行,是对被选点在value中的处理。函数PGT()是Spark中reduce函数的参数,即实现对三角形的筛选工作,不同于MapReduce的输出,Spark的输出可存储在内存中,以实现迭代计算的高效性。
4 实验结果及分析本章通过两部分实验验证GPT算法的高效性,实验是在两个人工生成数据集和两个真实数据集上进行,通过随机选点的方法比较两个算法的运行时间。
4.1 实验环境本文的所有实验在11个节点的集群上进行,其中包含1个Master节点负责任务的调度和集群管理,10个Worker节点负责存储数据和计算。每个节点的系统配置为:16核主频为2.20 GHz的AMD处理器,16 GB的RAM和1 TB的硬盘,节点之间通过1 Gb的网络连接,各节点用的是64位Ubuntu Linux12.01,部署的是Hadoop-1.2.1版本和Spark-1.6.1。
配置Hadoop,设置每个节点有10个Map slots和6个Reduce slots,采用默认的Hash分区函数,其他配置设置为默认值。为增强实验的说服力,同一组实验运行5次,取5次结果的平均值作为最终结果。
4.2 实验数据对于两种数据源作去重和格式化处理,并将数据处理为1-跳的形式。实验数据分为合成数据和真实数据,合成数据通过GTgraph[11]生成,包含DARPA HPCS SSCA (SSCA)和Recursive Matrix (R-MAT)数据,SSCA的参数设置:顶点数为220,极大团的大小为100;R-MAT设置顶点数为104,边与顶点的比值为1000。真实数据包含两种SOCIAL NETWORKS[12]数据,数据的分布情况如表 1所示。
| 表 1 实验数据 Table 1 Experimental data |
本节在合成数据集和真实数据集上比较两种算法的运行时间。实验采用随机选点,验证选点个数的不同对两种算法运行时间的影响。由于GT算法首先需要将一跳数据集全部转换为三角形数据集,这部分需要两轮MapReduce任务完成,经过5次测试,这部分的平均时间为3200 s。由于是处理部分点,在对比实验部分,不将这部分的时间计算在内;因此运行时间的统计分别为:GT算法为从全部三角形数据集中读取部分点的时间,PGT算法为从一跳数据集直接生产部分点的三角形数据集的时间。
图 2(a)、(b)分别是两种算法在合成数据集SSCA和R-MAT上的实验,图 2(c)、(d)分别是两种算法在真实数据集Orkut和Twitter上的实验。通过结果可以发现,GT算法和PGT算法都有很好的稳定性,而从运行时间上来看,在SSCA和R-MAT数据集上,GT算法的运行时间是PGT算法的3倍和4倍。随着输入数据量的增大,在真实数据集Orkut和Twitter上,GT算法的运行时间都是PGT算法运行时间的11倍。由此可见PGT算法在运行效率上有很大的提升。

|
图 2 GT和PGT算法在不同数据集上的运行时间对比 Figure 2 Runtime contrast of GT and PGT on different datasets |
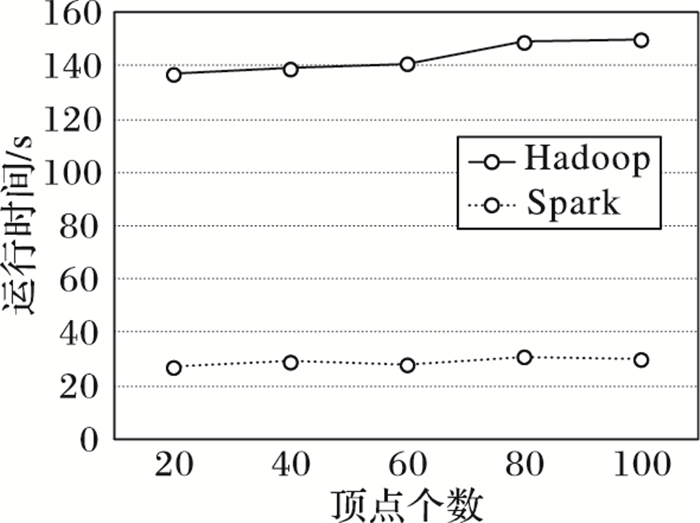
由于GT算法本身只有MapReduce实现,因此本节给出PGT算法在Hadoop和Spark系统上运行的对比实验,使用的数据集为图 2(d)的Twitter数据集,对比实验如图 3所示。
|
图 3 Spark与Hadoop上PGT算法运行时间对比 Figure 3 Runtime contrast of PGT algorithm on Spark and Hadoop |
从图 3结果可以看出,Spark系统在运行时间上比Hadoop系统有近7倍的性能提升,这主要因为Spark在迭代过程中未将结果写入磁盘,从而减少了对磁盘的读写操作。
5 结语本文提出一种改进的PGT算法,用于枚举部分点的三角形结构,并给出算法的MapReduce实现和Spark实现方法。该算法与传统算法相比,可以在三角形的生成过程中,只生成部分点的三角形结构,而避免对非筛选节点的三角形枚举工作,并最后在合成数据集和真实数据集上,验证该算法的高效性。三角形枚举是图数据研究中重要的应用,今后可通过本文的方法实现快速的三角形结构枚举。
| [1] | PARANJAPE A, BENSON A R, LESKOVEC J. Motifs in temporal networks[C]//Proceedings of the 2017 Tenth ACM International Conference on Web Search and Data Mining. New York:ACM, 2017:601-610. |
| [2] | WANG Z, CHEN Q, HOU B Y, et al. Parallelizing maximal clique and k-plex enumeration over graph data[J]. Journal of Parallel and Distributed Computing, 2017, 106: 79-91. DOI:10.1016/j.jpdc.2017.03.003 |
| [3] | COHEN J. Trusses:cohesive subgraphs for social network analysis[R]. Fort Meade, MD:National Security Agency, 2008. |
| [4] | 金宏桥, 董一鸿. 大数据下图三角计算的研究进展[J]. 电信科学, 2016, 32(6): 153-162. (JIN H Q, DONG Y H. Research progress of triangle counting in big data[J]. Telecommunications Science, 2016, 32(6): 153-162.) |
| [5] | SHAIK F, SUBRAMANYAM R, SOMAYAJULU D. Map-reduce based multiple sub-graph enumeration using dominating-set graph partition[J]. International Journal of Information Engineering and Electronic Business, 2017, 9(2): 36-44. DOI:10.5815/ijieeb |
| [6] | QIN L, YU J X, CHANG L J, et al. Scalable big graph processing in MapReduce[C]//Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data. New York:ACM, 2014:827-838. |
| [7] | SALIHOGLU S, WIDOM J. GPS:a graph processing system[C]//Proceedings of the 25th International Conference on Scientific and Statistical Database Management. New York:ACM, 2013:Article No. 22. |
| [8] | COHEN J. Graph twiddling in a MapReduce world[J]. Computing in Science & Engineering, 2009, 11(4): 29-41. |
| [9] | 王卓, 陈群, 李战怀, 等. 基于增量式分区策略的MapReduce数据均衡方法[J]. 计算机学报, 2016, 39(1): 19-35. (WANG Z, CHEN Q, LI Z H, et al. An incremental partitioning strategy for data balance on MapReduce[J]. Chinese Journal of Computers, 2016, 39(1): 19-35. DOI:10.11897/SP.J.1016.2016.00019) |
| [10] | ZHANG Y F, CHEN S M, WANG Q, et al. i2 MapReduce:incremental MapReduce for mining evolving big data[J]. IEEE Transactions on Knowledge and Data Engineering, 2015, 27(7): 1906-1919. DOI:10.1109/TKDE.2015.2397438 |
| [11] | BADER D A, MADDURI K. GTGraph:a synthetic graph generator suite[EB/OL].[2017-05-06]. https://www.researchgate.net/publication/228993783_GTGraph_A_synthetic_graph_generator_suite. |
| [12] | ROSSI R A, AHMED N K. The network data repository with interactive graph analytics and visualization[C]//Proceedings of the 2015 Twenty-Ninth AAAI Conference on Artificial Intelligence. Menlo Park:AAAI, 2015:4292-4293. https://www.semanticscholar.org/paper/The-Network-Data-Repository-with-Interactive-Graph-Rossi-Ahmed/93ee8e1c05d11d63aa3d61653b2c8bae75e0aecd |




