0 引言

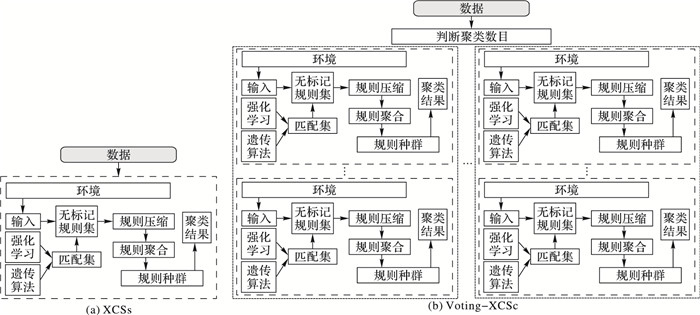
学习分类系统(Learning Classifier System, LCS)是一个动态感应环境、模拟认知的机器学习系统，它可根据环境反馈并通过强化学习^[1]来评估种群中的分类规则，进而借助遗传算法^[2-3]对种群进行进化，被认为是最常用的基于规则的学习工具之一。基于LCS框架，Wilson提出了复杂学习分类系统(eXtended Classifier System，XCS)^[4]和实值复杂学习分类系统(complex real Learning Classifier System, XCSR)^[5]，以处理样本连续实值属性问题。近年来，已有一些工作通过利用XCS进行聚类等无监督学习研究: Shi等^[6]提出了一种基于多规则表示的XCS聚类算法，每个数据点由规则对表示，并迭代合并包含共同数据点的规则; Shi等^[7]还提出了一种名为XCSc(XCS clustering)的聚类方法，该方法采用基于多规则的表示法，通过随机生成几个规则来初始化每个数据点, 同时，受Chameleon算法中使用的分层策略的启发，XCSc采用基于图的规则合并方法，能够处理复杂结构数据集; Qian等^[8]提出一种基于多轮投票的XCSc(Voting-XCSc)聚类方法，可以实现自动确定聚类簇数量。Voting-XCSc算法在XCSc^[7]算法基础上演变而来，二者区别如图 1所示。在Voting-XCSc中，当有新数据来自环境时，系统将自动检查整个规则种群，对于新数据，Voting-XCSc会基于一定规则生成规则匹配集，并计算规则匹配集中每条规则的相应奖励，之后Voting-XCSc通过强化学习机制更新规则的相应参数。Voting-XCSc属于无监督学习，一般在没有外部输入的情况下对未标记数据进行聚类分析。通过若干轮(需要设定最大学习次数)学习，Voting-XCSc对规则进行合并整合，从而生成规则集群，最后为每个新数据确定相应的集群。Voting-XCSc算法虽然可以自动确定聚类数目，但需要进行多轮学习，算法效率较低。

近邻传播聚类算法(Affinity Propagation, AP)^[8]将所有的数据点视为候选的簇代表点，避免聚类结果受限于初始簇代表点的选择，同时对于相似度矩阵的对称性没有要求。AP算法较为成功的特点是能够自动产生合理的聚类簇数目，在数据比较充足的情况下，AP能够准确地找出聚类代表点，其最终所获得的聚类效果往往也较为理想。然而，虽然AP算法同样解决了预先人为设定聚类簇数目的问题，但需要进行多轮迭代计算，同时由于AP算法是基于中心的聚类方法，它与其他基于中心的聚类方法一样，在紧凑的具有超球形分布的数据集上具有较好的聚类性能，但并不适合任意形状聚类问题。

为避免预先人为设定聚类簇数目，同时对任意形状的数据取得良好聚类效果，并保证一定的聚类算法效率，以适应未来流数据在线聚类需求，本文提出一种基于复杂学习分类系统(XCS)的密度聚类方法(Density XCS clustering，DXCSc)，主要贡献在于可自动确定聚类数目，聚类精度优于Voting-XCSc、AP等算法，且算法复杂度低于Voting-XCSc和AP算法。本算法以学习分类系统算法XCSc为框架，运用规则种群概念代表数据点集合，有效降低了表示大规模数据的复杂度，同时运用CFSFDP(Clustering by Fast Search and Find of Density Peaks)算法^[10]将各条规则重新视为二维数据点进行密度聚类，有效避免了Voting-XCSc、AP算法的多轮学习，取得良好的聚类效果。

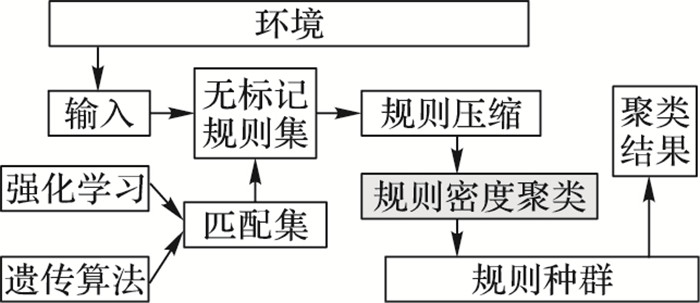
1 密度聚类学习分类系统框架与学习机制

本文提出的DXCSc算法(如图 2所示)与Voting-XCSc算法的主要不同在于：DXCSc算法不需要预先设定最大聚类数目，且不用进行k_max作为限定运算次数下的多轮计算，算法复杂度低于Voting-XCSc算法。DXCSc算法框图如图 2所示。

在聚类算法中，一般假定样本集$D = \left\{ {{\mathit{\boldsymbol{x}}_1}, {\mathit{\boldsymbol{x}}_2}, \cdots, {\mathit{\boldsymbol{x}}_m}} \right\}$包含m个无标记样本，每个样本${\mathit{\boldsymbol{x}}_i} = \left\{ {{x_{i1}}, {x_{i2}}, {x_{in}}} \right\}$是一个n维特征向量，则聚类算法将样本集D划分为k个不相交的簇$\left\{ {{C_l}\left| {l = 1, 2, \cdots, k} \right.} \right\}$，其中${C_{l'}}\bigcap\limits_{l' = l} {{C_l} = \emptyset } $且$D = \bigcup\limits_{l = 1}^k {{C_l}} $。相应地，本文用λ_j∈{1, 2, …, k}表示样本x_j的“簇标记”(cluster label)，即x_j∈C_λj。于是，聚类的结果可用包含m个元素的簇标记χ(x)表示。

本文在XCSc算法框架基础上，当新的数据来到并对应生成相关规则集合后，通过对重复冗余规则进行压缩，初步形成规则种群; 之后本文创新性地提出，将规则种群中的规则再次视为二维数据点，用对规则点的聚类取代对原始数据点的聚类，一条规则可代表大量数据点，从而可大量减少聚类所需计算量，并后续存在将高维数据降至低维的可能。其中对于每一个规则数据点i，计算i的局部密度ρ_i和与更高密度点之间的距离δ_i，二者定义如下所示：

$ {\rho _i} = \sum\limits_j {\chi \left( {{d_{ij}}-{d_c}} \right)} $

(1)

$ {\delta _i} = \mathop {\min }\limits_{j:{\rho _i} > {\rho _j}} \left( {{d_{ij}}} \right) $

(2)

其中，χ < 0时，χ(x)=1，当χ≥0时，χ(x)=0，其中d_ij是规则点i与规则点j之间的距离，d_c是用户指定的一个距离参数；ρ_i代表与规则点i距离小于δ_i的规则总数。式(2)中，δ_i代表了距离规则点i最近且密度大于规则点i的规则点j与i之间的距离。

本文将具有最高局部密度的规则点i的δ_i设定为$\mathop {\max }\limits_j \left( {{d_{ij}}} \right)$。本文提出的规则密度聚类方法主要有以下几步：1)计算规则种群中各规则点之间的距离；2)基于规则点之间的距离和用户设定的d_c计算每个规则点i的ρ_i；3)计算每个规则点i的距离δ_i。至此，参考CFSFDP算法^[10]，通过决策图方法人为选择ρ_i、δ_i值均较高的点就可以逐步算出簇中心，但是此方法存在的一个主要问题是，当数据分布存在较多密度极值点时，仅仅依靠规则密度搜索算法无法取得理想聚类效果。因此，本文采取Fuzzy-CFSFDP^[11]提出的方法，进一步优化了簇中心选择方式。如式(3)、(4)所示，EC_i代表预期的簇中心，σ(δ_i)是由式(2)计算所得的距离的标准差，μ(ρ_i)是ρ_i的平均值。根据CFSFDP算法，各簇中心间距离较远，因此簇中心数据点间距离应满足式(3)，与此同时，由于CFSFDP算法会产生具有较大距离δ_i和较小密度的噪声簇中心，因此，需要通过式(4)来分离预期簇中心的噪声。所以，当规则点i的ρ_i、δ_i满足上述式(3)、(4)时，方可认为该点为簇中心。

$ E{C_i} = \left( {{\delta _i}} \right) \ge 2\sigma \left( {{\delta _i}} \right) $

(3)

$ L{C_i} = E{C_i} \ge \mu \left( {{\rho _i}} \right) $

(4)

1.1 规则聚合(Merge)

在1.1节中，满足EC_i、LC_i条件而生成的初始子类数目较多，本文算法采用Chameleon算法^[11]对初始子类间距离进行了式(5)、(6)相关计算，主要进行类间相似性衡量比较，进而将相似性聚类子类进行合并得到最终聚类结果。Chameleon算法在融合子类的过程中，既考虑两个类之间的相对紧密情况RI_ij(类i与类j之间的相对互连性)，又考虑两个类的内部连接情况RC_ij(类i与类j之间的相对近似性)。

$ R{I_{ij}} = A{I_{ij}}/\left[{\left( {A{I_i} + A{I_j}} \right)/2} \right] $

(5)

$ R{C_{ij}} = \frac{{A{C_{ij}}}}{{\frac{{\left| {{G_i}} \right|}}{{\left| {{G_i} + {G_j}} \right|}}A{C_i} + \frac{{\left| {{G_j}} \right|}}{{\left| {{G_i} + {G_j}} \right|}}A{C_j}}} $

(6)

其中：AI_ij(绝对互连性)是将图G_i中点连接到图G_j中点的边权重之和。AI_i或AI_j(绝对内部互连)是属于图G_i或图G_j的最小切分平分线的边的权重之和。AC_ij(绝对近似性)是将图G_i中的点连接到图G_j中点的边平均权重。AC_i或AC_j(绝对内部接近度)是属于图G_i或图G_j最小切分平分线的边平均权重。

DXCSc算法具体内容如下所示：

输入：X={X₁, X₂, …, X_n}无监督数据集; d_c计算局部密度ρ_i所需半径;

输出：C={C₁, C₂, …, C_k}簇集合。

算法过程1：基于学习分类系统框架，通过强化学习及遗传学习模块，对输入数据生成规则种群，并对规则进行适当压缩。

算法过程2：对规则种群进行密度聚类。

2.1)计算各规则的局部密度ρ和δ。

2.2)采用Fuzzy-CFSFDP方法确定簇中心。

2.3)将每个规则划归至与其距离最近且局部密度更高的规则种群中。

算法过程3：对规则种群进行适当聚合。

3.1)对2.3)步骤中生成的规则种群中的每一对规则{C_i, C_j}，计算RI{C_i, C_j}*RC{C_i, C_j}^α。

3.2)将具有最高RI{C_i, C_j}*RC{C_i, C_j}^α值的规则对{C_i, C_j}合并。

3.3)重复3.1)、3.2)步，直至终止条件达到。

2 实验结果和分析 2.1 实验设置

对于实验中的参数设置，本文遵循Voting-XCSc^[8]中对应参数的相同值进行公平比较。种群最大规则数设为1000，学习率设为0.2，遗传算法中突变和交叉的概率分别为0.001和0.8，用于计算精度的参数α和v分别设置为0.1和5。此外，根据CFSFDP^[9]中分析，通过选择适当的参数d_c使得平均邻居数量在整个数据集中占比约1%至2%即可，因为在决策图中选择簇中心主要取决于数据点密度和高密度距离的相对关系，而不是绝对值，因此d_c的选择对最终聚类效果影响不大。实验计算机环境为：处理器为2.3 GHz Intel Core i5，内存为8 GB 1600 MHz DDR3，硬盘为320 GB，操作系统为Mac OS X EI Capitan，编程语言为Java、C++和Matlab。

2.2 典型数据集实验分析

本文首先使用Flame^[13]、Aggregation^[14]、D31^[15]、R15^[15]等典型数据集，测试并对比本文提出的DXCSc算法聚类效果。Flame数据集包含240个二维数据点，可分为2簇；Aggregation数据集包含788个二维数据点，可分为7簇；D31数据集包含3100个二维数据点，可分为31簇；R15数据集包含600个二维数据点，可分为15簇。

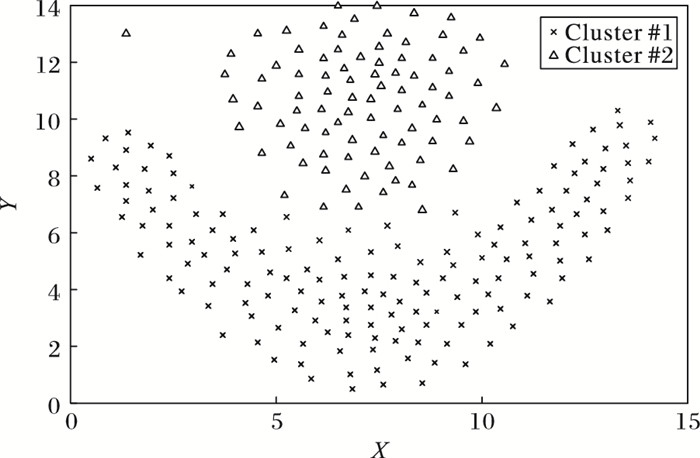
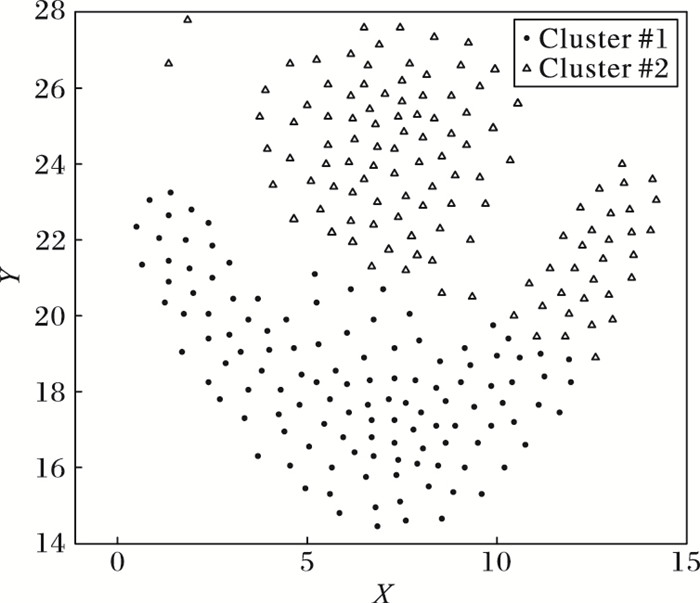
如图 3所示，DXCSc算法可以在无预先簇数目输入的情况下对任意形状的二维数据Flame Data进行有效聚类。

如图 4所示，K-means算法在预先输入簇数目(k_max=2)情况下，对任意形状的二维数据Flame Data聚类效果不是很好。

如图 5所示，AP算法虽然同样不需要预先设定簇数目，但对任意形状的二维数据Flame Data聚类效果也不好。此外，本文将上述算法分别在Aggregation^[14]、D31^[15]、R15^[15]数据集上进行了测试比对，实验结果表明: DXCSc算法在任意形状分布数据集Flame和超球形分布数据集D31、R15上都具有较好的聚类性能; 而K-means、AP算法只在超球形分布数据集上具有较好聚类性能，对任意形状数据集聚类效果不好。

如表 1所示，本文对DXCSc、K-means、AP以及Voting-XCSc算法在上述数据集上的聚类精度(Fitness)进行了比较，如表中结果所示，DXCSc在任意形状的二维数据集上可以取得良好的聚类效果。

与此同时，为确保评价指标的科学性，本文采用NMI(Normalized Mutual Information)评价指标对DXCSc、K-means、AP以及Voting-XCSc算法在上述数据集上的聚类效果进行了比较(如表 2所示)，该指标可用于衡量两个数据分布的吻合程度，取值范围为[0, 1]，该值越大表明聚类结果与真实情况越吻合。

2.3 真实数据集实验分析

本文采用UCI中的Iris、Wine、Ionosphere、Letter^[16]等真实数据集对上述算法进行了进一步验证。其中，Iris为鸢尾花卉数据集(数据实例数N=150，数据维度D=4，聚类簇数K=3)，是一类多重变量分析的数据集，可通过花萼长度、花萼宽度、花瓣长度、花瓣宽度4个属性预测鸢尾花卉属于Setosa、Versicolour、Virginica三个种类中的哪一类。Wine数据集(N=178，D=13，K=3)包含来自3种不同起源的葡萄酒的共178条记录，数据集中13个属性是葡萄酒的13种化学成分，通过化学分析可以来推断葡萄酒的起源。Ionosphere数据集(N=351，D=34，K=2)根据给定的电离层中的自由电子的雷达回波预测大气结构。Letter Recognition数据集(N=20000，D=16，K=2)将大量的黑白矩形像素显示的每一个字符标识为英文字母表中的26个大写字母之一。

如表 3所示，K-means算法在事先指定聚类簇数量k的情况下，聚类精度一般优于AP和DXCSc算法。在不指定聚类簇数量k的条件下，DXCSc算法精度优于AP算法。上述算法在未进行大量参数调整实验情况下，对真实数据的聚类效果并不是很好。

2.4 算法复杂度分析

在DXCSc算法过程1中，当有新数据输入时，学习分类系统遍历整个种群并更新相关规则参数，算法复杂度为O(n)，其中n为数据点数；在算法过程2中，需要O(n²)的时间来建立距离矩阵，得出任意两点间的距离，并计算局部密度ρ和δ；在算法过程3中，算法运行时间主要消耗在簇与簇之间的相似度计算和簇的融合更新之中，此部分算法复杂度为O(n log n)。综合分析，DXCSc的算法复杂度为O(n²+n log n)。K-means算法优点是简单实用，确定的k个划分到达平方误差最小，该算法当聚类是密集的，且类与类之间区别明显时，效果较好。对于处理大数据集，K-means算法相对可伸缩和高效的，计算的复杂度为O(nkt)(其中n是数据对象的数目，t是迭代的次数，k为簇数目); 虽然K-means算法复杂度相对较低，但需要用户预先设定聚类簇数目k，存在一定局限性。AP算法复杂度较高，为O(n² log n)。

基于上述分析，本文对实验所耗时间进行了比较分析，结果如表 4所示。AP算法复杂度较高，耗时较长，K-means算法与DXCSc算法耗时较为接近。

2.5 讨论

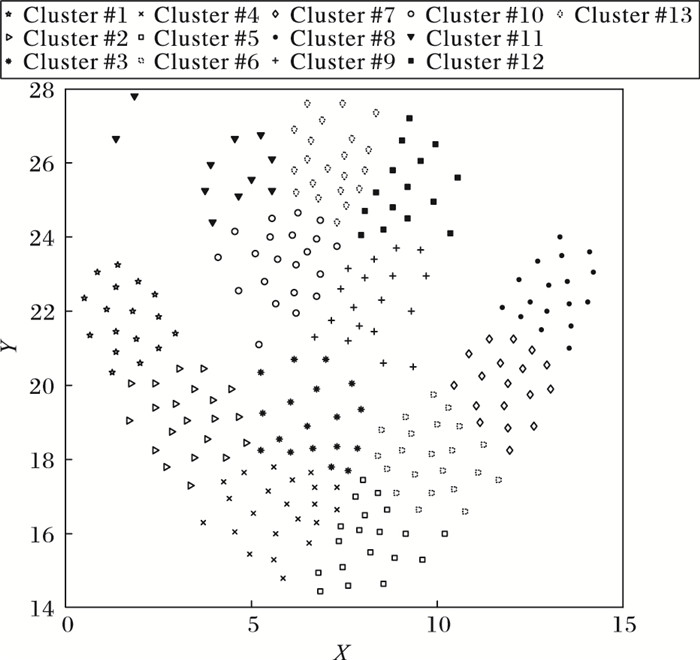
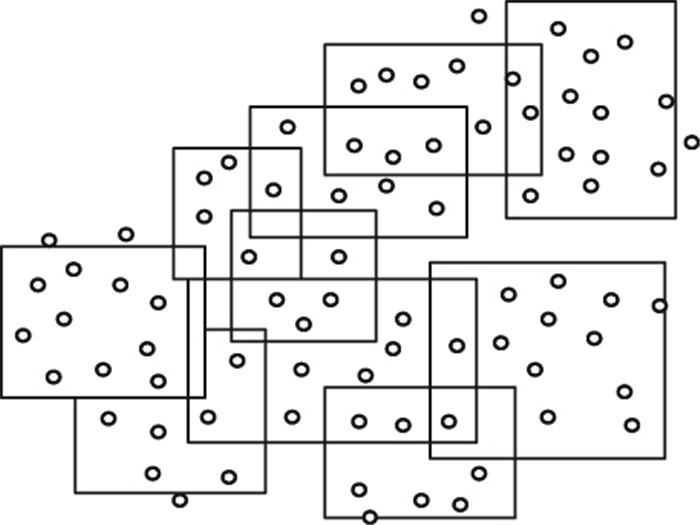
本文提出的DXCSc算法在任意形状的二维分布数据集上能够取得良好的聚类效果，主要取决于以下几个因素：首先，DXCSc采用学习分类系统框架后用规则代替原始二维数据点的表示方法，有效降低了数据表示的复杂度。具体如下，在DXCSc中，使用矩形作为规则的表示形式以处理连续值。规则可表示为(C_i, S_i)(i=1，2，…，d)，其中C_i为数据点的中心，S_i为拓展半径。当一个数据点I_i满足C_i-S_i≤I_i≤C_i+S_i时，则该点可由规则(C_i, S_i)表示。通过上述处理，海量的二维数据点就可以通过合并约减后的规则种群来表示，如图 6所示。

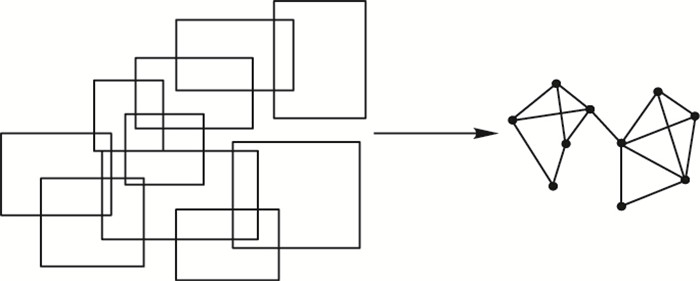
其次，DXCSc将合并约减后的规则再次表示为二维数据点(如图 7所示)，并应用密度聚类思想将上述数据点进行快速聚类，从而可以将Voting-XCSc的多轮学习转化为了单轮学习，避免了对原始数据的多次遍历。

3 结语

本文提出了一个新的基于学习分类系统的密度聚类方法(DXCSc)，用于研究学习分类系统在无监督环境下的聚类效果。DXCSc聚类方法的主要流程包含3个阶段:第一，DXCSc基于学习分类系统框架，通过强化学习及遗传学习模块，对输入数据生成规则种群，并对规则进行适当压缩；第二，DXCSc对规则种群进行密度聚类；第三，对规则种群进行适当聚合，生成最终的规则种群。本文通过一些数据集的无监督聚类实验说明了DXCSc的学习过程与效果。实验结果表明，DXCSc能够在不提前设定簇数量k的前提下，对无监督的典型二维数据取得较好的聚类效果，聚类精度优于AP、Voting-XCSc等算法。

下一步的工作有:首先，基于学习分类系统框架具有适应在线学习环境的特点，尝试把DXCS运用到二维流数据在线聚类中，并与一些更为复杂的流数据聚类算法比较性能。其次，设计面向流数据的Online Voting-XCSc算法。此外，可进一步将DXCSc算法扩展为面向高维数据以及高维流数据的聚类算法。