2. 山西省人民医院 CT室, 太原 030012
2. CT Room, Shanxi Provincial People's Hospital, Taiyuan Shanxi 030012, China
肺癌是发病率和死亡率最高的恶性肿瘤之一[1]。肺癌早期的检出对提高治愈率起着至关重要的作用[2]。计算机X射线断层扫描(Computed Tomography, CT)具有较高的组织分辨率,被广泛地应用于肺结节的筛查[3]。随着病灶区域成像精度的不断提高,CT扫描厚度不断减小,影像数据呈现爆炸式增长,由于肺部组织结构复杂和结节形状大小各异[4],医生对多层二维CT影像筛查结节并排除血管等其他组织干扰的工作难度很大,容易出现诊断疲劳,甚至可能造成漏诊和误诊[5]。因此,如何能够在不降低精度要求的前提下,快速、高效、精确地检出肺结节,对后续肺结节分割和良恶性诊断具有重大的意义。
Jia等[6]提出了一种基于图像区域平均灰度值和图像边缘能量的活动轮廓模型,用来分割和去除肺血管。Rezaie等[7]首先在原始图像上选择肿瘤可能存在的感兴趣区域,通过使用图像分割和图像阈值极限的确定指定肿瘤的面积,然后使用边缘检测滤波器检测肿瘤的边缘,通过计算具有较小误差百分比和更好分辨率的分形维数之后,确定疑似结节区域。另外根据结节的类圆特征,基于形态特征等的滤波器、聚类分析以及模型匹配等算法也被用于检测肺结节的应用中,吴平等[8]采用粗-精匹配思想,先使用改进绝对误差和(Sum of Absolute Differences, SAD)算法进行粗匹配找出候准匹配点,再采用归一化互相关算法在候准匹配点邻域内进行精确匹配找出最佳匹配点,来检测肺结节。Li等[9]构造选择性增强滤波器增强二维肺部CT图像中的圆、线区域,对疑似肺结节进行检测。Wang等[10]提出了基于形状约束Chan-Vese模型,结合计算粘附在结节候选物上的血液分支数量的候选结节的典型形状特征的分析,引入与球形增强滤波器结合的灰度级增强来提取候选结节及其球状轮廓区域,检测候选肺结节。Choi等[11]使用优化的多阈值和基于规则的剪枝技术检测候选结节。邱实等[12]以格式塔心理学为基础,以去除血管的新策略间接地对肺结节进行检测。
在肺结节的检测过程中,由于血管的密度、CT值等都与结节相似,而且疑似病灶区域过多,在病变区域内,部分结节和血管交叉,最终导致结节的检测敏感性不高而且存在较高的假阳性,降低结节检测的准确率。基于此,本文充分考虑结节和血管在三维图像中的形状结构的差异性,提出了基于三维形状指数(3D Shape Index,DSI)和Hessian矩阵特征值结合的结节检测方法。与已有的方法相比,在检测不同类型的结节时可以有效降低假阳性,具有较高的准确率。
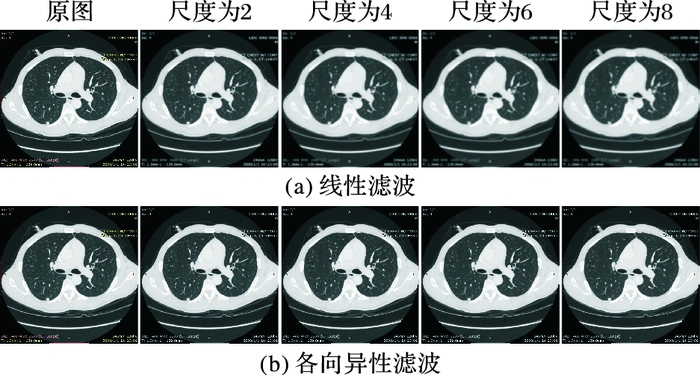
1 肺部序列CT图像预处理 1.1 各向异性滤波去噪由于CT设备等因素图像上存在噪声干扰,在进行肺结节检测前对CT图像进行去噪处理,如图 1所示线性滤波器去噪会导致边缘模糊,而各向异性扩散滤波则可以在降低噪声的同时保留甚至增强边缘信息。各向异性扩散滤波具有更低的敏感度,并更好地保留了图像中的结构细节,如结节边缘和血管边缘。因此,本文选择各向异性扩散滤波来平滑图像,降低噪声对肺结节检测以及三维分割算法的影响,提高检测的准确性,减少分割产生的空洞以及过分割现象。
|
图 1 不同尺度线性滤波与各向异性滤波去噪效果对比 Figure 1 Denoising effect comparison of linear filtering and anisotropic filtering at different scales |
人体肺部CT图像中肺实质区域在一张CT图像中所占比例较小,所在范围比较固定,左右肺实质区域相对于人体胸腔分布比较稳定,具有位置相对不变性,本文在序列CT图像预处理后,采用Liao等[13]提出的基于超像素的自生成神经网络序列肺实质图像的自动分割方法分割序列肺实质区域。如图 2所示为序列肺实质分割示意图。

|
图 2 序列肺实质分割 Figure 2 Segmentation of lung parenchymal image sequence |
肺结节直径一般在3~30 mm并且位于肺实质内呈类球形。虽然与肺血管相比,灰度值总体上相近,但是三维形状表现上差异性很大,因此,可以利用结节的三维特征将其与血管区分开。本文构建选择性增强滤波器——类球形增强滤波器,增强类球形的目标,抑制其他形状的目标。
2.1 高斯函数多尺度增强不用尺度空间上的高斯滤波函数对于复杂的医学影像具有高效的增强效果,结节灰度值呈Gaussian分布,对不同尺度不同类型的疑似肺结节,选取不同的尺度参数σ进行多尺度增强。根据高斯模板具有三维旋转对称性可得:σx=σy=σz=σ,三维高斯模板定义为式(1):
| $g(x,y,z)=\frac{1}{2\pi \sqrt{2\pi }{{\sigma }_{x}}{{\sigma }_{y}}{{\sigma }_{z}}}\exp (\frac{-{{x}^{2}}-{{y}^{2}}-{{z}^{2}}}{2{{\sigma }^{2}}})$ | (1) |
在三维体数据上使用服从高斯分布的球状模型模拟结节。本文用高斯函数来建立肺结节类球型b(x,y,z)数学模型定义为式(2):
| $b(x,y,z)=\exp (-\frac{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}{2{{\sigma }^{2}}})~$ | (2) |
Hessian矩阵描述了体素点附近的局部强度变化的二阶结构。在三维体数据中,三维图像I(x,y,z)中目标体素点为P,HP为P点的Hessian矩阵,由点P的二阶导数构建成三维图像的Hessian矩阵为一个3×3的实对称矩阵,具有3个实特征值。因此由Hessian矩阵的定义可得点P处的Hessian矩阵表达式如式(3) 所示:
| ${\mathit{\boldsymbol{H}}_p} = \left| {\frac{{{\partial ^2}I}}{{\partial {P^2}}}} \right| = \left[ {\begin{array}{*{20}{c}} {{I_{xx}}}&{{I_{xy}}}&{{I_{xz}}}\\ {{I_{yx}}}&{{I_{yy}}}&{{I_{yz}}}\\ {{I_{zx}}}&{{I_{zy}}}&{{I_{zz}}} \end{array}} \right]\;$ | (3) |
将Hessian矩阵的差分运算与高斯卷积相结合,通过改变高斯函数的标准偏移量来获得不同尺度σ下的线条滤波图像。三维高斯函数的表达式为式(4):
| $G(P,\sigma ) = \frac{1}{{\sqrt {{{(2\pi {\sigma ^2})}^3}} }}{{\rm{e}}^{ - {{\left\| x \right\|}^2}/2{\sigma ^2}}}$ | (4) |
根据高斯函数的卷积性质得图像Ⅰ如式(5) 所示:
| $I(P,\sigma ) = \frac{\partial }{{\partial P}}[I(P) * G(P,\sigma )] = I(P) * \frac{{\partial G(P,\sigma )}}{{\partial P}}\;$ | (5) |
结合高斯滤波图像的Hessian矩阵表达式如式(6) 所示:
| $\mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {I * {G_{{\rm{xx}}}}}&{I * {G_{xy}}}&{I * {G_{xz}}}\\ {I * {G_{yx}}}&{I * {G_{yy}}}&{I * {G_{yz}}}\\ {I * {G_{zx}}}&{I * {G_{zy}}}&{I * {G_{zz}}} \end{array}} \right]$ | (6) |
Hessian的特征值和特征向量可以描述图像I(P)的二阶导数的大小与方向。最大特征值相对应的特征向量代表着P点处曲率的最大方向,最小特征值相对应的特征向量则代表着P点处曲率的最小方向。
2.3 三维形状指数单独使用Hessian矩阵特征值来构建增强滤波器包含较多的假阳性,Koenderink等[14]提出了形状指数(Shape Index,SI)定义如式(7) 所示:
| $SI(p) = \frac{2}{\pi }\arctan \frac{{{\lambda _1} + {\lambda _2}}}{{{\lambda _1} - {\lambda _2}}}$ | (7) |
其中:λ1、λ2为Hessian最大最小特征值,结合两个主曲率提供信息,构建形状指标,比一对数字更能说明问题。
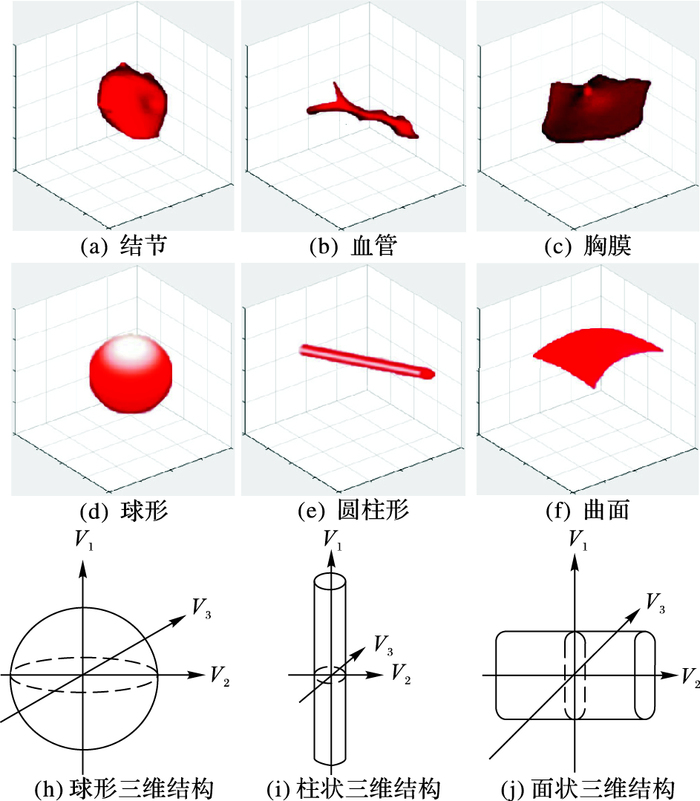
经典的表面曲率测量,例如高斯曲率和平均曲率,不能很好地指示局部形状; 仅用最大和最小曲率构建的SI,在二维图像上检测效果较好,但是面对复杂的肺部CT影像并不能很好地检测肺结节,而且存在较高的假阳性,因为结节、血管、胸膜等都是三维的实体,在形态上与标准的球、圆柱和曲面有一定的相似性。如图 3所示根据Hessian矩阵计算出来的特征值,可以得到三种不同类型的理想模型。
|
图 3 结节、血管、胸膜的三维效果图及其对应的数学模型和三维结构 Figure 3 Three-dimensional renderings and their corresponding mathematical model and three-dimensional structure of nodules, blood vessels and pleural |
Hessian矩阵特征值对应的特征向量两两正交,而且特征向量的方向对应着三维椭球各轴的主方向,特征值的大小对应着各轴的长度,它们共同反映了物体的形状和大小,而且对于不同的理想模型,其特征值的对应关系如表 1所示。
| 表 1 不同理想模型对应的Hessian矩阵特征值关系 Table 1 Eigenvalue relation of Hessian matrix corresponding to different ideal models |
肺结节检测根据三维特征可以很好地区分结节和血管以及其他组织。因此本文将形状指数SI扩展到三维体数据,计算三维体数据SI。使用三维曲率来更加完善地表示三维特征,能够较为准确地区分结节和血管,提高肺结节检测的准确率,降低假阳性。形状指数由二维扩展到三维过程如下:
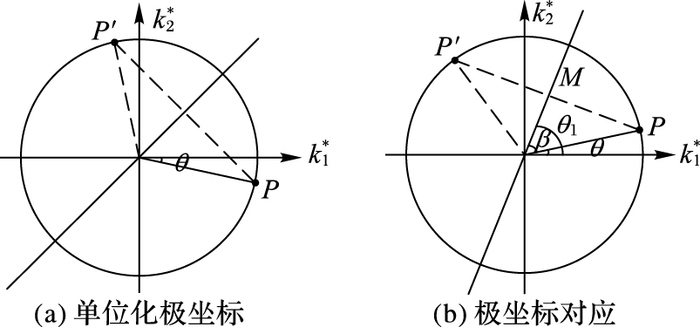
1) SI在二维上计算主曲率k1,k2,并将其单位化后变化到极坐标如图 4(a)所示。
|
图 4 极坐标的对应和转换关系 Figure 4 Correspondence and conversion of polar coordinates |
2) 如图 4(b)极坐标系中角度关系可得:θ1-θ=π/4,由此可知tan θ1=tan (θ+π/4) =(k1+k2)/(k1-k2),因此θ1=arctan[(k1+k2)/(k1-k2)]。
3) 最终得到形状指数:
| $\begin{array}{l} SI\left( p \right) = \frac{2}{{\rm{\pi }}}{\rm{ }}\arctan {\rm{ }}\frac{{{k_1} + {k_2}}}{{{k_1} - {k_2}}} \Rightarrow \\ \quad \quad SI\left( p \right) = \frac{2}{{\rm{\pi }}}{\rm{ }}\arctan {\rm{ }}\frac{{{k_1} + {k_2}}}{{\sqrt {{{({k_1} - {k_2})}^2}} }} \end{array}$ |
4) 计算可得cos β=(k1+k2)/$\sqrt 2 $,根据arctan和arccos关系可知:SI(p)=(2/π)arccos $\sqrt 2 $]-1。
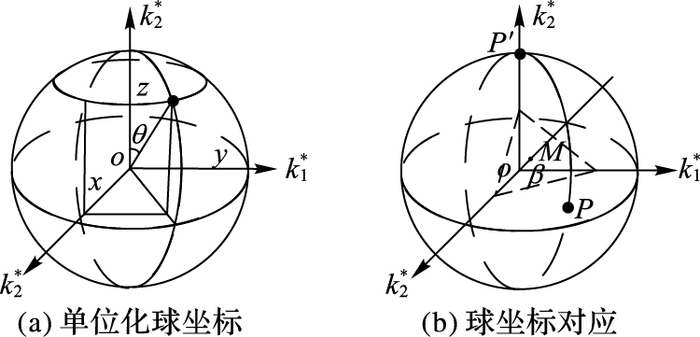
5) 在三维图像中,球面坐标(ρ,θ,φ)是球面坐标系上的点的表达式。设P(x,y,z)为空间内一点,其有三个主曲率k1、k2、k3,将其单位化后变化到球坐标如图 5(a)所示。
|
图 5 球坐标的对应和转换关系 Figure 5 Correspondence and conversion of spherical coordinates |
6) 根据第4) 步二维计算如图 5(b)推导可得:cos β=(k1+k2+k3)/$\sqrt 3 $。
7) 最终可得三维形状指数为式(8) 所示:
| $\begin{array}{l} DSI = \\ \frac{2}{{\rm{\pi }}}\arctan \frac{{{k_1} + {k_2} + {k_3}}}{{\sqrt {{{({k_1} - {k_2})}^2} + {{({k_1} - {k_3})}^2} + {{({k_2} - {k_3})}^2}} }} \end{array}$ | (8) |
由式(8) 可以得到DSI值,结合形状指数定义和实验分析,得到DSI所代表的具体形状如图 6所示。

|
图 6 DSI值的意义 Figure 6 Meaning of DSI value |
由图可以看出在0.75~0.875和0.125~0.25可以得到血管交叉区域如图 7(a)箭头指出所示,而在0.875~1和0.125~0可以得到结节区域如图 7(b)所示,根据得到的数值来设置滤波器的值,以此来得到结节区域。

|
图 7 血管和结节示意图 Figure 7 Blood vessels and nodules diagrammatic sketch |
Frangi等[15]总结三维体数据中Hessian矩阵特征值和结构之间的对应关系,根据三种不同的理想模型计算得到的特征值表示类球型、类管状、类面状三种类型如表 2所示。
| 表 2 Hessian矩阵特征值与结构之间的关系 Table 2 Relationship between eigenvalues and structure of Hessian matrix |
根据Hessian矩阵和本文计算得到的DSI,最终构建类球形滤波器结节检测函数V,如式(9) 所示:
| $V = \left\{ {\begin{array}{*{20}{l}} {\left| {{\lambda _3}} \right| \times \frac{{\left| {{\lambda _3}} \right|}}{{\left| {{\lambda _1}} \right|}},}&{({\lambda _{\rm{1}}} \approx {\lambda _{\rm{2}}} \approx {\lambda _{\rm{3}}}), 且满足式(8)}\\ 0&{其他} \end{array}} \right.$ | (9) |
综上所述,使用类球形滤波器结节检测函数进行结节检测的具体步骤如下:
算法1 类球形滤波器结节检测函数算法
1) 使用各向异性滤波对序列图像进行去噪。
2) 分割序列肺实质区域,并构建三维体数据Iin。
3) 确定经验范围内的高斯滤波尺度σ以及σ个数,并计算每个σ的值。
4) 对每一个尺度σn分别进行步骤5) ~10)。
5) 使用高斯滤波器平滑中三维体数据Iin。
6) 对每一个体素点分别进行步骤7) ~9)。
7) 计算Hessian矩阵以及其对应的特征值λ1、λ2、λ3。
8) 计算三维形状指数DSI。
9) 计算类球形结节检测函数V,并输出三维体数据Iout。
10) 终止体数据循环。
11) 终止尺度循环。
12) 最终输出不同尺度检测到的结节区域位置。
3 三维肺结节分割本文选择了结合置信连接的三维区域生长分割。在三维体数据利用切片之间的空间、纹理等信息进行整体分割,使用基于置信连接的区域增长方法,通过本文算法检测得到的结节位置作为区域增长的开始种子点,计算所有体素灰度值的平均值和标准差,根据指定的惩罚因子,乘以标准差,计算以期望为中心的灰度值范围如下所示:
| $I(X) \in \left[ {m - f\sigma ,m + f\sigma } \right]$ |
其中:X是图像I中的像素点,m和σ分别是当前区域灰度的平均值和标准差计算在范围内的邻域的灰度值作为分割区域,最终分割出三维肺结节。分割的步骤如下:
算法2 三维肺结节分割算法。
1) 根据类球形滤波器检测得到的结节多体素点位置坐标。
2) 将结节多体素点坐标作为区域增长的多种子点。
3) 计算肺实质中所有体素灰度值的平均值和标准差。
4) 根据指定的因子,乘以标准差,计算以期望为中心的灰度值范围,如果邻域的灰度值位于这个范围内就被包含在种子区域,否则就被排除。
5) 更新各部分权重,遍历所有体素点。
6) 最终完成结节的三维分割。
4 实验结果及分析本文算法的实验平台是Visual Studio 2010,Matlab 2014b,PC处理器为Intel Core i7-3770,主频3.40 GHz,内存8 GB。本文所使用的序列CT影像数据是来自LIDC公共数据库和山西省某大型医院,其中该医院使用的是美国通用公司的Discovery ST16 PET-CT,CT采集参数为150 mA、140 kV,层厚3.75 mm,CT图像大小为512×512。
实验中共选取100组病例数据,平均每个病例包含300张CT序列影像,CT层厚度为0.5~3.75 mm,图像大小为512×512。为了验证检测算法在不同类型肺部CT影像检测上的通用性和有效性,CT序列影像中的所有肺结节已经被医生标注。
4.1 定性比较在肺结节检测系统的假阳性结节主要为血管、血管交叉和血管弯曲等血管型假阳性结节,通过对比本文所提出的算法根据本文所提出的三维形状指数可以有效地区分结节和血管,能够去除较多的血管型假阳性结节,而且根据所有类型的结节在三维体数据上都呈现类球形,本文构建的三维类球形滤波器能够较好地检测出类球形结节(如血管牵拉结节、胸膜结节和磨玻璃结节)。
在此,本文展示了不同类型结节的检测效果图以及检测过程中的具体图示,主要步骤如下:首先将医师标注的CT序列数据构建三维体数据,在三维体数据上,根据本文提出的类球形滤波器对结节进行检测,最终将疑似结节区域显示出来,再通过多种子点的置信连接对疑似结节进行三维分割。通过对比本文所提算法能够较好地检测出其他三种类型较难检测的结节。
图 8为本文方法最终的肺结节检测的检测结果和分割结果。
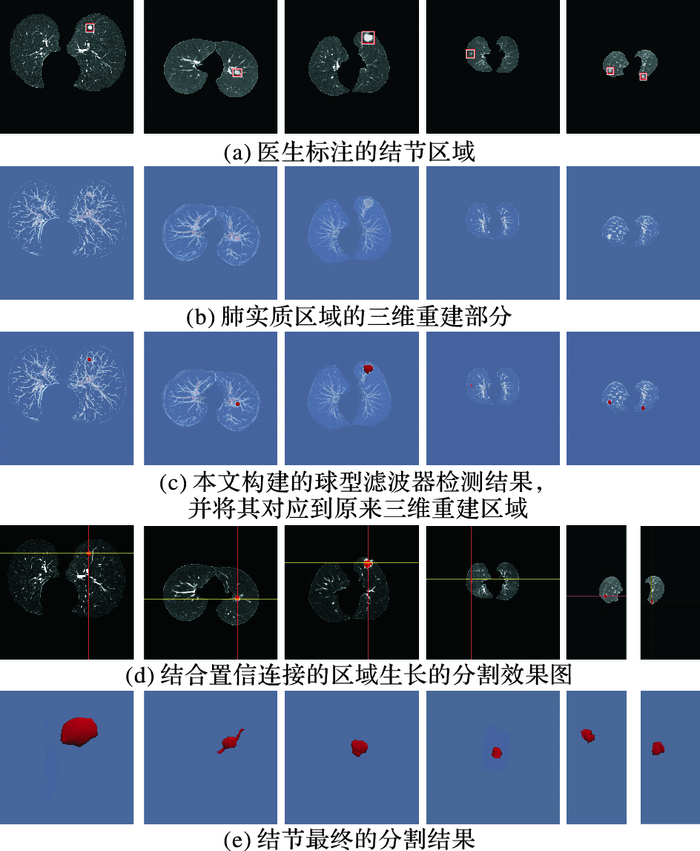
|
图 8 结节检测实验结果 Figure 8 Experimental results for different types of nodules |
由实验结果可知,本文的算法可以相对完整地检测出不同类型的结节,不仅对较易检测的孤立性肺结节有很好的检测效果;而且对胸膜牵拉型结节、血管粘连型结节和磨玻璃结节都有很好的检测效果。尤其是对磨玻璃这种特征不明显难以检测的结节也有很好的检测效果。
4.2 定量比较影像诊断实验检测的结果为阳性与阴性,在检测过程中对比金标准可能出现4种情况:诊断为阳性(真阳性(True Positive, TP))和对照被诊断为阴性(真阴性(True Negative, TN)),诊断为阴性(假阴性(False Negative, FN))和对照被诊断为阳性(假阳性(False Positive, FP))。对于肺结节检测算法的准确性通常是通过以下几个指标来完成:
准确率(Accuracy, ACC)是病例正确诊断为阳性与对照正确诊断为阴性的例数之和占总例数的百分率,计算公式为式(10):
| $ACC = \frac{{TP + TN}}{{TP + FP + TN + FN}}$ | (10) |
敏感度(Sensitivity, SE),实际患病且被诊断为阳性的概率就是敏感度,也称为真阳性率,计算公式为式(11):
| $SE = \frac{{TP}}{{TP + FN}}$ | (11) |
特异度(Specificity, SPE),实际未患病且被诊断为阴性的概率就是特异度,也称为真阴性,计算公式为式(12):
| $SPE = 1 - \frac{{FP}}{{FP + TN}}$ | (12) |
敏感性和特异性介于0~1。敏感度的值越大说明检测的真结节个数越多,漏检率越低,证明检测算法越有效;特异度的值越大说明检测算法检测到的假阳性个数越少,证明误检率越低,证明算法更有效。对比现有的肺结节CAD检测系统性能分析如表 4所示,本文方法可以检测的结节大小在3~30 mm,相比其他的检测方法具有较高的准确率,敏感度高,而且具有较高的特异性,证明可以去除较多的假阳性。
| 表 3 检测算法性能比较 Table 3 Performance comparison of detection algorithms |
| 表 4 与现有CAD检测系统比较 Table 4 Comparison with existing CAD detection system |
本文方法能够有效地检测出肺结节。与已有的肺结节CAD系统中检测方法相比,本文方法具有较高的敏感度和特异性,能够有效地降低假阳性。首先分割出序列肺实质图像,构建三维体数据,再利用本文提出的类球形滤波器结节检测函数增强结节区域,抑制其他组织,从而得到结节区域,能够很大程度上减少血管交叉型等假阳性结节。因此,本文提出的肺结节检测方法是一个高效、准确的方法,但是对于体积较小的结节检测和磨玻璃结节等灰度值较低的结节三维分割,需要后续进一步研究。
| [1] | SIEGEL R, MA J, ZOU Z, et al. Cancer statistics, 2014[J]. CA Cancer Journal for Clinicians, 2014, 64(1): 9-29. DOI:10.3322/caac.21208 |
| [2] | AOKAGE K, YOSHIDA J, HISHIDA T, et al. Limited resection for early-stage non-small cell lung cancer as function-preserving radical surgery:a review[J]. Japanese Journal of Clinical Oncology, 2016, 47(1): 7. |
| [3] | JIANG H. Computed Tomography:Principles, Design, Artifacts, and Recent Advances[M]. 2nd Edition. Bellingham, WA: SPIE, 2009: 1-388. |
| [4] | HENSCHKE C I, YIP R, YANKELEVITZ D F, et a1. Definition of a positive test result in computed tomography screening for lung cancer:a cohort study[J]. Annals of Internal Medicine, 2013, 158(4): 246-252. DOI:10.7326/0003-4819-158-4-201302190-00004 |
| [5] | MARTEN K, ENGELKE C. Computer-aided detection and automated CT volumetry of pulmonary nodules[J]. European Radiology, 2007, 17(4): 888-901. DOI:10.1007/s00330-006-0410-3 |
| [6] | JIA T, ZHANG H, MENG H. A novel lung nodules detection scheme based on vessel segmentation on CT images[J]. Bio-medical Materials and Engineering, 2014, 24(6): 3179-3186. |
| [7] | REZAIE A A, HABIBOGHLI A. Detection of lung nodules on medical images by the use of fractal segmentation[J]. International Journal of Interactive Multimedia and Artificial Intelligence, 2017, 4(5): 15-19. DOI:10.9781/ijimai.2017.452 |
| [8] | 吴平, 王彬, 薛洁, 等. 基于模板匹配的加速肺结节检测算法研究[J]. 计算机工程与应用, 2015, 51(7): 184-188. (WU P, WANG B, XUE J, et al. Research of accelerate detect of pulmonary nodules based on template matching algorithm[J]. Computer Engineering and Applications, 2015, 51(7): 184-188.) |
| [9] | LI Q, SONE S, DOI K. Selective enhancement filters for nodules, vessels, and airway walls in two and three-dimensional CT scans[J]. Medical Physics, 2003, 30(8): 2040-2051. DOI:10.1118/1.1581411 |
| [10] | WANG B, TIAN X, WANG Q, et al. Pulmonary nodule detection in CT images based on shape constraint CV model[J]. Medical Physics, 2015, 42(3): 1241. DOI:10.1118/1.4907961 |
| [11] | CHOI W-J, CHOI T-S. Genetic programming-based feature transform and classification for the automatic detection of pulmonary nodules on computed tomography images[J]. Information Sciences, 2012, 212(2): 57-78. |
| [12] | 邱实, 汶德胜, 冯筠, 等. 一种新策略的肺结节检测算法[J]. 电子学报, 2016, 44(6): 1413-1419. (QIU S, WEN D S, FENG J, et al. A new strategy lung nodules detection algorithm[J]. Acta Electronica Sinica, 2016, 44(6): 1413-1419.) |
| [13] | LIAO X, ZHAO J, CHENG J, et al. A segmentation method for lung parenchyma image sequences based on superpixels and a self-generating neural forest[J]. PloS One, 2016, 11(8): e0160556. DOI:10.1371/journal.pone.0160556 |
| [14] | KOENDERINK J J, VAN DOORN A J. Surface shape and curvature scales[J]. Image and Vision Computing, 1992, 10(8): 557-565. DOI:10.1016/0262-8856(92)90076-F |
| [15] | FRANGI A F, NIESSEN W J, HOOGEVEEN R M, et al. Model-based quantitation of 3-D magnetic resonance angiographic images[J]. IEEE Transactions on Medical Imaging, 1999, 18(10): 946-956. DOI:10.1109/42.811279 |
| [16] | NETTO S M B, SILVA A C, NUNES R A, et al. Analysis of directional patterns of lung nodules in computerized tomography using Getis statistics and their accumulated forms as malignancy and benignity indicators[J]. Pattern Recognition Letters, 2012, 33(13): 1734-1740. DOI:10.1016/j.patrec.2012.05.010 |
| [17] | 高婷, 龚敬, 王远军, 等. 检测肺结节的3维自适应模板匹配[J]. 中国图象图形学报, 2014, 19(9): 1384-1391. (GAO T, GONG J, WANG Y J, et al. Three dimensional adaptive template matching algorithm for lung nodule detection[J]. Journal of Image and Graphics, 2014, 19(9): 1384-1391. DOI:10.11834/jig.20140916) |
| [18] | TERAMOTO A, FUJITA H. Fast lung nodule detection in chest CT images using cylindrical nodule-enhancement flter[J]. International Journal of Computer Assisted Radiology and Surgery, 2013, 8(2): 193-205. DOI:10.1007/s11548-012-0767-5 |
| [19] | SANTOS A M, DE CARVALHO FILHO A O, SILVA A C, et al. Automatic detection of small lung nodules in 3D CT data using Gaussian mixture models, Tsallis entropy and SVM[J]. Engineering Applications of Artificial Intelligence, 2014, 36(C): 27-39. |
| [20] | CASCIO D, MAGRO R, FAUCI F, et al. Automatic detection of lung nodules in CT datasets based on stable 3D mass-spring models[J]. Computers in Biology and Medicine, 2012, 42(11): 1098-1109. DOI:10.1016/j.compbiomed.2012.09.002 |




