2. 河北工业大学 计算机科学与软件学院, 天津 300401;
3. 河北省大数据计算重点实验室, 天津 300401
2. School of Computer Science and Engineering, Hebei University of Technology, Tianjin 300401, China;
3. Hebei Province Key Laboratory of Big Data Calculation, Tianjin 300401, China
近年来,动态路径规划问题一直是机器人技术和人工智能领域的一个重要研究课题,同时也是机器人技术能够更广泛应用到其他领域的一个重要前提条件。当前常用的路径规划算法主要有栅格法[1]、人工势场法[2]、遗传算法[3]、神经网络[4]等,其中,人工势场法是目前比较成熟且高效的一种算法,但其主要用于解决静态环境下机器人路径规划问题,而对于解决动态环境下的运动路径规划问题并不理想,常由于斥力影响半径大于障碍物的半径而导致动态障碍物与机器人发生碰撞。为此本文提出了非完全等待策略与Morphine算法相结合的改进人工势场路径规划策略,从在单一动态环境和复杂动态环境下进行的实验结果可以看出,本文提出的改进策略在路径平滑性和规划路径步数上更优。
1 机器人路径规划方法 1.1 改进人工势场法人工势场法即根据地图的障碍物、目标点位置分别构建斥力场和引力场,通过斥力和引力相互作用构建人工虚拟势场,机器人在势场中规划出一条无碰撞路径。
在二维空间中设机器人的坐标向量为X=(x, y),目标点的坐标向量为Xd=(xd, yd),总势场Usum(X)可以表示为引力场函数Uatt(X)和斥力场函数Urep(X)之和,即:
| $ {U_{{\rm{sum}}}}\left( \mathit{\boldsymbol{X}} \right) = {U_{{\rm{att}}}}\left( \mathit{\boldsymbol{X}} \right) + {U_{{\rm{rep}}}}\left( \mathit{\boldsymbol{X}} \right) $ | (1) |
传统人工势场法的引力场函数Uatt(X)和斥力场函数Urep(X)计算公式如下:
| $ {U_{{\rm{att}}}}\left( \mathit{\boldsymbol{X}} \right) = 0.5\alpha {\rho ^2}(\mathit{\boldsymbol{X}}, {\mathit{\boldsymbol{X}}_o}) $ | (2) |
| $ \begin{array}{l} {U_{{\rm{rep}}}}\left( \mathit{\boldsymbol{X}} \right) = \\ \left\{ \begin{array}{l} 0.5\beta [1/\rho (\mathit{\boldsymbol{X}}, {\mathit{\boldsymbol{X}}_o})-1/{\rho _o}], \;\;\rho (\mathit{\boldsymbol{X}}, {\mathit{\boldsymbol{X}}_o}) < {\rho _o}\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\rho (\mathit{\boldsymbol{X}}, {\mathit{\boldsymbol{X}}_o}) \ge {\rho _o} \end{array} \right. \end{array} $ | (3) |
其中:α为引力的增益系数,是正数;β为斥力的增益系数,是正数;ρ(X, Xo)为机器人与障碍物之间的最短距离; ρo是一个大于零的常数,表示障碍物影响的距离,在ρo之外的机器人便不受此障碍物的影响。
改进人工势场法[5-7]引入机器人和目标点的相对位置和速度,公式如下:
| $ {U_{{\rm{att}}}}\left( {\mathit{\boldsymbol{p}}, \mathit{\boldsymbol{V}}} \right) = {\delta _p}{\left\| {\mathit{\boldsymbol{p}}-{\mathit{\boldsymbol{p}}_d}} \right\|^2} + {\delta _v}{\left\| {\mathit{\boldsymbol{V}}-{\mathit{\boldsymbol{V}}_d}} \right\|^2} $ | (4) |
其中:p为机器人当前位置,V为机器人当前速度,δp为相对位置引力系数,pd为目标点位置,Vd为目标点速度,δv为相对速度引力系数,‖p-pd‖为机器人与目标点之间的欧氏距离,‖V-Vd‖为机器人与目标点之间的相对速度。由此得出机器人所受目标点的引力,公式如下:
| $ {F_{{\rm{att}}}}\left( {\mathit{\boldsymbol{p}}, \mathit{\boldsymbol{V}}} \right) =-\nabla {U_{{\rm{att}}}}\left( {\mathit{\boldsymbol{p}}, \mathit{\boldsymbol{V}}} \right) =-{\nabla _p}{U_{{\rm{att}}}}\left( {\mathit{\boldsymbol{p}}, \mathit{\boldsymbol{V}}} \right)-{\nabla _v}{U_{{\rm{att}}}}\left( {\mathit{\boldsymbol{p}}, \mathit{\boldsymbol{V}}} \right) $ | (5) |
改进的斥力场函数可表示为:
| $ \begin{array}{l} {U_{{\rm{rep}}}}\left( {\mathit{\boldsymbol{p}}, \mathit{\boldsymbol{V}}} \right) = \\ \left\{ \begin{array}{l} {\beta _1}\left[{1/\left( {{\rho _{ro}}-{R_r}} \right)-1/{\rho _0}} \right] + {\beta _2}{\mathit{\boldsymbol{V}}_{ro}}, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;({\rho _{ro}} -{R_r}) \le {\rho _o}\& {\mathit{\boldsymbol{V}}_{ro}} > 0\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;({\rho _{ro}} -{R_r}) > {\rho _o}\& {V_{ro}} \le 0 \end{array} \right. \end{array} $ | (6) |
其中:Rr为机器人半径;β1与β2为可变因子;ρo为障碍物影响距离;ρro是指机器人与障碍物边界的距离;Vro为障碍物与机器人的相对速度。由此推出斥力公式:
| $ \begin{array}{l} {F_{{\rm{rep}}}}\left( {\mathit{\boldsymbol{p}}, \mathit{\boldsymbol{V}}} \right) = \\ \left\{ \begin{array}{l} {F_{{\rm{repp}}}} + {F_{{\rm{repv}}}}, \;\;({\rho _{ro}}-{R_r}) \le {\rho _o}\& {\mathit{\boldsymbol{V}}_{ro}} > 0\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;({\rho _{ro}}-{R_r}) > {\rho _o}\& {\mathit{\boldsymbol{V}}_{ro}} \le 0 \end{array} \right. \end{array} $ | (7) |
Morphine算法[8]即通过机器人获取环境信息后统计前方备选的多条弧线路径信息,选出最优通行路径。
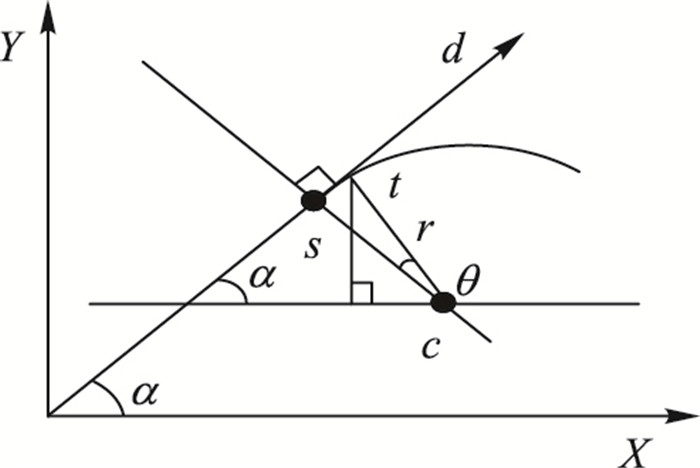
设已知机器人的起点s和目标点d的坐标, 机器人的方向角α(s和d的连线与x轴的夹角)、某一备选路径弧线的半径r, 如图 1所示,要画出备选路径弧线必须知道该弧线的圆心c的坐标及某一路径点t的坐标,其计算公式如式(8)~(9)所示:
|
图 1 弧线上某点坐标推导图 Figure 1 Coordinates of a point on the Arc |
| $ \left\{ \begin{array}{l} c\left( x \right) = s\left( x \right) + r\cdot\sin \alpha \\ c\left( y \right) = s\left( y \right)-r\cdot\cos \alpha \end{array} \right. $ | (8) |
| $ \left\{ \begin{array}{l} t{\rm{ }}\left( x \right) = c{\rm{ }}\left( x \right)-r\cdot\cos ({\rm{ \mathsf{ π} }}/2-\alpha + \theta )\\ t{\rm{ }}\left( y \right) = c{\rm{ }}\left( y \right) + r\cdot\sin ({\rm{ \mathsf{ π} }}/2-\alpha + \theta ) \end{array} \right. $ | (9) |
其中θ为路径点t的圆心角。
设定机器人路径寻优评估函数为:
| $ f = \left\{ \begin{array}{l} \infty, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;Arc \supset O\\ {\alpha _1}L + {\alpha _2}G + {\alpha _3}M, \; 其他 \end{array} \right. $ | (10) |
式中:Arc表示弧线,O表示障碍物,L为每条弧线路径长度;G为路径拐点参数;M为路径点t到目标点d的欧氏距离;α1、α2、α3为各参数的权值。当f值为无穷大时,弧线经过障碍物,机器人与障碍物碰撞,此路径不可取,选取f值最小的路径为机器人运行最优路径。
2 动态环境下机器人路径规划室内环境复杂多变,具有动态不确定性,移动机器人如何有效避障是完成路径规划的重点。本文在局部路径规划中采用滚动窗口预测障碍物,分析碰撞类型,分别采取不同避障策略,最终完成动态路径规划。
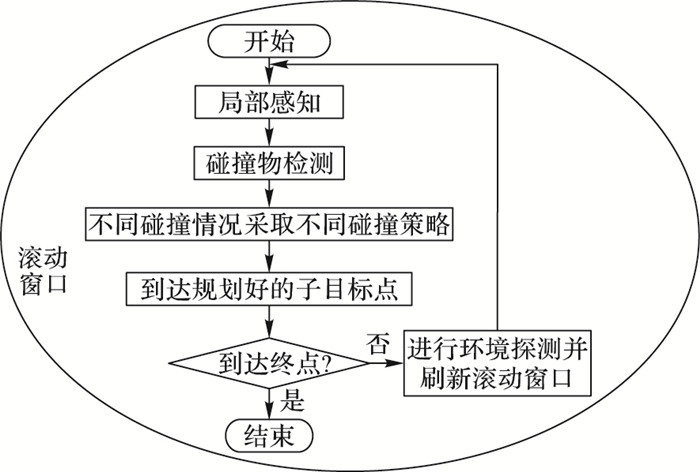
2.1 滚动窗口碰撞预测机器人在运动过程中采用滚动窗口[9]对周围的环境信息进行探测,预测在其规划好的全局路径中是否有障碍物出现; 若存在动态障碍物,则测定其速度与方向,预测其运动轨迹,制定有效的避碰策略。滚动窗口碰撞预测的流程如图 2所示,具体步骤如下:
|
图 2 滚动窗口碰撞预测流程 Figure 2 Collision prediction flow by rolling window |
1) 场景预测。机器人开始运动时,采用启发式方法,将传感器所探测到的局部环境信息转化为局部子目标[10],同时预测动态障碍物的运动轨迹,设定机器人每走一步用时Δt,通过预测Δt时间内机器人与动态障碍物两条运动轨迹之间的相对位置来预测二者是否会发生碰撞。
2) 滚动窗口更新优化。按照滚动窗口预测结果和环境信息,进行子目标的局部路径规划,采取相应策略有效避障,重新更新滚动窗口。
3) 反馈初始化。在新的滚动窗口范围内,根据此时传感器采集的信息,重新更新窗口内障碍物的运动状况和环境信息,以此循环预测。
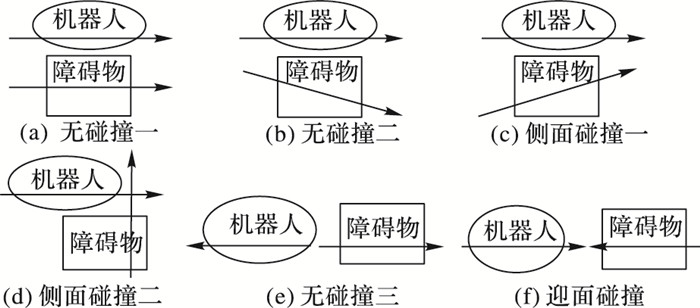
2.2 动态避障策略根据滚动窗口预测结果,分析机器人与动态障碍物运动轨迹是否存在交集,即是否存在碰撞,如图 3所示。机器人与动态障碍物相对运动的3种典型情况如下:
|
图 3 机器人与动态障碍物碰撞的几种典型情况 Figure 3 Several typical cases of collision between robot and dynamic obstacle |
1) 无碰撞。若两条运动轨迹不存在交集,如图 3(a)、(b)、(e)所示,此时机器人与障碍物在Δt范围内不会发生碰撞。
2) 侧面碰撞。若两条运动轨迹之间存在交集,如图 3(c)、(d)所示,机器人与动态障碍物将在Δt范围内发生侧面碰撞,此时机器人采取非完全等待策略[11]。假设障碍物的半径为R,障碍物斥力影响半径为r,当机器人在r范围内则开始等待,大于r则继续前进,称其为“完全等待”;但若机器人未等障碍物完全经过(还在影响半径r范围内)就继续前进,称其为“非完全等待”。
3) 迎面碰撞。若两条运动轨迹之间有交集,如图 3(f)所示,在Δt时间内机器人与动态障碍物发生迎面碰撞,则此时机器人采用Morphin算法作局部路径规划,当机器人不在动态障碍物影响半径r范围内时再用改进人工势场法作全局路径规划。
由于室内环境复杂多变,传统人工势场法存在障碍物附近目标不可达、易发生碰撞、狭窄通道等问题,本文提出采用改进人工势场法进行全局路径规划,当遇到狭窄通道时,采用Morphine算法进行局部路径规划。
2.3 动态路径规划机器人动态路径规划流程具体步骤如下。
步骤1 构建室内环境地图。
步骤2 采用改进人工势场法进行全局路径规划,且其目标点即机器人的势场全局最小点。
步骤3 机器人沿全局规划路径行走。
步骤4 通过滚动窗口预测动态障碍物,判断此障碍物是否会产生影响:若无影响,转步骤5;有影响,则转步骤6。
步骤5 判断是否到达目标点:若到达目标点路径规划结束;反之,返回步骤2。
步骤6 判断动态障碍物的运动方向和状态,采用相应的避障策略。
步骤7 判断是否避障成功:若成功返回步骤3;反之,返回步骤2。
3 实验结果及分析本文采用上述动态路径规划方法,分别设计单一和复杂两种动态障碍物环境进行20组实验验证,每类实验举一例说明。
3.1 单一环境动态路径规划 3.1.1 侧面碰撞假设机器人与动态障碍物发生侧面碰撞,其参数设定如表 1所示。
| 表 1 侧面碰撞参数列表 Table 1 Parameter list of side collision |
1) 机器人采取“完全等待”策略。
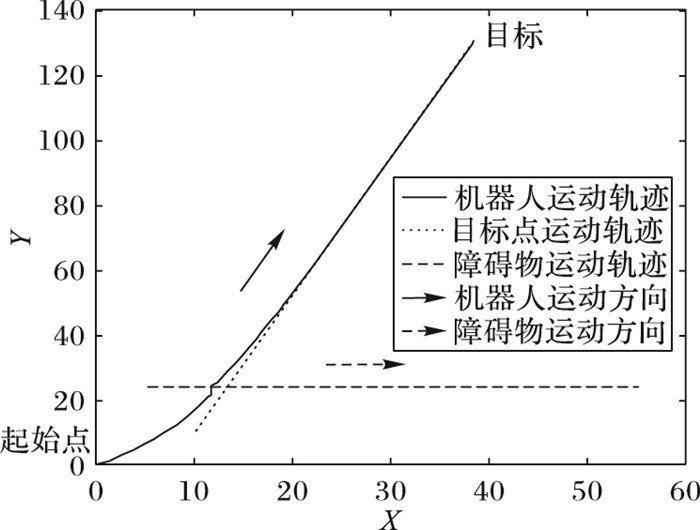
机器人采取“完全等待”策略的动态路径规划结果如图 4所示,机器人到达目标点步数为144步,且路径非常平滑。
|
图 4 完全等待动态路径规划 Figure 4 Completely waiting for dynamic path planning |
2) 机器人采取“非完全等待”策略。
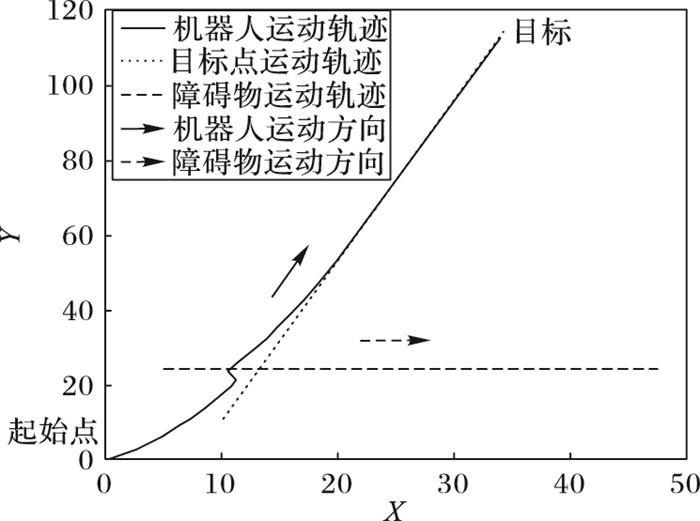
机器人采取“非完全等待”策略的动态路径规划结果如图 5所示,采取“非完全等待”策略的规划路径虽没有“完全等待”平滑,但机器人到达目标点步数为123步,小于“完全等待”规划步数。
|
图 5 非完全等待动态路径规划 Figure 5 Non-completely waiting for dynamic path panning |
同时在设定机器人步长为1的情况下选取3组实验数据作对比,结果如表 2所示,采取“非完全等待”策略在规划步数,即运动时间上要远小于“完全等待”策略。
| 表 2 两种等待策略步数对比 Table 2 Comparison of steps by two waiting strategies |
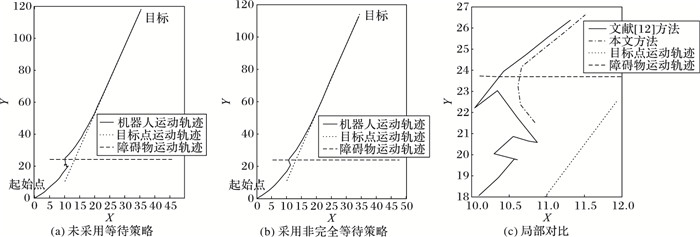
为再次证明“非完全等待”策略的有效性,本文与文献[12]方法作对比,实验环境不变,参数设定如表 1所示,实验结果如图 6所示,其中图 6(a)是采用文献[12]中的未采用等待策略的路径规划,图 6(b)是采用“非完全等待”策略的路径规划,图 6(c)是两种路径规划方法的局部避障放大对比图,由图 6(c)可以看出本文提出的非完全等待避障策略不会使机器人在受到巨大斥力情况下倒退行走,避障效果更优。
|
图 6 在一个障碍物的情形下侧面碰撞路径规划对比 Figure 6 Comparison of side collision path planning with one obstacle |
假设机器人与动态障碍物发生迎面碰撞,采取Morphine算法进行避障。为证明本文算法优越性,与文献[12]算法作对比,其参数设定如表 3所示,步长为1。
| 表 3 迎面碰撞参数列表 Table 3 Parameter list of face-to-face collision |
动态路径规划结果如图 7所示,其中图 7(a)为采用文献[12]人工势场算法的路径规划,图 7(b)为采用Morphine算法的路径规划,图 7(c)为两种方法局部避障放大对比图。不难看出未使用Morphine算法的机器人在遇到障碍物后会出现倒退现象,其运动到目标点的步数为169步,使用Morphine算法的机器人运动步数为159步。因此,本文算法在避障效果和路径规划步数上更优。

|
图 7 在一个障碍物的情形下迎面碰撞路径规划图 Figure 7 Comparison of face-to-face collision path planning with one obstacle |
建立复杂环境,在120×100的环境地图中设定8个静态障碍物和1个动态障碍物,机器人起始点坐标为(0, 0),目标点坐标为(100, 100),步长为1。
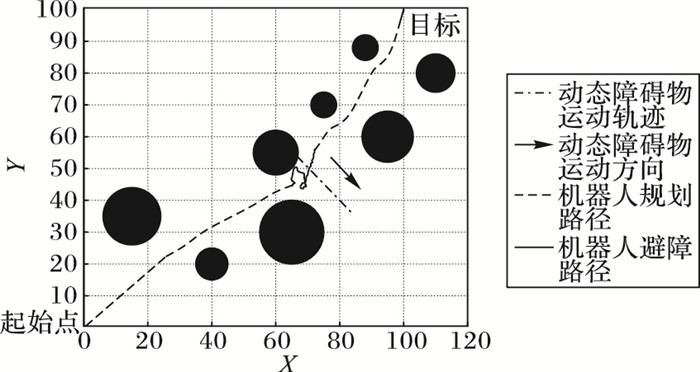
3.2.1 侧面碰撞设定动态障碍物起始点坐标为(69, 54),并向左下方运动,其半径为3,影响半径为6,采用传统人工势场法进行路径规划,如图 8所示,机器人整个动态避障的步数为45。
|
图 8 传统人工势场法避免侧面碰撞 Figure 8 Side collision avoidance by traditional artificial potential field method |
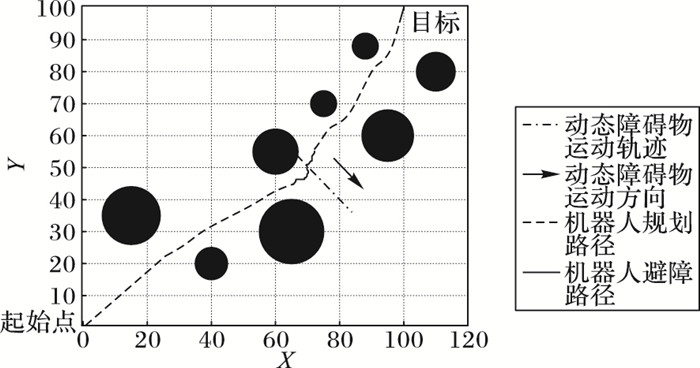
采用滚动窗口预测到机器人行至(65, 44)时将与动态障碍物发生侧面碰撞,于是采用本文提出的非完全等待进行避障,其动态路径规划如图 9所示,机器人整个动态避障的步数为33,可以明显看出采用非完全等待的避障策略的行进路径比传统避障方法的路径更平滑,所用步数更少。
|
图 9 非完全等待避障策略避免侧面碰撞 Figure 9 Side collision avoidance by non-completely waiting strategy |
设定动态障碍物的起始点坐标为(89, 78),并向左下方运动,其半径为3,影响半径为6,如图 10所示。采用常规避障方法,整个动态避障过程需要46步。

|
图 10 传统人工势场法避免迎面碰撞 Figure 10 Face-to-face collision avoidance by traditional artificial potential field method |
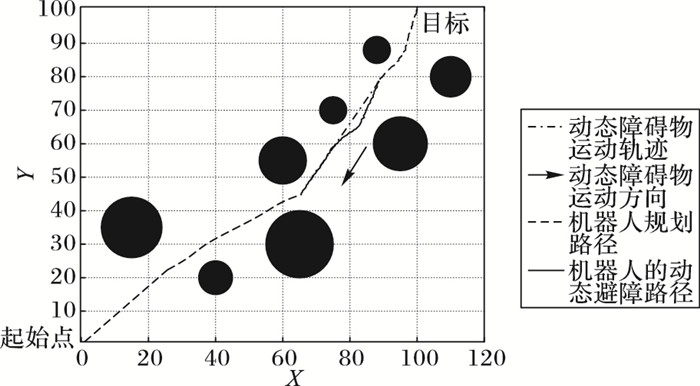
而在相同环境下,采用滚动窗口预测到机器人行至(74, 59)时将与动态障碍物发生迎面碰撞,采取Morphine算法进行局部避障,如图 11所示,实线为动态避障过程,整个动态避障过程需要40步,效果要优于传统人工势场法。
|
图 11 Morphine算法避免迎面碰撞 Figure 11 Face-to-face collision avoidance by Morphine algorithm |
本文在动态环境下提出非完全等待策略与Morphine算法相结合的改进人工势场法路径规划,并引入滚动窗口理论,对未知动态障碍物进行碰撞预测,分析碰撞模型进而采取相应的避障策略。通过对比实验可知,本文提出的改进策略具有更高的避障性能,且规划步数更少。
| [1] | WANG X, JIN Y, DING Z. A path planning algorithm of raster maps based on artificial potential field[C]//Proceedings of the 2015 Chinese Automation Congress. Piscataway, NJ:IEEE, 2015:627-632. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?reload=true&arnumber=7382575 |
| [2] | YE B, ZHAO M, WANG Y. Research of path planning method for mobile robot based on artificial potential field[C]//Proceedings of the 2011 International Conference on Multimedia Technology. Piscataway, NJ:IEEE, 2011:3192-3195. http://ieeexplore.ieee.org/document/6003004/ |
| [3] | OZDIKIS O. Genetic algorithms with random coordinates for route planning on a 3D terrain[C]//Proceedings of the 20115th International Conference on Genetic and Evolutionary Computing. Washington, DC:IEEE Computer Society, 2011:146-149. |
| [4] | JIANG M, YU Y, LIU X, et al. Fuzzy neural network based dynamic path planning[C]//Proceedings of the 2012 International Conference on Machine Learning and Cybernetics. Piscataway, NJ:IEEE, 2012:326-330. http://ieeexplore.ieee.org/document/6358934/ |
| [5] | CHEN L, LIU C, SHI H, et al. New robot planning algorithm based on improved artificial potential field[C]//Proceedings of the 3rd International Conference on Instrumentation, Measurement, Computer, Communication and Control. Washington, DC:IEEE Computer Society, 2013:228-232. http://ieeexplore.ieee.org/document/6840444/ |
| [6] | 罗胜华, 刘国荣, 蒋燕. 一种基于改进人工势场法的移动机器人路径规划[J]. 微计算机信息, 2009, 25(29): 188-190. (LUO S H, LIU G R, JIANG Y. A path planning of mobile robot based on improved artificial potential field method[J]. Microcomputer Information, 2009, 25(29): 188-190. DOI:10.3969/j.issn.2095-6835.2009.29.080) |
| [7] | 罗乾又, 张华, 王姮, 等. 改进人工势场法在机器人路径规划中的应用[J]. 计算机工程与设计, 2011, 32(4): 1411-1413. (LUO Q Y, ZHANG H, WANG H, et al. Application of improved artificial potential field approach in local path planning for mobile robot[J]. Computer Engineering and Design, 2011, 32(4): 1411-1413.) |
| [8] | 万晓风, 胡伟, 郑博嘉, 等. 基于改进蚁群算法与Morphin算法的机器人路径规划方法[J]. 科技导报, 2015, 33(3): 88-89. (WAN X F, HU W, ZHENG B J, et al. Robot path planning method based on improved ant colony algorithm and Morphin algorithm[J]. Science & Technology Review, 2015, 33(3): 88-89.) |
| [9] | 丛岩峰, 基于滚动优化原理的路径规划方法研究[D]. 长春: 吉林大学, 2007. (CONG Y F, The path planning method research based on rolling optimization theory[D]. Changchun:Jilin University, 2007.) http://cdmd.cnki.com.cn/article/cdmd-10183-2007093431.htm |
| [10] | LI X, XU H, LI M. A memory-based complete local search method with variable neighborhood structures for no-wait job shops[J]. International Journal of Advanced Manufacturing Technology, 2013, 87(5/6/7/8): 1401-1408. |
| [11] | BRANKE J, RG EN, MIDDENDORF M, et al. Waiting strategies for dynamic vehicle routing[J]. Transportation Science, 2005, 39(3): 298-312. DOI:10.1287/trsc.1040.0095 |
| [12] | LIU Z X, YANG L X, WANG J G. Soccer robot path planning based on evolutionary artificial field[J]. Advanced Materials Research, 2012, 568(8): 955-958. |




