2. 综合业务网理论及关键技术国家重点实验室(西安电子科技大学), 西安 710071
2. State Key Laboratory of Integrated Services Networks (Xidian University), Xi'an Shaanxi 710071, China
从1998年以来, 全球移动通信铁路系统(Global System for Mobile communication-Railway, GSM-R)已广泛地应用于列车通信和控制。然而, GSM-R仅仅只能提供200 Kb/s的数据率[1], 主要用于列车控制, 而不能为乘客提供宽带通信服务[2]。其后随着蜂窝移动通信的发展, 长期演进(Long Term Evolution, LTE)系统的建设和使用, 研究人员针对高铁场景提出LTE-R(LTE-Railway)的概念, 但是目前还没有形成标准, 尚有诸多的技术挑战[3]。另一方面, 在高速铁路上要求移动办公、娱乐的客户需求与日俱增。因此, GSM-R和现有的蜂窝移动通信系统均不能满足目前以及未来高铁用户对高速数据传输的需求[4]。故设计一个能够满足宽带数据传输需求的高铁移动通信系统非常紧迫且意义重大。而一个无线通信系统最基础的技术就是信道建模, 因此, 研究高速移动下的信道建模非常有意义。目前, 国内外对高速移动下的信道建模作了大量的研究。文献[5-8]研究了基于光线跟踪法的几何确定性模型(Geometry Based Deterministic Model, GBDM)的高铁传播信道。而在几何随机信道模型中, 高铁信道的脉冲响应通过波传播定律来表征。基于有效散射体的位置, 几何随机信道模型可以进一步分为规则形状几何随机模型(Regular-Shaped Geometry Based Stochastic Model, RS-GBSM), 例如单环[8]、双环和椭圆模型[10-12], 还有不规则形状几何随机模型(Irregular-Shaped Geometry Based Stochastic Model, IS-GBSM)[13]。非几何随机模型(Non-Geometrical Stochastic Model, NGSM)通过提供基本概率分布函数, 用一种完全随机的方式来表征在一个高铁传输信道的物理参数, 不需要假定散射体为任何的基本几何体[14-15]。文献[14]提出了一种基于高铁无线通信的有限状态马尔可夫链的NGSM。基于在高铁高架桥和狭窄通道场景的测量, 文献[15]提出了一种有限状态的马尔可夫信道。
以上研究主要针对的是高铁平原场景, 而高铁无线通信系统的发射机和接收机由于周围不同的地理环境而遭遇不同的信道条件。高铁环境一般被划分为以下几个主要场景:开阔地、高架桥、U型槽、山区、隧道和车站。综合考虑上述场景独特的设置和其他一些特殊的高铁场景, 高铁环境可以进一步划分为12种场景[16]。高铁在行驶途中会穿过一个或多个这些场景。而不同的场景, 它们的信道模型差异较大。在实际的高铁运行中, U型槽又是常见的场景, 大量出现在地下水丰富、地下水位较高、放坡条件受到限制的区域。目前对于高速移动下U型槽的信道建模的研究较少。文献[17]提出了基于U型槽的抽头延迟线模型和簇延迟线模型, 所提的建模方法都是只考虑了大尺度模型, 而没有考虑小尺度模型, 建模计算复杂度更高。除此之外, 现有的高速移动下U型槽的信道建模都是非时变性的, 而实际的信道是具有时变性和非平稳性的, 因此, 研究高速移动下U型槽的时变信道建模及其对高铁移动通信的影响, 可以丰富该领域的研究成果。
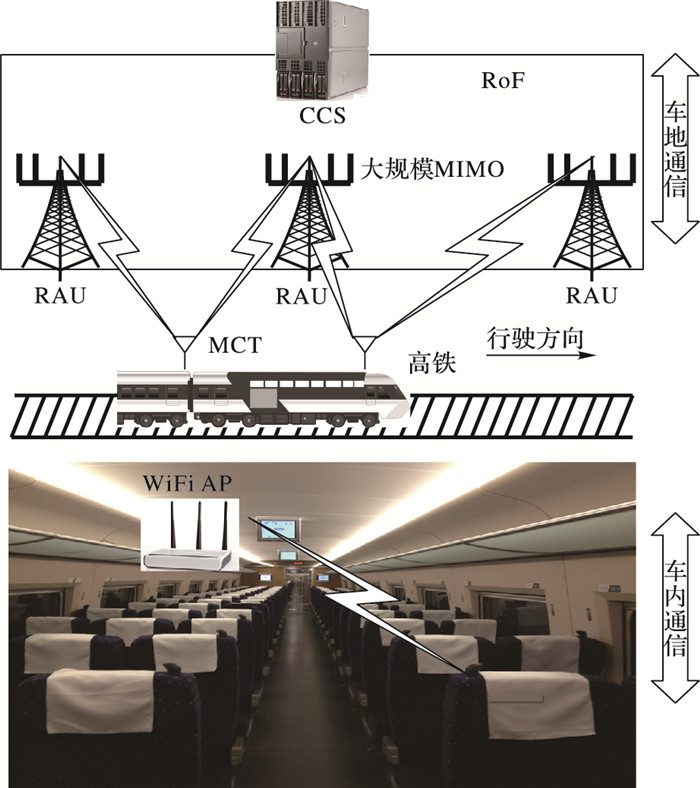
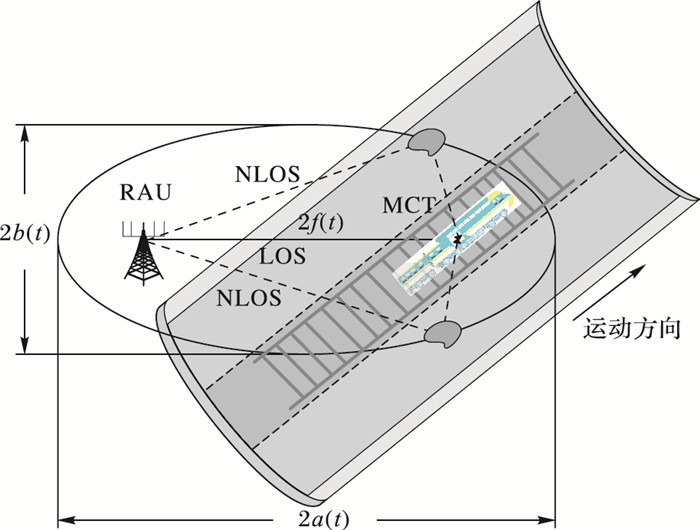
1 高铁移动通信系统模型本文考虑高铁移动车厢终端(Mobile Carriage Terminal, MCT)与铁路沿线的分布式远端天线单元(Remote Antenna Unit, RAU)之间的多输入多输出(Multiple Input Multiple Output, MIMO)通信系统, 以达到提高车厢内固定座位终端用户的语音和数据通信性能的目标。如图 1所示, 车内用户与基站之间的通信采用双层结构, 分别由两部分组成:一部分为车地通信, 即道旁的分布式MIMO中央控制基站(Central Control Station, CCS)和在其覆盖区内高速行驶的高铁车载MCT之间的车地通信, 列车位于U型槽内, 两侧的障碍物高于列车顶部; 另一部分为车内通信, 即高铁每节车厢顶部的车载MCT和车厢内WiFi接入点(Access Point, AP)之间的通信,以及WiFi AP与固定座位用户通信。MCT作为车地通信和车内通信的关键中间节点, 车内用户的服务质量(Quality of Service, QoS)需要通过MCT保障, 而MCT的QoS受限于车地通信的质量。本文主要研究其中的车地通信。
|
图 1 高速移动切换下分布式MIMO系统网络架构 Figure 1 Network architecture of distributed MIMO system under high-speed mobile handoff |
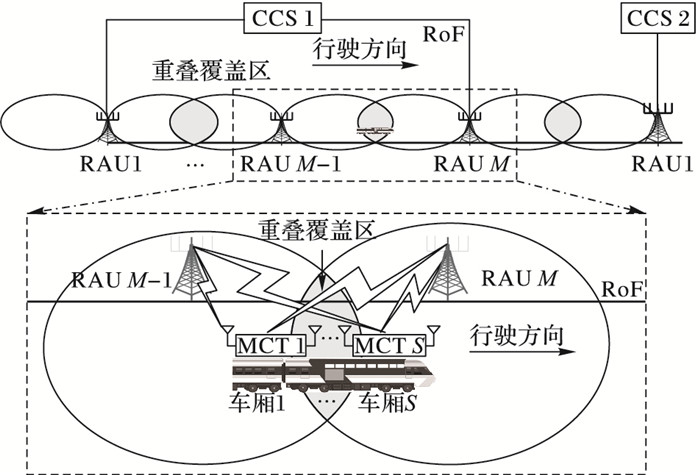
高速移动切换下分布式MIMO通信系统模型如图 2所示, 阴影部分为相邻RAU的重叠覆盖区, 高铁在此重叠区域内将同时与两个相邻RAU进行通信, 由于高铁速度非常快, 其将在非常短的时间内完成小区切换。每个CCS管理有M个RAU, 并且在同一个CCS内, 所有的RAU都工作在相同的频率, 即MCT在同一个CCS内的两个相邻RAU发生切换时, 工作频率不会发生变化, 这将大大减小系统的射频开销, 同时相邻MIMO RAU对MCT进行信号的复用和分集, 显然, 在两个CCS间相邻的两个RAU之间进行小区切换时, 将考虑频率切换问题。RAU均匀分布在高铁沿线, 每个RAU上有NT根天线, RAU和CCS通过光载无线电(Radio over Fiber, RoF)进行连接。高铁有S节车厢, 每节车厢顶部安装有1个MCT, 每个MCT有NR根天线。MCT通过RoF与车厢内的WiFi AP连接。分布式MIMO CCS和高铁MCT构成车地通信, MCT和WiFi AP以及WiFi AP和固定座位用户之间构成车内通信。
|
图 2 高速移动切换下分布式MIMO通信系统模型 Figure 2 Distributed MIMO communication system model under high-speed mobile handoff |
U型槽是在高铁无线通信中一个常见的场景。它代表了一种环境, 高铁通过U形地理狭窄通道的表面。U型槽场景被广泛应用于高铁建设, 确保铁路的光滑以及在通过山地时帮助火车达到高速。在这种场景下, 无线电传播的波形会由于两边陡峭的墙壁而受到严重的影响。
有研究表明U型槽两边陡峭的墙壁反射体较多, 故U型槽具有反射环境丰富、多径数量多等特点[17]。同时, 它还有较强的直射径, 因此, 该场景是一种强视距的场景。由于上述特点, U型槽场景的无线信道就具有非平稳性、较高的相关性以及较明显的多普勒效应。因为U型槽场景与高铁其他场景不同, 所以高铁中其他场景的信道模型并不完全适合U型槽。为此, 基于U型槽的特点, 本文对高速移动下的U型槽场景进行了信道建模。
2.2 U型槽时变信道建模为便于高速信道建模, 将实际的U型槽场景下高铁沿线的基于MIMO的RAU与车载MCT之间的车地通信场景抽象为一个几何模型, 具体建模过程如下。
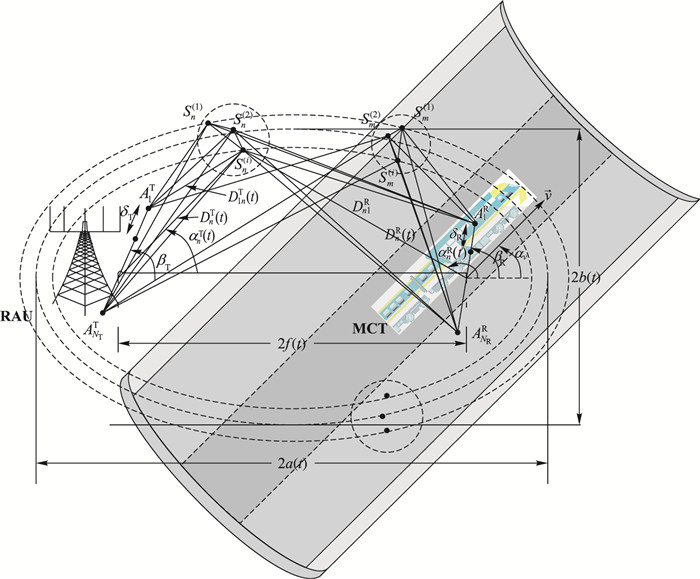
假定与某个路径长度相关联的全部局部散射体Sn(i)(n=1, 2, …, N)均处于同一椭圆上, 不同椭圆之间拥有共同的焦点, 即同焦椭圆。其中:Sn(1), Sn(2), …, Sn(i)位于同一个散射集群, 称之为第n个散射体簇, 且RAU和MCT分别位于椭圆焦点处, 两站相距2f(t), a(t)、b(t)分别为椭圆的长半轴短半轴长度, 整个模型基于U型槽环境, 如图 3所示。
|
图 3 U型槽下在椭圆上带有局部散射体Sn(i)的NT×NR MIMO信道的几何学椭圆时变散射模型 Figure 3 Geometric elliptic time-varying scattering model of NT×NR MIMO channel with local scatter Sn(i) on ellipse with U-shaped groove |
| 表 1 高速移动下U型槽几何学椭圆时变散射模型的主要参数 Table 1 Main parameters of elliptical time-varying scattering model for U-shaped groove under high-speed environment |
RAU为发射端, MCT为接收端。RAU与MCT分别配置有NT和NR个由天线单元组成的均匀线性天线阵列。RAU(MCT)天线阵的倾角为βT(βR), 天线阵中的天线单元间距为δT(δR)。由于天线尺寸相对于a(t)和f(t)而言较小, 则可假设不等式(NT-1)δT≪a(t)-f(t)和(NR-1)δR≪a(t)-f(t)成立。运动方向与x轴所成的夹角为αv。记第n个平面波的离开角(Angle of Departure, AOD)为αnT(t), 到达角(Angle of Arrival, AOA)为αnR(t),由此可得到从RAU第l根天线到MCT第k根天线时变模型的信道冲击响应(Channel Impulse Response, CIR)hkl(t):
| $ {h_{kl}}(t) = h_{kl}^{{\rm{LOS}}}(t) + h_{kl}^{{\rm{NLOS}}}(t) $ | (1) |
其中:hklLOS(t)为CIR的视距(Line of Sight, LOS)分量, 且
| $ h_{kl}^{{\rm{LOS}}}(t) = {E_{kl}}{\rm{exp}}\left( {{\rm{j}}\left( {{\theta _{kl}}-2\pi {f_{{\rm{max}}}}{\rm{cos}}(\alpha _n^{\rm{R}}(t)-{\alpha _v})t-2\pi {\lambda _0}f(t)} \right)} \right) $ | (2) |
其中:Ekl表示路径增益, 且
非视距(Non Line of Sight, NLOS)的CIR可表示为:
| $ h_{kl}^{{\rm{NLOS}}} = \sum\limits_{p = 1}^P {\sum\limits_{q = 1}^Q {h_{kl}^{pq}(t)} } $ | (3) |
其中:P描述无线电波从RAU到MCT所经历的最大散射次数;p表示散射次数;q表示由远及近的路径。例如hkl23(t)代表传输波经历2跳, 且其路径为由远及近的第3条路径, 即RAU→Sn(2)→Sn(1)→MCT(由远及近的原则),
散射分量可表示为:
| $ h_{kl}^{1q}(t) = \sqrt {\eta _{kl}^{1q}} {E_{kl}}\mathop {\lim }\limits_{{N^{1q}} \to \infty } \sum\limits_{{n^{{\rm{1}}q}} = 1}^{{N^{{\rm{1}}q}}} {{E_{{n^{{\rm{1}}q}}}}} {\rm{exp}}\left( {{\rm{j}}({\theta _{{n^{1q}}}}-{\mathit{\boldsymbol{k}}_{{n^1}q}} \cdot {\mathit{\boldsymbol{r}}_{\rm{R}}}-{k_0}{D_{{n^{1q}}}}(t))} \right) $ | (4) |
| $ \begin{align} & h_{kl}^{2q}(t)=\sqrt{\eta _{kl}^{2q}}{{E}_{kl}}\underset{\begin{smallmatrix} {{N}^{1q}}\to \infty \\ {{N}^{2q}}\to \infty \end{smallmatrix}}{\mathop{\lim }}\, \sum\limits_{{{n}^{\rm{1}q}}=1}^{{{N}^{\rm{2}q}}}{\sum\limits_{{{n}^{2q=1}}}^{{{N}^{2q}}}{{{E}_{{{n}^{1q}}}}}}\exp (j({{\theta }_{{{n}^{1q}}}}-{{\mathit{\boldsymbol{k}}}_{{{n}^{1q}}}}\cdot {{\mathit{\boldsymbol{r}}}_{\rm{R}}}-\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{k}_{0}}{{D}_{{{n}^{1q}}}}(t)))\times {{E}_{{{n}^{2q}}}}\exp (j({{\theta }_{{{n}^{2q}}}}-{{\mathit{\boldsymbol{k}}}_{{{n}^{2q}}}}\cdot {{\mathit{\boldsymbol{r}}}_{\rm{R}}}-\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{k}_{0}}{{D}_{{{n}^{2q}}}}(t))) \\ \end{align} $ | (5) |
| $ \begin{align} & h_{kl}^{3q}(t)=\sqrt{\eta _{kl}^{3q}}{{E}_{kl}}\underset{\begin{smallmatrix} {{N}^{1q}}\to \infty \\ {{N}^{2q}}\to \infty \\ {{N}^{3q}}\to \infty \end{smallmatrix}}{\mathop{\lim }}\, \sum\limits_{{{n}^{\rm{1}q}}=1}^{{{N}^{\rm{2}q}}}{\sum\limits_{{{n}^{2q=1}}}^{{{N}^{2q}}}{\sum\limits_{{{n}^{3q=1}}}^{{{N}^{3q}}}{{{E}_{{{n}^{1q}}}}}}}\exp (j({{\theta }_{{{n}^{1q}}}}-\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\mathit{\boldsymbol{k}}}_{{{n}^{1q}}}}\cdot {{\mathit{\boldsymbol{r}}}_{\rm{R}}}-{{k}_{0}}{{D}_{{{n}^{1q}}}}(t)))\times {{E}_{{{n}^{2q}}}}\exp (j({{\theta }_{{{n}^{2q}}}}-\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\mathit{\boldsymbol{k}}}_{{{n}^{2q}}}}\cdot {{\mathit{\boldsymbol{r}}}_{\rm{R}}}-{{k}_{0}}{{D}_{{{n}^{2q}}}}(t)))\times {{E}_{{{n}^{3q}}}}\exp (j({{\theta }_{{{n}^{3q}}}}-\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\mathit{\boldsymbol{k}}}_{{{n}^{3q}}}}\cdot {{\mathit{\boldsymbol{r}}}_{\rm{R}}}-{{k}_{0}}{{D}_{{{n}^{3q}}}}(t))) \\ \end{align} $ | (6) |
| $ \begin{align} & h_{kl}^{pq}(t)=\sqrt{\eta _{kl}^{pq}}{{E}_{kl}}\underset{\begin{matrix} {{N}^{1q}}\to \infty \\ \cdots \\ {{N}^{pq}}\to \infty \\ \end{matrix}}{\mathop{\lim }}\, \sum\limits_{{{n}^{1q}}=1}^{{{N}^{1q}}}{\cdots \sum\limits_{{{n}^{pq}}=1}^{{{N}^{pq}}}{{{E}_{{{n}^{1q}}}}}}\exp (j({{\theta }_{{{n}^{1q}}}}-\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\mathit{\boldsymbol{k}}}_{{{n}^{1q}}}}\cdot {{\mathit{\boldsymbol{r}}}_{\rm{R}}}-{{k}_{0}}{{D}_{{{n}^{1q}}}}(t)))\times \cdots \times \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{E}_{{{n}^{pq}}}}\exp (j({{\theta }_{{{n}^{pq}}}}-{{\mathit{\boldsymbol{k}}}_{{{n}^{pq}}}}\cdot {{\mathit{\boldsymbol{r}}}_{\rm{R}}}-{{k}_{0}}{{D}_{{{n}^{pq}}}}(t))) \\ \end{align} $ | (7) |
其中:ηklpq表示路径能量损耗因子; Nklpq为散射体簇区域内局部散射体个数, 假设其趋于无穷; knpq表示与第n个接收波相同方向的波向量; rR代表位于MCT的空间转换向量; k0是自由空间波数, k0=2π/λ0; Dnpq(t)表示从RAU AlT通过Sn(i)到MCT AkR的无线电波传播总距离长度; Enpq表示路径增益; θnpq表示相位偏移。
由于天线尺寸比a(t)、f(t)小, 因此可认为从RAU不同天线单元到达的(或传播到MCT不同天线单元的)无线电波, 由经过同一个局部Sn(i)产生的Enpq和θnpq近似相同。假设Sn(i)增益Enpq恒定:
| ${{E}_{{{n}^{pq}}}}\text{=1/}\sqrt{{{N}^{pq}}}$ | (8) |
式(7) 中的θnpq为独立同分布(Independent and Identically Distributed)随机变量, 所有变量均服从[0, 2π)的均匀分布,且在同一个散射体簇区域内可视作
| ${\mathit{\boldsymbol{k}}_{{n^{pq}}}} \cdot {\mathit{\boldsymbol{r}}_{\rm{R}}} =- 2\pi {f_{\max }}\cos \left( {\alpha _n^{\rm{R}}\left( t \right)- {\alpha _v}} \right)t$ | (9) |
| $ {k_0}{D_{{n^{pq}}}}\left( t \right) = \frac{{2{\rm{\pi }}}}{{{\lambda _0}}}(D_{l{n^{pq}}}^{\rm{T}}(t) + D_{{n^{pq}}k}^{\rm{R}}(t)) $ | (10) |
其中:DlnpqT(t)和DnpqkR(t)分别表示AlT到散射体簇和散射体簇到接收端AkR的距离。设两焦点距散射体簇距离分别为DnT(t)与DnR(t), 由于散射体簇区域半径远小于参数a(t)、f(t), 故可认为
| $ D_{ln}^{\rm{T}}\left( t \right) \approx D_n^{\rm{T}}\left( t \right)-({N_{\rm{T}}}-2l + 1)\frac{{{\delta _{\rm{T}}}}}{2}{\rm{cos}}(\alpha _n^{\rm{T}}(t)-{\beta _{\rm{T}}}) $ | (11) |
| $ D_{nk}^{\rm{R}}\left( t \right) \approx D_n^{\rm{R}}\left( t \right)-({N_{\rm{R}}}-2k + 1)\frac{{{\delta _{\rm{R}}}}}{2}{\rm{cos}}(\alpha _n^{\rm{R}}(t)-{\beta _{\rm{R}}}) $ | (12) |
其中:
| $ D_n^{\rm{T}}\left( t \right) = \frac{{{a^2}(t) + {f^2}(t) + 2a(t)f(t){\rm{cos}}\alpha _n^{\rm{R}}(t)}}{{a(t) + f(t){\rm{cos}}\alpha _n^{\rm{R}}(t)}} $ | (13) |
| $ D_n^{\rm{R}}(t) = \frac{{{b^2}(t)}}{{a(t) + f(t){\rm{cos}}\alpha _n^{\rm{R}}(t)}} $ | (14) |
将式(8)~(10) 代入式(7), 联立式(11)~(14) 得到高速环境下从RAU第l根天线到MCT第k根天线时变信道模型的复数信道增益为:
| $ \begin{array}{l} h_{kl}^{pq}(t) = \\ \sqrt {\eta _{kl}^{pq}} {E_{kl}}\mathop {\lim }\limits_{\begin{array}{*{20}{c}} {{N^{1q}} \to \infty }\\ { \cdot \cdot \cdot }\\ {{N^{pq}} \to \infty } \end{array}} \sum\limits_{n = 1}^N {\sum\limits_{{n^{1q}} = 1}^{{N^{1q}}} { \cdots \sum\limits_{{n^{pq}} = 1}^{{N^{pq}}} {\left( {\prod\limits_{j = 1}^q {{E_{{n^{jq}}}}} } \right)} } {a_{ln}}(t){b_{kn}}(t)} \times \\ \exp \left( {{\rm{j}}(2\pi {f_n}(t)t + {\theta _n} + {\theta _0})} \right) \end{array} $ | (15) |
其中:
| $\left\{ \begin{array}{l} {a_{ln}}\left( t \right) = \exp \left( {{\rm{j\pi }}({N_{\rm{T}}} - 2l + 1)\frac{{{\delta _{\rm{T}}}}}{{{\lambda _0}}}\cos (\alpha _n^{\rm{T}}(t) - {\beta _{\rm{T}}})} \right)\\ {b_{kn}}\left( t \right) = \exp \left( {{\rm{j\pi }}({N_{\rm{R}}} - 2k + 1)\frac{{{\delta _{\rm{R}}}}}{{{\lambda _0}}}\cos (\alpha _n^{\rm{R}}(t) - {\beta _{\rm{R}}})} \right)\\ {f_n}\left( t \right) = {f_{\max }}\cos (\alpha _n^{\rm{R}}(t) - {\alpha _v})\\ {\theta _n} = - (4{\rm{\pi }}a(t))/{\lambda _0} \end{array} \right.$ | (16) |
其中:fmax为最大多普勒频率, 表征的是信道中的多普勒效应。由fmax=v/fc可知, 当速度越大, 最大多普勒频率也相应地增大, 信道的多普勒效应也越明显。因此, 在高速环境下的信道建模需要考虑多普勒效应。另外, 由于θ0对高速信道模型的统计特性无影响, 因此式(15) 中θ0可设置为0。根据中心极限定理, 从有限同分布的任意一个总体中抽取样本量为m的样本, 当m充分大时, 样本均值的抽样分布近似服从正态分布。因为相位偏移θnpq为独立同分布的随机变量, 所有变量均服从[0, 2π)的均匀分布,故可知hklpq(t)是均值为0的复高斯过程,其包络|hklpq(t)|为瑞利分布。
在参考模型中, AOD αnT(t)和AOA αnR(t)是相关的, 因此可由αnR(t)表示αnT(t):
| $ \alpha _n^{\rm{T}}\left( t \right) = \left\{ \begin{array}{l} f(\alpha _n^{\rm{R}}(t)), \;\;\;\;\;\;\;{\rm{0}} < \alpha _n^{\rm{R}}(t) \le {\alpha _0}\\ f(\alpha _n^{\rm{R}}(t)) + \pi, \;\;\;{\alpha _0} < \alpha _n^{\rm{R}}(t) \le 2\pi-{\alpha _0}\\ f(\alpha _n^{\rm{R}}(t)) + 2\pi, \;\;{\rm{2}}\pi {\rm{-}}{\alpha _0} < \alpha _n^{\rm{R}}(t) \le 2\pi \end{array} \right. $ | (17) |
其中:
| $ f(\alpha _n^{\rm{R}}(t)) = \arctan \left[{\frac{{(\kappa _0^2-1)\sin (\alpha _n^{\rm{R}}(t))}}{{2{\kappa _0} + (\kappa _0^2 + 1)\cos (\alpha _n^{\rm{R}}(t))}}} \right] $ | (18) |
| ${\alpha _0} = {\rm{\pi }} - \arctan \left( {\frac{{\kappa _0^2 - 1}}{{2\kappa _0^2}}} \right)$ | (19) |
其中:κ0为椭圆离心率的倒数, 即κ0=1/e=a(t)/f(t)。
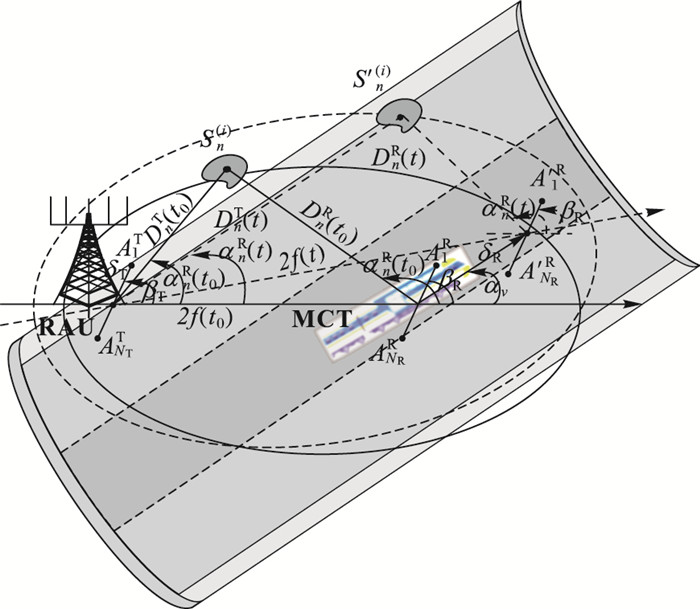
在图 4中, 由于MCT以速度v, 与x轴夹角αv的方向运动, 因此到达角AOA和椭圆焦点之间的距离2f(t)会随着时间发生变化。RAU与MCT之间的距离可通过几何关系得到
|
图 4 高铁U形槽信道模型中的时变角度参数 Figure 4 Time-varying angle parameters in high-speed train U-shaped channel model |
| $ \alpha _n^{\rm{R}}\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {{\alpha _v}-\arccos \left( {T\left( {\alpha _n^{\rm{R}}\left( t \right)} \right)} \right), }&{-{{ { π} }} < {\alpha _v} \le 0}\\ {{\alpha _v} + \arccos \left( {T\left( {\alpha _n^{\rm{R}}\left( t \right)} \right)} \right), }&{0 < {\alpha _v} \le {{ { π} }}} \end{array}} \right. $ | (20) |
其中:
| $ \begin{array}{l} T\left( {\alpha _n^{\rm{R}}\left( t \right)} \right) = \\ \frac{{vt-D_{nk}^{\rm{R}}\left( {{t_0}} \right)\cos \left( {{\alpha _v}-\alpha _n^{\rm{R}}\left( {{t_0}} \right)} \right)}}{{\sqrt {{{\left( {D_{nk}^{\rm{R}}\left( {{t_0}} \right)} \right)}^2} + {{\left( {vt} \right)}^2}-2D_{nk}^{\rm{R}}\left( {{t_0}} \right)vt\cos \left( {{\alpha _v} - \alpha _n^{\rm{R}}\left( {{t_0}} \right)} \right)} }} \end{array} $ | (21) |
至此, 完整地建模得到了高速移动下U型槽场景下的MIMO时变信道模型, 如式(1) 所示, 分别包含LOS和NLOS的CIR表达式。
综上, 高铁U型槽信道模型构建的步骤如下:
1) 设定高铁场景为U型槽场景, U型槽壁有无数的散射体簇, 以远端天线单元和高铁移动车厢终端分别作为椭圆的焦点建立一个椭圆的几何模型。
2) 根据步骤1) 获取当前时刻该场景下的距离、天线等参数。
3) 由步骤2) 得到当前时刻从RAU第l根天线到MCT第k根天线的CIR的视距分量。
4) 由步骤2) 得到当前时刻从RAU第l根天线到MCT第k根天线的复数信道增益。
5) 由步骤4) 得到当前时刻从RAU第l根天线到MCT第k根天线的CIR的非视距分量。
6) 结合步骤3) 和步骤5) 得到当前时刻从RAU第l根天线到MCT第k根天线的CIR。
7) 经过Δt时间以后, 若达到运行的时间, 则步骤6) 得到的CIR即为从RAU第l根天线到MCT第k根天线的时变CIR, 若没有达到运行时间, 则再回到步骤2)。
3 信道统计性能及仿真结果分析 3.1 统计性能首先, 将介绍应用于高速移动下U型槽时变信道模型的统计性能, 并给出各统计性能的数学表达式。
3.1.1 时变空时域互相关函数时变空时域互相关函数由MIMO高铁信道的两个任意的CIR之间的相关函数决定。[12]因为在高速移动下U型槽场景的时变信道模型的角度参数和发射机与接收机之间的距离是时变的, 故时变空时域互相关函数与时间和天线间的距离有关。时变空时域互相关函数的表达式如下:
| $ {R_h}\left( {t, \Delta {\delta _{\rm{T}}}, \Delta {\delta _{\rm{R}}}, \Delta t} \right) = {\rm{E}}\left\{ {{h_{kl}}(t)h_{{k^{'}}{l^{'}}}^*(t-\Delta t)} \right\} $ | (22) |
其中:t为时间; Δt为时间差; ΔδT为发射端天线间的距离; ΔδR为接收端天线间的距离; hk′l′*(t)表示hk′l′(t)的共轭。
3.1.2 时变自相关函数时变自相关函数是由MIMO高铁信道的任意CIR的自相关函数决定[12]。因为在高速移动下U型槽场景的时变信道模型是具有不稳定性的, 故时变自相关函数不仅与时间差Δt相关, 还与时间t相关。令时变空时域互相关函数的ΔδT与ΔδR为0, 即可得到时变自相关函数, 具体表达式如下:
| $ r\left( {t, \Delta t} \right) = E\left\{ {{h_{kl}}(t)h_{kl}^*(t-\Delta t)} \right\} = {R_h}\left( {t, 0, 0, \Delta t} \right) $ | (23) |
其中:t为时间; Δt为时间差; hkl*(t)为hkl(t)的共轭。式(23) 也给出了时变自相关函数与时变空时域互相关函数之间的关系式。
3.1.3 时变空域多普勒功率谱密度时变空域多普勒功率密度描述了高速移动下的信道频率色散参数, 是由移动台与基站间的相对运动或是信道中物体运动所引起的[12]。因为在高速移动下, 运动速度特别大, 多普勒效应比较明显, 故在仿真高速移动下U型槽场景的时变信道模型时, 需要考虑时变空域多普勒功率谱密度。具体表达式如下:
| $ \begin{array}{l} W\left( {t, \nu, \Delta {\delta _{\rm{T}}}, \Delta {\delta _{\rm{R}}}} \right) = \\ \int {{R_h}} \left( {t, \Delta {\delta _{\rm{T}}}, \Delta {\delta _{\rm{R}}}, \Delta t} \right)\exp \left( {-{\rm{j}}2\pi \nu \Delta t} \right){\rm{d}}\Delta t \end{array} $ | (24) |
其中:t为时间;Δt为时间差;ν为多普勒频移; ΔδT为发射端天线间的距离; ΔδR为接收端天线间的距离。由式(22) 可知,时变空域多普勒功率谱密度是由时变空时域互相关函数进行傅里叶变换得到的。
3.2 仿真结果及其分析为验证本文所提信道模型的合理性, 结合第2章所述的MIMO系统模型进行了验证。系统模型场景如图 5所示。
|
图 5 U型槽场景下的系统模型 Figure 5 System model of U-shaped scenario |
列车位于U型槽内, 在U型槽壁有无穷多散射体簇, 但在仿真中不可能做到无穷多的散射体簇, 故假设散射体簇的数目为50。该系统模型的主要仿真参数如表 2所示。
| 表 2 高速移动下U型槽时变信道模型的主要仿真参数 Table 2 Main simulation parameters of U-shaped time-varying channel model under high-speed mobile environment |
首先, 根据仿真参数得到了AlT到AkR和Al′T到Ak′R链路的时变空时域互相关函数, 如图 6~7所示。
|
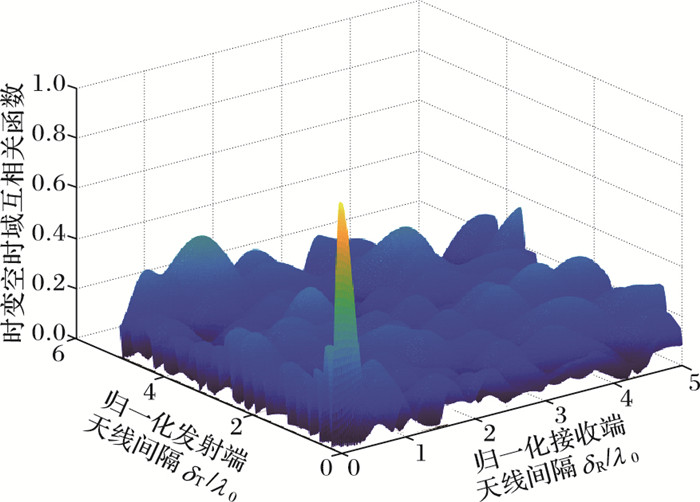
图 6 高速移动下U型槽时变信道模型含有视距分量的时变空时域互相关函数 Figure 6 Time-varying space-time cross-correlation function with line-of-sight component in time-varying channel model of U-shaped groove under high-speed mobile environment |
|
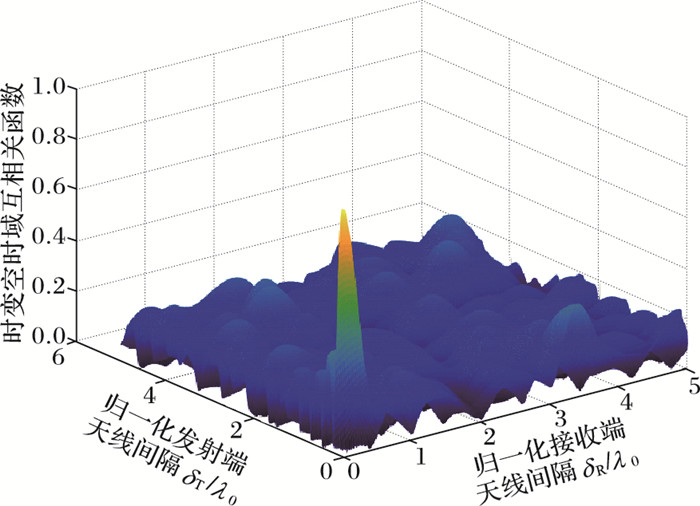
图 7 高速移动下U型槽时变信道模型不含视距分量的时变空时域互相关函数 Figure 7 Time-varying space-time cross-correlation function without line-of-sight component in time-varying channel model of U-shaped groove under high-speed mobile environment |
从图 6~7可看出,高速移动下U型槽时变信道模型在含有视距分量时的时变空时域互相关函数的值高于没有视距分量时的时变空时域互相关函数。这是因为加入视距分量后, 信道的相关性增强, 相关的性能下降。因此, 从图 6~7可以看出, 本文所提的信道模型是具有较高的相关性。
3.2.2 时变自相关函数通过将δT和δR设置为0, 从时变空时域互相关函数可以得到时变自相关函数, 如图 8所示。
|
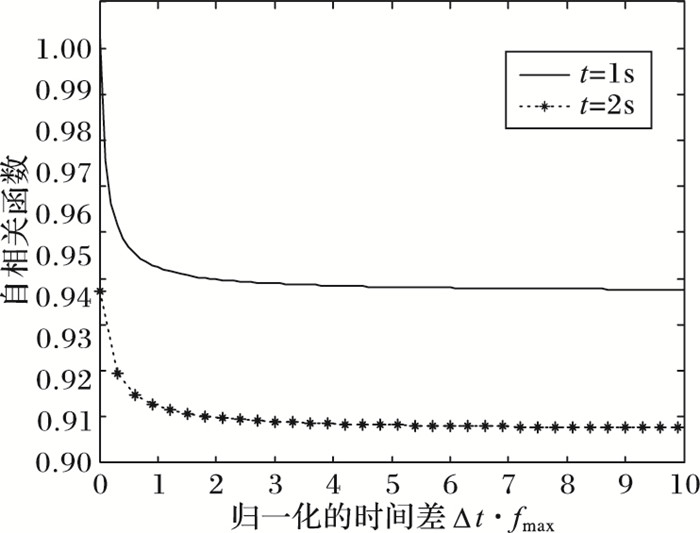
图 8 高速移动下U型槽时变信道模型的时变角度参数归一化的自相关函数 Figure 8 Normalized auto-correlation function of time-varying angle parameter in time-varying channel model of U-shaped groove under high-speed mobile environment |
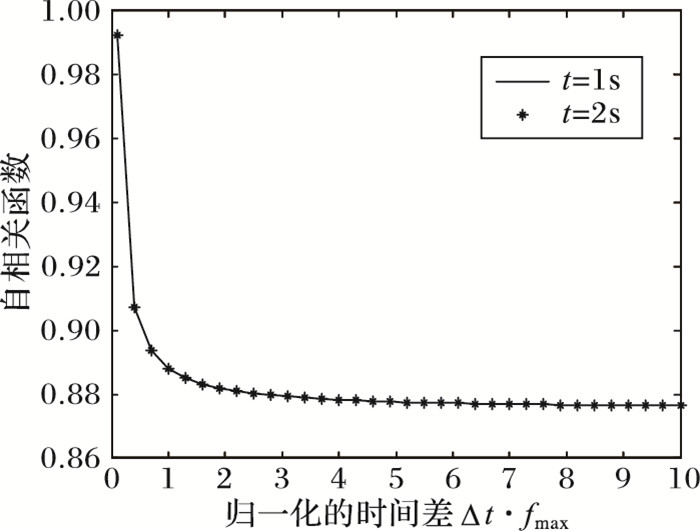
从图 8可看出,高速移动下U型槽时变信道模型的归一化自相关函数具有时变性, 而且自相关性也较高。首先, 因为加入了LOS分量, 信道的相关性会大幅提高;其次, 高速移动下U型槽时变信道模型是具有时变性的, 天线参数和发射端与接收端的距离也是时变参数, 故自相关函数随时间变化;并且由于高铁信道具有非平稳性, 自相关函数不仅与时间差Δt有关, 还与时间t相关。从图 9可以看出, 影响信道模型时变性的主要因素是角度参数, 若角度参数是非时变的, 则得到的自相关函数也是非时变的。图 8~9的结果验证了本文模型具有时变性以及高铁信道的非平稳性。
|
图 9 高速移动下U型槽时变信道模型的非时变角度参数的归一化的自相关函数 Figure 9 Normalized auto-correlation function of non-time-varying angularity of U-Shaped time-varying channel model under high-speed mobile environment |
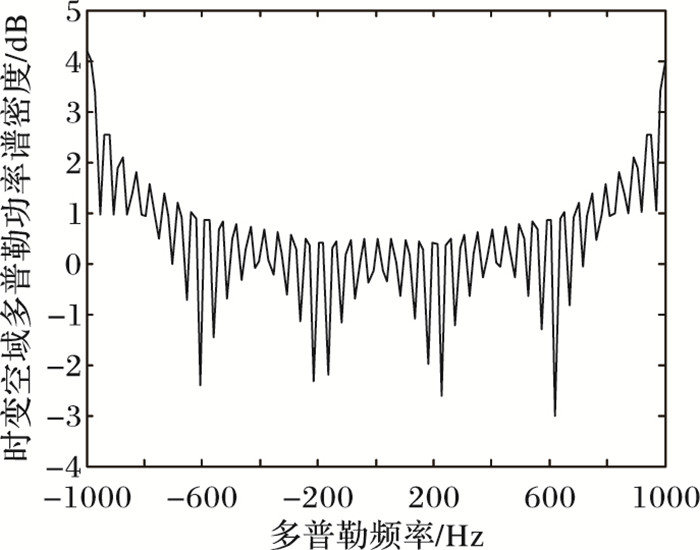
将时变空时域互相关函数进行傅里叶变换, 即可得到时变空域多普勒功率谱密度, 得到的仿真结果如图 10所示。
|
图 10 高速移动下U型槽时变信道模型的时变空域多普勒功率谱密度 Figure 10 Time-varying space Doppler power spectral density of U-shaped time-varying channel model under high-speed mobile environment |
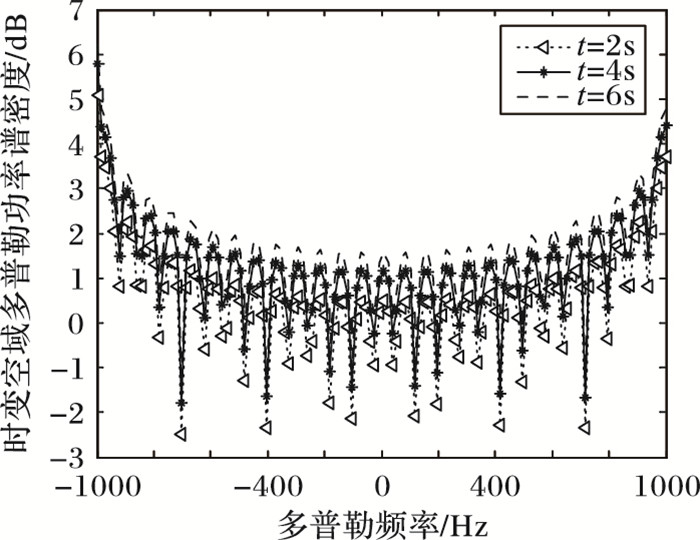
从图 10可看出,高速移动下U型槽时变信道模型的时变空域多普勒功率谱密度呈U型, 也称之为典型U型谱。多普勒频移是关于入射角的函数, 且关于入射角具有对称性。入射角变化时, 频率域会从fc变化到fc±fmax, 多普勒功率随着频率变化而变化, 因此时变空域多普勒功率谱密度呈U型。图 11显示了在不同时刻的高速移动场景下,U型槽时变信道模型下的时变空域多普勒功率谱密度, 因为本文所提的信道模型具有时变性, 所得的空域多普勒功率谱密度也具有时变性, 所以不同时刻下的多普勒功率谱密度函数也不同, 进一步验证了本文所提的信道模型具有时变性。
|
图 11 不同时刻的高速移动下U型槽时变信道模型的时变空域多普勒功率谱密度 Figure 11 Time-varying Doppler power spectral density in U-shaped time-varying channel model under high-speed mobile environment at different time |
本文通过计算不同统计性能的复杂度来分析统计性能开销。从表 3中本文所应用的不同统计性能的复杂度可以看出:时变自相关函数和时变空域多普勒功率谱密度的复杂度位于同一复杂度级别, 而时变空时域互相关函数更加复杂。这是因为它们都是基于CIR来计算的, 时变自相关函数和时变空域多普勒功率谱密度的循环次数仅与散射体簇的数目相关, 而时变空时域互相关函数的循环次数不仅与散射体簇的数目相关, 还与接收端和发射端天线数相关。此外, 本文也对比了以上三种统计性能进行完整运算的运行时间情况。仿真工具为Matlab 2014, 主机配置为2.6 GHz奔腾E5300 CPU, 内存2 GB, Windows 7.1操作系统, 仿真结果见表 3。可以看到, 时变空时域自相关函数的运行总时间略长于其他两种统计性能的运行总时间, 这是因为计算时变自相关函数和时变空域多普勒功率谱密度基于同一发射天线和接收天线, 而时变空时域互相关函数基于不同发射天线与接收天线, 计算更复杂, 这也与复杂度分析一致。
| 表 3 不同统计性能的对比 Table 3 Comparison of different statistical performance |
本文提出了一种高速移动下U型槽的时变信道模型, 采用几何随机分布理论以及波传播定律, 针对高铁典型场景U型槽建立出具体的几何分布模型, 分析散射体的变化规律, 推导视距分布、非视距分布、时变角度、时变多普勒扩展等参数的数学闭合表达式, 并给出了信道冲击响应的闭式解。仿真结果表明, 本文所提的信道模型具有时变性和较高的相关性, 体现了高铁信道的非平稳性,满足高速移动场景下无线信道的特性, 验证了所提的信道模型的合理性。
| [1] | GOLLER M. Application of GSM in high speed trains: measurements and simulations[C]//Proceedings of the 1995 IEE Colloquium on Radiocommunications in Transportation. Piscataway, NJ: IEEE, 1995: 1-7. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=465941 |
| [2] | BRISO C, CORTES C, ARQUES F J, et al. Requirements of GSM technology for the control of high speed trains[C]//Proceedings of the 13th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications. Piscataway, NJ: IEEE, 2002: 792-793. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1047330 |
| [3] | GUAN K, ZHONG Z, AI B. Assessment of LTE-R using high speed railway channel model[C]//Proceedings of the 2011 Third International Conference on Communications and Mobile Computing. Piscataway, NJ: IEEE, 2011: 461-464. http://ieeexplore.ieee.org/document/5931295/ |
| [4] | KASTELL K, BUG S, NAZAROV A, et al. Improvements in railway communication via GSM-R[C]//Proceedings of the IEEE 63rd Vehicular Technology Conference. Piscataway, NJ: IEEE, 2006: 3026-3030. |
| [5] | KNORZER S, BALDAUF M A, FUGEN T, et al. Channel analysis for an OFDM-MISO train communications system using different antennas[C]//Proceedings of the 2007 IEEE 66th Vehicular Technology Conference. Piscataway, NJ: IEEE, 2007: 809-813. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4349827 |
| [6] | GUAN K, ZHONG Z, AI B, KURNER T. Deterministic propagation modeling for the realistic high-speed railway environment[C]//Proceedings of the 2013 IEEE 77th Vehicular Technology Conference. Piscataway, NJ: IEEE, 2013: 1-5. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6692506 |
| [7] | CICHON D J, BECKER T C, WIESBECK W. Determination of time-variant radio links in high-speed train tunnels by ray optical modeling[C]//Proceedings of the 1995 Antennas and Propagation Society International Symposium. Piscataway, NJ: IEEE, 1995, 1: 508-511. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=530069 |
| [8] | CICHON D J, ZWICK T, WIESBECK W. Ray optical modeling of wireless communications in high-speed railway tunnels[C]//Proceedings of the IEEE 46th Vehicular Technology Conference, Mobile Technology for the Human Race. Piscataway, NJ: IEEE, 1996, 1: 546-550. |
| [9] | ZHENG Q, XU C, WU M. A novel MIMO channel model for high speed railway system[C]//Proceedings of the IEEE 14th International Conference on Communication Technology. Piscataway, NJ: IEEE, 2012: 31-35. |
| [10] | GHAZAL A, WANG C, HAAS H, et al. A non-stationary MIMO channel model for high speed train communication systems[C]//Proceedings of the IEEE 75th Vehicular Technology Conference. Piscataway, NJ: IEEE, 2012: 1-5. |
| [11] | GHAZAL A, WANG C, HAAS H, et al. A non-stationary geometry-based stochastic model for MIMO high-speed train channels[C]//Proceedings of the IEEE 12th International Conference on ITS Telecommunications. Piscataway, NJ: IEEE, 2012: 7-11. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6425292 |
| [12] | GHAZAL A, WANG C, AI B, et al. A nonstationary wideband MIMO channel model for high-mobility intelligent transportation systems[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(2): 885-897. |
| [13] | CHEN B, ZHONG Z. Geometry-based stochastic modeling for MIMO channel in high-speed mobile scenario[J]. International Journal of Antennas & Propagation, 2012, 2012: Article ID 184682. |
| [14] | LIN S, ZHONG Z, CAI L, et al. Finite state Markov modelling for high speed railway wireless communication channel[C]//Proceedings of the 2012 IEEE Global Communications Conference. Piscataway, NJ: IEEE, 2012: 5421-5426. http://ieeexplore.ieee.org/document/6503983/ |
| [15] | XUAN L, CHAO S, AI B, et al. Finite-state Markov modeling of fading channels: a field measurement in high-speed railways[C]//Proceedings of the 2013 IEEE/CIC International Conference on Communications in China. Piscataway, NJ: IEEE, 2013: 577-582. |
| [16] | AI B, HE R, ZHONG Z, et al. Radio wave propagation scene partitioning for high-speed rails[J]. International Journal of Antennas & Propagation, 2012(2012): Article ID 815232. |
| [17] | 邱佳慧, 陶成, 刘留, 等. U型槽无线信道多径传播特性测量与建模方法的研究[J]. 铁道学报, 2014, 36(1): 40-48. (QIU J H, TAO C, LIU L, et al. Research on measurement and modeling of wireless channel multipath propagation properties for U-shape cutting[J]. Journal of the China Railway Society, 2014, 36(1): 40-48.) |




