2. 西南交通大学 信息科学与技术学院, 成都 610031
2. College of Information Science and Technology, Southwest Jiaotong University, Chengdu Sichuan 610031, China
作为公共安全的重要保障,监控视频数量迅速增长,如何有效、智能处理视频图像大数据是建设安全、智能型城市的重要保障,其中面部图像是最重要的监控对象。因受到成像条件以及小样本问题的制约,面向海量人脸数据的自动人脸识别技术在公共安防领域还鲜有重大成功案例,最先进的自动人脸识别算法在类似美国波士顿马拉松爆炸案的恐怖案件调查过程中亦未能发挥效用。人脸识别专家Rowden等[1]于2014年进行了关于人类与机器视觉在人脸识别问题上性能的对比研究,成果表明在户外自由、非可控场景中,当前最先进、基于图像的人脸识别技术/系统仍无法达到人眼辨识水平。
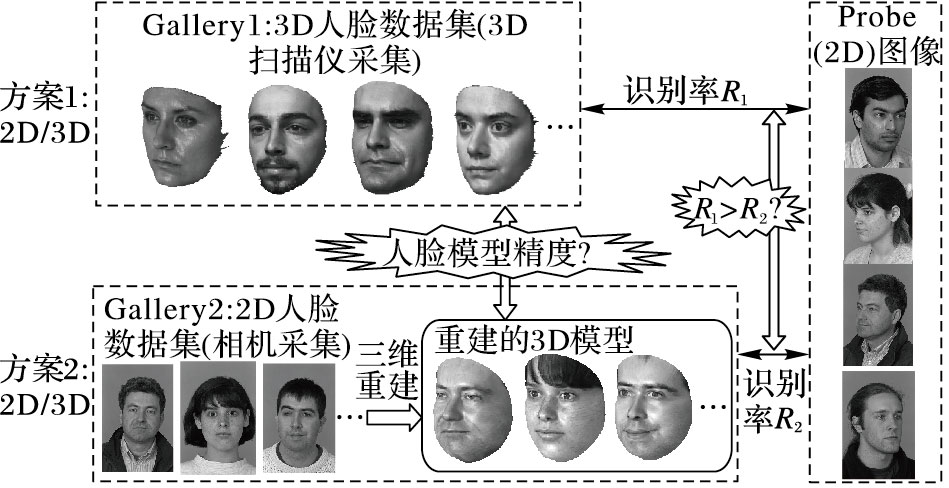
由于人脸天然具有三维形状,直观上基于三维人脸数据的识别是解决姿态问题行之有效的手段,学者采用三维面部法向量在人脸识别大挑战(Face Recognition Grand Challenge,FRGCv2) 三维人脸数据集[2]上获得了99.6%的准确率[3],验证了高质量三维人脸数据在人脸识别问题上的有效性。但是现有三维人脸采集技术对距离、运动速度、环境光照均有严格要求,并不适用于自由场景下的人脸采集,因此非用户配合的三维人脸识别从技术上还很难实现。图 1展示了一个可行的方案(简称方案1) ,即后台原型数据集(Gallery)采用三维人脸数据,前端测试集(Probe)依然采用二维图像,实现“2D/3D”的跨模态识别,以解决训练数据集的小样本问题,这类跨模态人脸识别研究刚起步;另一常见的方案(简称方案2) 是后台Gallery与Probe均是二维图像,对Gallery中的人脸图像进行三维重建,利用三维信息克服缓解姿态变化。方案2的优势是便于现有人脸识别系统的改进,且不需要额外硬件辅助。针对当前三维采集设备并未广泛使用的情况,本文旨在研究基于图像的三维人脸建模技术,并针对三维模型用于人脸识别的有效性进行评估。
|
图 1 2D/3D跨模态及基于三维重建的2D/2D人脸识别方案对比 Figure 1 Cross-modality 2D-3D face recognition vs. 3D assisted 2D/2D face recognition |
Yi等[4]将采用方案2的方法进一步分为4类:1) 虚拟正面合成;2) 多姿态投影;3) 模型参数拟合;4) 姿态自适应滤波。其中基于图像的三维人脸建模是这类方法一个关键问题,是本文的研究内容。
Blanz等[5]提出的三维形变模型(3D Morphable Model,3DMM)在三维人脸建模技术发展历上具有里程碑意义。对3DMM的优化、改进也成为了该领域的一个热点问题:学者们分别从提高建模效率[6]、融入表情因素[7]、建立完整头部模型[8]等角度对3DMM进一步完善和发展。为了简化优化过程,龚勋等[9]提出了基于特征点的算法,实现了采用单张图像、快速的人脸建模。
近年,Kemelmacher-Shlizerman等[10]基于人脸近似朗伯(Lambertain)凸表面的假设,利用球面谐波和一个三维人脸参考模型实现了单张人脸图像的建模,并进一步用互联网图片[11]和视频[12]作为训练集恢复人脸形状,但参考模型的选择对建模结果有一定影响。
从运动恢复结构(Structure From Motion,SFM)是三维重建的主流方法,近年在人脸建模方面取得了持续性的研究进展。Lin等[13]利用5张相差近45°的图像,实现了大范围变化下高精度的人脸建模,但需要建模对象的配合; Gonzalez-Mora等[14]在SFM算法中引入线性人脸模型作为先验知识,以提高在噪声、丢失信息情况下系统的鲁棒性。还有一些专家通过多张图像匹配点的对应关系建立方程组,并用非线性最小二乘法求解关键点的深度值。
本文在基于特征点的形变统计模型[15]的基础上,在SFM框架下实现多张图像的三维人脸建模,旨在进一步提高特征点的深度值估计精度。
1 基于图像的三维人脸形状建模本文人脸建模思路采用两步人脸建模(Two-Step Face Modeling,TSFM)方案[16]实现从粗到精的形状建模。
第1步 计算特征点的类三维坐标(Quasi-3D,Q-3D),(将其称之为类三维坐标是因为其坐标值是估计值)给定1张近正面人脸图像I0和n张非正面图像(I1,I2,…,In),通过计算特征点的深度值,由已知的二维坐标与深度估计值组合以获得Q-3D坐标。
第2步 将Q-3D特征点输入形变算法拟合整体形状,实现面部形状整体建模。
1.1 基于两张图像的特征点深度值估计在输入一张图像的情况下,Gong等[15]提出了基于稀疏线性模型的优化(Sparse Linear Model based Optimization,SLMO)算法,把所有特征点看成一个整体,然后利用训练库中的先验知识对缺失的特征点的坐标进行整体估计。本节将SLMO结合新的优化算法以提高深度值估计精度。
给定一张近正面图像I0和一张非正面图像Ii(1≤i≤n),s0和si分别是这两张图像上的k个特征点构成的二维形状向量,从而
| $\mathbf{s}_{0}^{{}}={{\left( \mathbf{p}_{0}^{\text{T}},\mathbf{p}_{2}^{\text{T}}\cdots \mathbf{p}_{k}^{\text{T}} \right)}^{\text{T}}}$ | (1) |
| $\mathbf{s}_{i}^{{}}={{\left( \mathbf{q}_{1}^{\text{T}},\mathbf{q}_{2}^{\text{T}}\cdots \mathbf{q}_{k}^{\text{T}} \right)}^{\text{T}}}$ | (2) |
其中,pk=(xk,yk)T,qk=(uk,vk)T分别是I0和Ii上的第k个特征点。
s0和si是同一个人的不同姿态下的形状,理论上s0可以通过旋转、缩放变换得到与si具有相同的姿态和大小的变换形状s′0,其中s′0=(p′1T,p′2T,…,p′kT)T。令σ是缩放因子,t=[Δx,Δy]T是平移向量,R(ω)是旋转矩阵,ω表示三个旋转角(α,β,γ),通过一个简单的成像模型,可以得到:
| $\left[ \begin{matrix} \mathbf{p}_{t}^{'} \\ z_{t}^{'} \\ \end{matrix} \right]=\sigma \cdot \left[ \begin{matrix} \mathbf{R} & \mathbf{t} \\ \end{matrix} \right]\cdot {{\left[ \mathbf{p}_{t}^{\text{T}},{{z}_{t}},1 \right]}^{\text{T}}}$ | (3) |
其中:zt是I0上第t个特征点的z坐标值,z′t是s′0的z坐标值。很明显,zt是未知量,通过式(3) 逐点计算p′t,一共存在k+6个未知量,即(α,β,γ,σ,Δx,Δy,z1,…,zk),根据已知的si,可以构建如下优化目标函数:
| $\min \left( d\left( \mathbf{s}_{0}^{\text{ }\!\!'\!\!\text{ }},\mathbf{s}_{i}^{{}} \right) \right)=\min {{\left\| \mathbf{s}_{0}^{'}-\mathbf{s}_{i}^{{}} \right\|}_{2}}$ | (4) |
本文采用粒子群优化算法[17]来优化这些未知量。ω和t的初始值通常可以设置为0,现有方法[18-19]通常采用三维人脸模板(如CANDIDE线框模型相应特征点的值z0={ z10,z2 0,…,zk0} 对深度值进行初始值[19],无法保证正常收敛。本节提出采用SLMO首先从单张正面图像估计出特征点的深度值,以获得比三维人脸模板更准确的深度值初始值,故二步深度值估计(Two-Step optimal Estimation,TSE)算法步骤如下。
算法1 两步深度值估计TSE算法。
输入:正面及侧面人脸图像上的两组二维特征点s0和si。
步骤1 采用SLMO从I0计算特征点深度值的初始值z0。
步骤2
a)将特征点的深度值z0固定,首先利用式(4) 优化旋转、平移参数和缩放因子,得到ω0、t0和σ0。
b)固定ω0、t0和σ0,通过求解式(4) 计算特征点的z坐标值。
输出:所有特征点的z坐标值z={z1,z2,…,zk}。
1.2 姿态与深度迭代优化算法从成像模型(3) 可以看出,姿态参数ω与深度值z二者相互影响,TSE算法采用了分步估计的策略。精确的姿态旋转角度能够进一步提高深度值计算精度。尽管通过估计算法无法获得绝对精确的角度值,但通过算法优化能够进一步提高旋转角的精度,进而获得一个折中的估计结果。另一方面,由于姿态参数ω与深度值z相互影响,要提高ω的估计精度,就需要更精确的深度值z。基于这一思路,本文提出将算法1变形为一个迭代方式,即姿态与深度迭代优化(Iterative Pose and Depth Optimization,IPDO)算法,归纳如下。
算法2 姿态与深度迭代优化IPDO算法。
输入:正面及侧面人脸图像的两组二维特征点s0和si,迭代最大次数N,收敛阈值τ。
步骤1 采用SLMO从I0计算特征点深度值的初始值z0,初值化循环指示器i=0。
步骤2
a)将特征点的深度值zi固定,首先利用式(4) 优化旋转、平移参数和缩放因子,得到ωi、ti和σi。
b)固定ωi、ti和σi,通过求解式(4) 计算特征点的z坐标值,得到zi,更新指示器i=i+1。
步骤3 如果italic>N或者‖zi-zi-1‖2<τ,退出;否则,跳至步骤2。
输出:所有特征点的z坐标值z={z1,z2,…,zk},并将其构造成类三维坐标Q-3D——由已知的二维形状s0和估计的深度值zi组合而成。
1.3 基于多张图像的深度值融合及整体形变IPDO算法解决了1张正面图像和1张非正面图像的深度值估计,当输入n(>1) 张非正面人脸图像时,将其与正面图像结合,可以为每个特征点计算得到n个深度值,采用平均值是一个常用的策略,但当数据量不大时(通常n∈[0, 5])容易受到噪声的影响,本文采用正态分布假设去除离群点。
给定第t个(1≤t≤k)特征点的n个估计值集合Ω={zt,1,zt,2,…,zt,n},根据第t个特征点的深度值的正态分布统计参数(均值t、均方差σt),可以排除一些异常点,从而获得一个包含n′个有效值的新集合:
| $\Sigma =\left\{ {{z}_{t,i}}\in \Omega \wedge {{z}_{t,i}}\in \left[ {{{\bar{z}}}_{t}}-3{{\sigma }_{t}},{{{\bar{z}}}_{t}}+3{{\sigma }_{t}} \right] \right\}$ | (5) |
其中zt和σt是通过训练集(包含225个三维人脸模型)得到的。根据Σ的平均值就可以计算第t个特征点的深度值:
| ${{z}_{t}}=\left\{ \begin{align} & \frac{1}{n'}\sum\limits_{i=1}^{n'}{{{z}_{t,i}}},\text{ if }\Sigma \ne \phi \\ & z_{t}^{0},\text{ if }\Sigma =\phi \\ \end{align} \right.$ | (6) |
其中zt0是由SLMO估计的第t个特征点的深度值,进而构造特征点的Q-3D坐标。
基于特征点的Q-3D坐标,采用径向基函数(Radial Basis Function,RBF)通过调整平均人脸模型实现模型形变,获得最终的三维人脸模型。
2 基于投影及相似度分析三维信息有效性评价为了客观评价三维人脸信息(既包括采集的高精度三维人脸,也包括重建的三维人脸)在跨姿态条件下人脸识别的有效性,本文将设计两者方案对其进行评价,并客观比较方案1(采用真实三维人脸模型)与方案2(采用的重建三维人脸模型)在人脸识别中的性能差异。鉴于本文的重点并非研究人脸识别涉及的特征提取、分类等问题,本章将以面部图像相似度度量为手段,从如下3方面对三维人脸信息进行评测。
1) 重建的三维人脸模型的精度评价。
由于三维人脸库中通过硬件设备采集的三维人脸模型作为人脸形状的真实值(Ground Truth)。真实三维人脸形状模型以及重建形状模型分别生成深度图,最后比较二者的差异。
2) 相似度S1和S2的比较。
对于输入的二维图像,首先估计其旋转角,然后将重建的三维人脸模型和真实三维人脸模型按照相应的角度进行投影,然后计算投影图与原始图像的相似度,分别用S1和S2表示。
3) 三维人脸模型在跨姿态人脸识别中的作用。
在2) 的基础上,采用人脸识别特征提取算法对三维模型投影图进行特征分析,然后进行闭集人脸识别测试,并与采用正面人脸图像的识别率进行对比,以验证三维信息在辅助人脸识别中的作用。特征提取采用局部相关分析匹配(Local Correlation Matching,LCM)算法[20]。
3 实验结果及分析本文实验在CPU:Intel i7 2.7 GHz,内存4 GB,操作系统:Windows 10的笔记本电脑上进行。
3.1 测试数据集为了验证文中提出深度估计算法的精度,在两个三维人脸数据集上进行实验,三维数据库中的人脸模型为特征点深度估计、三维人脸建模提供了用于对比的真实值(Ground Truth)。另外在二维人脸数据库IMM_Face[21]和FERET[22]上进行三维人脸建模,针对FERET中8个不同姿态子集进行了识别测试以验证三维信息。采用的两个三维人脸数据库如下。
1) SWJTU-HFDB多模人脸数据库。
针对跨模态、多模人脸识别等应用场景,本文采集了一个西南交通大学多模数据库(Southwest Jiaotong University-Hybrid Face Database,SWJTU-HFDB),包含同一个人4种不同模态数据:1) 二维高分辨率图像(用数码相机采集);2) 二维低分辨率图像(用监控摄像头采集);3) 三维高精度人脸模型(用结构光设备采集);4) 三维低精度人脸模型(用Kinect采集)。其中三维高精度人脸子集同时包含采集三维点云数据和纹理图像,共450个人脸模型,每个三维人脸模型均标定了76个特征点,是本文测试用到的数据集,下文简称SWJTU-3D数据集。
2) Bosphorus(BS) Database三维人脸数据库。
BS数据集[23]包括105个西方人,共4652个人脸模型。每个模型具有22个手动标注的特征点。数据通过商业结构光采集设备Inspeck Mega Capturor II 3D采集,同时采集了三维模型和纹理图像,其中三维模型包括约35000个顶点,二维纹理图像分辨率为1600×1200。
3.2 深度值估计精度验证为了量化评估文中提出的TSE和IPDO特征点深度估计的性能,本文将SWJTU-3D数据集中的正面人脸模型划分为训练集和测试集,每个集合包含225个模型。基于训练集合,生成一个平均人脸模型。为了验证不同姿态下的图像的估计效果,用三维模型投影生成了6种姿态的二维图像,分别为(10,10,0) ,(10,20,0) ,(10,30,0) ,(20,10,0) ,(20,20,0) ,(30,30,0) 。
以三维人脸数据库中三维人脸的特征点深度值为基准,采用两个量化评估标准,如下所示。
1) z坐标值平均误差e(ze,zg)及标准差σ(ze,zg):
| $e(\mathbf{z}_{e}^{{}},\mathbf{z}_{g}^{{}})=\frac{1}{k}\sum\limits_{t=1}^{k}{\left| {{z}_{e,t}}-{{z}_{g,t}} \right|}$ | (7) |
| $\sigma (\mathbf{z}_{e}^{{}},\mathbf{z}_{g}^{{}})=\sqrt{\frac{1}{k}\sum\limits_{t=1}^{k}{{{\left( {{z}_{e,t}}-{{z}_{g,t}}-e\left( \mathbf{z}_{e}^{{}},\mathbf{z}_{g}^{{}} \right) \right)}^{2}}}}$ | (8) |
其中:zg=[zg,1,zg,2,…,zg,k]T是真实三维人脸上的特征点深度真实值,ze=[ze,1,ze,2,…,ze,k]T是特征点深度的估计值。平均人脸模型上的特征点深度值与真实值的误差作为对比,即e(zavg,zg),σ(zavg,zg)。
2) 将所有特征点特征值组成向量,计算相关系数c(zg,ze)[19]作为相似度对比:
| $c\left( {{\mathbf{z}}_{g}},{{\mathbf{z}}_{e}} \right)=\frac{1}{k-1}\sum\limits_{t=1}^{k}{\left( \frac{{{z}_{g,t}}-{{{\bar{z}}}_{g}}}{{{\sigma }_{g}}} \right)\left( \frac{{{z}_{e,t}}-{{{\bar{z}}}_{e}}}{{{\sigma }_{e}}} \right)}$ | (9) |
其中:zg、σg是zg的均值和标准方差;ze、σe是ze的均值和标准差,根据定义可知c(zg,ze)越大意味着ze越接近zg。
首先,验证TSE、IPDO算法在6种不同姿态投影图像上的深度值估计精度。如前文所述,本文方法与现有方法如非线性最小二乘(Nonlinear Least-Squares,NLS)[19]算法的主要区别在于初始值的设置,TSE采用SLMO估计的值进行初始化,而NLS采用平均人脸上对应特征点的深度值。用NLS-like来表示用TSE的方法进行优化,但采用与NLS类似的初始化方法——采用平均人脸上的特征点深度值。如表 1所示,可以看到,不同角度对估计结果有一定的影响,但总体上波动不大,TSE由于采用了较准确的初始值,结果要优于NLS-like算法,能够获得1.5 mm以下的估计误差,而IPDO算法能够获得1.27 mm的平均估计误差。另外,所有估计算法均优于直接采用平均人脸模型(见Generic数据)。本实验结果验证了本文的算法能够有效地提高重建三维模型在轴方向的精度。
| 表 1 不同角度下图像的深度值估计对比 mm Table 1 Comparison of depth value estimation using different poses mm |
为了与现有深度估计算法通用模型算法(Genetic Algorithm,GA)[18]、非线性最小二乘法(Nonlinear Least-Squares Model with Symmetry and Regularization terms,NLS1_SR)[14]进行客观对比,在BS数据集上进行实验。与对比文献保持一致,用一张正面人脸和一张侧面人脸图像进行估计测试,其中侧面人脸图像分别来自5个不同的子集(P_R_D,P_R_SD,P_R_SU,PR_U,YR_R10) ,对比结果如表 2所示(其中: μ表示均值,std表示方差),可以看到,TSE与IPDO对于不同子集均具有鲁棒性,其性能优于GA和NLS1_SR算法,说明本文提出的方法性能稳定,可为后续进行整体三维建模提供条件。
| 表 2 在BS数据集上不同姿态角下深度值估计精度的对比 Table 2 Comparison of accuracy of depth value estimation using different profile images in BS database |
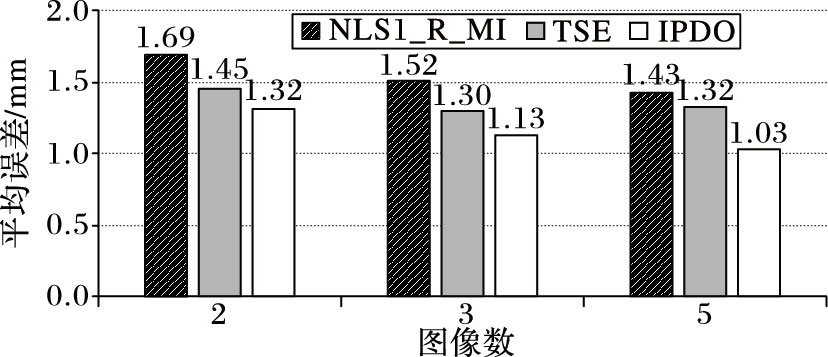
为验证1.3节所提出的基于多张图像的深度值融合策略的效果,在BS数据集上进行了测试,结果如图 2所示,可以看到不同算法采用多张图像均能够有效提高估计效果,同样地,IPDO能够获得最优的结果,本文提出的两个估计算法均优于NLS算法。算法运行时间对比如表 3(表 3中,NLS2为两步优化的非线性最小二乘(two-step optimization of Nonlinear Least-Squares)),可以看到在没有进行代码优化的情况下,TSE和IPDO能够具有较高的运行效率。
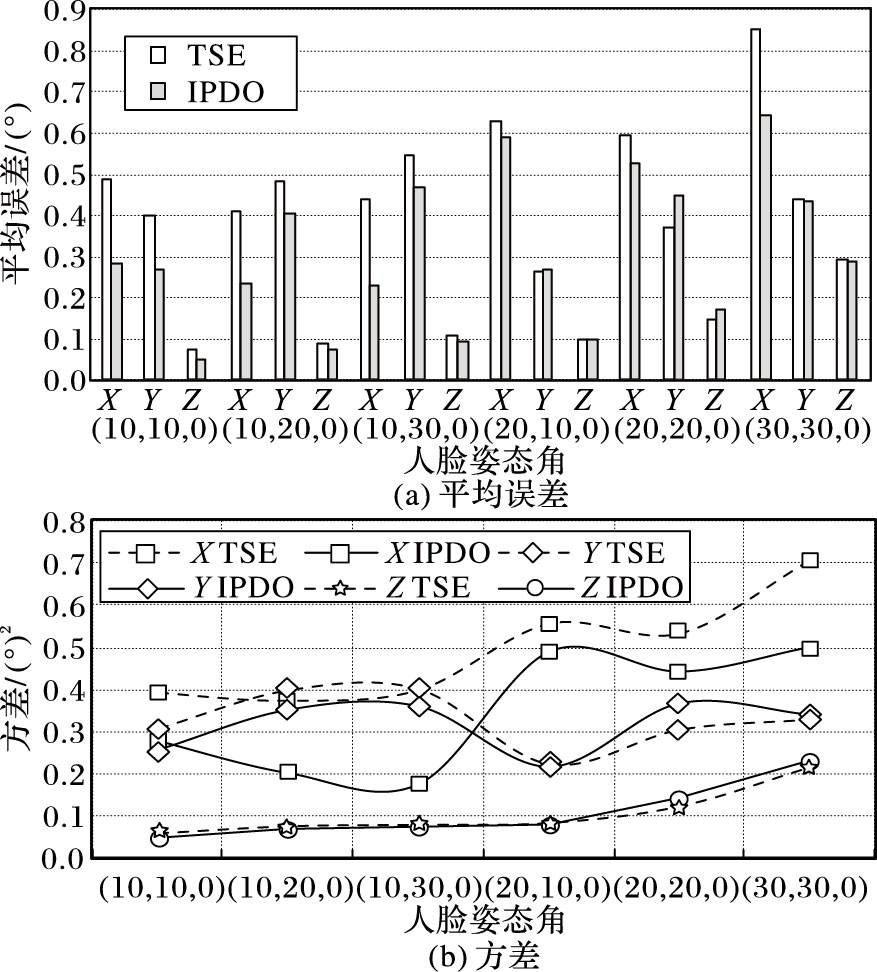
如1.2节所述,图像旋转角度估计会影响到深度值估计,进一步测试了TSE和IPDO在X、Y、Z三个方向上旋转角的估计误差,结果如图 3所示,可以看到由于IPDO进行了迭代,角度估计的平均误差和方差均小于TSE算法,从而也验证了迭代的有效性。
|
图 2 不同算法采用多张图像的深度估计误差 Figure 2 Comparison of depth estimation error of different methods by using multiple images |
| 表 3 算法运行时间(CPU 2.7 GHz,MEM 4 GB) Table 3 Time costs of different methods (CPU 2.7 GHz,MEM 4 GB) |
|
图 3 角度估计平均误差及方差 Figure 3 Angle estimation mean error and variance |
图 4展示了3组真实人脸照片的重建结果:分别来自公开库IMM_Face(Informatics and Mathematical Modelling Face)、FERET(The Facial Recognition Technology)[22]和BS(Bosphorus Database)[23]。左侧是输入的三维人脸照片,右侧是重建的三维人脸正面、侧面图,以及相应的几何模型。通过这些重建结果,可以看到本文算法能够还原出准确度高的人脸形状以及逼真的三维人脸模型。
另一方面,为了量化本文重建的三维人脸模型的精度,采用第2章的评价方案1,对BS数据库的纹理图像进行重建,并与该数据库的三维人脸模型进行深度图对比。基于深度图像的相似度对比结果如表 4,可以看到与平均模型、SRSD算法[24]、Heo等[25]的算法相比,本文IPDO+RBFs的重建结果相似度最高。

|
图 4 基于三维图像的三维人脸重建效果 Figure 4 3D face reconstruction results based on 3D images |
| 表 4 不同算法的深度图相似度比较 Table 4 Comparison of similarity of depth image with different methods |
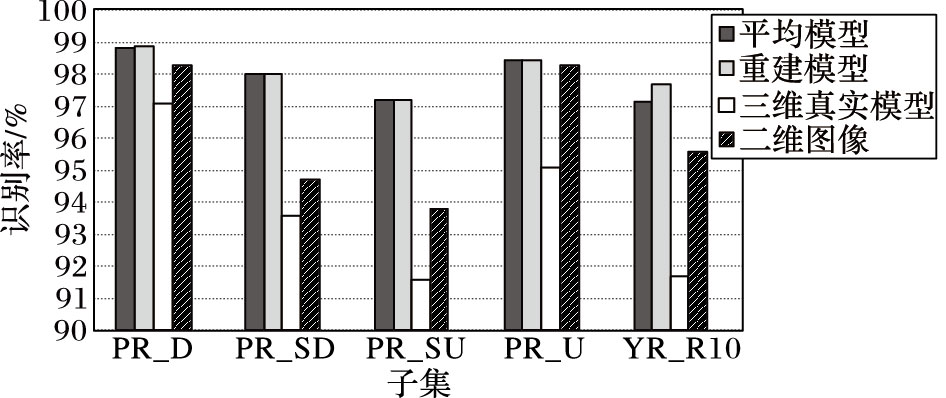
本节将采用第2章提出的评价方案2来验证三维人脸模型精度对人脸识别性能的影响。 实验数据采用BS人脸集的5个子集(PR_D、PR_SD、PR_SU、PR_U和YR_R10) ,子集的介绍请参考文献[23]。对于输入的二维图像,首先估计其旋转角,分别用3种三维模型(真实三维人脸模型、重建的人脸模型和平均人脸模型)按照根据该图像姿态进行投影,然后计算投影图像与二维图像之间的相似度,比较结果如图 5所示,结果表明重建的三维模型与平均模型的投影图与原始二维图像具有非常高的相似度,相反,真实的三维人脸投影相似度却反而低于重建的三维模型。这一实验结果表明,二维人脸识别更加注重图像外观特征,真实三维人脸虽然有很好的深度信息,但是纹理效果通常不如重建的人脸模型光滑。因存在毛刺或者不平滑现象而导致投影图与二维图像的相似度不高,这一结果表明:针对二维人脸识别应用,用于提供空间辅助信息的三维模型的准确性对于识别效果影响不大,纹理图像与对比图像的一致性更重要。
|
图 5 不同三维模型下二维图像之间相似度比较(BS数据库) Figure 5 Comparison of similarity of the captured 2D image and the projected image by using different 3D models (BS database) |
如第2章提出的评价方案3所述,为了验证重建的三维人脸模型对于大姿态角度变化下的人脸识别作用,本文对FERET数据库[22]中8个不同子集(分别是bb,bc,bd,be,bf,bg,bh,bi,角度从-60°到+60°之间变化)进行识别测试,特征提取算法采用LGXP[26]和LCM[20],分类采用最近邻,人脸图像尺寸归一化到64×64,采用传统基于瞳孔位置的尺度归一化方法,测试三种了Gallery构建方式下的人脸识别率。
1) 根据测试子集的角度,将重建的三维人脸模型进行投影,构建Gallery,用“3D-rec”表示;
2) 根据测试子集的角度,借助平均三维模型将正面图像合成相应角度的图像,构建Gallery,用“3D-avg”表示;
3) 直接采用正面人脸图像,用“2D”表示。
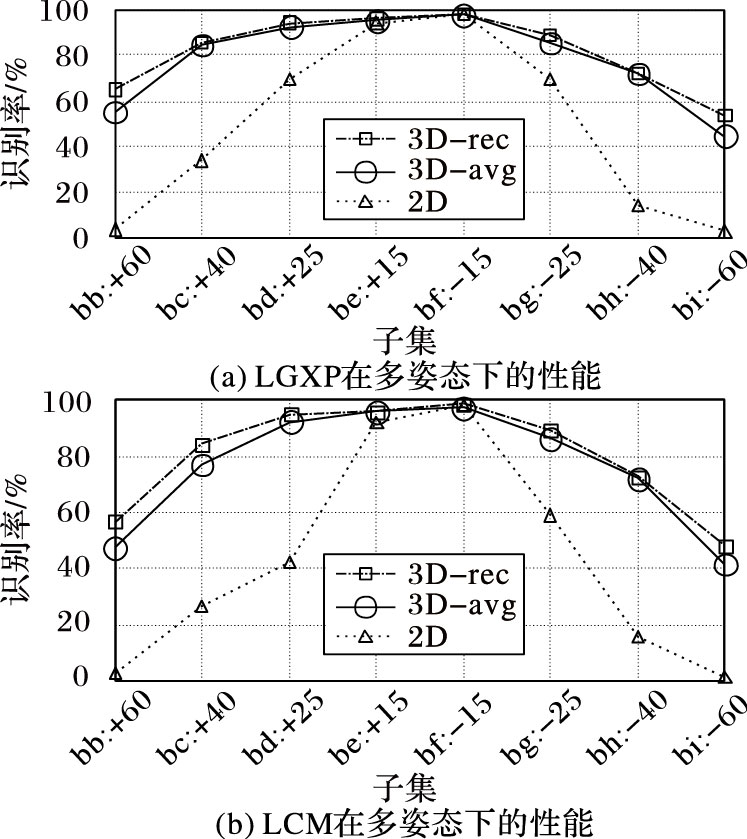
实验结果如图 6所示,可以看到曲线趋势有力地说明了利用三维模型相对直接采用正面图像可以大幅提高识别率,另一方面,采用重建的三维人脸相对直接使用平均人脸模型也可以提高识别率,这就验证了本文三维重建的有效性。图中表明LGXP和LCM在大角度情况下识别率并不高,主要原因如下。
|
图 6 基于三维模型的多姿态二维人脸识别率(FERET数据库) Figure 6 2D face recognition rate under multiple views with 3D models (FERET database) |
1) 简单地采用与正面图像一致的尺寸归一化方法,即将瞳孔间距归一化到相同尺度,通常对于正脸或者小姿态角的人脸图像有效,并不适用于对于大姿态角下的人脸匹配。
2) 仅采用特征提取和最近邻分类,未进行训练,导致鉴别性能不足。
以上两方面工作是跨姿态人脸识别研究的重点研究内容,而本文旨在验证三维信息对于姿态变化的有效性,故并未对以上两个问题进行深入研究。
4 结语本文主要研究基于图像实现人脸特征点深度值的精确计算,进而实现真实感的三维人脸建模,为人脸识别解决跨姿态问题奠定基础。基于图像的三维关键点重构分为姿态角估计及深度值估计两部分,二者相互影响。现有方法通常将其融合在一起统一计算导致深度值估计精度低,本文提出一个姿态及深度值迭代计算模型,实现了高精度的特征点深度值估计。进一步研究了多组深度值融合及整体形状建模。实验结果表明,重建的三维人脸形状接近真实模型,其投影图像与二维图像具有较高的相似度,验证了本文重建的三维人脸模型投影图像与二维图像具有较高的相似度,为下一步研究大姿态变化条件下人脸识别提供了有效手段。
| [1] | ROWDEN L B, BISHT S, KLONTZ J C, et al. Unconstrained face recognition:establishing baseline human performance via crowdsourcing[C]//Proceedings of the 2014 IEEE International Joint Conference on Biometrics. Piscataway, NJ:IEEE, 2014:1-8. |
| [2] | PHILLIPS P J, SCRUGGS W T, O'TOOLE A J, et al. FRVT 2006 and ICE 2006 large-scale experimental results[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32 (5) : 831-846. doi: 10.1109/TPAMI.2009.59 |
| [3] | MOHAMMADZADE H, HATZINAKOS D. Iterative closest normal point for 3D face recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35 (2) : 381-397. doi: 10.1109/TPAMI.2012.107 |
| [4] | YI D, LEI Z, LI S Z. Towards pose robust face recognition[C]//Proceedings of the 2013 IEEE International Conference on Computer Vision and Pattern Recognition. Piscataway, NJ:IEEE, 2013:3539-3545. |
| [5] | BLANZ V, VETTER T. A morphable model for the synthesis of 3D faces[C]//Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques. New York:ACM, 1999:187-194. |
| [6] | PATEL A, SMITH W A P. 3D morphable face models revisited[C]//Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ:IEEE, 2009:1327-1334. |
| [7] | WANG S, LAI S. Reconstructing 3D face model with associated expression deformation from a single face image via constructing a low-dimensional expression deformation manifold[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33 (10) : 2115-2121. doi: 10.1109/TPAMI.2011.88 |
| [8] | BUSTARD J D, NIXON M S. 3D morphable model construction for robust ear and face recognition[C]//Proceedings of the 2010 IEEE Conference Computer Vision and Pattern Recognition. Piscataway, NJ:IEEE, 2010:2582-2589. |
| [9] | 龚勋, 王国胤. 基于特征点的三维人脸形变模型[J]. 软件学报, 2009, 20 (3) : 724-733. ( GONG X, WANG G Y. 3D face deformable model based on feature points[J]. Journal of Software, 2009, 20 (3) : 724-733. ) |
| [10] | KEMELMACHER-SHLIZERMAN I, BASRI R. 3D face recon-struction from a single image using a single reference face shape[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33 (2) : 394-405. doi: 10.1109/TPAMI.2010.63 |
| [11] | KEMELMACHER-SHLIZERMAN I. Internet-based morphable model[C]//Proceedings of the 2013 IEEE International Conference on Computer Vision. Piscataway, NJ:IEEE, 2013:3256-3263. |
| [12] | SUWAJANAKORN S, KEMELMACHER-SHLIZERMAN I, SEITZ S. Total moving face reconstruction[C]//Proceedings of the 2014 European Conference on Computer Vision. Berlin:Springer, 2014:796-812. |
| [13] | LIN Y, MEDIONI G, CHOI J. Accurate 3D face reconstruction from weakly calibrated wide baseline images with profile contours[C]//Proceedings of the 2010 IEEE International Conference on Computer Vision and Pattern Recognition. Piscataway, NJ:IEEE, 2010:1490-1497. |
| [14] | GONZALEZ-MORA J, DE LA TORRE F, GUIL N, et al. Learning a generic 3D face model from 2D image databases using incremental structure from motion[J]. Image and Vision Computing, 2010, 28 (7) : 1117-1129. doi: 10.1016/j.imavis.2010.01.005 |
| [15] | GONG X, WANG G Y. Example-based learning for depth estimation of facial landmarks and its application in face modeling[J]. Chinese Journal of Electronics, 2010, 19 (4) : 676-680. |
| [16] | GONG X, WANG G Y, LI X X, et al. A statistical two-step method for 3D face reconstruction from single image[J]. Chinese Journal of Electronics, 2011, 20 (4) : 671-675. |
| [17] | KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of the 2013 IEEE International Conference on Neural Networks. Piscataway, NJ:IEEE, 1995:1942-1948. |
| [18] | KOO H, LAM K. Recovering the 3D shape and poses of face images based on the similarity transform[J]. Pattern Recognition Letters, 2008, 29 (6) : 712-723. doi: 10.1016/j.patrec.2007.11.018 |
| [19] | SUN Z, LAM K, GAO Q. Depth estimation of face images using the nonlinear least-squares model[J]. IEEE Transactions on Image Processing, 2013, 22 (1) : 17-30. doi: 10.1109/TIP.2012.2204269 |
| [20] | DE MARSICO M, NAPPI M, RICCIO D, et al. Robust face recognition for uncontrolled pose and illumination changes[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part A:Systems and Humans, 2013, 43 (1) : 149-163. doi: 10.1109/TSMCA.2012.2192427 |
| [21] | NORDSTROM M M, LARSEN M, SIERAKOWSKI J, et al. The IMM face database-an annotated dataset of 240 face images[R]. Copenhagen, Denmark:Technical University of Denmark, 2004. |
| [22] | PHILLIPS P J, WECHSLER H, HUANG J, et al. The FERET database and evaluation procedure for face-recognition algorithms[J]. Image and Vision Computing, 1998, 16 (5) : 295-306. doi: 10.1016/S0262-8856(97)00070-X |
| [23] | SAVRAN A, ALYUZ N, DIBEKLIOGLU H, et al. Bosphorus database for 3D face analysis[M]. Berlin: Springer, 2008 : 47 -56. |
| [24] | BLANZ V, MEHL A, VETTER T, et al. A statistical method for robust 3D surface reconstruction from sparse data[C]//Proceedings of the 2nd International Symposium on 3D Data Processing, Visualization. Washington, DC:IEEE Computer Society, 2004:293-300. |
| [25] | HEO J, SAVVIDES M. Rapid 3D face modeling using a frontal face and a profile face for accurate 2D pose synthesis[C]//Proceedings of the 2011 IEEE International Conference on Automatic Face & Gesture Recognition. Piscataway, NJ:IEEE, 2011:632-638. |
| [26] | XIE S, SHAN S, CHEN X, et al. Fusing local patterns of Gabor magnitude and phase for face recognition[J]. IEEE Transactions on Image Processing, 2010, 19 (5) : 1349-1361. doi: 10.1109/TIP.2010.2041397 |




