2. 电子工程学院 雷抗系, 合肥 230000
2. Department of Radar Countermeasures, Electronic Engineering Institute, Hefei Anhui 230000, China
线性调频(Linear Frequency Modulation,LFM)信号在通信、雷达、声呐等微波领域具有广泛的应用,其参数估计技术是电子侦察领域一个重要的研究课题[1-4]。
目前,LFM信号参数估计主要集中在调频率与中心频率这两个参数的研究,方法大致分为以下几类:极大似然(Maximum Likehood,ML)估计方法[5]、解线调(Dechirp)方法[6]、离散多项式变换(Discrete Polynomial Transform,DPT)[7-8]、时频分析与Rando(Hough)变换方法[9]、分数阶傅里叶变换(Fractional Fourier Transform,FrFT)方法[10-12]。从本质上讲,Dechirp方法与ML方法是等价的[13]。基于DPT的参数估计方法需要进行两次快速傅立叶变换(Fast Fourier Transform,FFT)并进行两次一维谱峰搜索,计算速度较快,但是受信噪比影响较大。基于时频分析(或模糊图)与Rando(或Hough)变换的方法利用LFM信号在时频域的直线特征,并借助Rando(Hough)变换的方法检测直线,提取信号参数。FrFT通过旋转频率空间,在特定阶次上聚集LFM信号的能量,从某种意义上等价于脉冲压缩。文献[10, 14]研究了基于FrFT的LFM信号调制参数与时延估计;文献[15]利用FrFT研究了LFM信号到达方向的高分辨估计问题;近年来,随着理论的发展,FrFT在LFM信号处理方面体现了特有的优势。
然而,电子侦察中的LFM信号参数估计问题更加棘手。信号到达时间、到达方向涉及到源定位问题[16-17];调频率、中心频率、脉冲宽度涉及到信号源识别问题[18]。因此,除调频率和中心频率外,侦察系统对信号到达时间、到达方向、脉冲宽度等参数也感兴趣。在多数情况下,调频率、中心频率、信号到达时间、脉冲宽度等参数在估计过程中是相互耦合的,并且受到接收机频率响应特性的影响,脉冲信号往往体现为不规则的“钟形”,这些问题都使得侦察系统中信号参数估计变得复杂。鉴于此,本文基于FrFT和部分相关,对LFM脉冲信号调频率、中心频率、到达时间、脉宽参数的估计问题进行了研究,并对参数估计误差进行分析。
1 LFM脉冲信号模型在电子侦察系统中,脉冲调制LFM信号模型可以表示为:
| $\begin{align} & x\left( t \right)=Ap\left( t-{{t}_{c}} \right)\exp \{j2\pi {{f}_{c}}\left( t-{{t}_{c}} \right)+ \\ & j\pi k{{(t-{{t}_{c}})}^{2}}\}+w\left( t \right) \\ \end{align}$ | (1) |
其中:A为脉冲幅度;tc为脉冲中心时刻; fc为中心频率;k为调频率;w(t)是0均值,方差为σ2的高斯噪声; p(·)为脉冲实包络。
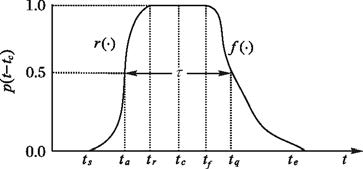
受接收机频率响应的影响,脉冲包络通常呈现为不规则的“钟形”。如图 1所示,r(·)、 f(·)为分别表示脉冲包络p(·)上升沿与下降沿的单调函数;ts为脉冲起始时刻;ta为脉冲上升到0.5的时刻(脉冲到达时刻);tr为脉冲幅度饱和时刻;tf为脉冲下降时刻;tq为脉冲下降到0.5的时刻;te为脉冲结束时刻。定义脉冲中心时刻tc=(ta+tq)/2,脉冲宽度τ=tq-ta。
|
图 1 脉冲实包络示意图 |
对于电子侦察系统,中心频率、调频率、脉宽参数有助于识别雷达,脉冲到达时间有助于实现目标的定位。因此,侦察系统感兴趣参数集$\xi ={{[{{f}_{c}},k,\tau ,{{t}_{a}}]}^{T}}$。
2 LFM脉冲全参数估计 2.1 调频率估计FrFT通过旋转时频平面实现对LFM信号的匹配处理,其最佳阶次FrFT的峰值信噪比等价于脉冲压缩,具有估计精度高、稳健性好等优点。信号s(t)的FrFT定义为:
| ${{X}_{s(t)}}\left( \alpha ,u \right)=\int{_{-\infty }^{-\infty }}s\left( t \right){{K}_{\alpha }}\left( u,t \right)\text{d}t$ | (2) |
其中:α为旋转角度;Kα(u,t)为变换核;u为变换后的频域。
对于给定LFM脉冲信号:
| $s\left( t \right)=\text{ }p\left( t \right)\text{exp}\left\{ j2\pi {{f}_{c}}t+j\pi k{{t}^{2}} \right\}$ | (3) |
其最佳变换阶次为α0=-arccot(k),FrFT的模表示为:
| $\begin{align} & |{{X}_{s(t)}}({{\alpha }_{0}},u)|= \\ & \sqrt{1+co{{t}^{2}}{{\alpha }_{0}}}~|\int{_{-\infty }^{+\infty }}p\left( t \right)\exp \{\text{j}2\pi ({{f}_{c}}-u~csc~{{\alpha }_{0}})t\}\text{d}t|\text{ } \\ \end{align}$ | (4) |
对应的谱峰位置:
| $\left\{ \begin{align} & {{\alpha }_{0}}=-\text{arc}\cot ~\left( k \right) \\ & {{u}_{0}}=\text{ }{{f}_{c}}\sin ~{{\alpha }_{0}} \\ \end{align} \right.$ | (5) |
在s(t)产生tc时延的情况下,二次相位调制率没有发生变化,最佳变换阶仍然为α0,FrFT的模表示为:
| $\begin{align} & |{{X}_{s(t-{{t}_{c}})}}({{\alpha }_{0}},u)|= \\ & \sqrt{1+{{\cot }^{2}}{{\alpha }_{0}}}|\int{_{-\infty }^{+\infty }}p(t-{{t}_{c}})\exp \left\{ \text{j}2\pi ({{f}_{c}}-k{{t}_{c}}-u\csc ~{{\alpha }_{0}})t \right\}\text{d}t|= \\ & \sqrt{1+{{\cot }^{2}}{{\alpha }_{0}}}|\int{_{-\infty }^{+\infty }}p\left( t \right)\exp \left\{ \text{j}2\pi ({{f}_{c}}-k{{t}_{c}}-u\csc ~{{\alpha }_{0}})t \right\}\text{d}t| \\ \end{align}$ | (6) |
对应的谱峰位置:
| $\left\{ \begin{align} & {{\alpha }_{0}}=-\text{arc}\cot \left( k \right) \\ & {{u}_{0}}=\sin ~{{\alpha }_{0}}({{f}_{c}}-k{{t}_{c}}) \\ \end{align} \right.$ | (7) |
式(5)和式(7)表明:在无时延条件下,LFM脉冲信号调频率和中心频率可直接通过FrFT的谱峰位置进行估计;在存在时延条件下,LFM脉冲信号的调频率依然可以通过FrFT的谱峰位置进行估计,而中心频率不能通过谱峰位置直接进行估计,因为,谱峰的位置受到调频率、中心频率和时延的共同调制。但是,在该条件下依然可以通过谱峰位置获得信号的时频关系。即无论信号是否存在时间延迟,FrFT均可以对LFM信号的调频率与时频关系进行估计,估计子为:
| $\begin{align} & \hat{k}=-\cot ({{\alpha }_{0}}) \\ & f=\hat{k}t+{{u}_{0}}\csc {{\alpha }_{0}} \\ \end{align}$ | (8) |
其中:第一个分式表征了LFM信号的调频率参数;第二个分式表征了LFM信号的时频关系。
2.2 调频率估计传统的脉冲到达时间估计通过检测脉冲的上升沿或上升沿斜率实现,一般要对脉冲幅度进行估计并且易受噪声影响,误差较大。2.1节对信号的调频率与时频关系进行了估计,因此,可先对信号进行相干积累提升信噪比,然后利用局部自相关[17]对脉冲其他参数进行估计,本文称之为部分相关方法,该方法无需对脉冲幅度进行估计且稳健性好于脉冲上升沿检测方法。
取部分积累脉宽τ0(一般不超过脉冲饱和时间长度),对LFM脉冲信号作相干积累,积累表达式如下:
| $\begin{align} & h(y)=|\int{_{y-\tau 0/2}^{y+\tau 0/2}}s(t-{{t}_{c}})\exp \{-2\text{j}\pi (\hat{k}y+ \\ & {{u}_{0}}\csc {{\alpha }_{0}})t-\text{j}\pi \hat{k}{{t}^{2}}\text{ }\!\!\}\!\!\text{ d}t| \\ \end{align}$ | (9) |
在忽略估计误差的条件下,信号s(t)的相位项被完全补偿,因此式(9)可理解为中心为y、脉宽为τ0的单位脉冲与信号包络p(t-tc)重叠的面积,因此
| $h\left( y \right)=\int{_{y-{{\tau }_{0}}/2}^{^{y+{{\tau }_{0}}/2}}}Ap(t-{{t}_{c}})\text{d}t$ | (10) |
记$P\left( x \right)\int{_{-\infty }^{x}}P\left( t \right)\text{d}t$,则h(y)表示为:
| $h\left( y \right)=A\left( P\left( y+\frac{{{\tau }_{0}}}{2}-{{t}_{c}} \right)-P\left( y-\frac{{{\tau }_{0}}}{2}-{{t}_{c}} \right) \right)$ | (11) |
将式(11)在y-tc处进行1阶泰勒展开:
| $\begin{align} & h\left( y \right)=A(P(y-{{t}_{c}})+\frac{{{\tau }_{0}}p(y-{{t}_{c}})}{2}+{{o}_{1}}({{\tau }^{2}}_{0})- \\ & P(y-{{t}_{c}})+\frac{{{\tau }_{0}}p(y-{{t}_{c}})}{2}-{{o}_{2}}(\tau _{0}^{2}))= \\ & A({{\tau }_{0}}p(y-{{t}_{c}})+{{o}_{1}}({{\tau }^{2}}_{0})-{{o}_{2}}({{\tau }^{2}}_{0})) \\ \end{align}$ | (12) |
其中:o1(·)、o2(·)为高阶项。通常情况下,“钟形”脉冲的上升沿与下降沿都是短暂的并且近似直线(高阶导数很小),除去上升沿与下降沿脉冲幅度为恒定值,因此高阶项可忽略,当y=ta时,有
| $h({{t}_{a}})\approx A{{\tau }_{0}}p({{t}_{a}}-{{t}_{c}})=A{{\tau }_{0}}/2$ | (13) |
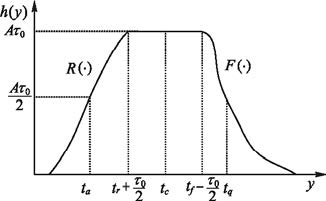
同理,可计算h(tq)≈Aτ0/2。图 2给出了积累曲线h(y)示意图,R(·)、F(·)为由脉冲上升沿和下降沿所确定的单调函数。
|
图 2 部分积累曲线 |
记h(y)的相关函数为C(z):
| $C\left( z \right)=\int{_{-\infty }^{+\infty }}h\left( 2z-y \right)h\left( y \right)\text{d}y$ | (14) |
如果R(·)、F(·)严格关于tc对称,则C(z)的最大值在z=tc处取得;如果R(·)、F(·)非严格对称,则C(z)的最大值在z=tc+Δt处取得,Δt取决于R(·),F(·)的函数形式。记估计量${{{\hat{t}}}_{c}}$:
| ${{{\hat{t}}}_{c}}=\arg \text{ }\underset{z}{\mathop{\max }}\,\left\{ C\left( z \right) \right\}$ | (15) |
对h(y)进行包络分割,提取h(y)的左半部分h-(y),其部分自相关为C-(z):
| ${{C}^{-}}\left( z \right)=\int{_{-\infty }^{+\infty }}{{h}^{-}}\left( z-y \right){{h}^{-}}\left( y \right)\text{d}y$ | (16) |
其中:
${{h}^{-}}\left( y \right)=\left\{ \begin{align} & h\left( y \right), y\le {{{\hat{t}}}_{c}} \\ & 0, y>{{{\hat{t}}}_{c}} \\ \end{align} \right.$
因为h-(y)单调不减,因此C-(z)的最大值在$z\in \left[ 2{{t}_{r}}+{{\tau }_{0}}+{{{\hat{t}}}_{c}}+{{t}_{r}}+{{\tau }_{0}}/2 \right]$内取得:
| $\begin{align} & {{C}^{-}}\left( z \right)={{(A{{\tau }_{0}})}^{2}}(z-2{{t}_{r}}-{{\tau }_{0}})+ \\ & 2A{{\tau }_{0}}\int{_{_{z-{{t}_{c}}}}^{{{t}_{r}}+{{\tau }_{0}}2}}R\left( y \right)\text{d}y \\ \end{align}$ | (17) |
对自变量求微分并令其等于0,得
| $\frac{\text{d}{{C}^{-}}_{i}\left( z \right)}{\text{d}z}={{(A{{\tau }_{0}})}^{2}}-2A{{\tau }_{0}}R(z-{{{\hat{t}}}_{c}})=0$ | (18) |
式(18)表明,$R(z-{{{\hat{t}}}_{c}})=A{{\tau }_{0}}/2$处取得最大值,即$z={{{\hat{t}}}_{c}}+{{t}_{a}}$。
以上分析表明,无论信号s(t)的上升沿与下降沿具有什么样的函数形式,只要h-(y)单调不减,${{{\hat{t}}}_{c}}\in \left[ {{t}_{r}}\text{+}{{\tau }_{0}}/2{{t}_{f}}-{{\tau }_{0}}/2 \right]$,脉冲到达时间的估计子由式(19)确定:
| $\left\{ \begin{align} & {{z}_{1}}=\underset{z}{\mathop{\arg \text{ max}}}\,\{{{C}^{-}}\left( z \right)\} \\ & {{z}_{2}}=\underset{z}{\mathop{\arg \text{ max}}}\,\left\{ C\left( z \right) \right\} \\ & {{{\hat{t}}}_{a}}={{z}_{1}}-{{z}_{2}} \\ \end{align} \right.$ | (19) |
与脉冲到达时间估计类似,提取h(y)的右半部分h+(y),并将其部分自相关表示为C+(z):
| ${{C}^{+}}\left( z \right)=\int{_{_{-\infty }}^{+\infty }}{{h}^{+}}\left( z-y \right){{h}^{+}}\left( y \right)\text{d}y$ | (20) |
其中:
| ${{h}^{+}}\left( y \right)=\left\{ \begin{align} & 0, y\le {{{\hat{t}}}_{c}} \\ & h\left( y \right),\text{ }y>{{{\hat{t}}}_{c}} \\ \end{align} \right.$ | (21) |
同理,C+(z)在$F\left( z-{{{\hat{t}}}_{c}} \right)=A{{\tau }_{0}}/2$处取得最大值,因此脉宽与中心频率估计子由式(22)确定:
| $\begin{align} & {{z}_{1}}=\underset{z}{\mathop{\arg \text{ max}}}\,\left\{ {{C}^{-}}(z) \right\} \\ & {{z}_{3}}=\underset{z}{\mathop{\arg \text{ max}}}\,\left\{ {{C}^{+}}(z) \right\} \\ & \hat{\tau }={{z}_{3}}-{{z}_{1}} \\ & {{{\hat{f}}}_{^{c}}}=\frac{\hat{k}({{z}_{3}}+{{z}_{1}}-2{{{\hat{t}}}_{c}})}{2}+{{u}_{0}}{{\csc }_{0}}{{\alpha }_{0}} \\ \end{align}$ | (22) |
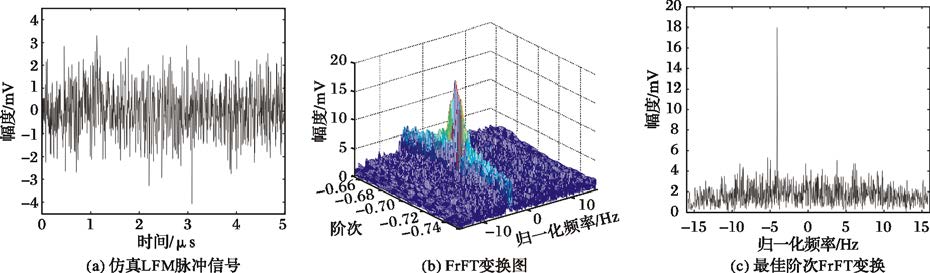
图 3(a)仿真幅度为1.0mV,中心时刻为4μs的LFM脉冲信号,中心频率设置10MHz,调频率设置5.0MHz/μs,噪声方差为1.0,对应信噪比0dB,采样率设置100MHz,脉冲包络为梯形,具体函数如式(23),式中时间单位为μs;图 3(b)给出FrFT时频图,图 3(c)给出了最佳阶次FrFT模值曲线。
| ${{p}_{1}}\left( t \right)=\text{ }\left\{ \begin{align} & 2t+5.5, -2.75\le t<-2.25 \\ & 1, -2.25\le t\le 2 \\ & -t+3, 2<t\le 3 \\ \end{align} \right.$ | (23) |
|
图 3 LFM脉冲信号及FrFT示意图 |
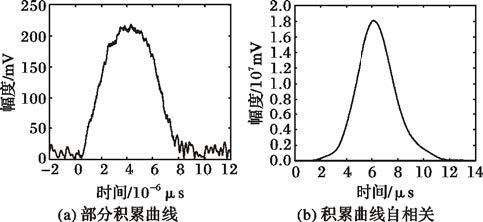
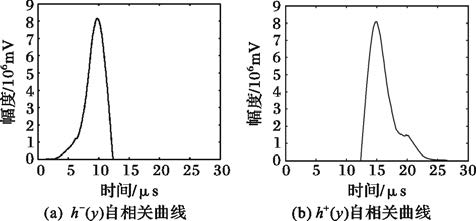
通常LFM脉冲信号的持续时间大于5μs,并且上升沿与下降沿时间非常短,取τ0=2μs。图 4为脉冲部分积累曲线及其对应的自相关函数,图 5为其积累曲线左半部分与右半部分的自相关函数曲线。表 1列出了参数集的估计值与真实值以作对比。
|
图 4 梯形包络部分积累 |
|
图 5 梯形包络分割自相关曲线 |
| 表 1 梯形包络脉冲参数估计与真实值对比 |
分析以上数据可知:在信噪比为0dB时,从时域几乎无法观察出脉冲包络,FrFT方法仍能够较为准确地估计信号的调频率。部分积累曲线的自相关函数较为平滑并且峰值明显,有利于参数集的估计。
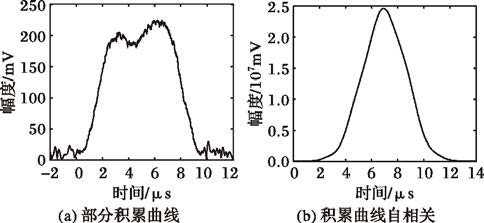
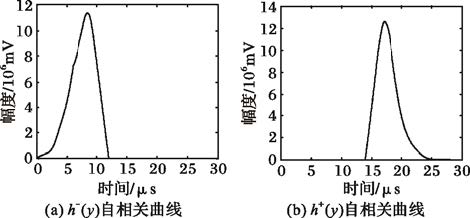
3.2 梯形包络参数估计仿真为研究更复杂的情况,调整脉冲包络的函数形式,设置脉冲上升沿与下降沿为余弦函数形式,脉冲包络函数如式(24),调制参数不变。图 6为脉冲部分积累曲线以及对应的自相关函数,图 7为积累曲线左半部分与右半部分的自相关函数曲线。表 2列出了参数集的估计值与真实值以作对比。
|
图 6 余弦型包络局部积累 |
|
图 7 余弦型包络分割自相关 |
| 表 2 余弦型脉冲参数估计与真实值对比 |
| ${{p}_{2}}\left( t \right)=\left\{ \begin{align} & \sin {{c}^{2}}\left( \frac{t+3}{0.9} \right), -3.9\le t<-2.5 \\ & 1, -2.5\le t\le 3 \\ & {{\cos }^{2}}\left( \frac{\left( t-3 \right)\pi }{1.6} \right), 3<t\le 3.8 \\ \end{align} \right.$ | (24) |
分析以上数据可知:虽然脉冲包络形式发生了变化,本文方法仍然能够较为准确地估计脉冲参数,表明该方法对上升沿与下降沿函数形式具有一定的稳健性。接下来主要对估计误差进行分析。
4 误差分析 4.1 信噪比对估计精度的影响首先推导信号参数估计的克拉美劳下界(Cramer Rao Low Bound,CRLB)[19-20]。记观测信号的离散形式:
| $\begin{align} & x\left[ n \right]=Ap(n-{{n}_{0}})\exp \{\text{j}2\pi {{f}_{c}}(n-{{n}_{c}})+ \\ & \text{j}\pi k{{(n-{{n}_{c}})}^{2}}\}+w\left[ n \right]= \\ & {{s}_{0}}\left[ n \right]+w\left[ n \right] \\ \end{align}$ | (25) |
则Fisher信息阵I(ξ)的对角元素:
| $\begin{align} & I{{\left( \xi \right)}_{11}}=\frac{{{\sigma }^{2}}}{4{{\pi }^{2}}{{A}^{2}}\sum\limits_{n=0}^{N-1}{{{\left( n-{{n}_{c}} \right)}^{2}}{{p}^{2}}\left[ n-{{n}_{c}} \right]}}=\frac{1}{4{{\pi }^{2}}SNR\sum\limits_{n=-{{n}_{c}}}^{L-1-{{n}_{c}}}{{{n}^{2}}{{p}^{2}}\left[ n \right]}} \\ & I{{\left( \xi \right)}_{22}}=\frac{{{\sigma }^{2}}}{{{\pi }^{2}}{{A}^{2}}\sum\limits_{n=0}^{N-1}{{{\left( n-{{n}_{c}} \right)}^{4}}{{p}^{2}}\left[ n-{{n}_{c}} \right]}}=\frac{1}{{{\pi }^{2}}SNR\sum\limits_{n=-{{n}_{c}}}^{N-1-{{n}_{c}}}{{{p}^{2}}\left[ n \right]}} \\ & I{{\left( \xi \right)}_{33}}=\frac{{{\sigma }^{2}}}{{{\sum\limits_{n=0}^{N-1}{\left| \frac{\partial {{s}_{0}}\left[ n \right]}{\partial {{n}_{a}}} \right|}}^{2}}}=\frac{{{\sigma }^{2}}}{{{f}_{s}}{{\int{_{0}^{{{T}_{s}}}\left| \frac{\partial {{s}_{0}}\left[ t \right]}{\partial t} \right|}}^{2}}\text{d}t}=\frac{{{\sigma }^{2}}}{\sigma _{f}^{2}{{f}_{s}}{{\int{_{0}^{{{T}_{s}}}\left| {{s}_{0}}\left( t \right) \right|}}^{2}}\text{d}t}=\frac{{{\sigma }^{2}}}{\sigma _{f}^{2}{{A}^{2}}\sum\limits_{n=-{{n}_{c}}}^{N-1-{{n}_{c}}}{{{p}^{2}}\left[ n \right]}}=\frac{1}{\sigma _{f}^{2}SNR\sum\limits_{n=-{{n}_{c}}}^{N-1-{{n}_{c}}}{{{p}^{2}}\left[ n \right]}} \\ & I{{\left( \xi \right)}_{44}}=\frac{{{\sigma }^{2}}}{\sum\limits_{n=0}^{N-1}{{{\left| \frac{\partial {{s}_{0}}\left[ n \right]}{\partial \tau } \right|}^{2}}}}=\frac{{{\sigma }^{2}}}{{{A}^{2}}\sum\limits_{n}{\left( {{\left( \frac{\partial r\left[ n \right]}{\partial n} \right)}^{2}}+{{\left( \frac{\partial f\left[ n \right]}{\partial n} \right)}^{2}} \right)}}=\frac{1}{SNR\sum\limits_{n}{\left( {{\left( \frac{\partial r\left[ n \right]}{\partial n} \right)}^{2}}+{{\left( \frac{\partial f\left[ n \right]}{\partial n} \right)}^{2}} \right)}} \\ \end{align}$ | (26) |
其中:SNR表示信噪比;Ts为信号持续时间;N为采样点数;σf2为信号的均方带宽。
${{\sigma }^{2}}_{f}=\frac{\int{_{0}^{{{T}_{s}}}}{{\left| \frac{\partial {{s}_{0}}\left( t \right)}{\partial t} \right|}^{2}}\text{d}t}{\int{_{0}^{{{T}_{s}}}}{{\left| {{s}_{0}}\left( t \right) \right|}^{2}}\text{d}t}$
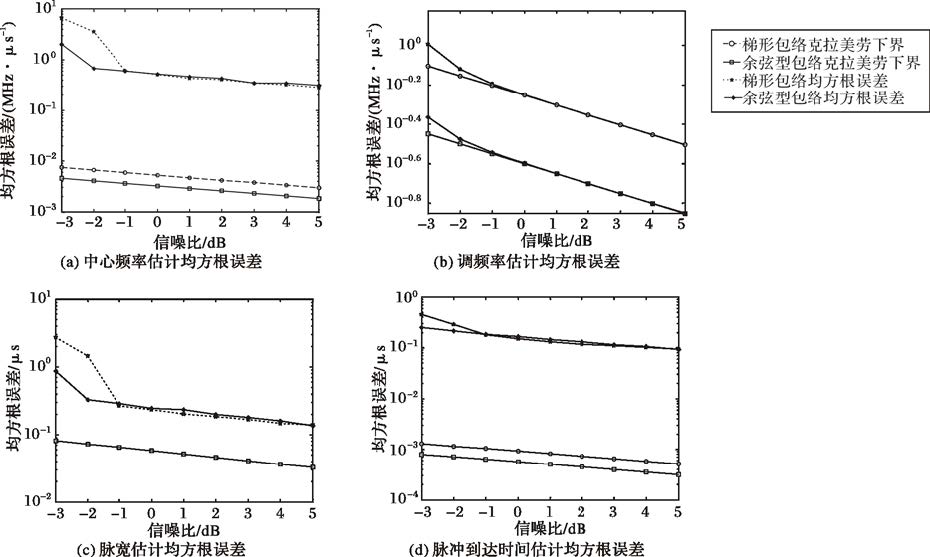
以上分析表明,信号参数估计的CRLB受到信噪比、信号带宽和信号包络的共同影响。图 8绘制了不同信噪比条件下估计参数的均方根误差曲线(500次蒙特卡罗实验)。
|
图 8 不同信噪比条件下参数估计均方根误差曲线 |
观察各参数估计误差曲线,调频率估计值均方根误差几乎达到CRLB,与文献[10]精度基本一致;中心频率估计值均方根误差约在10-1MHz数量级,文献[10]中约10-2MHz数量级;脉冲到达时间估计值均方根误差约在10-1μs数量级,与文献[14]相差约0.5μs;脉冲宽度估计值均方根误差约在10-1μs数量级。除调频率参数外,其他参数的估计误差均与CRLB(文献[10, 14]精度)存在一定距离,其本质原因有二:其一,各参数估计是存在相关性的,文献[10, 14]均是在假定部分基带参数(或部分调制参数)已知的条件下进行估计的,而本文中假定无任何调制参数、基带参数的先验信息,信息量更少,因此参数估计的精度略低一些;其二,调频率估计时FrFT对全脉冲进行相干积累,而其他参数估计仅仅对τ0时间长度进行了部分积累,因此估计误差大于CRLB。
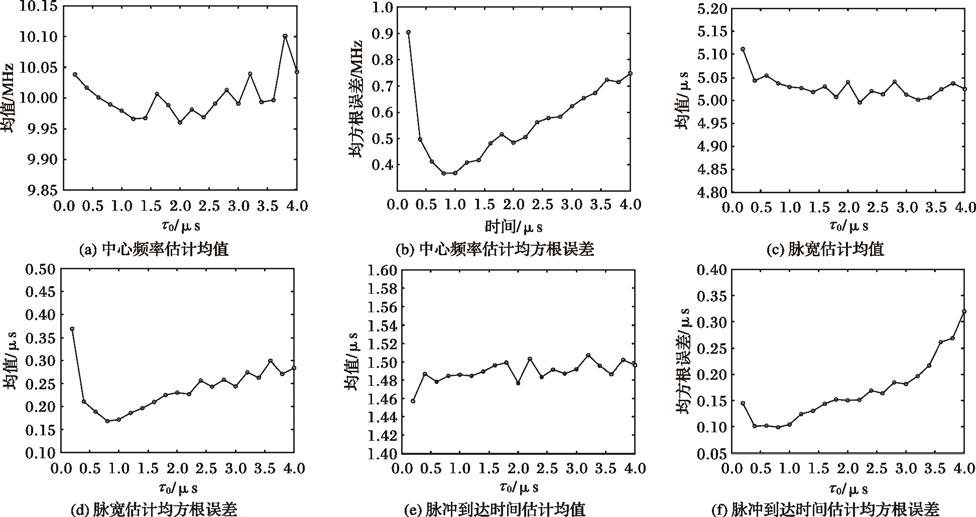
4.2 τ0对参数估计精度的影响积累脉宽τ0对参数估计精度会产生影响。当τ0过小时,局部积累函数的输出信噪比过低,导致参数估计稳健性降低;当τ0过大时,虽然局部积累函数的输出信噪比提高,但是积累函数可能发生畸变,同样不利于参数估计。以梯形脉冲包络为例,图 9绘制了0dB信噪比条件下,不同τ0值对参数估计的影响。
|
图 9 τ0对参数估计精度的影响 |
从图 9可看出:各参数估计的均值在真实值邻域内浮动,τ0的变化对估计均值影响不大。相对于均值曲线,误差均方根误差曲线要复杂一些。在τ0较小时,均方根误差随τ0的增大而减小;而当τ0超过一定值时,均方根误差随着τ0的增大呈上升趋势。接下来主要对均方根误差曲线进行分析。
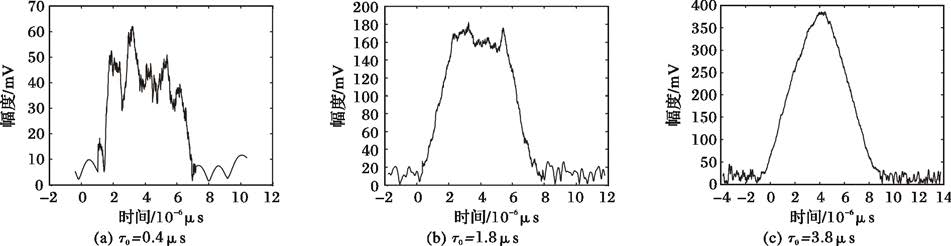
图 10为τ0不同取值时的部分积累曲线。分析图中数据,发现导致参数均方根误差随τ0的增大,出现先减小后增大的原因有二:其一,在τ0较小时,积累函数的信噪比较低,τ0的增加使得输出信噪比提高,进而使得参数均方根误差减小;而当τ0继续增大时,虽然输出信噪比增加,但是积累函数的最大平坦区间[ta+τ0/2,tf-τ0/2]长度急剧减小,上升段与下降段拖长,导致积累函数形状发生畸变,对参数估计产生不利因素。其二,在τ0较小时,积累函数的最大平坦值max{h(y)}≈Aτ0fs(fs为采样率),符合式(11)的理论推导;而τ0较大时,积累函数的最大平坦值max{h(y)}<Aτ0fs,与理论推导略有差异,这是计算机在积分过程中的累积误差引起的。鉴于此,参数均方根误差随着τ0的增大,出现先减小后增大的原因可以归结为:在τ0较小时,τ0的增大有利于提高积累函数的输出信噪比,对参数估计是有益的;当τ0增大到一定程度时,积累函数的畸变以及计算机累积误差将抵消信噪比的提升所带来的贡献,对参数估计式不利的。仿真研究发现,为获得高精度的参数估计,取τ0为实际脉冲持续时间的1/5~1/3较为合适。
|
图 10 不同τ0对应的部分积累曲线 |
与以往LFM信号调频率估计和中心频率估计不同,本文着眼于LFM脉冲信号的侦察问题,在信号包络不确知的条件下,对调频率、中心频率、信号到达时间、脉宽这一整套参数进行估计。基于FrFT与局部积累,推导了调频率、中心频率、信号到达时间、脉宽估计子,分析了信噪比和积累脉宽对参数估计误差的影响,给出了积累脉宽的选取范围。后续将研究积累脉宽的自适应选取问题。
| [1] |
ZAUGG E C, LONG D G. Generalized frequency scaling and backprojection for LFM-CW SAR processing[J].
IEEE Transactions on Geoscience and Remote Sensing, 2015, 53 (7) : 3600-3614.
doi: 10.1109/TGRS.2014.2380154 ( 0) 0)
|
| [2] |
GONG S, WEI X, LI X, et al. Mathematic principle of active jamming against wideband LFM radar[J].
Journal of Systems Engineering and Electronics, 2015, 26 (1) : 50-60.
doi: 10.1109/JSEE.2015.00008 ( 0) 0)
|
| [3] |
NGUYEN V K, TURLEY M D E. Bandwidth extrapolation of LFM signals for narrowband radar systems[J].
IEEE Transactions on Aerospace and Electronic Systems, 2015, 51 (1) : 702-712.
doi: 10.1109/TAES.2014.130525 ( 0) 0)
|
| [4] |
BOUCHIKHI A, BOUDRAA A O, CEXUS J C, et al. Analysis of multicomponent LFM signals by Teager Huang-Hough transform[J].
IEEE Transactions on Aerospace and Electronic Systems, 2014, 50 (2) : 1222-1233.
doi: 10.1109/TAES.2014.120202 ( 0) 0)
|
| [5] |
PELEG S, PORAT B. Linear FM signal parameter estimation from discrete-time observations[J].
IEEE Transactions on Aerospace and Electronic Systems, 1991, 27 (4) : 607-616.
doi: 10.1109/7.85033 ( 0) 0)
|
| [6] |
XIA X G. Discrete chirp-Fourier transform and its application to chirp rate estimation[J].
IEEE Transactions on Signal Processing, 2000, 48 (11) : 3122-3133.
doi: 10.1109/78.875469 ( 0) 0)
|
| [7] |
PELEG S, FRIEDLANDER B. Multicomponent signal analysis using the polynomial-phase transform[J].
IEEE Transactions on Aerospace and Electronic Systems, 1996, 32 (1) : 378-387.
doi: 10.1109/7.481277 ( 0) 0)
|
| [8] |
庞存锁. 基于离散多项式相位变换和分数阶傅里叶变换的加速目标检测算法[J].
电子学报, 2012, 40 (1) : 184-188.
( PANG C S. An accelerating target detection algorithm based on DPT and fractional Fourier transform[J].
Acta Electronica Sinica, 2012, 40 (1) : 184-188.
) ( 0) 0)
|
| [9] |
ZHANG Z, LUO M. New integral transforms for generalizing the Wigner distribution and ambiguity function[J].
IEEE Signal Processing Letters, 2015, 22 (4) : 460-464.
doi: 10.1109/LSP.2014.2362616 ( 0) 0)
|
| [10] |
QI L, TAO R, ZHOU S, et al. Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform[J].
Science in China Series F: Information Sciences, 2004, 47 (2) : 184-198.
doi: 10.1360/02yf0456 ( 0) 0)
|
| [11] |
COWELL D M J, FREEAR S. Separation of overlapping Linear Frequency Modulated (LFM) signals using the fractional Fourier transform[J].
IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2010, 57 (10) : 2324-2333.
doi: 10.1109/TUFFC.2010.1693 ( 0) 0)
|
| [12] |
罗蓬, 刘开华, 黄翔东, 等. 高精度 LFM 信号参数估计的谱校正方法[J].
系统工程与电子技术, 2011, 33 (6) : 1237-1242.
( LUO P, LIU K H, HUANG X D, et al. High-accuracy parameter estimation for LFM signals based on spectrum correction[J].
Systems Engineering and Electronics, 2011, 33 (6) : 1237-1242.
) ( 0) 0)
|
| [13] |
李文臣, 王雪松, 刘佳琪, 等. 线性调频参数估计方法的数学统一[J].
信号处理, 2009, 25 (8) : 1292-1297.
( LI W C, WANG X S, LIU J Q, et al. Mathematical unification of LFM parameters estimation methods[J].
Signal Processing, 2009, 25 (8) : 1292-1297.
) ( 0) 0)
|
| [14] |
TAO R, LI X M, LI Y L, et al. Time-delay estimation of chirp signals in the fractional Fourier domain[J].
IEEE Transactions on Signal Processing, 2009, 57 (7) : 2852-2855.
doi: 10.1109/TSP.2009.2020028 ( 0) 0)
|
| [15] |
杨小明, 陶然. 基于分数阶傅里叶变换的线性调频信号二维波达方向估计[J].
电子学报, 2008, 36 (9) : 1737-1740.
( YANG X M, TAO R. 2-D DOA Estimation of LFM signals based on fractional Fourier transform[J].
Acta Electronica Sinica, 2008, 36 (9) : 1737-1740.
) ( 0) 0)
|
| [16] |
YU J, ZHANG L, LIU K. Coherently distributed wideband LFM source localization[J].
IEEE Signal Processing Letters, 2015, 22 (4) : 504-508.
doi: 10.1109/LSP.2014.2363843 ( 0) 0)
|
| [17] |
CHAN Y T, LEE B H, INKOL R, et al. Estimation of pulse parameters by autoconvolution and least squares[J].
IEEE Transactions on Aerospace and Electronic Systems, 2010, 46 (1) : 363-374.
doi: 10.1109/TAES.2010.5417168 ( 0) 0)
|
| [18] |
ZHANG X D, SHI Y, BAO Z. A new feature vector using selected bispectra for signal classification with application in radar target recognition[J].
IEEE Transactions on Signal Processing, 2001, 49 (9) : 1875-1885.
doi: 10.1109/78.942617 ( 0) 0)
|
| [19] |
PELEG S, PORAT B. The Cramer-Rao lower bound for signals with constant amplitude and polynomial phase[J].
IEEE Transactions on Signal Processing, 1991, 39 (3) : 749-752.
doi: 10.1109/78.80864 ( 0) 0)
|
| [20] |
RISTIC B, BOASHASH B. Comments on "the Cramer-Rao lower bounds for signals with constant amplitude and polynomial phase"[J].
IEEE Transactions on Signal Processing, 1998, 46 (6) : 1708-1709.
doi: 10.1109/78.678501 ( 0) 0)
|




