2. 江苏省网络监控中心(南京信息工程大学), 南京 210044 ;
3. 计算机软件新技术国家重点实验室(南京大学), 南京 210023
2. Jiangsu Engineering Center of Network Monitoring (Nanjing University of Information Science and Technology), Nanjing Jiangsu 210044, China ;
3. State Key Laboratory for Novel Software Technology (Nanjing University), Nanjing Jiangsu 210023, China
随着云计算的发展、大数据时代的到来,云业务量呈指数级增长,云数据中心负载日益增加。云计算环境下的资源包括计算资源(CPU)、内存资源(RAM)、网络资源(带宽)、存储资源等,云计算资源分配问题实质上是解决大规模、多任务虚拟机资源分配、部署的问题。传统的分配方法必然会造成很多问题包括资源浪费、能源浪费、时间浪费等。
云计算平台通过对多种资源在云端进行整合,实现了对资源的统一管理和调度,并且依赖虚拟机节点执行各项任务[1]。因此云平台的资源分配需要根据当前各个虚拟机节点的资源需求,对资源进行合理的分配。主要注重资源分配的公平性和资源利用率的提高,前者充分保证了在资源有限的条件下,各虚拟机节点利益最大化,并且不会对其他节点造成不良影响;后者确保资源能够最大限度被利用,这也是云服务商追寻的目标之一,资源利用率的提高有助于节省成本、提高效率和服务质量。因此,如何更好地解决这两个问题是提高云数据中心整体性能的关键,具有很重要的理论和应用价值。
在已有的多资源公平分配的研究成果中,占优资源公平分配(Dominant Resource Fairness allocation,DRF)[2]、异构环境下的占优资源公平分配(DRF in Heterogeneous Cloud,DRFH)[3]和异构云计算体系结构下基于占优资源的多资源联合公平(Maximizing multi-resource Fairness based on Dominant Resource,MDRF)分配算法[4],都是基于“优势份额(Dominant Share)”的多资源公平分配算法,并且同时考虑分配的公平性和资源利用率,通过方法优化得到问题的最优解或近似最优解。DRF算法主要是在单个服务器上实现多资源的分配;DRFH算法将DRF的单服务器情况扩展到了多服务器情况,但资源利用率不高;MDRF算法在上述两个算法的基础上进行了优化,提高了系统的资源利用率,解决了具有相同优势资源用户的操作问题,但整个过程需遍历全局,略显复杂。
近年来,研究者们提出了各种各样的有关公平性的概念,如特殊应用的分配[5-6]、常用的公平性规则[7-8]、多资源公平性度量模型[9-11]等。目前,公平性评估方法主要通过构建评估函数来实现,而公平性评估方法对分配算法的选择、性能都具有重要的意义。文献[9]提出了基于5条基本公理的资源分配策略,并构建了基于单一资源的分配公平性评估框架,对特殊案例进行了分析验证,包括α-fairness[12]、 Jains index[13]、entropy、 Properties of fairness等;文献[10]在文献[9]的基础上结合DRF的核心思想,提出了一种基于Dominant Share的公平性统一度量框架,为多资源分配算法提供了定量的评估方法;文献[11]又在文献[10]的基础上提出一种适合于云计算的资源动态分配度量方法——DFE(Dynamic Fairness Evaluation),为动态资源公平分配算法的确定提供定量的依据。
本文在分析MDRF算法、公平性度量模型中影响资源利用率和公平性因素的基础上提出了多资源公平分配方法(Global Dominant Resource Fair allocation algorithm,GDRF)。该方法主要采用两步走的多轮分配方式,即先用最大最小公平思想及相关优先级参数确定每轮的分配名额,再根据全局优势资源共享比和全局优势资源权重的情况选定最优先分配用户进行具体分配。在分配时注重资源间的匹配度,使分配更合理化,整个过程注重公平性,具体的分配过程采用渐进填充方式,以资源利用率和公平性的提高为目标,作出最优的分配选择。
1 云数据中心建模和公平性分析在本文研究的云环境问题中,用户提交任务请求,然后由虚拟机来响应任务,最后由调度中心分配虚拟机到物理机完成各种服务。为了下文讨论方便,作以下约束:用户的优先级情况代替任务的优先级,用户的任务请求等同于虚拟机的请求,即用户任务过来将其映射到虚拟机上,虚拟机的虚拟资源量与任务请求资源量相等,并且这里规定一个用户对应的虚拟机是相同的;用户任务响应过程即是虚拟机部署过程也即是资源的分配过程。
1.1 数据中心资源模型在云计算的整个系统中,所有不同类型的物理机(服务器)组成了整个资源池,物理机集合P={p1,p2,…,pn},1≤n≤N,每个物理机都包含多种硬件资源,例如CPU、内存、磁盘等,因此资源类型R={r1,r2,…,rm},1≤m≤N,则Cj={C1,C2,…,Cn},1≤j≤n(为了表示的方便,当i、 j、r作为下标出现时,分别直接表示用户、物理机、资源),表示物理机所有的资源量,具体的物理机j对应的各资源集合为Cjr={Cj1,Cj2,…,Cjm},1≤r≤m,那么资源池中资源r的总量为:
| ${{S}_{r}}=\underset{j=1}{\mathop{\overset{n}{\mathop{\sum }}\,}}\,{{C}_{jr}}$ | (1) |
在云计算系统中用户是不可或缺的一部分,定义U={U1,U2,…,Uk},1≤k≤N为云系统资源共享用户集合,而各用户对于资源的请求di={d1,d2,…,dk},1≤i≤k,则用户i任务请求对应的虚拟机资源请求集合为dir={di1,di2,…,dim},用户i全局资源请求共享比(global resource share):
| ${{\mu }_{ir}}=\frac{{{d}_{ir}}}{{{S}_{r}}}=\frac{{{d}_{ir}}}{\sum\limits_{j=1}^{n}{{{C}_{jr}}}}$ | (2) |
对于式(2),若r=r*时,μir取得最大值,即μir*,那么称μir*为用户i的全局优势资源共享比(Global Dominant Resource Share,GDRS),而此时的r*则为用户i的全局优势资源,换句话说,在用户i请求任务的所有资源中,r*在资源池中占的比例最重。
1.2 资源利用率与权重分析建模在物理机中,对于每个物理机j,记Ojr={Oj1,Oj2,…,Ojm}为当前已被占有资源量,即当前已分配用户虚拟机资源总量,则该物理机当前的资源利用率可表示为:
| $~{{\eta }_{jr}}={{O}_{jr}}/{{C}_{jr}}$ | (3) |
物理机中资源的种类是多种多样的,这里需要关注所有资源的利用率,但由于在物理机中非优势资源的资源量很少,在分配中可能出现其资源利用率比优势资源的利用率大的情况,在求总体资源利用率时如果采用简单的累加式就显得本末倒置了,因此,本文按照物理机各资源量的比例(等效化后)来确定各资源利用率在w中的比例,其表达式为:
| $w=\underset{r=1}{\mathop{\overset{m}{\mathop{\sum }}\,}}\,\left( \frac{\left| {{C}_{jr}} \right|}{\left| {{C}_{j}} \right|}{{\eta }_{jr}} \right)$ | (4) |
从式(4)可看出,ηjr表示当前物理机资源r使用率,其表达式如式(3),w主要是用于求该物理机所有资源相对利用率之和,式中比值就是对上述情况的公式计算,在这里规定每个物理机中各资源间是等效的,即1单位量CPU与1单位量memory是等效的,其资源量数值可累加,表达式为:
| $\left| {{C}_{j}} \right|=\underset{r=1}{\mathop{\overset{m}{\mathop{\sum }}\,}}\,\left| {{C}_{jr}} \right|$ | (5) |
全局优势资源权重(Global Dominant Resource Weight,GDRW)用来衡量基于优势资源的用户在整个资源池的综合权重,其计算公式为:
| ${{\omega }_{i}}=\underset{r=1}{\mathop{\overset{m}{\mathop{\sum }}\,}}\,\frac{{{\mu }_{ir}}}{{{\mu }_{ir*}}}$ | (6) |
其中:r*为用户i的全局优势资源,在进行资源分配时,权重越高的用户虚拟机得到优先的分配。由于云计算服务计价模式采用按需分配,根据用户请求的资源数量和服务时间长度的实际情况进行收费[14]。因此,GDRW的值越高,说明用户单个虚拟机请求的资源量越大,故而服务费用也越高,进而可以拥有更高的优先权。此外,GDRW为具有相同优势资源的用户提供了分配优先级的量化指标,保证了资源分配的有序性。
1.3 公平性分析与建模虚拟机的分配过程主要是为了提高用户占优资源利用率和虚拟机数量,但同时也需要关注其他资源的情况,提高整体资源利用率,使服务器负载更均衡。在如今异构的云系统中,需求和资源的多样性使问题更加复杂,在这样的情况下,需要考虑的不仅仅是资源的瓶颈情况(包括占优资源),更多的是整个分配过程的公平性、合理性。
定义1 公平性(fairness)。用户受到平等的对待,他们的需求得到充分的满足或等效的满足,并合理地分配到服务器上。
虚拟机资源分配的公平性应当根据实际的请求情况来判断,所强调的公平是等效的公平分配。由于现阶段用户的需求非常复杂,包括不同的任务数量、资源种类、组合情况等,因此用户得到相同比例(或单位量)的任意一种系统资源都是等效的公平。此外,用户的请求都是视自己的情况而定的,在平等的情况下用户需求得到充分的满足也认为是公平的。分配的公平性不仅体现在分配过程中,也体现在分配的结果上,也就是物理机更合理均衡地接受这些分配。
根据面向优势份额的多资源分配公平性度量统一模型[15-17],其表达式为:
| $F=\text{sgn}\left( 1-\beta \right){{\left( \underset{j=1}{\mathop{\overset{n}{\mathop{\sum }}\,}}\,{{\left( \frac{{{\mu }_{j}}{{x}_{j}}}{\underset{k=1}{\overset{n}{\mathop{\sum }}}\,{{\mu }_{k}}{{x}_{k}}} \right)}^{1-\beta }} \right)}^{\frac{1}{\beta }}}{{\left( \underset{j=1}{\mathop{\overset{n}{\mathop{\sum }}\,}}\,{{\mu }_{j}}{{x}_{j}} \right)}^{\text{ }\lambda \text{ }}}$ | (7) |
其中: μj为优势份额;xj为任务数;sgn()表示符号。引入的参数 β∈R,λ∈R。公平性参数β,不同β值反映出不同的公平性类型,其大小决定了公平的强度;而λ强调资源利用率,该参数表明资源是否被最大化利用。式(7)是一个适用范围广、参数跨度大的模型,且仅适合用作最终的评估,并不符合本文的情况。根据文献[16],当β→1时,上述模型适合于比例公平性分配的评估,而在本文方案中,进行评估时主要是根据物理机的资源利用率即资源比例公平情况,这两者是相互适应的,因此,公平性度量模型为:
| $f=k{{\left( \underset{i=1}{\mathop{\overset{k}{\mathop{\sum }}\,}}\,{{\mu }_{ir*}}{{v}_{i}} \right)}^{w}}$ | (8) |
其中: μir*为用户i的优势资源共享比;vi表示用户i对应的虚拟机在当前物理机上分配的数量;w为物理机资源总利用率。式(8)主要用来度量用户虚拟机在具体分配到物理机时的公平性,f值越大则说明当前虚拟机的分配越公平,也是当前最适合的分配。式(8)用当前物理机所有资源的利用率作为考察因素,结合max-min fairness思想,尽可能使当前各资源利用率较低的得到本轮的分配,同时公平性度量值也是最大的,这也从一定程度上刻画了虚拟机分配到物理机上的适应度。
2 GDRF算法策略本文GDRF算法的多轮逐步分配的方式采用渐进填充[15]方法,它是max-min fairness的一种算法实现,最早被运用在网络的资源分配中。根据其思想本文将需要分配的用户虚拟机按照GDRF算法策略进行逐个的分配,直到所有用户的全部虚拟机分配完毕或者所有的物理机全被占用而无法填充为止。在之前的一些方案中已经解决了很多问题,但也有遗留问题,如没有对未确定占优资源的用户(用户任务请求资源中至少有两种资源的资源共享比相同且最大)的情况进行处理,这也是比较常见的问题,本文会在下面的方案中解决。
该策略的主要步骤如下:
步骤1 计算优先级。优先级在所有分配型案例中都是存在的,优先级数值的大小很大程度上直接影响着最终的分配结果,在整个分配方案中有着举足轻重的地位,需要根据用户的具体情况来确定用户的优先级。
步骤2 确定资格队列。分配方案采用多次少量的多轮分配方式,先确定该轮资格队列,再进行逐一的定位分配。资格队列的确定有助于用户更公平地得到分配服务。
步骤3 GDRF分配算法。在完成步骤1~2后就真正进入了分配环节,输入步骤2产生的资格队列,对队列中的多个用户进行最终优先级排序,然后选择优先级最高的进行分配,分配时选择与自身类型最相近的物理机,再遍历此类物理机寻找最适合当前虚拟机的物理机进行分配操作,接着进行下一轮分配。重复循环这样的操作,直至用户虚拟机全部分配完毕或物理机资源达到瓶颈无法继续分配为止。
2.1 优先级指标计算及排序根据用户的请求情况,计算出各用户的GDRS值并确定其全局优势资源,这里可能存在上面提到的无法确定优势资源的问题,有两个或多个资源的全局资源共享比是相同且最大的,本文方法是选择其中资源量数值最大的作为优势资源,若资源量也相等则随机选择资源作为优势资源;然后计算出用户的GDRW值,并将它们降序排列,留作后续用户优先级判断。
算法1 优先级计算。
输入 用户对应的虚拟机资源请求集Di,各物理机的资源量集Cj。
输出 用户全局优势资源共享比优先序列sort_GDRS,用户虚拟机的权重优先序列sort_GDRW。
用式(1)计算出资源池的资源总量Sr,用式(2)计算用户资源共享比集合μir
if 一个用户的μir有且仅有一个最大值 μir_max then
μir*= μir_max,并将该值添加到sort_GDRS中
else if 选取同时最大的几个值,这几个值对应资源有且仅有一个最大资源量dir_max then
μir*= μir_max,并将该值添加到sort_GDRS中
else μir*=random (对应dir_max最大的几个μir值),并将该值添加到sort_GDRS中
end if
end if
对sort_GDRS进行降序排列
用式(6)计算各用户虚拟机的权重值ωi,并添加到sort_GDRW中
对sort_GDRW进行降序排列
2.2 资格队列的确定定义2 资格队列(qualification queue)。相对于其他用户,资格队列中的用户拥有本轮被优先分配的权限。
当一大批用户请求过来时,本文采用多轮的分配形式(即少量多次)。首先以用户的个数作为每轮分配数,为了保障公平性,尽可能使每个用户得到分配,采用最大最小公平思想,在一轮分配中选取当前获得资源量最少的用户作为本轮的分配用户;若当前有多个用户获取资源量都最少,则选取GDRS值大的用户;当前两者都相同时,则选取GDRW值大的用户作为优先分配对象;若GDRW值还相等则随机选取用户,这样循环直到满足选取本轮用户数或总队列为空。
算法2 确定资格队列。
输入 用户的请求集D。
输出 当前资格队列QUE[](资格队列(名称)是数组)。
确定用户数量k,创建各用户已分配资源数组CON[k],创建资格队列QUE[k]
用户已分配资源数组CON[],设当前已分配资源量最少的用户数量为a,当前资格队列剩余名额为b
while b>0 && D为非空集 do
if a≤b then
将当前已分配资源量最少的用户加入资格队列QUE[]中,并累加其资源量到数组CON[]中,更新数据a,b
if b==0 then
输出当前资格队列QUE[],break
end if
else 选取这a个用户,根据算法1中计算的sort_GDRS,设当前DGRS值最大的个数为g,当前资格队列剩余名额为b
while b >0 do
if g≤b then
将这g个用户加入资格队列,改变数组CON[],更新数据g,b
if b= =0 then
输出当前资格队列QUE[],break
end if
else 取这g个用户,根据算法1中的sort_GDRW序列选择
用户加入资格队列直至队列全满
end if
end while
end if
end while
2.3 分配算法最后进行分配工作,首先在本轮有分配资格的队列用户中确定当前优先等级最高的一个用户,即选取GDRS值最大的一个用户,当GDRS值相同时按GDRW值降序选取,最终确定当前可被分配的用户;然后根据用户自身的优势资源情况,选择与其类型最相符的物理机集再进行最优分配(这样的选择既符合资源的类型需求,也符合物理机本身的性能要求,因为不同类型服务器之间各种服务效率的差距是巨大的,这样的选择可以达到共赢);最后根据上面建立的公平性度量模型,在未达到瓶颈资源过载界线的情况下,优先分配f值最大的物理机。这样便完成了一个用户的分配。后面的分配循环进行,直到用户虚拟机全部分配完毕或物理机资源达到瓶颈无法继续分配为止。
算法3 分配算法。
输入 资格队列QUE[],用户优先序列sort_GDRS,sort_GDRW,物理机集P={p1,p2,…,pn}。
输出 用户资源分配矩阵A。
while (资格队列QUE[]非空) do
if 有且仅有一个GDRS值最大的用户Ui then
fmax=0,pmax
for each pj in P do
if Ui_type= = pj_type
//判断物理机类型和虚拟机是否匹配
根据式(3)、(4)、(8)计算当前物理机的公平性评估值pj_ f
if fmax <pj_ f then
fmax= pj_ f,pmax= pj
end if
end if
end for
更新用户分配矩阵A中Ui和pj对应的数据项,更新资格队列QUE[
else 在多个GDRS值最大的用户中,选择其中GDRW值最大的用户Ui
fmax=0, pmax
for each pj in P do
if Ui_type== pj_type
根据式(3)、(4)、(8)计算当前物理机的公平性评估值
pj_ f
if fmax <pj_ f then
fmax= pj_ f,pmax= pj
end if
end if
end for
更新用户分配矩阵A中Ui和pj对应的数据项,更新资格队列QUE[]
end if
end while
2.4 GDRF算法公平性分析从算法的过程来看,多重优先级的设定和多轮的分配方式是算法公平性的一个体现。优先级的设定主要考虑了占优资源的情况,但同时也考虑到了非占优资源的情况,这里体现了资源间的公平;而每轮采用用户数作为目标数,体现了用户间的公平,如首次选取时必定是每个用户都能被选中,当各用户的任务的资源量相近时,几乎都是每轮每个用户都被选到,直到多轮后才会出现个别用户无法被选取的情况,这些都体现了用户间的公平。
从整个算法来分析,所有用户根据自己任务需求的资源份额能很好地在一个物理机或多个物理机上共同利用资源,也就是每个用户能更好地共享云资源池中的资源,而不是独占地利用资源池中的资源。用户不能通过谎报资源需求来获得更多的利益:首先虚拟机的租赁是以按需分配方式收费的,谎报资源需求量需要付出同等代价的;其次在GDRF算法中用户即使本轮因谎报资源需求获得更多的分配,但下几轮将无法再获得分配。在GDRF算法的分配中,若一个用户不减少分配量,那么另一个用户想增加分配量是不可能的,因为在GDRF分配的最终阶段是选择最适合的仍需分配的用户分配资源直到物理机资源耗尽为止。上面的这些都充分体现了GDRF算法的公平性。
3 实验评估针对GDRF算法,基于Google集群的数据集情况[16-17]设计了相关的模拟实验来对其特性进行评估分析,实验中的PC配置为:CPU主频2.20GHz,内存3GB,硬盘320GB,Windows 7操作系统,另外实验采用了CPU和memory两种资源,更通俗易懂。表 1为Google集群经过正则化处理后的资源配置,主要包括CPU和memory的量化关系,它们都是基于最大量进行了正则化处理,即最大量定为“1”,其他按比例缩小。
GDRF算法主要针对的是静态分配,所以本文设计的实验也是静态情况下的。文献[4]中MDRF已与之前两种方法进行比较并证明具有一定的优越性,因此本文仅与MDRF作对比,比较相同条件下虚拟机分配数量、资源利用率和公平性的情况。首先,以表 1中服务器的分布情况产生物理机,分别产生60台、120台、180台、240台和300台,并以此作为一个变量情况进行实验。
| 表 1 Google集群正则化处理后的环境配置 |
为了实验的方便,将物理机对应的资源量扩大100倍(如表 2所示),对应的用户的量也要有变化,因此选择用户的资源量(CPU,memory)从1~4随机组合产生20个。
| 表 2 60台物理机实验参数配置情况 |
这20个用户(如表 3所示)的资源组成几乎覆盖了所有组合情况,并且总体资源量呈正态分布,符合实际情况。
| 表 3 20台用户虚拟机参数配置情况 |
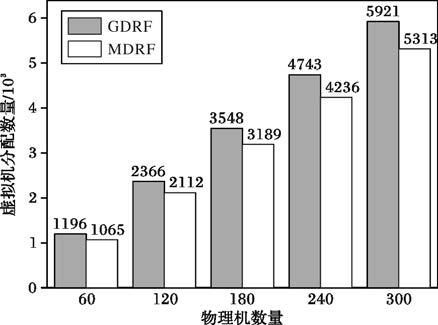
图 1为整个实验中两种方法所分配的虚拟机台数,从中可看出:在相同配置的情况下,GDRF算法分配的虚拟机台数明显多于MDRF算法,提高了约12%,并且随着物理机台数的增加,虚拟机数量呈稳定增长趋势。
|
图 1 虚拟机分配数 |
图 2是CPU利用率的结果比较,从中可看出:GDRF算法的CPU总利用率高于MDRF算法,表明在整个资源池中GDRF算法分配了更多的CPU资源;从物理机平均CPU利用率来看,GDRF也是占优的;还可看出,随着物理机数量的增加CPU利用率总体趋于平稳。

|
图 2 CPU资源利用率 |
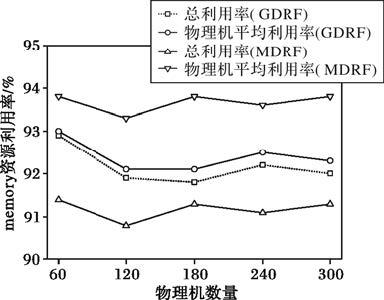
图 3为memory的资源利用率实验结果,从中可看出:GDRF的memory的总利用率高于MDRF,这从根本上说明了相同条件下GDRF算法分配的memory资源要多于MDRF,也就是GDRF优于MDRF。结合图 2~3可看出:memory的资源利用率远高于CPU,由于Google集群配置中CPU的总量要大于memory的总量,所以当用户请求的CPU、memory相对平衡时,memory的利用率必将高于CPU的。也因为这样的原因算法在分配时往往考虑CPU为主,memory则为瓶颈值,所以在图 3中出现了两种算法的物理机memory平均利用率会高于总利用率。另外图 3中GDRF的两条折线比较接近,而MDRF的距离很大,这是因为MDRF分配结果中有一大部分的物理机memory利用率很高,而小部分却很低,这样分配不均的情况导致了实验结果的差异,这也从侧面反映出GDRF算法分配资源的均衡性和稳定性。
|
图 3 memory资源利用率 |
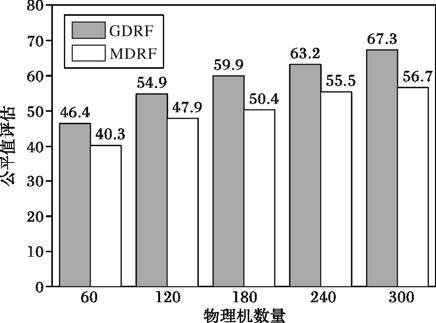
图 4为两种方法的总体公平值评估,从中可看出:GDRF算法的公平性评估值始终高于MDRF算法,提高了约15%,并且随着物理机数量的增加,评估值的差距越来越明显。
|
图 4 公平值评估 |
为了满足用户的需求,本文设计了公平性优化分配策略GDRF,根据用户的具体资源需求求出用户全局优势资源共享比、资源权重、资源利用率等数值,并且运用了多资源分配的公平性统一模型作为评估公式。在方法上本文采用多轮分配的两步走模式,即先确定资格队列,再具体分配,分配时按相关类型给予最优的分配,每一步都尽可能满足公平性原则,在用户的优先级上也采用了二级优先确定模式,使得资源的分配更加有序合理。实验结果也表明本文方案的优越性,使得系统的资源分配更均衡化,资源利用率更高,系统的工作效率也更高。进一步的研究方向是使其能更适应于动态环境下的分配情况。
| [1] |
XIAO Z, SONG W, CHEN Q. Dynamic resource allocation using virtual machines for cloud computing environment[J].
IEEE Transactions on Parallel and Distributed Systems, 2013, 24 (6) : 1107-1117.
doi: 10.1109/TPDS.2012.283 ( 0) 0)
|
| [2] |
GHODSI A, ZAHARIA M, HINDMAN B, et al. Dominant resource fairness: fair allocation of multiple resource types[C]//Proceedings of the 8th USENIX Conference on Networked Systems Design and Implementation. Berkeley: USENIX, 2011:24-37.
( 0) 0)
|
| [3] |
WANG W, LIANG B, LI B. Multi-resource fair allocation in heterogeneous cloud computing systems[J].
IEEE Transactions on Parallel and Distributed Systems, 2015 : 26.
( 0) 0)
|
| [4] |
王金海, 黄传河, 王晶, 等. 异构云计算体系结构及其多资源联合公平分配策略[J].
计算机研究与发展, 2015, 52 (6) : 1288-1302.
( WANG J H, HUANG C H, WANG J, et al. A heterogeneous cloud computing architecture and multi-resource-joint fairness allocation strategy[J].
Journal of Computer Research and Development, 2015, 52 (6) : 1288-1302.
) ( 0) 0)
|
| [5] |
KOKSAL C E, KASSAB H, BALAKRISHNAM H, et al. An analysis of short-term fairness in wireless media access protocols [C]//SIGMETRICS 2000: Proceedings of the 2000 ACM SIGMETRICS International Conference on Measurement and Modeling of Computer Systems. New York: ACM, 2000: 118-119.
( 0) 0)
|
| [6] |
BREDEL M, FIDLER M. Understanding fairness and its impact on quality of service in IEEE 802.11 [C]//Proceedings of the IEEE INFOCOM 2009. Piscataway, NJ: IEEE, 2009: 1098-1106.
( 0) 0)
|
| [7] |
PAO W, LOU W, CHEN Y, et al. Resource allocation for multiple input multiple output-orthogonal frequency division multiplexing-based space division multiple access systems[J].
IET Communications, 2014, 8 (18) : 3424-3434.
doi: 10.1049/iet-com.2014.0104 ( 0) 0)
|
| [8] |
PLA A, LOPEZ B, MURILLO J. Multi-dimensional fairness for auction-based resource allocation[J].
Knowledge-Based Systems, 2015, 73 : 134-148.
doi: 10.1016/j.knosys.2014.09.009 ( 0) 0)
|
| [9] |
LAN T, KAO D, CHIANG M, et al. An axiomatic theory of fairness in network resource allocation[C]//Proceedings of IEEE INFOCOM 2010. Piscataway, NJ: IEEE, 2010:1343-1351.
http://cn.bing.com/academic/profile?id=2122011919&encoded=0&v=paper_preview&mkt=zh-cn ( 0) 0)
|
| [10] |
WONG C J, SEN S, LAN T, et al. Multi-resource allocation: fairness-efficiency tradeoffs in a unifying framework[C]//Proceedings of the IEEE INFOCOM 2012. Piscataway, NJ: IEEE, 2012:1206-1214.
( 0) 0)
|
| [11] |
LU D, MA J F, XI N, et al. A universal fairness evaluation framework for resource allocation in cloud computing communications[J].
China Communications, 2015, 12 (5) : 113-122.
doi: 10.1109/CC.2015.7112034 ( 0) 0)
|
| [12] |
UCHIDA M, KUROSE J. An information-theoretic characterization of weighted α-proportional fairness[C]//Proceedings of IEEE INFOCOM 2009. Piscataway, NJ: IEEE, 2009: 1053-1061.
( 0) 0)
|
| [13] |
SEDIQ A B, GOHARY H, YANIKOMEROGLU H. Optimal tradeoff between efficiency and Jain's fairness index in resource allocation[C]//Proceedings of the 2012 IEEE 23rd International Symposium on Personal, Indoor and Mobile Radio Communications. Piscataway, NJ: IEEE, 2012:577-583.
( 0) 0)
|
| [14] |
XUE S J, SHI W L, XU X L. A heuristic scheduling algorithm based on PSO in the cloud computing environment[J].
International Journal of u-and e-Service, Science and Technology, 2016, 9 (1) : 349-362.
doi: 10.14257/ijunesst ( 0) 0)
|
| [15] |
GHODSI A, ZAHARIA M, SHENKER S, et al. Choosy: max-min fair sharing for datacenter jobs with constraints [C]//EuroSys 2013: Proceedings of the 8th ACM European Conference on Computer Systems. New York: ACM, 2013:365-378.
( 0) 0)
|
| [16] |
REISS C, WILKES J, HELLERSTEIN J L. Google cluster usage traces[EB/OL]. [2014-07-09].http://code.google.com/p/googleclusterdata.
( 0) 0)
|
| [17] |
REISS C, TUMANOV A, GANGER G R, et al. Heterogeneity and dynamicity of clouds at scale: Google trace analysis[C]//SoCC 2012: Proceedings of the Third ACM Symposium on Cloud Computing. New York: ACM, 2012: Article No. 7.
( 0) 0)
|




