随着自动化技术的发展,越来越多的机器人出现在我们生产和生活中,人与机器人之间的交互越来越频繁。人如何更好地与机器人打交道,是人机交互技术的研究的重点。目前,与工业机器人交互往往采用比较机械化的和专用手持式控制盒交互方式,如由ABB公司开发的Flex Pendant示教设备;沈阳新松机器人自动化公司设计的全按键式示教器等。近年来,人机交互技术向着愈来愈人性化和简单化的方向发展,其研究方向主要有表情、声音和手势识别技术。其中,手势是一种包含了较多信息量的人体语言,有着自然、友好、有效、直观等天然优势[1],因此,基于手势的人机交互正在成为一种新型和被广泛使用的人机交互方式。
国内外许多学者都对基于手势的人机交互方式进行了广泛的研究:Jain等[2]提出了使用智能手机内置加速计和蓝牙模块的人机交互系统捕捉操作员的手势动作,并用于控制机器人。Yuan等[3]在交通警察手背佩戴的加速计采集交警的手势动作和手掌姿态,将采集到的手势数据通过分类器进行手势识别,从而控制交通灯的状态转换。Kruse等[4]提出了使用Kinect传感器和力反馈器控制工业机器人的交互系统。Ren等[5]通过在手腕上缠上有色腕带来提取手势区域,提出了手指的地球移动距离(Finger-Earth Movers Distance,FEMD)算法,识别了数字0到9及加减乘除13个手势。曲贺[6]使用色调、饱和度、明度(Hue Saturation Value,HSV)空间皮肤颜色的分布快速提取人手的轮廓、手势中心,进而对手势进行分类,最终实现手势的识别。王松林等[7]提出了一种基于图像深度信息和人体骨骼信息的手指指尖识别方法和手掌轮廓检测算法。
目前,操作人员与工业机器人的交互方式往往还是采用比较机械化的和专用的手持式控制盒交互方式,本文设计了使用Kinect传感器作为手势采集设备并使用手势来对工业机器人进行控制的系统。在系统中,使用深度阈值法与手部骨骼点相结合的方法从Kinect红外摄像头获取的数据中准确地提取出手势图像。在提取过程中,操作员无需佩戴任何设备,对操作员所站位置没有要求,对背景环境也没要求。接着使用自编码网络与Softmax分类器结合的方法对手势进行识别,通过实验调优获得了满意的识别结果。最后通过手势操控工业机器人进行了仿真实验,实验在单手和双手手势下都取得了较好的效果,验证了手势操制工业机器人的可行性和可用性。
1 手势提取手势识别的关键步骤之一是手势区域定位与提取。但是,如何准确和快速地定位出图像中的手势区域,并分割出其中的手势是手势识别的一个难点。为了摆脱光照等自然环境的影响和解决复杂背景下对手势提取的影响,本文对Kinect获取的深度图像数据进行手势分割。
图 1(a)是由Kinect获取的深度图像,图 1(b)为对应的深度图像。由于深度数据没法直观展示,故将每个像素点上的深度数据转化成灰度数据之后就能够得到一幅灰度图像,采用的变换公式如下:
| $~{{D}_{gray}}={{D}_{depth}}\times 255\text{ }/{{D}_{max}}$ | (1) |
其中:Ddepth是每个像素点深度值,Dmax是整幅图像最大的深度值,Dgray是转换之后的灰度数据值。显然,在距离越近的地方,深度值越小,因而所计算出来的灰度值也就小,显示出来的对应图像颜色也就越深。因此,可以通过采用深度阈值的方法来提取手势图像。操作员在做手势或者动作时,手部通常会位于身体的最前方,这样就可以在获取到一幅图像的深度数据之后,找到最小的深度数据。考虑手掌的厚度,在深度数据上加上一个阈值进行分割,将灰度图像进行二值化,考虑到Kinect传感器在深度数据的获取上会存在着误差,所以在进行阈值分割时,需要在最小深度数据的基础上减去一个小的值,同时加上一个值,这样就可以得到图像中这段深度范围内的图像。处理函数如式(2)所示:
| $f(x) = \left\{ {\matrix{ {255,\matrix{ {} & {d - {D_1} \le x \le d - {D_2}} \cr } } \cr {0,\matrix{ {} & {x < d - {D_1},x > d + {D_2}} & {} \cr } } \cr } } \right.$ | (2) |
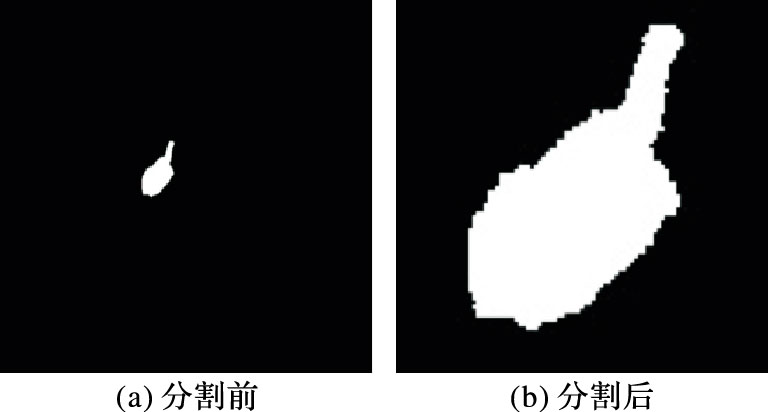
其中:D1依据经验取5,D2依据经验取4,可以依据识别效果作轻微调整。图像二值化之后得到结果如图 2(a)所示。Kinect的图像大小是640×480,而手势只占了其中的很小一部分,需要对图像中多余的黑色部分进行裁剪,以方便后期手势识别。裁剪多余黑色区域方法是寻找图像中最上最下最左最右的像素值为255的点,然后预留一些黑色区域,采用以上方法就可以确定分割区域,分割结果如图 2(b)所示。

|
图 1 彩色图像与深度图像 |
|
图 2 手势提取图 |
由图 2(a)可以看到基于深度阈值的方法能够非常简单且有效地处理出手势,这一切都是基于手部位于整个环境的最前端,一旦场景中有物体到深度摄像头的距离比操作者手部到摄像头的距离更要近或一样的距离时,那么就会对手势提取造成非常大的干扰,如图 3所示。

|
图 3 出现干扰物体 |
从图 3可以看到,在环境中有人或物体位于操作者前面时无法获取手势。同样地,如果是干扰因素与摄像头的距离和手势与摄像头的距离一样时,也会对手势提取造成很大的干扰。因此,本文在手势提取过程中,使用开放式的自然交互(Open Natural Interaction,OpenNI)[8]追踪手部关节点,以手部关节点深度值为分割值,再使用深度阈值法对手部区域的灰度图像进行阈值处理,对图 3的干扰情况提取后效果如图 4所示。利用手部骨骼节点辅助提取方法,解决了手部位姿一定要位于工作空间最前端的限制,再利用深度阈值法就完成了对手势的深度图像提取。

|
图 4 手部骨骼跟踪结果图 |
由于Kinect传感器使用激光散斑技术,当Kinect深度摄像头无法获取激光散斑图案时,所获取的深度图像就会出现噪声和空洞。为了保证后续手势识别的准确性及特征提取的准确度,对手势图像作一些滤波[9]及形态学操作。图 5(a)是通过阈值提取出来的手势图,图 5(b)是经滤波与形态学操作之后的手势图,可以看到处理过后图片明显在图像边缘更加平滑,手势图像更加清晰。

|
图 5 形态学处理前后对比 |
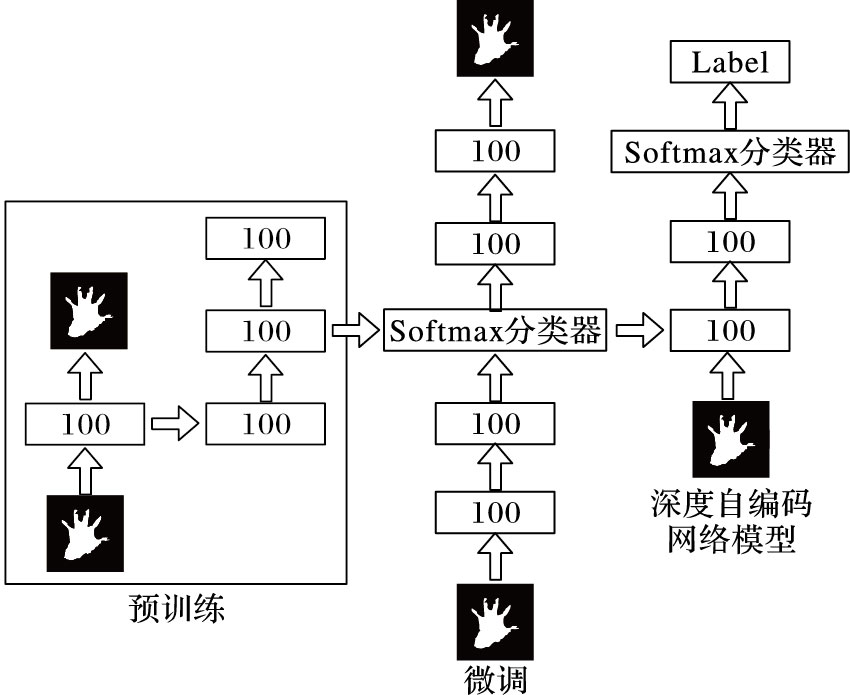
本文控制机器人的手势特征提取是基于深度学习的双隐藏层深度自编码网络,特征分类使用Softmax分类器。深度学习实际上起源于人工神经网络[10],通过模拟人类大脑神经系统建立分层结构模型,将上一层输出作为下一层输入逐层提取数据特征,从而获得更高层次的抽象特征。浅层学习在面对复杂函数的表示能力有限,而深度学习可以不受这个制约,实现复杂函数逼近。深度神经网络使用两段式学习过程:首先是预训练,将不带标签的手势数据作为网络输入,对网络隐藏层中各个参数进行训练;第二阶段是微调过程,将深度神经网络与分类器看作一个整体进行调整。经过两段式学习过程,可以得到最优的网络结构。图 6所示为本文设计的双层网络模型。
|
图 6 双层网络模型 |
为了实现对工业机器人的远程手势操控,本文设计了10个手势用于控制工业机器人。通过Kinect深度摄像头对5位人员的10个手势图片进行采集,每个手势采集30张图片,总计达1500张图片。其中,使用1000张用于训练图像,500张用于测试图像。每个图片是大小为50×50的二值图片共2500个维度。图 7列出了部分实验手势图片。

|
图 7 实验手势样例 |
自编码神经网络是一种新型的神经网络模型,属于无监督学习算法,能够实现图像重构与识别。它求解代价函数所利用的方法是反向传播算法和梯度下降法,自编码神经网络的目的是学习hW,b(x)函数。对于每一个输入x,该函数的输出都近似等于输入。稀疏自编码神经网络就是对自编码神经网络的隐藏单元施加一些限制,从而找出输入数据之间隐藏着的某种关联结构。如果输入数据的个数大于神经网络的隐藏层神经单元的个数,则使自编码神经网络学习输入数据的压缩表达;相反,若输入数据的个数小于或等于隐藏层神经单元的个数,这时就对隐藏层神经单元加入稀疏性限制,使得隐藏层大部分神经元处于抑制状态,只有极少数能够表示输入数据之间关联的那些神经元处于激活状态,这样自编码神经网络就能寻找出输入数据之间的相关性。定义激活与抑制的规则为:当该节点的输出接近于1时,就认为它被激活,而该节点输出接近于0的时候,则认为它被抑制。
本文使用aj(2)表示自编码神经网络中隐藏层神经元j 的激活度,还需要知道是哪一个输入x所产生激活度,故用aj(2)(x)来表示输入x对于隐藏神经元j产生的激活度。那么神经元j的平均活跃度${{\hat{\rho }}_{j}}$[13]可以用式(3)表示:
| ${\hat \rho _j} = {1 \over m}\sum\limits_{i = 1}^m {[a_j^{(2)}({x^{(i)}})]} $ | (3) |
其中:m表示样本的数量,在本文中训练时为1000,测试时为500。 对平均活跃度加上限制让${{\hat{\rho }}_{j}}$=ρ(ρ为稀疏性规则中的稀疏性参数)这样使得神经元的平均活跃度接近于某一个值,为了保持稀疏性,ρ通常是一个很小的数(如ρ=0.09),这样就使得神经元的激活度接近于0。在计算过程中会出现隐藏层的神经元平均激活度${{\hat{\rho }}_{j}}$和ρ有比较大差异的时候,为了缩小这一差异,在网络代价函数中添加惩罚因子,该因子用于惩罚${{\hat{\rho }}_{j}}$和ρ有显著不同的情况。本文使用的惩罚因子[13]如式(4)所示:
| $\sum\limits_{j=1}^{{{s}_{2}}}{\rho \log \frac{\rho }{{{{\hat{\rho }}}_{j}}}+(1-\rho )}\log \frac{1-\rho }{1-{{{\hat{\rho }}}_{j}}}$ | (4) |
其中:S2表示隐藏层中隐藏神经元的数量;索引j表示隐藏层中的每一个神经元。引入KL散度(Kullback-Leibler divergence)的概念,又称相对熵[13],则公式改写为:
| $\sum\limits_{j=1}^{{{s}_{2}}}{KL(}\left. \rho \right\|{{\hat{\rho }}_{j}})$ | (5) |
其中:
| ${{J}_{sparse}}(W,b)=J(W,b)+\beta \sum\limits_{j=1}^{{{s}_{2}}}{KL(\left. \rho \right\|{{{\hat{\rho }}}_{j}})}$ | (6) |
其中:J(W,b)为整体方差代价函数;β用于调节惩罚因子的权重。
2.4 分类及调优本文使用Softmax分类器对网络学习到的特征进行分类。Softmax分类器是一种非线性分类器,通过与无监督学习算法结合常常能取得比较好的识别率。微调是在完成网络预训练之后,将Softmax分类器加入网络看作一个整体再次调整深度自编码网络所有的参数。微调步骤[13-14]如下:
1) 进行一次前向传播,逐层计算出前向传播中每层的激励响应。
2) 计算输出层残差值:
| ${{\delta }^{({{n}_{l}})}}=-({{\nabla }_{{{a}^{{{n}_{l}}}}}}J)\bullet {f}'({{z}^{({{n}_{l}})}})$ |
由于本文是将Softmax分类器包括在网络中,则输出层就变成了Softmax分类器。在分类器中,输入数据标签用I表示,条件概率向量用P表示,那么分类器满足∇J=θT(I-P)。
3) 计算隐藏层残差值:
δ(l)=((W(l))δ(l+1))·f′(z(l))
4) 计算偏导数:
| $\left\{ \begin{align} & {{\nabla }_{{{W}^{(l)}}}}J(W,b;x,y)={{\delta }^{(l+1)}}{{({{a}^{(l)}})}^{T}} \\ & {{\nabla }_{{{b}^{(l)}}}}J(W,b;x,y)={{\delta }^{(l+1)}} \\ \end{align} \right.$ | (7) |
5) 更新权重参数:
| $\eqalign{ & \left\{ \matrix{ \Delta {W^{(l)}}: = \Delta {W^{(l)}} - \alpha [({1 \over m})\Delta {W^{(l)}}] + \lambda {W^{(l)}} \hfill \cr \Delta {b^{(l)}}: = \Delta {b^{(l)}} - \alpha [({1 \over m})\Delta {b^{(l)}}] \hfill \cr} \right. \cr & \left\{ \matrix{ {W^{(l)}} = {W^{(l)}} + {\nabla _{{W^{(l)}}}}J(W,b;x,y) \hfill \cr {b^{(l)}} = {b^{(l)}} + {\nabla _{{b^{(l)}}}}J(W,b;x,y) \hfill \cr} \right. \cr} $ | (8) |
对以上步骤经过多次迭代微调,可以对网络更进一步优化,提高网络的可用性。
2.5 手势识别实验手势识别实验目的有两个:第一是研究自编码神经网络中参数对于网络性能与识别率的影响,主要研究参数包括稀疏性参数ρ和隐藏层节点个数,同时还考虑微调对于改善网络性能的作用大小;第二是针对工业机器人操作控制,将要使用10个手势进行识别,并且通过实验得出识别这些手势最优的网络参数。
2.5.1 稀疏性与微调对识别率的影响稀疏性的目的是,网络在面对隐藏层神经元个数相当庞大时也能够学习到输入数据之间的关联信息,因而引入了稀疏性参数ρ,以验证ρ的大小对网络学习特征的影响,以及在完成网络训练之后,对网络整体进行调优处理,网络性能又会因此提高多少。本文的实验流程如下:1)数据预处理,将Kinect采集到的手势图像数据调整大小为50×50。2)选定训练数据与测试数据,对采集到的1500张手势图片,随机选取1000张用于训练数据,剩下500张用于测试数据。3)设定深度自编码神经网络参数:输入节点个数为2500个、隐藏神经元个数为50个、输出节点个数为2500个;权重衰减系数为λ1=3E-3,惩罚因子权重为β=3,分类器权重衰减系数λ2=1E-4。4)进行网络学习和特征分类,改变稀疏性参数ρ,记录实验结果。
本次实验ρ从0.005开始,以0.005的步长增加进行实验直到ρ=0.05,本文选取其中两次实验微调前和微调后的可视化训练结果进行分析。图 8(a)是ρ=0.005时,微调前后特征图,通过可视化训练结果可以明显地看到微调前训练得到的特征不够明显,比较模糊,在微调之后训练结果相对来说清晰很多。 选取另外一组图片对比,图 8(b)是ρ=0.040时微调前后对比图。同样可以看到微调之后比微调前学习的特征更加清晰。

|
图 8 微调前后对比图 |
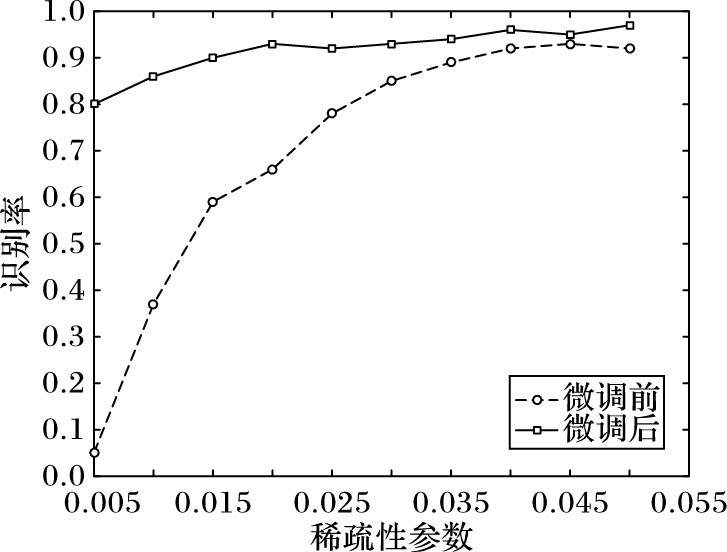
图 9展示了不同ρ在微调前与微调后网络识别率变化曲线。依据折线图,很容易看出微调对于识别率的提升有很大的帮助,特别是在ρ值比较小的情况下。也可以看到,不一定是稀疏性参数越小识别率越高,在本次实验中还出现了识别率下降的情况,对于ρ的设定需要依据具体情况而定。
|
图 9 稀疏性与微调对识别率的影响 |
隐藏层节点数目涉及到图像的特征提取,对网络识别率有着很大的影响。通常来说隐藏节点数目越多,学习到的特征也就越多,对图像的还原度也就越高。但是,隐藏节点数目越多网络的计算量也会相应增加许多,而且过多的隐藏层节点会学习到重复度很高的特征,这些重复度很高的特征对于图像识别并不会带来很大改善。本实验目的在于探寻最优的隐藏层节点个数。实验流程前三步和网络参数与2.5.1节相同,只是在第四步时改变隐藏层神经节点数目,记录实验结果,重复第四步。本次实验隐藏层节点数从50开始每次以50步长增长直到400。本文选取其中两次训练结果进行分析,图 10(a)和(b)是隐藏节点数为50时,微调前后得到的特征图。对比可以看出,微调后的结果在细节方面更加清晰,更有利于图像局部特征的描述。

|
图 10 隐藏节点数为50和200微调前后对比图 |
选取另外一组数据,图 10(c)和(d)是当节点数为200时,微调前后的学习特征结果图。可以看到同样是微调之后效果更好。当隐藏层节点数从50增加到200时,学习到的特征更加明显,也就是说在一定范围内增加隐藏层节点数可提高识别率。
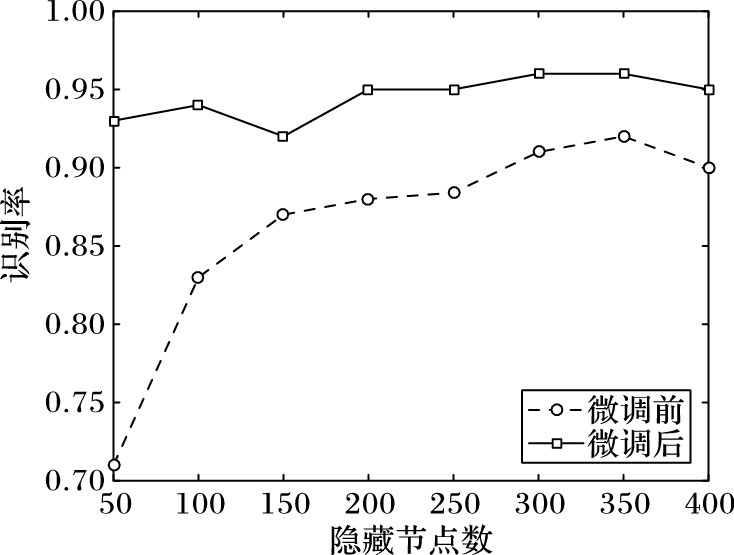
从图 11所示的识别率曲线可以看出,增加隐藏层节点数目对于微调之后的识别率并没有太多的提升,其中一个原因是因为在微调后最低的识别率已经接近了95%。但是,增加隐藏层节点数目对于微调前的识别率却有着显著提升。隐藏层节点数目越少,微调所起作用就越大。
|
图 11 隐藏层节点数对识别率的影响 |
经过实验分析可得,增加隐藏层节点数对于识别率提升有一定的作用,当数目超过阈值之后,提升效果就不明显了,反而增加更多节点数会带来更多的计算量,以及有可能造成过拟合的情况。但是节点数目也不能太少,太少会导致学习的特征过少,识别率较低。
2.5.3 最优网络配置在工业机器人手势操作控制系统中,会使用到手势识别模块,为提高手势识别准确率,对稀疏性参数和隐藏层节点数两个参数进行调优。使用的图片为2500维度,输入层为2500个节点,第一个隐藏层节点配置值从50开始以每次50步长增长到300,第二个隐藏层节点配置同第一个隐藏层配置一样。稀疏性参数从0.005开始每次以0.005的步长增长,直到0.05,其他参数值与上面两次实验中的数据一样。通过实验发现对于大部分的ρ值,在隐藏层节点数增加到100之后,识别率几乎不再增长,于是本文选定100作为网络隐藏层节点数。当ρ=0.035时,识别率达到了99.846%。于是本文将隐藏层节点个数设置为100个,稀疏性参数值ρ设定为0.035。图 12是基于上面参数学习到的特征,可以看到特征清晰,细节描述清楚,非常有利于手势识别。

|
图 12 学习到的100个特征 |
手势识别控制系统主要有两种控制模式,分别为单手模式和双手模式。单手模式即单手控制,启动程序,当成功连接服务器之后,打开Kinect传感器,单手在保持手势不变的情况下,工业机器人会一直按照手势代表的指令进行运动,直到无法继续执行动作。在单手模式下,所识别的9个手势分别代表的指令如图 13(a)所示。Kinect传感器以每秒30帧的速率扫描当前画面,将实时处理得到的结果发送给服务端,服务端发送相应的命令给工业机器人。
双手模式下的手势命令有:左手手势代表工业机器人关节,工业机器人为6自由度机器人,加上末端夹具(机械手),左手定义的手势有7个;右手用于控制关节运动,由于每个关节可以往两个方向运动,加上停止手势,右手使用三个手势,在左手手势代表控制机械手的时候,右手的手势代表的是保持原来状态、夹具打开、夹具关闭这三种动作,由于人手的对称性,本文将右手手势,作对称性变化就得到了左手手势,因此在识别的时候,仍然只需要识别10种手势。左手手势如图 13(b)所示,右手手势如图 13(c)所示。左手和右手的这10个手势涵盖了工业机器人运动所用到的所有动作。通过这10个手势,就能够完全控制工业机器人的相关动作和作业。
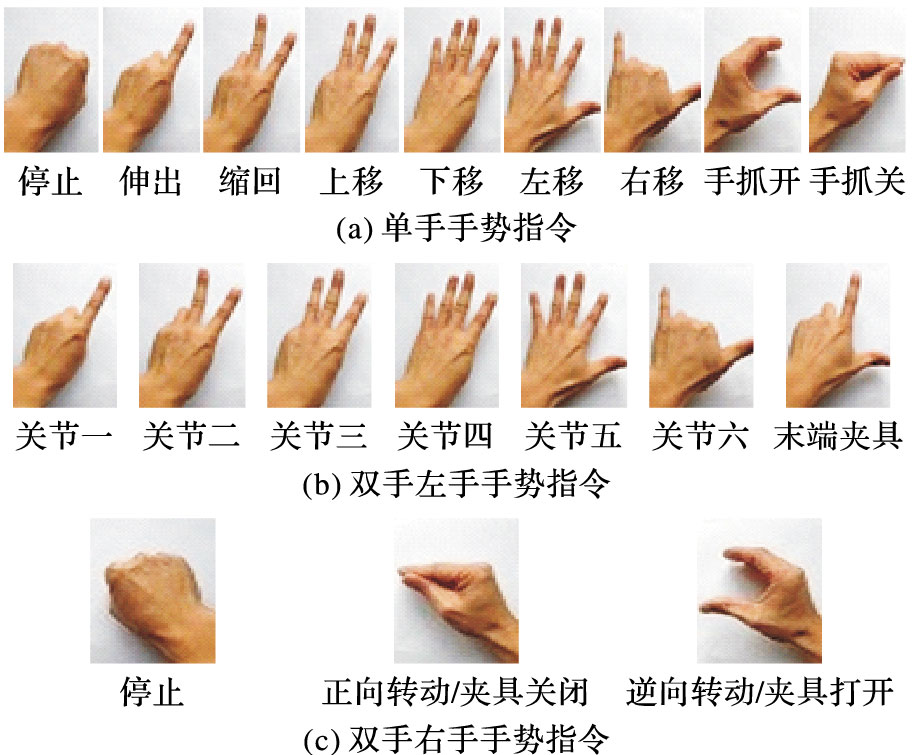
|
图 13 手势指令图 |
仿真平台[11-12]由本地服务器端和远程客户端组成,通过WinSock进行通信,采用基于状态反馈的实时仿真方法。客户端向服务器端发送简单的命令,服务器端返回执行命令后的状态信息,信息交流量小,能保证系统的实时性要求。本文在此仿真平台上通过手势控制工业机器人完成插销作业(Peg-In-Hole)实验,单手和双手操作模式实验过程分别如图 14~15所示。
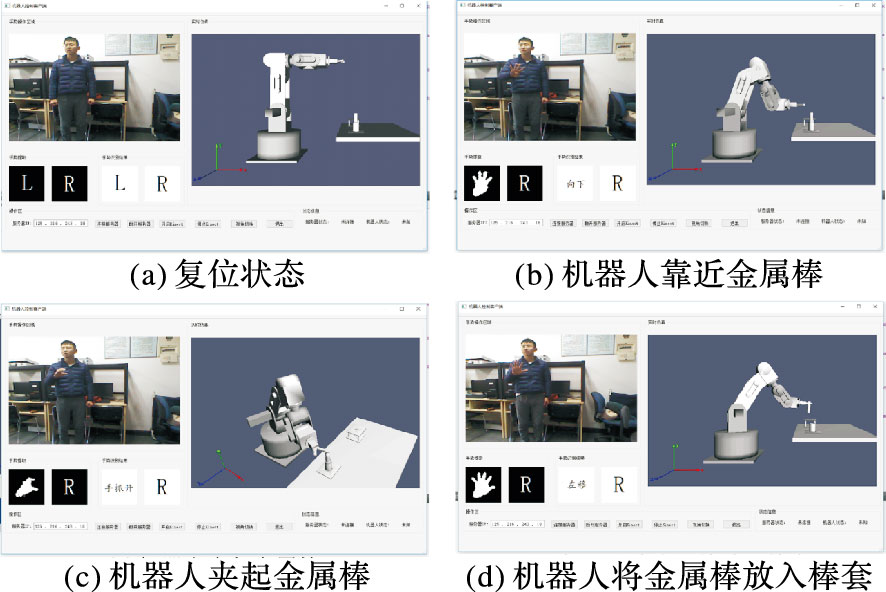
|
图 14 单手操作模式控制机器人完成插销实验 |
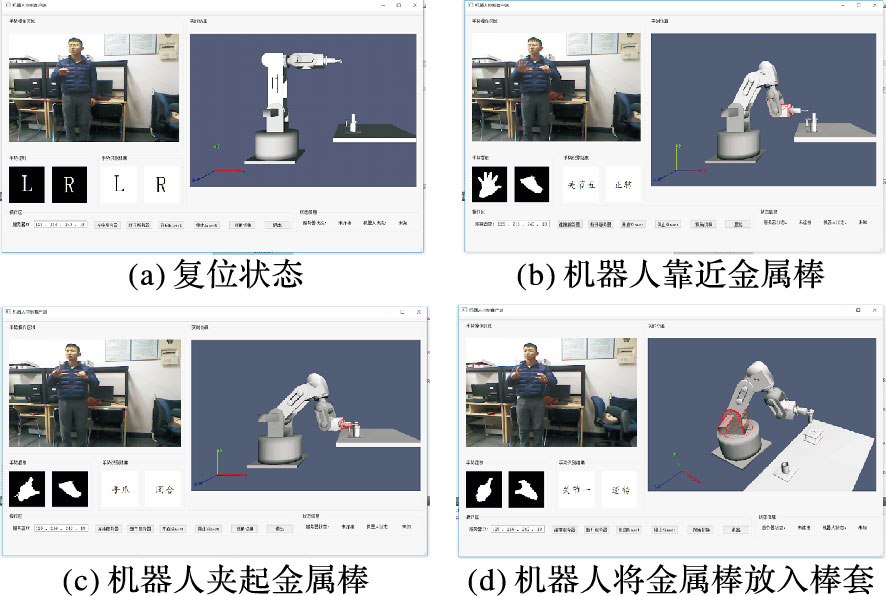
|
图 15 双手操作模式控制机器人完成插销实验 |
两种模式各重复4次,表 1记录了每次操作所用的时间(单位为s)。在本地模拟仿真实验中,通过单手、双手两种方式实现了对本地仿真工业机器人的精准操控,准确地完成了插销作业实验。操作员能够通过对本地仿真工业机器人控制熟悉实际工业机器人操作,为实际工业机器人控制提供帮助。
| 表 1 模拟仿真控制任务完成时间 |
本文利用Kinect传感器,实现了用手势对6自由度工业机器人的操作控制。利用深度阈值法与手部骨骼追踪相结合的方法,提取出了清晰的手势图像。该方法不受光照,不受背景环境的影响,具有较高的鲁棒性;使用自编码深度神经网络加Softmax分类器的手势识别方法,在本文设计的10种工业机器人控制手势集中识别准确率达到99.846%,具有很高的识别准确度;能够在0.01 s内完成手势识别;设计的手势简单、自然。在仿真实验平台上,直接用手势操控工业机器人完成了Peg-In-Hole的实验,所需时间不到3 min,表明手势操控工业机器人的可行性,为工业机器人的自然交互提供了便利。
| [1] | WONGPHATI M, OSAWA H, IMAI M. User-defined gestures for controlling primitive motions of an end effector[J]. Advanced Robotics, 2015, 29 (4) : 225-238. doi: 10.1080/01691864.2014.978371 |
| [2] | JAIN M, ADITI A L, KHAN M F, et al. Wireless gesture control robot:an analysis[J]. International Journal of Research in Computer and Communication Engineering, 2012, 1 (10) : 855-857. |
| [3] | YUAN T, WANG B. Accelerometer-based Chinese traffic police gesture recognition system[J]. Chinese Journal of Electronics, 2010, 19 (2) : 270-274. |
| [4] | KRUSE D, WEN J T, RADKE R J. A sensor-based dual-arm tele-robotic system[J]. IEEE Transactions on Automation Science and Engineering, 2014, 12 (1) : 4-18. |
| [5] | REN Z, YUAN J S, ZHANG Z Y. Robust hand gesture recognition based on finger-earth mover's distance with a commodity depth camera[C]//MM'11:Proceedings of the 19th ACM International Conference on Multimedia. New York:ACM, 2011:1093-1096. |
| [6] | 曲贺.人与机器人交互中手势控制技术的研究[D].哈尔滨:哈尔滨工业大学,2013:17-23. ( QU H. Research on gesture control technology based on interaction with robot[D]. Harbin:Harbin Institute of Technology, 2013:17-23. ) |
| [7] | 王松林, 徐文胜. 基于Kinect深度信息与骨骼信息的手指尖识别方法[J]. 计算机工程与应用, 2016, 52 (3) : 169-173. ( WANG S L, XU W S. Fingertips recognition based on Kinect depth and skeleton data[J]. Computer Engineering and Applications, 2016, 52 (3) : 169-173. ) |
| [8] | OpenNI. OpenNI[EB/OL].[2016-03-17]. http://www.Openni.org. |
| [9] | TOMASI C, MADNDUCHI R. Bilateral filtering for gray and color images[C]//Proceedings of the 6th International Conference on Computer Vision. Washington, DC:IEEE Computer Society,1998:839-846. |
| [10] | 尹宝才, 王文通, 王立春. 深度学习研究综述[J]. 北京工业大学学报, 2015, 41 (1) : 48-59. ( YIN B C, WANG W T, WANG L C. Review of deep learning[J]. Journal of Beijing University of Technology, 2015, 41 (1) : 48-59. ) |
| [11] | 张建生, 肖南峰. 机器人远程控制系统的实时仿真与实现[J]. 计算机工程与应用, 2009, 45 (14) : 245-248. ( ZHANG J S, XIAO N F. Real-time simulation and realization of robot control system[J]. Computer Engineering and Applications, 2009, 45 (14) : 245-248. ) |
| [12] | 甘志刚, 肖南峰. 仿人机器人三维实时仿真系统的研究与实现[J]. 系统仿真学报, 2007, 19 (11) : 2444-2448. ( GAN Z G, XIAO N F. Research and implementation of 3D simulation system for biped humanoid robot[J]. Journal of System Simulation, 2007, 19 (11) : 2444-2448. ) |
| [13] | NG A. Sparse autoencoder[EB/OL].[2016-03-25]. http://nlp.stanford.edu/~socherr/sparseAutoencoder_2011new.pdf. |
| [14] | 邓力,俞栋.深度学习:方法及应用[M].谢磊,译.北京:机械工业出版社,2016:30-37. ( DENG L, YU D. Deep Learning:Methods and Application[M]. XIE L, translated. Beijing:China Machine Press, 2016:30-37. ) |




