2. 曲阜师范大学 软件学院, 山东 曲阜 273100
2. School of Software Engineering, Qufu Normal University, Qufu Shandong 273100, China
社交媒体以及各专业领域时刻都在产生大量的数据[1],而这些数据需经过合适的处理才能为人所用。传统的机器学习算法对于处理大规模数据并不实用。因此,如何在现有技术上改进和创新来高效地分类处理信息成为当前的研究热点。目前,常用的分类算法有支持向量机(Support Vector Machine,SVM)、朴素贝叶斯、K-最近邻 (K-Nearest Neighbor,KNN)、神经网络等[2]。其中,KNN分类算法因其稳定性、鲁棒性和高准确率等优点被广泛运用于机器学习和数据挖掘中。但KNN分类算法有以下缺点:1) K值需通过实验验证取值;2)KNN分类算法作为一种惰性算法,在分类阶段,每个待测样本都需要与训练集中所有样本做相似度计算从而找出K个最近邻并由此来确定样本最终分类,其时间复杂度与训练样本数量成正比;3)当样本分布不均衡时,有可能影响分类效果[3]。同时,随着数据信息的不断增加,传统的数据处理架构已经不能满足数据分析和处理的需求,提高算法的时间效率和扩展性成为亟需解决的问题。
近几年国内外研究者主要对KNN分类算法的分类效果和分类效率进行研究与优化。针对KNN算法本身,文献[4]在KNN中引入信赖值提高分类鲁棒性和准确率;文献[5]中对KNN进行加权并在UCI数据集中验证分析。针对KNN的并行化主要有以下几种常用手段:1)基于多核设备进行的并行化。文献[6]在多核上实现了KNN;多核设备有几十个核的并发处理能力,将数据存储在Global Memory中,处理速度较快。2)基于Hadoop平台的并行化。文献[7]在MapReduce上实现了KNN算法,提高了KNN的执行效率;文献[8]也将KNN应用到Hadoop平台中,得出KNN在Hadoop平台中具有较好的加速比。MapReduce框架[9]和它在Hadoop[10]中的开源应用是有效处理大数据集的突破,通过分布式系统来处理数据,节点在失效时不会影响程序运行。但研究者们在实验中发现多核设备受单节点限制易导致耦合度过于紧密且可扩展性低。以及Hadoop平台中MapReduce的限制性[11]:在迭代计算过程中每轮的作业启动开销过大,磁盘I/O的开销也使得执行效率下降。而Spark框架[12]克服了以上问题,它通过内存计算策略来加速处理分布式计算。此框架允许用户将数据存储在内存中重复查询使用,使其更加实用于在线、迭代和数据流算法。
本文主要研究实现KNN分类算法的并行化,并在并行化实现过程中对传统KNN算法进行了优化:首先在文献[13]提出的优化的K-medoids聚类算法的基础上引入收缩因子,对聚类过程中收敛较慢的簇进行一次裁剪,然后在聚类结束后通过判定函数对训练集进行二次裁剪,最后在分类过程对K值进行循环迭代并获得最终分类结果。本文算法在并行化优化基础上减少了KNN算法中相似度的冗余计算,提高了执行效率。
1 相关工作 1.1 KNN分类算法KNN分类算法是惰性算法,它的基本思想为:计算待测样本与已知样本的相似度,找出与待测样本相似度最大的K个最近邻样本,K个样本中大多数属于哪个类别则待分类样本也属于这个类别,并具有这个类别上样本的特性。
KNN具体实现的步骤:假设训练样本集为D,其中有N个类别C1,C2,…,CN,样本集D的总数为M,特征向量维度阈值为n。D中的一个样本的特征向量表示为:di={xi1,xi2,…,xij,…,xin}(0<i≤M)。其中,xij表示di的第j维的权重(0<j≤n)。待分类文本的特征向量形式为d={X1,X2,…,Xj,…,Xn},Xj表示d的第j维的权重(0<j≤n)。余弦相似度计算式如式(1)。
| $Sim(d,di)=\frac{\sum\limits_{j=1}^{n}{Xjxij}}{\sqrt{\sum\limits_{i=1}^{n}{X_{j}^{2}}}\sqrt{\sum\limits_{i=1}^{n}{X_{ij}^{2}}}}$ | (1) |
相似度计算完毕后,得出待分类样本的K个最近邻样本。并通过式(2)计算待测样本属于每个样本的权重,并归类。
| $W(d,Cj)=\sum\limits_{i=1}^{K}{Sim(d,di)}y(di,Cj)$ | (2) |
其中
Spark 是由加州大学伯克利分校AMP实验室研发的一种基于内存的计算框架,使用Scala语言进行构建。Spark框架给出了并行运算的两个主要的架构:在数据集上创建弹性分布式数据集 (Resilient Distributed Dataset,RDD)和并行运算操作。其中RDD是Spark框架的核心和基础,并且提供了一个强大的分布式内存并行计算引擎,支持快速的迭代计算。
RDD是一种分布式的内存抽象概念,在集群中的多个节点上进行分区,表示只读分区记录的集合。通过多台机器上不同RDD联合分区的控制,能够减少机器之间的数据混合(Data Shuffling)。在Spark中,所有RDD都只能通过在稳定物理存储中的数据集或已有的RDD上执行一些确定性操作来创建:1)在文件共享系统中获取,如Hadoop分布式文件系统(Hadoop Distributed File System,HDFS)。2)通过驱动程序中用来并行计算的Scala集合进行创建(例如:在驱动程序中构建的一个array对象)。3)转换现有的RDD。4)进行持久化来改变现有的RDD。并行操作包括两种类型:转换(transform)和动作(action)。转换表示从现有的RDD 创建一个新的RDD,动作则表示在RDD上执行计算,结果返回一个普通的类型值或将RDD中的数据输出到存储系统中[15]。
用户对RDD的控制还可以通过缓存和分区两个方面来控制。通过将RDD在多个并发操作之间缓存起来,进而加速后期对该RDD的重用。RDD也允许用户根据关键字(key)来指定分区顺序,将数据划分到各个分区中。
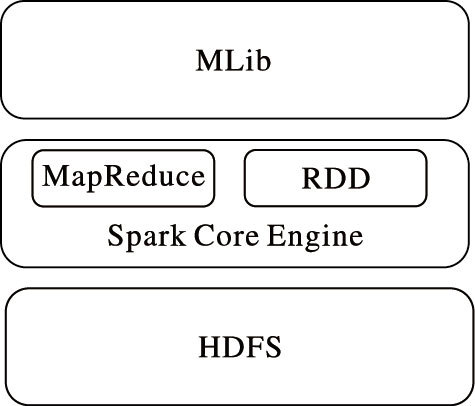
图 1为Spark基本架构。计算框架包含MapReduce框架,它在Hadoop的基础上进行了一些架构上的改良。Spark与Hadoop不同点在于,Spark的中间输出结果可以保存在内存当中,从而不需要再次读写HDFS。因此,利用Spark并行化处理框架可以极大提高迭代计算过程效率。
|
图 1 Spark框架 |
Hadoop是前几年出现的广为使用的大数据平台,而随着基于内存计算的Spark框架系统的发展,国内外开始将机器学习和数据挖掘的并行化算法关注到Spark框架中。
2 优化KNN分类算法的并行化传统KNN算法虽然简单有效,但因其计算过程中待测样本要与所有训练集进行相似度计算,算法时间与样本数量成正比。因此,在当前大数据背景下,KNN分类算法的效率问题尤为凸显[16]。针对KNN算法计算量大的问题,本文在文献[13]中心点优化的K-medoids算法中引入收缩因子对训练集进行聚类裁剪,通过簇数迭代K值确定最终分类结果,并在Spark计算框架下实现并行化。在Spark框架中RDD的使用大大缩短了算法迭代过程中I/O的花费时间,而且采用Spark中并行运算操作减少了运算时间。
2.1 基于聚类裁剪的KNN分类算法K-medoids聚类算法是一种应用广泛的传统聚类算法,计算简单,有着较高的鲁棒性。但K-medoids聚类算法在初始化时其中心点的选取比较敏感,并且在中心点的替换过程中使用全局替换方法,效率较低[17]。因此本文采用文献[13]中优化的K-medoids算法对训练集进行聚类裁剪,并引入收缩因子来消除增长缓慢的类簇对训练集进行初步裁剪。聚类结束后利用判定函数对聚类进行二次裁剪。最后在分类计算过程中迭代K值并获得最终分类结果。收缩因子公式为:
| $dk=di+\delta (Oi-di)$ | (3) |
其中:dk表示第k个样本的特征向量;di表示训练样本D中一个样本的特征向量; Oi表示聚类中心;δ表示收缩因子。
假设训练集为D,样本总数为M,共包含C1,C2,…,CN,N个类别。训练集裁剪步骤如下。
算法1 基于优化K-medoids聚类的KNN分类。
输入 训练集D;
输出 分类结果。
1) K-medoids初始中心点选择与优化。
a) 对于训练集D划分为m个类簇,其中m=3*N。
b) 随机选取簇心Oi (0<i≤m)。
c) 计算D中Oi到非簇心的余弦相似度,并按相似度初步聚类。
d) 在每个初始的簇中,以簇内每个点作为中心点,计算中心点到簇中其他样本的相似度距离和,选取距离和最小的点作为新的簇心Oi。引入收缩因子δ,将增长缓慢的簇删减掉(若δ取值很小,易形成非常小且距中心点很远的簇,通过实验对比将δ初始值设置为0.5),并调整聚类中心。
2) 对替换中心点搜索的优化。
a) 选择一个没有被选择过的中心点。替换中心点集A不再使用全局的非中心点集,而是在Oi的一定范围内。此范围指距离Oi最近的j(指迭代次数,0<j<m)个簇包含的非中心点样本区域。
b) 在候选集A中选择一个未被选择过的非中心点Qi,并计算Qi与Oi间平方差,并记录在新的集合Q中,直到集合A中的点都被比较过为止。
c) 如果集合Q中最小值小于零,即min(Q)<0,则采用Q中最小值所对应的点替换原中心点,并得到m个新的中心点。
d) 最后把剩余的样本分配给相似度最大的中心点所属的簇,由步骤1)开始重复执行。
e) 若min(Q)≥0结束算法,并得到m个类簇及簇心。
3) 二次裁剪训练集。
计算待测样本与m个簇心的相似度距离,如果Sim(D,Oi)<Ei(E为第i个簇的簇内样本与该簇中心点的最小相似度),则说明待测样本与该簇内样本间相似度极低,因此把该簇所包含的样本删减掉;否则将该簇加入到新的训练集中。
4) 迭代K值,获取分类结果。
a) 计算得出的每个类Ci 中的样本数Ni,并计算出每个簇的样本平均值
b) 对K值循环迭代获取距离最近的样本,1≤K≤avg,将每次K值获得的最邻近文本存到一个集合U中(U1,U2,…,Ui)。
c) 计算集合Ui中样本数目Sumi,若Sumi≤K,则继续循环迭代,di∈Ci;若Sumi>K,则结束迭代过程。
d) 若存在一个样本与每个聚类中心距离相同,则将该样本分到样本数目最大的类别中,即di∈Ci,如果Sumi>Sumj,那么di∈Ui。
e) 调整整个算法,直到每个数据都分配到对应的类别中不再改变。
通过引入收缩因子的高效K-medoids聚类算法对训练样本进行两次裁剪,减少了待测样本与训练样本比较次数,缩小了分类算法的计算规模,提高了KNN算法的执行效率。
2.2 KNN算法的并行化KNN过程主要是进行大量相似度计算找出K个最近邻,通过并行化可大大提高计算速度。改进后的KNN算法有很多的迭代计算而 Spark框架中RDD底层接口是基于迭代器的,从而使得数据访问变得更加高效同时避免了大量中间结构对内存的消耗,不需要进行磁盘间的I/O操作,可以大大提高计算效率。用户对RDD的控制还可以通过缓存和分区两个方面来控制,通过将RDD在多个并发操作之间缓存起来,进而加速后期对该RDD的重用。
由于并行过程中每次迭代都需要进行一次MapReduce操作比较耗时,本文对迭代计算过程进行了局部优化。将数据通过RDD分区机制分到P个分区当中,每个分区pi中首先基于自己分区内的数据进行迭代计算,计算结果与判定函数比较后等待本地经过系统再对P个分区得到的值进行比较,再将计算值分给每个分区,每个分区再次进行比较迭代,直到迭代结束。
Master服务器分配不同的数据块给不同的节点进行Map过程,不同的Map过程之间相互独立、并行,计算过程以〈key,value〉的形式读入并以此形式将中间结果传递给Reduce。Reduce过程对中间结果进行处理以〈key,value〉进行合并输出。
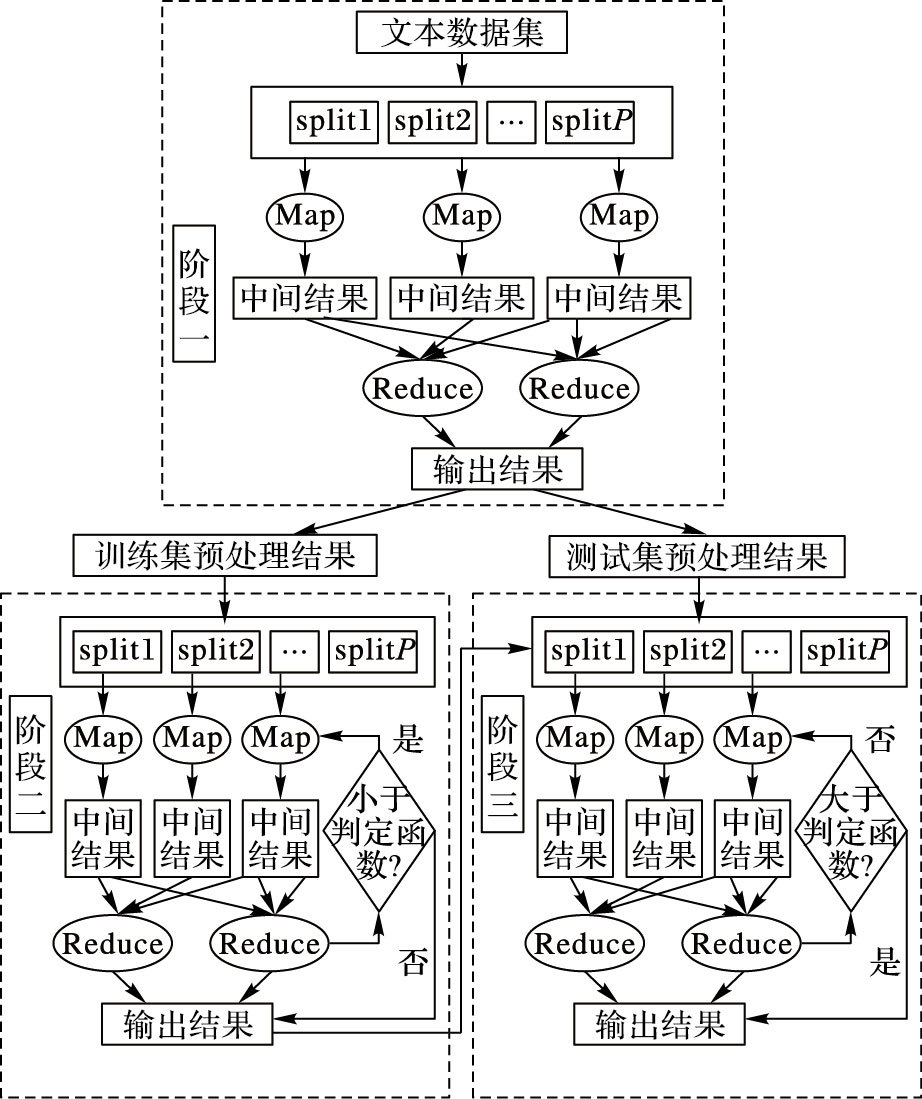
本文将并行化过程分为三部分,预处理、训练集聚类裁剪和最终分类过程。全部分类过程主要需要三对MapReduce函数,分别是对数据集进行去处理的PreMap与PreReduce,对训练集进行聚类的ClusterMap、ClusterReduce与KNN分类算法的函数KNNMap、KNNReduce函数。图 2给出了算法整体过程。
|
图 2 并行化KNN运行过程 |
预处理阶段如图 2中阶段一所示。本文采用中国科学院分词软件ICTCLAS2015对数据集进行分词、去除停用词等预处理。它提供了在Hadoop上去停词的源码。去停词结果以〈key,value〉形式给出,此形式可以用TF-IDF(Term Frequency-Inverse Document Frequency)对向量中每一维的权重进行计算,计算结果以〈word,textID〉形式进行表示。在Map过程运行之前,将训练集上传至HDFS中,借助分布式缓存机制将训练集分发给每一个节点,然后Map函数通过静态的方法UseDistributedCache()实现对缓存数据的调用。
2.2.2 聚类并行化此过程与图 2中阶段二相对应。将训练集结果读取调用,并将各数据作为创建出新的RDD,通过Cache操作将RDD数据进行缓存。通过文档ID与文档特征向量即〈textID,Vector〉键值对形式进行计算。Map过程主要计算每个数据对象到簇心的相似度距离并将其分到所对应的类簇中,并对簇心进行优化替换。Reduce过程主要根据中间结果判断是否进行下一步迭代。
算法2 分类训练集聚类过程并行化。
输入 训练集D〈textID,Vector〉,训练集样本数n;
输出 m个聚类。
1) 将训练集D在HDFS中读取,并创建出新的RDD。
2) 创建存储对象。
3) ClusterMap:
a) 读取对应分区;
b) 指定簇数m;
c) 为每个簇随机选择簇心Oi,并初步划分;
d) 根据2.1节中聚类过程算法1步骤2对簇心进行替换优化。
4) ClusterReduce:计算判定函数min(Q)。若min(Q)<0,则采用Q中最小值所对应的点替换原中心点,并得到m个新的中心点,并重复步骤3)~4);反之,结束算法获得m个簇、簇心及簇内样本数目。
2.2.3 并行化分类过程具体实现步骤将待测样本集的预处理结果在本地进行缓存,并调用算法1中聚类结果。利用Map过程计算待测样本与训练样本聚类后的簇心进行相似度比较,将相似度较低的聚类删减掉,比较待测样本与其余训练样本间相似度,迭代K值。Reduce过程结合Map过程的中间结果判定是否进行下一步迭代,并进行规约操作输出结果。此过程如图 2中的阶段三,具体步骤如下。
算法3 分类过程并行化。
输入 测试集S〈textID,Vector〉;
输出 测试集分类文本y个。
1) 建立KNNNode对象来存储测试集与训练集样本间的距离和训练样本的类别。
2) 调用算法2训练样本的聚类结果:m个聚类结果,簇内数目Ni。
3) KNNMap:
a) 读取对应分区。
b) 遍历本节点训练集簇类中心点,得到待测样本与簇心的余弦相似度Sim(d,Oi)。
c) 二次裁剪。如果Sim(d,Oi)<Ei,将该簇所包含的样本删减掉,否则将该簇加入到新的训练集Dnew中。
d) 调用得出的每个类Ci中的样本数Ni,并计算出每个簇的样本平均值。
e) 对K值循环迭代获取距离最近的样本,1≤K≤avg,将每次K值获得的最邻近文本存到一个集合U中(U1,U2,…,Ui)。
4) KNNReduce过程:
a) 计算集合Ui中样本数目Sumi,若Sumi≤K,则继续循环迭代,di∈Ci ;若Sumi>K,则结束迭代过程。
b) 若存在一个样本与每个聚类中心距离相同,则将该样本分到样本数目最大的类别中,即di∈Ci,如果Sumi≤Sumj,那么di∈Ui。
c) 调整整个算法,直到每个类都分配到对应的类别中不再改变,并获得最终分类。
分类过程进行了大量的迭代运算,而Spark框架中的RDD使得中间结果得以保存在内存当中,减少了磁盘的重复读写操作,提高了I/O速度,大大缩短了运算时间。同时,使用Spark中的迭代计算在内部完成,减少了耗时。KNN算法的并行化,提高了算法的执行效率,使算法更适用于当前的大数据环境。
2.3 时间复杂度分析通过对KNN算法的分析,计算相似度距离是算法中最耗时的。传统的KNN分类算法时间复杂度为O(r1r2),r1为训练样本个数,r2为测试样本个数。本文算法对训练集进行特征选取后将聚类收敛较慢的训练集以及与待测样本相似度较低的簇进行裁剪生成新的训练集,数目为r3,显然,r3<r1。因此本文聚类改进的KNN方法与传统分类方法的时间复杂度关系为:O(r3r2)<O(r1r2)。
本文并行化将大的数据块通过RDD分区为小的数据分区,每个节点负责本地数据,KNN算法的时间复杂度也被分散到g个节点当中。而本文基于Spark的时间复杂度为,O(r3r2)/g,其中g为节点数目。
3 实验结果与分析 3.1 实验环境与数据集本文实验在Hadoop平台的YARN上部署Spark框架,在Vcenter中创建了6台虚拟机,其中包含1个Master节点和5个Slave节点。算法使用Java实现。虚拟机中操作系统均为Ubuntu 14.04.3 -Server-amd64版本,Hadoop版本为2.6.0,Spark版本为1.4.0,Java开发包版本为jdk1.7.0_79,程序开发工具为Eclipse Mars.1 Release (4.5.1)。
本文实验采用Sogou实验室提供的分类语料库,选取其中搜狐新闻网站整理过的新闻语料以及对应的分类信息。本文实验所用语料库分为财经、互联网、健康、教育、军事、旅游、体育、文化、招聘等20大类,每个类别中有2 000篇文本,共40 000篇文档。根据需要每个类别中随机选取500篇文本,共10 000篇作为训练集。为了实验结果的有效性和全面性,将其余数据分为不同规模的测试集,如表 1所示。
| 表 1 测试集 |
在Spark计算框架中对得到的新训练文本集Dnew进行下一步的KNN文本分类处理,并在分类过程中迭代K值并获取最终分类结果。最后通过比较准确率、运行时间、加速比来验证算法的执行性能。加速比公式为:
| $Speedup(g)=\frac{在一个节点上使用的时间}{在g个节点上使用的时间}$ | (4) |
准确率公式:
| $Pc=\frac{分类正确的文本数}{真正包含的文本数}$ | (5) |
实验首先以准确率(Pc)与运行时间(T)为指标在单一节点上对传统KNN分类算法、文献[18]中基于K-medoids的改进KNN算法、本文优化KNN分类算法以及4个节点下的本文基于Spark框架的优化KNN分类算法进行了比较。如表 2所示。
| 表 2 四种算法性能比较 |
通过表 2可以看出,D1、D2测试集样本数据较少时,单一节点上的本文优化聚类裁剪算法准确率比传统KNN算法低了0.9~1.7个百分点,较文献[18]中算法低了0.3~0.8个百分点。这是由于经过裁剪后的算法为近似算法,当数据量较小时对分类准确率有所影响。但在运行时间方面,本文优化后的裁剪算法较文献[18]中算法缩短了13%~24%,较传统KNN分类算法缩短了25%~37%,这是因为优化后的聚类算法对训练集进行了两次裁剪,减少了相似度的冗余计算,提高了分类效率。而在Spark框架下的并行化计算准确率较其他算法稍有降低,这是由于并行算法将数据进行了分区计算。但传统算法耗费时间是Spark框架下算法时间的3.92~31.90倍。为了直观比较给出了时间折线图,如图 3所示。

|
图 3 四种算法运行时间比较 |
由图 3可得,单一节点中本文优化的KNN分类算法优于传统KNN分类算法和文献[18]中改进KNN分类算法。从测试数据集D4开始,三种单一节点算法运行时间增长加快,这是由于传统架构下的算法不适用于大数据环境。而基于Spark框架的并行化算法在测试集规模增长的情况下运行时间平缓增加,并远小于单一节点上各KNN分类算法的运行时间。
比较4个节点时,Spark框架与文献[18]中Hadoop平台下算法在5个不同规模数据集运行时间,如图 4所示。

|
图 4 两种架构运行时间比较 |
由图 4可以看出,在Hadoop平台处理较小数据集D1、D2时,使用时间较长,这是由于Hadoop平台处理在I/O计算时花费较多时间,在小样本集中尤为凸显。而Spark框架在各数据集下平缓增长并优于Hadoop。
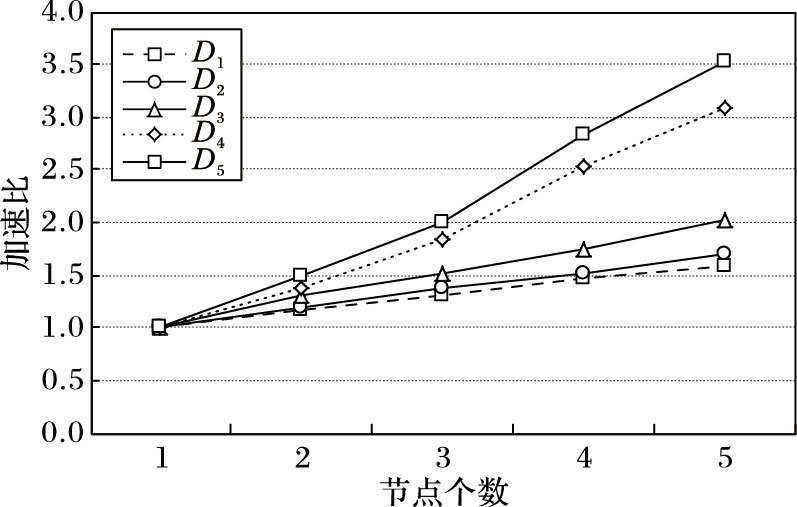
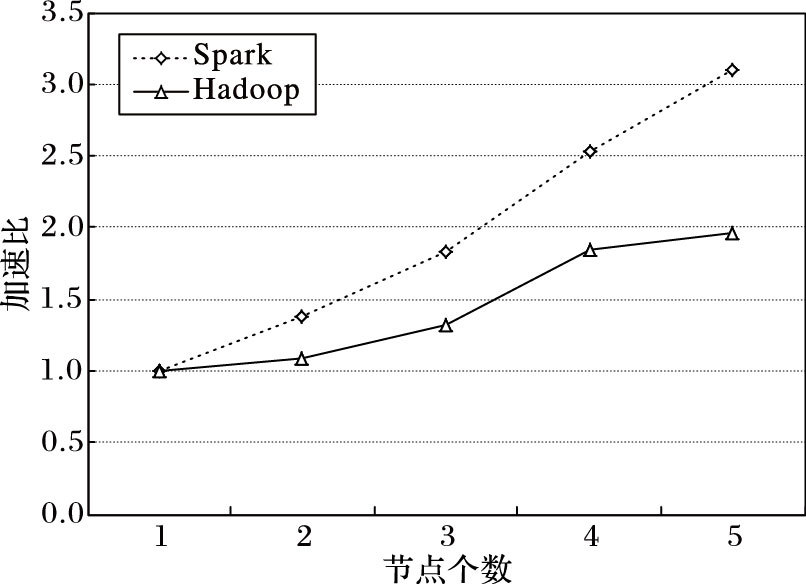
加速比主要用于衡量一个系统的扩展性能。图 5~6给出了不同规模的5个测试集的加速比以及Hadoop与Spark的在数据集D4中的加速比比较。
|
图 5 基于Spark框架优化KNN算法加速比 |
|
图 6 两种架构加速比比较(D4数据集) |
由图 5可得,Spark框架中加速比随着节点个数增长并保持一个线性的增长,并在节点数增加为4个时,加速比快速提高,即多个节点能够很好地缩短分类过程所需时间,这说明Spark框架在处理KNN分类算法上具有较好的加速比。可以预见,当节点数更多时,这种性能优势将更加明显。另外数据规模越大加速比越大,表示本文算法对大规模数据集的处理存在优势。图 6直观地显示出在D4数据集下Spark框架的加速比要优于Hadoop。随着节点数目增加,Hadoop越来越趋于平缓,这是由于节点数目增加使得节点间通信量及时间开销增大,可见Hadoop磁盘I/O对于算法的限制。由此可见Spark框架具有较好的加速比且优于Hadoop平台,适用于大数据环境。
4 结语本文针对KNN分类算法计算效率低的问题以及当前的大数据背景,使用优化的聚类算法对训练集进行裁剪并运用于Spark框架中实现并行化,有效地减少了分类过程中相似度的冗余计算,提高了分类效率,并能够适应当前的大数据环境。实验结果表明本文提出的算法与传统KNN分类算法、基于K-medoids的KNN算法以及Hadoop平台下的KNN算法相比在中文文本分类的时间效率上有明显提高。但由实验结果亦可知,本文算法与传统算法在分类准确率上基本持平。后续研究可以考虑如何进一步提高分类准确率。
| [1] | KALEGELE K, SASAI K, TAKAHASHI H, et al. Four decades of data mining in network and systems management[J]. IEEE Transactions on Knowledge & Data Engineering, 2015, 27 (10) : 2700-2716. |
| [2] | 苏金树, 张博锋, 徐昕. 基于机器学习的文本分类技术研究进展[J]. 软件学报, 2006, 17 (9) : 1848-1859. ( SU J S, ZHANG B F, XU X. Advances in machine learning based text categorization[J]. Journal of Software, 2006, 17 (9) : 1848-1859. doi: 10.1360/jos171848 ) |
| [3] | LIU W, CHAWLA S. Class confidence weighted kNN algorithms for imbalanced data sets[C]//Proceedings of the 15th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining, LNCS 6635. Berlin:Springer, 2011:345-356. |
| [4] | LIU Z G, PAN Q, DEZERT J. A new belief-based K-nearest neighbor classification method[J]. Pattern Recognition, 2013, 46 (3) : 834-844. doi: 10.1016/j.patcog.2012.10.001 |
| [5] | ZHANG L, ZHANG C J, XU Q Y, et al. Weigted-KNN and its application on UCI[C]//Proceedings of the 2015 IEEE International Conference on Information and Automation. Piscataway, NJ:IEEE, 2015:1748-1750. |
| [6] | 刘闯.基于多核计算的分类数据挖掘算法研究[D].南京:南京航空航天大学,2011:12-20. ( LIU C. Research on classification algorithms based on multicore computing[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2011:12-20. ) |
| [7] | ANCHALIA P P, ROY K. The k-nearest neighbor algorithm using MapReduce paradigm[C]//Proceedings of the 20145th International Conference on ISMS (Intelligent Systems, Modelling and Simulation). Piscataway, NJ:IEEE, 2014:513-518. |
| [8] | LU S P, TONG W Q, CHEN Z J. Implementation of the KNN algorithm based on Hadoop[C]//Proceedings of the 2015 International Conference on Smart and Sustainable City and Big Data. London:IET, 2015:123-126. |
| [9] | DEAN J, GHEMAWAT S. MapReduce:simplified data processing on large clusters[C]//OSDI'04:Proceedings of the 6th Conference on Symposium on Operating Systems Design and Implementation. Berkeley, CA:USENIX Association, 2004, 6:137-149. |
| [10] | GHEMAWAT S, GOBIOFF H, LEUNG S T. The Google file system[J]. ACM SIGOPS Operating Systems Review, 2003, 37 (5) : 29-43. doi: 10.1145/1165389 |
| [11] | GROLINGER K, HAYES M, HIGASHINO W A, et al. Challenges for MapReduce in big data[C]//Proceedings of the 2014 IEEE World Congress on Services. Piscataway, NJ:IEEE, 2014:182-189. |
| [12] | ZAHARIA M, CHOWDHURY M, DAS T, et al. Resilient distributed datasets:a fault-tolerant abstraction for in-memory cluster computing[C]//NSDI'12:Proceedings of the 9th Usenix Conference on Networked Systems Design and Implementation. Berkeley, CA:USENIX Association, 2012:141-146. |
| [13] | 夏宁霞, 苏一丹, 覃希. 一种高效的K-medoids聚类算法[J]. 计算机应用研究, 2010, 27 (12) : 4517-4519. ( XIA N X, SU Y D, QIN X. Efficient K-medoids clustering algorithm[J]. Application Research of Computers, 2010, 27 (12) : 4517-4519. ) |
| [14] | COVER T, HART P. Nearest neighbor pattern classification[J]. IEEE Transactions on Information Theory, 1967, 13 (1) : 21-27. doi: 10.1109/TIT.1967.1053964 |
| [15] | ZAHARIA M, CHOWDHURY M, FRANKLIN,M J, et al. Spark:cluster computing with working sets[C]//Proceedings of the 20102nd Usenix Conference on Hot Topics in Cloud Computing. Berkeley, CA:USENIX Association, 2010:1765-1773. |
| [16] | NIU K, ZHAO F, ZHANG S B. A fast classification algorithm for big data based on KNN[J]. Journal of Applied Sciences, 2013, 13 (12) : 2208-2212. doi: 10.3923/jas.2013.2208.2212 |
| [17] | CHEN X Q, PENG H, HU J S. K-medoids substitution clustering method and a new clustering validity index method[C]//WCICA 2006:Proceedings of the 20066th World Congress on Intelligent Control and Automation. Piscataway, NJ:IEEE, 2006:5896-5900. |
| [18] | 罗贤锋, 祝胜林, 陈泽健, 等. 基于K-Medoids聚类的改进KNN文本分类算法[J]. 计算机工程与设计, 2014, 35 (11) : 3864-3867. ( LUO X F, ZHU S L, CHEN Z J, et al. Improved KNN text categorization algorithm based on K-Medoids algorithm[J]. Computer Engineering and Design, 2014, 35 (11) : 3864-3867. ) |




