YAN Mengdi, born in 1993, M. S. candidate. Her research interests include network communication and control
QIN Linlin, born in 1975, Ph. D., senior engineer. Her research interests include artificial environment modeling and control, hybrid system
WU Gang, born in 1964, Ph. D., professor. His research interests include advanced control and optimization, new energy vehicle
文件类型是指文件存储在计算机中使用的特殊编码方式, 计算机根据文件类型来识别内部存储。每一种类型的文件, 都对应着一种或多种存储格式和访问方式。文件类型识别即通过某种途径判别文件所属类型的过程。为了保证计算机信息安全, 需要设计出能准确且快速地判断出文件的真实类型的方法。
在工程应用中, 可以分别使用基于文件的后缀名、基于文件的特征标识、基于文件的二进制内容这三种方法来识别文件实体的真实类型[1]。Windows操作系统采用文件后缀名来标识文件类型;另一种方法是利用特征标识, 即魔数信息来识别文件类型。基于后缀名和基于魔数的方法都有识别效率高的优点, 但是在识别正确率方面却有明显的不足。此外, 通过更改文件魔数信息或者文件的后缀名可以隐藏文件的真实类型, 某些恶意用户可以借此来骗取用户访问,控制病毒传播,掩盖违法信息。
除了以上两种方法, McDaniel等[2]首次统计文件内容的某些特定字节(特征值), 以特征值的频率分布生成文件类型的“指纹”, 依此识别文件类型。这种算法不依赖于文件名和文件特征标识, 不易被篡改误导;但识别正确率不高。Li等[3]以文献[2]中提出的算法为基础, 通过建立文件内容的n-gram模型对算法进行了扩展, 并使用多个指纹的聚类算法判断文件类型, 提高了识别正确率;但是此方法无法有效地识别相同文件类型中统计特征值有很大差异的文件。
此外, 在文本分类领域, K近邻(K Nearest Neighbors, KNN)算法因其简单、有效、非参数化而得到了广泛应用[4-5]。但传统KNN分类算法效率低下, 可从缩减训练集规模、对文本进行降维处理等方面着手降低算法的计算开销[6]。
本文提出的文件类型判别方法是一种新的混合算法, 基于基本KNN分类算法, 利用主成分分析(Principal Component Analysis, PCA)方法对文件的向量空间模型先降维处理, 对降维后的文件通过聚类算法得到该类文件的多个质心, 用聚类质心代表全部的训练样本, 从而减少了KNN分类器的输入。为减小样本分布不均对分类结果可能产生的影响, 使用经加权修正后的KNN算法。实验结果表明使用本文算法分类文件具有较高的精度;另外因为使用了聚类和降维算法, 显著地减少了分类时间。
1 文件类型特征模型建立 1.1 文件的向量空间模型建立文件的特征值模型V:
| $V = \left( {{m_0}/\max, {m_1}/\max, ..., {m_{255}}/\max } \right)$ | (1) |
其中:mi是字节值为i的字节的个数[7], max为{m0, m1…, m255}中的最大值。不同类型的文件字节值分布会有很大差异, 为便于分类, 将文件的向量空间模型中每一维的值都除以最大值, 数值归一化到[0, 1]内。
1.2 文件内容截取算法读取整个文件的字节值并统计每个值的频率分布会花费大量的计算时间, 文献[3]中提出一种内容截取算法, 即用文件某一部分内容的字节值代替整个文件的, 这种方法的引入可以有效减少分类计算时间。文献[3]中实验证明, 该算法不会降低分类准确性。
本文借鉴上述算法, 分别截取文件头部1 KB、文件中间任意位置1 KB进行对比实验。实验结果表明文件中某段位置的字节分布可以很好地代表整个文件的特性。
2 PCA和KNN算法描述 2.1 PCA算法描述主成分分析是一种统计方法, 通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量, 转换后的这组变量叫主成分。
主成分分析方法是一种对数据进行降维的方法, 它的基本思想如下:将具有一定相关性的多个原始变量, 通过组合变换, 得到一组互相无关的综合变量。从中选取几个较少的能够在很大程度上反映原始变量信息的综合变量, 就是主成分。主成分之间是互不相关的, 且是原始变量的线性组合[8]。
主成分分析方法的计算步骤如下:
1) 获取训练样本特征矩阵:
| $\mathit{\boldsymbol{X}} = {\left\{ {\mathit{\boldsymbol{x}}_1^T, \mathit{\boldsymbol{x}}_2^T...\mathit{\boldsymbol{x}}_n^T} \right\}^T}$ |
其中:n表示训练样本数, xi为第i个样本文件的字节频率分布, 是一个m维的行向量。
2) 计算X的协方差矩阵S :
| $\mathit{\boldsymbol{S}} = \frac{1}{n}\sum\limits_{i = 1}^n {({\mathit{\boldsymbol{x}}_i}}-\overline x ){({\mathit{\boldsymbol{x}}_i}-\mathit{\boldsymbol{\overline x}} )^T}$ | (2) |
其中
3) 计算协方差矩阵S的特征值λ和特征向量e。
4) 按照从大到小的顺序, 依次排列特征值, (λ1≥λ2≥…≥λn), 依此来选择特征值组成特征向量矩阵。
5) 根据需要的维数选择p(p < m)个重要的主成分, p的选取根据成分的累积贡献率来决定, 一般要求累积贡献率达到85%以上, 这样才能保证综合变量能包含原始变量的大多数信息。
6) 计算主成分得分, 以达到降维的目的。
2.2 KNN算法描述K近邻分类算法的核心思想是:如果一个样本在特征空间中的K个最相邻的样本中大多数属于某一个类别, 则该样本也属于这个类别, 并具有这个类别上样本的特性。KNN算法中, 所选择的邻居都是已经正确分类的对象。该算法只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
假定所有样本对应于m维空间Rm中的点[9], 一个样本的最近邻是根据标准的欧氏距离定义的。f: Rm→T, 其中T={t1, t2,…,ts}表示训练集中共有s个判别类别。f(xi)表示对测试样本集中第i个样本xi的估计, 它是指距离xi最近的k个训练样本中最普遍的f值。
| $\overline f ({x_i}) \leftarrow \mathop {\arg \max }\limits_{t \in T} \sum\limits_{j = 1}^k {\delta (t, f({x_j}} ))$ | (3) |
其中:
| $\delta (a, b) = \left\{ \begin{array}{l} 1, a = b\\ 0, 其他 \end{array} \right.$ | (4) |
尽管PCA算法的引入, 降低了训练样本的维数, 节约了计算开销, 但是该分类算法仍然存在两大缺陷:第一个是需要消耗大量的存储空间以存储所有训练样本, 第二个是需要进行繁重的距离计算。本文对此不足进行了改进, 提出在对测试样本进行分类之前, 先对训练样本文件进行预处理, 即先将训练样本集按类型分组, 对每组样本用聚类算法得到该类文件的多个质心位置, 以这些质心作为代表点和未知样本计算距离, 选取距离样本最近的K个质心, 统计这K个质心中大多数质心所属的类, 这个类别就是待分类样本所属的类别。不用和所有样本点都计算距离, 大幅减小了算法的时间开销。
本文使用K-means算法对样本进行聚类, 计算步骤如下:
1) 从数据集中随机选取K个点作为初始质心;
2) 计算每个点到这K个质心的距离, 将每个点指派到最近的质心, 形成K个类簇;
3) 重新计算各个类簇的质心, 即每个类内部点的均值;
4) 重复步骤2)和3), 直到质心不再变动。
算法的最终截止条件:一般是迭代次数达到最大设定值或者目标函数达到了最优解。
目标函数会根据实际选择的距离度量而不同, 如果选择的是欧氏距离, 那么最小化对象到其簇质心的距离的平方和就是目标函数。目标函数如下:
| $\min \sum\limits_{i = 1}^k {\sum\limits_{x \in {C_i}} {d{{\left( {{c_i}, x} \right)}^2}} } $ | (5) |
其中欧氏距离计算公式为:
| $d(x, y) = \sqrt {\sum\limits_{i = 1}^m {{{({x_i}-{y_i})}^2}} } $ | (6) |
如果选择的是余弦相似度, 那么最大化对象到其簇质心的余弦相似度和就是目标函数, 目标函数如下:
| $\max \sum\limits_{i = 1}^k {\sum\limits_{x \in {C_i}} {\cos \left( {{c_i}, x} \right)} } $ | (7) |
其中余弦相似度的计算公式为:
| $\begin{array}{c} \cos \left( {\mathit{\boldsymbol{x, y}}} \right) = \frac{{\mathit{\boldsymbol{x}} \bullet \mathit{\boldsymbol{y}}}}{{{\rm{||}}\mathit{\boldsymbol{x}}|| \times ||\mathit{\boldsymbol{y}}||}} = \\ \frac{{\sum\limits_{i = 1}^m {({\mathit{\boldsymbol{x}}_i} \times {\mathit{\boldsymbol{y}}_i})} }}{{\sqrt {\sum\limits_{i = 1}^m {{{\left( {{\mathit{\boldsymbol{x}}_i}} \right)}^2}} } \times \sqrt {\sum\limits_{i = 1}^m {{{\left( {{\mathit{\boldsymbol{y}}_i}} \right)}^2}} } }} \end{array} $ | (8) |
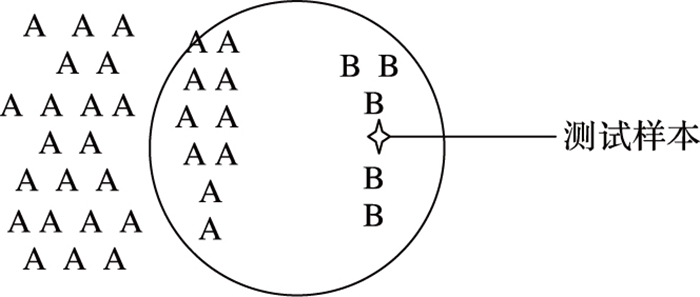
基本KNN算法在训练样本分布不均时, 分类的准确率会有所下降。如图 1所示, 因为样本的不均匀分布, 属于B类的样本被误判到了A类[10]。
|
图 1 训练样本分布不均匀对训练结果影响示例图(K=15) |
由图 1可见, 基本KNN算法在样本的数量分布不均匀时, 有个明显的不足之处, 即其中一个类的样本数量很大, 而其他类样本数量较小时, 当对一个未知类型的样本进行分类时, 得到的前K个邻近样本中的大多数都属于大数量的类。但是这类样本并不接近目标样本, 而数量小的这类样本很接近目标样本, 这个时候我们有理由认为该样本属于数量小的样本所属的一类。
为了将距离远近的因素也考虑在内, 采用加权的方法改进, 对于和测试样本距离小的邻居赋给较大的权值, 和测试样本距离大的邻居赋给较小的权值, 避免因某些类样本数量过大导致误判的情况。
| $\overline f ({\boldsymbol{x}_i}) \leftarrow \mathop {\arg \max }\limits_{t \in T} \sum\limits_{j = 1}^k {{w_j}} \delta (t, f({\boldsymbol{x}_j}))$ | (9) |
修正权值
| ${w_j} = \frac{{\cos ({\boldsymbol{x}_i}, {\boldsymbol{x}_j})}}{{d{{({\boldsymbol{x}_i}, {\boldsymbol{x}_j})}^2}}}$ | (10) |
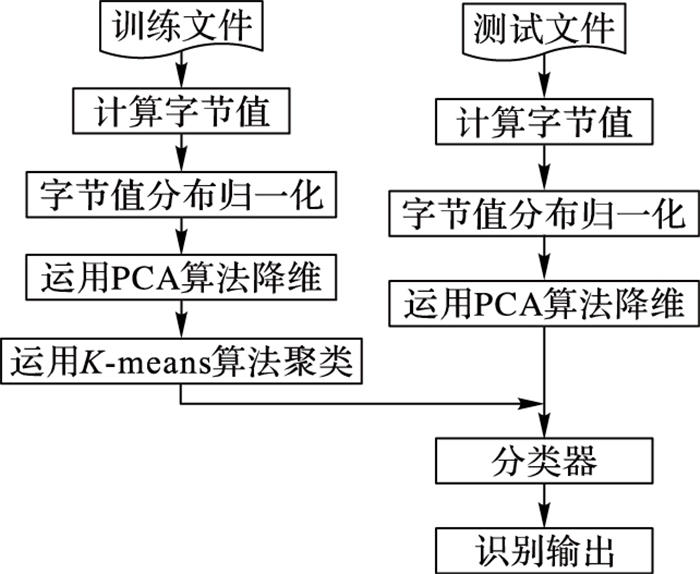
图 2为本文算法的识别流程, 训练样本和测试样本均需经过计算字节值、字节值分布归一化和运用PCA算法降维等过程。其中已知具体类型的训练样本比待分类的测试样本多一个步骤, 即先使用K-means聚类算法, 获取到远少于样本数的样本类质心, 输入分类器。预处理后, 将测试样本输入分类器, 计算出与之最接近的K个类质心, 得到最多的那个文件的类型, 作为分类器的识别结果输出。
|
图 2 文件类型识别流程 |
实验平台:Inter Core i5-3470四核四线程3.20 GHz处理器; 三级缓存6 MB; 4 GB内存; 在Matlab 7.0下进行仿真实验。
4.2 实验数据本文针对5种常见类型(doc、exe、html、jpg、pdf)的文件进行仿真实验, 对于每种文件类型, 准备200个文本作为训练样本, 50个文本作为测试样本, 每个文本的大小最小为10 KB, 最大为100 MB, 文件大小随机分布。文中实验所用的数据集的信息如表 1所示。文件均为在搜索引擎中使用“filetype:.后缀名”搜索下载得到, 或者从各个计算机中随机选取得到, 均为可靠文件[11]。
| 表 1 实验所用数据集 |
| 表 2 一些常用类型文件的魔数字节 |
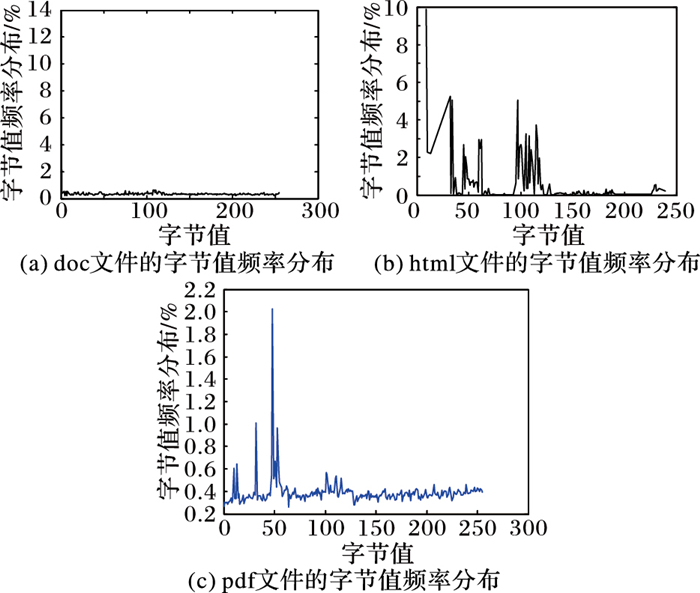
图 3为分别读取doc、html和pdf三种类型文件的二进制内容, 得到的文件字节值频率分布曲线。由图 3中可以看出, 不同类型文件的字节值分布有很大差异, 可以作为文件的“特征”[13-14]。
|
图 3 不同类型文件字节值频率对比 |
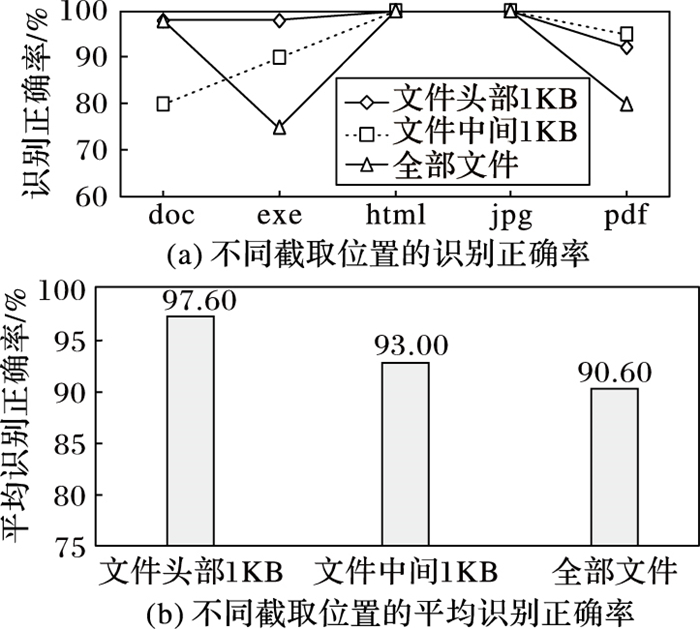
图 4为分别截取文件头部1 KB、文件中间1 KB、全部文件内容, 运用基本KNN分类器得到的识别正确率和平均识别正确率对比。图中实验结果验证了1.2节的算法, 对本文算法的验证实验即建立在截取文件头部1 KB的基础上。
|
图 4 不同截取位置分类性能 |
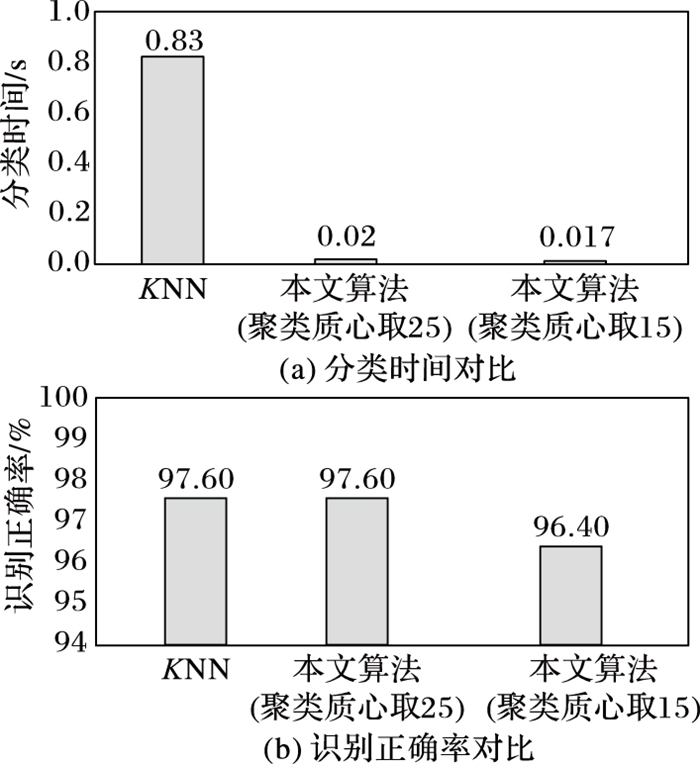
使用基本KNN算法(其中K取10), 本文算法(聚类质心分别取25和15, 样本空间由256维降至10维)进行对比实验, 对分类时间和分类的平均正确率记录如图 5。
|
图 5 不同算法分类性能 |
由图 5可以看出, 本文算法在时间性能方面优于基本KNN算法, 且分类识别的正确率基本不变。基本KNN算法分类的时间为0.83 s, 本文算法因聚类质心数的选取而不同, 分类时间分别为0.02 s和0.017 s。本文算法和基本KNN算法的识别正确率均在96%和98%之间, 基本不变。
5 结语本文基于现有的通过文件二进制内容识别文件类型的方法, 利用K近邻的分类思想, 针对算法中计算量大、样本数较多时分类时间较长, 样本的不均匀分布会使分类产生误判的情况, 提出基于降维和聚类的加权K近邻算法。最后对算法进行了实验验证, 并与基本K近邻算法进行了比较分析, 所提算法显著提高了文件识别的效率, 保持了较好的识别效果。但是仍然存在不足之处, 对于office系列的文件(doc、ppt、xls), 有极其相似的字节频率分布特征, 该算法无法判断出具体类型, 将来进一步研究新的特征提取方法, 以便有效地判别字节频率分布相近的文件。
| [1] | HICKOK D, LESNIAK D, ROWE M. File type detection technology[EB/OL].[2015-10-10]. http://www.micsymposium.org/mics_2005/papers/paper7.pdf. |
| [2] | McDANIEL M, HEYDARI M H. Content based file type detection algorithms[C]//Proceedings of the 36th Annual Hawaii International Conference on System Sciences. Washington, DC:IEEE Computer Society, 2003:332a. |
| [3] | LI W, WANG K, STOLFO S J, et al. Fileprints:identifying file types by n-gram analysis[C]//Proceedings of the 6th IEEE Systems, Man and Cybernetics Information Assurance Workshop. Piscataway, NJ:IEEE, 2005:64-71. |
| [4] | 胡元, 石冰. 基于区域划分的KNN文本快速分类算法研究[J]. 计算机科学, 2012, 39 (10) : 182-186. ( HU Y, SHI B. Fast KNN text classification algorithm based on area division[J]. Computer Science, 2012, 39 (10) : 182-186. ) |
| [5] | SONG Q, NI J, WANG G. A fast clustering-based feature subset selection algorithm for high-dimensional data[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25 (1) : 1-14. doi: 10.1109/TKDE.2011.181 |
| [6] | 张永, 孟晓飞. 基于投影追踪的KNN文本分类算法的加速策略[J]. 科学技术与工程, 2014, 36 (14) : 92-96. ( ZHANG Y, MENG X F. Accelerated K-nearest neighbors text classification algorithm[J]. Science Technology and Engineering, 2014, 36 (14) : 92-96. ) |
| [7] | 郑洁, 罗军勇, 卢斌. 基于统计特征值的文件类型识别算法[J]. 计算机工程, 2007, 33 (1) : 142-144. ( ZHENG J, LUO J Y, LU B. Documents type identification based on statistical characteristic[J]. Computer Engineering, 2007, 33 (1) : 142-144. ) |
| [8] | 史淼, 刘锋. 基于PCA和KNN混合算法的文本分类方法[J]. 电脑知识与技术, 2015, 11 (10) : 169-171. ( SHI M, LIU F. A hybrid algorithm for text classification based PCA and KNN[J]. Journal of Computer Knowledge and Technology, 2015, 11 (10) : 169-171. ) |
| [9] | 陈振洲, 李磊, 姚正安. 基于SVM的特征加权KNN算法[J]. 中山大学学报(自然科学版), 2005, 44 (1) : 17-20. ( CHEN Z Z, LI L, YAO Z A. Feature-weighted K-nearest neighbor algorithm with SVM[J]. Journal of Acta Scientiarum Naturalium Universitatis Sunyatseni, 2005, 44 (1) : 17-20. ) |
| [10] | 沈志斌, 白清源.基于加权修正的KNN文本分类算法[C]//第二十五届中国数据库学术会议论文集.重庆:计算机科学, 2008, 38(10A):220-225. ( SHEN Z B, BAI Q Y. KNN text classification method based weight modify[C]//NDBC 2008:Proceedings of the 25th National DataBase Conference. Chongqing:Computer Science, 2008, 38(10A):220-225. ) |
| [11] | 曹鼎, 罗军勇, 尹美娟. 基于变长元组的文件类型识别算法[J]. 计算机应用, 2011, 31 (7) : 1894-1900. ( CAO D, LUO J Y, YIN M J. Variable length gram based file type identification algorithm[J]. Journal of Computer Applications, 2011, 31 (7) : 1894-1900. ) |
| [12] | PANG G, JIN H, JIANG S. CenKNN:a scalable and effective text classifier[J]. Data Mining and Knowledge Discovery, 2015, 29 (3) : 593-625. doi: 10.1007/s10618-014-0358-x |
| [13] | EVENSEN J D, LINDAHL S, GOODWIN M. File-type detection using naive Bayes and n-gram analysis[EB/OL].[2015-10-10]. http://ojs.bibsys.no/index.php/NISK/article/download/99/88. |
| [14] | AHMED I, LHEE K S, SHIN H, et al. Content-based file-type identification using cosine similarity and a divide-and-conquer approach[J]. IETE Technical Review, 2010, 27 (6) : 465-477. doi: 10.4103/0256-4602.67149 |




