2. 武汉大学水利水电学院水资源与水电工程科学国家重点实验室, 武汉 430072
2. State Key Laboratory of Water Resource & Hydropower Engineering Science, School of Water Resources and Hydropower Engineering, Wuhan University, Wuhan 430072, China
0 引言
在土壤-地下水环境中,重质非水相流体(dense non-aqueous phase liquid,DNAPL)污染日益严重。其低水溶性、弱迁移性与强穿透性,给污染监测与修复带来了挑战[1-2]。掌握DNAPL在污染区域的分布特征对于选取适当的预防和治理措施至关重要。众多研究者的研究表明,DNAPL的理化特性[3-5]、泄漏速率[1, 6]、持留特征[7-8]、介质孔隙特性[9]、介质非均质性[1-2, 10]及地下水流速[11-13]对DNAPL在多孔介质中的运移分布特征有一定影响[14],其中介质非均质性是控制DNAPL污染源结构特征的主要因素[1-2, 10]。例如,当DNAPL运移至细砂透镜体时将聚积于其上部并侧向扩散,运移至粗砂透镜体时则沿粗砂构成的优势通道下渗。非均质透镜体使DNAPL的运移路径延长[10]。天然条件下,地下介质呈现出一定的非均质性。为刻画DNAPL的迁移规律与污染源区的结构特征,需进行参数估计以描述水文地质参数的非均质性。
非线性回归方法与贝叶斯方法在多相流参数估计领域应用广泛[15-19],如Gauss-Newton与Marquardt-Levenberg算法等。王景瑞等[16]基于iTOUGH2[20]软件中的Marquardt-Levenberg算法估计了均质承压含水层的导水系数并与FEFLOW推估结果对比,发现两者吻合较好。陆乐等[18-19]基于贝叶斯方法,针对具有5个参数分区的二维承压水非稳定流问题,推估其水文地质参数,获得了精度较高的全局最优解。值得注意的是,非线性回归方法与贝叶斯方法大多用于推估低维含水层参数,对于复杂非均质场下的多相流高维参数估计问题,其计算成本很高,不具适用性[21-23]。
集合卡尔曼滤波(ensemble Kalman filter,EnKF)[24]结合了传统卡尔曼滤波[25]与样本统计方法,以较低的计算成本获取观测数据与参数间的相关信息,显著提高了计算效率[26],广泛适用于油藏模拟中的多相流参数估计问题,尤其是对于高维参数估计具有较好的适用性与较高的计算效率。例如:Geir等[27]针对热储模拟问题,基于EnKF方法,联合动态变量(压力和饱和度等)与静态参数(渗透率等),获得了较好的同化效果;Jahanbakhshi等[28]将基于样本统计的卡尔曼滤波方法用于多孔介质多相流问题,同化测井历史观测资料以推估绝对渗透率场分布,得到了较高的参数估计精度;Panzeri等[29]将随机矩方程与EnKF方法结合,避免了繁复的蒙特卡洛分析,提高了计算效率;针对强非线性对传统EnKF方法的不一致性影响,Liao等[30]与Man等[31]提出TEnKF(transformed ensemble Kalman filter)与RAPCKF(restart adaptive probabilistic collocation based Kalman filter)方法加以改进,在一定程度上避免了非物理值的出现;Erdal等[32]针对EnKF方法在强非线性非高斯问题中的不适应性问题,采用状态变量转换策略,改善了参数推估与状态预测效果。
虽然EnKF方法在油藏模拟等领域应用广泛,但针对DNAPL渗漏运移中的多相流参数估计的应用研究偏少,且多数研究基于理想数值算例来分析EnKF的参数估计效果,实际问题中EnKF方法的真实性能有待研究。由于水文地质参数的非均质性显著影响DNAPL污染源区的结构特征,本文针对DNAPL污染物在饱和多孔介质中的渗漏问题,提出了基于多相流运移模型的集合卡尔曼滤波同化方案,融合DNAPL饱和度观测数据以推估非均质渗透率参数空间分布,构建了实际与理想算例,以期探究EnKF方法对非均质渗透率场的估计效果和观测频率、观测点数目与观测点位置分布对EnKF同化效果的影响。
1 研究方法 1.1 多相流运移模型针对多相流运移问题,根据达西定律并考虑DNAPL、水和空气3种组分及系统热平衡,可得质量平衡控制方程[33-36]:
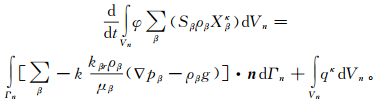 (1)
(1) 式中:t为时间;φ为孔隙度;Sβ为β相饱和度;ρβ为β相密度;Xβκ为组分κ(κ=1, 2, 3,分别代表DNAPL、水和空气3种组分)在β相中的质量分数;Vn为任意渗流区的体积;Γn为渗流区面积;k为介质绝对渗透率;kβr为β相相对渗透率;μβ为β相黏滞系数;pβ为β相压力;g为重力加速度;n为内法线单位向量;qκ为单位体积生成或消耗组分的速率。
本文基于多相流模拟程序T2VOC[37]求解式(1) 以模拟DNAPL的运移过程。
1.2 集合卡尔曼滤波作为一种基于蒙特卡洛抽样的数据同化方法,EnKF结合了滤波方法与集合预报。定义z为模型的状态向量,本文中指DNAPL饱和度。模型的观测向量可表示为
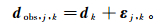 (2)
(2) 式中:dobs, j, k为样本j在tk时刻的观测向量;dk为tk时刻的实际观测值;εj, k为样本j在tk时刻的观测误差(假定其为高斯白噪声)。
对于任意样本j,同化更新前后状态向量的关系[24]可表示为
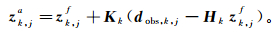 (3)
(3) 式中:zk, ja、zk, jf分别为为状态向量的分析值和预报值;Hk为tk时刻的观测矩阵;Hk zk, jf为与观测值dobs, j, k对应的模型预测值;Kk为第k同化步的卡尔曼增益项,其具体形式[25]为
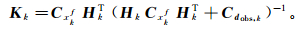 (4)
(4) 式中:Cxkf为状态向量协方差矩阵;Cdobs, k为观测误差矩阵;HkT为Hk的转置。Cxkf[24]可表示为
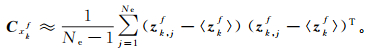 (5)
(5) 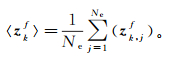 (6)
(6) 式中:Ne为样本数。
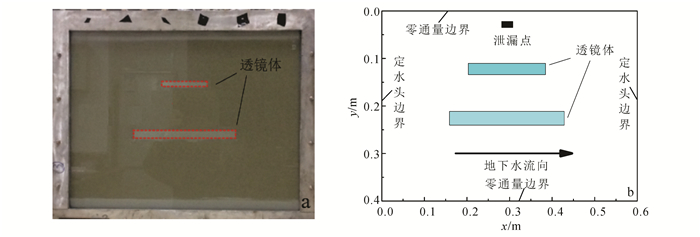
2 实例分析 2.1 实例介绍本节的实验数据自文献[2, 10, 14, 38],依托光透法实测砂箱中DNAPL饱和度数据,展开数据同化,以验证EnKF方法的实际效果。
砂箱模型见图 1a,尺寸为0.6 m×0.4 m×0.012 m(概化为二维问题)。背景介质与上下两层透镜体介质分别采用渗透率为2.6×10-10、0.35×10-10和0.22×10-10 m2的石英砂,并以此作为渗透率参照值(真实值)。利用注射泵将PCE(四氯乙烯)以5.4×10-15 kg/s的恒定速率由泄漏点注入砂箱,地下水流速由蠕动泵控制为1 m/d。
采用透射光系统监测砂箱中DNAPL饱和度分布[38-39],可获得10个不同时刻的PCE饱和度分布作为观测值。经高燕维等[38]验证,将光透法获取的砂箱区域PCE饱和度累加统计得到的总体积,与实际PCE注入量有较好的吻合,相对误差低于5%。本节取光透法观测误差为5%。
基于上述实验研究,本文构造了相应的数值模型以分析实例中EnKF方法融合饱和度观测数据,进而推估渗透率参数的效果。模拟研究区概化为二维xy剖面,将x与y方向分别均匀离散为35个和38个单元,共剖分为1 330个网格。区域上下两侧为零通量边界,左右两侧为定水头边界,见图 1b。区域内完全饱水,初始DNAPL饱和度为0。假设表面无降雨入渗,无蒸散发,温度保持为25 ℃,且不考虑相关热物理参数。确定性模型采用T2VOC程序,不考虑模型误差。研究区内均布80个观测点。
本节重点在于层状非均质渗透率参数估计,因此算例中只考虑渗透率k的不确定性。基于K-L展开法[40-41]生成服从对数高斯分布的初始样本,其中x向相关长度为0.09 m,y向相关长度为0.03 m。考虑到初始分布对同化效果影响较大,过强的离散性将导致确定性模型T2VOC计算不收敛,本例所取初始样本与参照场较为接近,其统计特征如下:ln k~N(-21.15, 0.01);样本数取100;模型总模拟时间与砂箱实验[10]保持一致,设为1 000 s,均匀离散为10个同化步段;80个观测点每个同化步均提供DNAPL饱和度的光透法观测数据。
2.2 同化效果为评价EnKF方法的参数估计效果,引入均方根误差RMSE与集合离散度ES(ensemble spread)作为评判指标。RMSE表示同化值与参照值之间的差异,其值越小说明同化值与参照场越接近,即参数估计效果越好;ES反映同化方法的收敛速度,其下降越快代表同化过程收敛越快。其计算公式分别为:
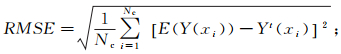 (7)
(7) 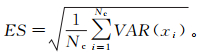 (8)
(8) 式中:Nc为格点数目,本文为1 330;Yt(xi)为第i格点渗透率对数ln k的参照值;E(Y(xi))为同化后第i格点的样本均值;VAR(xi)为第i格点处样本间的方差。
由于本例中DNAPL渗漏范围有限,且饱和度观测数据仅对DNAPL流经区域(图 2)的渗透率具有推估效果,故同化过程中只更新中上部渗漏集中区域的渗透率参数值,见图 3。
|
| a.第3同化步;b.第6同化步;c.第10同化步。Sn为DNAPL饱和度。 图 2 实际算例不同时刻的DNAPL饱和度分布 Figure 2 Temporal evolutions of the DNAPL saturation distribution |
|
|
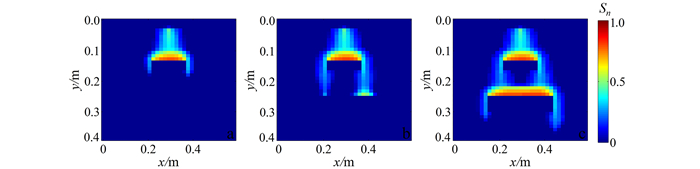
|
| a.参照k场;b.初始k场;c.同化后的k场。图中黑框为参数更新区域。 图 3 实际算例不同时刻的参数估计效果 Figure 3 Temporal evolutions of the permeability parameter estimates |
|
|
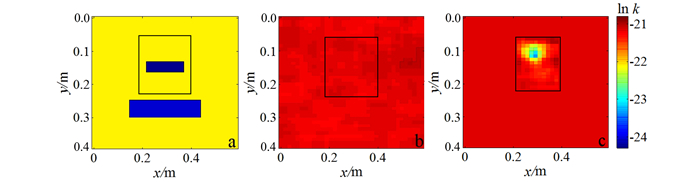
图 3为EnKF推估得到的渗透率集合均值。可见初始随机场未能反映参照场的分布特征,随着观测数据的融入,DNAPL渗漏集中区域内的渗透率向真值趋近。图 4a中RMSE值不断下降也说明了EnKF方法在实际污染渗漏问题中的参数估计效果;RMSE曲线后期有小幅上升,可能是因为EnKF更新参数导致了参数与饱和度变量之间不再服从既有的多相流控制方程,即非一致性,造成误差不断积累[42]。ES曲线变化见图 4b。同时注意到,由于选取DNAPL饱和度作为观测变量,其影响范围有限(图 2),导致EnKF无法有效推估整个研究区的非均质参数分布。
|
| 图 4 实际算例ln k场同化效果 Figure 4 RMSE and ES between estimated and real logarithmic permeability field as a function of step |
|
|
由上述实际算例可知,DNAPL饱和度观测数据的局限性导致了EnKF方法的参数估计效果不良。为进一步分析EnKF方法在DNAPL渗漏运移问题中的参数估计效果,本节在上述实际算例基础上将DNAPL泄露点增加为5个,以增大DNAPL饱和度的影响范围,如图 5a所示,介质渗透率调整为随机非均质。区域内均布80个观测点,如图 5b所示。
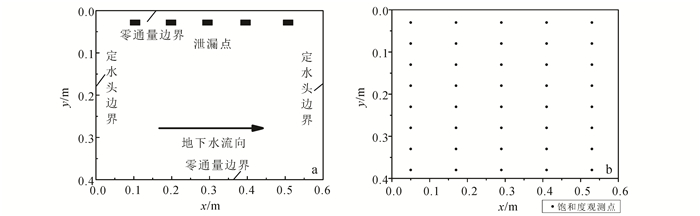
|
| a.多相流概念模型;b.观测点布置。 图 5 多相流概念模型与观测点布置 Figure 5 Multiphase flow concept model and configuration of the observation location |
|
|
假设渗透率场服从对数高斯分布[43]。渗透率参照场(用kref表示)与初始场均由K-L展开法生成,其统计特征分别为:ln kref~N(-21.66, 0.01),ln k~N(-22.07, 0.01)。为验证EnKF方法的有效性,假设DNAPL饱和度观测误差服从均值为0、方差为0.000 1的高斯分布。其余参数设置和边界条件与实际算例相同。
模拟中首先根据渗透率参照场运行确定性模型T2VOC,获得不同时刻的DNAPL饱和度参照值,添加观测误差生成伪观测数据。基于EnKF融合伪观测数据以推估渗透率参数,将结果与参照值对比以分析同化效果。
3.2 同化效果图 6为不同时刻推估所得的渗透率集合均值。由图 6可见:初始k场无法反映参照场的分布特征;随着饱和度观测数据不断融入,同化估计值与参照值越来越吻合;同化后研究区边缘处k值与参照值仍有一定差异,这是因为DNAPL的运移范围有限,且饱和度观测数据的影响范围较小。在非饱和带水流模拟中,史良胜等[44]将地下水位与含水量观测数据等信息联合运用,改善了参数估计和含水量预测的精度。针对DNAPL渗漏运移问题,应进一步研究联合同化多种观测信息(溶解态NAPL溶度与地球物理数据等),以充分发掘不同类型信息的数据价值,提高参数推估精度。
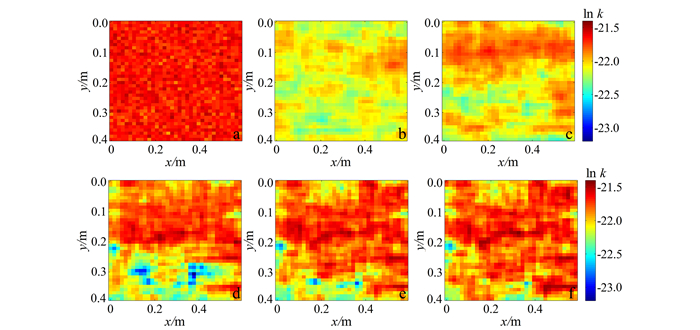
|
| a.参照k场;b.初始k场;c.第1同化步后的k场;d.第4同化步后的k场;e.第7同化步后的k场;f.第10同化步后的k场。 图 6 理想算例不同时刻的参数估计效果 Figure 6 Temporal evolutions of the permeability parameter estimates in the synthetic example |
|
|
由图 7a可知:最终RMSE为0.33,同化结果较好地刻画了参照场的空间分布,说明基于EnKF方法同化饱和度观测数据,可有效地推估非均质渗透率场分布;RMSE曲线随时间逐渐下降并趋于稳定,前期RMSE减小较快,第6同化步之后,饱和度观测数据对于参数k的校正效果有限,这是由于后期DNAPL已经运移到底部,整个区域内饱和度变幅较小导致其更新强度有限。图 7b中ES曲线更充分说明了上述规律,同化前期样本收敛速度较快,说明更新强度较大,这与前人的结论类似[45-47]。崔凯鹏等[48]指出处于水头波动较大时期的水头观测数据,对同化系统具有更高的数据价值。据此推断,在实际应用中若经费条件允许,可在同化前期增加观测点数目以改善参数估计效果。
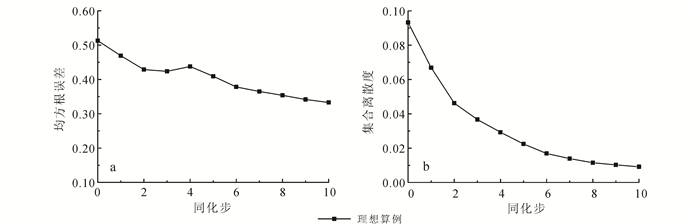
|
| 图 7 理想算例ln k场同化效果 Figure 7 RMSE and ES between estimated and real logarithmic permeability field as a function of step in the synthetic example |
|
|
一般认为随观测频率提高,同化效果将得到改善[47]。但过高的观测时间密度可能会产生信息冗余,对同化系统带来误差,造成不良的影响[48]。本节在3.1节算例的基础上将融合观测数据的次数减少为5次和3次,所得的RMSE与ES曲线见图 8。
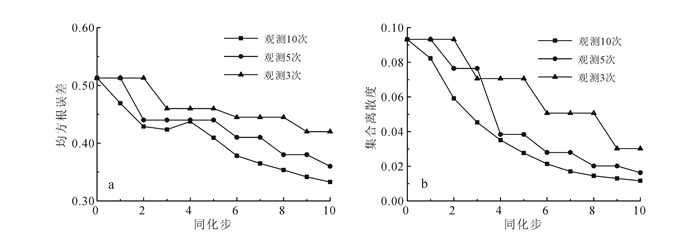
|
| 图 8 不同观测频率下ln k场同化效果 Figure 8 RMSE and ES between estimated and real logarithmic permeability field as a function of step for various frequency |
|
|
由图 8a可知:当观测频率为5次时,其RMSE曲线下降较快,且在同化结束时具有较低的RMSE值;然而由观测5次提高为观测10次,最终RMSE值由0.36降低为0.34,改善效果并不显著。可能的原因是相邻观测信息的时间间隔较短,其间差异性较小,导致单次同化的更新效果不显著。对于本模型,即使只观测5次,也可获得与观测10次相近的推估精度。结果表明针对本模型,利用频率较低的观测序列也可获得较好的参数估计效果,与文献[47]中关于观测频率的影响分析结果类似。
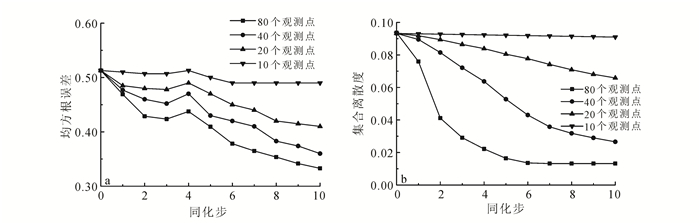
4.2 观测点布置密度监测地下水污染过程中的取样工作将耗费大量人力物力,故研究DNAPL饱和度观测点数目对同化结果的影响,对于节约工作成本、提高投入效率具有重要意义。本节选取在空间均匀分布的观测点,数目分别为80、40、20和10。与参照场对比,其RMSE与ES曲线如图 9所示。
|
| 图 9 不同观测布置密度下ln k场同化效果 Figure 9 RMSE and ES between estimated and real logarithmic permeability field as a function of numbers for various observations |
|
|
由图 9a可知:只布设10个观测点时,EnKF无法有效估计渗透率场;随着观测点加密,渗透率估计值与参照值越来越接近;注意到布设40、80个观测点时的参数估计精度较高,最终RMSE值分别为0.36与0.33,但布设40个观测点时观测成本较低且与布设80个观测点具有相近的精度。因此,针对本模型,40个观测点更为经济可行。实际中确定观测点数目时应综合考虑观测成本与参数估计精度。注意到随着观测点数目的增多,对于同化的改善效果逐渐减弱,这是因为:对于影响半径较小的观测数据(如DNAPL饱和度),在改善观测点附近的参数估计的同时,可能歪曲距离较远处的参数估计,增大观测密度可能给同化带来负面影响[49];EnKF方法中观测点具有全局影响,观测点影响范围重叠将导致参数的过度更新[45, 48]。
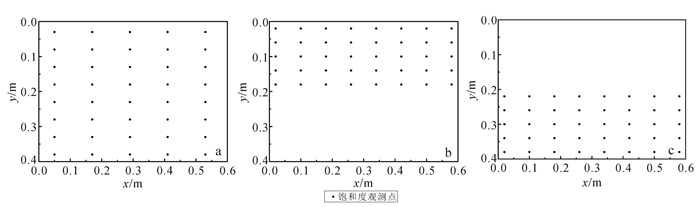
4.3 观测点位置分布不同观测位置获得的饱和度数据变幅不同,对于参数估计的数据价值也有所差异。为研究观测点位置分布对同化效果的影响,为优化观测点布置提供参考,本节考虑40个观测点分别分布在整个区域(图 10a)、上部(图 10b)和下部(图 10c)时3种不同的空间分布。
|
| a.观测点均匀分布;b.观测点在上部;c.观测点在下部。 图 10 不同的观测位置分布 Figure 10 Different configuration of the observation location |
|
|
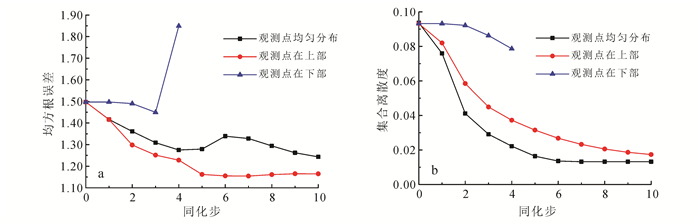
由图 11a可知:3种观测布置方式中,将40个观测点布置在上半部时,具有最低的RMSE值1.15,说明其参数估计效果最好;而将观测点布置在下半部时,RMSE曲线大幅上升,确定性模型T2VOC计算不收敛导致数值模拟终止;原因是模拟初期DNAPL尚未达到下部区域,此时下部观测点的饱和度数据不具有参数更新效果。图 11b则表明了观测上部时算法收敛速度快。曹少华等[45]与崔凯鹏等[48]指出,同等经费条件下,可优先布设状态变化较大处的监测井以求最大化监测数据的效用。据此推断,实际中应在污染集中或饱和度变幅较大的区域多布观测点,以获取较高的参数估计精度。
|
| 图 11 不同观测点位置分布下ln k场同化效果 Figure 11 RMSE and ES between estimated and real logarithmic permeability field as a function of step for various observation configuration |
|
|
本研究针对具体的DNAPL污染运移问题,构建了基于集合卡尔曼滤波方法和多相流运移模型的数据同化方案,融合DNAPL饱和度观测数据来推估非均质介质渗透率空间分布。基于二维砂箱实际与理想算例,验证了同化方法的参数估计效果,探讨了观测频率、观测点布置密度与观测点布置对同化效果的影响。研究表明:
1) 基于EnKF方法同化DNAPL饱和度观测数据可较好地推估非均质介质渗透率空间分布。由本文实际与理想多相流算例可知,如仅选取NAPL饱和度作为观测变量,其影响范围有限,需要在整个研究区范围内布置足够的观测点才能有效推估非均质参数分布。未来可联合其他类型的观测数据(例如溶解态NAPL溶度),从而提高推估非均质参数的精度。
2) 参数估计精度随观测数据时空密度的增大而提高,随观测数据不断加密,估计精度改善幅度逐渐下降,实际中需综合考虑观测成本与推估精度。
3) 观测点数目一定时,观测点位置分布对参数估计效果有一定影响,在污染集中或饱和度变幅较大的区域多布观测点,可获得较高的估计精度。
| [1] |
施小清, 姜蓓蕾, 吴吉春, 等. 非均质介质中重非水相污染物运移受泄漏速率影响数值分析[J].
水科学进展, 2012, 23(3): 376-382.
Shi Xiaoqing, Jiang Beilei, Wu Jichun, et al. Numerical Analysis of the Effect of Leakage Rate on Dense Non-Aqueous Phase Liquid Transport in Heterogonous Porous Media[J]. Advances in Water Science, 2012, 23(3): 376-382. |
| [2] |
郑菲, 高燕维, 施小清, 等. 地下水流速及介质非均质性对重非水相流体运移的影响[J].
水利学报, 2015, 46(8): 925-933.
Zheng Fei, Gao Yanwei, Shi Xiaoqing, et al. Influence of Groundwater Flow Velocity and Geological Heterogeneity on DNAPL Migration in Saturated Porous Media[J]. Journal of Hydraulic Engineering, 2015, 46(8): 925-933. |
| [3] | Gerhard J I, Pang T W, Kueper B H. Time Scales of DNAPL Migration in Sandy Aquifers Examined via Numerical Simulation[J]. Ground Water, 2007, 45(2): 147-157. DOI:10.1111/gwat.2007.45.issue-2 |
| [4] |
杨宾, 李慧颖, 伍斌, 等. 4种NAPLs污染物在二维砂箱中的指进锋面形态特征研究[J].
环境科学, 2013, 34(4): 1545-1552.
Yang Bin, Li Huiying, Wu Bin, et al. Sand Box Study on Fingering Front Morphology for NAPLs Infiltrated in Homogeneous Porous Media[J]. Environmental Science, 2013, 34(4): 1545-1552. |
| [5] |
黄倩, 王锦国, 陈舟, 等. 黏滞性对LNAPL在非饱和多孔介质中优先流影响的试验研究[J].
河海大学学报(自然科学版), 2015, 43(1): 66-71.
Huang Qian, Wang Jinguo, Chen Zhou, et al. Experimental Study of Impacts of Viscosity of LNAPL on Preferential Flow in Unsaturated Porous Media[J]. Journal of Hohai University(Natural Sciences), 2015, 43(1): 66-71. |
| [6] | Nsir K, Schäfer G, Roupert R D C, et al. Laboratory Experiments on DNAPL Gravity Fingering in Water-Saturated Porous Media[J]. International Journal of Multiphase Flow, 2012, 40: 83-92. DOI:10.1016/j.ijmultiphaseflow.2011.12.003 |
| [7] |
施小清, 吴吉春, 刘德朋, 等. 饱和介质中重非水相液体运移的数值模拟及敏感性分析[J].
南京大学学报(自然科学版), 2011, 47(3): 299-307.
Shi Xiaoqing, Wu Jichun, Liu Depeng, et al. Numerical Simulation of Transportation of Dense Non Aqueous Phase Liquids in the Subsurface Environment[J]. Journal of Nanjing University (Nature Science), 2011, 47(3): 299-307. |
| [8] | Fagerlund F, Niemi A, Illangasekare T H. Modeling of Nonaqueous Phase Liquid (NAPL) Migration in Heterogeneous Saturated Media: Effects of Hysteresis and Fluid Immobility in Constitutive Relations[J]. Water Resources Research, 2006, 44: 893-897. |
| [9] |
白静, 赵勇胜, 陈子方, 等. 孔隙介质特性影响Tween80溶液冲洗修复NAPL污染含水层模拟实验[J].
吉林大学学报(地球科学版), 2012, 42(增刊3): 239-244.
Bai Jing, Zhao Yongsheng, Chen Zifang, et al. Experimental Simulation of Porous Medium Characteristics on Tween80 Solution Flushing of NAPL from Contaminated Aquifer[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(Sup.3): 239-244. |
| [10] |
郑菲, 高燕维, 孙媛媛, 等. 污染源区结构特征对Tween 80去除DNAPL效果的影响[J].
中国环境科学, 2016, 36(7): 2035-2042.
Zheng Fei, Gao Yanwei, Sun Yuanyuan, et al. The Influence of Source-Zone Architecture on DNAPL Removal by Tween 80 Flushing[J]. Environmental Science, 2016, 36(7): 2035-2042. |
| [11] |
程洲, 吴吉春, 徐红霞, 等. DNAPL在透镜体及表面活性剂作用下的运移研究[J].
中国环境科学, 2014, 34(11): 2888-2896.
Cheng Zhou, Wu Jichun, Xu Hongxia, et al. Investigation of the Migration Characteristic of DNAPL in Aquifer with Lenses and Under the Action of Surfactant Flushing[J]. China Environmental Science, 2014, 34(11): 2888-2896. |
| [12] |
张蔚, 施小清, 吴剑锋, 等. 渗透率空间变异性对重非水相流体运移的影响[J].
高校地质学报, 2013, 19(4): 677-682.
Zhang Wei, Shi Xiaoqing, Wu Jianfeng, et al. Impacts of the Spatial Variation of Permeability on the Transport of Dense Non-Aqueous Phase Liquids in Porous Media[J]. Geological Journal of China Universities, 2013, 19(4): 677-682. |
| [13] | Yang Z, Zandin H, Niemi A, et al. The Role of Geological Heterogeneity and Variability in Water Infiltration on Non-Aqueous Phase Liquid Migration[J]. Environmental Earth Sciences, 2013, 68(7): 2085-2097. DOI:10.1007/s12665-012-1894-6 |
| [14] |
邓亚平, 郑菲, 施小清, 等. 多孔介质中DNAPLs运移行为研究进展[J].
南京大学学报(自然科学), 2016, 52(3): 409-420.
Deng Yaping, Zheng Fei, Shi Xiaoqing, et al. Review on the Transport of Dense Non-Aqueous Phase Liquids in Porous Media[J]. Journal of Nanjing University (Natural Sciences), 2016, 52(3): 409-420. |
| [15] | Yeh W W. Review: Optimization Methods for Groun-dwater Modeling and Management[J]. Hydrogeology Journal, 2015, 23(6): 1051-1065. DOI:10.1007/s10040-015-1260-3 |
| [16] |
王景瑞, 胡立堂, 尹文杰. iTOUGH2反演模型在地下水模拟中的应用[J].
水文地质工程地质, 2015, 42(1): 35-41.
Wang Jingrui, Hu Litang, Yin Wenjie. Application of iTOUGH2 to Groundwater Modeling[J]. Hydrogeology & Engineering Geology, 2015, 42(1): 35-41. |
| [17] | Lee S J, Mcpherson B J, Vasquez F G. Leakage Pathway Estimation Using iTOUGH2 in a Multiphase Flow System for Geologic CO2 Storage[J]. Environmental Earth Sciences, 2015, 74(6): 5111-5128. DOI:10.1007/s12665-015-4523-3 |
| [18] |
陆乐, 吴吉春. 地下水数值模拟不确定性的贝叶斯分析[J].
水利学报, 2010, 41(3): 264-271.
Lu Le, Wu Jichun. Bayesian Analysis of Uncertainties in Groundwater Numerical Simulation[J]. Journal of Hydraulic Engineering, 2010, 41(3): 264-271. |
| [19] |
陆乐, 吴吉春, 陈景雅. 基于贝叶斯方法的水文地质参数识别[J].
水文地质工程地质, 2008, 35(5): 58-63.
Lu Le, Wu Jichun, Chen Jingya, et al. Identification of Hydrogeological Parameters Based on the Bayesian Method[J]. Hydrogeology & Engineering Geology, 2008, 35(5): 58-63. |
| [20] | Finsterle S. iTOUGH2 User's Guide[R]. Berkeley:Lawrence Berkeley National Laboratory, 1999. |
| [21] | Liang B. An Ensemble Kalman Filter Modulefor Au-tomatic History Matching[D]. Austin: University of Texas, 2007. |
| [22] | Oliver D S, Chen Y. Recent Progress on Reservoir History Matching: A Review[J]. Computational Geosciences, 2011, 15(1): 185-221. DOI:10.1007/s10596-010-9194-2 |
| [23] | Oliver D S, Reynolds A C, Liu N. Inverse Theory for Petroleum Reservoir Characterization and History Matching[J]. Journal of Affective Disorders, 2008, 175C: 488-493. |
| [24] | Evensen G. Sequential Data Assimilation with a No-nlinear Quasi-Geostrophic Model Using Monte Carlo Methods to Forecast Error Statistics[J]. Journal of Geophysical Research, 1994, 99(C5): 10143-10162. DOI:10.1029/94JC00572 |
| [25] | Kalman R E. A New Approach to Linear Filtering and Prediction Theory[J]. J Basic Eng Trans Asme, 1960, 82D(1): 35-45. |
| [26] | Song X, Shi L, Ye M, et al. Numerical Comparison of Iterative Ensemble Kalman filters for Unsaturated Flow Inverse Modeling[J]. Vadose Zone Journal, 2014, 13(2): 1-12. |
| [27] | Geir N, Johnsen L M, Aanonsen S I, et al. Reservoir Monitoring and Continuous Model Updating Using Ensemble Kalman Filter[J]. Society of Petroleum Engineers Journal, 2003, 10(1): 66-74. |
| [28] | Jahanbakhshi S, Pishyaie M R, Boozarjomehry R B. Joint Estimation of Absolute and Relative Permeabilities Using Ensemble-Based Kalman Filter[J]. Journal of Natural Gas Science and Engineering, 2015, 26: 1232-1245. DOI:10.1016/j.jngse.2015.08.029 |
| [29] | Panzeri M, Riva M, Guadagnini A, et al. Data Assi-milation and Parameter Estimation via Ensemble Kalman Filter Coupled with Stochastic Moment Equations of Transient Groundwater Flow[J]. Water Resources Research, 2013, 49: 1334-1344. DOI:10.1002/wrcr.20113 |
| [30] | Liao Q, Zhang D. Data Assimilation for Strongly Nonlinear Problems by Transformed Ensemble Kalman Filter[J]. Society of Petroleum Engineers Journal, 2015, 20(1): 202-221. |
| [31] | Man J, Li W, Zeng L, et al. Data Assimilation for Unsaturated Flow Models with Restart Adaptive Probabilistic Collocation Based Kalman Filter[J]. Advances in Water Resources, 2016, 92: 258-270. DOI:10.1016/j.advwatres.2016.03.016 |
| [32] | Erdal D, Rahman M A, Neuweiler I. The Importance of State Transformations when Using the Ensemble Kalman filter for Unsaturated Flow Modeling: Dealing with Strong Nonlinearities[J]. Advances in Water Resources, 2015, 86: 354-365. DOI:10.1016/j.advwatres.2015.09.008 |
| [33] | Pruess K, Oldenburg C, Moridis G. TOUGH2 User's Guide Version 2.0[R]. Berkeley: Lawrence Berkeley National Laboratory, 1999. |
| [34] |
杨艳林, 许天福, 李佳琦, 等. 应用TOUGH模拟二氧化碳地质储存过程的复杂地质体建模技术与实现[J].
吉林大学学报(地球科学版), 2014, 44(4): 1307-1313.
Yang Yanlin, Xu Tianfu, Li Jiaqi, et al. Complex Geological Body Modeling and Implementation of CO2 Geological Storage Simulation Using TOUGH[J]. Journal of Jilin University (Earth Science Edition), 2014, 44(4): 1307-1313. |
| [35] |
郭亮亮, 张延军, 许天福, 等. 大庆徐家围子不同储层改造的干热岩潜力评估[J].
吉林大学学报(地球科学版), 2016, 46(2): 525-535.
Guo Liangliang, Zhang Yanjun, Xu Tianfu, et al. Evaluation of Hot Dry Rock Resource Potential Under Different Reservoir Conditions in Xujiaweizi Area, Daqing[J]. Journal of Jilin University(Earth Science Edition), 2016, 46(2): 525-535. |
| [36] |
李正伟, 张延军, 郭亮亮, 等. 松辽盆地北部干热岩开发水热产出预测[J].
吉林大学学报(地球科学版), 2015, 45(4): 1189-1197.
Li Zhengwei, Zhang Yanjun, Guo Liangliang, et al. Prediction of Hydrothermal Production from Hot Dry Rock Development in Northern Songliao Basin.[J]. Journal of Jilin University(Earth Science Edition), 2015, 45(4): 1189-1197. |
| [37] | Falta R W, Pruess K, Finsterle S, et al. T2VOC User's Guide[R]. Berkeley: Lawrence Berkeley National Laboratory, 1995. |
| [38] |
高燕维, 郑菲, 施小清, 等. 基于透射光法探讨水流流速对DNAPL运移分布的影响[J].
环境科学, 2015, 36(7): 2532-2539.
Gao Yanwei, Zheng Fei, Shi Xiaoqing, et al. Laboratory Investigation of DNAPL Migration Behavior and Distribution at Varying Flow Velocities Based on Light Transmission Method[J]. Environmental Science, 2015, 36(7): 2532-2539. |
| [39] |
章艳红, 叶淑君, 吴吉春. 光透法定量两相流中流体饱和度的模型及其应用[J].
环境科学, 2014, 35(6): 2120-2128.
Zhang Yanhong, Ye Shujun, Wu Jichun. Models for Quantification of Fluid Saturation in Two-Phase Flow System by Light Transmission Method and Its Application[J]. Environmental Science, 2014, 35(6): 2120-2128. |
| [40] |
史良胜, 杨金忠, 李少龙, 等. 基于KL-Galerkin解法的地下水流动随机分析[J].
四川大学学报(工程科学版), 2005, 37(5): 31-35.
Shi Liangsheng, Yang Jinzhong, Li Shaolong, et al. Stochastic Analysis of Subsurface Flow Based on KL-Galerkin Method[J]. Journal of Sichuan University(Engineering Science Edition), 2005, 37(5): 31-35. |
| [41] |
史良胜, 杨金忠, 陈伏龙, 等. Karhunen-Loeve展开在土性各向异性随机场模拟中的应用研究[J].
岩土力学, 2007, 28(11): 2303-2308.
Shi Liangsheng, Yang Jinzhong, Chen Fulong, et al. Research on Application of Karhunen-Loeve Expansion to Simulating Anisotropic Random Field of Soil Property[J]. Rock and Soil Mechanics, 2007, 28(11): 2303-2308. DOI:10.3969/j.issn.1000-7598.2007.11.010 |
| [42] |
张秋汝, 史良胜, 林琳, 等. 非饱和土壤水的集合卡尔曼滤波:Ⅱ:不一致性问题解决方法比较[J].
水利学报, 2015, 46(12): 1470-1478.
Zhang Qiuru, Shi Liangsheng, Lin Lin, et al. Ensemble Kalman Filter for Unsaturated Soil Water Flow: Ⅱ:Comparison of Methods to Deal with Inconsistency[J]. Journal of Hydraulic Engineering, 2015, 46(12): 1470-1478. |
| [43] |
施小清, 吴吉春, 袁永生. 渗透系数空间变异性研究[J].
水科学进展, 2005, 16(2): 210-215.
Shi Xiaoqing, Wu Jichun, Yuan Yongsheng. Study on the Spatial Variability of Hydraulic Conductivity[J]. Advances in Water Science, 2005, 16(2): 210-215. |
| [44] |
史良胜, 张秋汝, 宋雪航, 等. 地下水位在非饱和水流数据同化中的应用[J].
水科学进展, 2015, 26(3): 404-412.
Shi Liangsheng, Zhang Qiuru, Song Xuehang, et al. Application of Groundwater Level Data to Data Assimilation for Unsaturated Flow[J]. Advances in Water Science, 2015, 26(3): 404-412. |
| [45] |
曹少华, 曾献奎, 蒋建国, 等. 基于局域化集合卡尔曼滤波的含水层弥散度场识别研究[J].
南京大学学报(自然科学), 2016, 52(3): 429-437.
Cao Shaohua, Zeng Xiankui, Jiang Jianguo, et al. An Approach Based on Localized Ensemble Kalman Filter to Identify Groundwater Dispersivity Field[J]. Journal of Nanjing University (Natural Sciences), 2016, 52(3): 429-437. |
| [46] |
宋雪航, 史良胜, 杨金忠. 基于集合卡尔曼滤波的潜水动态预测方法[J].
武汉大学学报(工学版), 2014, 47(3): 324-331.
Song Xuehang, Shi Liangsheng, Yang Jinzhong. Application of Ensemble Kalman Filter to Phreatic Water Flow[J]. Journal of Wuhan University (Engineering Science Edition), 2014, 47(3): 324-331. |
| [47] | Chen Y, Zhang D. Data Assimilation for Transient Flow in Geologic Formations via Ensemble Kalman Filter[J]. Advances in Water Resources, 2006, 29(8): 1107-1122. DOI:10.1016/j.advwatres.2005.09.007 |
| [48] |
崔凯鹏, 吴吉春. 观测数据时空密度对集合卡尔曼滤波计算精度的影响[J].
水利学报, 2013, 44(8): 915-923.
Cui Kaipeng, Wu Jichun. Effect of Observation Data Time/Spatial Density on Ensemble Kalman Filter[J]. Journal of Hydraulic Engineering, 2013, 44(8): 915-923. |
| [49] | Nan T, Wu J. Groundwater Parameter Estimation Using the Ensemble Kalman Filter with Localization[J]. Hydrogeology Journal, 2011, 19(3): 547-561. DOI:10.1007/s10040-010-0679-9 |