2. 吉林市松城建设工程质量检测中心, 吉林 吉林 132000
2. Songcheng Construction Engineering Quality Testing Center of Jilin, Jilin 132000, Jilin, China
0 引言
随着地下矿产资源勘探深度的增加,硬岩钻进的技术难题越来越突出。硬岩钻进困难的主要原因是硬岩致密、强度高、研磨性强、破碎功大。而振动有利于破碎岩石[1-2],在岩石受到合理共振时,其内部会快速产生破损,强度急剧下降,此时,岩石会很容易被破碎。利用共振碎岩也会使钻井速度和钻头寿命大幅度提高。学者们针对振动碎岩作了大量研究,取得了一定的成果[3-4];然而,大多数研究涉及的振动频率较低,与完整致密硬岩的固有频率 (一般为20~38 kHz) 相差悬殊,且对于超声波频率范围内的振动碎岩机理的研究基本属于空白。岩石内部含有随机分布的微裂纹、微孔隙等细观缺陷[5-6],在载荷作用下,这些细观缺陷将发生不可逆的演化,从而导致岩石宏观力学性能的劣化。因此,研究超声波作用下岩石内部裂纹的扩展规律对提高超声波振动碎岩效率具有重要意义。
数值模拟与室内实验相结合的方法被看成是研究岩石内部裂纹扩展规律的有效途径。Cho等[7]通过霍普金森层裂实验考察了应变率对凝灰岩动态拉伸强度的影响,并利用有限元方法分析后认为,由于岩石内部非均匀性引起的应力集中和重新分布,抗拉强度随应变率的增大而增大。Whittles等[8]通过室内落重试验与离散元数值模拟相结合的方法研究了岩样动态断裂过程,分析了应变率和冲击能量对岩石强度以及微裂纹产生数目的影响。Tay等[9]模拟了岩石在冲击作用下的内部裂缝扩展,分别以最大主应力和最大环向应力为强度判定准则,将单元弱化方法引入有限元,改善了以往连续介质求解不连续的问题。Armero等[10]将有限单元嵌入非连续算法,以最大法向应力建立抗拉强度准则,并将裂缝尖端的扩展速度作为重要指标纳入计算方程,分析了岩石裂缝扩展过程,与试验吻合较好。
研究[11-12]表明,岩石材料具有非均匀性,其内部在承受载荷以前已存在随机分布的微裂纹,这类材料的破坏过程受控于其中原有的微裂纹。非均匀性是材料物理力学性质在空间上的非连续性,从细观角度分析,岩石是一种典型的非均匀材料。岩石材料细观结构非均匀性是造成岩石强度差异的主要原因[13],因此,在研究岩石内部损伤过程中不能忽略岩石的非均匀性。建立在统计方法理论基础上的数值模拟方法被看成是解决非均匀性问题的有效途径,这种方法的特点在于运用统计方法来反映由细观单元构成的整体的复杂的力学行为[14]。Weibull [15]最早提出了用概率的方法描述材料的非均匀性,他认为材料局部最薄弱处的破坏将导致整体破坏,因此可以用具有门槛值的幂函数律来描述强度极值分布律。前苏联学者Bonkob[16]认为只有当非均匀材料中构成部分的破裂累计到一定程度后材料才能发生宏观破裂,他利用正态分布函数推导出了破裂发生概率方程。此后又有一些学者在Weibull和Bonkob的理论基础上进行了许多研究[17-18],取得了一定成果。本文采用数值模拟与试验相结合的方法,分析超声波振动下岩石内部原有裂纹的扩展过程,并分析了岩石非均匀性对裂纹扩展过程的影响。
1 数值模拟方法本文将边长0.020 m的正方形岩样模型离散成3 407个二维三角形实体结构单元,初始裂纹长0.005 m,并在模型底端施加约束。考虑到岩石在动静组合加载条件下的破坏强度比单独动载作用下的破坏强度小[19-20],因此在模型顶端施加垂直向下的、振幅40 μm、频率20 kHz的正弦振动及400 N的静压力。岩石的泊松比与密度分别为0.2和2 950 kg/m3。令全部单元的弹性模量服从正态分布以体现岩石的非均匀性,该分布可以按照如下的概率密度函数来定义:
 (1)
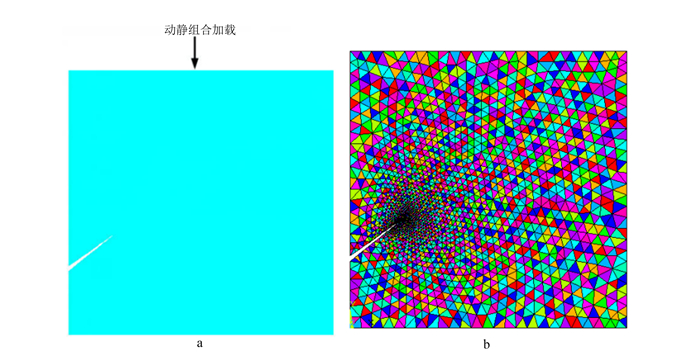
(1) 式中:f(x) 为某一弹性模量值x在总体单元中出现的概率;μ为弹性模量均值,其值为55 Gpa;σ2为岩石的非均匀系数,体现了岩石的不均匀程度,σ越小,岩石越均匀,σ越大,岩石越不均匀。图 1为模型示意图和网格划分情况。
|
| 图 1 模型示意图 (a) 及网格划分情况 (b) Figure 1 Sketch map of the model (a) and its mesh generation condition (b) |
|
|
通过ANSYS瞬态分析完全法对模型进行计算,在计算前进行了如下假设:1) 假设岩石为非均匀的弹脆性体,且认为初始情况下岩石内部除了初始裂纹外无孔隙且不渗透;2) 由于超声波振动振幅很小,岩石的惯性可忽略;3) 破坏准则满足第二强度理论,即当模型内任一单元的最大伸长应变ε1达到了单向拉伸断裂时最大伸长应变的极限值时,此单元就发生断裂破坏,其内部各节点应力为0 MPa,模型应力重新分布直至平衡;4) 由于岩石强度随损伤加剧而降低,强度准则门限值随时间略微减小。
根据以上4点假设,计算具体步骤如下:1) 在每步加载过程中,采用迭代法计算所有节点的位移及应力,直至整个系统达到平衡;2) 根据破坏准则对所有单元的应力状态进行破坏判定,如果满足破坏准则,则根据假设3) 进行死亡处理,并重复步骤1),否则,系统在此次加载过程中达到了真正的平衡。
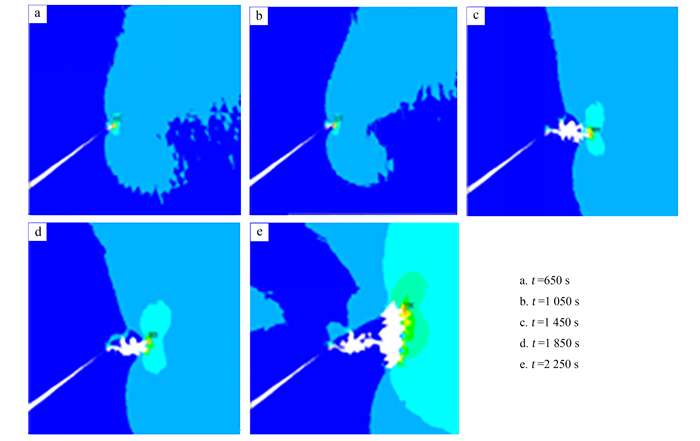
2 超声波振动作用下岩石内部原始裂纹扩展 2.1 数值模拟分析采用ANSYS瞬态分析法对400 N静载与振幅40 μm、频率20 kHz的正弦动载共同作用下岩石内部初始裂纹的扩展情况进行分析。图 2为岩石内部裂纹随时间 (t) 的扩展情况,岩石的非均匀系数为5。由图 2可知,岩石内部原始裂纹首先于裂纹尖端处开始扩展。裂纹尖端处为高应力区,受岩石非均匀性影响,应力等值线具有一定的离散性。根据模拟结果,可将岩石材料原始裂纹在超声波振动下的扩展过程分为萌生、扩展、贯通3个阶段:首先,原始裂纹尖端处某些孤立的节点上产生应力集中,这些节点开裂形成微孔隙,此时为第1阶段 (图 2a、b);随着振动时间的增加,微孔隙不断向四周缓慢延伸,最终沿某一方向形成主裂纹,主裂纹上伴有随机分布的次裂纹,并在主裂纹附近出现新的节点开裂现象,此时为第2阶段 (图 2c、d);随着微孔隙、微裂纹的不断开裂、延伸,这些细观缺陷之间开始相互贯通,形成大面积不规则裂纹,此时为第3阶段 (图 2e)。
|
| 图 2 岩石内部裂纹随时间扩展情况 Figure 2 Extension situation of rock internal cracks over time |
|
|
在对岩石细观结构的研究中,获取不同条件下岩石内部结构的图像并对其进行分析是主要的研究手段,CT识别技术为超声波振动下岩石细观结构变化研究提供了可能[21]。为了验证数值模拟结果的准确性,分别对施加超声波振动300、600、900 s时的岩石试样进行CT扫描及压裂处理,具体试验过程如下:1) 选取完整性和非均匀性较好的花岗岩,根据岩石常规力学性能的测试要求制作直径40 mm、长径比2:1的标准岩样,并对岩样两端进行研磨,使其不平行度小于0.02 mm;采用SY-1型声波测试仪测试各试样的完整性系数,选取完整性系数相近的试样进行试验以降低岩石非均匀性对实验结果的影响。2) 在特制的ZJS-2000型超声波振动装置上分3组进行试验,每组的振动时间分别为300、600、900 s,每组3~5个试样。该装置如图 3所示,由振动器、电源、支架3部分构成,在支架顶端施加400 N竖向静载荷,通过电源驱动振动器施加频率为20 kHz的超声波动载,所施加的动静载荷与数值模拟一致。3) 对各组试样进行CT扫描,每个试样每次扫描100层,选取典型层面的CT图像进行分析。4) 使用WEW-1000D型微机液压万能实验机对各试样进行压裂试验,观测岩石破碎形态。

|
| 图 3 ZJS-2000型超声波振动装置 Figure 3 ZJS-2000 ultrasonic vibration device |
|
|
图 4为典型层面的CT图像,可以看出:当t=300 s和600 s时,岩石内部变化不明显,损伤过程处于节点开裂阶段;随着振动时间的增加,原始裂纹处微孔隙不断扩展形成裂纹,损伤过程逐渐进入第2、第3阶段,当t=900 s时,可以明显看到裂纹在试样圆心处贯通。图 5为不同振动时间下各岩石试样的破碎形态:当t=300 s和600 s时,岩石碎块数较多,这是由于,振动实验所施加的最大静载荷为500 N,远小于岩石的极限抗压强度,岩石内部的结构变化以其受到与岩石试样固有频率相近的超声波动载作用和内应力集中于原始裂纹尖端处导致的裂纹扩展为主;随着振动时间的增加,岩石内部微裂纹相互贯通,形成较大裂纹,当t=900 s时,在压裂过程中试件沿较大裂纹劈裂,碎块数明显减少,在试样垂直方向出现明显的凹形破碎面。分析图 5可知,随着振动时间的增加,试样压裂后的碎块数不断减少,岩石的破碎面越来越明显。CT成像实验与压裂实验很好地验证了数值模拟结论。

|
| 图 4 CT扫描图像 Figure 4 Images for the CT scan test |
|
|

|
| 图 5 不同振动时间的岩石破碎形态 Figure 5 Fragmented morphology of rock under different duration of vibration |
|
|
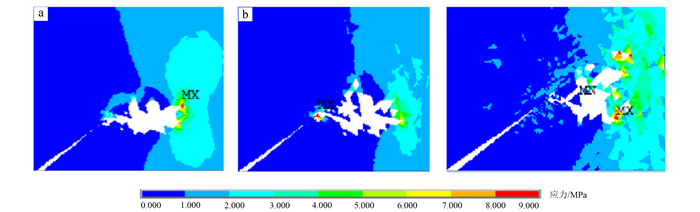
图 6为1 850 s时不同非均匀系数下岩石原始裂纹处局部放大图。对比分析图 6a、b、c可知,受岩石非均匀性影响,即使施加的荷载与振动时间相同,岩石内部的裂纹扩展情况也各不相同:非均匀系数为1时,裂纹尖端处等效应力场分布比较均匀;非均匀系数为5时,等效应力场已具有一定的离散性;非均匀系数为15时,等效应力场离散性十分明显,应力场不连续。根据最大正应力准则,岩石内部高应力区将首先满足破坏准则,产生细观结构上的不可逆变化。显然,随着岩石非均匀系数的增大,其内部应力场分布的离散性增强,进而增大裂纹扩展的随机性。持续振动1 850 s时:非均匀系数为1的岩石内部主裂纹及次裂纹向四周延伸;非均匀系数为5的岩石内部裂纹延伸过程已基本完成,裂纹之间出现相互贯通的趋势;而非均匀系数为15的岩石内部已经出现明显的裂纹贯通现象。可以看出,随着非均匀系数的增加,岩石原始裂纹的扩展效率逐渐增大。
|
| MX.应力最大处;MN.应力最小处。 a.非均匀系数为1;b .非均匀系数为5;c .非均匀系数为15。 图 6 岩石原始裂纹处局部放大图 Figure 6 Partial enlarged images of rock original crack |
|
|
损伤是在外载和环境的作用下,由细观结构缺陷引起的材料或结构的劣化过程。在细观损伤力学中,为了描述岩石内部的微孔隙、微裂纹等细观缺陷的演化过程,引入了抽象的“损伤变量”概念。以二维模型为例,假定材料劣化的主要机制是由于微缺陷导致的有效承载面积减小,则损伤因子可定义为
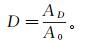 (2)
(2) 式中:A0为材料的原始面积 (mm2);AD为出现损伤的面积 (mm2);D为损伤因子。实际材料的损伤因子介于0和1之间:D=0时材料无损伤,D=1时材料完全损伤。由式 (2) 可知,岩石经过超声波振动一定时间后的损伤因子Dt可表示为
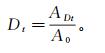 (3)
(3) 式中,ADt为t时刻的损伤面积 (mm2)。令A0=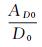
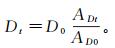 (4)
(4) 式中:D0为初始损伤因子;AD0为初始损伤面积 (mm2)。设Kt为t时刻的损伤增量因子,且Kt=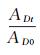
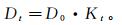 (5)
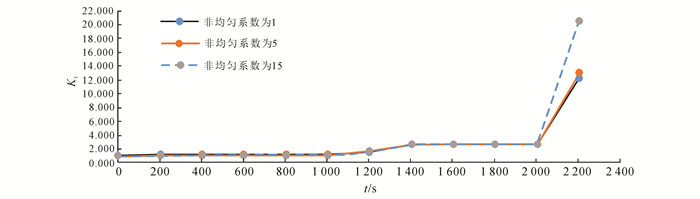
(5) 图 7为不同非均匀系数下Kt随时间的变化情况,岩石初始损伤因子D0为0.002。由图 7可知:当t小于2 000 s时,Kt变化不明显;当t大于2 000 s时,Kt随时间急剧增大,当t=2 200 s时非均匀系数为1、5、15对应的Kt值分别为12.188、12.950和20.513,非均匀系数为15对应的Kt值明显大于前两者。
|
| 图 7 不同非均匀系数下Kt随时间变化情况 Figure 7 Relation curve of Kt against time under different homogeneity coefficients |
|
|
结合公式 (5) 和图 7分析可知,某一时刻的损伤增量因子与非均匀系数的响应关系和损伤因子D0有关。D0存在一个临界值:当D0低于该值时,随着非均匀系数的增大,Kt变化不大,岩石非均匀性对损伤因子几乎没影响;当D0高于该值时,Kt值随着非均匀系数的增大而急剧增大,岩石非均匀性对损伤因子的影响不容忽视。本文中的损伤因子临界值约为0.005 4。
4 结论1) 采用有限元与统计技术相结合的方法,建立岩石二维非均匀性模型,对超声波振动下岩石内部原始裂纹的扩展过程进行数值模拟分析,并通过振动实验对模拟结果进行验证。超声波振动下岩石内部原始裂纹扩展过程主要分为萌生、扩展、贯通3个阶段。
2) 原始裂纹扩展过程与岩石非均匀性之间存在紧密联系。随着非均匀系数的增加,裂纹尖端的等效应力场越来越离散,裂纹扩展的随机性增强,裂纹扩展效率逐渐加快。
3) 引入了损伤增量因子的概念,某一时刻损伤增量因子与非均匀系数的响应关系和岩石的损伤因子D0有关。损伤因子D0存在一个临界值:当D0低于该值时,随着非均匀系数的增大,损伤增量因子变化不大;当D0高于该值时,损伤增量因子随非均匀系数的增大而急剧增大。
| [1] | Atalah A. Effect of Rock Trenching Vibrations on Ne-arby Structures[J]. Journal of Construction Engineering and Management, 2008, 134: 234-241. DOI:10.1061/(ASCE)0733-9364(2008)134:4(234) |
| [2] | Xu G Y, Yan C B. Numerical Simulation for Influence of Excavation and Blasting Vibration on Stability of Mined-Out Area[J]. Journal of Central South University of Technology, 2006, 13: 577-583. DOI:10.1007/s11771-006-0091-8 |
| [3] | Roussy R. The Development of Sonic Drilling Techno-logy[J]. Geodrilling International, 2002, 10: 12-14. |
| [4] | Oothoudt T. Sonic Drilling:An Environmental Impe-rative[J]. Geodrilling International, 1998, 2: 14-16. |
| [5] | Nikolic M, Ibrahimbegovic A. Rock Mechanics Model Capable of Representing Initial Heterogeneities and Full Set of 3D Failure Mechanisms[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 290: 209-227. DOI:10.1016/j.cma.2015.02.024 |
| [6] | Zhong J H. Macro-Fracture Mode and Micro-Fracture Mechanism of Shale[J]. Petroleum Exploration and Development, 2015, 42(2): 269-276. DOI:10.1016/S1876-3804(15)30016-1 |
| [7] | Cho S H, Ogata Y, Kaneko K. Strain-Rate Depen-dency of the Dynamic Tensile Strength of Rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(5): 763-777. DOI:10.1016/S1365-1609(03)00072-8 |
| [8] | Whittles D N, Kingman S, Lowndes I, et al. Labo-ratory and Numerical Investigation into the Characteristics of Rock Fragmentation[J]. Minerals Engineering, 2006, 19(14): 1418-1429. DOI:10.1016/j.mineng.2006.02.004 |
| [9] | Tay T E, Tan V B C, Deng M. Element-Failure Concepts for Dynamic Fracture and Delamination in Low-Velocity Impact of Composites[J]. International Journal of Solids and Structures, 2003, 40(3): 555-571. DOI:10.1016/S0020-7683(02)00623-6 |
| [10] | Armero F, Linder C. Numerical Simulation of Dyna-mic Fracture Using Finite Elements with Embedded Discontinuities[J]. International Journal of Fracture, 2009, 160(2): 119-141. DOI:10.1007/s10704-009-9413-9 |
| [11] | 修立君, 邵明礼, 唐华风, 等. 松辽盆地白垩系营城组火山岩孔缝单元类型和特征[J]. 吉林大学学报 (地球科学版), 2016, 46(1): 11-22. Xiu Lijun, Shao Mingli, Tang Huafeng, et al. Types and Characteristics of Volcanic Reservior Pore-Fracture Units of Cretaceous Yingcheng Formation in Songliao Basin[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(1): 11-22. |
| [12] | 王冠民, 熊周海, 张婕. 岩性差异对泥页岩可压裂性的影响分析[J]. 吉林大学学报 (地球科学版), 2016, 46(4): 1081-1089. Wang Guanmin, Xiong Zhouhai, Zhang Jie. The Impact of Lithology Differences to Shale Fracturing[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(4): 1081-1089. |
| [13] | 杨蔚为, 郑永来, 邓树新. 单元体弹性模量分布对岩石单轴抗压强度影响数值模拟[J]. 长江科学院院报, 2014, 31(9): 84-87. Yang Weiwei, Zheng Yonglai, Deng Shuxin. The Numerical Simulation for the Influence of the Distribution of Unit Elastic Modulus Against Rock Uniaxial Compressive[J]. Journal of Yangtze River Scientific Research Institute, 2014, 31(9): 84-87. |
| [14] | 李志宏. 爆生气体作用下岩石裂纹扩展机理与数值模拟[D]. 西安: 西安理工大学, 2006. Li Zhihong.Mechanism and Numerical Simulation of Rock's Crack Propagaion Under Detonation Gas[D]. Xi'an:Xi'an University of Technology, 2006. |
| [15] | Weibull W A. Statistical Theory of the Strength of Materials[C]//Proceedings of Royal Swedish Institute Engineering Researching. Stockholm:[s.n.]. 1939:1-50. |
| [16] | 沃尔科夫C Д. 强度统计理论[M]. 吴学蔺译. 北京: 科学出版社, 1965. Bonkob С Д.Statistical Strength Theory[M].Translated by Wu Xuelin.Beijing:Science Press, 1965. |
| [17] | 唐春安. 岩石破裂过程中的灾变[M]. 北京: 煤炭工业出版社, 1993. Tang Chun'an. The Catastrophe in the Process of Rock Failure[M]. Beijing: Coal Industry Publishing House, 1993. |
| [18] | Hudson J A, Faihurst C. Tensile Strength Weibull's Theory and a General Statistical Approach to Rock Failure[C]//The Proceeding of Civil Engineering Materials Conference. Southampoton:Srtucture, Solid Mechnics and Engineering Design, 1969:901-904. |
| [19] | Zhang C, Zhang Y J, Li Z W. Experimental Study of Seepage Characteristics of Single Rock Fracture Based on Stress States and Stress History[J]. Global Geology, 2016, 19(3): 1-5. |
| [20] | 马春德. 一维动静组合加载下岩石力学特性的试验研究[D]. 长沙: 中南大学, 2004. Ma Chunde. The Experimental Study of Mechanics Characteristics of Rock Subjected to One-Dimensional Coupled Static and Dynamic Loads[D]. Changsha:Central South University, 2004. |
| [21] | 刘慧. 基于CT图像处理的冻结岩石细观结构及损伤力学特性研究[D]. 西安: 西安科技大学, 2013. Liu Hui.Study on Meso-Structure and Damage Mechanical Characteristics of Frozen Rock Based on CT Image Processing[D]. Xi'an:Xi'an University of Science and Technology, 2013. |



