2. 中国石油塔里木油田公司勘探开发研究院, 新疆 库尔勒 841000 ;
3. 中国石油大学(北京)地球物理与信息工程学院, 北京 102249
2. Research Institute of Exploration and Development, Tarim Oilfield Company, PetroChina, Korla 841000, Xinjiang, China ;
3. College of Geophysics and Information Engineering, China University of Petroleum, Beijing 102249, China
0 引言
陆上地震资料面波非常发育。面波是一种频率低、视速度低、能量强、呈扫帚状频散的规则干扰波,其振幅随着深度的增加而快速衰减[1]。面波是降低反射波地震资料信噪比的重要原因之一,严重影响后续处理和解释质量。因此,如何压制面波一直受到地震资料处理研究人员的关注。
地震资料野外采集观测系统设计的重要一环就是压制面波,其主要是进行检波点组合设计,但是与面波相同频带的反射信号也受到压制。目前工业上常用的压制面波方法主要是基于倾角滤波的方法,如区域滤波、f-k滤波和频率特性的方法如分频异常振幅压制等[2-6]。区域滤波法仅仅考虑了面波频率较低、局部区域分布的特点,压制面波时会伤害相应频带的有效波;而f-k滤波或者多道倾角滤波技术不能区分低频的有效信号和面波;考虑到面波的优势频带主要集中在低频端,可以采用分频滤波的方法进行面波压制。虽然面波一般具有较低的频率,但有效信号的低频成分也与其重合。这些低频有效信号对陡倾角成像、缝洞型储层成像或其他方法如全波形反演、地震反演等技术的有效应用具有重要作用。因此,研发高保真的保幅去面波方法至关重要。
面波在不均匀介质中传播时的频散现象是面波勘探的基础。通过对面波的研究分析,可以很好地刻画浅层近地表结构特征,同时可以对深层准确成像提供一定的帮助。面波模拟去噪方法是一种利用面波而去除面波的手段,通过对面波的分析、反演和模拟,再减去面波干扰。该方法能够在不伤害有效信号的同时很好地去除大部分面波[7]。近些年兴起的曲波变换是一种新的信号分析和图像处理方法,它在保持传统小波多尺度性的同时还具有多方向性和各向异性,更加适合表示地震波前特征。因此,可以对地震数据进行理想的稀疏表示。许多学者在利用曲波变换进行地震资料噪声压制方面做了很多工作[8-13],在面波压制方面取得了优于小波域处理的效果[14-16]。曲波具有很强的方向性,能同时获得对图像平滑区域和边缘部分的稀疏表达。通过将地震数据分为多个尺度和方向,根据有效波和面波在不同尺度不同方向特征的差异,利用有效波和面波在曲波域不重叠的特性,可以对剩余面波进行进一步的压制。
随着油气勘探开发精细程度的不断提高,地球物理工作者越来越重视面波衰减方法和保护有效低频信号的研究。目前基于十字交叉排列的FKK面波压制技术,难以达到理想的去噪效果,严重影响地震资料低频信号保幅性[17-18]。本文提出一种面波模拟和曲波变换的联合面波衰减技术,并用实际数据处理结果验证本次研究方法的有效性。
1 方法原理 1.1 面波模拟如何保幅压制面波噪声一直是地震处理的关键。本次处理先采用面波模拟的方法逐级压制强能量的第一阶、第二阶、第三阶面波,再采用曲波变换技术压制残余面波,达到最大限度保持有效信号的目的。
面波模拟主要分为以下三个步骤。
1) 面波频散曲线提取
基于频率波数(f-k)法提取面波频散曲线。
频率波数域分析方法是可以对多道地震信号d(x,t)进行计算频散曲线的一种有效方法。它对多道面波记录d(x,t)分别沿时间和空间方向作傅里叶变换,便可以将时空域数据d(x,t)变换到f-k域,即:
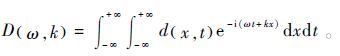 (1)
(1) 其中:ω是圆频率;k是波数,与波长λ的关系为k=1/λ;Dω,k是面波地震记录的f-k域表达。
在得到的面波频率波数谱上,拾取每一个频率上最大频散能量所对应的波数,由f和k便可求得面波以此频率成分谐波传播时的相速度vR=f/k。这样,将所有峰值频率及其对应的相速度vR连成一线,便可以获得面波的频散曲线。
2)面波频散曲线反演
根据频散曲线可以得到f-vR的关系。瑞雷波相速度vR由下列非线性隐函数特征方程F确定:
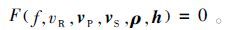 (2)
(2) 其中:向量vPvS、ρ、h分别为纵波速度、横波速度、密度和厚度。vR与f有关。通过不同反演算法便可以反演出浅层的速度模型等信息。
3) 面波正演模拟
通过频散曲线反演获得近地表地层参数(如横波速度、纵波速度等)以后,采用采用交错网格有限差分数值模拟方法对面波进行正演模拟,得到面波记录[19]。为了避免对位移计算二阶导数,引进质点振动速度vx、vy、vz,即位移的一阶导数,则三维各向同性介质瑞雷面波数值模拟推导公式由速度和应力的一阶弹性波方程可表示为
 (3)
(3) 式中:vx,vy,vz是质点速度在x、y、z三个方向的分量;σxx、σyy、σzz分别是质点在x、y、z方向的正应力;τxy、τxz、τyz分别是xy、xz、yz平面内的剪应力;ρ是密度;λ和μ是拉梅常数。
采用边界PML(perfectly matched layer)吸收法,通过傅里叶分析方法,可以得到不同差分精度的稳定条件:
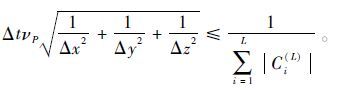 (4)
(4) 式中:Δx,Δy,Δz为三维交错网格间隔;L是空间差分阶数的一半;
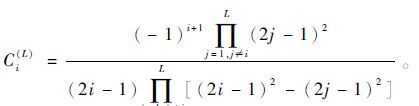
从实际地震记录中减去正演模拟的面波,便去除了大部分高能量面波噪声。
1.2 曲波变换曲波变换结合了小波变换的多尺度特点和脊波变换的各向异性特点,能够对信号进行理想的稀疏表示;在系数项个数相同的情况下,曲波变换的误差最小。因此,曲波变换更适用于信号分析,可以在压制噪声的同时保护有效信号,达到更好的去噪效果。
1) 二维曲波变换
定义尺度为2-j、方位角为θl、位置为xk(j,l)=Rθl-12-jk1,2-j/2k2的曲波为
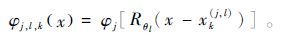 (5)
(5) 式中:j,l∈Z;k=k1,k2为位移参量;x为空间位置参量;(R,θ)为频率域下的极坐标;Rθl表示以θl为弧度的旋转。曲波系数c可以简单地表示为两个元素f∈L2(R2)和φj,l,k的内积(R2代表二维空间):
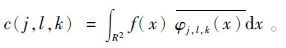
式中:f(x)为x的函数;φj,l,k(x)是φj,l,k(x)的共轭。连续曲波变换在频率域进行。频率域的曲波系数为
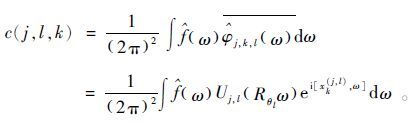 (6)
(6) 二维曲波变换处理三维数据时,没有充分利用三维数据体内所包含的丰富信息。三维曲波变换针对沿着二维曲面上有边缘奇异值的数据,给出了最佳的描述方法,具有敏感的方向特性以及各向异性,能更好地捕捉二维变换所缺失的整体信息。为此,引入了三维曲波变换。
2) 三维曲波变换
三维曲波变换保持了二维曲波变换的性质,它似一个拥有抛物线尺度性质的锲形体作为其频率域支撑。在算法上,三维曲波变换同样也表示为两个元素f∈L2R3和φj,l,k的内积,即
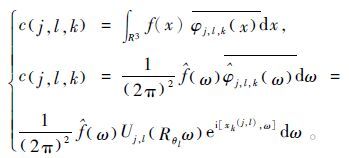 (7)
(7) 其中:j,l∈Z;k=k1,k2,k3为位移参量; x=(x1,x2,x3)为空间位置参量;φj,l,kω的离散表达式为
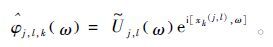 (8)
(8) 式中:Uj,l为频率窗,表示为射线窗Wj和角度窗Vj,l的乘积形式,即
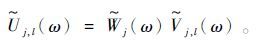 (9)
(9) 其中:
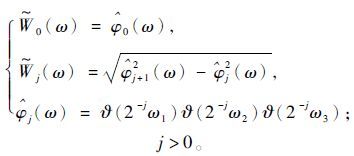 (10)
(10) 式中:j是低通圆滑函数;ω1,ω2,ω3分别为三维笛卡尔网格形式频率正方体的3个坐标轴。
离散三维曲波变换的基函数分割体有6个面,以第1部分(ω1 >0)为例,假设(1,αl,βl)是楔形中心线的方向,角窗口函数定义为
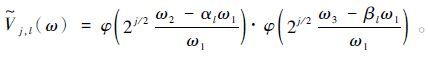 (11)
(11) 对于其他5个部分,交换W1与W2或W1与W3进行类似定义。
1.3 三维曲波阈值迭代法实现消除信号的残余面波噪声采用阈值方法,其关键是阈值和阈值函数的确定。地震数据变换到Curvelet域,在不同的分解尺度和方向上有效波和面波的能量和分布各有不同,如果能够选择合适的分解层次[20],则可对含有面波但同时含有较多有效信号的尺度选择合适的分解层次再次进行分解(多级分解),使面波和有效信号在不同分解尺度和方向上得到更好的分离。然后对面波分布的尺度和方向区域的曲波系数置零,最终得到压制面波后的数据。
鉴于此,采用多级曲波分解和稀疏约束阈值迭代方法[21]:
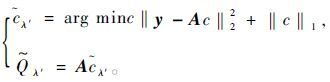 (12)
(12) 式中:y是含噪地震数据;λ′为拉格朗日算子;A表示三维曲波逆变换;Qλ′是最终输出结果。
公式(11)问题是通过迭代阈值技术来求解的,其迭代序列为
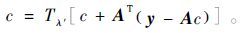 (13)
(13) 式中:AT表示曲波正变换;Tλ′为软阈值函数,其表达式为
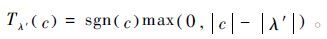 (14)
(14) 阈值根据如下公式选择:
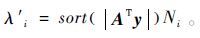 (15)
(15) 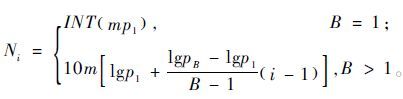 (16)
(16) 其中:sort(·)为数据排序;INT(·)为取整;m为噪声经曲波变换后的曲波系数个数;B表示总的外循环次数;p1为第一次外循环保留的曲波系数百分比;pi为最后一次外循环保留的曲波系数百分比;i为当前循环次数。
2 实际资料去噪塔里木盆地某工区表层调查表明该区的表层结构为低速和高速两层结构:低速层厚度一般为7.5 m,速度为293.5~700.2 m/s;高速层顶界面为一个较平缓的高速顶,速度为1 635~1 788 m/s。面波和浅层多次折射波是该区地震资料的主要噪音,能量较强、分布的时间空间范围大,对反射波造成强干扰。在面波分布带内反射波基本被面波淹没,使反射波记录面貌变差,反射波信噪比低,面波信噪比高,这为面波信息的识别、提取和分析提供了前提。从地震记录(图 1)上可以看出,面波以基阶、一阶、二阶和更高阶存在,同时频散面波也存在(图 2a)。针对该区主要噪音特点,对面波衰减采用如下步骤:先用面波模拟衰减高能量面波,然后压制浅层多次折射波,最后衰减剩余面波。

|
| 图 1 面波模拟法衰减噪音前(a)、后(b)地震记录 Figure 1 Comparison of seismic data before (a) and after (b) the application of surface wave simulation method |
|
|
|
| 图 2 模拟的基阶(a)、一阶(b)和二阶(c)面波噪声 Figure 2 Simulation of surface wave (the basic order(a),the first order (b),the second order(c)) |
|
|
由于数据的有限带宽,地表的非均匀性、特定地下条件和仪器的接收因素,相速度频散是一个区域而不是一个曲线;这些区域的重叠可以导致频散模式识别错误。Rayleigh面波的模式识别错误,可能会导致反演结果的错误。由于频散曲线可能非连续及跳跃,为了防止对速度估计不足或过估,必须准确制作和拾取频散曲线。根据数据特征选择方位角和偏移距范围,切除地滚波以上的能量,产生f-k谱并进行不同阶模式拾取。为了减少近源效应,在产生f-k谱的时候剔除近炮检距,远炮检距数据缺少高频并具有较低信噪比也需要剔除。同时要保证选取的偏移距长度范围适中,如果太短会难以观察到长波长效应,太长会使得横向的变化不明显。
根据高精度f-k谱拾取的频散曲线进行面波正演模拟,然后从数据中自适应减去模拟出的面波噪声。图 1是该方法单炮记录去噪前、后的效果。图 2为模拟的基阶、一阶和二阶面波噪声,难以见到有效信号。图 3是该方法单炮记录去噪前、后的叠加效果。由于采集因素影响,从图 1b和图 3b上可以看出,剖面上还残留更高阶面波和频散面波,需要进一步衰减。
|
| 图 3 面波模拟法衰减噪音前(a)、后(b)叠加对比 Figure 3 Comparison of stack section before (a) and after (b) the application of surface wave simulation method |
|
|
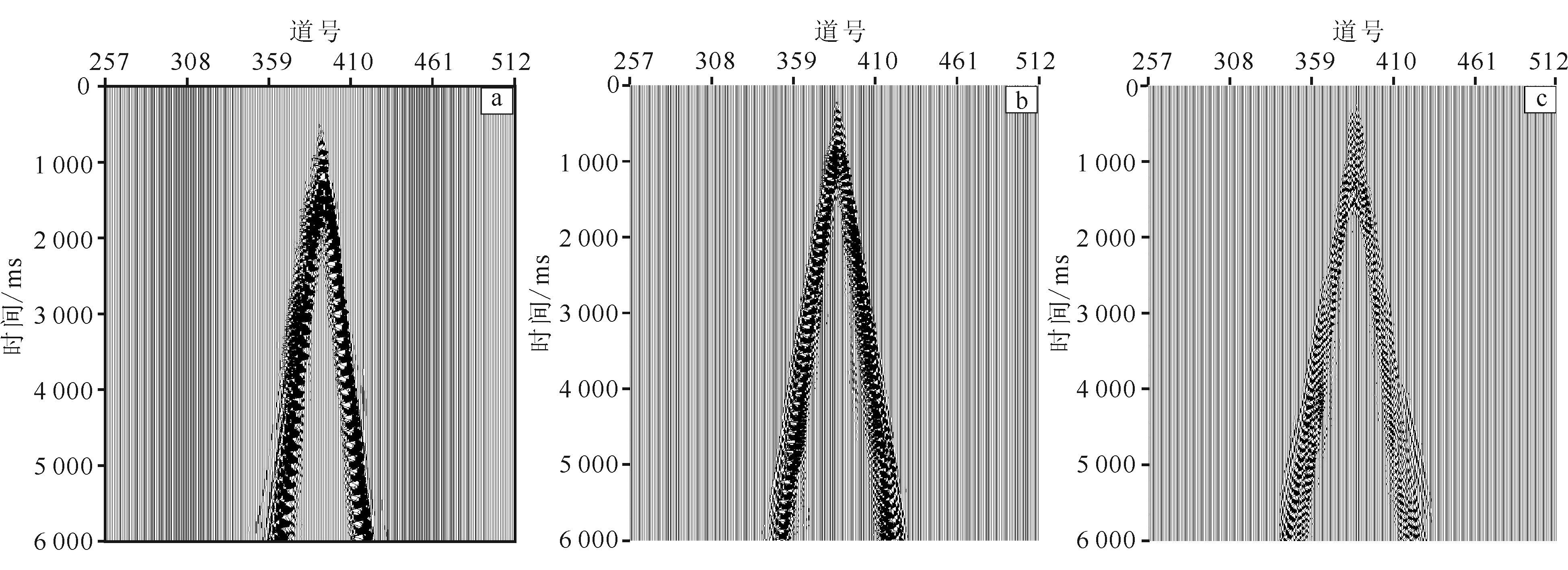
用曲波变换衰减剩余更高阶面波和频散面波之前,对数据进行反褶积处理,压制浅层多次折射波。如图 4a为浅层多次折射波压制后的炮集,图 4b为曲波变换法衰减剩余面波之后的炮集,图 5为相应的叠加剖面对比。由图 4、图 5可以看出,高阶面波和频散面波衰减效果好,大大提高了资料信噪比。

|
| 图 4 曲波变换衰减噪音前(a)、后(b)单炮对比 Figure 4 Comparison of seismic data before (a) and after (b) the application of curvelet transform |
|
|

|
| 图 5 曲波变换衰减噪音前(a)、后(b)叠加对比 Figure 5 Comparison of stack section before (a) and after (b) the application of curvelet transform |
|
|
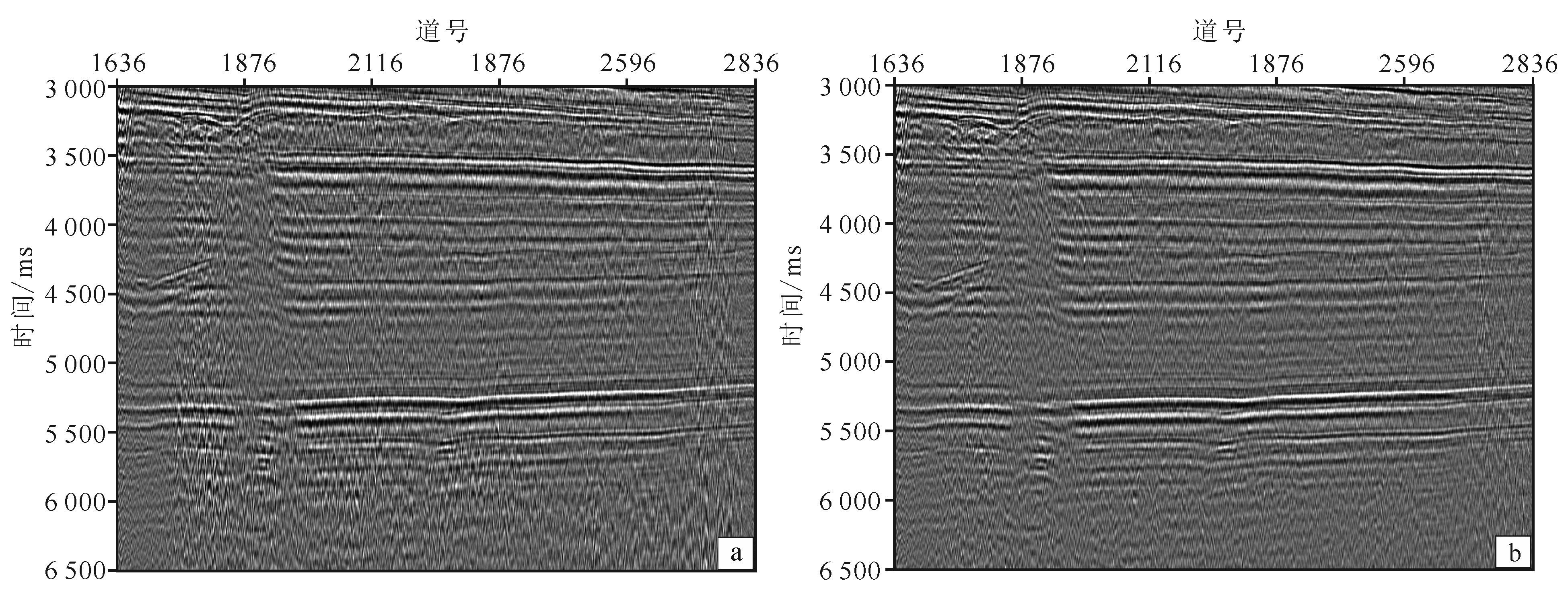
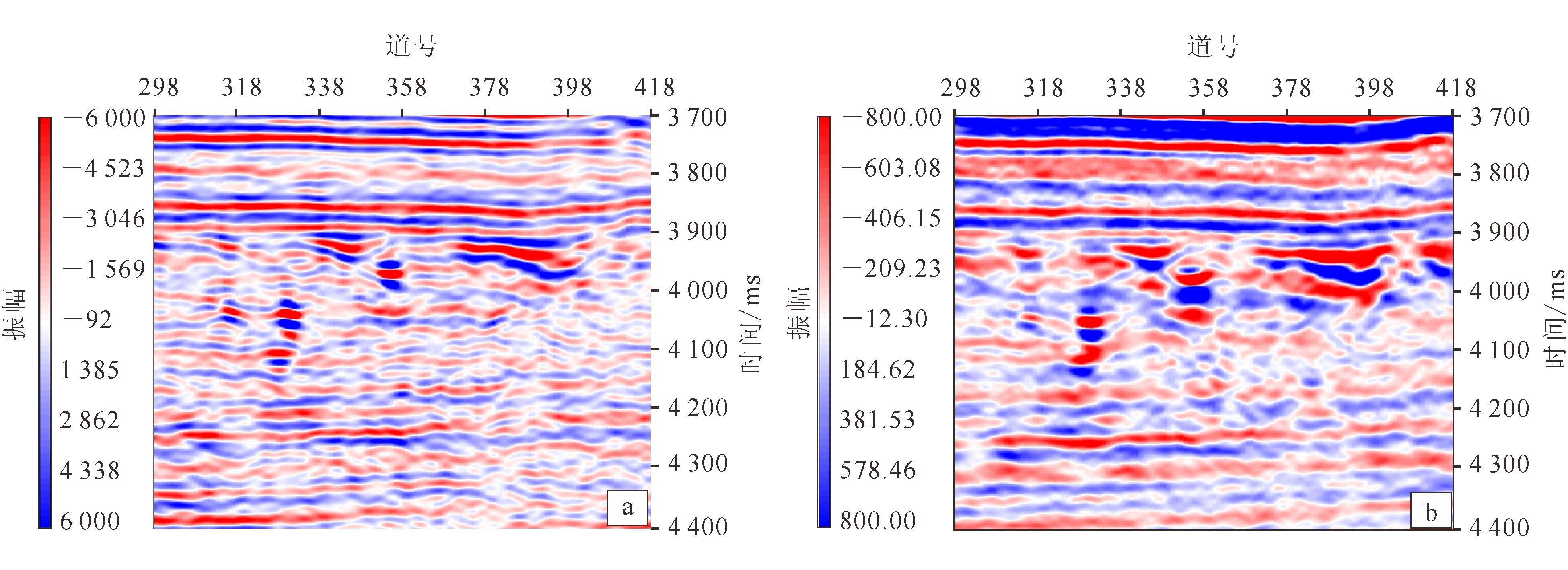
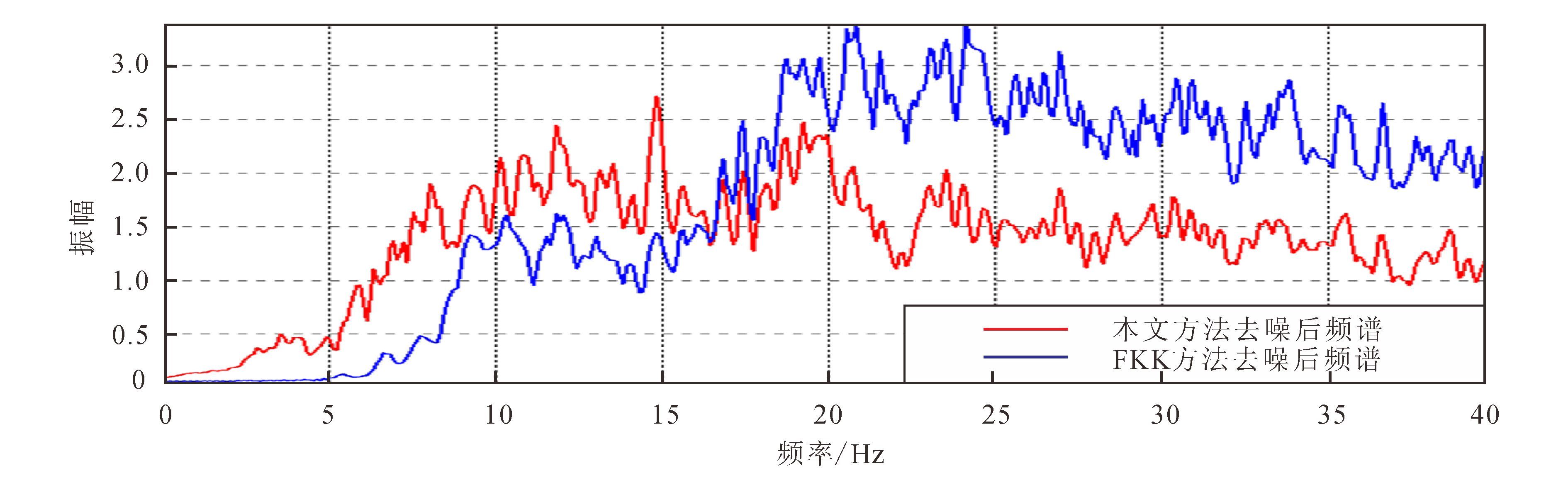
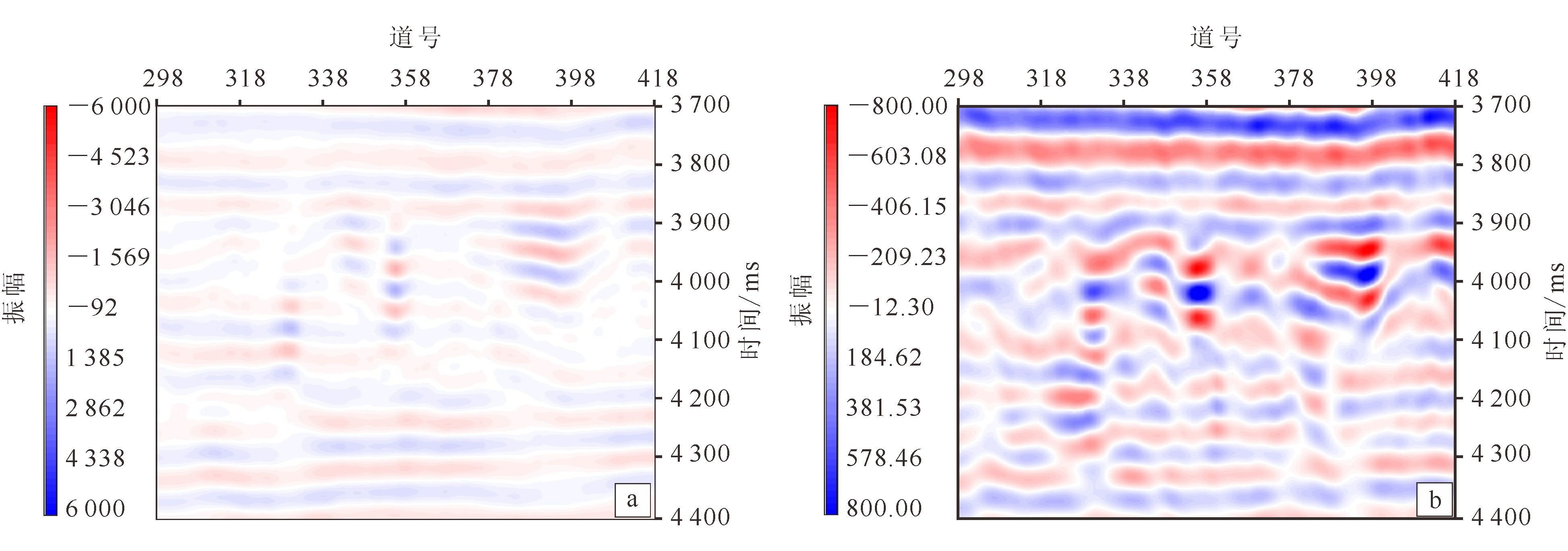
为高保真保幅压制面波噪声,进行了面波模拟正演方法和曲波变换联合去噪技术研究,去噪效果如图 6-8所示。由图 6-8可以看出,本文方法对面波的衰减较常规三维FKK压制方法优势明显,去噪后的叠前时间偏移剖面保留更多有效信号低频信息。由于本文方法去噪后的资料低频信息相对更丰富,更有利于叠前反演、流体检测等技术应用。
|
| 图 6 常规三维FKK去噪(a)与本文方法去噪后(b)PSTM(叠前时间偏移)对比 Figure 6 Comparison of PSTM between 3D FFK(a) and above method(b) |
|
|
|
| 图 7 常规三维FKK与本文方法去噪后频谱对比 Figure 7 Comparison of frequency spectrum between 3D FFK and above method |
|
|
|
| 图 8 常规FKK去噪(a)与本文方法去噪(b)PSTM低频部分对比(6~12 Hz) Figure 8 Comparison of low frequency (6~12 Hz) of PSTM between 3D FFK (a) and above method (b) |
|
|
本文介绍了一种基于面波模拟和曲波变换方法的面波衰减技术。该方法依据面波与反射信号的差异,对低频、高能量的基阶面波采用面波模拟法压制,对剩余的残余面波采用曲波变换方法压制,避免了常规方法依据单一特性进行信噪分离带来的有效信号损伤。在保护低频有效信号的前提下,与常规三维FKK处理方法相比,表明本文方法压制面波更彻底,是一种相对保幅的面波压制方法。实际地震资料处理结果验证了本文方法的优越性,说明具有广阔的应用前景。
| [1] | 渥·伊尔马滋. 地震资料分析:地震资料处理、反演和解释:上册 [M]. 北京: 石油工业出版社, 2006 : 658 -713 . Yilmaz O. Seismic Data Analysis:Processing, Inversion and Interpretation of Seismic Data:Volume I [M]. Beijing: Petroleum Industry Press, 2006 : 658 -713 . |
| [2] | 张军华. 地震资料去噪方法:原理、算法、编程及应用 [M]. 北京: 中国石油大学出版社, 2011 : 70 -95 . Zhang Junhua. Seismic Data Denoising Method:Theory,Algorithm,Programming and Application [M]. Beijing: China University of Petroleum Press, 2011 : 70 -95 . |
| [3] | 孔庆丰. 基于Hilbert-Huang变换的面波压制方法研究[J]. 石油物探 , 2012, 51 (5) : 446-450. Kong Qingfeng. Surface Wave Suppressing Method Based on Hilbert-Huang Transform[J]. Geophysical Prospecting for Petroleum , 2012, 51 (5) : 446-450. |
| [4] | 董烈乾, 李振春, 杨少春, 等. 基于经验模态分解的f-x域面波压制方法[J]. 石油地球物理勘探 , 2013, 48 (1) : 42-48. Dong Lieqian, Li Zhenchun, Yang Shaochun, et al. Ground Roll Suppression in f-x Domain Based on Empirical Mode Decomposition[J]. Oil Geophysical Prospecting , 2013, 48 (1) : 42-48. |
| [5] | 王德营, 李振春, 黄建平, 等. 一种分尺度的面波压制方法[J]. 石油学报 , 2014, 35 (2) : 303-309. Wang Deying, Li Zhenchun, Huang Jianping, et al. A Surface Wave Suppression Method Based on Scale-Partition[J]. Acta Petrolei Sinica , 2014, 35 (2) : 303-309. |
| [6] | Lu J, Wang Y, Yang C Y. Instantaneous Polarization Fil-tering Focused on Suppression of Surface Wave[J]. Applied Geophysics , 2010, 7 (1) : 88-97. DOI:10.1007/s11770-010-0001-6 |
| [7] | Strobbia C, Laake A, Vermeer P, et al. Surface Waves Use Them Then Lose Them[J]. Near Surface Geophysics , 2011, 9 (6) : 503-514. |
| [8] | Herrmann F J, Wang D L, Hennenfent G, et al. Curvelet-Based Seismic Data Processing:A Multiscale and Nonlinear Approach[J]. Geophysics , 2008, 73 (1) : A1-A5. DOI:10.1190/1.2799517 |
| [9] | 张恒磊, 张云翠, 宋双, 等. 基于Curvelet域的叠前地震资料去噪方法[J]. 石油地球物理勘探 , 2008, 43 (5) : 508-513. Zhang Henglei, Zhang Yuncui, Song Shuang, et al. Curvelet Domain-Based Prestack Seismic Data Denoise Method[J]. Oil Geophysical Prospecting , 2008, 43 (5) : 508-513. |
| [10] | 仝中飞, 王德利, 刘冰. 基于Curvelet变换阈值法的地震数据去噪方法[J]. 吉林大学学报(地球科学版) , 2008, 38 (Sup.1) : 48-52. Tong Zhongfei, Wang Deli, Liu Bing. Seismic Data Denoise Based on Curvelet Transform with the Threshold Method[J]. Journal of Jilin University (Earth Science Edition) , 2008, 38 (Sup.1) : 48-52. |
| [11] | 吴爱弟, 赵秀玲. 基于曲波变换的地震信号去噪方法[J]. 中国石油大学学报(自然科学版) , 2010, 34 (3) : 30-33. Wu Aidi, Zhao Xiuling. Seismic Signal Denoising Method Based on Curvelet Transform[J]. Journal of China University of Petroleum (Edition of Natural Science) , 2010, 34 (3) : 30-33. |
| [12] | 董烈乾, 李振春, 王德营, 等. 第二代Curvelet变换压制面波方法[J]. 石油地球物理勘探 , 2011, 46 (6) : 897-904. Dong Lieqian, Li Zhenchun, Wang Deying, et al. The Surface Wave Suppression Using the Second Generation Curvelet Transform[J]. Oil Geophysical Prospecting , 2011, 46 (6) : 897-904. |
| [13] | 姜宇东, 杨勤勇, 何柯, 等. 基于曲波变换的地面微地震资料去噪方法研究[J]. 石油物探 , 2012, 51 (6) : 620-624. Jiang Yudong, Yang Qinyong, He Ke, et al. Surface Microseismic Date Denoising Method Based on Curvelet Transform[J]. Geophysical Prospecting for Petroleum , 2012, 51 (6) : 620-624. |
| [14] | 张之涵, 孙成禹, 姚永强, 等. 三维曲波变换在地震资料去噪处理中的应用研究[J]. 石油物探 , 2014, 53 (4) : 421-429. Zhang Zhihan, Sun Chengyu, Yao Yongqiang, et al. Research on the Application of 3D Curvelet Transform to Seismic Data Denoising[J]. Geophysical Prospecting for Petroleum , 2014, 53 (4) : 421-429. |
| [15] | Wang D L, Saab R, Yilmaz O, et al. Bayesian Ground-Roll Separation by Curvelet-Domain Sparsity Promotion[J]. Geophysics , 2008, 73 (5) : A33-A38. DOI:10.1190/1.2952571 |
| [16] | Zheng J J, Yin X Y, Zhang G Z, et al. The Surface Wave Suppression Using the Second Generation Curvelet Transform[J]. Applied Geophysics , 2010, 7 (4) : 325-335. DOI:10.1007/s11770-010-0257-x |
| [17] | 吴长江. 三维锥形滤波器压制面波的应用效果分析[J]. 工程地球物理学报 , 2010, 7 (1) : 15-18. Wu Changjiang. Application of 3-D Cone-Shaped Filter to Surface Wave Suppression and Its Analysis[J]. Chinese Journal of Engineering Geophysics , 2010, 7 (1) : 15-18. |
| [18] | 石颖, 裴江云, 林春华, 等. 十字交叉排列面波压制方法及应用[J]. 东北石油大学学报 , 2012, 36 (5) : 29-32. Shi Ying, Pei Jiangyun, Lin Chunhua, et al. Surface Wave Suppressing and Application Based on Cross-Spread Approach[J]. Journal of Northeast Petroleum University , 2012, 36 (5) : 29-32. |
| [19] | 张少梅.地震资料面波正演模拟及去噪技术研究[D].青岛:中国石油大学(华东),2011. Zhang Shaomei. Study of Surface Wave Forward Simulation and Denoising Technology[D]. Qingdao:China University of Petroleum(Huadong),2011. http://cdmd.cnki.com.cn/Article/CDMD-11941-2010221062.htm |
| [20] | 邓乐翔.瑞雷波场正演模拟及频散曲线提取[D].西安:长安大学,2010. Deng Lexiang.Rayleigh Wave Field Simulation Modeling and Frequency Dispersion Curves of Extraction[D].Xi'an:Chang'an University,2010. http://cdmd.cnki.com.cn/Article/CDMD-11941-2010221062.htm |
| [21] | Daubechies I, Defrise M, De Mol C. An Iterative Thre-sholding Algorithm for Linear Inverse Problems with a Sparsity Constraint[J]. Communications on Pure and Applied Mathematics , 2004, 57 (11) : 1413-1457. DOI:10.1002/(ISSN)1097-0312 |
| [22] | 孟阁阁, 王德利, 陈鑫. 基于三维曲波变换的地震数据去噪方法研究[J]. 石油物探 , 2014, 53 (3) : 313-323. Meng Gege, Wang Deli, Chen Xin. Study on Seismic Data Denoising Method Based on 3D Curvelet Transform[J]. Geophysical Prospecting for Petroleum , 2014, 53 (3) : 313-323. |


