2. 武汉工程大学资源与土木工程学院, 武汉 430073
2. School of Resource and civil engineering, Wuhan Institute of Technology, Wuhan 430073, China
0 引言
地震滑坡是地震引起岩体或土体沿一个滑坡面滑移一定距离的现象。其在地震发生时及滞后一段时间都有可能发生。当发生强震时,由地震引发的滑坡崩塌造成的危害有时可能比地震本身还要严重,尤其在山区。我国处在世界两大地震带中间,属于大陆地震多发的国家之一,因地震而导致的滑坡及水土流失也是最严重的地区之一。在我国,多震的西部地区是地震滑坡的主要发生地,而边坡地震崩滑以川滇两省为首[1, 2]。
地震滑坡相关问题已得到国内外学者的广泛研究。其中,前人对地震滑坡的统计分析、分类、空间分布规律以及影响因素等方面获得了重要的成果,并在地震滑坡的危险性分析上也取得了一定的进展[3, 4, 5, 6, 7, 8]。尽管如此,地震滑坡的危险性区划在评价单元及分析模型上仍需进一步完善。
笔者以“4·20”芦山地震为例,选择芦山县为研究区,从地形数据中提取斜坡作为评价单元,并构建基于遗传算法的神经网络的评价模型,完成芦山县地震滑坡危险性区划图,以期为芦山县地震灾后预警及评估提供决策支持,同时为地震滑坡危险性区划研究提供新的技术手段。
1 研究区概况及数据源发生于2013年4月20日的芦山地震是继2008年汶川地震后沿龙门山断裂带发生的又一起破坏性地震[9]。芦山县,隶属于四川省雅安市,位于四川盆地西缘,位于102°52′E103°11′E,30°01′N30°49′N,面积达1 364.42 km2。该区域河谷深切,地形起伏大,海拔最低541 m,最高5 279 m。属内陆亚热带湿润气候,气候温和,雨量充沛。研究区的地层岩性主要有二叠系碳酸盐岩和火山岩、石炭系的碳酸盐岩、震旦系白云岩和石灰岩。此次地震震中位于芦山县,是地震诱发滑坡的主要地区[10]。
笔者采用的数据源有:①1∶50 000数字化地形图,用于生成30 m数字高程模型,并从中提取地形地貌、斜坡单元、水文特征等信息;②1∶250 000数字化地质图,从中提取地层岩性、断层、斜坡结构等信息;③2013年10月9日的Landsat ETM+卫星遥感影像1景,轨道号为130/39,用于提取植被指数等信息;④地震参数中的地震峰值加速度(PGA)和加速度反应谱峰值(PSA),由美国联邦地质调查局USGS发布;⑤震后无人机航空影像数据(0.4 m和0.6 m分辨率)。通过遥感解译和野外调查,最终提取了226个地震诱发滑坡,其中最大的面积为0.089 km2,最小的为0.000 1 km2,平均滑坡面积为0.005 km2(图 1)。所有数据转化为格网形式,大小统一为30 m×30 m。
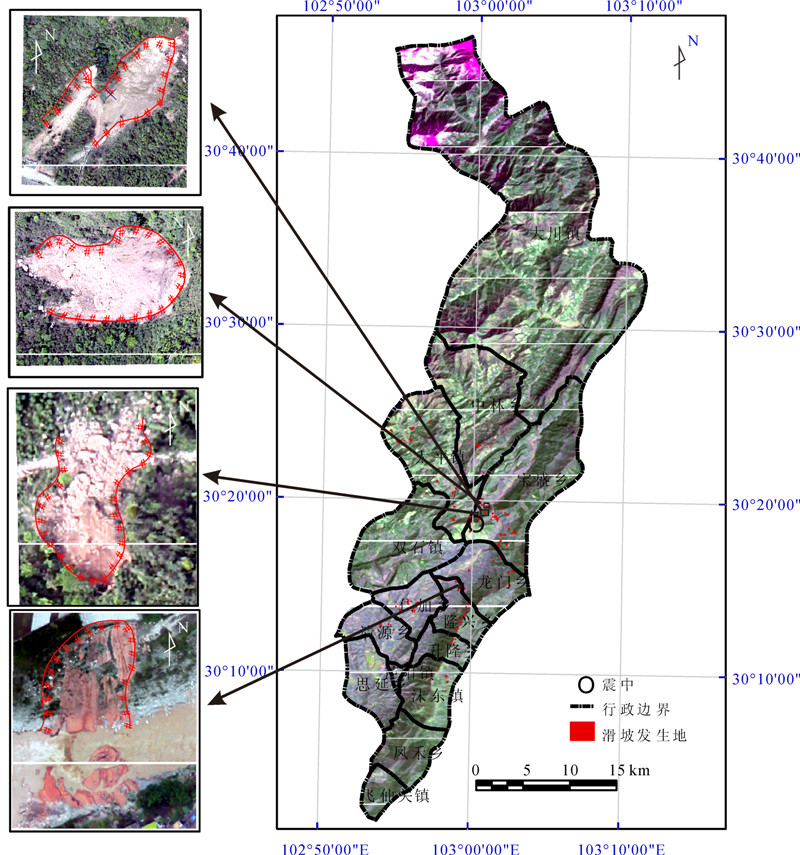 |
| 图 1 研究区滑坡分布及样例图 Fig. 1 Landslide distribution and samples of the study area |
| |
地震滑坡的发生受到多种因素的影响,前人[11, 12, 13]对此做了大量的研究。通过对已有成果的分析,将影响因素分为地形地貌因素、基础地质、水文因素、地表覆被因素和地震诱发因素5大类;根据已有的研究成果,提取地面高程、坡度、坡向、斜坡形态、地层、斜坡结构、断层平均距离(简称断层)、水系平均距离(简称水系)、植被指数(NDVI)、PGA和PSA 11个地震滑坡评价因子;为了确保评价因子之间的独立性,应用皮尔森(Pearson)积矩相关系数对11个评价因子进行相关分析并得出统计结果(表 1)。其中,除PSA和PGA的相关系数为0.841外,其余因子的相关系数均小于0.500。可认为地震诱发因素的两个因子(PGA和PSA)有较强的相关性,而其余因子的相关性较低。考虑到PGA是地震分析的主要因素[12],最后剔除PSA,将剩余10个因子作为地震滑坡的评价因子。
|
Pearson 相关性 | 坡向 | 高程 | NDVI | PGA | PSA | 水系 | 坡度 | 地层 | 断层 | 斜坡结构 | 斜坡形态 |
| 坡向 | 1.000 | ||||||||||
| 高程 | -0.068 | 1.000 | |||||||||
| NDVI | 0.294 | 0.062 | 1.000 | ||||||||
| PGA | 0.002 | -0.505 | 0.044 | 1.000 | |||||||
| PSA | 0.001 | -0.491 | -0.044 | 0.841 | 1.000 | ||||||
| 水系 | -0.002 | 0.297 | 0.097 | 0.009 | -0.030 | 1.000 | |||||
| 坡度 | 0.030 | 0.502 | 0.158 | -0.320 | -0.365 | 0.092 | 1.000 | ||||
| 地层 | 0.042 | -0.438 | 0.186 | 0.488 | 0.440 | 0.036 | -0.240 | 1.000 | |||
| 断层 | 0.014 | -0.324 | -0.183 | 0.156 | 0.139 | -0.104 | -0.298 | 0.105 | 1.000 | ||
| 斜坡结构 | -0.305 | 0.081 | -0.026 | -0.046 | -0.031 | -0.016 | 0.088 | -0.82 | -0.71 | 1.000 | |
| 斜坡形态 | -0.083 | 0.029 | -0.050 | -0.015 | -0.019 | 0.011 | 0.034 | -0.003 | -0.004 | 0.055 | 1.000 |
评价单元作为开展滑坡危险性分析的基本单位,其大小和边界与评价结果有直接关系。在以往的研究中多采用格网单元,其缺点是切割了斜坡整体性;而笔者采用斜坡单元作为评价单元,可克服该缺点,其划分方法为“集水区重叠法”。主要步骤有:先对正、反向数字高程数据进行无洼地填充,然后计算河流流向并生成累计流量图,在此基础上计算河流网络;接着绘制集水区,通过正、反集水区重叠切割和人工修编得到斜坡单元划分图[14, 15, 16]。通过该划分方法,将研究区划分出24 164个斜坡单元。
2.3 评价模型构建构建科学合理的评价模型是确定评价因子对地震滑坡的影响程度,从而挖掘出两者之间关系的重要技术。笔者采用遗传算法结合神经网络的方法构建评价模型。遗传算法(GA)是模仿生物进化思想得出的一种自适应启发式全局搜索算法,而神经网络适合处理规则不明确的复杂问题。将两者结合,通过遗传算法优化BP神经网络权值,从而使神经网络在继承了神经网络自身的广泛映射能力的基础上,具有自适应、增强式学习的能力[17],使之能更好地反映地震滑坡和评价因子之间的关系。具体步骤如下:
1)设置基本参数:BP神经网络输入层、隐含层及输出层的节点数目、种群规模、终止进化代数、交叉概率和变异概率。遗传种群的个体是神经网络的网络权值,将其看成一个整体,编成浮点数编码的染色体,初始种群随机生成。
2)由适应度函数计算种群中每个个体的适应度值。
3)根据代沟值大小通过随机遍历采样法选择算子选择出母体。对该母体分别按交叉概率和变异概率执行交叉和变异,得到待选个体群。依据适应值最小原则选择出新一代种群。
4)如果新一代种群的个体的适应度值满足设定的阈值条件,或者达到了进化代数的最大值,则算法结束,否则迭代数+1转到步骤2)。
5)根据搜索得到的最佳染色体还原到神经网络权值,建立评价模型。
3 地震滑坡危险性评价 3.1 评价因子数据处理由于评价因子数据在数据类型、数值范围及量纲上存在多处不同,在建模之前需对所有数据进行标准化处理。
首先,将数据进行分类。对于连续数据,容易分类的(如坡向)按照常规方法分类;更多的不易分类的(如高程、坡度、断层、水系、NDVI、PGA等)则按自然断点法离散化为排序数据。其中高程等参数采用整数,而NDVI取值是-1~1的小数,由美国USGS提供的PGA值是带有两位小数的小数值,为了保证精度要求,NDVI取三位小数,PGA取两位小数(表 2)。对于离散数据,可按照各自的规则进行分类。如根据岩层的特征将其分为7类(表 3),斜坡结构类型根据斜坡坡度、坡向、下伏地层倾向、倾角这四者在空间上的相互关系及组合可划分为:块状岩体、近水平层状坡、顺向坡、斜向坡、逆向坡、横向坡6大类[15],斜坡形态则可根据平面曲率与剖面曲率的组合分为9类:X/O,X/I,X/GR,V/O,V/I,V/GR,GE/O,GE/I,GE/GR。其中,/左侧的X、V、GE分别表示凸形坡、凹形坡、直线坡,/右侧的O、I、GR分别表示外向形坡、内向型坡、直坡[18]。
| 评价因子 | 分类标准 |
| 坡向 | E,SE,S,SW,W,NW,N,NE |
| 坡度/(°) | [0,10),[10,21),[21,31),[31,41),[41,81] |
| 高程/m | [541,1 190),[1 190,1 797),[1 797,2 528),[2 528,3 526),[3 526,5 279] |
| NDVI | [-1.000,-0.043),[-0.043,0.139),[0.139,0.247),[0.247,0.325),[0.325,1.000] |
| PGA | [0.01,0.15),[0.15,0.26),[0.26,0.38),[0.38,0.48),[0.48,0.61] |
| 断层/m | [0,1 102),[1 102,2 504),[2 504,4 074),[4 074,5 744),[5 744,8 517] |
| 水系/m | [0,499),[499,1 061),[1 061,1 655),[1 655,2 311),[2 311,3 967] |
| 岩层 | 1,2,3,4,5,6,7 |
| 斜坡结构 | 块状岩体、近水平层状坡、顺向坡、斜向坡、逆向坡、横向坡 |
| 斜坡形态 | X/O,X/I,X/GR,V/O,V/I,V/GR,GE/O,GE/I,GE/GR |
注:岩层分类标准中的17对应表3中的编号。
| 编号 | 地层名称 | 岩性描述 |
| 1 | 现代河漫滩冲积物、三级阶地冲击物 | 粉质黏土、砂岩、洪水平原冲积砂砾石 |
| 2 | 白垩系灌口组、夹关组 | 泥岩、砂泥岩、泥灰岩、细砂岩 |
| 3 | 芦山组,二叠系吴家坪组、梁山组、阳新组,三叠系须家河组,侏罗系沙溪庙组、遂宁组、蓬莱镇组, 下第三系名山组 | 红褐泥岩、石英粉砂岩、砂岩、砾岩、生屑灰岩和页岩交替、石英砂岩 |
| 4 | 泥盆系养马坝组、沙窝子组,石炭系雪宝顶组、西沟组,二叠系三道桥组,三叠系飞仙关组 | 微晶灰岩、生物碎屑灰岩和石英砂岩、石灰岩角砾岩、粉砂质泥岩 |
| 5 | 奥陶系宝塔组,泥盆系观雾山组,三叠系雷口坡组、嘉陵江组 | 粉砂岩、石英砂岩、白云灰岩、白云岩、泥灰岩 |
| 6 | 二叠系大石包组、峨眉山玄武岩组 | 玄武岩、闪长岩、英云闪长岩、辉长岩、花岗岩、花岗闪长岩 |
| 7 | 康定(岩)群、黄水河群、盐井群、泥盆系危关组、二叠系菠莰沟组 | 变粗玄岩、变玄武岩、绢云母石英片岩、板岩、石英砂岩、绢云母千枚岩、石英粗面岩 |
然后按照平均值法对数据进行归一化,取值范围为-1~1。
最后,将斜坡单元内的评价因子数据按照统计的方法进行规整。对于连续型数据采取统计斜坡单元内平均值的方式给斜坡单元赋值,如一个斜坡单元内断层的距离为整个单元内所有格网的平均断层距离。对于离散型数据则采取统计单元内占比例最大的类型赋值,如一个斜坡单元内的地层属性是该单元内占比例最大的地层类别。
3.2 样本及参数设置随机选取70%的滑坡及与滑坡样本数量相同的非滑坡区作为训练样本。基于遗传算法的神经网络参数设置包括:BP神经网络输入层、隐含层及输出层的节点数目,激励函数,种群规模,适应度函数,终止进化代数,交叉概率和变异概率。其中:输入层和输出层是由本次评价对象决定的,评价因子有10个,所以BP网络的输入层为10,结果为滑坡的“发生”和“不发生”两类,BP网络的输出层可用1个输出节点表达;激励函数选择Sigmond函数;适应度函数的公式为
终止进化代数为150;种群规模为60。式(1)中:f(xi)为第i个训练样本的危险性指数值;yi为第i个训练样本的样本值;n为训练样本大小;f为适应度函数值。
代沟、变异概率、交叉概率和隐含层节点数对算法性能将产生影响,通过试验我们对这几项数据进行了测试,原则是每组试验中只改变一个参数的数值,其他参数保持不变。首先对代沟参数进行测试,选择最好的参数后再进行其他参数测试;以此类推,得到正确率趋势图(图 2)。
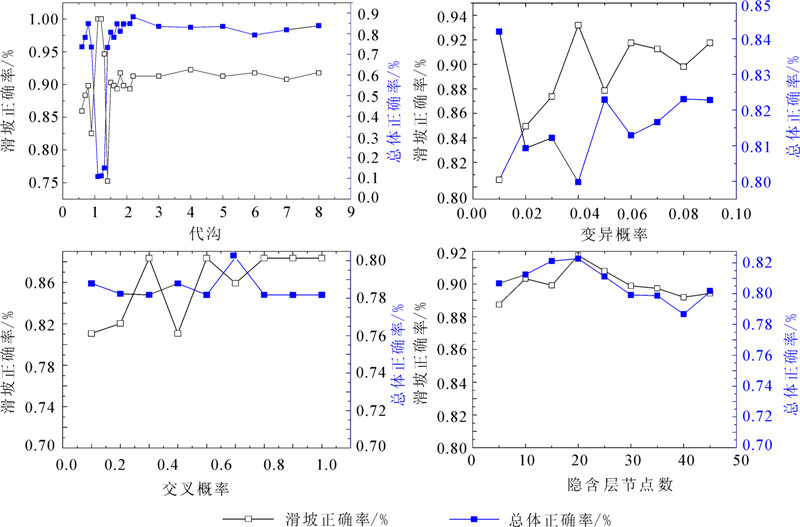 |
| 图 2 不同参数的正确率趋势图 Fig. 2 Accuracy trend of different parameters |
| |
通过综合比较滑坡正确率和总体正确率的实验结果,发现当代沟、变异概率、交叉概率和隐含层节点数分别为1.9,0.09,0.7,20时总体正确率结果最好。因此选择这些参数构建本文的评价模型。
3.3 危险性评价分区利用构建的评价模型计算研究区内每个斜坡单元的危险性指数,取值范围为0~1,越接近1说明危险性越高。然后将数据导入到斜坡单元属性中,并利用自然断点法(划分的危险性指数范围见表 4和表 5)将危险性进行分区,得到芦山地区地震滑坡的危险性分区图(图 3a)。
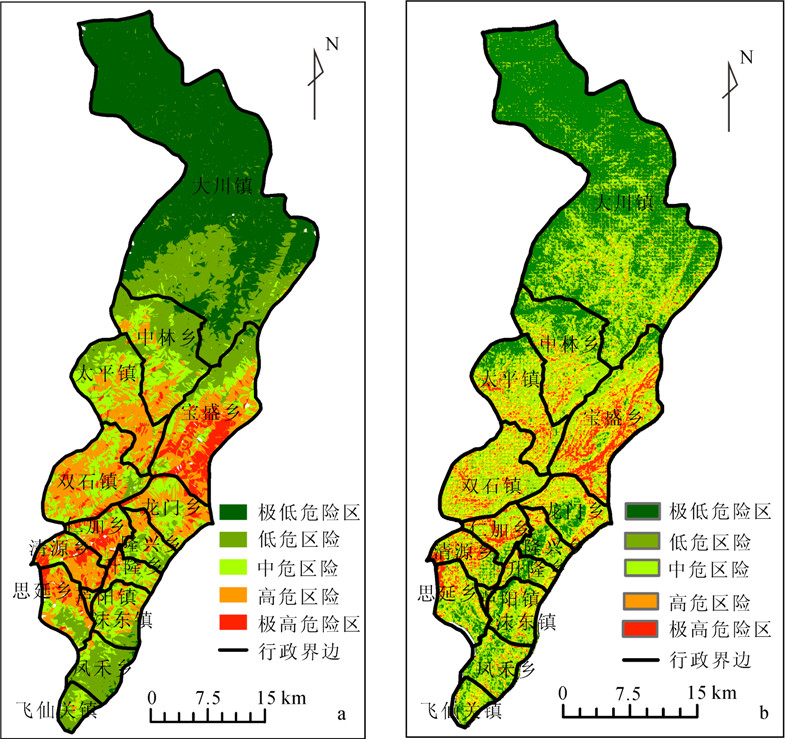 |
| a.斜坡单元; b.格网单元。 图 3 地震滑坡危险性分区图 Fig. 3 Risk zoning of earthquake-induced landslide |
| |
| 危险性分区 | 危险性指数范围 | 分区面积/ km2 | 面积所占 比例 | 分区内 滑坡点个数 | 滑坡所占 比例 | 滑坡密度/ (个/km2) |
| 极低危险区 | 0~0.188 25 | 443.959 30 | 0.376 36 | 0.000 00 | 0.000 00 | 0.000 00 |
| 低危险区 | 0.188 26~0.391 52 | 301.262 07 | 0.255 39 | 29.000 00 | 0.073 79 | 0.096 26 |
| 中危险区 | 0.391 53~0.593 98 | 227.223 01 | 0.192 62 | 87.000 00 | 0.221 37 | 0.382 88 |
| 高危险区 | 0.593 99~0.788 87 | 146.874 72 | 0.124 51 | 121.000 00 | 0.307 89 | 0.823 83 |
| 极高危险区 | 0.788 88~1.000 00 | 60.297 72 | 0.051 12 | 156.000 00 | 0.396 95 | 2.587 16 |
| 总计 | 1 179.616 82 | 1.000 00 | 393.000 00 | 1.000 00 |
| 危险性分区 | 危险性指数范围 | 分区面积/ km2 | 面积所占 比例 | 分区内 滑坡点个数 | 滑坡所占 比例 | 滑坡密度/ (个/km2) |
| 极低危险区 | 0~0.093 74 | 388.150 92 | 0.334 01 | 0.000 00 | 0.000 00 | 0.000 00 |
| 低危险区 | 0.093 75~0.397 78 | 285.762 59 | 0.245 90 | 7.000 00 | 0.033 97 | 0.024 50 |
| 中危险区 | 0.397 79~0.592 00 | 194.872 51 | 0.167 69 | 40.000 00 | 0.194 18 | 0.205 26 |
| 高危险区 | 0.592 01~0.791 00 | 229.237 41 | 0.197 26 | 70.000 00 | 0.339 81 | 0.305 36 |
| 极高危险区 | 0.792 01~1.000 00 | 64.072 20 | 0.055 14 | 89.000 00 | 0.432 04 | 1.389 06 |
| 总计 | 1 162.095 63 | 1.000 00 | 206.000 00 | 1.000 00 |
为了比较斜坡单元和格网单元区划结果的准确性,笔者用同样的评价模型对格网单元的数据(为了控制数据量,格网大小为100 m×100 m)进行了试验,其危险性分区图见图 3b,而两者的定量化统计结果则见表 4和表 5。从表 4、5可知,格网单元的滑坡正确率为92.6%(包含极高危险区、高危险区和中危险区),斜坡单元的滑坡正确率为96.6%。因此斜坡单元的正确率比格网单元高。
同时,不确定性分析也是地震滑坡危险性分析的主要方面,是区划结果可利用性的一个参考指标。为此,采用受试者工作特征曲线(ROC)来进行结果分析比较。ROC 曲线是根据一系列不同的二分类方式,以危险性指数为纵坐标,1-特异性(即错分率)为横坐标绘制的曲线。曲线越陡,则模型的准确性越高;同时ROC曲线下的面积越大也能说明模型的预测评价能力越强。本文的评价模型每次均随机抽样完成评价,通过对5次数据的结果进行分析,得到5次评价结果的ROC曲线图(图 4)。从图 4可见,ROC曲线位置及曲线下面积大小相当,可说明本模型稳定,结果可利用性较高。
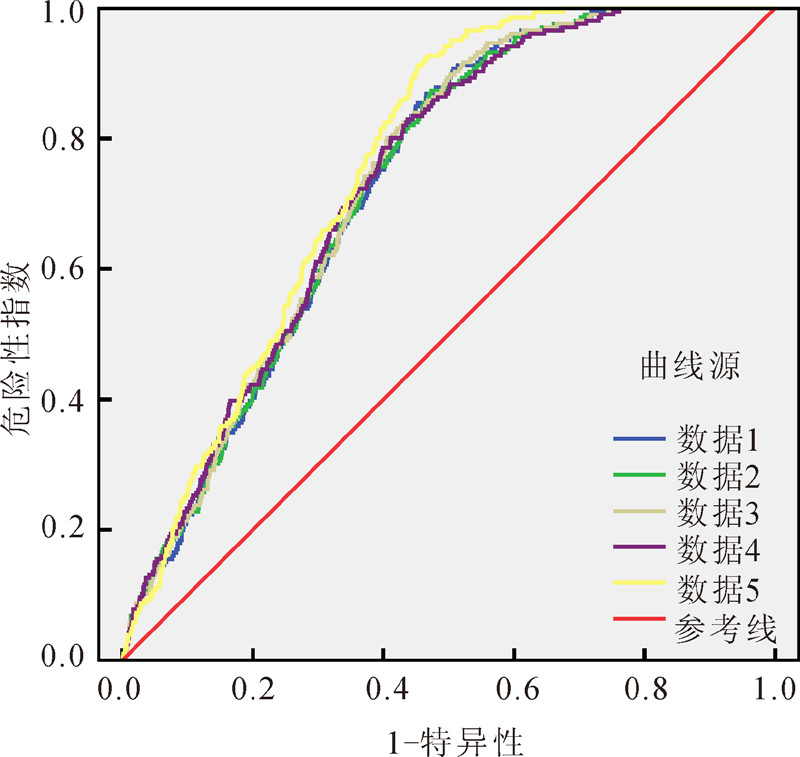 |
| 图 4 不同数据的危险性评价ROC曲线图 Fig. 4 Risk forecast ROC figure of different data |
| |
1)本文通过相关性分析,对地震滑坡的评价因子进行了选择,结果表明地面高程、坡度、坡向、斜坡形态、地层、斜坡结构、断层平均距离、水系平均距离、植被指数、地震峰值加速度两两之间相关性较低,可用来进行危险性分析。
2)对评价模型的代沟、变异概率、交叉概率和隐含层节点数等参数进行了多组测试,最终选择了适合评价模型的参数。
3)根据评价模型计算地震滑坡危险性指数并生成危险性分区图。通过对基于斜坡单元和格网单元的区划结果比较,以及基于斜坡单元的多组随机抽样结果的ROC曲线图分析,发现斜坡单元支持下基于遗传算法的神经网络地震滑坡危险性评价模型具有准确性高、性能稳定、数据量小的优势,其结果可为地震灾后预警及评估提供参考依据。
| [1] | 李树德,任秀生,岳升阳,等. 地震滑坡研究[J]. 水土保持研究,2001,8(2): 24-25. Li Shude, Ren Xiusheng, Yue Shengyang, et al. Study of Earthquake-Landslide[J]. Research of Soil and Water Conservation, 2001,8(2): 24-25. |
| [2] | 李忠生. 国内外地震滑坡灾害研究综述[J]. 灾害学, 2003,18(4): 65-71. Li Zhongsheng. The State of the Art of the Research on Seismic Landslide Hazard at Home and Abroad[J]. Journal of Catastrophology, 2003,18(4): 65-71. |
| [3] | 乔建平, 蒲晓虹, 王萌,等. 大地震诱发滑坡的分布特点及危险性区划研究[J]. 灾害学, 2009,24(2): 25-29. Qiao Jianping, Pu Xiaohong, Wang Meng, et al. A Study on Characteristics of Distribution of Earthquake-Induced Landslides and Hazard Zoning[J]. Journal of Catastrophology, 2009,24(2): 25-29. |
| [4] | 徐桂弘. 地震诱发滑坡的危险性分析与预测[J]. 内陆地震, 2008,22(2): 188-192. Xu Guihong. Analysis and Prediction of Danger of Landslide Caused Earthquakes[J]. Inland Earthquake, 2008,22(2): 188-192. |
| [5] | 许冲, 戴福初, 姚鑫,等. 基于GIS与确定性系数分析方法的汶川地震滑坡易发性评价[J]. 工程地质学报, 2010,18(1): 15-26. Xu Chong, Dai Fuchu, Yao Xin, et al. GIS Platform and Certainty Factor Analysis Method Based Wenchuan Earthquake-Induced Landslide Susceptibility Evaluation[J]. Journal of Engineering Geology, 2010,18(1): 15-26. |
| [6] | 陈晓利, 叶洪, 程菊红. GIS技术在区域地震滑坡危险性预测中的应用:以龙陵地震滑坡为例[J]. 工程地质学报, 2006,14(3): 333-338. Chen Xiaoli, Ye Hong, Cheng Juhong. Use of GIS in Regional Risk Assessment of Earthquake Induced Landslides:A Case Study of Earthquake Induced Landslides in Longling in 1976[J]. Journal of Engineering Geology, 2006,14(3): 333-338. |
| [7] | 许冲, 戴福初, 姚鑫,等. GIS支持下基于层次分析法的汶川地震区滑坡易发性评价[J]. 岩石力学与工程学报, 2009,28(增刊2): 3978-3985. Xu Chong, Dai Fuchu,Yao Xin, et al. GIS-Based Landslide Susceptibility Assessment Using Analytical Hierarchy Process in Wenchuan Earthquake Region[J]. Chinese Journal of Rock Mechanics and Engineering, 2009,28(Sup.2): 3978-3985. |
| [8] | Keefer D K. Investigating Landslides Caused by Ear-thquakes: A Historical Review[J]. Surveys in Geophysics, 2002, 23(6): 473-510. |
| [9] | 孟宪纲, 薄万举, 刘志广,等. 芦山7.0级地震与巴颜喀拉块体中东段的活动性[J]. 吉林大学学报:地球科学版,2014,44(5):1705-1711. Meng Xiangang, Bo Wanju, Liu Zhiguang, et al. Activity in the Middle East of Bayan Har Block with Lushan Ms 7.0 Earthquake[J]. Journal of Jilin University:Earth Science Edition,2014,44(5): 1705-1711. |
| [10] | 常鸣, 唐川, 李为乐,等."4·20"芦山地震地质灾害遥感快速解译与空间分析[J]. 成都理工大学学报:自然科学版, 2013,40(3): 275-281. Chang Ming, Tang Chuan, Li Weile, et al. Image Interpretation and Spatial Analysis of Geohazards Induced by "4·20"Lushan Earthquake in Epicenter Area[J]. Journal of Chengdu University of Technology: Science & Technology Edition, 2013,40(3): 275-281. |
| [11] | 陈晓利, 冉洪流, 祁生文. 1976年龙陵地震诱发滑坡的影响因子敏感性分析[J]. 北京大学学报:自然科学版, 2009,45(1): 104-110. Chen Xiaoli, Ran Hongliu, Qi Shengwen. Triggering Factors Susceptibility of Earthquake-Induced Landslides in 1976 Longling Earthquake[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2009,45(1): 104-110. |
| [12] | 王秀英, 聂高众, 马牧军. 地震滑坡灾害评估中地震影响因素的联合应用[J]. 地震学报, 2012,34(1): 76-84. Wang Xiuying, Nie Gaozhong, Ma Mujun. Application of Multiple Ground Motion Factors in Earthquake-Induced Landslide Hazard Evaluation[J]. Acta Seismologica Sinica, 2012,34(1): 76-84. |
| [13] | 侯景瑞, 袁中夏. 汶川地震滑坡与影响因素[J]. 西北地震学报, 2011,33(增刊1): 398-402. Hou Jingrui, Yuan Zhongxia. Influence Factors of the Landslides Caused by Wenchuan Earthquake[J]. Northwestern Seismological Journal, 2011,33(Sup.1): 398-402. |
| [14] | 彭令. 三峡库区滑坡灾害风险评估研究[D]. 武汉:中国地质大学, 2013. Peng Ling. Landslide Risk Sssessment in the Three Gorges Reservoir[D]. Wuhan:China University of Geosciences,2013. |
| [15] | 丁辉. 基于遥感技术滑坡灾害区划研究[D]. 西安:长安大学, 2011. Ding Hui. Study on Landslides Geo-Hazard Zoning[D].Xi'an: Chang'an University, 2011. |
| [16] | 武雪玲, 任福, 牛瑞卿,等. 斜坡单元支持下的滑坡易发性评价支持向量机模型[J]. 武汉大学学报:信息科学版, 2013,38(12): 1499-1503. Wu Xueling, Ren Fu, Niu Ruiqing, et al. Landslide Spatial Prediction Based on Slope Units and Suppert Vector Machines[J]. Geomatics and Information Science of Wuhan University, 2013,38(12): 1499-1503. |
| [17] | 田旭光, 宋彤, 刘宇新. 结合遗传算法优化BP神经网络的结构和参数[J]. 计算机应用与软件, 2004,21(6): 69-71. Tian Xuguang, Song Tong,Liu Yuxin. Optimizing the Structure and Parameters of BP Neural Network Based on Genetic Algorithm[J]. Computer Applications and Software, 2004,21(6): 69-71. |
| [18] | 李景富, 牛瑞卿. 基于GIS的斜坡结构图自动化制图方法研究[J]. 人民长江, 2009,40(19): 38-40. Li Jingfu, Niu Ruiqing. Automated Mapping Method of Slope Structure Image Based on GIS[J].Yangtze River, 2009,40(19): 38-40. |




