2. 重庆大学土木工程学院, 重庆 400044;
3. 长安大学地质工程与测绘学院, 西安 710054;
4. 中铁第四勘察设计院集团有限公司, 武汉 430063
2. School of Civil Engineering, Chongqing University, Chongqing 400044, China;
3. College of Geological Engineering and Geomatics, Chang'an University, Xi'an 710054, China;
4. China Railway Siyuan Survey and Design Group Co., Ltd., Wuhan 430063, China
0 引言
反倾边坡一般较稳定,但在特殊的工程地质条件下反倾边坡却有可能发育深层倾倒,进而转变为大型深层滑坡,如锦屏水文站滑坡即由倾倒发育而成,两岸斜坡的倾倒变形深度均超过220 m[1]。西部地区水电工程的建设揭露了许多反倾边坡的倾倒变形现象,如狮子坪二古溪倾倒[2]、拉西瓦果卜倾倒[3]、苗尾坝址区倾倒[4]等,其对工程建设与安全运营造成了巨大的潜在威胁。
倾倒变形是一种较典型的重力时效变形过程,离心模型试验通过高速旋转的离心力形成远大于模型自重的重力场[5],对边坡施加体力,能够更加真实地再现倾倒变形过程。已有部分学者[6-9]将离心试验应用于反倾边坡的研究中,取得了良好的效果,但其高昂的试验成本限制了大规模应用。数值模拟可重复性强,且可提供较丰富的数据,实时记录模型变形破坏过程,可作为试验研究的有效补充。目前反倾边坡研究常用的数值方法有有限元法[10]、离散元法(discrete element method)[11]、DDA(discontinuous deformation analysis)法[12]等。反倾边坡通常不存在典型滑动面,其破裂面的形成取决于岩层的断裂,而离散元法可充分考虑不连续面的影响,并实现岩层的变形与破裂,在研究反倾边坡方面具有独特的优势。如:程东幸等[13]基于龙滩岸坡的单因素分析得出,坡角和倾角都大于40°时,反倾边坡才可能发生比较明显的倾倒;蔡跃等[14]根据不连续理论,讨论了坡高、倾角以及岩层厚度等几个重要影响因素的相互关系;李明霞等[15]通过UDEC/3DEC软件对多种主控因素的单因素分析,认为层面力学参数的影响最为显著。
现有的数值模拟研究大多较好地考虑了层面、层厚、坡角、倾角等参数对反倾边坡的影响[13-15],但由于未考虑或无法实现岩层的断裂,反倾边坡破裂面形成机制仍有待研究。本文基于离心模型试验,对反倾边坡的倾倒变形过程进行了离散元数值模拟,通过在岩层内预置大量随机微裂隙,以实现较真实的岩层断裂;在此基础上,共进行了170组数值试验,通过单因素分析,研究坡角、倾角对边坡稳定及破坏模式的影响,通过正交试验分析,研究材料参数的影响,以期进一步深入研究反倾边坡变形机理。
1 离散元数值模型的构建 1.1 离散元数值方法与模型建立离散元法(DEM)是一种分析离散介质变形和运动趋势的有力工具,在20世纪80年代被引入我国,其适用于求解非连续介质大变形问题,广泛应用于节理化岩体、碎裂结构岩质边坡的变形破坏分析。DEM区别于其他数值方法的主要特征在于:其能反映块体之间接触面的滑移、分离和翻转等不连续变形,还能计算块体内部的变形和应力分布状态;其可以用于求解非线性大位移和动力稳定问题,利用显式时间差分解法来求解动力平衡方程。反倾边坡的变形破坏受结构面的影响十分显著,且岩层的弯折破裂对其整体破裂面的形成具有重要影响,基于此,将离散元法应用于反倾边坡变形破坏机理的研究中是十分合适的。
Adhikary等[6, 16]采用脆性和柔性相似材料开展了7组不同结构反倾边坡倾倒变形的离心模型试验,取得了良好效果。本文以其中的脆性材料模型(IGM-01)作为原型,并在岩层间预置了大量的随机裂隙,通过离散元数值模拟,先实现对反倾边坡离心模型试验过程的还原;进而通过改变数值模型倾角、坡角等关键参数,研究反倾边坡倾倒变形的影响因素,以获得反倾边坡破裂面起裂与延展特征。
反倾边坡数值模型与离心模型试验的物理模型边坡几何尺寸及主要结构相同,如图 1所示,其岩层倾角80°,坡角61°,坡高330 mm。为简化起见,模型暂未考虑层面外的其他结构面,在岩层内预置泰森多边形随机裂隙,网格最大边长15 mm,最小边长5 mm,共划分3 672个块体。模型左右两侧及底部为固定边界,顶部及坡面为自由边界。为实现大变形,设置模型块体为刚性块体。
层面采用常用的面接触-库仑滑移节理模型(Coulomb slip-area contact),需要节理黏聚力cj、节理摩擦角φj、节理抗拉强度σtj、节理法向刚度Kn、节理剪切刚度Ks等5个参数[17]。其中,cj、φj和σtj参考物理模型参数进行取值,Kn值采用Diederichs等[18]推导的下列方程估算:
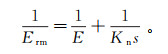 (1)
(1) 式中:Erm和E分别为岩体和完整岩石的弹性模量,Pa;s为节理间距,m。
层内微节理采用面接触-具有残余强度的库仑滑移模型(Coulomb slip with residual strength-area contact),该模型适用于描述内部开裂[19],需要黏聚力cij、内摩擦角φij、抗拉强度σit、残余黏聚力cijr、残余内摩擦角φijr、残余抗拉强度σitr、微节理法向刚度Kin和微节理剪切刚度Kis等8个参数。其中cij、φij、σit、cijr、φijr、σitr等前6个参数代表完整岩石的强度,与物理模型一致。物理模型边坡材料为钛铁矿砂和15% 石膏混合料,模型参数见表 1。
微节理法向刚度Kin使用Cho等[20]提出的公式确定:
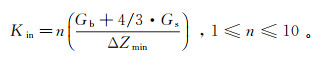 (2)
(2) 式中:n为附加调整系数;Gb和Gs为别为块体的体积模量和剪切模量,Pa,结合物理模型参数综合取值;ΔZmin为垂直方向上与接触面相邻区域的最小宽度,m。通过多次试算与微调,最终参数见表 2。
| 模型参数 | 刚性块体 | 层内微节理 | 层面 |
| 密度/(kg/m3) | 2 380 | — | — |
| 抗拉强度/MPa | 1.4 | 1.4 | 0 |
| 法向刚度/(1010 N/m) | — | 28.0 | 8.0 |
| 剪切刚度/(1010 N/m) | — | 25.0 | 7.5 |
| 黏聚力/MPa | 3.4 | 3.4 | 1.5 |
| 内摩擦角/(°) | 22 | 22 | 15 |
| 残余摩擦角/(°) | 18 | 18 | 12 |
离心模型试验通过逐步提高离心机转速,逐级增加模型的加速度场和有效自重,实现对边坡倾倒变形的模拟。因此,数值模拟模仿离心机加载过程,首先对边坡施加自重荷载(1g),计算至初始平衡,之后间隔5g逐级增加重力,每级加载设置足够的时间步(最大20万步),以保证稳定的模型响应。当检测到最大不平衡力小于1×10-5 N时,当级加载自动结束。
离心模型试验通过激光位移传感器和线性电压位移传感器(LVDT)监测模型位移,位移观测点(位观点)位置如图 1a所示。为实现对数值模拟结果的对比验证,在数值模型边坡坡面相同位置布置位观点,同时在坡体内等间距布置若干个位观点(图 1b),以分析坡体不同位置的变形特征。
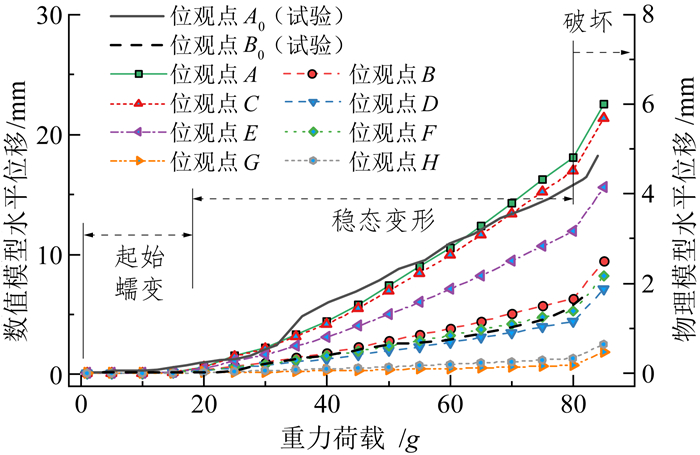
从加载结束后的边坡变形特征和水平位移-荷载曲线两个方面对数值模拟与离心模型试验的结果进行对比验证。由图 2可见,二者的最终变形形态均呈现明显的“叠合悬臂梁”式破坏特征,最深部破裂面呈直线形,破裂面与原始岩层层面方向的夹角均约70°。从二者的水平位移-荷载曲线(图 3)角度分析可知,边坡均在加载至80g后迅速破坏,破坏前位移较小(< 5 mm),发生破坏后边坡瞬间整体失稳,可见数值模拟与物理试验的变形破坏过程吻合较好,仅位移量值存在一定差异,验证了模拟方案的有效性。
进一步分析水平位移-荷载曲线(图 3)可见,反倾边坡的变形破坏过程可明显分为3个阶段:①起始蠕变阶段,0~20g,位移量极小,坡体内无变形,岩体为弹性变形;②稳态变形阶段,20g~80g,位移曲线近似线性增大,边坡变形体向前均匀倾倒,此变形不可逆,为重力时效累进变形;③失稳破坏阶段,80g及以后,整体破裂面贯通,坡体位移量骤增,变形体向前快速倾倒,边坡整体失稳。将破裂面贯通时的荷载值称为破坏荷载Gf,由图 3可见,数值模型边坡的破坏荷载Gf为80g。
|
| 图 3 水平位移-荷载曲线 Fig. 3 Horizontal displacement-load curve |
|
|
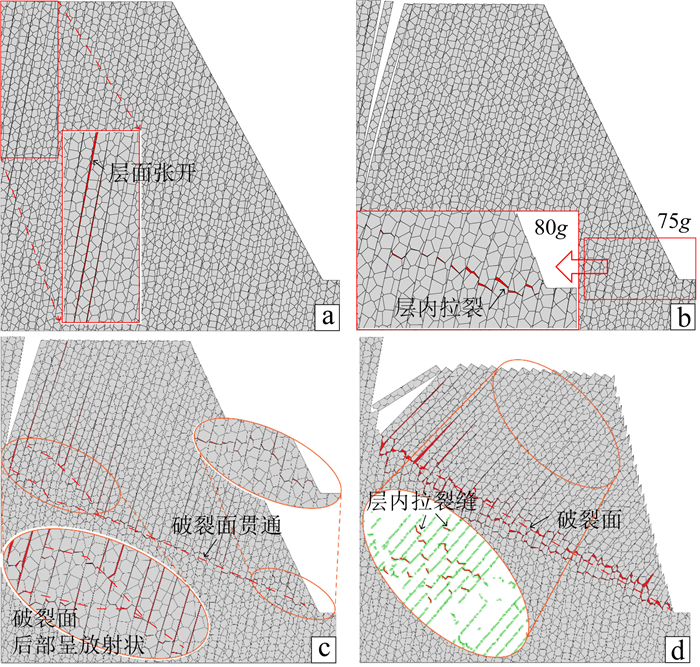
数值模型在起始蠕变阶段变形极小,宏观上几不可见。但当边坡进入稳态变形阶段(阶段②)后,首先在坡顶后缘出现较明显的拉张裂缝(图 4a),说明边坡变形体已向临空面方向发生缓慢的倾倒变形。
|
| a. 35g;b. 75g~80g;c. 85g;d. 90g。 图 4 数值模型宏观变形 Fig. 4 Macroscopic deformation of numerical model |
|
|
之后边坡变形体持续向前较均匀的弯曲直至加载至75g时,变形岩层发生较明显的弯曲,边坡临空面处岩层可见轻微的相对错动,但坡体除后缘的拉张裂缝外其他部位尚未出现明显的破坏现象(图 4b)。加载至破坏荷载Gf(80g)时,边坡进入临界破坏状态,坡脚已发育局部横向拉张裂隙(图 4b)。
继续增重一级(85g),横向裂隙在坡体内贯通(图 4c),破裂面形成。破裂面在一级荷载内迅速成型,符合实际调查得出的脆性岩石反倾边坡“折而立断”的变形特征[4]。此时后缘岩层的拉张脱层现象明显。
继续进行一级加载(90g)后,边坡破裂面附近的拉裂区明显扩大(图 4d),后缘进一步强烈拉张,并由岩层折断坠覆;岩层间剪切错动强烈,坡顶及坡面已呈明显的锯齿状,坡脚岩体有明显的挤出趋势,变形体中上部已可见次级拉裂区。此时边坡的变形现象已与物理实验的破坏形态(图 2a)非常接近。对比可见,数值模型的破裂面同样呈现明显的直线形,破裂面中后部逐渐延向上伸出斜率更大的局部拉裂;整体破裂面与原始岩层间夹角为70°,与物理模型边坡高度接近,进一步验证了模拟方案的有效性。
根据模拟结果可对边坡的进一步变形趋势做出合理推测:继续加载,坡脚岩体断裂、坠覆,与母体脱离而在坡脚形成空腔,进而使上部岩体失去支撑,变形加剧;之后,变形体内自下而上形成多级破裂带,且各破裂带均接近垂直于其各自下方临近处岩层;最后,变形体由外向内沿不同的破裂面逐级折断、垮落,形成渐进后退式破坏。
2.2 塑性区塑性区特征可反映岩石的变形屈服情况。模拟表明,边坡在80g时,坡脚发育零星屈服面,在85g时,屈服面沿近垂直层面方向遍布坡体。图 5为破坏后典型时刻的塑性区分布图。由图 5a可见:在85g时,最新屈服面位于塑性区最上部,说明岩层的屈服呈近直线型由下向上扇形扩展;在90g时,主破裂带处的屈服面更加密集,但范围并未明显扩大,而是在变形体上部发育了新的屈服区,与次级破裂带位置基本一致。由于塑性区计算采用变形体,岩层的变形趋势稍弱,但整体上塑性区的分布与演变与横向裂隙的演变一致,佐证了前文的判断。

|
| a. 85g塑性区;b. 90g塑性区。黑圈为最新屈服面位置,紫圈为历史屈服面位置。 图 5 数值模型变形破坏与塑性区 Fig. 5 Deformation and plastic zone of numerical model |
|
|
在坡体内典型位置呈网状布置6个位观点(C—H),位置如图 1b所示,各点的水平位移-荷载曲线见图 3。对比各点的位移大小不难发现,水平方向上(点C—A、点D—F—B、点G—H),位移越靠边坡临空面量值越大;竖直方向上(点C—D、A—E—F—G、B—H),越靠近坡顶,位移量越大。位于破裂面以下的位移点(点G)全程位移量均极小,而破裂面以上的各位移点的位移趋势高度接近,验证了反倾边坡的“叠合悬臂梁”式变形特征,即变形体各处具有相似的动力学特征。
边坡位移云图表明,加载初期(20g以前),位移场无明显指向性(图 6a),位移由坡顶放射状递减;进入稳态变形阶段后,位移场逐渐沿层面渐变(图 6b),相同岩层越靠外侧位移越大;破裂面贯通以后(85g),位移集中于破裂面以上,沿层面向外侧递增。
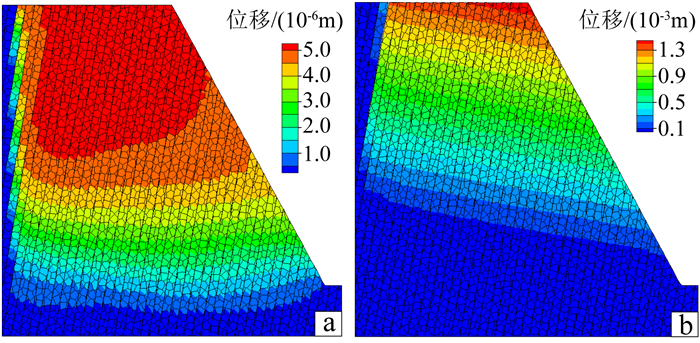
|
| a. 20g;b. 35g。 图 6 数值模型位移场 Fig. 6 Displacement field of numerical model |
|
|
倾角和坡角对反倾边坡的变形破坏机制具有重要影响,从其对破坏荷载Gf、临界位移df、破裂面产状以及破坏模式的影响角度分别进行探讨。
3.1 对破坏荷载的影响试算得出,当岩层倾角α或边坡坡角β小于35°时,边坡极难发生破坏,因此α、β均在35°~90°区间内等间隔5°取值,共进行144组数值试验。对坡体内出现典型破裂面的边坡进行统计,引入临界系数κ评价边坡稳定性,定义为
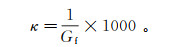 (3)
(3) κ值越大,边坡达到破坏所需荷载越小,稳定性越差。将计算结果绘制成二维气泡图(图 7),其可直观反映倾角和坡角对κ值的耦合影响规律。
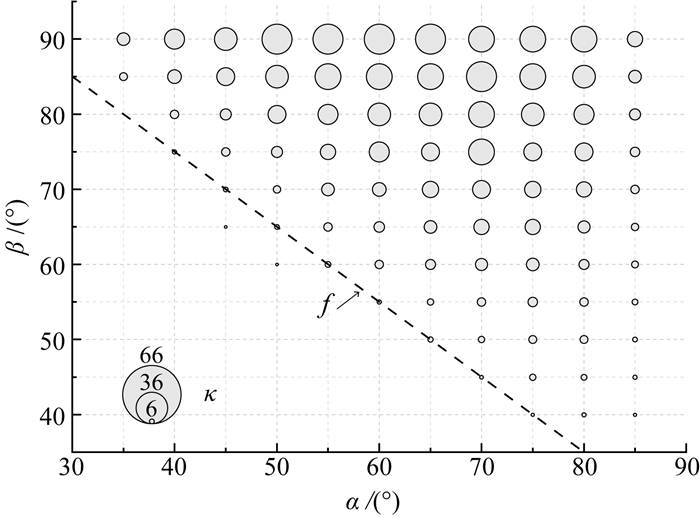
|
| f为倾角与坡角的组合关系函数。气泡直径代表κ值大小。 图 7 临界系数气泡图 Fig. 7 Critical coefficient bubble diagram |
|
|
由图 7明显可见,发生破坏的边坡均落在倾角-坡角气泡图的右上三角区域,可见理想状态下,当倾角与坡角的值满足一定条件时,反倾边坡才能发生破坏。根据图 7的统计,易发生倾倒破坏的反倾边坡的倾角和坡角一般满足如下函数关系:
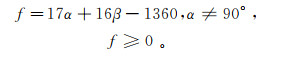
进一步分析坡角、倾角对Gf的单因素影响规律,结果见图 8。由图 8a可见,坡角一定时,Gf均随倾角的增大而先减小后增大。倾角α较小时,岩层临空条件差,倾倒弯矩的力臂较短,随着倾角的增大,力臂增长,倾倒弯矩逐渐增大;因此,当α较小(一般小于60°)时,Gf随α增大而迅速减小。当α足够大时,重力沿垂直层面方向的分量已变得较小,虽然力臂较长,但弯矩变小,因而α增大到近直立时,Gf反而逐渐增大。Gf最小值通常处于α为70°~80°区间,此时岩层所受弯矩最大,边坡稳定性最差。当α无限接近于90°时,无论坡角如何改变,边坡均不破坏;此时岩层完全直立,重力几乎没有垂直层面方向的分量,岩层缺少沿水平方向位移的推动力。

|
| a. 保持坡角β相同; b. 保持倾角α相同。 图 8 破坏荷载随倾角和坡角的变化 Fig. 8 Relationship of failure load with dip and slope angle |
|
|
图 8b表明,当倾角α一定时,Gf随坡角β单调变化,β越大,Gf值越小,边坡越容易破坏。在大多数倾角-坡角组合中,β大于60°时,Gf曲线斜率明显减小,Gf值稳定在较小的水平,可见当β大于60°时,边坡更易破坏。
对岩层进行简化的受力分析,如图 9所示,取坡顶A′点,分析其作用在坡脚C′点处的弯矩。假设A′点重力为G,则其垂直层面方向的分量为
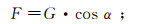
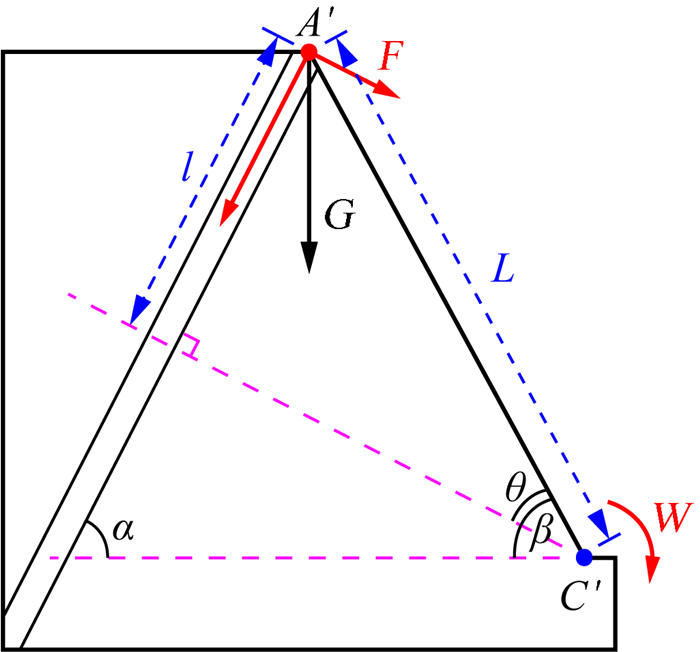
|
| 图 9 岩层受力分析简图 Fig. 9 Sketch of force analysis of rock layer |
|
|
设坡面长度为L,则力臂长度为
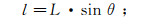
A′点岩层作用在C′点处的弯矩为
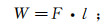
根据几何关系,整理可得
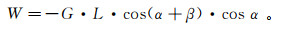
式中:F为垂直层面方向的分量,N;l为力臂长度,m;W为弯矩,N·m。G与L值恒定,假设其乘积为1。将倾角和坡角值代入,可得图 10所示关系曲线。不难发现,各坡角下,随着α增大,弯矩先增大后减小。对比图 8a可见,只有当W-α曲线中弯矩接近或达到峰值以后,具有对应的倾角、坡角组合的边坡才会发生破坏。坡角为90°时,弯矩值已减小为0.0,印证了前文的分析。此外,当倾角、坡角均较小时,弯矩为负值,即方向相反,从力学角度验证了此时边坡极难破坏。
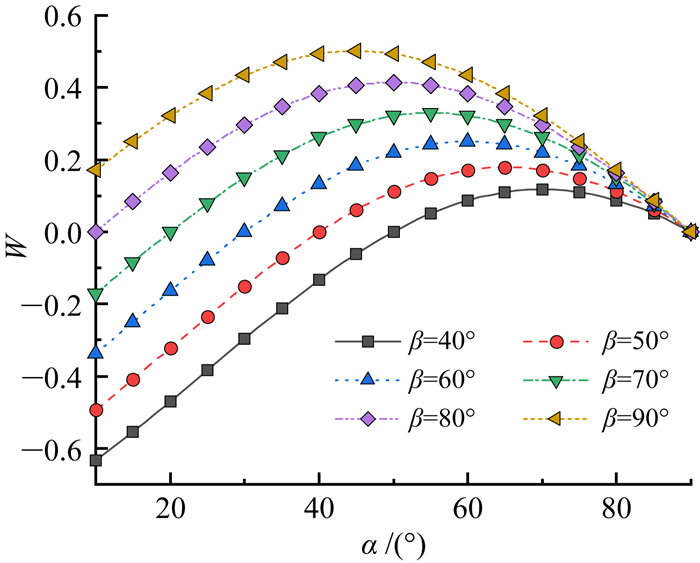
|
| 图 10 岩层弯矩与倾角关系图 Fig. 10 Relation between bending moment and dip angle |
|
|
破裂面贯通时的坡体位移值(记为临界位移df)反映了边坡稳态时效变形程度的强弱,由于实际倾倒边斜坡大多处于该阶段[21],因此该阶段的位移阈值对反倾边坡的监测预警有指示作用。图 11表明,该位移随倾角增大而近似幂函数增大,且倾角较大时,位移值增速更快。

|
| R为相关系数。 图 11 坡顶位移随倾角的变化 Fig. 11 Relationship of top displacement with dip angle |
|
|
部分学者研究认为反倾边坡的破裂面通常与层面法向呈5°~11°的夹角[6, 19],总结本文数值模型的破裂面与层面法向的夹角(γn-f)发现,γn-f随岩层倾角的增大而近似线性增大,同时破裂面与水平面的夹角(γh-f)则随倾角增大而线性减小(图 12a)。当坡形一定时,γh-f直接影响变形体体积,即原岩倾角越大,破裂面倾角越小,变形体规模越大,边坡变形的潜在威胁也就更大。而当倾角一定时,坡角改变对γn-f的影响很小,但坡角的增大使坡面与破裂面间夹角(γs-f)直线增大(图 12b),即变形体规模显著增大。
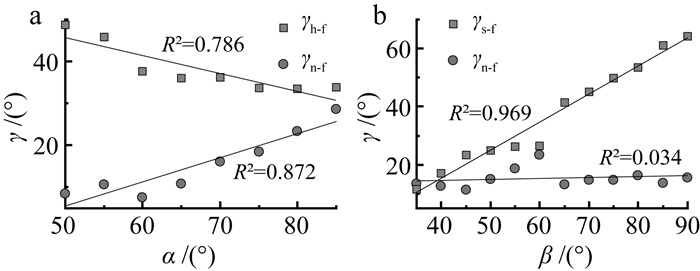
|
| 图 12 倾角、坡角对破裂面与层面法向夹角的影响 Fig. 12 Relation of γ with dip and slope angle |
|
|
对不同倾角、坡角组合下的边坡破坏模式进行归纳汇总(图 13)发现,反倾边坡主要存在3种破坏模式,并且受倾角和坡角关系的直接影响,具体表现为:

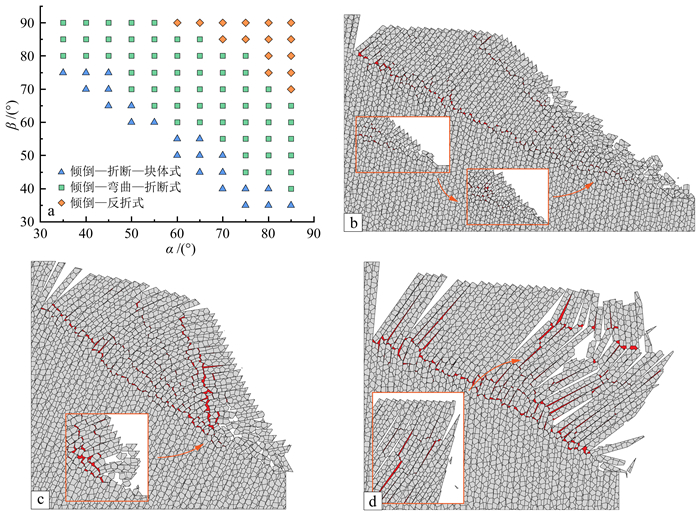
|
| a. 破坏模式汇总;b. 倾倒—折断—块体式;c. 倾倒—弯曲—折断式;d. 倾倒—反折式。 图 13 倾角和坡角对破坏模式的影响 Fig. 13 Relation of failure mode with dip and slope angle |
|
|
1) 倾倒—折断—块体式破坏
在倾角较大而坡角较小,加载至Gf时,破裂面贯通后,坡脚岩体随即折断、挤出,进而在变形体浅层形成二级破裂面;之后该面以上岩体很快即破碎成块,自下而上呈崩塌式垮落,原有层序几不可辨,堆积于坡脚(图 13b)。
2) 倾倒—弯曲—折断式破坏
倾角、坡角均中等时,边坡发生倾倒—弯曲—折断式破坏。底裂面贯通后,上部岩体在重力弯矩作用下持续弯曲,导致自下而上逐渐形成多条破裂带,破裂面与其下部临近处岩体变形后折断前的层面法向小角度相交(图 13c);随着弯曲程度的增大,坡脚岩体首先折断而脱离母体,进而引起上部较浅层破裂面以上岩体垮落、坠覆。岩层仍基本保持原有层序。
3) 倾倒—反折式破坏
当倾角、坡角均较大时,发生倾倒—反折式破坏。破裂面贯通初期,变形岩体保持原始层型向前倾倒,岩层间拉张脱层强烈发育,中前部岩层在加载到一定程度后发生折断,折断面以下岩体继续向前倾倒,倾倒程度加剧;而折断面以上岩体变形滞后,逐渐形成反向弯曲,变形体形成“S”形失稳破坏(图 13d),上部岩层层序发生倒转。吴昊等[8]在以平板玻璃为相似材料的离心模型试验中,发现在边坡倾角和坡角较大时存在类似变形现象。
4 基于正交设计的参数敏感性分析除倾角、坡角等关键性边坡结构条件外,岩层及层面的物理力学性质对反倾边坡变形破坏的影响也不容忽视。但由于影响因素众多,若一一对比进行单因素分析将造成海量的工作量,几乎不可能实现。因此,本节基于正交设计原理,对岩体力学参数进行敏感性分析。
4.1 正交试验原理正交设计法仅挑选代表点开展试验,各数据点均衡分散、齐整可比,试验效率高[22]。正交试验对全部因素而言是部分试验,但对其中任两个因素却是重复次数相同的全面试验[23],且各因素间可进行有效的横向对比。
在设计好正交因素水平后,可通过SPSS软件内嵌专用模块自动生成正交表,依据正交表所列参数组合开展试验,并对结果进行极差分析。极差分析基本原理为:设Mij表示第i水平、第j列下各工况计算结果平均值,第j列因素的极差Rj为Mij中的最大值与最小值之差:
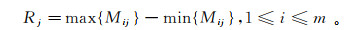
式中,m为水平数,文中m=5。极差Rj反映了第j列因素的水平变动时试验指标的最大变动幅度,文中j=t、c、φ、ρ、η。研究[22]表明,Rj越大,表明该因素敏感性越高,其水平改变对指标影响越显著。
4.2 正交表格设计正交试验组模型边坡的倾角、坡角与初始模型(即通过物理模型校核的数值模型)一致。经多次试算,层内随机裂隙的参数对边坡的宏观影响较小,因此岩石参数中仅考虑密度ρ的影响。实际倾倒边坡多具有软硬互层结构[4],为考虑软硬岩性差异,引入密度比η,并定义为硬岩与软岩密度的比值,赋值时保持硬岩参数不变。层面参数的影响显著,特别是黏聚力c、内摩擦角φ值[15],重点考虑其影响,在初始参数基础上各增减二级取值。同时考虑层厚t的影响,最终取5个因素,每因素设5个水平,为L25(55)正交试验,各因素水平取值见表 3。
| 水平 | t/mm | c/kPa | φ/(°) | ρ/(kg·m-3) | η |
| 1 | 10 | 5 | 5 | 1 380 | 1.0 |
| 2 | 15 | 10 | 10 | 1 880 | 1.5 |
| 3 | 20 | 15 | 15 | 2 380 | 2.0 |
| 4 | 25 | 20 | 20 | 2 880 | 2.5 |
| 5 | 30 | 25 | 25 | 3 380 | 3.0 |
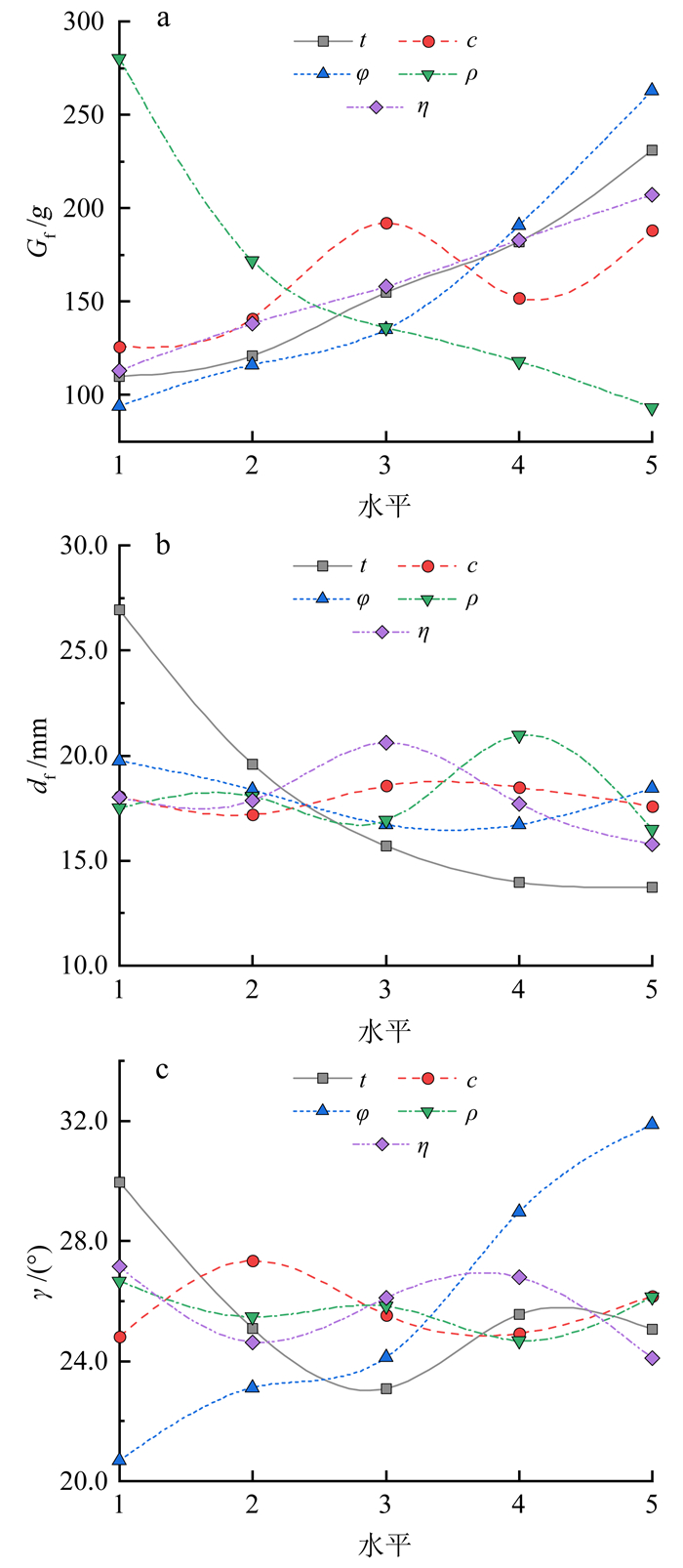
同样选取破坏荷载Gf、临界位移df、破裂面倾角γ等3个敏感性评价指标。极差分析结果及直观分析曲线分别见表 4与图 14。
| 水平 | Gf /g | ||||
| t | c | φ | ρ | η | |
| 1 | 110 | 126 | 94 | 280 | 113 |
| 2 | 121 | 141 | 116 | 172 | 138 |
| 3 | 155 | 192 | 135 | 136 | 158 |
| 4 | 182 | 152 | 191 | 118 | 183 |
| 5 | 231 | 188 | 263 | 93 | 207 |
| Rj | 121 | 66 | 169 | 187 | 94 |
| 排序 | Rρ>Rφ>Rt>Rη>Rc | ||||
| 水平 | df/mm | ||||
| t | c | φ | ρ | η | |
| 1 | 26.9 | 18.1 | 19.7 | 17.5 | 18.0 |
| 2 | 19.6 | 17.2 | 18.4 | 18.1 | 17.9 |
| 3 | 15.7 | 18.6 | 16.7 | 16.9 | 20.6 |
| 4 | 14.0 | 18.5 | 16.7 | 21.0 | 17.7 |
| 5 | 13.8 | 17.6 | 18.4 | 16.5 | 15.8 |
| Rj | 13.1 | 1.4 | 3.0 | 4.5 | 4.8 |
| 排序 | Rt>Rη>Rρ>Rφ>Rc | ||||
| 水平 | γ /(°) | ||||
| t | c | φ | ρ | η | |
| 1 | 30.0 | 24.8 | 20.7 | 26.7 | 27.1 |
| 2 | 25.1 | 27.3 | 23.1 | 25.5 | 24.6 |
| 3 | 23.1 | 25.5 | 24.1 | 25.8 | 26.1 |
| 4 | 25.6 | 24.9 | 29.0 | 24.7 | 26.8 |
| 5 | 25.1 | 26.2 | 31.9 | 26.1 | 24.1 |
| Rj | 6.9 | 2.5 | 11.2 | 2.0 | 3.1 |
| 排序 | Rφ>Rt>Rη>Rc>Rρ | ||||
|
| a. 破坏荷载Gf;b. 临界位移df;c. 破裂面倾角γ。 图 14 因素影响直观分析曲线 Fig. 14 Factors influencing visual analysis curve |
|
|
极差分析(表 4)可得,各因素对Gf的敏感性从大到小依次为ρ、φ、t、η、c。其中,Gf随密度ρ的增大而单调递减,而随其他参数(φ、t、η)单调递增(图 14a)。ρ越大,岩体自身可提供的倾倒力矩越大,因而不利于边坡稳定;而层面c、φ越大,层面的抗错动能力越强,岩层间相对错动难以发生,岩层的整体性变强,削弱了岩层变形的空间,有利于坡体稳定;层厚t越大,岩层抗折断能力越强,边坡稳定性也就越好;密度比η的增大导致Gf线性增大。
对数据进行线性拟合(表 5)可见,各因素对Gf的影响均近似线性相关,其中η的线性相关性最好,t、φ次之。
| 因素 | 拟合公式 | R2 |
| t | y=30.3x+68.9 | 0.959 3 |
| c | y=13.5x+119.3 | 0.537 8 |
| φ | y=41.3x+35.9 | 0.922 7 |
| ρ | y=-42.8x+288.2 | 0.857 1 |
| η | y=23.3x+89.9 | 0.998 9 |
对临界位移df而言,受模型尺寸限制,各参数的整体影响较小,极差Rj最大为13.1 mm(表 4),当边坡规模足够大时,该位移将相当可观。极差分析可见,t、η、ρ对df的影响较大,而层面c、φ影响较小;说明稳态阶段位移量主要受层厚及密度等岩层自身力学性质的控制,而受层面的影响较小。由图 14b可见,df与t呈较好的幂函数相关关系。
正交试验组坡形一致,因此破裂面倾角γ直接影响变形体的体量。极差分析(表 4)表明,层面内摩擦角φ对γ起主控影响,γ随φ的增大而近似线性增大(图 14c),即变形范围线性减小。
5 讨论一般而言,反倾边坡的稳定性较好,因此,反倾边坡的变形破坏问题常常被忽视。基于上文大量的数值模拟,对反倾边坡的变形稳定性及灾害防治进行探讨。
无论试验还是模拟,反倾边坡的变形均存在较长时期的时效变形阶段,其变形是一个渐进的过程,而一旦岩层弯曲到一定程度,整体破裂面瞬间形成,坡体快速失稳。因此,从变形的角度判断反倾边坡的稳定性是可行的。早期的倾倒变形一般只发育沿层面的相对错动,表现在坡体表面形成一系列反坡台坎,而岩层内尚未出现较多的拉张裂隙,此时,边坡可视为相对稳定。一旦岩层内(特别是坡脚处岩体)可见较多次生拉张裂隙时,反倾边坡的稳定性问题需引起足够重视。实际工程中,边坡的内部变形通常比较隐蔽,需通过勘探平硐等揭露,如西部多个水电工程通过平硐揭露了众多大型倾倒体,取得了良好效果[24-26]。
特定的倾角与坡角的组合关系是反倾边坡形成倾倒变形的必要条件,模拟结果表明,二者之和小于120°时,边坡极难破坏。因此,工程实践中可通过二者之和快速地对此类边坡的稳定性进行初步评判,从而决定是否需要采取进一步措施。当倾角越大时,破裂面倾角越小,边坡潜在变形范围将很大,在软岩为主边坡(如千枚岩、板岩、片岩等)或软硬互层岩质边坡中,岩层即使发生较大弯曲也不会完全折断,此时反倾边坡将容易形成深层倾倒变形体,并有可能形成巨型滑坡。西南地区已有多个真实案例,如澜沧江苗尾水电站坝址区[24],未倾倒岩体倾角约80°,地层为岩性较强的变质砂岩、千枚岩、板岩等软硬互层岩体,该处形成了左坝肩、右坝肩、右岸坝前边坡等多个变形深度超过200 m的大型深层倾倒变形体。又如澜沧江古水水电站坝址区争岗滑坡[25],其为倾倒变形转化而成的巨型滑坡,正常岩层倾角大于70°,岩性同样为软硬相间的变质岩组合。
不论何种破坏模式,模拟结果表明,反倾边坡的破坏均从坡脚附近开始发育,当坡脚岩体起裂或坠覆后,上部岩体均难以维持稳定。因此,加固边坡坡脚对于控制反倾边坡的变形可起到良好作用。实际工程中,压脚措施也已有成功案例。如苗尾右坝肩边坡在开挖期间[26],坡脚的小规模开挖即引起坡肩产生16道宏观裂缝,裂缝宽度不断加大,而当在坡脚堆载压脚后,边坡上部变形得到了很好的控制。
此外,模拟表明,变形早期岩层间的相对错动是岩体产生进一步拉张变形的必要条件,若能在此阶段限制这种相对错动,则可较好地增强边坡的稳定性。可尝试通过锚固、注浆等增加层面的抗剪力实现。
反倾边坡的反折式破坏在已有离心模型试验[8]、底摩擦试验[27]中也存在类似变形现象,此外,三峡库区巫山独龙段7#反倾岸坡中可见明显的S型变形现象[11],说明此类变形客观存在。推测这是由于倾倒体不同部位间惯性的差异以及下部岩体的阻挡作用下形成的,并可沿岩层的反弯点形成不同规模的整体破裂面。
自然界中的天然斜坡常具有复杂的岩体结构,同时受到多种外界因素的影响,如河流下切导致的强烈的卸荷作用和表生改造[28-29],区域高地应力环境等[30]。而青藏高原东南缘的深切河谷地带恰是深层倾倒变形体的高发区[24-26],因而实际反倾边坡的变形破坏机理更加复杂,仍需进一步研究。
6 结论1) 反倾边坡倾倒变形过程可分为起始蠕变、稳态变形和失稳破坏3个阶段。起始阶段坡内无可见变形;稳态变形阶段位移线性增大,伴随轻微的层间拉张和相对错动,为重力时效累进变形;进入破坏阶段后,破裂面贯通,变形体快速向前倾倒变形。
2) 坡内横向裂隙首先在坡脚零星发育,之后自下而上迅速贯穿坡体,形成整体破裂面。之后,边坡变形体内逐渐发育多条破裂面,最终形成渐进后退式破坏。
3) 倾角与坡角直接影响反倾边坡稳定性及其破坏模式。受弯矩大小的控制,破坏荷载随倾角增大先减小后增大;坡角越大,边坡越容易破坏,破坏荷载与坡角幂函数相关。反倾边坡存在倾倒—折断—块体式、倾倒—弯曲—折断式、倾倒—反折式三种破坏模式。
4) 正交试验表明,层厚、层面的黏聚力、层面的内摩擦角、密度、密度比等参数对反倾边坡倾倒变形影响显著,破坏荷载与层厚、层面的内摩擦角、密度比等参数高度线性相关。临界位移受层厚影响明显,破裂面倾角则受层面内摩擦角控制。
| [1] |
黄润秋. 20世纪以来中国的大型滑坡及其发生机制[J]. 岩石力学与工程学报, 2007, 26(3): 433-454. Huang Runqiu. Large-Scale Landslides and Their Sliding Mechanisms in China Since the 20th Century[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 433-454. DOI:10.3321/j.issn:1000-6915.2007.03.001 |
| [2] |
Liu M, Liu F Z, Huang R Q, et al. Deep-Seated Large-Scale Toppling Failure in Metamorphic Rocks: A Case Study of the Erguxi Slope in Southwest China[J]. Journal of Mountain Science, 2016, 13(12): 2094-2110. DOI:10.1007/s11629-015-3803-4 |
| [3] |
Lin P, Liu X L, Hu S Y, et al. Large Deformation Analysis of a High Steep Slope Relating to the Laxiwa Reservoir, China[J]. Rock Mechanics and Rock Engineering, 2016, 49: 2253-2276. DOI:10.1007/s00603-016-0925-0 |
| [4] |
黄润秋, 李渝生, 严明. 斜坡倾倒变形的工程地质分析[J]. 工程地质学报, 2017, 25(5): 1165-1181. Huang Runqiu, Li Yusheng, Yan Ming. The Implication and Evaluation of Toppling Failure in Engineering Geology Practice[J]. Journal of Engineering Geology, 2017, 25(5): 1165-1181. |
| [5] |
包承纲. 我国岩土离心模拟技术的应用与发展[J]. 长江科学院院报, 2013, 30(11): 55-66, 71. Bao Chenggang. Application and Development of Centrifugal Modeling Technology for Geotechnical Engineering in China[J]. Journal of Yangtze River Scientific Research Institute, 2013, 30(11): 55-66, 71. DOI:10.3969/j.issn.1001-5485.2013.11.012 |
| [6] |
Adhikary D P, Dyskin A V, Jewell R J, et al. A Study of the Mechanism of Flexural Toppling Failure of Rock Slopes[J]. Rock Mechanics and Rock Engineering, 1997, 30(2): 75-93. DOI:10.1007/BF01020126 |
| [7] |
汪小刚, 张建红, 赵毓芝, 等. 用离心模型研究岩石边坡的倾倒破坏[J]. 岩土工程学报, 1996, 18(5): 14-21. Wang Xiaogang, Zhang Jianhong, Zhao Yuzhi, et al. Investigations on Mechanism of Slope Toppling Failure by Centrifuge Model Testing[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(5): 14-21. DOI:10.3321/j.issn:1000-4548.1996.05.003 |
| [8] |
吴昊, 赵维, 年廷凯, 等. 反倾层状岩质边坡倾倒破坏的离心模型试验研究[J]. 水利学报, 2018, 49(2): 223-231. Wu Hao, Zhao Wei, Nian Tingkai, et al. Study on the Anti-Dip Layered Rock Slope Toppling Failure Based on Centrifuge Model Test[J]. Journal of Hydraulic Engineering, 2018, 49(2): 223-231. |
| [9] |
黄达, 马昊, 孟秋杰, 等. 软硬互层岩质反倾边坡弯曲倾倒离心模型试验与数值模拟研究[J]. 岩土工程学报, 2020, 42(7): 1286-1295. Huang Da, Ma Hao, Meng Qiujie, et al. Centrifugal Model Test and Numerical Simulation for Anaclinal Rock Slopes with Soft-Hard Interbedded Structures[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(7): 1286-1295. |
| [10] |
Leandro R A, Iván G, Roberto M. Analysisof a Complex Toppling-Circular Slope Failure[J]. Engineering Geology, 2010, 114(1): 93-104. |
| [11] |
马昊, 黄达, 石林. 基于断距-层厚特征统计的反倾边坡S型破坏演化数值模拟[J]. 工程地质学报, 2020, 28(6): 1160-117. Ma Hao, Huang Da, Shi Lin. Numerical Simulationof S-Shaped Failure Evolution of Anti-Dip Slope Based on Statistics of Broken Length and Layer Thickness[J]. Journal of Engineering Geology, 2020, 28(6): 1160-1171. |
| [12] |
孙东亚, 彭一江, 王兴珍. DDA数值方法在岩质边坡倾倒破坏分析中的应用[J]. 岩石力学与工程学报, 2002, 21(1): 39-42. Sun Dongya, Peng Yijiang, Wang Xingzhen. Application of DDA Method in Stability Analysis of Topple Rock Slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(1): 39-42. DOI:10.3321/j.issn:1000-6915.2002.01.008 |
| [13] |
程东幸, 刘大安, 丁恩保, 等. 层状反倾岩质边坡影响因素及反倾条件分析[J]. 岩土工程学报, 2005, 27(11): 1362-1366. Cheng Dongxing, Liu Daan, Ding Enbao, et al. Analysis on Influential Factors and Toppling Conditions of Toppling Rock Slope[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(11): 1362-1366. DOI:10.3321/j.issn:1000-4548.2005.11.027 |
| [14] |
蔡跃, 三谷泰浩, 江琦哲郎. 反倾层状岩体边坡稳定性的数值分析[J]. 岩石力学与工程学报, 2008, 27(12): 2517-2522. Cai Yue, Mitani Yasuhiro, Esaki Tetsuro. Numerical Analysis of Stability for an Antidip Stratified Rock Slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(12): 2517-2522. DOI:10.3321/j.issn:1000-6915.2008.12.018 |
| [15] |
李明霞, 董联杰. 层状反倾边坡变形特征及影响因素分析[J]. 计算力学学报, 2015, 32(6): 831-837. Li Mingxia, Dong Lianjie. Analysis on Influential Factors and Deformation Characteristics of Toppling Slope[J]. Chinese Journal of Computational Mechanics, 2015, 32(6): 831-837. |
| [16] |
Adhikary D P, Dyskin A V. Modelling of Progressive and Instantaneous Failures of Foliated Rock Slopes[J]. Rock Mechanics and Rock Engineering, 2007, 40(4): 349-362. DOI:10.1007/s00603-006-0085-8 |
| [17] |
Itasca Consulting Group Inc. UDEC (Universal Distinct Element Code), Version 6.0[Z]. Minneapolis: Itasca, 2014.
|
| [18] |
Diederichs M S, Kaiser P K. Stability of Large Excavation in Laminated Hard Rock Masses: The Voussoir Analogue Revisited[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(1): 97-117. DOI:10.1016/S0148-9062(98)00180-6 |
| [19] |
Zheng Y, Chen C X, Liu T T, et al. Study on the Mechanisms of Flexural Toppling Failure in Anti-Inclined Rock Slopes Using Numerical and Limit Equilibrium Models[J]. Engineering Geology, 2018, 237: 116-128. DOI:10.1016/j.enggeo.2018.02.006 |
| [20] |
Cho N, Martin C D, Sego D C. A Clumped Particle Model for Rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(7): 997-1010. DOI:10.1016/j.ijrmms.2007.02.002 |
| [21] |
赵华, 李文龙, 卫俊杰, 等. 反倾边坡倾倒变形演化过程的模型试验研究[J]. 工程地质学报, 2018, 26(3): 749-757. Zhao Hua, Li Wenlong, Wei Junjie, et al. Model Test Study on Toppling Deformation Evolution Process of Counter-Tilt Slope[J]. Journal of Engineering Geology, 2018, 26(3): 749-757. |
| [22] |
刘毅, 赵斌滨, 殷坤龙, 等. 基于正交设计的麻柳林滑坡稳定性敏感分析[J]. 地球科学, 2019, 44(2): 677-684. Liu Yi, Zhao Binbin, Yin Kunlong, et al. Sensitivity Analysis of Maliulin Landslide Stability Based on Orthogonal Design[J]. Earth Science, 2019, 44(2): 677-684. |
| [23] |
倪恒, 刘佑荣, 龙治国. 正交设计在滑坡敏感性分析中的应用[J]. 岩石力学与工程学报, 2002, 21(7): 989-992. Ni Heng, Liu Yourong, Long Zhiguo. Applications of Orthogonal Design to Sensitivity Analysis of Landslide[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(7): 989-992. DOI:10.3321/j.issn:1000-6915.2002.07.010 |
| [24] |
游昆骏. 澜沧江苗尾水电站右坝肩边坡倾倒岩体开挖变形晌应及稳定性研究[D]. 成都: 成都理工大学, 2014. You Kunjun. Study on Deformation Response and Stability of Toppling Deformation Rock by Excavation at Right Bank Abutment of Miaowei Hydropower Station on Lancang River[D]. Chengdu: Chengdu University of Technology, 2014. |
| [25] |
赵永辉. 澜沧江古水水电站争岗巨型滑坡形成机理及演化过程研究[D]. 成都: 成都理工大学, 2016. Zhao Yonghui. Research on the Formation and Evolution Mechanism of Zhenggang Giant Landslide of Gushui Hydropower Station on Lancang River[D]. Chengdu: Chengdu University of Technology, 2016. |
| [26] |
贺宇航. 澜沧江苗尾水电站坝肩倾倒岩体开挖变形响应研究[D]. 成都: 成都理工大学, 2015. He Yuhang. Study on Deformation Response of Toppling Deformation Rock by Excavation at Miaowei Hydropower Station on Lancang River[D]. Chengdu: Chengdu University of Technology, 2015. |
| [27] |
张御阳, 裴向军, 唐皓, 等. 反倾岩坡倾倒变形结构面影响效应研究[J]. 工程地质学报, 2018, 26(4): 844-851. Zhang Yuyang, Pei Xiangjun, Tang Hao, et al. Experimental Tests for Impact of Structural Surfaces to Toppling Deformation in Anti-Dipped Rock Slopes[J]. Journal of Engineering Geology, 2018, 26(4): 844-851. |
| [28] |
王梓龙, 裴向军, 张御阳, 等. 松动岩体工程特性研究: 以雅砻江楞古水电站松动岩体为例[J]. 吉林大学学报(地球科学版), 2019, 49(5): 1376-1388. Wang Zilong, Pei Xiangjun, Zhang Yuyang, et al. Engineering Characteristics of Loose Rock Mass: Taking Loose Rock Mass of Lenggu Hydropower Station in Yalong River as an Example[J]. Journal of Jilin University (Earth Science Edition), 2019, 49(5): 1376-1388. |
| [29] |
白永健, 王运生, 葛华, 等. 金沙江深切河谷百胜滑坡演化过程及成因机制[J]. 吉林大学学报(地球科学版), 2019, 49(6): 1680-1688. Bai Yongjian, Wang Yunsheng, Ge Hua, et al. Formation Evolution and Genetic Mechanism of Baisheng Landslide in the Deep-Incised Valley of Jinsha River[J]. Journal of Jilin University (Earth Science Edition), 2019, 49(6): 1680-1688. |
| [30] |
欧小强, 王奭, 李永亮, 等. 拉林铁路板块缝合带隧道地应力分析[J]. 吉林大学学报(地球科学版), 2019, 49(6): 1689-1697. Ou Xiaoqiang, Wang Shi, Li Yongliang, et al. In-Situ Stress Analysis of Tunnel in Plate Suture Zone of Lhasa-Nyingchi Railway[J]. Journal of Jilin University (Earth Science Edition), 2019, 49(6): 1689-1697. |





