2. 中国石油吉林油田公司乾安采油厂, 吉林 松原 138000
2. Qian'an Oil Factory, Jilin Oilfield, PetroChina, Songyuan 138000, Jilin, China
0 引言
在地震数据处理中常常需要将地震资料从时间-空间域转换到其他数据域中,分析其在不同数据域中所表现的特征,实现地震数据处理任务。例如,使目标信号与其他信号在变换域中具有不同的稀疏特征,可以进行信噪分离。函数投影变换方法在地震数据处理中有着广泛的应用,可以根据地震数据同相轴斜率p的差异,实现信噪分离、缺失地震道插值和平面波分解等重要的应用。如τ-p域[1-5]、p-f域[6-8]、p-x域[9-10]和t-x-p域[11-12]等变换方法可以在不同的视角下,分析地震资料的相关属性。
Radon变换是由Radon[13]提出的一种积分变换,其中线性Radon变换的本质是对原函数做空间转换,即将原平面内的点映射到另一平面上,且原平面内一条直线上所有的点在另一平面上都位于同一点。Claerbout等[14]将该变换方法引入到地震勘探中,称为τ-p变换。由于面波、直达波、反射波等的形态与p密切相关,通过τ-p变换方法,可以区分不同斜率的信号成分,将目标信号与其他信号的性质特征表现得直观和明确,有利于进行信号分析和处理。
不同于常规τ-p变换的计算方法,本文提出了基于径向道变换的τ-p变换和基于斜率分解的τ-p变换。本文阐述了两种τ-p变换方法的基本原理,通过对理论模型进行测试,并对比常规τ-p变换方法,分析所提及方法的正反变换精度和计算效率,最后通过反射波和面波的信噪分离处理实例,进一步测试本文方法的有效性。
1 理论基础地震勘探中的τ-p变换基本原理是将原始地震数据沿着不同斜率的直线方程(t=τ+px)进行积分,将t-x域数据d(t, x)变换为τ-p域数据m(τ, p),t-x域内的一条直线对应τ-p域内一个点(或一团能量团),即原始数据作如下变换:
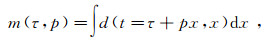 (1)
(1) 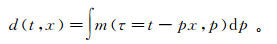 (2)
(2) 式中:x为炮检距;t为双程旅行时;τ为截距时间;p表示积分路径直线的斜率。在频率域内的τ-p正反变换形式如下:
 (3)
(3) 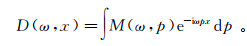 (4)
(4) 式中:D(ω, x)和M(ω, p)分别为数据d(t, x)和m(τ, p)沿时间方向作一维Fourier变换的结果;ω为频率。
观察τ-p正反变换公式可以看到,在传统的τ-p变换方法中,正变换和反变换过程都是通过积分(叠加的原理)实现的,即正反变换的过程可以看成是沿不同方向一定次数的叠加。这样的积分变换过程,使得正反变换后的数据幅值发生很大的偏差。同时,若采用时间域方法,需要考虑叠加路径上采样点的插值方法;若采用频率域方法,则需要根据采样定理考虑数据采样关系,以及可能会产生的吉布斯效应等。这些因素都影响着传统τ-p变换方法的变换精度和分辨率。
为了保证正反变换后数据幅值的稳定,以及提高变换方法的分辨率,可以根据数学反问题框架构建正反变换的目标函数,然后利用数值计算方法来求取最小二乘解[15]。例如,根据线性算子定义频率域τ-p反变换,可得如下数据域和变换域的关系:
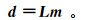 (5)
(5) 式中:d和m分别为d(ω, x)与m(ω, p)各频率分量的矩阵形式;L为τ-p反变换算子。建立最小平方意义下线性反演误差的目标函数:
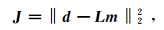 (6)
(6) 即可得到τ-p反变换算子。目前常规的τ-p变换采用求解数学反问题的技术思路,在求解目标函数时采用的数值计算方法(迭代算法)不尽相同;本文提出的两种实现τ-p正反变换的方法,先将数据分别转换到f-k域或t-x-p域,然后通过进一步处理来实现τ-p变换。
1.1 基于径向道变换的τ-p变换实现方法根据刘清林[16]对频率域τ-p变换的数学推导,以及Averbuch等[17]对快速倾斜叠加(fast slant stack)原理的阐述,τ-p域数据与t-x域数据,以及其二维Fourier变换域数据存在对应关系。对t-x域数据d(t, x)作二维Fourier变换正反变换,可得下式:
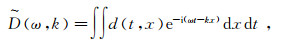 (7)
(7) 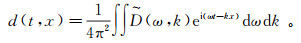 (8)
(8) 式中: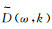
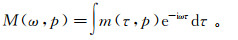 (9)
(9) 令k=ωp,t=τ+px,并代入公式(7),可得
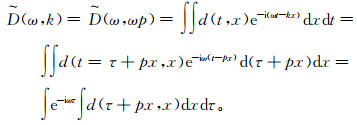 (10)
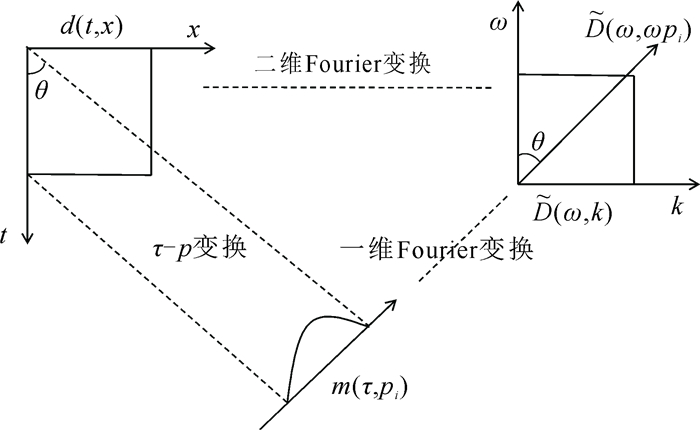
(10) 可知τ-p域数据m(τ, p)的一维Fourier变换数据M(ω, p)对应t-x域数据的二维Fourier变换数据(即f-k域) 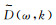
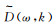
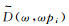
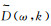
|
| 图 1 投影切片定理示意图 Fig. 1 Schematic diagram of projection-slice theorem |
|
|
利用投影切片定理实现τ-p变换,需要取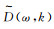
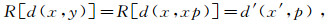 (11)
(11) 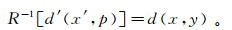 (12)
(12)
|
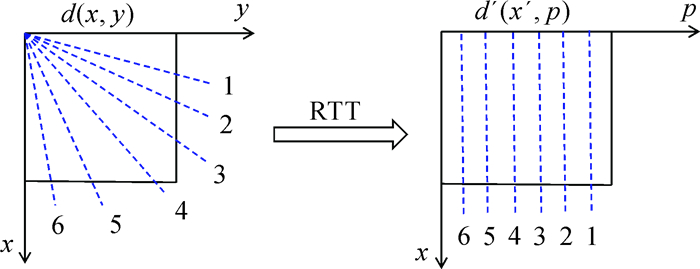
| 图中数字1—6代表数据切片。 图 2 径向道变换示意图 Fig. 2 Schematic diagram of radial trace transform |
|
|
式中:x′=x-x0;p=(y-y0)/(x-x0),(x0, y0)为径向道变换原点;d′(x′, p)为径向道变换后的数据。这里令原点为(0,0),如图 2所示,在d(x, y)中沿径向选取的数据切片1—6规则排布在d′(x′, p)中时需要进行插值。高阶B样条插值方法[19]能够提供高精度的插值结果,可以作为径向道变换的插值算子核心。
基于高插值精度径向道变换技术,并结合投影切片定理,τ-p正反变换过程可以按如下流程进行。
正变换步骤:
1) 将地震数据d(t, x)作二维Fourier变换后得到
2) 利用公式(11)对频域数据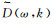
3) 对数据M(ω, p)作一维Fourier反变换即可得τ-p域数据m(τ, p)。
同理,反变换步骤:
1) τ-p域数据m(τ, p)作一维Fourier变换得到M(ω, p)。
2) 对频域数据M(ω, p)作径向道反变换得到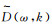
3) 再将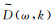
基于径向道变换方法并结合投影切片定理,利用快速Fourier变换算法和高精度径向道变换技术,可以实现对地震数据的τ-p变换。
1.2 基于斜率分解的τ-p变换实现方法斜率分解方法最早由Ottolini[11]提出,包括了两种方法:交叉叠加和局部倾斜叠加,将地震数据从t-x域分解变换到t-x-p域。Ghosh等[12]提出了一种由局部时频分解[20]发展而来的斜率分解算法。张雪冰等[21]提出了基于局部均值分解的时频分解方法。局部时频分解过程可以表示为
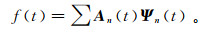 (13)
(13) 式中:f(t)为时间序列;Ψn(t)为基函数;An为随时间变化的系数。在L2范数下建立如下目标函数:
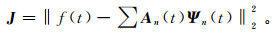 (14)
(14) 公式(14)为数学欠定问题,可以利用整形正则化[22]作为约束条件:
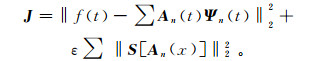 (15)
(15) 式中:ε为正则化参数;S为整形正则化算子。
类似于时频分解的思路,可以构建斜率分解算法。对二维数据d(t, x)沿时间t轴作一维Fourier变换得到D(ω, x),若对数据D(ω, x)沿炮检距x轴作局部时频分解,可以表示为
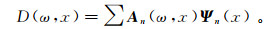 (16)
(16) 式中:Ψn(x)=ei2πnkx。将k=pω代入式(16),则对数据D(ω, x)进行斜率分解可表示为
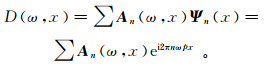 (17)
(17) 依照局部时频分解理论,可以构建数据D(ω, x)斜率分解的目标函数:
 (18)
(18) 对目标函数进行求解,进而可将f-x数据分解,得到f-x-p域数据。利用这样的斜率分解方法,再对数据进行简单线性拉伸(linear moveout,LMO)处理,就可以得到τ-p域数据,具体步骤如下:
1) 对原始数据沿时间t轴做Fourier变换,使t-x域数据变换到f-x域。
2) 对每个频率分量(切片)应用斜率分解方法,从而将f-x域数据变换到f-x-p域。
3) 通过Fourier反变换将数据由f-x-p域转到t-x-p域。
4) 对t-x-p域数据进行线性拉伸可以转换到τ-x-p域,沿着x轴进行叠加即得到τ-p域数据。
相应的反变换较为简单,只需要将τ-x-p域数据作反线性拉伸,得到t-x-p域数据,再将数据沿着p轴进行叠加,即可恢复成原始t-x域数据。
利用斜率分解方法可以得到中间结果t-x-p和τ-x-p域数据,基于不同信号在t、x和p 3个不同维度上的变化规律,可以更直观地对不同成分的信号进行区分[20]。
2 理论模型分析为验证文中提出的τ-p变换实现方法的有效性,建立了一个多层反射地震同相轴理论模型(图 3),地震子波主频为15 Hz,道间距为25 m,共有128道,并且在该模型中部加入AVO(amplitude versus offset)现象。为了测试本文提出的τ-p正反变换效果,选取基于共轭梯度法求解目标函数(公式(6))的常规方法进行对比。
|
| 图 3 理论模型 Fig. 3 Synthetic model |
|
|
利用本文提出的两种实现方法以及常规方法对模型数据进行τ-p正变换,结果如图 4所示。从图 4中可以看出,各条同相轴在不同方法实现的τ-p域内都能表现出正确的形态,证明了本文方法的有效性。仔细对比本文提出两种方法和常规方法,基于径向道变换的τ-p正变换存在一些线性虚假干扰,基于斜率分解的τ-p正变换效果比较理想,而常规方法实现的τ-p正变换存在较基于径向道变换的τ-p正变换更加严重的虚假干扰,尤其在零倾角范围附近。
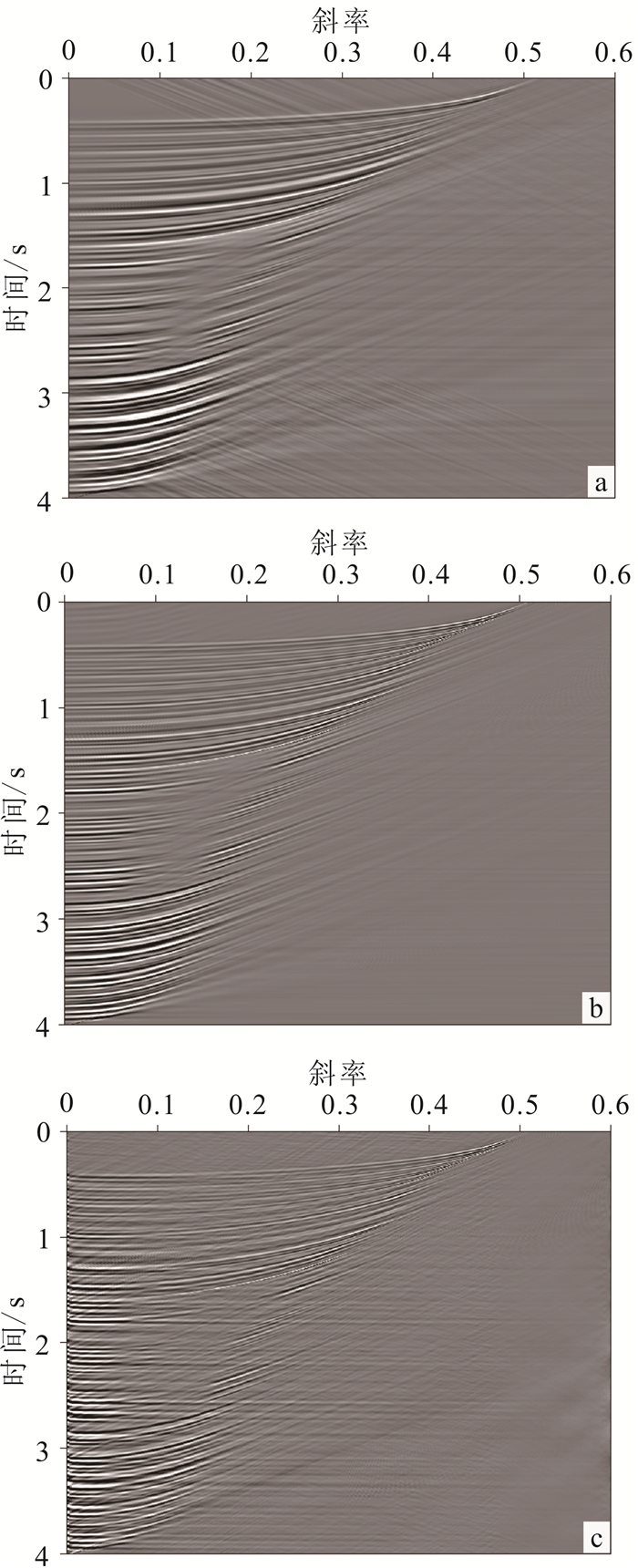
|
| a.基于径向道变换;b.基于斜率分解;c.常规方法。 图 4 不同τ-p正变换结果对比 Fig. 4 Comparison of different forward τ-p transforms |
|
|
接下来,对不同的τ-p域数据进行反变换,结果如图 5所示。3种方法恢复的t-x域数据直观上同相轴清晰,没有引入噪声干扰。
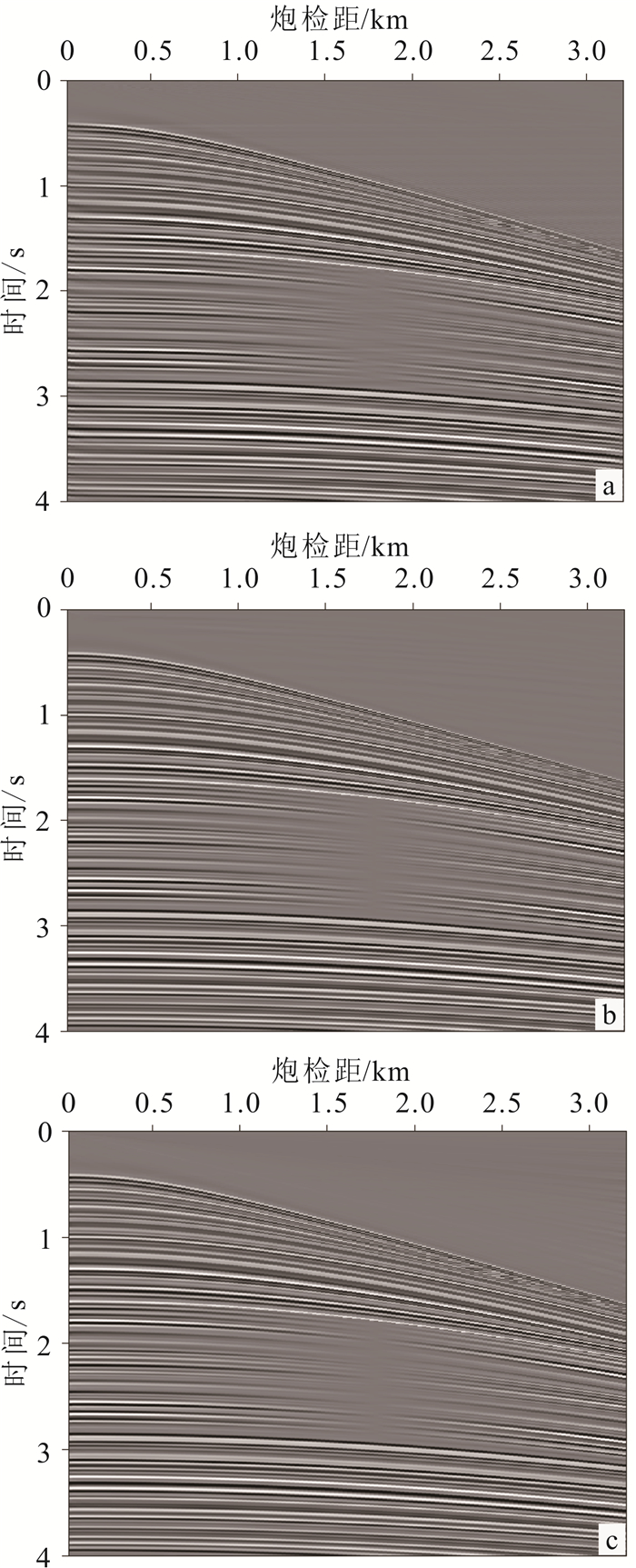
|
| a.基于径向道变换;b.基于斜率分解;c.常规方法。 图 5 不同τ-p反变换结果对比 Fig. 5 Comparison of different inverse τ-p transforms |
|
|
为了更加准确地对比各方法数据重构的精度,将反变换得到的结果与原始数据作差,可以得到对应的误差剖面,结果如6所示。基于径向道变换的τ-p变换方法存在一定的误差,引入了一些近水平的虚假信息(图 6a),而基于斜率分解的τ-p变换方法(图 6b)和常规方法(图 6c)能够较好地恢复原始数据信息。
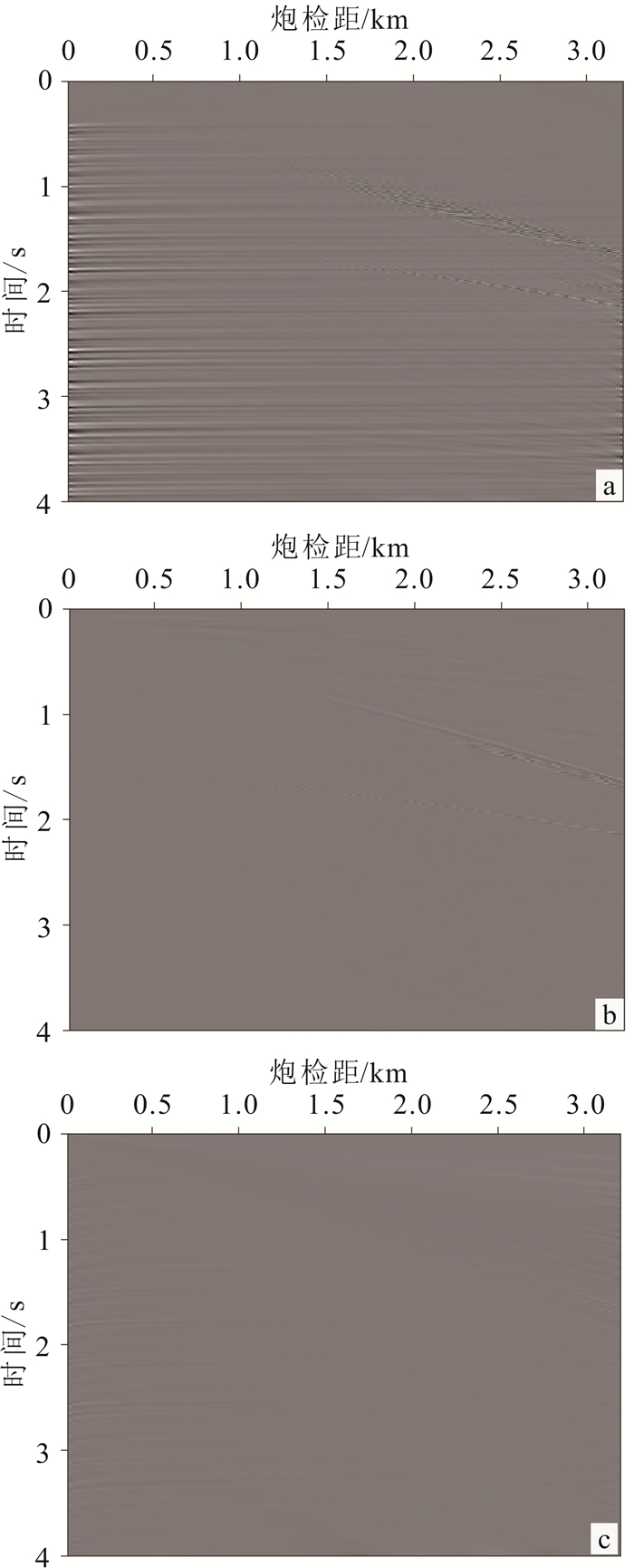
|
| a.基于径向道变换;b.基于斜率分解;c.常规方法。 图 6 不同τ-p变换方法误差对比 Fig. 6 Comparison of error for different τ-p transforms |
|
|
表 1列出了3种方法的计算时间,计算中采用Intel Xeon E5-2695-v4处理器,单核主频2.10 GHz。根据数据比较可知:基于径向道变换的τ-p变换方法在更短的时间内完成了对数据的正反变换,数据能够得到比较合理的恢复,其误差产生的原因主要是对数据作径向道变换时,径向切片上的采样点需要进行插值处理,提高插值精度能够降低误差的幅值;基于斜率分解的τ-p变换计算效率较常规方法更低,但是该方法对应的变换域精度更高。
| 方法名称 | 正变换耗时/s | 反变换耗时/s |
| 基于径向道变换 | 0.369 543 | 0.319 656 |
| 基于斜率分解 | 118.223 317 | 4.752 845 |
| 常规方法 | 63.071 789 | 0.981 368 |
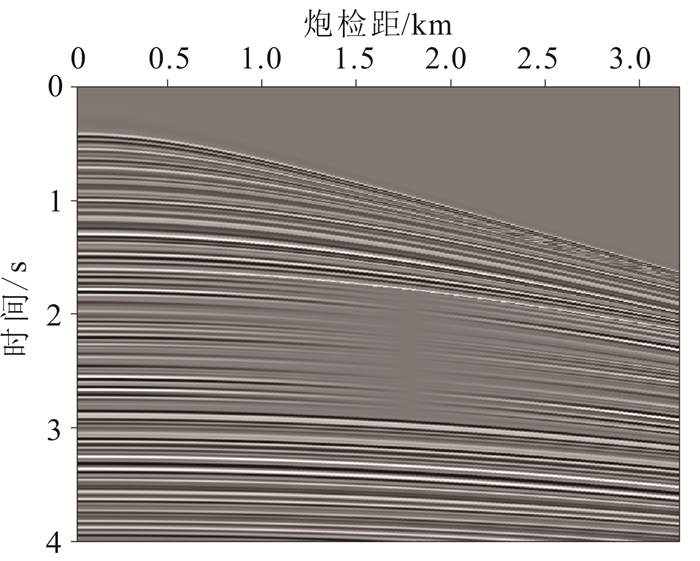
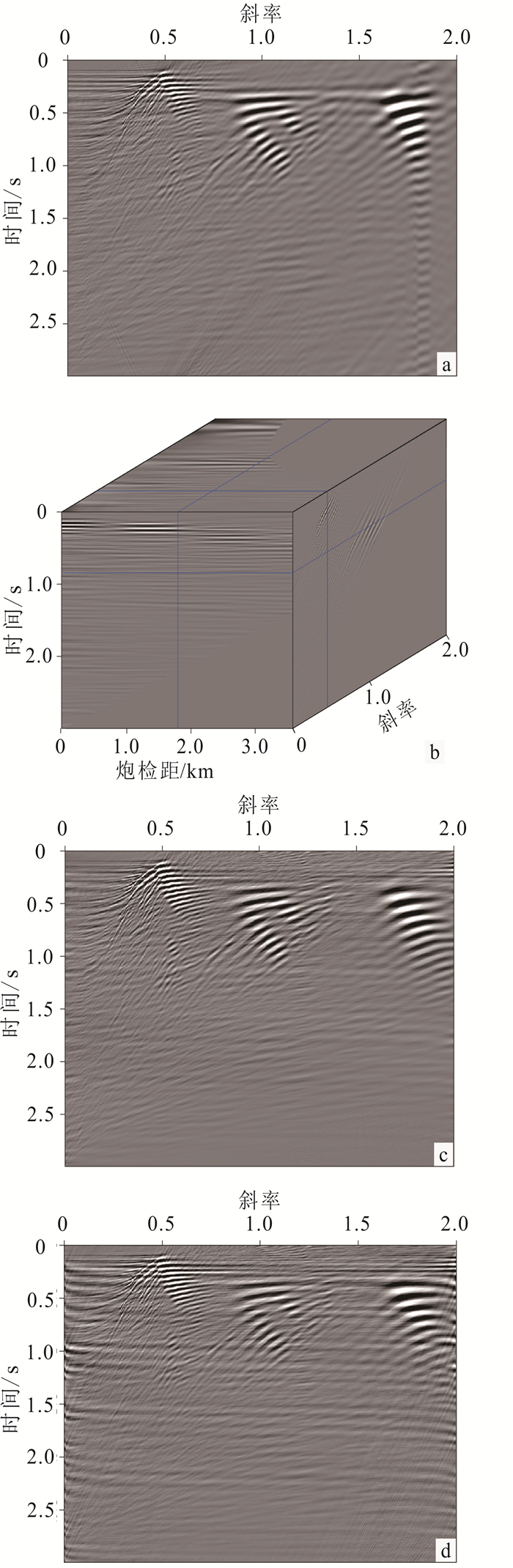
在实际数据测试中,选取某地区陆上含面波干扰的单炮记录(图 7)进行去噪处理。该数据共120道,道间距为30 m。选取初始斜率p0=0,斜率采样间隔dp=0.005,斜率采样数np=401,根据选定的斜率范围,使用3种方法(基于径向道变换、基于斜率分解和常规方法)分别进行τ-p正变换,得到如图 8所示的结果。基于斜率分解的τ-p变换实现方法还可以得到τ-x-p域数据的中间处理结果(图 8b),这一结果能够用来设计高维度的处理算子。从图 8可以看出,面波噪声在τ-p变换域的浅层和大斜率位置处汇聚。
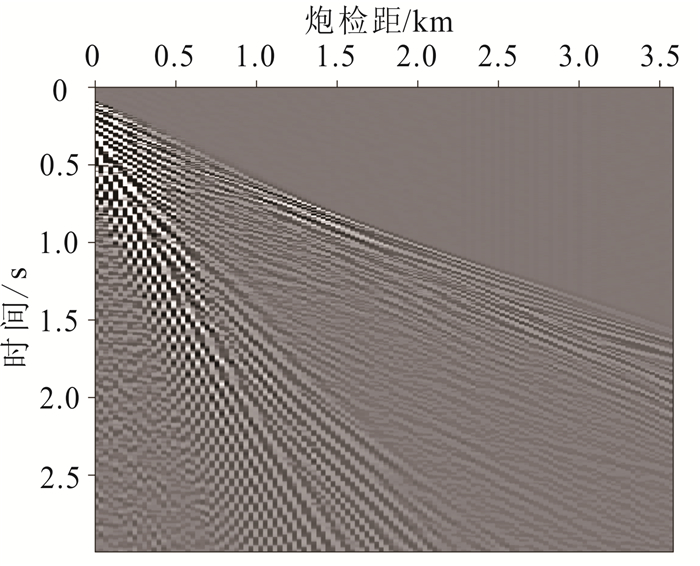
|
| 图 7 含面波单炮记录 Fig. 7 Shot gather containing ground roll |
|
|
|
| a.基于径向道变换;b.基于斜率分解方法生成的τ-x-p域数据;c.基于斜率分解;d.常规方法。 图 8 3种不同实现方法的τ-p变换域 Fig. 8 Shot gather in τ-p transform domains by using different implementations |
|
|
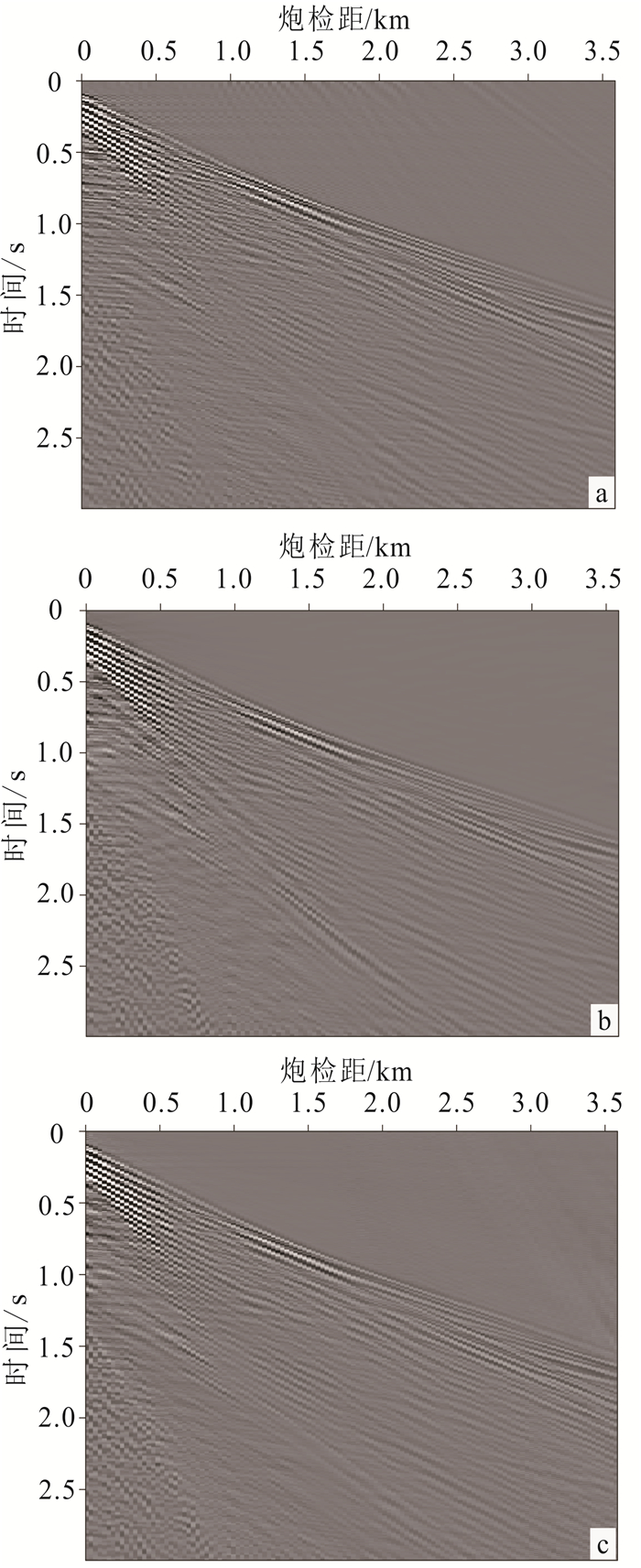
对3个变换域内的面波能量团进行切除,切除结果进行反变换后得到去噪结果,如图 9所示。从图 9可以看到,基于径向道变换和基于斜率分解的方法都能较好地实现面波噪声的压制流程。基于径向道变换的τ-p变换实现方法噪声压制效果与常规方法相近,目标信号能够得到有效的保留,但是计算效率更高,这种优势在高维数据处理中具有更加明显的优势;基于斜率分解的τ-p变换实现方法具有更高的正反变换精度,引入更少的干扰,同时还能够提供冗余变换维度(τ-x-p域),为设计更加灵活的滤波算子提供有效变换域。
|
| a.基于径向道变换;b.基于斜率分解;c.常规方法。 图 9 不同τ-p变换实现方法的噪声压制处理结果 Fig. 9 Denoising results by τ-p transforms base on different implementations |
|
|
1) 本文提出了基于径向道变换的τ-p变换方法和基于斜率分解的τ-p变换方法。
2) 基于径向道变换的τ-p变换方法以投影切片定理为核心,以径向道变换为工具,同时借助快速Fourier算法和高阶B样条插值,在保证较高计算精度的同时拥有较常规方法更快的计算速度。数据测试结果突出了基于径向道变换的τ-p变换方法在计算速度方面的优势,可作为大规模地震数据的处理工具。
3) 基于斜率分解的τ-p变换方法运用稳定的斜率分解方法,在变换过程中数据分解出t、x、p 3个维度的信息,提供了冗余变换维度。理论模型和实际数据的处理结果表明基于斜率分解的τ-p变换方法拥有较常规τ-p变换方法更高的变换精度,并为数据分析提供更加灵活的变换域。
致谢: 美国德州大学奥斯汀分校经济地质局Sergey Fomel教授在本研究过程中与通信作者进行了讨论并给出了建议,在此表示感谢。
| [1] |
Stoffa P L, Buhl P, Diebold J B, et al. Direct Mapping of Seismic Data to the Domain of Intercept Time and Ray Parameter:A Plane-Wave Decomposition[J]. Geophysics, 1981, 46(3): 255-267. DOI:10.1190/1.1441197 |
| [2] |
Durrani T S, Bisset D. The Radon Transform and Its Properties[J]. Geophysics, 1984, 49(8): 1180-1187. DOI:10.1190/1.1441747 |
| [3] |
Turner G. Aliasing in the Tau-p Transform and the Removal of Spatially Aliased Coherent Noise[J]. Geophysics, 1990, 55(11): 1496-503. DOI:10.1190/1.1442797 |
| [4] |
Yilmaz Öz. Seismic Data Analysis:Processing, Inversion, and Interpretation of Seismic Data[M]. Katras: Society of Exploration Geophysicists, 2001.
|
| [5] |
Wilson C, Guitton A. Teleseismic Wavefield Interpolation and Signal Extraction Using High-Resolution Linear Radon Transforms[J]. Geophysical Journal International, 2007, 168(1): 171-181. DOI:10.1111/j.1365-246X.2006.03163.x |
| [6] |
Levin S A. Frequency-Dip Formulation of Wave-Theoretic Migration in Stratified Media:Acoustical Imaging[M]. Boston: Springer, 1980.
|
| [7] |
Forbriger T. Inversion of Shallow-Seismic Wavefields:Ⅰ:Wavefield Transformation[J]. Geophysical Journal International, 2003, 153(3): 719-734. DOI:10.1046/j.1365-246X.2003.01929.x |
| [8] |
Dev A, McMechan G A. Spatial Antialias Filtering in the Slowness-Frequency Domain[J]. Geophysics, 2009, 74(2): V35-V42. DOI:10.1190/1.3052115 |
| [9] |
McMechan G A. Px Imaging by Localized Slant Stacks of Tx Data[J]. Geophysical Journal International, 1983, 72(1): 213-221. DOI:10.1111/j.1365-246X.1983.tb02813.x |
| [10] |
Tang R, Carswell A, Moon W. Velocity Analysis in the p-x Plane from a Slant Stack Wavefield[J]. Geophysical Prospecting, 1984, 32(6): 1016-1032. DOI:10.1111/j.1365-2478.1984.tb00752.x |
| [11] |
Ottolini R. Signal/Noise Separation in Dip Space[J]. SEP Report, 1983, 37: 143-149. |
| [12] |
Ghosh S, Fomel S. Multiple Suppression in the t-x-p Domain[C]//SEG Technical Program Expanded Abstracts 2012. Las Vegas: Society of Exploration Geophysicists, 2012: 1-6.
|
| [13] |
Radon J. Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten, Ber Verh Sächs Akad Wiss Leipzig[J]. Math-Nat kl, 1917, 69: 262-277. |
| [14] |
Claerbout J F, Johnson A G. Extrapolation of Time-Dependent Waveforms Along Their Path of Propagation[J]. Geophysical Journal International, 1971, 26(1): 285-293. |
| [15] |
Claerbout J F. Earth Soundings Analysis:Processing Versus Inversion[M]. Boston: Blackwell Scientific Publications, 1992.
|
| [16] |
刘清林. Tau-p变换的频率域算法及Tau-p域的偏移处理[J]. 长春地质学院学报, 1986, 16(4): 77-80. Liu Qinglin. The Calculating Method of Tau-p Transform in F-K Domain and Migration Method in Tau-p Domain[J]. Journal of Changchun University of Earth Science, 1986, 16(4): 77-80. |
| [17] |
Averbuch A, Coifman R R, Donoho D L, et al. Fast Slant Stack:A Notion of Radon Transform for Data in a Cartesian Grid Which Is Rapidly Computible, Algebraically Exact, Geometrically Faithful and Invertible[J]. SIAM Scientific Computing, 2001, 37(3): 192-206. |
| [18] |
Claerbout J F. Slant-Stacks and Radial Traces[R]. Stanford: Stanford Exploration Project, 1975: 1-12.
|
| [19] |
Fomel S. Inverse B-Spline Interpolation[R]. Stanford: Stanford Exploration Project, 2000.
|
| [20] |
Liu Y, Fomel S. Seismic Data Analysis Using Local Time-Frequency Decomposition[J]. Geophysical Prospecting, 2012, 61(3): 516-525. |
| [21] |
张雪冰, 刘财, 刘洋, 等. 基于局部均值分解的地震信号时频分解方法[J]. 吉林大学学报(地球科学版), 2017, 47(5): 1562-1571. Zhang Xuebing, Liu Cai, Liu Yang, et al. Seismic Data Time-Frequency Decomposition Based on Local Mean Decomposition[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(5): 1562-1571. |
| [22] |
Fomel S. Shaping Regularization in Geophysical-Estimation Problems[J]. Geophysics, 2007, 72(2): R29-R36. DOI:10.1190/1.2433716 |



