2. 中国电子科技集团公司光电研究院, 天津 300308;
3. 中水东北勘测设计研究有限责任公司, 长春 130061
2. Academy of Opto-Electronics, China Electronic Technology Group Corporation, Tianjin 300308, China;
3. China Water Northeastern Investigation, Design & Research Co., Ltd., Changchun 130061, China
0 引言
横波速度是浅地表的关键地震参数,也是其地层动力学特征的关键参数[1]。因此,如何采取有效的近地表地震勘探工作方式和数据处理流程实现高精度的横波速度评价一直是浅地表地球物理学界的研究热点。浅地表介质通常是极其不均匀的,经干涉形成的面波在其中传播时会发生频散现象。与体波相比,面波能量的衰减比体波的几何扩散慢。且面波的能量在浅地表地震波场中占据主导地位,以垂向震源激发的瑞雷波约占地震波场能量的70%,以横向震源激发的勒夫波约占地震波场能量的90%[2]。正是面波的大振幅特性,使利用面波频散特性的多道分析技术(multi-channel analysis of surface waves, MASW和multi-channel analysis of love waves, MALW)成为一种流行的横波速度评价方法[3-6]。
在过去,地球物理学者对勒夫波的关注明显弱于瑞雷波[7]。除其横向振动的激发和测量难度较大之外,另一个原因是人们普遍认为只有正速度梯度的地层才会产生勒夫波,而在高速层下存在低速软夹层时不会观测到明显的勒夫波,这限制了前人对勒夫波的研究。然而,Safani[8]的研究表明,在存在低速软夹层时产生的勒夫波更加明显。与此同时,Zeng等[9]分析了瑞雷波和勒夫波对横波速度和层厚的敏感性,分析结果表明在大多数频率范围内勒夫波对横波速度和层厚更加敏感。Luo等[10]则模拟了勒夫波在弹性介质中的传播,并分析了勒夫波的频散特征。对于利用面波的频散特性实现横波速度的评价方法,必不可少的一个步骤就是频散曲线反演。1999年,Xia等[3]采取奇异值分解和Levenberg-Marquardt(L-M)方法实现了瑞雷波基模式频散曲线的反演。L-M方法实质上是一种线性反演方法。线性反演方法是一种基于泰勒展开式的局部优化方法,如果无法建立一个较为准确的初始模型,通常情况下难以揭露真实模型的特征。随着计算能力的提高,非线性反演方法提供了一个解决面波频散曲线反演的思路。2008年,宋先海等[11]将确定性非线性寻优算法广义模式识别(generalized pattern search, GPS)引入瑞雷波反演中。2011年,Hamimu等[12]则研究了勒夫波对夹层的分辨能力,指出在频散曲线反演中加入更高模式的勒夫波会明显提高横波速度评价结果的可靠性。同年,Dal等[13]应用进化类优化方法联合反演了多层模型的瑞雷波和勒夫波的频散曲线。2011年,Socco等[14]采取蒙特卡洛算法联合反演了多模式斯通利波和勒夫波,实现了对洋壳的横波速度评价,并分析了斯通利波和勒夫波的横向分辨率。Xia等[4]于2012年在前人的研究基础上提出了勒夫波多道分析(MALW),并详细描述了MALW在横波速度评价上的优势。Xie等[15]于2015年应用快速模拟退火方法反演了横向同性介质中的勒夫波。Fang等[16]则通过面波频率域射线追踪方法直接实现了对介质3D横波速度结构的描述。与此同时,Wang等[17]基于一阶微扰理论实现了多模式的瑞雷波和勒夫波反演,并引入了广义最小残差法。Dalton等[18]于2017年系统地研究了瑞雷波和勒夫波对模型参数的敏感性,并给出了从频散曲线中计算层厚度的最优频率,同时指出基模式面波对半空间以上的地层参数更敏感,高模式面波对半空间和半空间以上的地层参数都很敏感。
面波反演参数的敏感度分析表明,横波速度和厚度是影响相速度的主要参数[2-3]。将地层划为等厚的薄层是面波反演中经常采用的一种策略;然而当勘探深度很深时,会令反演系统参数过多,使反演结果不稳定。为克服这个缺点,需要降低系统的复杂度,同时兼顾浅层分辨率。为此,本文采取线性映射方法实现GPS算法在面波频散曲线变厚度反演中的应用。为深入分析实现多模式瑞雷波和勒夫波反演的可能性,本文首先采用高阶交错网格有限差分法实现两层模型的瑞雷波和勒夫波数值模拟,应用τ-p变换形成频散能量图,并分析瑞雷波和勒夫波的频散特征。为深入理解泊松比、基模式和多模式面波对最终横波速度评价结果的影响,以及说明面波非线性反演的特征,本文采用GPS算法实现对含软弱夹层四层模型的反演,并分析各因素对最终反演结果的影响。
1 两层模型中瑞雷波和勒夫波的传播对于二维各向同性弹性介质,满足胡克定律的瑞雷波弹性波速度-应力方程为[19]:
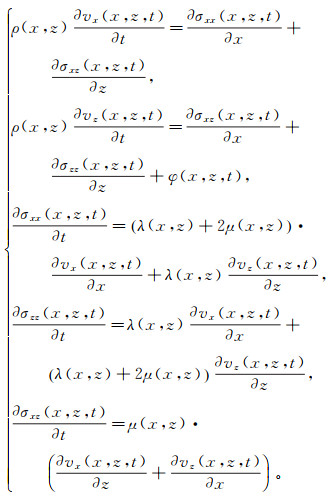 (1)
(1) 满足胡克定律的勒夫波弹性波速度-应力方程为[20]:
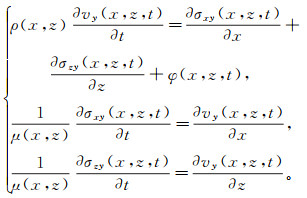 (2)
(2) 其中:
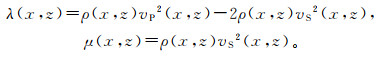
式中:ρ(x, z)为介质密度;vx(x, z, t)、vz(x, z, t)和vy(x, z, t)为质点速度;σxx(x, z, t)、σzz(x, z, t)、σxz(x, z, t)、σxy(x, z, t)和σzy(x, z, t)为质点应力;vP(x, z)和vS(x, z)分别为介质的纵波速度和横波速度;φ(x, z, t)是震源项。对于瑞雷波,φ(x, z, t)加载到垂向振动分量vz(x, z, t)上;对于勒夫波,φ(x, z, t)加载到横向振动分量vy(x, z, t)上。
以上正演方程可以通过高阶交错网格有限差分法求解[19-20]。对于瑞雷波仿真和勒夫波仿真,分别采取横向各向同性介质替换法[21]和应力镜像法[22]实现模型上部的自由边界条件;模型左侧、下侧和右侧的吸收边界条件则由双轴完全匹配层技术来实现[23]。
为深入认识瑞雷波和勒夫波的频散规律,本文设计了一个两层递增型地质模型,分别模拟瑞雷波和勒夫波在其中的传播。表 1给出了具体的模型参数,对于勒夫波模拟,参数不包含纵波速度。令两层模型的空间网格Δx=Δz=0.5 m,网格剖分为301×141,即模型深度为70 m,横向长度为150 m;时间域采样间隔Δt=0.000 2 s;震源是主频为20 Hz延迟时间为0.02 s的Ricker子波,并将其布置在(15 m, 0 m)处,初始偏移距为1 m,共记录120道;吸收网格点数为40,理论反射系数是0.000 1;时间模拟精度为2阶,空间模拟精度为10阶。瑞雷波记录时间为1.2 s,勒夫波记录时间为1.5 s。
| 层序号 | vP/(m/s) | vS/(m/s) | ρ/(g/cm3) | h/m |
| 1 | 368 | 150 | 2.0 | 10 |
| 2 | 780 | 450 | 2.0 | ∞ |
| 注:h.层厚度。 | ||||
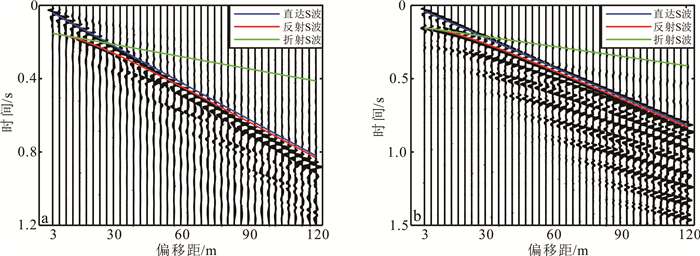
图 1给出了两层递增型地质模型的面波模拟记录,为清晰显示振动图,图中的道间距已调节为3 m,共40道。图 1可以观察到因频散而呈扫帚状的面波,且地震记录中面波占据了绝大部分的能量。相比瑞雷波,图 1a中的纵波能量很弱,很难观察到连续的纵波同相轴,换言之,很难不经过复杂的数据处理步骤从实测记录中提取出纵波信息。这里的子波延迟时间仅仅为0.02 s,然而实际地震子波的延迟时间很长,而且浅地表存在大量的薄层,令初至的直达波、反射波时差很小。这令拾取纵波初至时间时很容易造成波型误判,给利用纵波中直达波、反射波带来了巨大的困难。实际的垂向分量地震记录可以观测到折射波[24-25],然而,利用折射波信息仅能实现粗略分层和厚度估计,当地层中存在软弱夹层时,折射波反演的结果会出现明显的深度和速度误差,这是折射波勘探的缺陷。图 1中给出了初至的横波直达波、反射波、折射波的理论走时曲线。基模式瑞雷波高频部分的相速度大约是表层横波速度的0.92倍[2],体现在图 1a中就是横波直达波的走时略小于初至的瑞雷波的走时。从图 1a中观察到的走时大于初至瑞雷波的波组,主要是由多次干涉形成的高阶瑞雷波,体现于振动图中的特征是慢度小,走时长。基模式勒夫波高频部分的相速度趋近于表层横波速度[2],体现于图 1b中就是横波直达波的走时基本和初至的勒夫波一致。勒夫波的高阶模式是由横波多次反射波叠加干涉形成的[26],表现为振动图中的特点就是多次反射波与高阶模式的勒夫波耦合在一起。勒夫波的视周期通常很长,这给利用横波多次反射波带来了很大的难度。总之,利用浅地表地震波场中的体波信息是比较困难的。
|
| a.瑞雷波vz分量归一化振动图;b.勒夫波vy分量归一化振动图。 图 1 两层递增型地质模型面波模拟记录 Fig. 1 Simulation of surface waves for two-layer incremental geophysical model |
|
|
图 2是两层递增型地质模型面波频散分析结果,用来频散分析的面波记录的初始偏移距是5 m,道间距是1 m,共116道,频散能量图的频率范围是0.5~100 Hz。从图 2a可以看出,瑞雷波在两层模型中传播时占据主导地位的是基模式瑞雷波。从图 2b中可以看出,各模式勒夫波能量分配较均匀,换言之,对于高速半空间的地质模型,易于从勒夫波的频散能量图中拾取多模式频散曲线。仔细观察图 2a,4~6 Hz处基模式瑞雷波的相速度和第二模式瑞雷波的相速度很接近,这是瑞雷波独有的“模式接吻”现象[28]。在处理实测数据时,这个特点很容易造成模式误判,令反演结果不可信。从图 2a中还可以看出,大约60 Hz处第九模式和第十模式瑞雷波存在“模式接吻”现象,第十一模式和第十二模式瑞雷波在大约80 Hz处存在“模式接吻”现象,第十三模式和第十四模式瑞雷波在大约95 Hz处存在“模式接吻”现象。相比瑞雷波,更容易从勒夫波记录中提取出多模式频散曲线。
GPS算法本质上是一种搜索寻优算法,其寻优策略可以概括为从初始模型m0出发,按照方向变化策略在每次迭代过程中给出多个试触模型,从其中选择最优模型,然后重复迭代,直至满足目标函数评价要求。迭代序列可以表示为
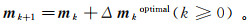 (3)
(3) 式中:Δmk为每次迭代过程中的下降方向矩阵;Δmkoptim al为按照评价方法在矩阵Δmk中选取的最优下降方向。Δmk可以表示为
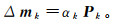 (4)
(4) 式中:αk为第k次迭代时的步长;Pk为下降方向模式矩阵。为最大程度防止迭代序列陷入局部极小值,这里令Pk为最大正基模式[29]。对于变量数为N的反演系统,M为N阶单位矩阵,则Pk具有以下形式:
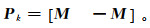 (5)
(5) 若第k次迭代成功预测最优下降方向,则扩大步长;否则保留上一次迭代的模型,减小步长,重新寻优。即
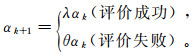 (6)
(6) 式中:λ为扩张因子;θ为收缩因子。
给定m0、α0、λ、θ,则可以按照上述框架完成迭代反演。问题的关键在于面波频散曲线反演中厚度与横波速度范围不一致,无法同步更新。为解决这个问题,本文应用线性映射方法,将厚度变量由厚度空间映射到速度空间,以便同步更新。若横波速度的上、下界分别为vSu、vSl,厚度的上、下界分别为hu、hl,则在每次迭代时的方向更新过程中,将h由厚度空间映射到速度空间,在评价时,将h由速度空间映射回厚度空间,实现速度和厚度同步更新。h由厚度空间映射到速度空间时的斜率k和截距b的表达式如下:
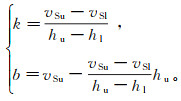 (7)
(7) 遵循相同思路,很容易实现速度空间到厚度空间的映射。
2.2 含软弱夹层四层地质模型面波频散曲线反演应用GPS算法实现面波变厚度反演,定义评价函数如下:
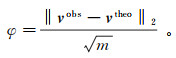 (8)
(8) 式中:vob s和vtheo分别为测量的和由正演计算得出的面波相速度向量;m为基模式面波频散曲线的频点数。为定量评价数值测试中每个反演结果的精度,定义横波速度和层厚度的误差EvS和Eh:
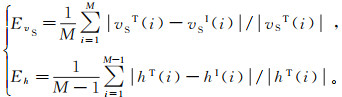 (9)
(9) 式中:vST(i)和vSI(i)分别为第i层的真实横波速度和横波速度反演结果;hT(i)和hI (i)分别为第i层的真实层厚度和层厚度反演结果;M是总地层数。
为比较瑞雷波和勒夫波对横波速度的评价能力,设计含软弱夹层地质模型测试瑞雷波和勒夫波的横波速度评价能力,模型中的参数差异已足够显著。模型具体的参数如表 2所示,泊松比为0.4。
| 层序号 | vP/(m/s) | vS/(m/s) | ρ/(g/cm3) | h/m |
| 1 | 735.0 | 300 | 1.8 | 2 |
| 2 | 367.5 | 150 | 1.8 | 4 |
| 3 | 980.0 | 400 | 1.8 | 6 |
| 4 | 1 470.0 | 600 | 1.8 | ∞ |
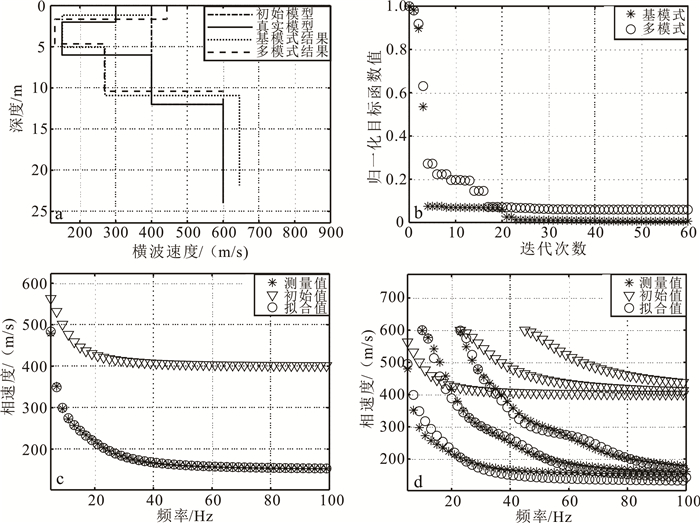
为便于比较,下文测试中的各参数设为:初始步长α0=10 m/s,λ=3,θ=0.4,vSu=800 m/s,vSl=80 m/s,hu=10 m,hl=1 m,最大迭代次数为60。频散曲线的频率范围是5~100 Hz,间隔是1 Hz。初始模型设置为[400 m/s 400 m/s 400 m/s 600 m/s 2 m 3 m 7 m],共包含7个参数,第1到第4个参数给出了初始模型第1到第4层的速度,第5到7个参数给出了初始模型第1到第3层的厚度。初始模型与真实模型的差距已经十分显著。此时,采取局部寻优算法是不可能反演成功的。瑞雷波反演过程中,假定泊松比和密度是已知的,且在反演过程中保持不变,多模式反演中的模式数量为3。图 3和图 4分别是瑞雷波和勒夫波的基模式和多模式频散曲线反演结果,为显示清晰,图中频率间隔已调节至2 Hz。
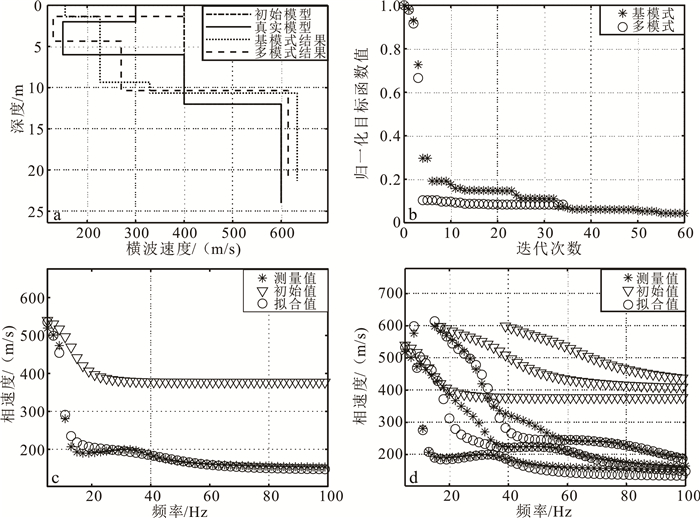
|
| a.横波速度剖面;b.目标函数值的变化曲线;c.基模式频散曲线;d.多模式频散曲线。 图 3 含软弱夹层四层地质模型的瑞雷波基模式和多模式反演结果 Fig. 3 Inversion results of base and multi-mode Rayleigh waves for four-layer geophysical model with a weak interlayer |
|
|
|
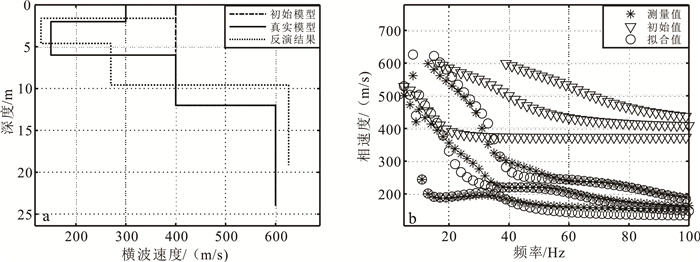
| a.横波速度剖面;b.目标函数值的变化曲线;c.基模式频散曲线;d.多模式频散曲线。 图 4 含软弱夹层四层地质模型的勒夫波基模式和多模式反演结果 Fig. 4 Inversion results of base and multi-mode Love waves for four-layer geophysical model with a weak interlayer |
|
|
从图 3a中可以看出,在初始模型很拙劣时,单独反演基模式瑞雷波频散曲线不能重建地层中含有软弱夹层这一特征,而单独反演基模式勒夫波则能重建地层中含有软弱夹层这一特征(图 4a)。当高模式瑞雷波加入到反演中后,地层中含有软弱夹层这一关键特征则能够被揭露(图 3a),而且迭代次数远小于基模式反演(图 3b)。基模式瑞雷波反演中,拟合的频散曲线与测量值误差主要存在于15~30 Hz(图 3c),而这段频带的频散曲线形态恰恰是地层中含有软弱夹层的指示,这提示我们可以通过观察频散曲线形态给出一个良好的初始模型,从而能令基模式瑞雷波反演成功地评价地层的横波速度结构。从图 3d中可以看出,在8 Hz和35 Hz附近,基模式瑞雷波的相速度与第二模式瑞雷波相速度很接近,发生“模式接吻”,对应于实测数据则很容易模式误判。与瑞雷波相比,勒夫波不存在“模式接吻”的现象(图 4d),高模式勒夫波加入到反演后,反演结果则能够完全重建半空间横波速度;这说明基模式勒夫波对半空间以上的地层参数较敏感,而高模式勒夫波的加入提高了对半空间横波速度的敏感性,这也与此前Dalton等[18]的分析结果一致。
表 3是各方法反演结果的精度统计表,可以得出:高模式瑞雷波的加入会明显地提高横波速度和层厚度的反演精度;高模式勒夫波的加入可以略微地提高层厚度的反演精度,然而横波速度反演精度却有所下降,误差变大。从图 4a的反演结果可以看出,多模式勒夫波反演结果增加的误差主要来源于第1层和第2层,而第1层是表层高速层,第2层是软弱夹层,这两个地层都是异常层;这说明高模式勒夫波的加入会提高反演系统对半空间以上异常层的敏感性,从而使反演结果过度估计。
| 反演方法 | EvS | Eh |
| 基模式瑞雷波反演 | 0.306 6 | 0.693 9 |
| 多模式瑞雷波反演 | 0.203 8 | 0.191 5 |
| 基模式勒夫波反演 | 0.184 6 | 0.156 9 |
| 多模式勒夫波反演 | 0.234 6 | 0.156 1 |
在瑞雷波反演测试中,假定地层的泊松比是已知的,而实际数据处理很难精确地估计出地层泊松比。为认识泊松比误差对横波速度评价结果的影响,在相同的初始模型和反演参数条件下,分析泊松比估计值偏低和偏高时对反演结果的影响。图 5是泊松比为0.33时的反演结果,图 6是泊松比为0.45时的反演结果。
|
| a.横波速度剖面;b.多模式频散曲线。 图 5 泊松比估计值偏低时瑞雷波的横波速度评价结果 Fig. 5 Evaluation results of S-wave velocity in Rayleigh waves with low estimated Poisson's ratio |
|
|

|
| a.横波速度剖面;b.多模式频散曲线。 图 6 泊松比估计值偏高时瑞雷波的横波速度评价结果 Fig. 6 Evaluation results of S-wave velocity in Rayleigh waves with high estimated Poisson's ratio |
|
|
泊松比估计值偏低或偏高时,多模式瑞雷波反演均能重建地层中存在软弱夹层这一关键特征(图 5和图 6)。若能避免瑞雷波数据处理中的模式误判现象,则即使在泊松比值估计不准时多模式瑞雷波反演仍能够重建地层的结构特征。高模式瑞雷波的加入会显著地提高反演系统的鲁棒性。
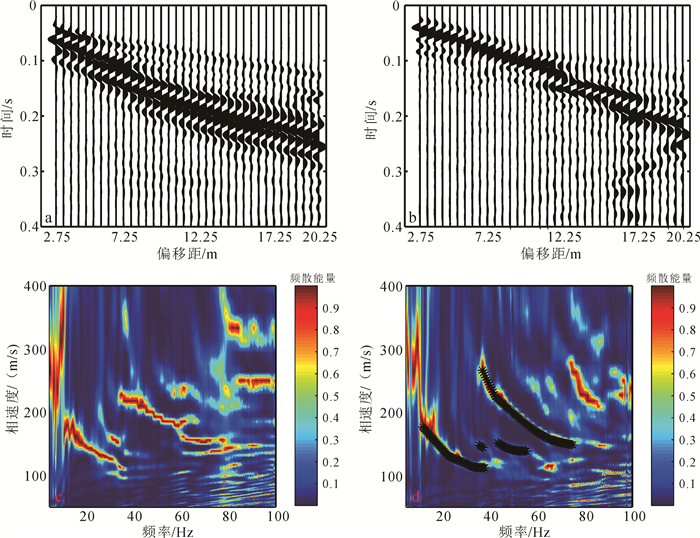
3 勒夫波实测数据分析以上算例已经说明勒夫波对横波速度更敏感。为进一步分析勒夫波的横波速度评价能力,利用GPS算法对在斯洛文尼亚西北部塞耶特村采集的勒夫波数据进行了分析。此次勒夫波调查的目的是为了确定地下是否有历史建筑地基的遗存。每个检波器可以记录两个成180°角的横向振动。在频散分析前,将两组横向振动记录相减,以去除记录中的纵波[30]。记录的初始偏移距是2.75 m,道间距是0.5 m,共36道,时间域采样间隔是0.000 25 s,记录的总时间为1.2 s。图 7a、b分别是震源左、右侧激发的归一化振动图,为清晰显示记录中的主要波型,仅显示0.4 s内的记录;图 7c、d分别是由高分辨线性拉东变换[31]计算得出震源左、右侧激发的勒夫波记录和频散能量图,频率范围是5~100 Hz。
|
| a.震源左侧激发的实测地震记录;b.震源右侧激发的实测地震记录;c.震源左侧激发炮集的频散能量图;d.震源右侧激发炮集的频散能量图。 图 7 塞耶特村地震数据与频散能量图 Fig. 7 Seismic data and dispersion energy image of Cˇachtice village |
|
|
记录中能量主要集中于小于0.3 s的部分,从中可以清晰地看到直达波、折射波、发散的勒夫波(图 7a、b)。在时间大于0.3 s的记录中还可以观察到散射波,这是由SH波传播到测区附近围墙的地基时所产生的(图 7b)。从图 7a、b可以看出,左侧和右侧激发的勒夫波记录的折射波的出现时间和盲区距离差异较大,这说明测线下的介质具有很强的横向不均匀性。图 7c、d中的频散能量聚焦也存在着很大的不同,这从另一个角度说明了介质的横向不均匀性。从图 7c、d可以观察到,基模式勒夫波的频散能量只延续到大约35 Hz处。为令反演结果更加准确,只拾取频散能量中最可靠的各模式频散曲线,如图 7d中的黑色星形线所示。
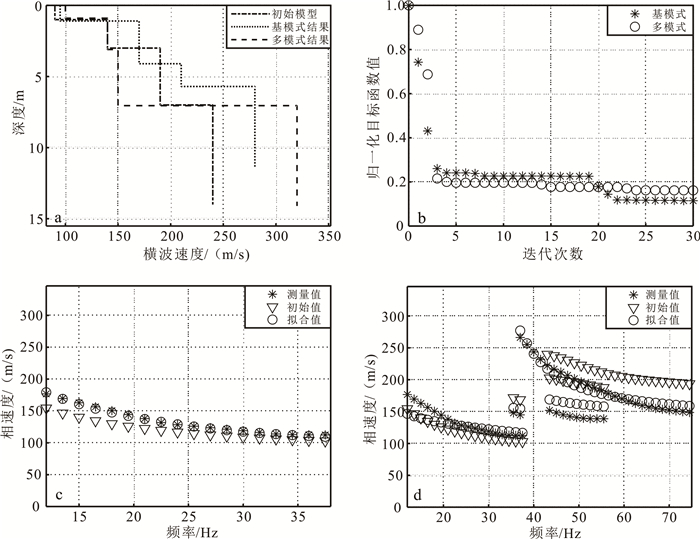
按照上文描述的方法分别实现基模式和多模式勒夫波的反演。令反演的初始模型为[90 m/s 140 m/s 190 m/s 240 m/s 1 m 2 m 4 m],第1至第4层密度在反演过程中保持不变,为[1.5 g/cm3 1.6 g/cm3 1.7 g/cm3 1.8 g/cm3]。α0=5 m/s,λ=2,θ=0.5,vSu=400 m/s,vSl=50 m/s,hu=6 m,hl=0.5 m,最大迭代次数为30。图 8是反演结果,为清晰显示频散曲线拟合情况,图 8c、d的频率间隔已调成1.5 Hz。基模式勒夫波的反演结果是[95 m/s 170 m/s 210 m/s 280 m/s 1.10 m 3.00 m 1.60 m],多模式勒夫波的反演结果是[100 m/s 140 m/s 150 m/s 320 m/s 0.90 m 2.20 m 3.95 m]。
|
| a.横波速度剖面;b.目标函数值的变化曲线;c.基模式频散曲线;d.多模式频散曲线。 图 8 塞耶特村数据反演结果 Fig. 8 Inversion results of field data acquired fromCˇachtice village |
|
|
相比初始模型的目标函数值,基模式和多模式勒夫波反演的目标函数下降量都足够显著(图 8b)。基模式和多模式勒夫波频散曲线反演给出的结果都是递增型地层,相比于基模式勒夫波频散曲线反演,多模式勒夫波频散曲线反演的深度更深,这说明高模式勒夫波的穿透深度更深(图 8a)。本次勘探的目的是确定测线下是否有历史建筑的遗迹,而建筑地基的横波速度远大于反演结果的横波速度。因此,笔者确信地下不存在历史建筑的遗迹,这与Dokter等[30]此前的结论也是一致的。
4 结论1) 对于瑞雷波反演,高模式瑞雷波的加入会显著提高横波速度评价结果的精度。然而,多模式瑞雷波的频散曲线总存在“模式接吻”现象,处理实测数据时很容易模式误判,令反演结果的可靠性降低。
2) 与瑞雷波相比,勒夫波能量分配均匀,易于提取多模式频散曲线,不存在“模式接吻”现象,且反演系统更为简单。基模式勒夫波对横波速度更敏感,即使在初始模型很拙劣时,基模式勒夫波反演仍能够揭露出地层的结构特征。高模式勒夫波则可以有效提升半空间横波速度的评价精度。
3) 应用本文中提出的面波频散曲线变厚度反演方法处理塞耶特村勒夫波数据。结果表明,基模式和多模式勒夫波反演给出的反演结果都是递增型的横波速度结构,且高模式勒夫波的穿透深度更深。根据反演结果的横波速度范围,笔者确信测线下没有历史建筑的遗迹。
致谢: 爱丁堡大学地球科学学院格兰特研究所的Dokter博士将在斯洛文尼亚西北部塞耶特村采集的勒夫波数据分享给我们,以令我们能够将本文中的方法应用于实测数据,全体作者在此表示感谢。
| [1] |
Yilmaz Ö, Eser M, Berilgen M. A Case Study of Seismic Zonation in Municipal Areas[J]. The Leading Edge, 2006, 25(3): 319-330. DOI:10.1190/1.2184100 |
| [2] |
夏江海. 高频面波方法[M]. 武汉: 中国地质大学出版社, 2015. Xia Jianghai. High-Frequency Surface Wave Method[M]. Wuhan: Press of China University of Geosciences, 2015. |
| [3] |
Xia J, Miller R D, Park C B. Estimation of Near-Surface Shear-Wave Velocity by Inversion of Rayleigh Waves[J]. Geophysics, 1999, 64(3): 691-700. DOI:10.1190/1.1444578 |
| [4] |
Xia J, Xu Y, Luo Y, et al. Advantages of Using Multichannel Analysis of Love Waves (MALW) to Estimate Near-Surface Shear-Wave Velocity[J]. Surveys in Geophysics, 2012, 33(5): 841-860. DOI:10.1007/s10712-012-9174-2 |
| [5] |
McMechan G A, Yedlin M J. Analysis of Dispersive Waves by Wave Field Transformation[J]. Geophysics, 1981, 46(6): 869-874. DOI:10.1190/1.1441225 |
| [6] |
Park C B, Miller R D, Xia J. Multichannel Analysis of Surface Waves[J]. Geophysics, 1999, 64(3): 800-808. DOI:10.1190/1.1444590 |
| [7] |
Steeples D W. Near-Surface Geophysics:75 Years of Progress[J]. The Leading Edge, 2005, 24(Sup. 1): S82-S85. |
| [8] |
Safani J. Surface Wave Dispersion Modeling by Full-Wavefield Reflectivity and Inversion for Shallow Subsurface Imaging[D]. Kyoto: Kyoto University, 2007.
|
| [9] |
Zeng C, Xia J, Liang Q, et al. Comparative Analysis on Sensitivities of Love and Rayleigh Waves[C]//SEG Technical Program Expanded Abstracts. San Antonio: Society of Exploration Geophysicists, 2007: 1138-1141.
|
| [10] |
Luo Y, Xia J, Xu Y, et al. Finite-Difference Modeling and Dispersion Analysis of High-Frequency Love Waves for Near-Surface Applications[J]. Pure and Applied Geophysics, 2010, 167(12): 1525-1536. DOI:10.1007/s00024-010-0144-7 |
| [11] |
Song X H, Li D Y, Gu H M, et al. Insights into Performance of Pattern Search Algorithms for High-Frequency Surface Wave Analysis[J]. Computers & Geosciences, 2009, 35(8): 1603-1619. |
| [12] |
Hamimu L, Nawawi M, Safani J. Utilization of Multimode Love Wave Dispersion Curve Inversion for Geotechnical Site Investigation[J]. Journal of Geophysics and Engineering, 2011, 8(2): 341-350. DOI:10.1088/1742-2132/8/2/019 |
| [13] |
Dal Moro G, Ferigo F. Joint Analysis of Rayleigh-and Love-Wave Dispersion:Issues, Criteria and Improvements[J]. Journal of Applied Geophysics, 2011, 75(3): 573-589. DOI:10.1016/j.jappgeo.2011.09.008 |
| [14] |
Socco L V, Boiero D, Maraschini M, et al. On the Use of the Norwegian Geotechnical Institute's Prototype Seabed-Coupled Shear Wave Vibrator for Shallow Soil Characterization:Ⅱ:Joint Inversion of Multimodal Love and Scholte Surface Waves[J]. Geophysics Journal International, 2011, 185(1): 237-252. DOI:10.1111/j.1365-246X.2011.04961.x |
| [15] |
Xie H, Liu L. Near-Surface Anisotropic Structure Characterization by Love Wave Inversion for Assessing Ground Conditions in Urban Areas[J]. Journal of Earth Science, 2015, 26(6): 807-812. DOI:10.1007/s12583-015-0619-7 |
| [16] |
Fang H, Yao H, Zhang H, et al. Direct Inversion of Surface Wave Dispersion for Three-Dimensional Shallow Crustal Structure Based on Ray Tracing:Methodology and Application[J]. Geophysical Journal International, 2015, 201(3): 1251-1263. DOI:10.1093/gji/ggv080 |
| [17] |
Wang N, Montagner J P, Burgos G, et al. Intrinsic, Versus, Extrinsic Seismic Anisotropy:Surface Wave Phase Velocity Inversion[J]. Comptes Rendus Geoscience, 2015, 347(2): 66-76. DOI:10.1016/j.crte.2015.02.010 |
| [18] |
Dalton D R, Slawinski M A, Stachura P, et al. Sensitivity of Love and Quasi-Rayleigh Waves to Model Parameters[J]. Quarterly Journal of Mechanics & Applied Mathematics, 2017, 70(2): 103-130. |
| [19] |
Virieux J. P-SV Wave Propagation in Heterogenous Media:Velocity-Stress Finite-Difference Method[J]. Geophysics, 1986, 51(4): 889-901. DOI:10.1190/1.1442147 |
| [20] |
Virieux J. SH-Wave Propagation in Heterogenous Media:Velocity-Stress Finite-Difference Method[J]. Geophysics, 1984, 49(11): 1933-1942. DOI:10.1190/1.1441605 |
| [21] |
Mittet R. Free-Surface Boundary Conditions for Elastic Staggered-Grid Modeling Schemes[J]. Geophysics, 2002, 67(5): 1616-1623. DOI:10.1190/1.1512752 |
| [22] |
Graves R W. Simulating Seismic Wave Propagation in 3D Elastic Media Using Staggered-Grid Finite Differences[J]. Bulletin of the Seismological Society of America, 1996, 86(4): 1091-1106. |
| [23] |
Collino F, Tsogka C. Application of the Perfectly Matched Absorbing Layer Model to the Linear Elastodynamic Problem in Anisotropic Heterogeneous Media[J]. Geophysics, 2006, 66(1): 294-307. |
| [24] |
刘四新, 朱怡诺, 王旭东, 等. 工程地震折射波解释方法研究进展[J]. 吉林大学学报(地球科学版), 2018, 48(2): 350-363. Liu Sixin, Zhu Yinuo, Wang Xudong, et al. Progress of Engineering Seismic Refraction Interpretation[J]. Journal of Jilin University (Earth Science Edition), 2018, 48(2): 350-363. |
| [25] |
林松, 李媛, 程邈, 等. 嘉鱼断裂西向延伸与第四系活动特征[J]. 吉林大学学报(地球科学版), 2018, 48(5): 1501-1511. Lin Song, Li Yuan, Cheng Miao, et al. Westward Extension and Quaternary Activity Charracteristics of Jiayu Fault[J]. Journal of Jilin University (Earth Science Edition), 2018, 48(5): 1501-1511. |
| [26] |
Levshin A L, Ritzwoller M H, Shapiro N M. The Use of Crustal Higher Modes to Constrain Crustal Structures Across Central Asia[J]. Geophysical Journal International, 2005, 160(3): 961-972. DOI:10.1111/j.1365-246X.2005.02535.x |
| [27] |
凡友华.层状介质中瑞利面波频散曲线正反演研究[D].哈尔滨: 哈尔滨工业大学, 2001. Fan Youhua. Research of Forward and Inversion for Rayleigh Wave Dispersion Curve in Layered Medium[D]. Harbin: Harbin Institute of Technology, 2001. http://d.wanfangdata.com.cn/Thesis/Y392387 |
| [28] |
Gao L, Xia J, Pan Y, et al. Reason and Condition for Mode Kissing in MASW Method[J]. Pure and Applied Geophysics, 2016, 173(5): 1627-1638. DOI:10.1007/s00024-015-1208-5 |
| [29] |
韩飞, 王者江, 闫英伟. 基于广义模式识别面波基模式频散曲线反演研究[J]. CT理论与应用研究, 2017, 26(3): 309-320. Han Fei, Wang Zhejiang, Yan Yingwei. Research on Inversion of Surface Wave Base Mode Dispersion Curve Based on Generalized Pattern Search[J]. CT Theory and Applications, 2017, 26(3): 309-320. |
| [30] |
Dokter E, K hn D, Wilken D, et al. Full-Waveform Inversion of SH- and Love-Wave Data in Near-Surface Prospecting[J]. Geophysical Prospecting, 2017, 65(S1): 216-236. |
| [31] |
Luo Y, Xia J, Miller R D, et al. Rayleigh-Wave Dispersive Energy Imaging Using a High-Resolution Linear Radon Transform[J]. Pure and Applied Geophysics, 2008, 165(5): 903-922. DOI:10.1007/s00024-008-0338-4 |




