2. 广州市金融服务创新与风险管理研究基地,广东 广州 510640
2. Guangzhou Financial Services Innovation and Risk Management Research Base, Guangzhou 510640, Guangdong, China
经证监会批准,我国首只场内交易的期权产品“华夏上证50ETF期权”于2015年2月9日在上海证券交易所上市交易,开启了中国资本市场期待已久的“期权元年”,丰富了我国资本市场上的金融产品,增加了风险管理的手段。
期权的定价和对冲问题一直是学术界研究的热点,对资本市场上期权、结构化产品的设计和交易有着重大意义。Black和Scholes(BS)及Merton对期权的定价和对冲研究做出了开创性的贡献,他们设定股票价格变动模型为布朗运动的随机扩散模型,通过伊藤引理和积分变换求解随机微分方程得到了欧式看涨和看跌期权的精确价格。[1-2]他们提出的模型称为BSM模型,它假设波动率为常数、无交易费用、连续时间对冲,这与实际市场情况不相符,直接应用BSM模型可能带来较大的对冲误差。对此,学者们在BSM模型的基础上不断对模型加以改进。例如: Merton在BSM模型的基础上加入服从泊松过程的跳跃部分来描述股价的跳跃现象;[3]Heston放松BSM模型中波动率为常量的限制,提出了Heston随机波动模型[4],他假设波动率服从CIR模型;[5]Bakshi等假设股票价格服从随机利率、随机波动率以及泊松跳跃过程的模型,全面考虑市场上影响期权价格的波动率风险、利率风险、跳跃风险等主要风险,提出了BCC模型,该模型具有更高的自由度,可以根据市场数据来校准模型的参数,通过傅里叶变换得到精确的期权定价公式。[6]
期权对冲最常见的方法为delta对冲,即投资组合中标的股票的投资份额等于期权价格关于标的股票价格的一阶导数,每一期都根据delta值来调整投资策略。Heston模型、BCC模型都可通过计算delta值来调整股票头寸对冲风险。在波动率为常数的假设下,Leland根据交易费用的比例相应的调整波动率改进了对冲误差。[7]Boyle等人在Cox-Ross-Rubinstein 二叉树定价模型的基础上研究了考虑交易费用的期权对冲问题。[8]Nguyen等人研究了考虑随机波动率和交易费用的期权对冲问题,改进了Leland调整波动率的方法。[9]
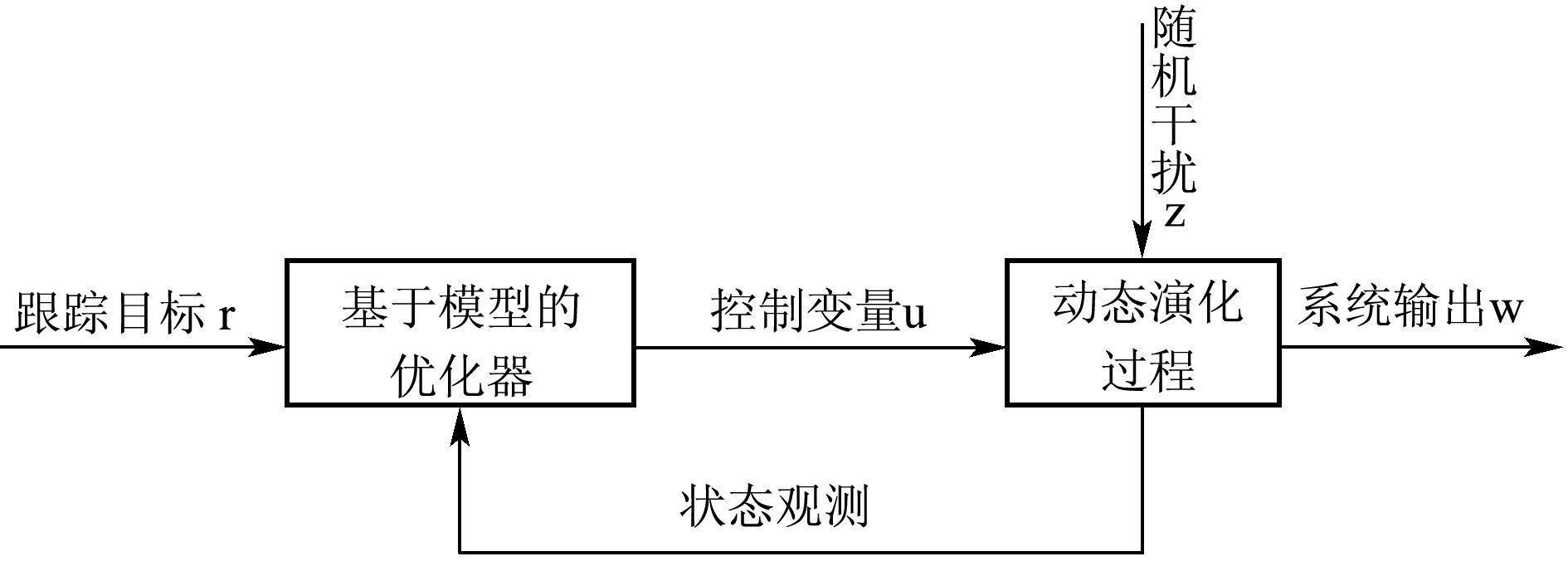
从控制论的角度可以将期权动态对冲看成一个跟踪控制问题。从市场上得到的标的股票价格、利率、期权价格等公开信息看作系统的观测值,系统的控制变量为股票、债券的投资金额或者投资份数,系统的输出变量为由股票和债券构成的投资组合价值,系统的控制目标是在给定投资组合的初始金额等于卖出期权价格的条件下,采用合适的控制方法使得投资组合动态跟踪期权的价值,跟踪误差越接近零越好,且尽可能地排除随机因素的干扰。该系统的方框图如图 1所示。
|
图 1 控制系统的方框图 |
控制论中的随机最优控制可以解决多阶段的期权对冲问题,通过哈密顿-雅可比-贝尔曼(Hamilton-Jacobi-Bellman)偏微分方程来求解。Gondzio和Zhao等人分别把定价和对冲问题转化成随机线性规划问题,通过多阶段随机规划求解。[10-11]这种方法的主要不足是模拟树的节点会随着仿真周期的数量呈现指数倍增长,因此通常情况下每个节点只考虑2个或者3个分叉情况。Primbs把对冲问题转化成一个线性二次型(LQR)调控问题,采用两种方法考虑交易费用,一是在目标函数中加入交易成本作为惩罚项,将对冲问题转化为无约束的随机线性二次型问题;[12]另一种方法是通过随机模型预测控制来处理交易费用约束,求解一个有限时域的二次规划问题。[13]Bemporad等人提出了基于情景树模拟的随机模型预测控制方法,将期权到期时的系统状态映射到较短时刻,根据考虑交易费用与否选择跟踪误差的方差或者条件在险价值(Condition Value at Risk,CVaR)作为目标函数,应用相应的优化方法得到了一个次优解。[14-15]尹力博等人研究了人民币外汇期权的对冲问题,考虑不同资产收益率的随机波动与汇率的随机波动,构建整体风险控制和后验优化风险再调整的外汇期权组合风险综合管理机制,通过基于离散情景树的多阶段随机规划求解最优对冲策略。[16]
上述关于期权对冲问题的研究工作考虑随机波动率风险的比较多,而考虑随机利率和跳跃风险的较少。本文选择随机波动率、随机利率和跳跃风险的BCC模型作为股票价格的预测模型研究欧式期权的动态对冲问题。在不考虑交易费用的情况下,建立以跟踪误差的方差最小化为控制目标的优化控制模型。在考虑交易费用的情况下,建立以跟踪误差的CVaR最小化为控制目标的优化控制模型。并且,通过蒙特卡洛仿真对基于随机模型预测控制的对冲方法和delta对冲方法的效果进行对比分析。进一步使用华夏上证50ETF期权合约的实际数据进行实证分析,结果验证了基于随机模型预测控制方法解决期权对冲问题的有效性。
一、 构建资产价格变动模型 (一) 股票价格模型BCC模型包含了随机波动率、跳跃风险和随机短期利率,使用BCC模型来描述股票价格变动对市场风险的考虑较为全面。给定一个流域概率空间(Ω,γ,F,P),截至日期为T,0<T<∞,Ω代表连续的状态空间,γ表示σ-代数,F表示流域,P表示实际的概率测度。其中股票价格由包括随机波动率、跳扩散的Bates模型[17]来描述:
| $d{{S}_{t}}=({{r}_{t}}-{{r}_{J}}){{S}_{t}}dt+\sqrt{{{v}_{t}}}{{S}_{t}}d{{Z}_{t}}^{1}+{{J}_{t}}{{S}_{t}}d{{N}_{t}}$ | (1a) |
| $d{{v}_{t}}={{\kappa }_{v}}({{\theta }_{v}}-{{v}_{t}})dt+{{\sigma }_{v}}\sqrt{{{v}_{t}}}d{{Z}_{t}}^{2}$ | (1b) |
其中,St表示t时刻股票S的价格,rt表示t时刻无风险利率,rJ=λ(exp(μJ+δ2/2)-1)表示跳跃的偏移修正,vt表示t时刻方差,θv表示方差的长期均值,κv表示vt回归θv的速度,σv表示股票价格方差的波动系数,Zt1、Zt2表示标准布朗运动,Nt表示强度为λ的泊松过程,t时刻跳跃Jt的分布为log(1+Jt)≈N(log(1+μJ)-0.5δ2,δ2),N表示标准正态分布随机变量的累积分布函数。
随机利率通过著名的CIR平方根扩散模型[5]来描述:
| $d{{r}_{t}}={{\kappa }_{r}}({{\theta }_{r}}-{{r}_{t}})dt+{{\sigma }_{r}}{{\sqrt{r}}_{t}}d{{Z}_{t}}^{3}$ | (1c) |
其中,rt表示t时刻的短期利率,θr表示短期利率的长期均值,κr表示短期利率rt回归长期均值的速度,σr表示短期利率的波动系数,Zt3表示标准的布朗运动。
上述的随机过程是适应于流域F的,三个布朗运动的相关性为dZt1dZt2=ρdt,dZt1dZt3=dZt2dZt3=0,Nt独立于Ztn,n=1,2,3。
当前时刻为t,T(T>t)时刻到期支付1单位货币的零息债券在当前时刻的价格为:
| ${{B}_{t}}\left( T \right)={{E}_{t}}^{Q}({{e}^{-\int_{t}^{T}{{{r}_{u}}du}}})$ | (2) |
其中,E表示风险中性Q测度下的期望符号。BCC模型是一个具有代表性的通用模型,包含了以下广泛使用的定价模型:(a) BSM模型:几何布朗运动是模型的不确定性来源,而波动率和利率都是常量;(b) Merton 跳跃模型:在BSM模型的基础上加上了呈对数正态分布的跳跃部分;(c) Heston随机波动模型:比较流行的随机波动率模型,而其短期利率是固定常量;(d) Bates 随机波动率跳扩散模型:在Heston模型的基础上加上了跳跃部分。
经典BSM模型如下:
| $dS\left( t \right)=\mu S\left( t \right)dt+\sigma S\left( t \right)d{{z}^{S}}$ | (3) |
其中,μ为漂移参数,σ为波动率。本文在离散的时间点对股票、期权等变量进行估值计算,需要对价格模型进行离散化处理,把时间段[0,T]划分为M段,每段间隔Δt=T/M,t∈{0,Δt,2Δt,…,T},得到BSM模型的离散形式:
| $S\left( t \right)=S\left( s \right)\cdot \exp ((\mu -0.5{{\sigma }^{2}})\Delta t+\sigma \sqrt{\Delta t}{{z}^{S}})$ | (4) |
连续时间的BCC模型经过离散化处理后的表达式如下:
| ${{S}_{t}}={{S}_{s}}({{e}^{\left( {{{\bar{r}}}_{t}}-{{r}_{J}}-{{v}_{t}}/2 \right)\Delta t+\sqrt{{{v}_{t}}}\sqrt{\Delta t}{{Z}_{t}}^{1}}}+({{e}^{{{\mu }_{J}}+\delta {{z}_{t}}^{4}}}-1){{y}_{t}})$ | (5a) |
| ${{{\tilde{v}}}_{t}}={{{\tilde{v}}}_{s}}+{{\kappa }_{v}}({{\theta }_{v}}-{{{\tilde{v}}}_{s}}^{+})\Delta t+{{\sigma }_{v}}\sqrt{{{{\tilde{v}}}_{s}}^{+}}\sqrt{\Delta t}{{Z}_{t}}^{2},{{v}_{t}}={{{\tilde{v}}}_{t}}^{+}$ | (5b) |
| ${{{\tilde{v}}}_{t}}={{{\tilde{v}}}_{s}}+{{\kappa }_{r}}({{\theta }_{r}}-{{{\tilde{v}}}_{s}}^{+})\Delta t+{{\sigma }_{r}}\sqrt{{{{\tilde{v}}}_{s}}^{+}}\sqrt{\Delta t}{{Z}_{t}}^{3},{{r}_{t}}={{{\tilde{v}}}_{t}}^{+}$ | (5c) |
其中,s=t-Δt,rt=(rt+rs)/2,yt表示强度为λ的泊松分布随机变量,Ztn, n=1,2,3,4表示标准正态分布随机变量,Zt1和Zt2的相关系数为ρ,其他随机变量不相关,x+表示max[0,x]。
(二) 欧式期权定价公式对于上面得到标的股票价格变动模型,可以通过蒙特卡洛仿真和积分运算两种方法得到欧式期权的定价公式。
设置好仿真步长Δt,对离散化的BCC模型进行I次蒙特卡洛仿真,增大仿真次数、缩减仿真步长以及采取控制变量等方法有助于提高仿真结果的精度,在风险中性测度下可以得到欧式看涨期权价格:
| ${{C}_{0}}^{MCS}={{B}_{0}}\left( T \right)\frac{1}{T}\sum\limits_{i=1}^{I}{\max [{{S}_{T,i}}-k,0]}$ | (6) |
标的股票价格变动服从BSM模型时,得到欧式看涨期权的公式如下:
| ${{C}_{t}}={{S}_{t}}\phi ({{h}_{+}})-K{{e}^{-r(T-t)}}\phi ({{h}_{-}})$ | (7) |
其中,t为当前时刻,T为到期日,r为无风险利率,σ为波动率,K为敲定价格,φ(x)表示标准正态随机变量的累积分布函数在x点的值,h+=(ln(Pt/K)+(r+0.5σ2)(T-t))/(σ$\sqrt{T-1}$),h-=h+-σ$\sqrt{T-1}$。
当标的股票价格变动服从BCC模型时,参考 Carr等人和Lewis的傅里叶变换方法对股票价格服从BCC模型的欧式期权进行定价。[18-19]BCC模型由Heston随机波动模型和Merton 跳跃模型以及CIR利率模型构成,首先构造驱动资产价格演化的随机过程的特征函数,Heston随机波动模型的特征函数φ0H如式(8)所示:
| ${{\varphi }_{0}}^{H}\left( u,T \right)=exp({{H}_{1}}\left( u,T \right)+{{H}_{2}}\left( u,T \right){{v}_{0}})$ | (8) |
其中,c1=κvθv,
Merton 跳跃模型的特征函数φ0M(u,T)如式(9)所示:
| ${{\varphi }_{0}}^{M}\left( u,T \right)=\exp ((iu\omega +\lambda ({{e}^{iu{{\mu }_{J}}-{{u}^{2}}{{\delta }^{2}}/2}}-1))T)$ | (9) |
其中,ω=-λ(eμJ+0.5δ2-1)。由于Hestons随机波动模型和Merton 跳跃模型中的随机变量不相关,得到BCC模型的特征函数如下:
| ${{\varphi }_{0}}^{BCC}\left( u,T \right)={{\varphi }_{0}}^{H}\left( u,T \right){{\varphi }_{0}}^{M}\left( u,T \right)$ | (10) |
得到特征函数后通过傅里叶积分得到欧式期权的定价公式 (11):
| $\begin{align} & {{C}_{0}}\left( K,T \right)={{S}_{0}}-{{B}_{0}}\left( T \right)\sqrt{{{S}_{0}}K}\frac{1}{\pi }\int_{0}^{\infty }{{}} \\ & Re[{{e}^{-iuk}}{{\varphi }_{0}}\left( u-i/2,T \right)]\frac{du}{{{u}^{2}}+1/4} \\ \end{align}$ | (11) |
其中,k=log(S0/K),S0为t=0时刻股票价格,K为期权的敲定价格,T为期权的到期日,φ0为BCC模型的特征函数。假设当前时刻t=0,折现因子B0(T)为T时刻支付1单位货币的零息债券的现值,在CIR模型中的表达式如下:
| ${B_0}(T) = {b_1}(T)exp( - {b_2}(T){r_0})$ | (12) |
其中,
| $\begin{align} & {{b}_{1}}\left( T \right)={{\left[ \frac{2\gamma {{e}^{\left( {{\kappa }_{r}}+\gamma \right)T/2}}}{2\gamma +({{\kappa }_{r}}+\gamma )({{e}^{\gamma T}}-1)} \right]}^{\frac{2{{\kappa }_{r}}{{\theta }_{r}}}{\sigma _{r}^{2}}}}, \\ & {{b}_{2}}\left( T \right)=\frac{2({{e}^{\gamma T}}-1)}{2\gamma +({{\kappa }_{r}}+\gamma )({{e}^{\gamma T}}-1)}, \\ & \gamma =\sqrt{{{\kappa }_{r}}^{2}+2{{\sigma }_{r}}^{2}}. \\ \end{align}$ |
假设投资组合由一支股票S和债券B构成,期权的卖方动态管理投资组合来跟踪期权价格,使得投资组合价值在到期日的时候尽可能她等于期权价值。在时间段[tΔT,(t+1)ΔT],t=0,1,…,T,令u0(t)表示分配在无风险债券上的财富,u1(t)表示标的股票的购买份额。
在不考虑交易费用的情况下,t时刻的投资组合价值为:
| $w\left( t \right)={{u}_{0}}\left( t \right)+S\left( t \right){{u}_{1}}\left( t \right)$ | (13) |
其中,S(t)为t时刻标的股票的价格,这里假设股票价格在交易前交易后的瞬间是一样的。投资组合为标准的自融资投资组合,则投资组合的动态方程如下:
| $w\left( t+1 \right)=\left( 1+r\left( t \right) \right)w\left( t \right)+b\left( t \right){{u}_{1}}\left( t \right)$ | (14) |
其中,b(t)=S(t+1)-(1+r(t))S(t)。投资组合的初始条件w(0)等于投资者购买期权的价格,即w(0)=C0(K,T)。
由于实际市场上买卖股票会产生一定的交易费用,所以在这里假设股票交易费用h(t)与每次交易股票的数量|u1(t)-u1(t-1)|成比例:
| $h\left( t \right)=\varepsilon |{{u}_{1}}\left( t \right)-{{u}_{1}}\left( t-1 \right)|S\left( t \right)$ | (15) |
其中,ε为股票交易金额的费用比率。
令w(t-)表示t时刻投资策略调整前一瞬间的投资组合资产价值,w(t+)表示t时刻投资策略调整后一瞬间的投资组合资产价值,在考虑交易费用的情况下,
| $w({{t}^{+}})=w({{t}^{-}})-h\left( t \right)$ | (16) |
| $w({{\left( t+1 \right)}^{-}})=\left( 1+r\left( t \right) \right)(w({{t}^{-}})-h\left( t \right))+b\left( t \right){{u}_{1}}\left( t \right)$ | (17) |
投资组合的初始条件w(0-)等于投资者购买期权的价格,即w(0-)=C0(K,T)。
二、 基于情景模拟的随机模型预测控制 (一) 不考虑交易费用的控制模型基于上文给出的股票价格、期权定价公式以及投资组合模型,我们可以把期权动态对冲问题看成控制理论中的随机参考跟踪问题,其中投资组合w(t)为系统的输出变量,股票的投资份额u1(t)为系统的控制变量,期权价格c(t)为w(t)的跟踪目标。控制目标为对可能出现的资产价格S(t)尽量使得投资组合在期权到期日的价值w(T)等于期权价值c(T)。定义跟踪误差为e(t)=w(t)-c(t), 则控制目标为最小化|e(t)|,在不考虑交易费用的情况下通过最小化跟踪误差的方差来实现。
下面通过基于情景模拟和随机规划的随机模型预测控制来求解最小方差问题。首先我们根据当前时刻从市场上得到关于股票价格、利率、波动率等信息,采用上文中的股票价格变动模型和相应期权定价模型进行预测,模拟出M个未来可能出现的资产价格情景,每个情景对应着相关随机过程的一个实现,每个情景发生的概率为πj,j=1,2,…,M,0<πj≤1,π1+π2+…+πM=1。
本文将优化时域从[t,T]缩短为[t,min{t+N,T}],N≥1,采用滚动求解有限时域的优化控制问题来降低复杂性,这种方法通常被称作滚动时域控制(Receding Horizon Control,RHC)或者模型预测控制(Model Predictive Control,MPC)。本文我们选取N=1的特殊情况,而且假设在时间段t+1到T实现可以实现期权的完美对冲。在交易时刻t=0,1,…,T-1,通过求解下面的有限时域的随机动态优化问题得到最优的投资组合控制变量u1(t):
| $\begin{align} & \underset{{{u}_{1}}\left( t \right)}{\mathop{\min }}\,Va{{r}_{{{m}_{t+1}}}}[w(t+1,{{m}_{t+1}})-c(t+1,{{m}_{t+1}})] \\ & s.t.w(t+1,{{m}_{t+1}})=\left( 1+r\left( t \right) \right)w\left( t \right)+b(t,{{m}_{t+1}}){{u}_{1}}\left( t \right) \\ \end{align}$ | (18) |
其中,mt+1表示在t+1时刻市场的状态,这由资产价格变动模型中的随机过程决定。上述问题是一步预测最小方差问题,只需要优化求解一个变量u1(t),极大的减少了需要优化求解的变量,而且t+1时刻后情景树没有进一步的分支,因此情景模拟数量M可以设置得大一些,模拟更多的情景。通过优化w(t+1)-c(t+1)的采样方差,上述问题可以转化为简单的最小二乘问题:
| $\mathop {\min }\limits_{{u_1}\left( t \right)} {\mkern 1mu} \sum\limits_{j = 1}^M {{\pi ^j}} {({e^j}\left( {t + 1} \right) - ({1 \over M}\sum\limits_{j = 1}^M {{e^j}} \left( {t + 1} \right)))^2}$ | (19) |
其中,ej(t+1)=wj(t+1)-cj(t+1),wj(t+1)=(1+r(t))wj(t)+bj(t)u1(t)是对应每种情景j=1,2,…,M下的将来的投资组合财富,πj是相应情景出现的概率,0≤πj≤1,
在考虑交易费用情况下,Bemporad等人证明了跟踪误差的方差这一目标函数不受交易费用的影响,所以不合适作为控制目标。[15]因此需要对目标函数进行改进,在这里采用条件在险价值(CVaR)作为跟踪控制的目标函数。令f(u1,s):R1+k→R是关于决策变量u1的损失函数,在这里f(u,s)=|e(t+1)|,s∈Rk对应各种模拟情景下的随机变量,令p(s)表示S的概率密度函数,给定一个固定概率β,0≤β<1,典型的取值β=90%,95%,99%,则CVaR的定义为在发生概率为1-β条件下的平均损失:
| ${{\varphi }_{\beta }}({{u}_{1}})=\frac{1}{1-\beta }\int_{f\left( {{u}_{1}},s \right)\ge {{\ell }_{\beta }}({{u}_{1}})}{f({{u}_{1}},s)p\left( s \right)ds}$ | (20) |
其中,$\ell $β(u1)=min{$\ell $∈R:ψ(u1,$\ell $)≥β},ψ(u1,$\ell $)表示损失函数不超过$\ell $的概率:
| $\psi ({{u}_{1}},\ell )=\int_{f\left( {{u}_{1}},s \right)\le \ell }{p\left( s \right)ds}$ | (21) |
Rockafellar等人表示β-CVaR可以写成[20]:
| ${{\varphi }_{\beta }}({{u}_{1}})=\underset{\ell \in R}{\mathop{\min }}\,+\frac{1}{1-\beta {{\int }_{s\in R}}}{{[f({{u}_{1}},s)-\ell ]}^{+}}p\left( s \right)ds$ | (22) |
其中,[f]+=max{f,0}。在这里可以通过对模拟产生的M个情景采样来近似s的分布,sj相应的概率为πj,j=1,…M,则φβ(u1)可以近似表示为:
| ${{{\tilde{\varphi }}}_{\beta }}({{u}_{1}})=\ell +\frac{1}{1-\beta }\sum\limits_{j=1}^{M}{{{\pi }_{j}}}{{[f({{u}_{1}},{{s}^{j}})-\ell ]}^{+}}$ | (23) |
最后,以CVaR为目标函数的期权动态对冲问题可以转化为线性规划问题:
| $\begin{align} & \underset{{{u}_{1}}\left( t \right),\ell ,{{\{{{v}_{j}}\}}_{j=1}}^{M},\tau }{\mathop{\min }}\,\ell +\frac{1}{1-\beta }\sum\limits_{j=1}^{M}{{{\pi }_{j}}}{{v}_{j}} \\ & s.t.{{v}_{j}}\ge {{w}^{j}}({{\left( t+1 \right)}^{-}})-{{c}^{j}}\left( t+1 \right)-\tau -\ell \\ & {{v}_{j}}\ge {{w}^{j}}({{\left( t+1 \right)}^{-}})+{{c}^{j}}\left( t+1 \right)+\tau -\ell \\ & \tau \ge \varepsilon ({{u}_{1}}\left( t \right)-{{u}_{1}}\left( t-1 \right))S\left( t \right) \\ & \tau \ge -\varepsilon ({{u}_{1}}\left( t \right)-{{u}_{1}}\left( t-1 \right))S\left( t \right) \\ & {{v}_{j}}\ge 0,j=1,...,M \\ \end{align}$ | (24) |
上述随机模型预测控制的流程总结如下:
下面对随机模型预测控制方法解决期权对冲问题的有效性进行仿真验证,并和经典的delta对冲进行对比。首先在不考虑交易费用的条件下,设定股票价格变动服从BCC模型,并且股票价格的预测模型也是BCC模型,以跟踪误差的方差最小化为控制目标。设置模型中的参数如下:SMPC中情景预测数M=100,预测长度N=1,仿真期权到期时间为T=0.5年,动态对冲的时间间隔ΔT=0.02年,股票的初始价格S0=100,敲定价格K=100,CIR利率模型的参数r0=0.04,κr=0.3,θr=0.04,σr=0.1,波动率模型的参数v0=0.01,κv=1.5,θv=0.02,σv=0.15,股票价格模型的参数λ=0.25,μJ=-0.2, δ=0.1, ρ=0.1,蒙特卡洛仿真次数为500次。
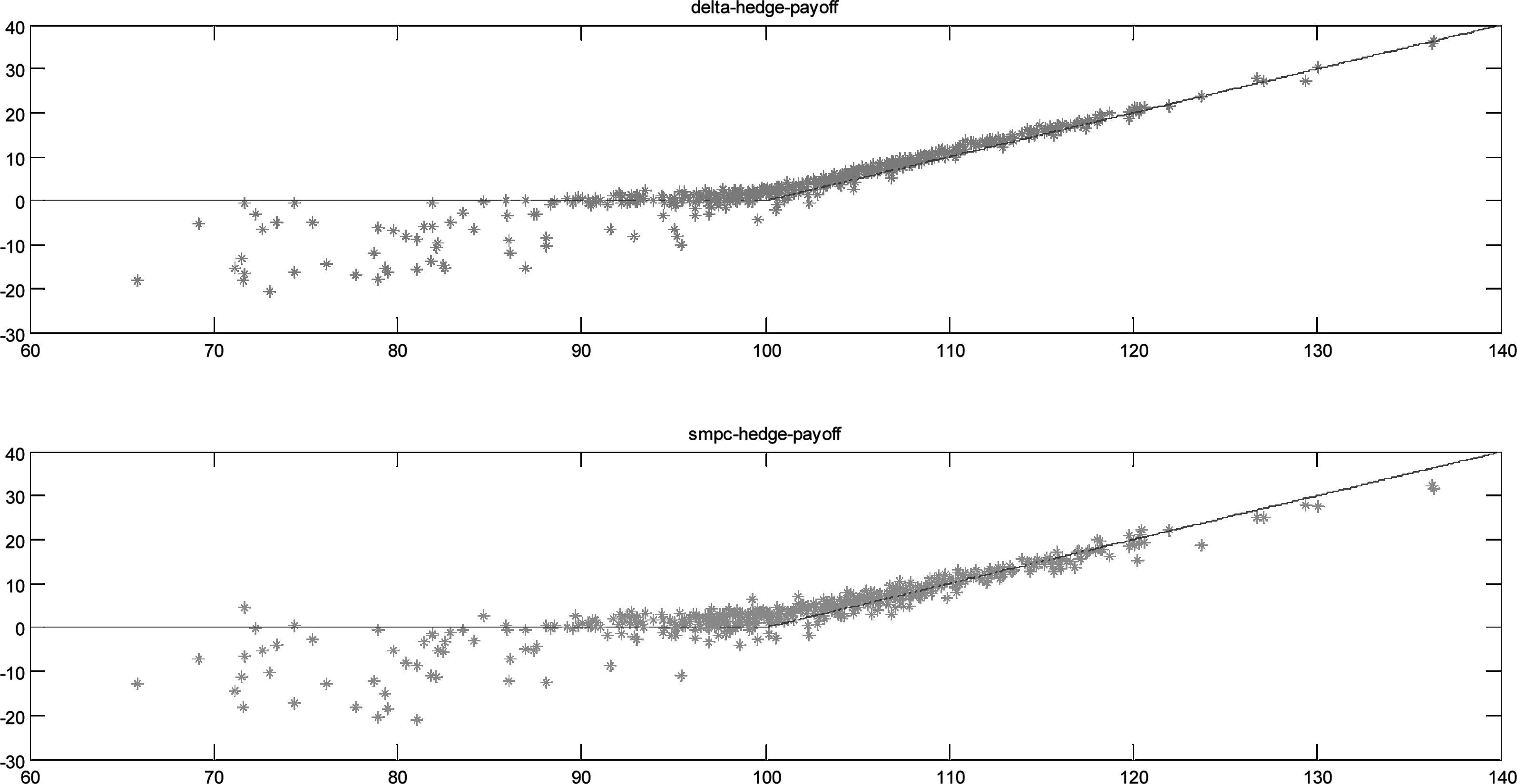
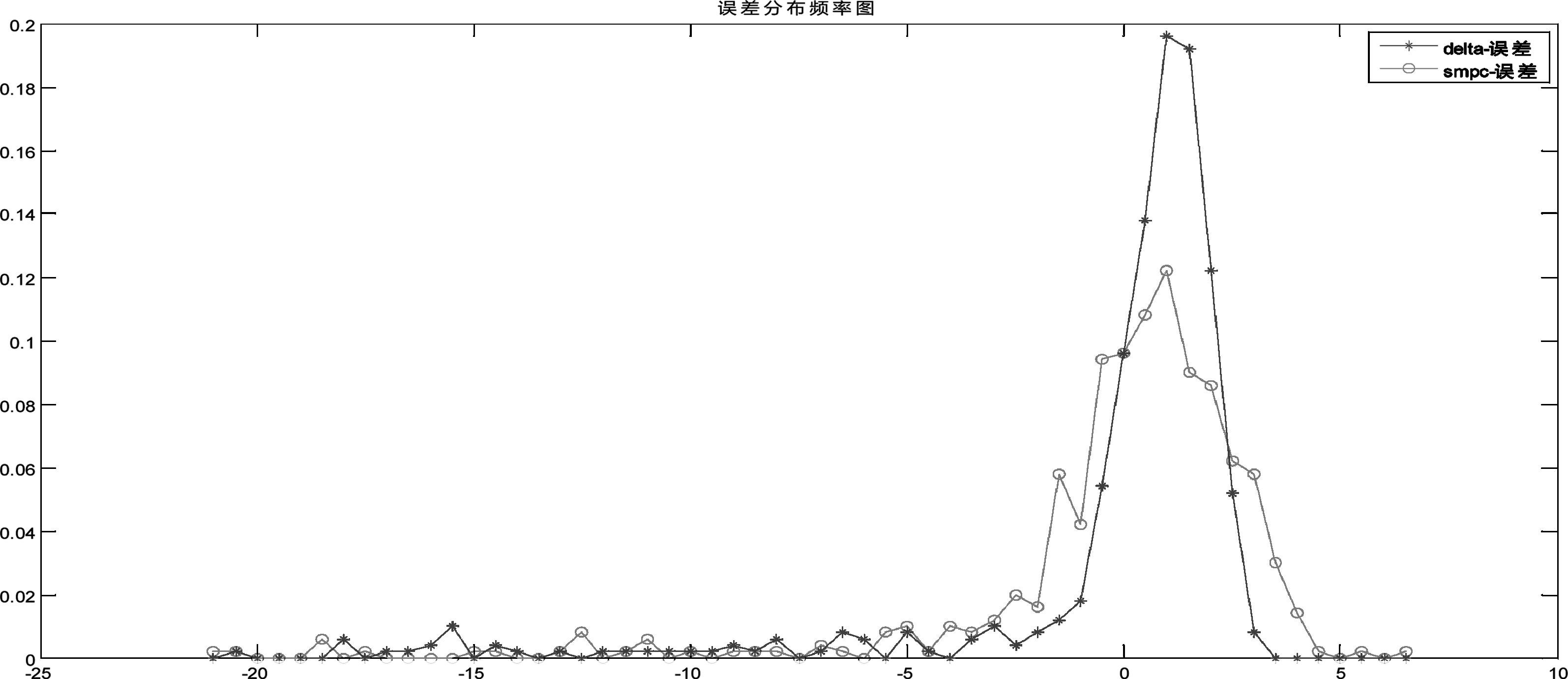
通过图 2可以看出,delta对冲和SMPC对冲两种方法整体上能达到跟踪期权回报的目标,但是当期权处于虚值状态时跟踪误差较大;从图 3可以看出SMPC对冲的误差分布相对均匀,而delta对冲的误差分布左偏。表 1中CVaR统计量的结果表明SMPC对冲的风险要小于delta对冲的风险。
|
图 2 到期日delta对冲和SMPC对冲投资组合价值与期权价值对比 |
|
图 3 delta对冲和SMPC对冲误差的频率分布图 |
| 表 1 对冲误差相关统计量 |
接下来进行考虑交易费用的仿真,设定股票价格变动服从BSM模型,并且预测模型也是BSM模型,以跟踪误差的95%-CVaR为目标函数。设置模型中的参数如下:初始价格S0=100,敲定价格K=100,到期日T=10/360年,无风险利率r=0.05,波动率sigma=0.3,仿真步长M = 10,交易费用比率ε设置为1%,总共仿真500次。
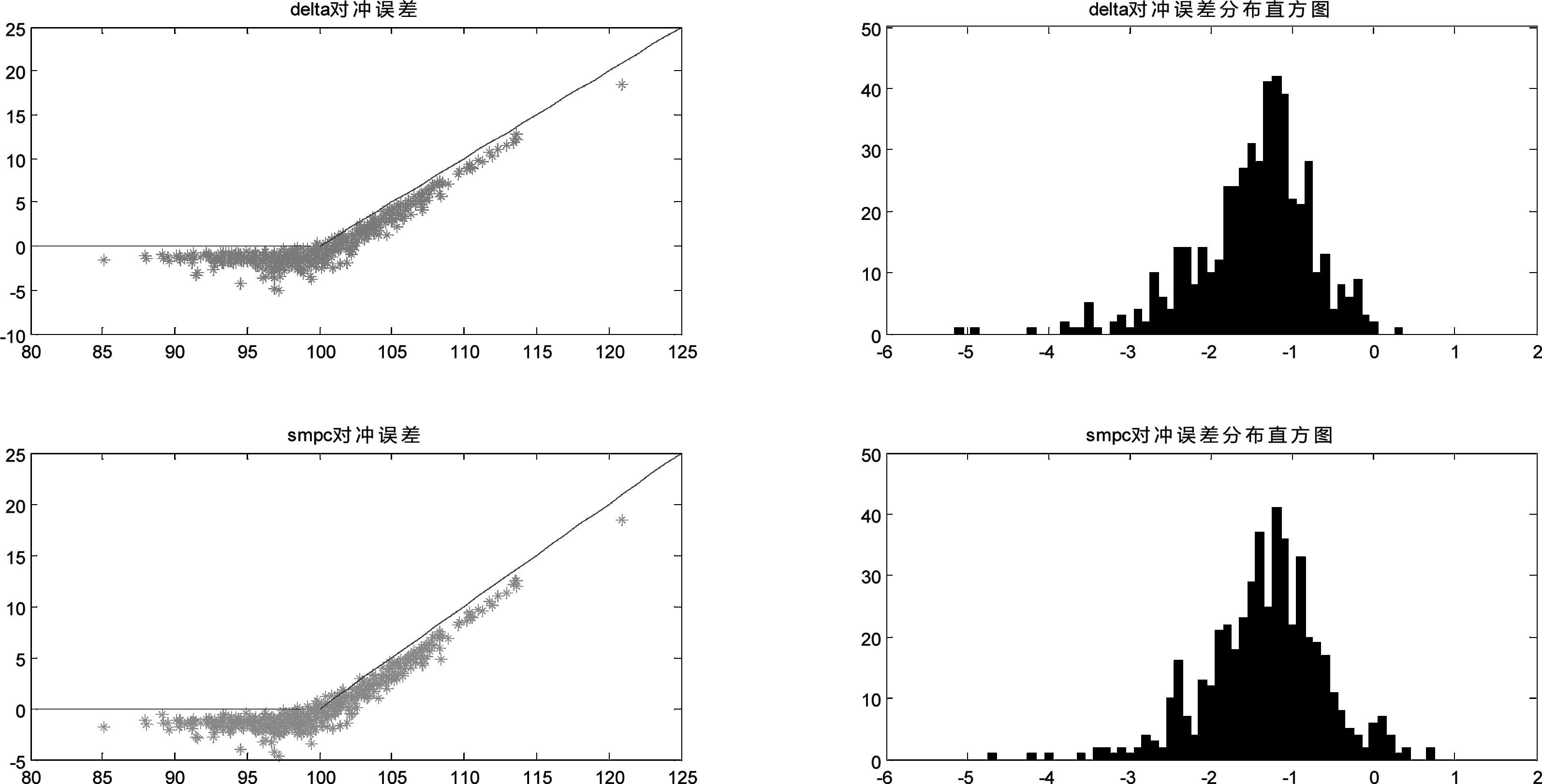
图 4左边为到期日delta对冲和SMPC对冲的投资组合价值与期权价值对比,右边为对冲误差的分布图,可以看出交易费用因素对动态对冲的结果有较大影响。从表 2中跟踪误差的各项统计量可以看出SMPC方法要优于delta对冲。
|
图 4 到期日delta对冲和SMPC对冲的效果对比 |
| 表 2 考虑交易费用的delta对冲和SMPC对冲的误差统计量 |
接下来通过Wind数据终端下载华夏上证50ETF期权的数据进行实证,选取的合约为2016年2月到期的看涨期权,敲定价格1.90元,预测模型选择相对简单BSM模型,无风险利率取一年期的上海银行间同业拆借利率,波动率是根据市场上期权的实际价格倒推得到的隐含波动率,交易费设置为千分之五,合约开始日期为2016年1月27日,到期日为2016年2月24日。动态对冲的结果如图 5所示,动态对冲的过程中股票投资决策如表 3所示,结果也证明了SMPC方法的有效性。
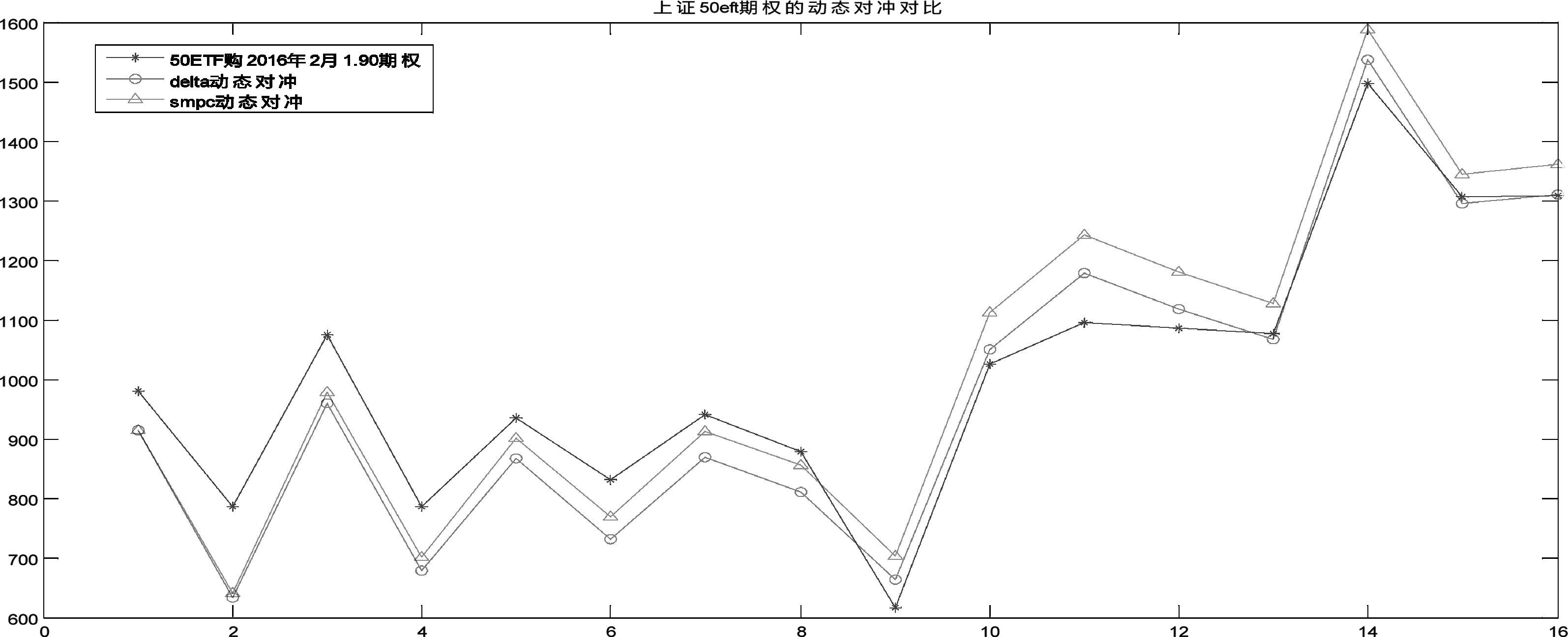
|
图 5 华夏上证50ETF期权动态对冲结果 |
| 表 3 华夏上证50ETF期权动态对冲过程中的投资决策 |
期权的动态对冲是一个经典的金融问题,具有很强的应用价值。本文通过随机模型预测控制来解决期权的动态对冲问题,随机模型预测控制具有很强的通用性,预测模型可以采用BSM、Heston、BCC等多种描述股票价格变动的模型,而且最小化跟踪误差的方差或者CVaR都可以作为控制目标,还能够显式处理交易费用,应用灵活。通过最小二乘法、线性规划等较为简单的算法就可以得到优化的控制量。最后通过蒙特卡洛仿真和实际市场中的数据验证了随机模型预测控制的实用性,其动态对冲的结果优于delta对冲。
| [1] | Scholes M S, Black F S. The Pricing of Options and Other Corporate Liabilities[J]. Journal of Political Economy, 1973,81(3): 637–54. DOI: 10.1086/260062 |
| [2] | Merton R C. A Rational Theory of Option Pricing[J]. Bell Journal of Economics & Management Science, 1973,4(1): 141–183. |
| [3] | Merton R C. Option Prices When Underlying Stock Returns Are Discontinuous[J]. Journal of Financial Economics, 1976,3(1-2): 125–144. DOI: 10.1016/0304-405X(76)90022-2 |
| [4] | Heston S L. A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options[J]. Review of Financial Studies, 1993,6(2): 327–343. DOI: 10.1093/rfs/6.2.327 |
| [5] | Cox J C, Ingersoll J E, Ross S A. A Theory of the Term Structure of Interest Rates[J]. Econometrica, 1985,53(2): 385–407. DOI: 10.2307/1911242 |
| [6] | Bakshi G, Cao C, Chen Z. Empirical Performance of Alternative Option Pricing Models[J]. Journal of Finance, 1997,52(5): 2003–2049. DOI: 10.1111/j.1540-6261.1997.tb02749.x |
| [7] | Leland H. Option Pricing and Replication with Transactions Costs[J]. Research Program in Finance Working Papers, 1985,40(5): 1283–1301. |
| [8] | Boyle P P, Vorst T. Option Replication in Discrete Time with Transaction Costs[J]. Journal of Finance, 1992,47(1): 271–293. DOI: 10.1111/j.1540-6261.1992.tb03986.x |
| [9] | Nguyen T H, Pergamenshchikov S. Approximate hedging problem with transaction costs in stochastic volatility markets[J]. Mathematical Finance, 2015,25(4): 702–723. DOI: 10.1111/mafi.2015.25.issue-4 |
| [10] | Gondzio J, Kouwenberg R, Vorst T. Hedging options under transaction costs and stochastic volatility ☆[J]. Journal of Economic Dynamics & Control, 2003,27(6): 1045–1068. |
| [11] | Zhao Y, Ziemba W T. A stochastic programming model using an endogenously determined worst case risk measure for dynamic asset allocation[J]. Mathematical Programming, 2000,89(2): 293–309. |
| [12] | Primbs J A. LQR and receding horizon approaches to multi-dimensional option hedging under transaction costs[C]//Glenn YM.Proceedings of the 2010 American Control Conference (ACC), Baltimare Maryland VSA:IEEE, 2010: 6891-6896. |
| [13] | Primbs J A. Dynamic hedging of basket options under proportional transaction costs using receding horizon control[J]. International Journal of Control, 2009,82(10): 1841–1855. DOI: 10.1080/00207170902783341 |
| [14] | Bemporad A, Gabbriellini T, Puglia L, et al. Scenario-based stochastic model predictive control for dynamic option hedging[C]//Lalrtk M.49th IEEE Conference on Decision and Control (CDC),Atlanta,GAVSA:IEEE, 2010:6089-6094. |
| [15] | Bemporad A, Puglia L, Gabbriellini T. A stochastic model predictive control approach to dynamic option hedging with transaction costs[C]// Rahmat S.Proceedings of the 2011 American Control Conference.San Francisco.CA.VSA:IEE 2011:3862-3867. |
| [16] | 尹力博, 韩立岩. 人民币外汇期权套保策略:基于随机规划模型[J]. 管理科学学报, 2012, 15(11): 31–44. |
| [17] | Bates D S. Jumps and Stochastic Volatility: Exchange Rate Processes Implicit in thePHLX Deutschemark Options[J]. Review of Financial Studies, 1996,9(1): 69–107. DOI: 10.1093/rfs/9.1.69 |
| [18] | Carr P, Madan D B. Option Valuation Using the Fast Fourier Transform[J]. Journal of Computational Finance, 1999,2(4): 61–73. DOI: 10.21314/JCF.1999.043 |
| [19] | Lewis A L. A Simple Option Formula for General Jump-Diffusion and Other Exponential Levy Processes[J]. SSRN Electronic Journal, 2010,9(11): 1–24. |
| [20] | Rockafellar R T, Uryasev S. Optimization of Conditional Value-At-Risk[J]. Journal of Risk, 1999,29(1): 1071–1074. |
 2016, Vol. 18
2016, Vol. 18
