战略性新兴产业是引导经济社会发展、推动我国现代化建设的重要力量,对经济高质量发展有重要的支撑作用。在我国经济由高速增长向高质量发展转变的背景下,战略性新兴产业的地位尤为重要。自2010年起,发展战略性新兴产业成为国家层面的重大战略,发布于2010年的《国务院关于加快培育和发展战略性新兴产业的决定》首次阐述了国家发展战略性新兴产业的政策。近年来,战略性新兴产业在经济发展中的作用愈发突出。培育壮大新兴产业不仅对地区经济发展[1]、提升区域竞争力[2]具有重要的推动作用,也有助于促进形成强大国内市场[3],保障经济社会平稳运行,实现高质量发展。
战略性新兴产业这一概念由我国提出并大规模践行,具有一定独特性,因此以战略性新兴产业为主题的研究主要集中于国内。在战略性新兴产业发展的初期,相关的研究集中于产业的含义与特征、发展环境、政策导向[4]、选择和培育问题[5]等议题。近年来,随着战略性新兴产业的发展,相关研究的内容逐渐丰富,研究的广度和深度均有所拓展,研究热点集中于产业政策[6-9]、产业集聚[10-11]、科技创新等方面。
创新是战略性新兴产业发展研究中的一个重要议题。创新是新兴产业发展的核心[12],不仅对新兴产业高质量发展具有促进作用[13],也对区域经济发展[14]、产业转型升级有重要影响[15],因此许多学者对战略性新兴产业研发创新相关的问题进行了探讨。对于战略性新兴产业的创新能力现状,邵云飞等[16]发现战略性新兴产业的整体创新能力较弱且东西部差距明显。在影响因素方面,有学者通过实证研究发现政府创新补贴[6, 17]、产业集聚[18]、大规模市场[19]等因素可以促进战略性新兴产业的创新活动,同时环境不确定性对新兴产业企业研发创新有负面影响[20]。在产业政策方面,刘晓龙等[21]从科学技术发展保障的角度,理论阐述了发展战略性新兴产业需要强化顶层设计,协调科研力量,健全人才激励机制的观点。创新驱动是战略性新兴产业的重要特点之一,创新对产业发展的重要作用已得到证明,同时各类因素对战略性新兴产业创新的影响已经得到广泛的研究。
高效率是新时代经济发展的趋势与要求之一,在认识到创新重要性的基础上,部分研究更深入地从效率的角度入手,考察战略性新兴产业创新活动的效率。战略性新兴产业创新活动等经济活动的效率通常使用全要素生产率进行度量。在测算产业层面的全要素生产率时,多数研究采取生产前沿分析方法,通过测算全要素生产率的相对效率来对比分析不同个体间的效率差异。在效率测算的具体方法层面,部分研究使用SFA方法进行测算[22-24],而更多研究采用数据包络分析(DEA)方法。有较多研究使用DEA方法测算特定地区或若干产业创新活动的效率,并从时间、区域、细分产业等角度详细地分析创新效率的特征[25-27]。进一步地,有研究将相对效率值计算结果作为因变量,使用计量手段考察各类因素对创新效率的影响[28]。此类对战略性新兴产业创新效率的研究大多数仅限于研发创新活动单一阶段的考察,即从投入研发资源到产出创新成果的过程,只有乔威威等[25]的研究进一步地考察了创新成果的应用成效。
研发创新投入的最终目的在于产出经济效益,若需要更完整地刻画技术创新活动的总体效率,需要将创新成果转化过程的效率纳入考察。在此类研究中,常用的建模手段是两阶段建模,即将从研发投入到经济效益产出的总过程拆分为创新技术的生产过程与经济效益的实现过程,并结合DEA等前沿分析方法进行效率测算。这一类两阶段建模方法的使用案例,较早的有官建成等[29]在对于区域创新系统的研究中的运用,该研究将区域创新活动分为技术产出阶段和经济产出阶段以及二者的综合阶段,技术产出阶段投入创新活动的人力、财力并产出专利,经济产出阶段投入专利并产出经济效益,使用DEA方法与C2R模型计算并评价了区域创新系统的技术有效性、经济有效性和综合有效性。余泳泽[30]在对高技术产业创新效率的研究中同样使用了专利作为两阶段的中间品,并使用DEA-Malmquist指数法对各阶段的效率和影响因素进行了实证分析。黄薇[31]在对保险机构资金运用效率的研究中建立了资源型两阶段DEA效率评估模型,在早期独立型两阶段DEA与序列型两阶段DEA模型的基础上做出改进,模型中第二阶段的投入不完全由第一阶段的输出构成。冯志军等[32]在对高技术产业研发创新效率的研究中使用了资源约束型两阶段DEA模型,且基于现实中存在创新要素非线性流动的网络化特征,使用了初始投入同时被高技术开发和高技术经济转化两个子阶段所消耗的模型设定。乔威威等[25]使用两阶段建模DEA方法,结合问卷调查数据,分析了上海市战略性新兴产业技术创新效率。该研究开展时间较早,受到数据和研究方法前沿进展的限制,因此分析范围较窄且程度较浅。
本文从战略性新兴产业研发创新活动效率的角度切入,在DEA方法的框架下,通过两阶段建模综合考虑创新专利研发阶段与创新成果的经济效益转化阶段的效率,结合战略性新兴产业上市公司数据集进行测算,并从时间、区域角度对我国战略性新兴产业研发创新活动的效率分布特征进行分析。相较于与主题相近的乔威威等[25]的研究,本文在数据和方法方面具有创新点。数据方面,样本范围涵盖了全国范围内的战略性新兴产业,地理空间范围更广、时间更长且数据更新,可以更全面地反映近年来我国战略性新兴产业的研发创新活动效率,同时实现了对研发创新效率区域差异的分析。方法方面,结合DEA-Malmquist指数法将研发创新活动各阶段的效率值进行分解,实现对效率值及其分解项动态变化的分析,更详细地刻画战略性新兴产业研发创新效率特征。
二、两阶段DEA效率评估模型构建 (一) DEA-Malmquist指数法DEA法是产业生产研究中常用的全要素生产率的测算方法,最早由Charnes等人于1978年提出。使用DEA方法测算全要素生产率可得到各决策单元全要素生产率的相对值,即相对效率,通过相对效率值的比较对各决策单元的全要素生产率进行分析。DEA方法的优势在于无须设定具体的生产函数形式,可以避免主观因素对全要素生产率测算结果造成的误差,同时在实际操作上较为简便,因此在全要素生产率的研究中被广泛使用。当前使用DEA方法计算全要素生产率有三种主流的模型形式,分别是规模报酬不变假设下的CCR模型、考虑可变规模报酬的BCC模型以及测算跨期效率变化的DEA-Malmquist指数模型。本文所使用的样本数据结构为平衡面板数据,因此选用DEA-Malmquist指数法测算战略性新兴产业全要素生产率相对效率以及跨时期的效率变化。
DEA-Malmquist指数法定义的全要素生产率指数(MPI)的计算公式见式(1)。
| $\operatorname{MPI}\left(x^{t+1}, y^{t+1}, x^t, y^t\right)=\left(\operatorname{MPI}^t \times \operatorname{MPI}^{t+1}\right)^{\frac{1}{2}}=\left[\frac{E^t\left(x^{t+1}, y^{t+1}\right)}{E^t\left(x^t, y^t\right)} \times \frac{E^{t+1}\left(x^{t+1}, y^{t+1}\right)}{E^{t+1}\left(x^t, y^t\right)}\right]^{\frac{1}{2}}$ | (1) |
式(1)左侧的MPI为跨期全要素生产率变化,等于t期与t+1期全要素生产率的几何平均值;xt与yt分别为t期的要素投入与要素产出;Et(·)为t期的距离函数。指数计算结果MPI>1代表t期到t+1期全要素生产率上升;MPI<1代表t期到t+1期全要素生产率下降;MPI=1则代表t期到t+1期全要素生产率相对不变。全要素生产率变化MPI又可分解为相对效率变化(EFFCH)和技术变化(TECH),公式表达见式(2)。
| $\mathrm{MPI}=\mathrm{EFFCH} \times \mathrm{TECH}$ | (2) |
EFFCH代表决策单元与当期技术前沿的相对距离;TECH代表技术前沿的变化,即所有决策单元最高效率的跨期变动。EFFCH又可分解为纯技术效率变化(PECH)和规模效率变化(SECH),公式表达见式(3)。
| $\mathrm{EFFCH}=\mathrm{PECH} \times \mathrm{SECH}$ | (3) |
PECH代表决策单元的生产效率变动;SECH代表规模报酬可变的假设下,伴随经济规模变化带来的效率变动。
(二) 两阶段DEA效率评估模型在考察技术创新等包含多个生产环节的生产过程时,传统的DEA模型通常仅考虑初始的投入与最终的产出,而忽略中间步骤的投入与产出,将多环节生产过程视为一个“黑箱”,无法考察中间环节的生产率特征。为了更详细地刻画战略性新兴产业创新活动从研发投入到实现经济效益的整个过程,本文参考官建成等[29]、余泳泽[30]、黄薇[31]等研究者使用的两阶段建模方法,将战略性新兴产业的研发投入-产出过程分解为创新专利研发阶段与经济效益转化阶段,结合DEA-Malmquist指数法,构建两阶段DEA效率评估模型,对战略性新兴产业的创新活动进行分阶段的效率评估。
两阶段DEA效率评估建模机理如图 1所示。
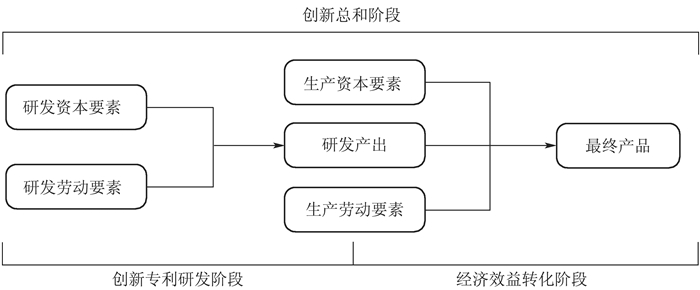
|
图 1 两阶段DEA效率评估建模机理 |
第一阶段为创新专利研发阶段,投入创新研发所需要的资本要素和劳动要素,产出创新成果作为中间品。中间品使用同类研究常用的专利来代表。第二阶段为创新成果的经济效益转化阶段,创新活动产出的专利通过参与最终产品的生产从而转化为经济效益。第二阶段投入前一阶段产出的中间品,以及最终产品生产所需的资本要素和劳动要素,产出最终的经济效益。假定在第一阶段产出的中间品在第二阶段的生产过程中被完全消耗,不存在中间品的剩余。为了考察从创新投入到经济效益转化的全过程综合效率,参考官建成等[29]及黄薇[31]的建模方法,将创新专利研发阶段与经济效益转化阶段序贯加和,定义为创新活动的总和阶段。在创新总和阶段中,投入要素为创新活动全过程的各阶段投入之和,包括创新研发所需要的资本要素和劳动要素以及最终产品生产所需的资本要素和劳动要素;产出品为创新活动全过程的各阶段产出之和,等同于模型第二阶段的最终产品。
(三) 投入产出指标选择创新专利研发阶段的投入-产出机理与一般产品生产基本一致,投入研发所需的资本和劳动力,产出研发成果。创新专利研发阶段的投入指标为研发资本存量、研发费用、研发人员数,产出指标为专利申请数。指标选取理由与处理方法解释如下:
研发资本存量:使用研发资本存量反映创新专利研发活动资本投入中固定资本的使用量。上市公司数据集中不直接代表研发资本存量的指标,因此通过永续盘存法计算研发资本存量。对于研发投入-产出的处理方法,可分为两类。一类处理方法是使用永续盘存法进行研发资本存量的计算,然后使用与一般产品生产相同的方法处理技术研发过程[33-34];另一类处理方法是使用设定的滞后期对技术研发投入-产出过程进行处理[35-36]。设定滞后期的做法优点在于操作上较为简便,缺点在于滞后期时长设定主观性较强,没有一个受到广泛认可的通行的滞后期长度。从现实角度考虑,创新专利生产过程是比较复杂的,不同专利的研发时长可能差异巨大,因此简单地设定一个滞后期用于所有创新专利生产过程缺乏合理性。本文采用永续盘存法计算研发资本存量,参考肖文等[33]的做法,在创新专利研发阶段使用适中的10%的折旧率进行计算。使用“研发投入金额”指标结合“资本化研发投入占研发投入的比例”计算各企业每年的研发投入资本化和费用化的金额。初始研发资本存量的确定采用基期前推的方法,将基期前推10年至2000年,并设定基期的研发资本存量为0,使用价格指数折算每年研发投入金额的实际值,在10%的折旧率设定下按照永续盘存法的公式计算研发资本存量。
研发费用:使用研发费用反映创新专利研发活动资本投入中当期消耗的费用。研发费用具体数值为计算研发资本存量过程中同时得到的资本费用化金额。
研发人员数:使用研发人员数反映创新专利研发活动的人员投入。
专利申请数:使用专利申请数反映创新专利研发活动的产出。专利数是可量化的研发成果指标,在同类研究中被广泛使用。专利数的具体指标通常存在两种选择,一种是专利申请数,另一种是专利授权数。由于专利授权可能受到审批延迟的影响,不能及时地反映专利的产出情况,因此选择专利申请数作为专利的具体指标更为合理。专利的定义范围包含了发明专利、使用新型专利、外观设计专利三类。
经济效益转化阶段的投入产出指标选择与一般产品生产过程的投入产出基本一致。同类研究中对企业层级全要素生产率的测算,常见的投入指标有员工数量、固定资产投入、资本投入等,常见的产出指标有净利润、营业收入、总产值等。结合数据集中所具有的指标,经济效益转化阶段选取的投入指标为固定资产净额、员工数量、专利申请数;产出指标为净利润和营业收入。指标选取理由解释如下:
固定资产净额:使用固定资产净额反映最终产品生产过程的资本投入。上市公司数据集中的固定资产净额已扣除折旧等扣减项,可以无偏误地反映企业当期资本投入水平。
员工数量:使用员工数量反映最终产品生产过程的劳动投入。参与产品生产过程的员工数量为员工总数扣减研发人员数的余值。
专利申请数:基于两阶段模型的特点,在最终产品生产阶段加入创新要素的投入。作为创新专利研发阶段的延续,使用专利申请数作为经济效益转化阶段的创新要素投入指标。
净利润:使用净利润作为企业产出水平的指标之一。企业经营的目的在于盈利,净利润很好地反映了企业的盈利能力。
营业收入:营业收入指标反映企业经营能力。DEA方法不排斥经济意义上存在重复的指标,因此加入同类研究常用的营业收入指标,作为企业经营能力的代表,从不同角度反映企业的产出水平,同时不会与净利润指标产生冲突。
在使用两阶段DEA效率评估模型测度创新效率的研究中,新产品的产值与销售收入是一类常用于度量创新成果转化的变量,利用到此类指标的研究均以高新技术产业为样本,并使用相应的年鉴数据。由于本文使用的数据集为上市公司数据集中的战略性新兴产业企业,在企业层面并未统计新产品相关的指标,因此无法使用新产品的产值或收入作为经济效益转化阶段的产出指标。同时,由于新产品的营收是企业总体营收的一个子集,净利润与营业收入指标包含了新产品的部分,使用总体营收指标可以涵盖新产品营收的信息,足以反映创新成果经济转化的情况。
创新总和阶段将创新专利生产阶段与最终产品生产阶段的投入产出相加,并抵消中间品,将整个生产过程视为一个黑箱过程。创新总和阶段的投入指标为固定资产净额、员工数量、研发资本存量,产出指标为净利润与营业收入。在模型设定中,创新专利生产阶段产出的专利完全投入最终产品生产阶段并完全消耗。
三、数据与计算方法 (一) 数据来源本研究使用的数据包括上市公司财务报表数据和上市公司研发创新数据,数据来自国泰安数据库和中国研究数据服务平台。
由于不存在专门的战略性新兴产业年鉴或数据库,因此本文采用上市公司数据集,使用关键词匹配的方法对照上市公司的主营业务与经营范围描述,筛选各年从属于战略性新兴产业的上市公司,作为全体新兴产业企业的样本。参照国家统计局《战略性新兴产业分类(2018)》的定义,战略性新兴产业共含9类,其中数字创意产业和相关服务业为新加入的产业类目,数字创意产业相关的研究与数据较少,相关服务业的定义尚不清晰,因此这两类产业不纳入研究范围。其余7类战略性新兴产业分别为:新一代信息技术产业、高端装备制造产业、新材料产业、生物产业、新能源汽车产业、新能源产业、节能环保产业。参照《战略性新兴产业分类(2018)》挑选属于各类产业的关键词,并通过测试删除、修改了其中容易引发歧义的关键词。用于筛选的各产业关键词列表如表 1所示。
| 表 1 战略性新兴产业关键词 |
使用表 1中的关键词匹配上市公司数据集中的“主营业务”和“经营范围”条目,筛选从属于战略性新兴产业的企业。由于不同企业与战略性新兴产业的关联程度不同,若将所有包含关键词的企业全部纳入样本范围则会造成样本范围过大,因此对采用不同筛选方式得到的企业做差异化处理。将通过“主营业务”条目匹配得到的企业定义为战略性新兴产业核心企业,即战略性新兴产业相关业务为公司主要业务的企业;同时将通过“经营范围”条目匹配得到,且“主营业务”不包含关键词的企业定义为关联企业,即战略性新兴产业相关业务非公司主要业务的企业。为避免过度计算新兴产业的经济规模,将关联企业的经济规模数值乘以一定的系数,纳入新兴产业规模的计算。由于无法确定关联企业新兴产业业务的比例,也无法得知企业间经济活动的关系网络,因此通过设定一个简单模型,从平均意义上度量关联企业的新兴产业相关经济活动的比例。假设任一企业i与样本内的全部N家上市公司企业之间都存在等量的经济业务关系,则企业i的经济活动中有1/N的比例与另一企业j存在关联。又设定新兴产业核心企业的权重为1,核心企业的总数为n1,关联企业的总数为n2,平均每家企业与新兴产业的业务关联比例为γ。设定每家企业的经济活动总量为1,则可得到等式γ=(n1+γ×n2)/N,即新兴产业的经济活动比例等于核心企业经济活动规模与关联企业经济活动中关联新兴产业的比例之和除以全体企业经济活动总规模。等式经过简单数学变换为γ=n1/(N-n2),即任一企业i的经济活动中有n1/(N-n2)的比例与新兴产业相关联。将关联企业的经济规模乘以系数γ加入战略性新兴产业规模的计算。样本期内上市公司数据集中共4 652家企业,有1 639家企业与战略性新兴产业相关,其中核心企业376家,关联企业1 362家,由此可得到γ的数值约为0.114。
按照关键词筛选得到的战略性新兴产业各行业企业数量在31个省(自治区、直辖市)的分布如表 2所示。
| 表 2 31个省(自治区、直辖市)各类新兴产业企业数量 |
由于部分企业业务范围较广,涵盖了多个战略性新兴产业行业,因此各产业的企业数量加总可能大于新兴产业企业数量总计值。由表 2可以看到,战略性新兴产业数量最多的为广东省,共有416家企业从属于战略性新兴产业的范畴,其中核心企业有60家。新兴产业企业数量较多的省、市包括江苏省、北京市、浙江省、上海市等,新兴产业企业数量较少的省(自治区、直辖市)包括西藏自治区、青海省、宁夏回族自治区、贵州省等。除香港特别行政区、澳门特别行政区与台湾省数据缺失外,每个省级行政区均有从属于战略性新兴产业的企业。从行业角度比较,从属于新一代信息技术产业的企业最多,为852家;从属于新材料产业的企业最少,为71家;其余产业的企业数量均介于160至330之间。
(二) 数据描述性统计基于数据完整性与数据质量的考虑,考察年限设定为2016—2020年。DEA-Malmquis指数法要求数据结构为平衡面板数据,战略性新兴产业省级数据集在2015年及之后满足平衡面板数据的要求。又由于2015年是新加入省份,即青海省首年拥有战略性新兴产业企业的时点,考虑到研发的投入-产出过程存在时滞[33, 35-36],首年的研发投入即带来相应成果产出并实现经济效益转化的可能性较小,为保证后续分析的可信性,将起始年份延后一年,使用2016年作为后续分析的起始年份。同时,2021年及之后的企业数据指标缺失较多。综上原因,使用2016—2020年作为后续研究的年限。所有数据在企业层级的描述性统计如表 3所示。
| 表 3 企业数据描述性统计 |
企业层级的数据中存在少量缺失值,加总到省级行政区层级后进行处理。核心企业的所有经济变量全部参与加总,关联企业的所有经济变量乘以新兴产业经济关联比例γ后加总。
使用DEA-Malmquist指数法测算全要素生产率相对效率需要定义决策单元(DMU),本文将战略性新兴产业上市公司的投入产出指标数据加总到省级行政区层级,将每个省作为决策单元进行计算。企业数据加总后得到的数据集包含31个省(自治区、直辖市),时间范围为2016—2020年,共155条数据,数据结构为平衡面板数据。描述性统计如表 4所示。
| 表 4 省级加总数据描述性统计 |
由于数据集为面板数据的结构,包含每个个体多年的信息,存在货币价值变动的问题,固定资产、利润、收益等货币指标的名义价值变动会导致效率值计算结果产生偏误,因此需要将所有货币指标的名义值换算为真实值。由于国家统计局所公布的价格指数中没有可以与固定资产、研发投入等指标较好地匹配的价格指数,因此统一使用以1978年为基期的GDP指数对所有货币类指标进行平减,得到货币类指标的真实值。
在DEA效率值计算过程中,部分产出指标如净利润、专利申请数存在零值和负值将导致计算结果出错,因此参考沈江建等[37]对于负产出的处理方法,以及马占新等[38]对于零产出的处理方法,将所有净利润数值同向变换至正数以消除净利润的负值;将专利申请数的零值调整为极小正数以消除专利申请数的零值。
四、效率值计算结果分析使用DEA-Malmquist指数法计算各决策单元的全要素生产率跨期变动以及效率变化的分解项。由于本文关注给定投入下的最大化产出,因此模型使用产出导向的效率值计算方法。
效率值计算结果数据总量较大,无法全部展示,因此给出效率值计算结果的描述性统计,刻画效率值的总体特征,后续从时间和个体两个维度分别对效率值计算结果进行分析。表 5至表 7分别报告了创新专利研发阶段、经济效益转化阶段与创新总和阶段全要素生产率及分解项的描述性统计结果。
| 表 5 创新专利研发阶段效率值计算结果描述性统计 |
| 表 6 经济效益转化阶段效率值计算结果描述性统计 |
| 表 7 创新总和阶段效率值计算结果描述性统计 |
观察极值的分布。从表 5可以看到,创新专利研发阶段纯技术效率变化的最大值达到13.173 5,该数值出现于西藏自治区2019—2020年的效率变化样本,由于西藏自治区纳入战略性新兴产业范畴的企业仅2家,企业数量相对极少,因此出现这一数值结果存在一定偶然性因素。这一相对较大的数值导致相对效率变化和全要素生产率变化同样出现较大的最大值。除此条数据外,其余数据均在与均值距离三个标准差的范围之内。经济效益转化阶段和创新总和阶段没有出现异常的效率值极值。
对比不同生产阶段效率值分布情况。创新专利研发阶段的部分效率值分解项的平均数和中位数存在较大差异,相对效率变化的平均值约为1.869 0,而中位数约为1.187 3,表示相对效率变化极大值对于数值总体分布影响较大;规模效率变化的平均值约为1.642 7,中位数约为1.051 9,同样表示规模效率变化极大值对于数值总体分布存在较大影响。经济效益转化阶段和创新总和阶段的各效率值平均值和中位数均在1附近,总体分布较为均匀。
对比不同生产阶段效率值离散程度。经济效益转化阶段和创新总和阶段的效率值标准差总体上小于创新专利研发阶段的效率值标准差。这一结果表明创新专利研发阶段各决策单元效率值的离散程度明显大于成果转化阶段的效率值,意味着相较于一般产品生产的效率差异,各决策单元创新研发的效率差异较大。
(一) 跨期效率分析以年为时间单位计算效率值可能存在由于时间延迟导致的效率值异常。例如,专利的产出、申请与生产应用之间可能存在数据无法刻画的延迟,前后两期均投入研发创新资源,而专利申请由于未知的随机因素延迟至后一时期,导致前一时期创新专利研发效率偏低,而后一时期效率偏高;同时,若专利未申请而直接投入实际的产品生产过程,又会对创新专利经济效益转化阶段的效率值产生不可预测的影响。后续分析分别从个体和时间维度对效率值进行平均,以减少潜在的由于时期迟滞导致的效率值极端数值对经济意义分析的影响。
从时间维度进行分析,对不同时期31个省(自治区、直辖市)的效率值及分解项进行平均,刻画每个时期我国战略性新兴产业效率变化的总体特征。表 8至表 10分别报告了创新专利研发阶段、经济效益转化阶段以及创新总和阶段的全要素生产率变化以及生产率变动的分解项。
| 表 8 创新专利研发阶段生产率变化 |
| 表 9 经济效益转化阶段生产率变化 |
| 表 10 创新总和阶段生产率变化 |
图 2以折线图形式直观呈现了三个生产阶段全要素生产率变化的趋势。
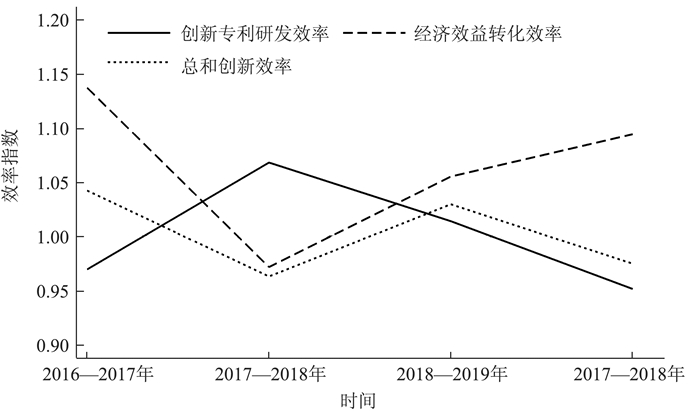
|
图 2 全要素生产率变化趋势 |
结合表 8和图 2的结果可以看到,2016—2020年,战略性新兴产业整体研发创新活动全要素生产率变化趋势为先上升后下降,在2017—2018年达到最大值,相对前一时期的效率提高达到6.82%。5年间研发创新活动的全要素生产率整体呈现缓慢上升趋势,平均年均增长率约为0.08%。研发创新活动的相对效率变化在2016—2017年达到3.5940,其余时期内保持较高的增长率,5年内平均增长率为186.90%,这一数值体现了战略性新兴产业创新研发活动追赶技术前沿的速度极快。研发创新活动的技术变化效率值相对较低,5年内平均技术变化率小于1,意味着创新活动前沿技术的效率总体呈现降低的趋势。相对效率的分解项纯技术效率变化和规模效率变化总体上都呈现上升的趋势,意味研发创新活动整体上呈现规模报酬递增的特点,同时,研发创新的技术效率总体呈现上升的变化趋势。
结合表 9和图 2的结果可以看到,2016—2020年,战略性新兴产业研发创新成果经济效益转化的全要素生产率总体呈现上升趋势,最大值为2016—2017年的1.137 2,仅2017—2018年间效率值下降,5年内年平均增长率约为6.46%。研发成果经济效益转化的相对效率变化总体呈现先下降后上升的趋势,5年间平均效率值变动为-2.54%。研发成果经济效益转化的技术变化5年间平均增长率约为11.55%,总体上前沿技术效率有较明显的提升。相对效率变化的分解项纯技术效率变化总体呈现下降的趋势,5年平均变化率约为-2.07%;规模效率变化总体幅度平均值小于0.01%,趋势上呈现先下降后上升的状态。
结合表 10和图 2结果可以看到,2016—2020年,战略性新兴产业创新活动全过程全要素生产率呈波动趋势,在正负5%的区间内波动,5年平均全要素生产率变化约为0.25%。相对效率和纯技术效率总体降低,技术变化和规模效率变化总体提升,各效率值的5年平均变化幅度均在3%以内。
总体上看,战略性新兴产业研发创新活动的全要素生产率处于缓慢增长的状态,这一增长状态由较高的相对效率变化和较低的技术前沿效率增长共同构成。这个特点意味着在战略性新兴产业的创新活动中,各决策单元对于技术前沿的追赶速度极快,产业中一旦有新技术产生,便可以极快的速度扩散至整个产业,提高整个产业的创新效率。同时,产业整体的技术前沿效率下降意味着前沿技术的研发动力不足,效率较差。在样本期内,战略性新兴产业的创新活动总体呈现规模报酬递增的特点,因此增加创新投入的规模有利于促进战略性新兴产业研发创新活动的效率。
战略性新兴产业研发创新成果的经济效益转化,本质上是有专利因素参与的一般消费产品生产过程,其效率变化是创新要素、资本要素和劳动要素综合作用的结果。经济效益转化过程的全要素生产率变化总体较为平稳,效率增长幅度适中。创新驱动下的最终产品生产的技术前沿变化提升幅度较大,前沿技术的效率提高明显,但与创新活动相比,经济效益转化阶段技术扩散的速度较慢。在样本期内,战略性新兴产业创新成果经济效益转化总体上呈现规模报酬不变的特征。
战略性新兴产业研发创新活动的全过程作为两阶段的总和,其全要素生产率变化幅度总体上介于研发创新活动全要素生产率和经济效益转化全要素生产率之间。在2019年之前,研发创新全过程的总和效率值变动趋势与经济效益转化阶段更为紧密;2019年之后,综合效率值变动与创新专利研发效率变动趋势更加接近。这一现象反映了创新专利研发阶段的经济活动比重增加,对比成果转化阶段存在相对上升的趋势,与近年来我国各产业创新研发投入整体增加,创新活动旺盛的现象相一致。
(二) 个体效率分析从个体维度进行分析,对不同省(自治区、直辖市)的各时期全要素生产率变化进行平均,刻画不同省(自治区、直辖市)战略性新兴产业效率变化的基本特征。表 11报告了31个省(自治区、直辖市)的全要素生产率平均值。
| 表 11 31个省(自治区、直辖市)全要素生产率平均值 |
将31个省(自治区、直辖市)的创新专利研发阶段全要素生产率与经济效益转化阶段全要素生产率绘制于2×2矩阵图,如图 3所示。
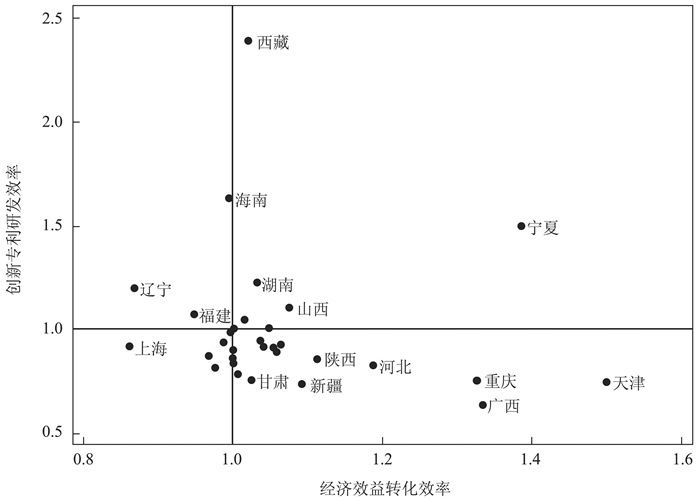
|
图 3 两阶段创新效率矩阵 |
图 3以两个阶段的全要素生产率变化相对不变,即MPI=1为界,划分为四个象限。左下区域内的为创新专利研发效率和经济效益转化效率均较低的样本,右下区域内的为创新专利研发效率较低而经济效益转化效率较高的样本,左上区域内的为创新专利研发效率较高而经济效益转化效率较低的样本,右上区域内的为创新专利研发效率和经济效益转化效率均较高的样本。
结合表 11和图 3的结果可以看到,大多数省(自治区、直辖市)分布于两阶段效率年平均变化幅度均较小的区域。出现效率极高值的省(自治区、直辖市),如西藏自治区、海南省、宁夏回族自治区所拥有的战略性新兴产业企业数量均较少,因此其对战略性新兴产业总体的效率影响有限。拥有战略性新兴产业企业数量较多的省份,如广东省、江苏省、浙江省等,其年平均效率值分布较接近矩阵中心,即代表效率值平均变化程度较小的区域。
从创新专利研发全要素生产率的角度观察,不同省(自治区、直辖市)创新专利研发阶段的效率值差异较大,最大值为西藏自治区的2.382 3,其次为海南省的1.629 9;较多省份处于创新专利研发平均效率变化小于1的区域,即相对效率平均降低的区域。从经济效益转化全要素生产率的角度观察,不同省份创新成果经济效益转化的效率值差异相对较小,较多省份分布于平均效率变化大于1的区域,最大值为天津市的1.498 4。
综合观察两阶段的效率值计算结果,明显呈现出“创新效率低,转化效率低”特征的是上海市,四川省、安徽省、贵州省同样呈现“创新效率低,转化效率低”的特征,但效率值变化幅度较小,相对不明显。明显呈现出“创新效率低,转化效率高”特征的有天津市、重庆市、广西壮族自治区、河北省等,呈现此特征的省(自治区、直辖市)数量在四种类型中最多。明显呈现出“创新效率高,转化效率低”的有辽宁省和福建省,海南省也存在此特征,但转化效率低的特征相对不明显。明显呈现出“创新效率高,转化效率高”的是宁夏回族自治区,同呈现此特征但程度较低的省份有湖南省、山西省、吉林省、西藏自治区。此外,部分省(自治区、直辖市)如浙江省、内蒙古自治区、黑龙江省、湖北省、江西省的年平均经济效益转化效率几乎处于不变的状态,浙江省、北京市的年平均创新专利研发效率几乎处于不变的状态。
对于创新专利研发效率与经济效益转化效率矩阵中的四类省(自治区、直辖市),效率角度最优的状态为“创新效率高,转化效率高”,但能实现此高效状态的省(自治区、直辖市)数量较少,大多处于“创新效率低,转化效率高”的状态,对于此类省(自治区、直辖市),效率改进的主要方向为提升创新专利研发的效率。对于处于“创新效率高,转化效率低”的省(自治区、直辖市),效率改进的方向是提高经济效益转化的效率,可以通过产业生产过程的效率改进实现。对于“创新效率低,转化效率低”的省(自治区、直辖市),从研发效率和经济效益转化效率方面着手均可实现有意义的效率改进。
五、结论与政策建议本文建立了研发创新的两阶段DEA效率评估模型,筛选战略性新兴产业上市公司样本作为产业整体的代表,通过DEA-Malmquist指数法测算了我国31个省(自治区、直辖市)战略性新兴产业创新专利研发阶段、研发成果经济效益转化阶段以及创新总和阶段的全要素生产率变化以及分解效率值,并从时间和省(自治区、直辖市)个体的角度详细分析了创新活动各个阶段的效率值特征。
在战略性新兴产业创新活动效率特征方面,主要结论有:
第一,2016—2020年,我国战略性新兴产业创新活动的全要素生产率总体呈现上升趋势,创新专利研发活动全要素生产率年平均提升0.08%,创新成果经济效益转化全要素生产率年平均提升6.46%,创新活动总体全要素生产率年平均提升0.25%。
第二,31个省(自治区、直辖市)战略性新兴产业的创新专利研发效率总体处于较低水平,创新成果的经济效益转化效率总体处于中高水平。
第三,样本期内研发创新活动整体呈现规模报酬递增的特点,创新成果的经济效益转化整体呈现规模报酬不变的特点。
总结研究内容可以发现,我国战略性新兴产业创新研发活动存在“高效应用,低效研发”的现象,主要表现在:
第一,在创新研发与转化的层面,31个省(自治区、直辖市)的效率值总体上呈现研发效率较低而转化效率较高的状态,即创新成果的转化与应用较为容易,而创新专利的产出较为困难。一方面,由于创新成果的经济效益转化过程与一般消费品生产的关系密切,得益于我国大部分地区完善的工业体系,在战略性新兴产业领域内创新成果的转化难度相对较低,因此体现出较高的效率。另一方面,随着技术研发的深入,简单的技术成果被发掘殆尽,产出新成果的难度逐渐提升,因此体现出研发投入的物质、人力要素增加,而产出的成果不等比例增加的低效率现象。
第二,在创新研发活动层面,同样存在类似于高效应用而低效研发的现象。创新研发活动追赶前沿新技术的速度快、效率高,然而技术前沿的效率却没有提高,反而呈现下降的趋势。技术前沿的效率下降有可能是由于前沿技术研究本身的高难度与高随机性所致,也可能意味着前沿技术开发进入了技术上的瓶颈期。
需要辨析的是,相较于我国科技与经济“两张皮”的主流观点,本文发现的“高效应用,低效研发”现象与该观点的研究角度和讨论范围存在差异。首先,在研究角度方面,科技与经济“两张皮”通常指科研单位与生产单位相脱离,导致科研成果的经济效益转化不畅[39]。科研成果的转化效果通常从数量上进行度量,而从效率方面进行考察,则会导致结论在表面上与主流观点存在一定出入。其次,在研究对象方面,本文的研究基于上市公司企业数据,考察的创新技术研发与成果转化均为发生在企业内部的经济活动,从主体上看均为“两张皮”的经济一侧,而纯科研单位,即“两张皮”的科技一侧不在研究范围内。相较于独立的科研机构,企业内部的研发活动通常基于实际生产的需求,与生产活动的结合更加紧密,以此实现科研成果转化的相对高效。因此,本文的发现与“两张皮”的主流观点不矛盾,同时强调了研发与生产紧密结合对于提高经济效率的重要性。
最后,基于研究发现,对于我国战略性新兴产业研发创新活动提出政策建议:
一是增加研发创新投入以提高创新效率。样本期内战略性新兴产业研发创新活动整体上呈现规模报酬递增的特点。因此,若需要提高产业的创新效率,增加创新要素投入规模很可能是一条简单且可行的产业政策路径。具体的政策手段包括直接增加研发创新活动所需的资本与劳动要素投入量,以及通过产业集群化发展的手段在一定区域实现研发创新活动的集聚。
二是鼓励前沿科技研发。前沿“硬核科技”是战略性新兴产业乃至国家的核心竞争力,同时前沿技术的研发存在随机性强、难度高的特征,因此表面的经济效益低不可能成为放弃前沿技术研发的理由。相反,政府应鼓励前沿技术的开发,在保证财政资金、人力投入的同时,鼓励市场科研力量投入,以灵活、高效、创新性的方式进行前沿技术的开发。通过提升技术前沿,利用新兴产业新技术扩散快的特性,将前沿技术成果快速推广至整个产业,提升产业整体技术水平,增强新兴产业的整体竞争力。
三是基于企业需求,执行针对性的产业政策。实证结果显示创新研发效率高的省(自治区、直辖市)所拥有的战略性新兴产业企业数量均较少,这可能是由于企业数量少的省(自治区、直辖市)在产业政策制定方面具有更强的针对性,通过针对性的产业政策助力少数企业提高效率,即可带动全省的新兴产业总体效率提升。战略性新兴产业企业数量较多的省(自治区、直辖市)创新效率通常处于平均值附近,由于企业数量较多,研发、经营状况复杂,因此产业政策较难具体顾及各企业的发展需求。提高此类省(自治区、直辖市)的新兴产业总体创新研发活动效率,需要地方政府深入企业,了解各新兴产业企业的具体诉求,使用针对性的产业政策手段助力企业提高技术研发与成果转化效率。
| [1] |
陶金国, 刘海艳. 战略性新兴产业集聚、空间溢出效应与区域经济增长质量[J]. 统计与信息论坛, 2020, 35(5): 26-34. |
| [2] |
张晴. 战略性新兴产业集聚与区域经济竞争力关系的实证检验[J]. 统计与决策, 2017(12): 134-136. DOI:10.13546/j.cnki.tjyjc.2017.12.032 |
| [3] |
何立峰. 促进形成强大国内市场 大力推动经济高质量发展[J]. 宏观经济管理, 2019(2): 1-4. DOI:10.19709/j.cnki.11-3199/f.2019.02.002 |
| [4] |
李晓华, 吕铁. 战略性新兴产业的特征与政策导向研究[J]. 宏观经济研究, 2010(9): 20-26. DOI:10.16304/j.cnki.11-3952/f.2010.09.002 |
| [5] |
刘洪昌. 中国战略性新兴产业的选择原则及培育政策取向研究[J]. 科学学与科学技术管理, 2011, 32(3): 87-92. |
| [6] |
陆国庆, 王舟, 张春宇. 中国战略性新兴产业政府创新补贴的绩效研究[J]. 经济研究, 2014, 49(7): 44-55. |
| [7] |
肖兴志, 王伊攀. 政府补贴与企业社会资本投资决策——来自战略性新兴产业的经验证据[J]. 中国工业经济, 2014(9): 148-160. DOI:10.19581/j.cnki.ciejournal.2014.09.012 |
| [8] |
余东华, 吕逸楠. 政府不当干预与战略性新兴产业产能过剩——以中国光伏产业为例[J]. 中国工业经济, 2015(10): 53-68. DOI:10.19581/j.cnki.ciejournal.2015.10.005 |
| [9] |
曲丽娜, 刘钧霆. 经济政策不确定性、政府补贴与企业创新[J]. 统计与决策, 2022, 38(6): 169-174. |
| [10] |
郭轶舟, 冯华. 我国战略性产业的地理集中度系数及其要素贡献度测算[J]. 统计与决策, 2018, 34(21): 126-130. |
| [11] |
王欢芳, 张幸, 熊曦, 等. 中国生物产业的空间集聚度及其变动趋势——基于上市公司的经验数据[J]. 经济地理, 2018, 38(8): 101-107. |
| [12] |
芮明杰. 构建现代产业体系的战略思路、目标与路径[J]. 中国工业经济, 2018(9): 24-40. |
| [13] |
李小青, 何玮萱, 霍雨丹, 等. 数字化创新如何影响企业高质量发展——数字金融水平的调节作用[J]. 首都经济贸易大学学报, 2022, 24(1): 80-95. DOI:10.13504/j.cnki.issn1008-2700.2022.01.007 |
| [14] |
李新安. 区域创新能力对经济发展质量提升的驱动作用研究[J]. 区域经济评论, 2020(2): 65-74. |
| [15] |
刘嘉琳, 汤吉军. 东北地区战略性新兴产业与传统产业融合发展研究——基于动态演化博弈模型分析[J]. 经济问题探索, 2020(11): 95-104. |
| [16] |
邵云飞, 穆荣平, 李刚磊. 我国战略性新兴产业创新能力评价及政策研究[J]. 科技进步与对策, 2020, 37(2): 66-73. |
| [17] |
闫俊周, 齐念念, 童超. 政府补贴与金融支持如何影响创新效率?——来自中国战略性新兴产业上市公司的经验证据[J]. 软科学, 2020, 34(12): 41-46. DOI:10.13956/j.ss.1001-8409.2020.12.07 |
| [18] |
石璋铭, 徐道宣. 集聚促进战略性新兴产业创新生态系统发展的实证分析[J]. 科技进步与对策, 2018, 35(23): 92-98. |
| [19] |
黄先海, 张胜利. 中国战略性新兴产业的发展路径选择: 大国市场诱致[J]. 中国工业经济, 2019(11): 60-78. DOI:10.19581/j.cnki.ciejournal.2019.11.004 |
| [20] |
谢伟峰, 陈省宏. 环境不确定性、会计稳健性与公司研发创新——来自战略性新兴产业民营A股上市公司的经验证据[J]. 科技管理研究, 2021, 41(3): 109-116. |
| [21] |
刘晓龙, 葛琴, 崔磊磊, 等. 新时期我国战略性新兴产业发展宏观研究[J]. 中国工程科学, 2020, 22(2): 9-14. |
| [22] |
邬龙, 张永安. 基于SFA的区域战略性新兴产业创新效率分析——以北京医药和信息技术产业为例[J]. 科学学与科学技术管理, 2013, 34(10): 95-102. |
| [23] |
龚立新, 吕晓军. 政府补贴与企业技术创新效率——来自2009-2013年战略性新兴产业上市公司的证据[J]. 河南大学学报(社会科学版), 2018, 58(2): 22-29. DOI:10.15991/j.cnki.411028.2018.02.004 |
| [24] |
刘素坤, 王乐, 何文韬, 等. 国际化程度对企业创新效率的影响——基于战略性新兴产业[J]. 经济问题, 2022(3): 95-103. |
| [25] |
乔威威, 罗鄂湘, 钱省三. 基于DEA的企业技术创新效率研究——以上海战略性新兴产业为例[J]. 技术与创新管理, 2014, 35(6): 562-566, 631. DOI:10.14090/j.cnki.jscx.2014.06.004 |
| [26] |
黄海霞, 张治河. 中国战略性新兴产业的技术创新效率——基于DEA-Malmquist指数模型[J]. 技术经济, 2015, 34(1): 21-27, 68. |
| [27] |
刘晖, 刘轶芳, 乔晗, 等. 我国战略性新兴产业技术创新效率研究[J]. 系统工程理论与实践, 2015, 35(9): 2296-2303. |
| [28] |
刘继兵, 王定超, 夏玲. 政府补助对战略性新兴产业创新效率影响研究[J]. 科技进步与对策, 2014, 31(23): 56-61. |
| [29] |
官建成, 何颖. 基于DEA方法的区域创新系统的评价[J]. 科学学研究, 2005(2): 265-272. |
| [30] |
余泳泽. 我国高技术产业技术创新效率及其影响因素研究——基于价值链视角下的两阶段分析[J]. 经济科学, 2009(4): 62-74. |
| [31] |
黄薇. 中国保险机构资金运用效率研究: 基于资源型两阶段DEA模型[J]. 经济研究, 2009, 44(8): 37-49. |
| [32] |
冯志军, 陈伟. 中国高技术产业研发创新效率研究——基于资源约束型两阶段DEA模型的新视角[J]. 系统工程理论与实践, 2014, 34(5): 1202-1212. |
| [33] |
肖文, 林高榜. 政府支持、研发管理与技术创新效率——基于中国工业行业的实证分析[J]. 管理世界, 2014(4): 71-80. |
| [34] |
原毅军, 刘浩, 白楠. 中国生产性服务业全要素生产率测度——基于非参数Malmquist指数方法的研究[J]. 中国软科学, 2009(1): 159-167. |
| [35] |
向小东, 陈丽芬. 制造业技术创新效率评价模型及其应用研究[J]. 运筹与管理, 2016, 25(1): 215-223. |
| [36] |
张凯煌, 千庆兰. 中国新能源汽车产业创新网络特征及其多维邻近性成因[J]. 地理研究, 2021, 40(8): 2170-2187. |
| [37] |
沈江建, 龙文. 负产出在DEA模型中的处理——基于软件DEAP的运用[C]//中国管理现代化研究会, 复旦管理学奖励基金会. 第十届(2015)中国管理学年会论文集. 2015: 267-272.
|
| [38] |
马占新, 唐焕文. 关于DEA有效性在数据变换下的不变性[J]. 系统工程学报, 1999(2): 27-32. |
| [39] |
周元, 梁洪力, 王海燕. 论中国创新悖论: "两张皮"与"76%"[J]. 科学管理研究, 2015, 33(3): 1-4. |
 2023, Vol. 25
2023, Vol. 25
