2. 华南理工大学 金融工程研究中心, 广东 广州 510006
2. Research Center of Financial Engineering, South China University of Technology, Guangzhou 510006, Guangdong, China
期权广泛运用于风险管理和投机交易。我国于2015年2月上市了首个场内期权——上证50ETF期权,此后又于2019年12月上市了以沪深300指数和沪深300ETF为标的的场内期权。我国期权市场规模逐步扩大,交易日趋活跃,上证50ETF期权和沪深300ETF期权均已成为全球主要股票期权品种。上海证券交易所公布的数据显示,上证50ETF期权2020年全年日均成交213.37万张,相比2016年日均成交32.41万张,增长了558%。投资者可以运用期权构建灵活的交易策略来满足不同的投资需求,同时也可以运用期权市场的交易数据对其现货市场的投资决策进行指导。例如,投资者可以根据期权的隐含波动率大小来判断股票市场的风险。
期权多种执行价格和多种期限的特征,使其价格包含了丰富的信息。首先,同一标的的期权具有看涨和看跌、不同到期期限以及不同行权价格,这使得期权的价格信息具有价格宽度和时间跨度;其次,期权的期限结构特征使其能够直接反映市场对标的资产未来价格的期望,其隐含信息具有前瞻性;最后,期权市场的参与者包括了诸多的套利、投机和对冲交易者,使得期权的价格能充分反映不同市场交易者的信息。因此,投资者通常采用期权隐含的信息来预测标的资产价格未来收益。
已有文献主要从期权价格中提取隐含信息,研究其能否解释标的资产未来价格变动。比较常见的隐含信息包括隐含波动率、隐含偏度和隐含峰度等不同阶矩的信息,这些都被证实是市场收益的有效预测因子,能反映标的资产价格未来的走势特征。不同的阶矩仅反映了标的资产价格的总体特征,其尾部特征也有可能解释未来收益的一部分变动。这类反映尾部特征的隐含信息被称为“隐含尾部风险”,通常使用虚值期权数据度量。在已有文献中,Pan等[1]证明杠杆更高的虚值期权包含的有效信息更多。Andersen等[2]发现使用虚值期权提取出的隐含尾部风险在预测市场月收益时起到重要作用。由于我国期权市场发展较晚,现有的文献涉及对我国期权市场的研究较少,本文对我国期权市场隐含尾部风险信息的研究是对我国期权市场研究的一个补充。本文以上证50ETF期权为对象,采用深度虚值期权定价公式,从期权价格数据中提取期权隐含尾部风险,旨在验证我国期权市场隐含尾部风险信息对市场未来走势的预测能力。
二、文献综述已有文献关于期权隐含信息的研究主要包括隐含信息的提取和对未来收益预测。在模型构建方面,其主要的区别在于信息提取方法和信息构建方式的不同。在应用方面,其主要的区别在于预测对象和研究市场的不同。
首先,从期权中提取信息的方法可以分为无模型方法和有模型方法,区别在于是否需要借助具体的期权定价公式[3]。无模型方法的优势在于不存在拟合估计偏差,但是该方法通常数学推导复杂,不易理解和扩展。郑振龙[3]认为有模型方法涉及的许多假定可能与实际不符,像Black-Scholes期权定价公式[4],其前提假设为标的资产价格呈现几何布朗运动。这一假定无法描述收益率分布的尖峰肥尾特征。已有大量的文献对这一假定进行了改进,如Merton[5]假设标的资产遵循跳跃-扩散过程,并推出Merton跳跃-扩散模型;White等[6]基于随机波动的期权定价公式将波动率自身作为随机过程进行建模。而近期,随着极值理论在风险管理领域广受关注,基于极值理论的期权定价公式也相继被提出。极值理论主要描述用何种分布形式来拟合极端值数据,因此能够有效刻画标的资产的肥尾特征。Markose等[7]提出了基于广义极值分布的期权定价公式,并证明无论是样本内还是样本外,该定价公式的准确性都高于Black-Scholes期权定价公式。Hamidieh[8]提出了基于广义帕累托分布的深度虚值期权定价公式,并证明该公式能够很好地捕捉标的资产“肥尾负偏”的特征。
其次,在信息构建方式方面,学者们从期权中提取的信息主要反映标的资产价格的整体特征,如隐含波动率、隐含偏度和隐含峰度等不同阶矩风险。但是,郭婧等[9]指出这类不同阶矩的风险指标测量的是资产价格变化的不确定性,而引起实质性损益的是资产下行风险和上行风险,即尾部风险。许多学者对此有类似的看法,因此,近几年的文献开始关注期权隐含的尾部风险信息。刘天宇[10]对比分析了基于期权数据计算的隐含VaR与基于历史数据计算的VaR,发现前者要优于后者;Wang等[11]发现在经济衰退的时候,隐含尾部风险指标与标的资产未来一日收益间的关系会增强;陈坚等[12]研究了美国SP500指数期权市场,认为在实际投资组合的构建和风险管理中,应该充分考虑期权价格中所隐含的尾部风险信息,从而提高投资收益并减少风险暴露。
最后,在应用方面,多数研究主要针对国外的期权市场,如SP500指数期权或者个股期权。对于我国的期权市场,较早的研究受限于期权数据不足,研究存在一定的局限性。在2017年以后,随着期权数据量的增加,一些研究开始关注上证50ETF期权的定价问题以及期权上市后对股票市场波动率的影响。例如,杨兴林等[13]在正态分布、广义t分布和Edgeworth渐进分布这三种假设下,对上证50ETF期权进行了定价分析。也有部分学者研究了上证50ETF期权的隐含信息,主要集中在隐含波动率、隐含偏度等信息。例如,郑振龙[3]研究了上证50ETF期权的隐含波动率和实现波动率之间的关系以及中美之间隐含波动率差异比较;倪中新等[14]研究了上证50ETF期权隐含波动率微笑形态中包含的信息;王琳玉等[15]通过自回归滑动平均模型提取期权隐含高阶矩新息,分析其对股票收益的预测作用。
综上所述,期权隐含尾部风险信息是针对现存隐含信息的重要补充,其信息价值在国外市场得到了证实,但现有研究并未针对我国期权市场隐含尾部风险信息进行研究。上证50ETF期权上市交易至今已有七年时间。在这段时间,我国股票市场经历了多次大波动,如2015年的股灾、2016年初的市场熔断、2018年的熊市、2020年的新冠疫情暴发等。因此,研究我国期权市场隐含尾部风险信息并验证其对股市未来收益的预测作用,对于指导投资有重要价值。
本文参考Wang等[11]采用极值理论下的深度虚值期权定价公式,计算得到上证50ETF期权隐含尾部收益因子和隐含尾部损失因子,用于度量期权隐含尾部风险,并检验其对上证50指数未来收益的预测能力。本文的主要贡献为:一是相较于现有研究我国期权市场的文献,本文研究了上证50ETF期权的隐含尾部风险信息及其对市场的预测能力,是对现有期权隐含信息研究的补充;二是考虑到我国期权市场的期权数量少、执行价格覆盖率较低,遇到市场极端时期虚值期权数量不足,本文给出了一套动态调整期权样本的选择方法来解决期权数据不足的问题。
三、隐含尾部风险因子计算 (一) 极值理论传统的期权定价公式需要假设标的资产价格或者收益率的分布。本文在研究期权隐含尾部风险时采用的模型与之不同,只关注标的资产价格超阈值部分的分布,从而可以有效获得关于标的资产价格尾部变化的信息。
假设{xi}(i=1, 2,…, n)为独立且同分布的随机变量序列,其总体分布函数为F(x),属于极值分布中的“最大值吸引场”,则存在常数列{an>0}和{bn},使得当n→∞时,归一化最大值统计量(max(xi)-bn)/an,收敛于一个非退化的分布函数。这个分布函数只有可能是广义极值分布(generalized extreme value distribution,GEV)族中的一种。
根据极值理论的第二定理①和F(x)属于极值分布中的“最大值吸引场”这一事实,对于x超过极端阈值μ的部分,即x-μ|x>μ,当μ充分大的时候,其分布将会近似广义帕累托分布(generalized pareto distribution,GPD),即为:
① 极值理论的第二定理,又称为PBdH定理。该定理说明,对于充分大的阈值,多数未知分布函数的变量,其超额条件分布函数都可以用广义帕累托分布很好地近似。
| $ G(x-\mu \mid x>\mu)=\left\{\begin{array}{cc} 1-\left(1+\xi \frac{x-\mu}{\beta}\right)^{-\frac{1}{\xi}} & \xi \neq 0 \\ 1-\exp \left(-\frac{x-\mu}{\beta}\right) & \xi=0 \end{array}\right. $ | (1) |
其中,β和ξ为变量x右尾分布的尺度参数和形状参数。同理,对于x低于极端阈值h的部分,即h-x|x < h,当h充分小时,其分布将近似为:
| $ G(h-x \mid x<h)=\left\{\begin{array}{c} 1-\left(1+\xi^* \frac{h-x}{\beta^*}\right)^{-\frac{1}{\xi^*}} \xi^* \neq 0 \\ 1-\exp \left(-\frac{h-x}{\beta^*}\right) \quad \xi^*=0 \end{array}\right. $ | (2) |
其中,β*和ξ*为变量x左尾分布的尺度参数和形状参数。
极值理论中的近似关系使研究者不必关注随机变量(如资产价格)的真实分布,有效增加模型的实用性。如果我们假设ξ和ξ*都小于1,x为标的资产价格,那么标的资产价格x的右尾分布期望值(极端收益)和左尾分布期望值(极端损失)可以分别表示为:
| $ E(x-\mu \mid x>\mu)=\frac{\beta}{1-\xi} $ | (3) |
| $ E(h-x \mid x<h)=\frac{\beta^*}{1-\xi^*} $ | (4) |
基于极值理论提出的期权定价公式有两种,一种是Markose等[7]提出的基于广义极值分布的期权定价公式,另一种是Hamidieh[8]提出的基于广义帕累托分布的深度虚值期权定价公式。由于广义帕累托分布只针对尾部进行建模,适用于对尾部风险信息的提取,因此,本文使用第二种期权定价公式。Hamidieh[8]给出的深度虚值看涨期权和深度虚值看跌期权的定价公式为:
| $ C\left(K_i\right)=C(K)\left[\frac{\xi}{\beta}\left(K_i-K\right)+1\right]^{1-\frac{1}{\xi}} $ | (5) |
| $ P\left(K_i^*\right)=P\left(K^*\right)\left[\frac{\xi^*}{\beta^*}\left(K^*-K_i^*\right)+1\right]^{1-\frac{1}{\xi^*}} $ | (6) |
其中,C(K)和P(K*)为执行价格K下的看涨和看跌期权价格;ξ和β为右尾分布的形状参数和尺度参数;ξ*和β*为左尾分布的形状参数和尺度参数。对于看涨期权,K为充分大的可以作为有效阈值的执行价格,Ki大于K,并随着指标i的增大而增大;对于看跌期权,K*为充分小的可以作为有效阈值的执行价格,Ki*小于K*,并随着指标i的增大而减小。
本文参考Wang等[11]的方法,利用期权价格分别计算左右尾分布的形状参数和尺度参数。在每个交易日下,对于同一到期日的期权,通过最小化期权理论价格和市场价格的离差平方和,得到右尾(左尾)分布的形状参数估计值
| $ \{\hat{\xi}, \hat{\beta}\}=\operatorname{argmin}_{\xi, \beta} \sum\limits_{i=1}^n \frac{V\left(K_i\right)}{\mathrm{TV}}\left[C_{\mathrm{MKT}}\left(K_i\right)-C\left(K_i\right)\right]^2 $ | (7) |
| $ \left\{\hat{\xi}^*, \hat{\beta}^*\right\}=\operatorname{argmin}_{\xi^*, \beta^*} \sum\limits_{i=1}^{n^*} \frac{V\left(K_i^*\right)}{\mathrm{TV}}\left[P_{\mathrm{MKT}}\left(K_i^*\right)-P\left(K_i^*\right)\right]^2 $ | (8) |
其中,CMKT(Ki)和PMKT(Ki*)分别为看涨期权和看跌期权的市场价格;C(Ki)和P(Ki*)分别为对应的理论价值;V(Ki)/TV为期权的交易量与总交易量的比值。考虑到期权交易量越大,期权定价越准确,本文将交易量与总交易量的比值作为拟合时的权重,用于提高参数估计值的准确性。
根据式(3)和式(4),可以得到隐含尾部收益因子(implied tail gain,ITL)和隐含尾部损失因子(implied tail loss,ITL)的计算公式:
| $ \mathrm{ITG}_t=\frac{\hat{\beta}}{(1-\hat{\xi}) S_t} $ | (9) |
| $ \mathrm{ITL}_t=\frac{\hat{\beta}^*}{\left(1-\hat{\xi}^*\right) S_t} $ | (10) |
其中,
本文研究对象是上证50ETF期权,是国内上市时间最久的场内期权,其标的资产为交易型指数基金上证50ETF。每一交易日,上证50ETF期权存在四个不同期限的合约,即当月到期、下月到期、下季到期与下下季到期。本文选取2015年2月9日到2021年9月30日交易的所有上证50ETF期权合约,期间总计2 800支期权,并参考上证50ETF波动率指数(iVIX)编制方案,使用当月到期或者下月到期的期权合约计算隐含尾部收益因子和隐含尾部损失因子。同时参考Bliss等[16]的研究,对期权样本进行如下的数据清洗过程:一是为减轻“到期日效应”对实证结果的影响,对期限不足10个日历日的样本进行剔除;二是同时剔除买卖均价小于0.001元和明显违背无套利条件的期权样本,因为这些期权存在微观结构噪音。进行数据清洗后,不同类型期权的日合约数如表 1所示。
| 表 1 不同类型期权的日合约数占比 |
为了在估计参数时有足够的样本保证参数估计值的准确性,同时也为了尽可能贴近期权定价公式中阈值尽可能大(对于看涨期权)或尽可能小(对于看跌期权)的假设条件,Wang等[11]在美国市场上选用深度虚值期权。但我国期权市场的期权数量少、执行价格覆盖率低,完全选用深度虚值期权会导致期权数据不足以用于参数估计。因此,为了解决市场极端时期深度虚值期权不足,甚至虚值期权不足的问题,本文采用如下方法在每个交易日动态调整期权的选择:
(1) 当虚值期权合约数小于4个时,选择执行价格最高的4个看涨期权或者执行价格最低的4个看跌期权;
(2) 当虚值期权合约数大于等于4个,小于等于8个时,选择全部的虚值期权;
(3) 当虚值期权合约数大于8个时,选择执行价格高于50%分位点的虚值看涨期权或者执行价格小于50%分位点的虚值看跌期权。
采用上述方法,本文在每个交易日选出适合参数估计的期权样本,最终样本包括1 619个交易日,每个交易日平均使用5.25支看涨期权估计隐含尾部收益因子,使用5.66支看跌期权估计隐含尾部损失因子。
五、实证研究 (一) 隐含尾部风险因子期权隐含尾部信息衡量了期权市场参与者预判未来市场发生大幅波动的概率。其中,隐含尾部收益因子(ITL)的数值越大表示投资者对现货市场未来大幅上涨越有信心,而隐含尾部损失因子(ITL)的数值越大表示投资者对现货市场未来大幅下跌的预感越强烈。采用式(9)和式(10),计算得到期权隐含尾部收益因子和隐含尾部损失因子的时间序列,如图 1所示。
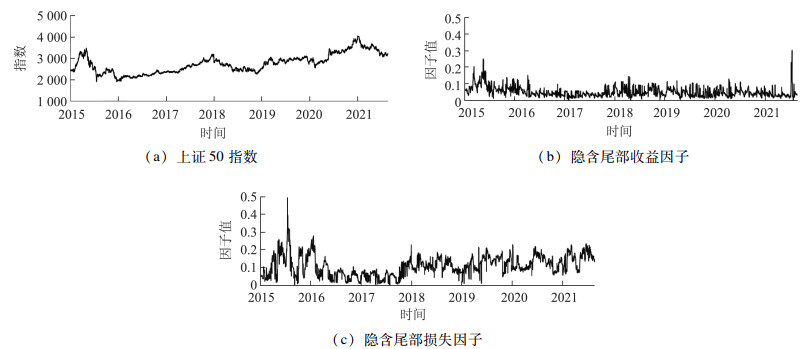
|
图 1 上证50指数以及上证50ETF期权隐含尾部损益因子(2015年2月9日到2021年9月30日) |
2015年,我国股市经历了一轮快速的大涨和大跌。从图 1可以看出,期权市场在此期间也经历了大幅的变化:首先,隐含尾部收益因子和隐含尾部损失因子的数值不断增大,表明市场分歧的不断加深,期权交易者预知市场有较大的波动;其次,隐含尾部损失因子继续扩大,超过隐含尾部收益因子,说明市场看跌观念逐步占据市场;最后,隐含尾部收益因子和隐含尾部损失因子回落到低位波动,说明市场进入盘整期。同样地,在2018年受中美贸易摩擦的影响,我国市场全年处于熊市中,隐含尾部损失因子和隐含尾部收益因子开始出现较大波动,且平均值也出现上升,说明市场波动加大,隐含尾部损失因子表现要强于隐含尾部收益因子,说明市场悲观预期一直占据主导地位。此后,2020—2021年,市场一直受疫情的影响,存在较大不确定性,表现出隐含尾部风险因子总体波动较大。
比较有趣的发现是,进入2021年9月,隐含尾部收益因子突然增大,说明市场预计指数会有较大的反弹,同时期的上证50指数也确实在9月开始触底反弹,结束了2021年初以来的持续下跌。
表 2给出了ITG和ITL的统计值。可以看到,ITL的均值和方差均明显大于ITL,说明市场下跌的风险更明显反映到期权价格中,投资者更倾向于在市场下跌时,采用看跌期权来进行投机或者对冲市场下跌的风险。同时,隐含尾部损失因子数值波动较大,说明预期市场下跌存在较大的不稳定性。总之,该结果表明我国期权市场所隐含的左右尾特征存在较大的差异。
| 表 2 隐含尾部风险统计特征 |
为了验证我国上证50ETF期权隐含尾部风险对上证50指数的预测作用,本文选用隐含尾部收益因子和隐含尾部损失因子,对上证50指数的未来一个月累计收益进行回归分析。参考王琳玉等[15]和倪中新等[14]的研究,本文引入了可能影响指数未来收益的指标作为控制变量,包括股息率(D/P)、成交量(Vol)、近一个月回报(Month_LR)、市场风险因子(MKT_RF)、规模因子(SMB)、账面市值比因子(HML)和动量因子(UMD)。表 3给出控制变量的统计特征。
| 表 3 控制变量的统计特征 |
为研究当期的隐含尾部收益因子和隐含尾部损失因子对未来一个月上证50指数累计收益rt, t+τ的影响,构建如下回归模型:
| $ r_{t, t+\tau}=\beta_0+\beta_1 \mathrm{ITG}_t+\beta_2 \mathrm{ITL}_t+\beta_{\text {contrr }} \text { Contrs }_t+\varepsilon_t $ | (11) |
其中,β1和β2分别为隐含尾部收益因子和隐含尾部损失因子对未来股指收益的回归系数;βcontrs为控制变量Contrs的回归系数;rt, t+τ为上证50指数从t时刻到t+τ时刻的收益率; εt残差项。
表 4给出了隐含尾部风险对未来一个月收益率的回归结果。列(1)和(2)为隐含尾部损益因子的单变量回归,列(3)、列(4)和列(5)为加入控制变量后的多变量回归。在单变量回归模型下,隐含尾部收益因子对上证50指数未来一个月的收益率具有显著的预测能力,其β系数的估计值在1%的显著性水平下统计显著,并且β小于0,说明看涨期权市场上存在过度乐观情绪,这与现有文献中的结果一致①。隐含尾部损失因子同样对未来收益有显著的预测能力,其β系数的估计值同样小于0,但此时的系数小于0,说明看跌期权市场上的隐含信息能预测市场下跌。当看跌期权市场的参与者认为市场出现大幅下跌的可能性较大时,未来市场将会向下移动,这与大多数文献认同的风险补偿观念相反,但符合Wang等[11]提出的“信息有效假设”②。模型加入控制变量后未影响隐含尾部风险因子的显著性,说明隐含尾部风险的预测能力是稳健的。
| 表 4 隐含尾部风险对未来一个月收益率的回归结果 |
① 王琳玉等[15]认为正偏的资产价值倾向于被高估,最终导致负偏的收益;崔海蓉等[17]发现投资者会因为羊群效应造成看涨期权价格相对过高,但实际上标的收益率并未上升反而下降。
② Wang等[11]提出“信息有效假设”,在该假设条件下期权市场参与者对未来市场的判断是准确的,隐含尾部收益因子的增大,意味着市场参与者看涨,那么未来一段时间市场收益为正。
(三) 隐含尾部风险与隐含高阶矩过往文献所研究的期权隐含信息主要是隐含高阶矩[15]、隐含波动率偏斜[17]和隐含偏度风险溢酬[18]等。这些因子都被证明能够预测未来收益。那么隐含尾部风险是否包含这些因子所不包含的信息呢?
本文使用隐含高阶矩作为代表进行接下来的研究。原因在于隐含高阶矩是其余几个期权隐含信息的基础,同时隐含高阶矩中的隐含波动率实际应用广泛,像美国CBOE的VIX指数和中国上交所的iVIX指数。参考Bali等[19]的无模型方法计算隐含高阶矩,其中包括隐含波动率(implied volatility,IV)、隐含偏度(implied skewness,IS)和隐含峰度(implied kurtosis,IK)。表 5为期权隐含信息间的相关性,从表 5中可以看到,隐含尾部收益因子与隐含波动率间的相关性为0.28,以隐含峰度间的相关性接近0.5,隐含尾部损失因子与隐含波动率和隐含峰度间的相关性都超过了0.5。
| 表 5 期权隐含信息间的相关性 |
本文首先比较隐含尾部风险与隐含高阶矩对未来收益的预测能力。表 6为隐含高阶矩对未来一个月收益率的回归结果。与表 4中的单变量回归结果进行比较可以发现,ITL和ITL的R2小于隐含波动率和隐含偏度的R2,但大于隐含峰度的R2,说明隐含尾部风险与隐含高阶矩具有类似的预测能力。那么剔除隐含高阶矩后的隐含尾部风险是否仍然含有对未来市场变化的信息呢?
| 表 6 隐含高阶矩对未来一个月收益率的回归结 |
本文采用正交化方法从隐含尾部风险中剔除隐含高阶矩信息。具体方法是,对隐含尾部风险作关于隐含高阶矩的多元回归,将回归后得到的残差项作为隐含尾部风险新息。隐含尾部收益新息记为ITGres,隐含尾部损失新息记为ITLres。采用隐含尾部风险新息代替式(11)中的隐含尾部风险,再对未来一个月上证50指数累计收益rt, t+τ进行回归。
表 7和表 8分别为隐含尾部收益新息和隐含尾部损失新息对上证50指数未来一个月收益的回归结果,其中样本A对应整个期间(2015年2月9日至2021年9月30日)、样本B对应发展初期(2015年2月9日至2016年7月29日)、样本C对应发展期(2016年8月1日至2021年9月30日),区间划分方式参考崔海蓉等[17]。
| 表 7 隐含尾部收益新息对上证50指数未来一个月收益率的回归结果 |
| 表 8 隐含尾部损失新息对上证50指数未来一个月收益率的回归结果 |
首先观察样本A的回归结果,在加入控制变量之前,隐含尾部收益新息对上证50指数未来一个月收益的解释能力显著,并且其β系数的估计值与隐含尾部收益因子保持方向上的一致性,但引入其他影响因素后,隐含尾部收益新息的预测变得不显著。再观察样本B和样本C的回归结果,可以发现,隐含尾部收益新息的预测能力随着期权市场的发展出现了明显的变化,从一开始的稳健性显著到不显著,说明看涨期权市场上过度乐观情绪的出现有所缓和,但仍然不满足“信息有效假设”,即对市场作出有效的判断。
同样我们可以观察到表 8结果,在样本A中,隐含尾部损失新息对上证50指数未来一个月收益的解释能力并不显著,说明从整个期间看,隐含尾部损失因子还没有包含多于隐含高阶矩的信息。但观察样本B和样本C的回归结果,隐含尾部损失新息的预测能力随着期权市场的发展也出现了明显的变化,从一开始的不显著到显著。结合其β系数的估计值在样本C中显著小于0,说明看跌期权市场的参与者对尾部风险的判断能力有所提高,在期权市场的发展期,隐含尾部损失新息能够包含出更多更有效的信息。
(四) 隐含尾部风险与投资者情绪现有研究发现,市场价格容易受到投资者情绪的影响。期权隐含尾部风险是从期权市场价格提取得到的,那么,投资者情绪也将会影响到隐含尾部风险。由于我国期权市场经历了不同的发展阶段,本文将进一步分析不同时期的投资者情绪与隐含尾部风险信息的关系。
本文参考崔海荣等[17]的研究,选取股票换手率(MTurn)、看涨看跌期权交易量比率(P/C_Vol)、看涨看跌期权持仓量比率(P/C_Pos)和股票融资融券余额比(Margin)这四个指标,通过主成分分析法提取出第一个主成分作为投资者情绪指数,记为Senti。四个指标的统计性描述如表 9所示,从中可以看出,股票换手率具有较明显的正偏和高峰特征,其也是反映投资者情绪的主要指标。因为,相较于期权交易与融资融券交易,普通股票交易并没有对参与者进行限制,所能覆盖的群体更广泛。
| 表 9 变量的描述性统计 |
投资者情绪指数的时间序列如图 2所示。可以看出,投资者情绪指标在2018年以前的波动程度明显高于2018年以后,说明市场在经过一段时期的发展后,投资者情绪的稳定性会明显提高,市场上过度乐观或者过度悲观情绪出现的次数也会明显减少,市场趋于理性。但与图 1进行比较时,我们无法对隐含尾部风险与投资者情绪间的关系进行准确判断,因此接下来使用相关性分析对其进行研究。
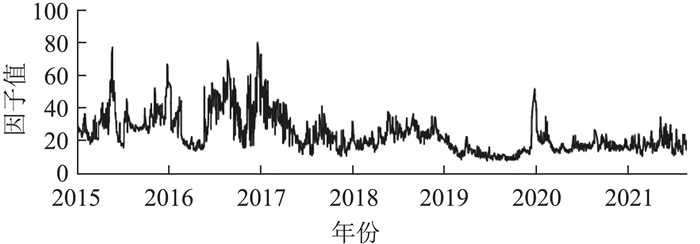
|
图 2 投资者情绪指数 |
隐含尾部风险新息与投资者情绪指数间的相关性如表 10所示。从表 10可以看出,隐含尾部风险新息与投资者情绪间存在显著的相关性,其中隐含尾部风险新息与投资者情绪间存在正相关性。说明当隐含尾部收益因子走高,期权投资者对未来市场上涨表示看好的时候,投资者情绪是高涨的,但往往也是不理性的。而隐含尾部损失新息与投资者情绪间存在负相关关系,说明隐含尾部损失新息的高点,也是投资者情绪的低点。
| 表 10 隐含尾部风险新息与投资者情绪相关性分析 |
进一步,本文参考崔海荣等[17]的研究,验证市场处于不同发展阶段时投资者情绪对隐含尾部风险信息的影响,构建模型如下:
| $ \mathrm{ITG}_t^{\text {res }}=\alpha+\beta \text { Senti }_t+\varepsilon_t $ | (12) |
| $ \mathrm{ITL}_t^{\text {res }}=\alpha+\beta S \text {enti }_t+\varepsilon_t $ | (13) |
其中,Senti表示投资者情绪。
在前面的实证分析中,隐含尾部收益新息在发展初期对未来收益呈负向预测作用,到发展期这一现象消失;隐含尾部损失新息在发展初期对未来收益没有预测作用,随后在发展期对未来收益呈负向预测作用,说明期权投资者变的可以预测未来损失。
表 11给出在不同发展阶段下,由式(12)和式(13)得到的隐含尾部风险新息与投资者情绪间的回归结果。可以看出,隐含尾部收益新息与投资者情绪在发展期不再有显著的相关性。这说明在发展初期,看涨期权市场确实对极端收益存在过度乐观的情绪,但到了发展期,期权市场上的非理性行为有所消退。隐含尾部损失新息则始终与投资者情绪存在显著的相关性,这说明看跌期权市场上的参与者始终受到投资者情绪的影响。从相关系数和R2来看,到了发展期,隐含尾部损失新息更容易受到投资者情绪的影响,因此其所包含的信息也更有价值。
| 表 11 投资者情绪对隐含尾部风险新息的回归结果 |
期权市场隐含信息一直是学术研究的重点,但目前学术界提出的大多数因子反映的都是标的资产价格的整体分布特征。本文利用Hamidieh[8]所提出的深度虚值期权定价公式,首次在我国期权市场分析隐含的尾部风险特征,并研究其对未来收益的预测能力。主要结论如下:
首先,隐含尾部收益因子对上证50指数未来一个月的收益率具有显著的负向预测能力,说明看涨期权市场上的乐观情绪往往是过度的,即当看涨期权暴涨时,市场较大概率会反向下跌。同时,隐含尾部损失因子对上证50指数未来一个月的收益率也具有显著的负向预测能力,当看跌期权市场参与者认为市场出现大幅下跌的可能性较大时,未来市场将会向下移动,跟随看跌期权价格的极端变化,可以有效预测市场下跌。
其次,从整个样本期看,隐含尾部风险不含有多于隐含高阶矩的新信息,但如果将样本分成不同的发展阶段,其含有的新信息会有所体现。具体来看,隐含尾部收益新息的预测能力随着期权市场的发展出现了明显的变化,从一开始的显著到不显著,说明看涨期权市场上过度乐观情绪的出现有所缓和。隐含尾部损失新息的预测能力随着期权市场的发展也出现了明显的变化,从一开始的不显著到显著为负,说明看跌期权市场的参与者对尾部风险的判断能力有所提高。
最后,投资者情绪能够在一定程度上解释期权隐含尾部风险与未来收益间关系的变化。隐含尾部收益新息在市场发展初期表现出的过度情绪源于市场的非理性行为,并且这一非理性行为随着市场的发展有所消退。看跌期权市场价格更容易受到投资者情绪的影响,也正因如此,隐含尾部损失所包含的信息更有价值。
| [1] |
PAN J, POTESHMAN A M. The information in option volume for future stock prices[J]. The review of financial studies, 2006, 19(3): 871-908. DOI:10.1093/rfs/hhj024 |
| [2] |
ANDERSEN T G, FUSARI N, TODOROV V. The risk premia embedded in index options[J]. Journal of financial economics, 2015, 117(3): 558-584. DOI:10.1016/j.jfineco.2015.06.005 |
| [3] |
郑振龙. 资产价格隐含信息分析框架: 目标、方法与应用[J]. 经济学动态, 2012(3): 33-40. |
| [4] |
BLACK F, SCHOLES M. The pricing of options and corporate liabilities[J]. Journal of political economy, 1973, 81: 637-654. DOI:10.1086/260062 |
| [5] |
MERTON R C. Option pricing when underlying stock returns are discontinuous[J]. Journal of financial economics, 1976, 3(1): 125-144. |
| [6] |
WHITE A D, HULL J C. The pricing of options on assets with stochastic volatilities[J]. The journal of finance, 1987, 42(2): 281-300. DOI:10.1111/j.1540-6261.1987.tb02568.x |
| [7] |
MARKOSE S, ALENTORN A. The generalized extreme value distribution, implied tail index, and option pricing[J]. Journal of derivatives, 2011, 18(3): 35-60. DOI:10.3905/jod.2011.18.3.035 |
| [8] |
HAMIDIEH K. Estimating the tail shape parameter from option prices[J]. Journal of risk, 2017, 19(6): 85-110. DOI:10.21314/JOR.2017.366 |
| [9] |
郭婧, 倪中新, 肖洁. 上证50ETF期权隐含波动风险对资本市场风险的预警能力分析[J]. 统计与信息论坛, 2021, 36(4): 60-71. DOI:10.3969/j.issn.1007-3116.2021.04.007 |
| [10] |
刘天宇. 期权隐含概率分布、极值分布与尾部风险[D]. 厦门: 厦门大学, 2017.
|
| [11] |
WANG Y H, YEN K C. The information content of option-implied tail risk on the future returns of the underlying asset[J]. Journal of futures markets, 2018, 38(4): 493-510. DOI:10.1002/fut.21887 |
| [12] |
陈坚, 张轶凡, 洪集民. 期权隐含尾部风险及其对股票收益率的预测[J]. 管理科学学报, 2019, 22(10): 72-81. DOI:10.3969/j.issn.1007-9807.2019.10.006 |
| [13] |
杨兴林, 王鹏. 基于时变波动率的50ETF参数欧式期权定价[J]. 数理统计与管理, 2018, 37(1): 162-178. |
| [14] |
倪中新, 郭婧, 王琳玉. 上证50ETF期权隐含波动率微笑形态的风险信息容量研究[J]. 财经研究, 2020, 46(4): 155-169. |
| [15] |
王琳玉, 倪中新, 郭婧. 上证50ETF隐含高阶矩风险对股票收益的预测研究[J]. 统计研究, 2020, 37(12): 75-90. |
| [16] |
BLISS R R, PANIGIRTZOGLOU N. Testing the stability of implied probability density functions[J]. Journal of banking & finance, 2002, 26: 381-422. |
| [17] |
崔海蓉, 李晶晶, 鲁训法. 买卖权平价关系偏离能预测现货市场收益吗?——基于上证50ETF期权的实证研究[J]. 金融发展研究, 2021(8): 57-65. |
| [18] |
陈蓉, 林秀雀. 波动率偏斜与风险中性偏度能预测尾部风险吗[J]. 管理科学学报, 2016, 19(8): 113-126. |
| [19] |
BALI T G, HU J, MURRAY S. Option implied volatility, skewness, and kurtosis and the cross-section of expected stock returns [R]. Georgetown: Georgetown McDonough school of business research paper, 2019.
|
 2023, Vol. 25
2023, Vol. 25
