在平台经济环境下,月度活跃用户数(monthly active user, MAU)俨然成为评价第三方电商平台运营绩效的一项重要指标。但是,相较于活跃用户,平台上不活跃的用户体量更大,常常被形象地称为“安静的大众”与“活跃的小众”。这些不活跃的平台用户对其他用户的影响诚然不如活跃用户;但是,作为网络口碑营销的受众,他们人数众多,贡献了企业销售收入的绝大多数。因此,领域专家非常重视对市场中“安静的大众”在产品口碑营销中表现出的行为和偏好的研究。例如,电子商务中非主流产品“热销”的长尾现象,就被解释为“安静的大众”用户有限理性的产品购买决策偏好[1]。实践中,企业也非常重视这些“安静的大众”对企业口碑营销的反应,即关心平台用户在口碑营销中表现出的行为或偏好对产品口碑营销效果的影响。因为,只有在明晰多数平台用户对企业网络口碑营销的反应后,企业才能制订出高效的口碑营销策略。
网络口碑营销受到信息发布方、信息接收方、社会关系网络、口碑信息本身等多方因素的影响,且口碑信息扩散过程具有天然的随机性和不确定性,研究难度非常大。当前,网络口碑营销的研究主要从产品口碑的信息扩散模型和平台用户之间社会关系网络两个方面展开。在这些研究工作中,平台用户(信息接收方)在口碑营销过程中的行为多被简化为一个随机选择,如用户受产品口碑影响或不受其影响。然而,随着相关实证研究的深入,平台用户在口碑营销过程中的表现被证实为一个复杂的随机选择函数,即用户传播产品口碑信息的兴趣或口碑营销的参与度会随着其在社会关系网络中的“邻居们”对产品口碑的知晓率而呈现“U”形变化[2]。本文即是在此实证研究结果的基础上,构建更加贴近现实的产品口碑扩散和口碑营销模型,并以多智能体建模与仿真的研究方法,仿真分析平台用户之间复杂社会关系网络对口碑营销效果的影响以及平台用户表现出的U形偏好对口碑营销效果的影响。
二、文献综述以微博、微信等为代表的网络平台上的信息扩散,信息传播路径和扩散结果通常难以预测。多数话题会短暂引起少数用户的注意和转发,随后则被淹没在其他信息扩散之中。但是,少数话题会迅速扩散,并逐步发酵,最终成为社会热点问题。如此信息扩散的不可预见性和不可复制性,领域专家通常从平台用户在口碑营销/口碑扩散中表现出的异质性以及平台用户之间的社会关系网络两个方面去解读。
平台用户在口碑营销和口碑扩散中表现出的行为因素研究,领域专家通常在经典的信息扩散模型上扩展,模型中引入更加贴近现实世界中平台用户行为偏好的因素或参数。此类研究工作较多,近几年代表工作包括:在产品口碑扩散的Bass模型基础上,将信息扩散的参数由常数值改为指数函数,从而模拟信息扩散的强度不断增加[3];或者考虑正面、负面信息的同步扩散和相互影响[4]以及相关信息(迭代产品的口碑信息)叠加影响[5];考虑口碑信息扩散过程中多个话题同时扩散时的交互影响,提出了口碑信息扩散和网络拓扑演化的信息传播动力学模型[6];将病毒扩散SIS(Susceptible-Infected-Susceptible)模型与谣言传播Maki-Thomson模型结合起来,分析多层社会关系网络环境下的扩散过程[7];将口碑信息扩散看作是不完全信息环境下的演化博弈过程,采用类似囚徒困境式的收益矩阵刻画用户行为和后果[8]等。
对平台用户的社会关系网络的研究,主要是指分析社会关系网络的网络结构、关键节点等对口碑信息扩散的影响。近几年,代表性工作包括:将平台用户的社会关系网络划分为两个子网络,考虑子网络内部信息扩散和子网络之间信息扩散的差异性[9];分析社会关系网络为小世界网络时,网络特征属性如平均路径长度等与信息扩散之间的关系[10];多层超网络环境下的信息扩散研究,构建信息扩散过程中关键节点的识别指标(多层加权度指标)[6, 11];采用多指标体系对信息扩散效果进行综合评价[12];对病毒扩散SIR(Susceptible-Infected-Recovered)模型进行扩展,分析了加权网络下的信息扩散过程[13];分析病毒扩散SIS模型在时变、多层复杂网络环境下的应用[14];同时考虑多层网络和网络中的社团结构,引入信息包传播的系统动力学模型分析社团结构对信息扩散的影响[15]以及识别信息扩散中意见领袖[16]、信息转发中的关键节点(“推手”节点)[17]等。
以上这些研究工作中,平台用户在口碑信息扩散中表现出的行为偏好刻画较为简单。例如,在病毒扩散SIR、SIS模型中,平台用户传播产品口碑信息的行为用一个简单的随机变量进行刻画,即传播概率[7, 13, 14];在Bass模型中,平台用户受产品口碑的影响同样描述为一个随机变量,即内部影响因子[3]。随着实证研究的深入,平台用户在口碑信息扩散中表现出的非线性、非理性的行为特征被逐渐被发现,如演化博弈模型中的非理性行为[8]、从众行为中的非线性特征[3]等。但是,这些实证研究的成果由于涉及的消费者行为模型过于复杂,并没有被引入口碑扩散模型之中。进而,这些真实的平台用户行为偏好对口碑信息扩散的影响也就无从谈起。
鉴于理论研究与企业实践之间的巨大鸿沟,本文结合最新的实证研究成果,侧重研究平台用户复杂的口碑传播行为对口碑营销效果的影响。相较于前人的研究,本文的最大创新之处是对平台用户口碑传播行为的刻画更加贴近现实,研究结论更加真实可信。为了能够再现平台用户在口碑营销中表现出的非线性行为,本文在多智能体建模方法的指导下,通过模型仿真实现问题求解。因此,本文除了问题模型的创新外,研究方法也是对传统数学建模分析的丰富和扩展。
三、平台用户间产品口碑扩散的模型构建 (一). 平台用户传播产品口碑信息的随机模型根据最新实证研究成果[2],本文定义网络中用户传播产品口碑信息的概率αU (0<αU≤1)为下面所示的分段线性函数(k≥1;0<a<b<1):
| $ {\alpha _{\rm{U}}} = {\rm{Prob}}\left( r \right) = \left\{ \begin{array}{l} \frac{{br\left( {1 - k} \right)}}{a} + kb\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {0 \le r < a} \right)\\ b\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {a \le r \le 1 - a} \right)\\ - \frac{{br\left( {1 - k} \right)}}{a} + \frac{b}{a}\left( {ak - k + 1} \right)\;\;\;\;\left( {1 - a < r \le 1} \right) \end{array} \right. $ | (1) |
| $ b = \frac{1}{{ak - a + 1}} $ | (2) |
其中,参数r定义为经过归一化处理后网络中所有节点的度指标,即首先统计得到网络中所有节点的度指标最大值(Dmax)和最小值(Dmin),然后采用极差公式计算得到归一化处理后的节点度指标(D)值r:
| $ r = \left( {D - {D_{\min }}} \right)/\left( {{D_{\max }} - {D_{\min }}} \right) $ | (3) |
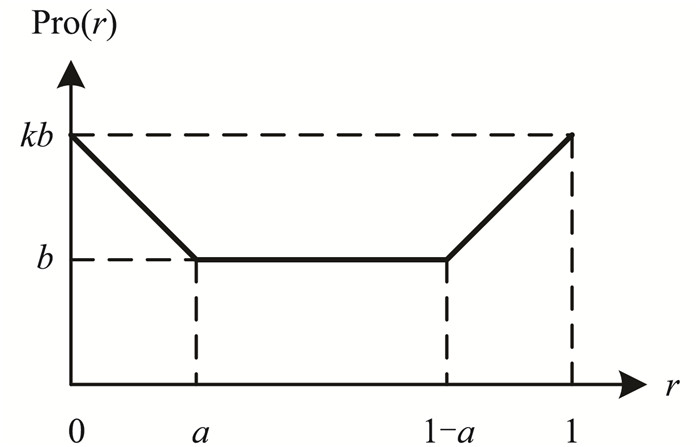
其中,“安静的大众”是指节点度r位于[a, 1-a]的用户,这些用户传播口碑信息的可能性Pro(r)=b。“活跃的小众”是指在网络中朋友数量很少(0≤r<a)或很多(1-a < r≤1)的用户。朋友数量很少的用户(0≤r < a)为了避免被“边缘化”而更倾向于传播产品口碑信息,即Pro(r)>b;而朋友数量很多的用户(1-a < r≤1)为了维系其社会关系网络中意见领袖的地位,也更倾向于传播产品口碑信息[2]。并且,随着朋友数量不断减少或增多,其传播口碑信息的可能性呈现线性增长(斜率为k)。
根据公式(1)描述的分段线性函数,绘制其图形。如图 1所示,该分段线性函数为一个U形曲线。
|
图 1 平台用户传播产品口碑信息的概率 |
此函数描述了平台用户因网络朋友数量多少而表现出传播产品口碑信息的概率差异化。
为了与经典的SIR模型对比,我们也计算了公式(1)对应的常数值形式的传播概率αC,即:
| $ {\alpha _{\rm{C}}} = {\rm{Prob}}\left( r \right) = \lambda \left( {0 < \lambda \le 1} \right) $ | (4) |
此时,由全概率公式,公式(1)所示U形曲线的参数与公式(4)所示常数值λ的关系为:
| $ \lambda = b\left( {ak - a + 1} \right) \cdot $ | (5) |
本文以产品口碑扩散的经典模型——SIR模型,再现平台用户之间产品口碑信息传播的过程。在此模型下,定义平台上用户传播口碑信息的概率为αU,放弃传播口碑信息的概率为μ(0<μ≤1):
第一步,初始化网络上所有平台用户/网络节点的状态为S(“易感者”)。
第二步,从所有节点中随机挑选出1个节点,定义其状态为I(“传播者”),即口碑营销的起始节点。
第三步,从状态为I的网络节点中,随机选出一个节点i,并从节点i的所有相邻节点中随机选出一个节点j。
第四步,如果节点j的状态为S,那么节点j以概率αU转移为状态I,表示节点j从节点i处感知到产品口碑信息(节点i的状态保持为I不变);如果节点j的状态为I或R(“潜水者”),那么节点i以概率μ转移为状态R,表示节点i不再继续向邻居节点传播产品口碑(节点j的状态保持不变)。
以上所示的口碑扩散过程可以用状态转移描述为:
| $ \left\{ \begin{align} & \text{I}\left( i \right)+\text{S}\left( j \right)\xrightarrow{{{\alpha }_{\text{U}}}}\text{I}\left( i \right)+\text{I}\left( j \right) \\ & \text{I}\left( i \right)+\text{I}\left( j \right)\xrightarrow{\mu }\text{R}\left( i \right)+\text{I}\left( j \right) \\ & \text{I}\left( i \right)+\text{R}\left( j \right)\xrightarrow{\mu }\text{R}\left( i \right)+\text{R}\left( j \right) \\ \end{align} \right. $ | (6) |
第五步,重复第三、第四步,直到网络中不再存在状态为I的节点。
第六步,统计状态为R的节点的总数, 其占总节点数量的比例即是产品口碑信息扩散的范围指标——网络覆盖率指标。
如上所示,由于平台上用户的朋友数量(节点度指标)差异较大,使得用户传播口碑信息的概率αU差异巨大,从而导致产品口碑信息扩散难以采用传统的动力学分析方法进行数学分析和求解。因此,本文采用信息扩散分析中常用的多智能体建模分析方法,建立平台上产品口碑信息扩散的多智能体模型,通过计算机仿真实现问题求解。
(三). 产品口碑扩散的多智能体模型在多智能体建模方法论指导下,平台上的产品口碑扩散被“分解”为每位平台用户的传播行为的“汇总”,即复杂系统理论中的“涌现(emergence)”机制。在多智能体建模方法论下的产品口碑信息扩散仿真描述如下:
第一步:系统初始化。
首先,生成N个智能体对象,用于代表平台上N个用户。
其次,引入社会关系网络,建立智能体对象/用户之间的关系。
最后,计算每个智能体对象的邻居数量,即节点度指标(D)。应用公式(1),计算每个智能体对象传播口碑信息的概率。
第二步:初始化所有智能体对象的状态为S,并以前文描述的SIR模型再现信息扩散的整个过程。
第三步:统计产品口碑信息扩散结束后,状态为R的智能体对象的总数,并计算得到此类智能体的总占比,即口碑信息扩散的最终结果——网络覆盖率指标C。
第四步:重复第二、第三步所示的信息扩散过程M次。
第五步:以M次重复仿真得到的网络覆盖率指标的平均值作为产品口碑扩散的最终结果。
四、模型仿真分析为了研究平台用户在产品口碑营销中表现出的行为特征对口碑扩散和口碑营销效果的影响,我们以复杂网络分析工具Pajek生成了一个小世界网络,并在多智能体仿真平台Netlogo上以代码实现了产品口碑信息扩散的多智能体模型。具体参数设置如表 1所示。
| 表 1 多智能体模型中参数设置 |
为了检验模型的正确性,我们设置参数k =1.0(其他参数不变)。根据公式(1),可以知道此时U形曲线退化为一条直线——常数,即经典SIR模型。
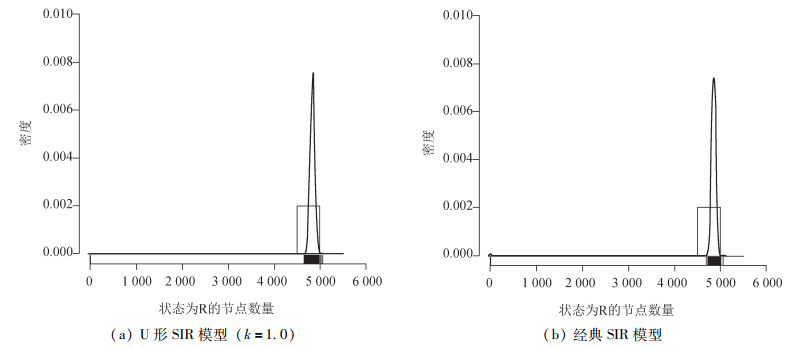
图 2为重复仿真1 000次得到的数据结果,为了对比,我们同时也对经典的SIR模型重复仿真1 000次。可以看出,两个模型仿真结果的数据分布完全一致;而且,本文模型仿真结果也得到了前期仿真所发现的“双峰”现象,即存在信息扩散不开的现象[9]。
|
图 2 重复仿真1 000次的数据统计直方图 |
表 2给出了重复仿真1 000次的仿真结果。
| 表 2 重复仿真结果的描述统计 |
对两个模型的仿真结果进一步做方差齐性检验和单因素方差分析。其中,方差齐性检验计算得到的显著性为0.519,远大于0.05,表明两组数据的方差相等;单因素方差分析计算得到的显著性(p值)为0.904,也远大于0.05,表明两组数据平均值相等,也无显著差异。
两个模型重复仿真的结果平均值相等、方差相等,据此可以认为两个模型的仿真结果相同。因此,可以确认本文实现的产品口碑扩散模型的正确性。
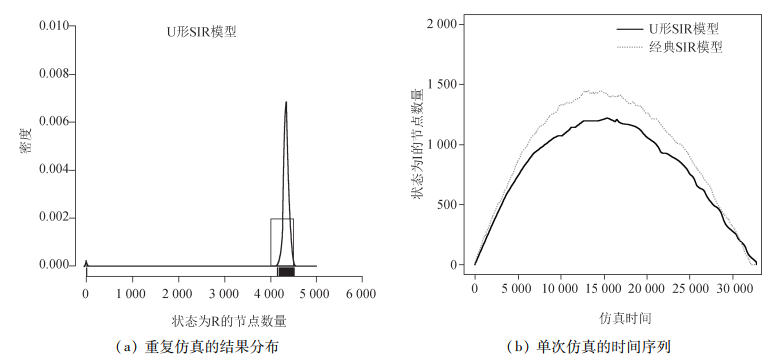
(二). 仿真结果分析以表 1所示模型参数,进行仿真。重复仿真1 000次,得到基础模型的仿真结果如图 3所示。
|
图 3 基础模型的仿真结果 |
如图 3所示,与经典SIR模型的仿真结果相比,本文的U形SIR模型仿真得到的结果(仿真结束时状态为R的节点数量)显著较小,而且,产品口碑信息扩散的速度要更慢。这个仿真结果能够用平台用户的U形行为模型解释,即U形曲线暗示网络中多数用户传播口碑信息的兴趣要低于经典SIR模型中的兴趣值,因此,其口碑扩散的速度和结果要低于经典SIR模型的扩散速度和结果。详细的统计数据如表 3所示。
| 表 3 基准模型重复仿真的结果(状态为R的节点数量) |
根据仿真结果,计算得到信息扩散的网络覆盖率指标C(U型SIR模型网络覆盖率为CU,经典SIR模型网络覆盖率其Cc)为:
| $ \left\{ \begin{array}{l} {C_{\rm{U}}} = 4310.67/10000 = 43.10\% \\ {C_{\rm{C}}} = 4846.22/10000 = 48.46\% \end{array} \right. $ | (7) |
根据计算结果,可以得到以下结论:
现实世界中,平台用户在产品口碑传播中表现出的异质性,即用户可以分为“安静的大众”和“活跃的小众”,显著降低口碑扩散的网络覆盖率指标。如果企业忽视平台用户这样的行为偏好,认为所有用户传播口碑的概率相同,必将高估口碑营销的效果。进而,企业基于此分析作出的口碑营销策略决策,必然带来较高的成本。
五、参数分析下面分别分析平台用户传播概率U形曲线和信息扩散SIR模型中的参数对产品口碑信息扩散的影响。
(一). 参数k对产品口碑扩散的影响参数k值越高,表明朋友数量越少或越多的平台用户就越倾向于传播信息,即两类用户传播口碑信息的概率差异越大。并且,“活跃的小众”传播口碑信息概率越大,普通平台用户(“安静的大众”)传播信息的概率就越小。
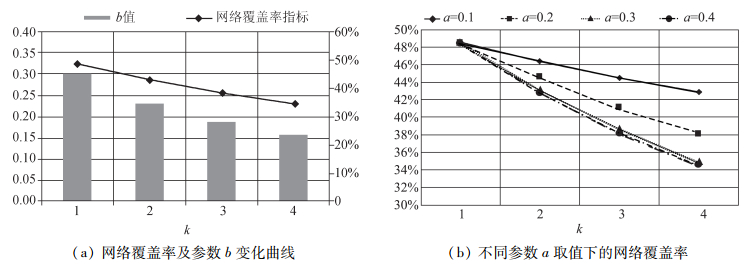
图 4为k分别等于2、3或4时,产品口碑扩散的效果(参数k=1给出的是经典SIR模型的数据)。
|
图 4 U型曲线参数k对信息扩散的影响 |
如图 4所示,随着参数k取值增加,产品口碑扩散的效果在下降。在小世界网络中,“安静的大众”数量显著多于“活跃的小众”数量。因此,参数k值增加引起这些“安静的大众”用户传播产品口碑信息的意愿下降,产品口碑扩散的最终结果就变差。
(1) 随着参数k值增加,产品口碑扩散的网络覆盖率指标呈现单调下降趋势,且呈线性趋势明显。
以a=0.3为例,采用线性回归拟合得到的回归模型为:
| $ {C_{\rm{U}}} = - 0.0452k + 0.5258 $ | (8) |
(2) 随着参数a值增加,网络中“安静的大众”用户传播产品口碑信息的概率下降,网络覆盖率下降更快。但是,当参数a取值大于0.3时,网络覆盖率的变化差异变小。
鉴于参数k值增加导致“安静的大众”用户的传播信息的意愿下降,下面仿真分析当改变信息扩散SIR模型中的参数λ时信息扩散的结果。
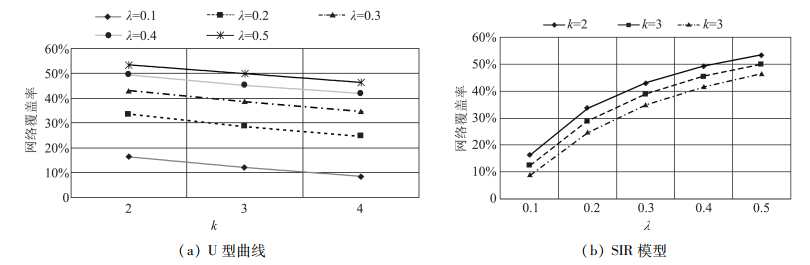
从两个不同维度看参数λ和参数k对产品口碑扩散的影响,结果如图 5所示。从中可以发现:
|
图 5 参数k对产品口碑信息扩散的影响(不同的参数取值) |
(1) SIR模型中的参数λ能够有效提高产品口碑扩散的网络覆盖率指标,且参数λ的影响力呈现边际效应递减的特点。
(2) 参数k对产品口碑扩散的影响相对简单。不同的参数λ组合下,产品口碑扩散的网络覆盖率指标呈现简单的线性下降趋势。
(二). 参数a对产品口碑扩散的影响参数a值越小,模型越接近经典SIR模型。此时,U形曲线所示“安静的大众”用户就越多(范围为[a, 1-a])。并且,当参数a值越小,“安静的大众”用户参与传播产品口碑信息的概率也在上升。
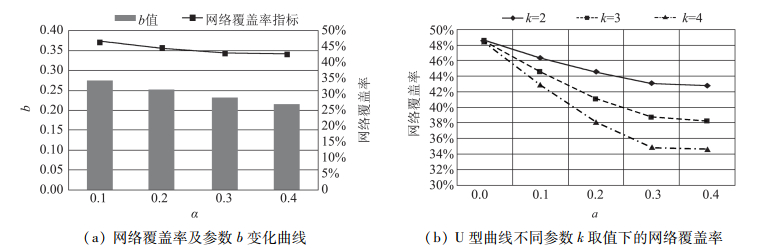
图 6为a分别等于0.1、0.2、0.3或0.4时的产品口碑的扩散效果(参数a=0.0时给出的是经典SIR模型的仿真结果)。
|
图 6 参数a对产品口碑信息扩散的影响 |
如图 6所示,随着参数a取值的增加,产品口碑信息扩散的网络覆盖率指标在单调下降。但是,当参数取值a=0.3,网络覆盖率指标值变化较小,呈现为水平态势。以k=2为例,拟合最好的曲线为对数曲线,即:
| $ {C_{\rm{U}}} = - 0.037\ln \left( a \right) + 0.4861 $ | (9) |
(1) 随着网络中的“安静的大众”用户数量增加,即[a, 1-a]范围的增加,且“安静的大众”用户的产品口碑扩散概率增加,即b值增大,即产品口碑信息扩散的效果逐步增加。
(2) 参数a取值为0.3后,产品口碑信息扩散的效果变化不大,这表明平台用户节点度主要集中在[0.3, 0.7]段。当超过这个范围之后,由于用户数量变化较少,对产品口碑信息扩散的影响不大。
鉴于参数a值增加导致“安静的大众”用户的数量增多,且这些用户传播产品口碑信息的概率增加,下面继续分析当改变信息扩散SIR模型中的参数λ时产品口碑扩散的结果。
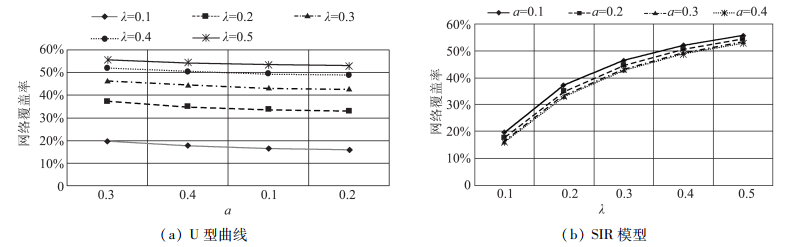
如图 7所示,从两个不同维度看参数λ和参数a对产品口碑扩散的影响,可以发现:
|
图 7 参数a对产品口碑信息扩散的影响(不同的参数λ取值) |
(1) 相比于参数λ,参数a对产品口碑扩散的影响较小,即产品口碑扩散效果的差异主要由参数λ决定。
(2)相比于参数k,参数a对产品口碑信息扩散的影响也相对较小。
(三). 参数λ对产品口碑扩散的影响参数λ定义了平台用户对传播信息的兴趣,即参数λ取值越大,其越倾向于接受产品口碑信息并成为该产品口碑信息的传播者。下面对比不同参数λ值下产品口碑信息扩散的效果。根据公式(4)所示的参数之间的关系,我们设定参数λ的变化范围为[0.1, 0.6]。
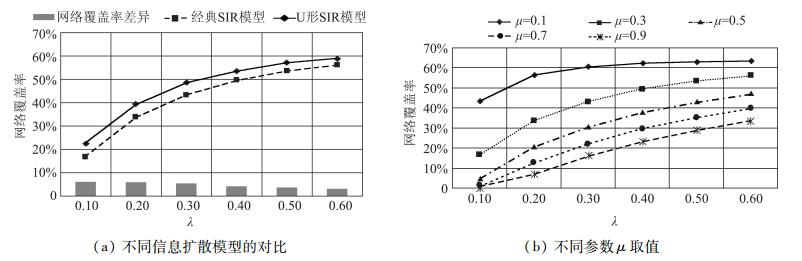
图 8为参数λ对产品口碑信息扩散的影响,并且也给出了不同的参数μ对产品口碑信息扩散的影响。
|
图 8 SIR模型参数λ对信息扩散的影响 |
从图 8可以看出,随着参数λ取值增大,产品口碑扩散的网络覆盖率在提高。
(1) 随着平台用户传播口碑信息的兴趣增加,产品口碑扩散的效果在增强。并且,随着参数λ取值增大,两个模型的传播效果差异在缩小,即平台用户的异质性影响在衰减。
(2) 随着平台用户传播产品口碑信息的兴趣更加持久,即参数μ取值越小,产品口碑扩散的效果随之增大。同样,随着参数μ取值增大,参数λ的影响效果变化在降低。
以μ=0.3为例,下面给出了拟合最好的回归曲线形式:
| $ {C_{\rm{U}}} = 0.2238\ln \left( \lambda \right) + 0.1747 $ | (10) |
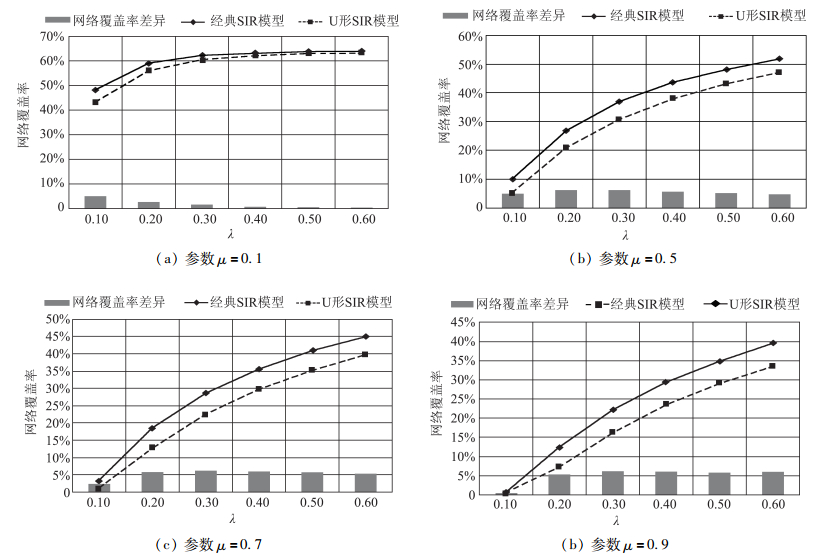
图 9为不同参数μ取值下,不同产品口碑信息扩散模型的效果对比。
|
图 9 SIR模型参数μ对产品口碑信息扩散的影响 |
如图 9所示,经典SIR模型中参数λ对产品口碑扩散的影响与U形SIR模型影响相同。另外,需要指出的是,当参数λ≪μ时,两个模型的差异性也在降低。这表明,此时μ参数对产品口碑扩散占据主导地位。
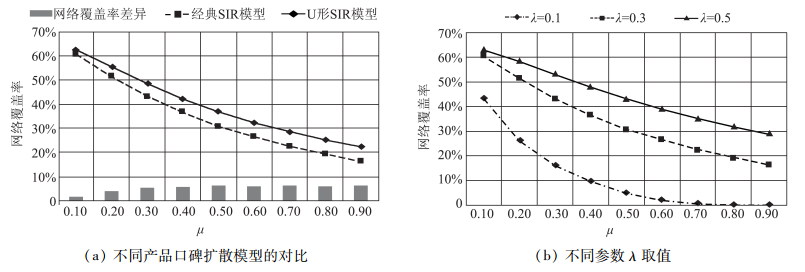
(四). 参数μ对产品口碑扩散的影响在信息扩散SIR模型中,参数μ定义了平台用户对传播信息的兴趣持久性,即参数μ取值越大,其越容易放弃传播产品口碑信息成为“潜水者”。因此,参数μ取值越大,口碑扩散的效果越差,反之则越好。图 10为参数μ对产品口碑扩散的影响,同时给出了不同参数λ对产品口碑扩散的影响。
|
图 10 SIR模型参数μ对产品口碑扩散的影响 |
如图 10所示,随着平台用户传播信息的兴趣迅速衰减,即参数μ取值逐渐增大,信息扩散的效果明显变差。
(1) 随着平台用户传播产品口碑信息的兴趣降低,产品口碑扩散的网络覆盖率指标呈现指数形式的衰减。并且,随着参数μ的增大,两个模型的仿真结果差异不断增大。
以λ=0.3为例,下面给出了参数μ与产品信息扩散的结果——网络覆盖率指标的关系模型:
| $ {C_{\rm{U}}} = 0.7094 \cdot \exp \left( { - 0.165 \cdot \mu } \right) $ | (11) |
(2) 当参数μ保持不变时,参数λ增大引起的网络覆盖率指标的增加程度不断下降,即参数λ对网络覆盖率指标的变化呈现边际效应递减特征。
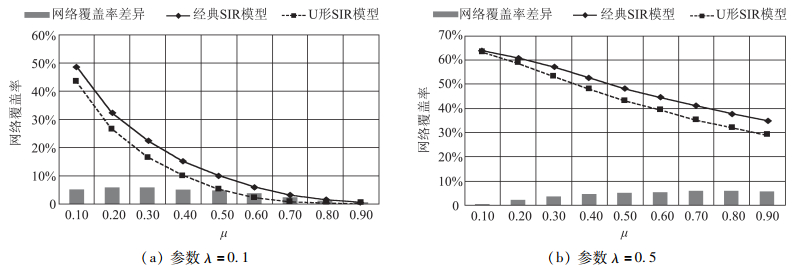
图 11为不同参数λ取值下,不同产品口碑扩散模型的效果对比。
|
图 11 SIR模型参数λ对产品口碑信息扩散的影响 |
如图 11所示,不同参数λ取值下,参数μ对产品口碑扩散的影响表现一致。并且,当参数μ与参数λ数值接近时,两个模型的产品口碑扩散效果差异更大。而当两个参数差异较大时(λ≪μ或μ≪λ),两个模型的仿真结果更加接近。
六、结论与启示本文结合最新的实证研究成果,研究平台经济环境下产品口碑扩散及产品口碑营销的效果。通过构建研究问题的多智能体模型,包括平台用户之间社会关系网络,采用仿真方法研究平台用户在产品口碑扩散的差异化表现对口碑营销的影响。
(一). 仿真结果小结仿真结果的数据分析表明:平台用户差异化表现降低了产品口碑营销的营销效果。
(1) 对比经典SIR模型和U形SIR模型的仿真结果可以发现,当社交平台上的平台用户在口碑营销中表现出较强的异质性,即“活跃的小众”用户的口碑营销参与积极性显著高于“安静的大众”用户的口碑营销参与积极性时,即使所有用户的口碑营销参与积极性的平均值保持不变,企业口碑营销的效果也会下降。如果企业希望提高产品口碑营销的效果,则需要提高“安静的大众”用户的口碑营销参与度。
(2) 对比不同U形SIR模型中参数k的仿真结果,当社交平台上“活跃的小众”用户的口碑营销参与积极性越强于“安静的大众”用户的口碑营销参与积极性(参数k取值越大)时,企业口碑营销的效果就越差,并呈现线性下降的趋势。因此,如果企业希望提高产品口碑营销的效果,则需要提高“安静的大众”用户的口碑营销参与积极性,从而降低不同用户口碑营销参与积极性的差异性,即降低参数k值。
(3) 对比不同U形SIR模型中参数a的仿真结果,当社交平台上“活跃的小众”用户数量越多(参数a取值越小),企业口碑营销的效果越差,并呈现线性下降的趋势。但是,平台用户之间社会关系网络的小世界特性,“活跃的小众”用户数量无法随着参数a取值减少而成比例下降,因此企业口碑营销的效果存在下限。
(4) 对比不同U形SIR模型中参数λ的仿真结果,当平台用户参与口碑营销的意愿更强(参数λ取值越大),企业口碑营销的效果越好。但是,随着平台用户参与口碑营销的意愿增加,其对口碑营销效果的影响呈现边际效应递减的趋势。因此,从成本效率的视角来看,试图不断刺激所有平台用户的参与口碑营销意愿并不经济。
(5) 对比不同U形SIR模型中参数μ的仿真结果,当平台用户参与口碑营销的概率更耐久(参数μ取值越小),企业口碑营销的效果越好。当平台用户参与口碑营销的概率更短暂,企业口碑营销的效果越差,并呈现边际效应递减的趋势。
(6) 对照不同参数λ和参数μ的仿真结果可以发现,当平台用户参与口碑营销的概率较强而且更加持久(μ≪λ)时,或者当平台用户参与口碑营销的概率较小而且意愿更加短暂(λ≪μ)时,平台用户的异质性对口碑营销效果的影响并不显著,即企业口碑营销的效果可以用简化后的经典SIR模型分析得到。
(二)管理启示
根据以上结论,可以得到以下管理启示:
(1) 针对社交平台上的平台用户展开口碑营销,需要通过营销努力提高平台用户中大众用户的口碑营销热情。在实践中,企业应通过激励机制促进“安静的大众”用户积极参与口碑营销,避免“安静的大众”与“活跃的小众”用户的口碑营销热情反差过大。
(2) 从成本效率的角度出发,追求提高所有平台用户的口碑营销热情并不高效,其将导致营销努力的边际效应递减。在实践中,最有效的口碑营销努力应该是尝试多种方式同步进行,如提高用户受口碑营销影响的转化率,并同时制造一系列“衍生”话题维系平台用户参与口碑营销的热情。
(3) 如果平台用户对参与产品口碑营销的热情非常高或非常低,此时对于口碑营销效果的估计可以忽略平台用户的异质性,即假定平台用户完全同质。在实践中,在这两种情景下,企业可以通过口碑营销的早期反应,对口碑营销的效果作出准确率较高的预测。
| [1] |
ZHANG L. Intellectual property strategy and the long tail: evidence from the recorded music industry[J]. Management science, 2018, 64(1): 24-42. DOI:10.1287/mnsc.2016.2562 |
| [2] |
SUN M, ZHANG X, ZHU F. U-shaped conformity in online social networks[J]. Marketing science, 2019, 38(3): 461-480. DOI:10.1287/mksc.2018.1133 |
| [3] |
李萧薇, 刘铁忠, 鲁云蒙. 基于BASS模型的公众危化品危害信息扩散行为研究[J]. 管理学报, 2019, 16(11): 1703-1711. DOI:10.3969/j.issn.1672-884x.2019.11.015 |
| [4] |
任建超, 韩青. 基于食品安全事件异质性的信息扩散过程研究[J]. 系统工程理论与实践, 2017, 37(11): 2833-2843. DOI:10.12011/1000-6788(2017)11-2833-11 |
| [5] |
李锋, 林宁, 庄东. 迭代产品病毒式线上口碑营销下的库存优化[J]. 华南理工大学学报(社会科学版), 2017, 19(6): 55-67. |
| [6] |
刘小洋, 何道兵. 基于突发公共事件的信息传播动力学模型与舆情演化研究[J]. 计算机科学, 2019, 46(5): 320-326. |
| [7] |
SILVA P C V, VELASQUEZ-ROJAS F, CONNAUGHTON C, et al. Epidemic spreading with awareness and different timescales in multiplex networks[J]. Physical review E, 2019, 100(3): 032313. DOI:10.1103/PhysRevE.100.032313 |
| [8] |
张卫东, 李松涛, 梁恩平. 基于完全信息博弈模型的社交媒体用户跟随行为研究[J]. 情报科学, 2019, 37(8): 114-119. |
| [9] |
OESTEREICH A L, PIRES M A, CROKIDAKIS N. Three-state opinion dynamics in modular networks[J]. Physical review E, 2019, 100(3): 032312. DOI:10.1103/PhysRevE.100.032312 |
| [10] |
李锋, 魏莹. 小世界网络下病毒式信息传播的仿真分析[J]. 系统仿真学报, 2019, 31(9): 1790-1801. |
| [11] |
朱晓霞, 胡小雪. 多层社交网络中节点影响力的识别[J]. 情报理论与实践, 2019, 42(1): 105-111. |
| [12] |
李锋, 庄东. 社会网络的多层次特性对口碑营销营销的综合评价[J]. 华南理工大学学报(社会科学版), 2016, 18(5): 1-8. |
| [13] |
ZHU Y, WANG W, TANG M, et al. Social contagions on weighted networks[J]. Physical review E, 2017, 96(1): 012306. |
| [14] |
LIU Q, XIONG X, ZHANG Q, et al. Epidemic spreading on time-varying multiplex networks[J]. Physical review E, 2018, 98(6): 062303. |
| [15] |
李凯, 安实, 孟建芳. 基于社团结构的多层复杂网络中信息传播机制研究[J]. 情报理论与实践, 2019, 42(3): 134-138. |
| [16] |
李锋, 王妍沣, 胡锦亚. 比特币交易P2P网站中意见领袖的识别与分析[J]. 华南理工大学学报(社会科学版), 2019, 21(6): 64-73. |
| [17] |
李锋, 阳斯. 线上口碑信息扩散中关键"推手"节点的识别及评价研究[J]. 华南理工大学学报(社会科学版), 2018, 20(4): 35-44. |
 2021, Vol. 23
2021, Vol. 23
