2. 华南理工大学 计算机科学与工程学院, 广东 广州 510640
2. School of Computer Science and Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China
随着人们生活品质的提高和生活节奏的加快,人们对于冷链品的需求体量也越来越大。为保持新鲜食品以及冷冻食品从供应地到接收地的品质,冷链物流应运而生。由于运输产品易腐变质的特性,需要在合适的低温环境进行预冷、转运、存贮和配送,相应增加制冷设施,这造成冷链物流比普通物流配送过程产生更多的二氧化碳,成本比普通物流要高出40%~60%。随着能源价格的调整,冷链物流的成本总体上呈现持续走高的趋势[1-2]。根据我国冷链物流起步较晚、基础薄弱、标准体系不完善等情况,政府出台了相应政策来规范冷链物流行业的发展。目前,冷链物流行业还存在基础设施相对落后、专业化水平不高、有效监管不足等问题。2017年国务院办公厅颁布的《加快发展冷链物流保障食品安全促进消费升级的意见》指出:希望到2020年,我国能初步建立一个覆盖广泛、布局合理、衔接顺畅的冷链基础设施网络,基本建立“标准健全、全程温控、应用广泛、绿色安全”的冷链物流服务体系。冷链物流体系建设关键不是强调“冷”,而是强调“链”。节点中断问题频发使追求精益化的整个供应链面临挑战[3],给企业带来额外的缺货成本、货损成本,给冷链品公司日常运营带来很大的不便。例如,2019年因为蔬菜、水果价格居高不下而引发的“水果自由”①问题之中,其售价的70%是用来补贴流通过程中的损失[4],其中就包含供应节点中断带来的腐损问题。综上,考虑冷链物流网络中的节点存在中断风险情景下,研究如何构建引入碳排放成本的冷链物流网络规划,采取有效措施提高冷链效率,防止冷链中断对于企业自身、消费者和整个社会环境来说无疑具有重要意义。
① 受极端天气等季节性因素的影响,车厘子等鲜果价格上涨,这引发社会大众对于收入与水果价格的讨论。
本文研究在冷链物流网络中工厂-冷藏仓库两层节点存在中断风险的情况下,应该如何规划物流网络,进行仓库选址和流量分配,如何增强节点弹性能力,满足弹性系数要求。另外,响应碳减排政策,在数学建模时考虑加入碳排放成本,提高冷链物流的效率,并最小化物流总成本,为冷链物流企业设计物流网络进行决策支持。
二、研究综述结合国家标准(GB/T18354—2006),冷链物流网络(CCLN)的定义是:“根据物品特性,为了保持其品质、降低物流成本、提高物流服务水平,采用冷链技术将物品由原产地到消费者手中的实体流通中一直保持低温状态,在这过程中包含的所有物流系统组织和设施的集合。”[5]尽管冷链物流运输中物流成本居高不下,但合理的物流网络规划可以更好地控制运输过程,从而减少损耗,这引起了国内外广大学者对冷链物流规划问题的关注。学者们对冷链物流网络的研究重点聚焦于网络模式选择、网络规划与建立、网络中心点选择和配送路径的选择等方面[6],对于不同的优化方向,学者们所构建的模型和求解方法不尽相同。
在冷链物流网络规划模型建立方面,Bogataj等[7]分析了影响冷链物流系统中易腐败品的品质的各种因素,建立了以最低货损率为目标的冷链物流网络优化模型,并通过在时域内得到的公式和在频率空间中的公式相结合来求解该模型。Wang等[8]研究了生鲜食品冷链投资与定价决策,建立了以冷链物流中各成员利润最大化为目标的冷链物流网络优化模型,其研究结果确定了冷链建设和广告的最优投资水平以及最优定价。Hsiao等[9]将质量水平引入冷链物流网络规划研究中,综合考虑了送货员劳务费、燃油费、温度设定费、碳排放成本、缺货成本、质量替换成本,并开发了一种基于生物地理学的优化算法(BBO)求解物流网络规划问题。Qin等[10]为了在冷链物流路径优化问题中同时考虑成本、顾客满意度和碳排放,基于成本效益的思想,提出了以单位满意顾客成本最小为目标的综合冷链车辆路径优化模型。梁海红[11]结合生鲜农产品易损耗的特点,构建了具有互联网时代特点的农产品物流配送中心选址模型。陈靖等[12]以物流速递服务企业为研究对象,在随机配送服务需求场景下,受车辆运载能力限制与客户产品新鲜度要求的约束,分析企业包含冷链硬件能力等环境参数与集配数量、客户服务水平相关指标的关系,对生鲜品的物流集配问题进行建模。吴芳芸等[13]基于轴辐式理论研究了生鲜品运输开始节点至目的地节点新鲜度最大为约束条件的冷链物流网络优化模型,其中成本综合考虑了冷链物流运输成本、制冷成本和货损成本。袁群等[14]研究的冷链物流网络设计以总成本最低为目标函数,综合考虑时间窗、货物品质及客户服务水平,利用混合遗传算法对模型求解。杨晓芳等[15]结合冷链运输对时间的敏感性,建立了客户满意度最大化和物流成本最小化的双目标优化模型进行冷链物流网络设计。陈淑童等[16]以配送中心费用最少为目标并考虑货损成本情形下,构建了考虑时效和货损的混合整数线性规划模型,分析了时间与货损率的变化对冷链物流网络构建的影响。但以上文献较少考虑碳排放量因素,也较少将碳排放量转化为碳税作为冷链物流网络规划的成本之中。
在冷链物流网络规划优化算法方面,张文峰等[17]提出了非线性混合整数规划模型,利用量子粒子群算法,对冷链物流网络的网点布局和运输进行优化。杨华龙等[18]建立了考虑了货物损失的速度的冷链物流网络规划模型,并利用遗传算法求解该模型。肖建华等[3]构建了考虑节点应急能力的弹性供应链网络优化模型,针对问题复杂度高的特点,引入基于最短增广链法的改进遗传算法对模型进行求解。Osvaid等[19]采用禁忌搜索的启发式算法求解有生命周期的易腐产品冷链配送分布的车辆路线模型。Yu[20]利用最短路径搜索模型对,实现了云计算环境下冷链物流配送船舶航线的在线规划算法优化设计,提高云计算环境下冷链物流配送的效率。李军涛等[21]建立基于碳排放量、配送总成本和客户满意度的多目标配送路径优化模型来解决冷链物流路径规划问题。丁秋雷等[22]的研究针对干扰事件导致鲜活农产品冷链物流配送难的情况,以生成扰动最小的调整方案为突破口,运用干扰管理思想,分析干扰事件对厂商、顾客和第三方物流配送商三个行为主体的影响,采用改进的蚁群算法——混合蚁群算法进行求解配送优化模型,并证明该方法相较于重调度方法能够生成综合考虑多个主体的利益的解决方案。鲍春玲等[23]提出引入一个虚拟车场将多配送中心问题转化为单配送中心问题的改进遗传算法求解路径优化问题,结果发现联合配送在冷链配送费用和碳排放成本两方面远远低于传统分区配送。刘虹等[24]构建了考虑客户厌恶度的冷链物流配送优化问题模型,采用了微粒群算法与局部搜索算法进行优化求解。陈久梅等[25]建立了生鲜农产品多隔室车辆路径优化模型,利用粒子群算法进行了求解。蔡浩原等[26]考虑鲜活农产品的变质函数和配送时间的惩罚函数,采用人工蜂群算法对带有时间窗的鲜活农产品冷链物流路径优化模型进行了求解。王维军等[27]采用改进的智能水滴算法对带时间窗的冷链物流配送路径优化模型进行求解冷链物流网络规划问题。任腾等[28]基于客户满意度对低碳冷链车辆规划进行建模并采用改进型蚁群算法高效求解。但上述文献在应用算法时,均未考虑不确定节点中断情景下[3, 29, 30],如何进行冷链物流网络设计。同时运用复杂模型的决策变量降维的方法上,也缺少有效的措施。因此,本文的主要创新点在于:一是响应碳减排政策,将碳排放量转化为碳税计入冷链物流网络规划的成本之中。二是考虑冷链物流中两级节点中断情况并采用改进的遗传算法求解模型。
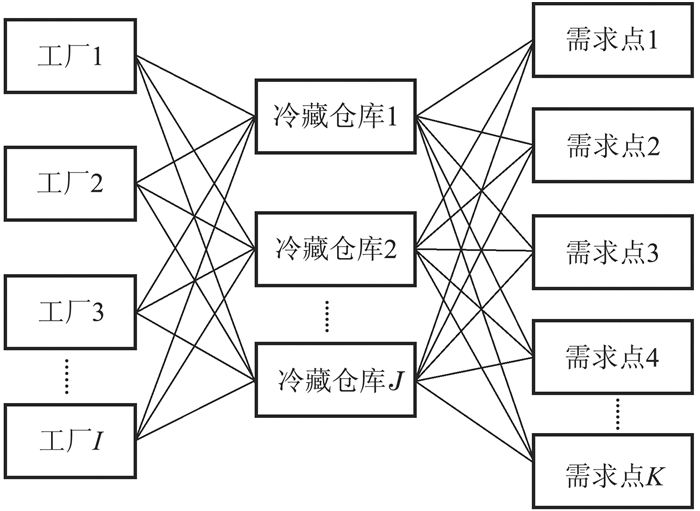
三、问题描述与模型构建 (一) 问题描述冷链物流网络一般包括工厂—冷藏仓库—需求点。如图 1所示,本文研究的是一个由I个工厂、J个冷藏仓库、K个需求点组成的三级冷链物流网络。冷链物流的起始节点是工厂,通过冷链运输至冷藏仓库,再由冷藏仓库运输到各个城市需求点。工厂和冷藏仓库的供应能力和需求能力已知,需要从候选仓库中选取合适的冷藏仓库组成冷链物流网络。从企业的角度来说,当工厂节点、冷藏仓库节点发生中断时,需求点会因为供应中断问题产生缺货成本。同时,以冷链物流网络中总成本最小化为目标,包括货损成本、碳排放成本和运输成本等。虽然碳排放成本发生在物流节点和物流运输两个环节,但实际上物流节点产生的碳排放量较于运输过程少很多,所以仅考虑物流运输产生的碳排放成本。综上,本文研究的是节点存在中断风险的情况下“选址-库存-路径”问题,具体细分为以下问题:一是确定仓库选址个数的冷链物流网络情况下,冷藏仓库应该位于何处?多大规模?二是如何合理将工厂生产的冷链产品分配给冷链仓库?如何合理规划冷链仓库到需求点的运输数量和运输路线?三是如何增强节点弹性能力,满足弹性系数要求?四是如何在冷链物流网络规划设计中融入碳排放量?
|
图 1 三级冷链物流配送网络模式 |
对于问题的相关费用、供需能力和节点失效情况的假设如下:
(1) 在冷链中心仓库选址之前,工厂建设已经完成,工厂最大供应能力和单位弹性供应成本已知。企业对于冷链仓库的固定投资费用、最大容量也已经了解,并且确定了仓库的选址个数。
(2) 企业根据多年信息系统采集到的数据,能预估需求量。
(3) 运输同一类物品,一个需求点只能由一个冷藏中心仓库提供配送。
(4) 冷藏仓库之间的需求是相互独立的,不存在互相调货的情况。
(5) 节点中断情况仅发生在工厂和冷藏仓库两个层级,同级节点只考虑单个节点失效的情况,不同层级可以同时失效,即最多两个冷链物流网络的节点发生失效。
(6) 当冷链物流销售网络节点发生中断时候,原本经过节点的产品不在节点产生流量,产品的数量会根据企业能够承受的物流网络弹性进行弹性供应、弹性储备,使物流整体仍能够正常运行。
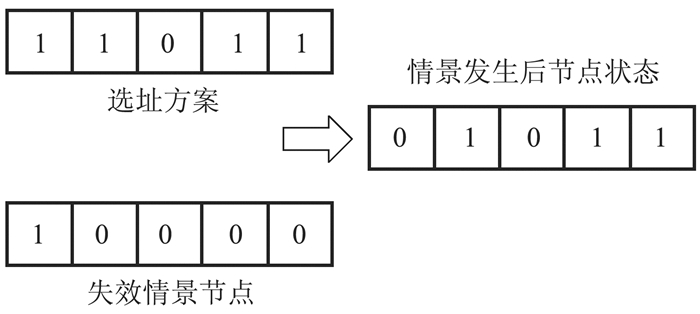
(三) 模型建立 1. 情景表示利用情景描述法来刻画发生节点中断风险的状况及其发生概率。冷链物流网络中的节点状态只有两种:中断(发生失效,由于不可抗力如发生自然灾害导致节点不能正常运转)和正常运作(不发生失效)。假定一个有2个工厂—3个冷藏仓库—k个需求点的冷链物流,那么全部的中断情景有12种:{(10100), (10010), (10001), (01100), (01010), (01001), (00100), (00010), (00001), (10000), (01000), (00000)}。各节点状态发生的概率累乘作为各情景发生的概率。选址方案、中断情景和该情景下的节点状态的关系如图 2所示。编码过程中,有5个仓库可以进行选址,0代表没有选择该仓库,1代表选择该仓库,当前选址方案为冷藏仓库1、2、4、5。中断情景编码中,1代表该节点中断发生,0代表没有中断。情景发生后只有仓库2、4和5能够正常运转。
|
图 2 选址方案、中断情景和情景发生后的节点状态的关系 |
本文涉及的符号及其含义如表 1。
| 表 1 各符号含义表 |
由于冷链物流在运输过程中使用制冷设备,导致了冷链物流的高耗能、高排放的特点,为此,本文的碳税成本考虑了运输过程和物流节点产生的碳排放。同时冷链物流需要低温冷藏货物,随时间变化应考虑运输产品的货损成本。碳排放成本发生在物流节点和物流运输两个环节[31-32],本文主要参考杨建华等[32]的研究,物流节点的碳排放产生在备选冷库中分担的固定成本和备选冷库中的变动碳排放成本,运输过程中产生的二氧化碳排放量=冷链运输环节单位产品单位距离变动碳排放×实际运输量×运输距离,再乘以碳税为冷链运输过程中的碳排放成本。
综上,以冷链物流总成本最小化为目标的冷链物流网络规划模型为:
其中
| $ \begin{gathered} \min C=C_{1}+C_{2}+C_{3}+C_{4}+C_{5}+C_{6}+C_{7}+C_{8} \\ C_{1}=\sum\limits_{s \in S} p_{s} \sum\limits_{j \in J} \sum\limits_{k \in K} Q_{j k}^{s} P\left(1-\mathrm{e}^{-\beta t_{j k}}\right) \\ C_{2}=\alpha\left(\sum\limits_{s \in S} p_{s} \sum\limits_{i \in I} \sum\limits_{j \in J} E_{d} d_{i j} Q_{i j}^{s}+\sum\limits_{s \in S} p_{s} \sum\limits_{j \in J} \sum\limits_{k \in K} E_{d} d_{j k} Q_{j k}^{s}\right) \\ C_{3}=\alpha\left(\sum\limits_{j \in J} f_{j} Y_{j}+\sum\limits_{s \in S} p_{s} \sum\limits_{i \in I} \sum\limits_{j \in J} v_{j} Q_{i j}^{s}\right) \\ C_{4}=\sum\limits_{s \in S} p_{s} \sum\limits_{i \in I} \sum\limits_{j \in J} C_{i j} Q_{i j}^{s} d_{i j}+\sum\limits_{s \in S} p_{s} \sum\limits_{j \in J} \sum\limits_{k \in K} C_{j k} Q_{j k} d_{j k} \end{gathered} $ |
| $ \begin{gathered} C_{5}=\sum\limits_{j \in J} Y_{j} C_{i f} \\ C_{6}=\sum\limits_{i \in I} C_{r i} R_{i} \\ C_{7}=\sum\limits_{j \in M} C_{r j} R_{j} Y_{j} \\ C_{8}=\sum\limits_{s \in S} p_{s} \operatorname{Soc}\left(\sum\limits_{k \in K} D_{k}^{s}-\sum\limits_{j \in J} \sum\limits_{k \in K} Q_{j k}^{s}\right) \end{gathered} $ |
| $ \text{s.t.} \quad\quad\quad\quad\quad \sum\limits_{j \in J} \sum\limits_{k \in K} Q_{j k}^{s} / \sum\limits_{k \in K} D_{k}^{s} \geqslant R, s \in S $ | (1) |
| $ \sum\limits_{j \in J} Q_{i j}^{s} \leqslant\left(\operatorname{Cap}_{i}+R_{i}\right)\left(1-y_{i}^{s}\right), i \in I, s \in S $ | (2) |
| $ \sum\limits_{\mathrm{k} \in K} Q_{j k}^{s} \leqslant\left(\mathrm{Cap}_{j}+R_{j}\right) Y_{j}\left(1-y_{j}^{s}\right), j \in J, s \in S $ | (3) |
| $ \sum\limits_{i \in I} Q_{i j}^{s}+R_{j} \geqslant \sum\limits_{k \in K} Q_{j k}^{s}, j \in J, s \in S $ | (4) |
| $ \sum\limits_{j \in J} Q_{j k}^{s} \leqslant D_{k}^{s}, k \in K, s \in S $ | (5) |
| $ X_{j k}^{s} \geqslant Q_{j k}^{s} / D_{k}^{s}, j \in J, k \in K, s \in S $ | (6) |
| $ \sum\limits_{j \in J} X_{j k}^{s} \leqslant 1, k \in K, s \in S $ | (7) |
| $ \sum\limits_{j \in J} Y_{j}=W $ | (8) |
| $ \frac{d_{j k} X_{j k} Y_{j}}{v} \leqslant h $ | (9) |
| $ Q_{i j}^{s}, Q_{j k}^{s}, R_{i}, R_{j} \geqslant 0, i \in I, j \in J, k \in K, s \in S $ | (10) |
| $ Y_{j}, X_{j k}^{s}, y_{i}^{s}, y_{j}^{s} \in\{0, 1\}, i \in I, j \in J, k \in K, s \in S $ | (11) |
目标函数代表冷链物流总成本最小化,包括冷链产品在运输过程之中的货损成本C1、运输过程碳排放成本C2、物流节点碳排放成本C3、内向和外向运输成本C4、固定成本C5、弹性供应成本C6、弹性库存成本C7和缺货损失成本C8。式(1)表示整个冷链物流网络的弹性约束;式(2)表示节点失效情景之下工厂的供应能力应该不超过其最大供应能力与弹性供应能力之和;式(3)表示每个冷藏仓库的运往需求点的运量不超过其最大容量与弹性库存之和;式(4)表示在任何节点失效的情景之下,冷藏仓库实际运往需求点的运量之和不超过其工厂实际供应量和弹性库存之和;式(5)表示任何情景冷藏仓库对需求点的实际供应量之和不超过该地需求量;式(6)表示若情景s下冷藏仓库j向需求点k提供配送,则Xjks为1,反之为0;式(7)表示每个需求点只能由一个冷藏仓库供应冷链品;式(8)表示冷藏仓库选址个数为W;式(9)表示冷链产品时效性约束;式(10)表示非负约束;式(11)表示决策变量只能取0或1,其中0代表未选中该节点,1代表选择该节点。
四、改进遗传算法由于冷链物流网络系统中存在较多约束条件、网络节点数、随机参数等因素,比传统的有容量约束固定费用的网络设计问题情况更复杂,属于NP-hard的问题。这类问题一般采用启发式算法求解。遗传算法对目标函数可微性和凸性均无要求,具有极强的鲁棒性,因此在求解组合优化问题的时候具有巨大的优势[33]。同时,本文涉及的问题较为复杂,约束太多,而且维度也高,导致可行域被分割得很零散,形成一个个孤岛,造成求解的空间复杂,正常的遗传算法很难进行有效的搜索约束条件,因此需要采用自适应的改进遗传算法进行降维。
本文采用的模拟二进制交叉算子改进遗传算法对问题决策变量进行了一定的降维。我们将问题划分成若干个较为独立的部分,通过不同的群体独立地求解这些部分,可以从不同的角度寻求和优化解决方案,有助于增加解决方案的多样性和鲁棒性[34]。模型中主要包括两类决策变量,即选址等整数变量和运输量等实数变量,本文采用的算法对问题中的所有决策变量进行了统一的实数编码进行求解。算法的求解过程主要采用模拟二进制的交叉算子,根据如下规则进行压缩:首先,在得到一个解后,不同作用的变量会被分别处理:Qij与Xij代表对应的运输量和节点,因此可根据Qij的大小将Xij压缩为0或1,代表是否进行对应的运输供应,而不用额外求解Xij;类似地,Xjk根据Qjks给出的结果,取最大的为1;求解结果方案的选址Yj是根据遗传算法(GA)给出的结果,将最大的三个对应选址地点的变量取值为1,其余转换为0,然后根据选址Yj值,对不需要进行供应的线路的对应变量Qij和Qjk取为0。其次,根据场景节点变化情况对Qij进行调整,以满足问题的约束;通过约束对Ri进行优化,Ri变为原来的值与满足约束的值之间较大的值,保证Ri满足约束;Rj根据Qij与Qjk的值,取刚刚好满足约束值和0之间较大的值,即如果约束值为负,则本身已满足约束,不需要弹性库存,则此时Rj取值为0,否则取最小能满足约束的值。
经过修改和删除这些中间变量后,目标函数的最终模型公式更清晰地显示出来,与决策变量关系也更清晰,有助于缩减问题的解决空间,降低问题规模,从而提高优化求解的效率。结合模拟二进制交叉算子的改进,遗传算法可以及时发现新的个体在种群中扩散, 使种群中个体能向最优解的方向行进,从而提高算法的搜索效用[35]。
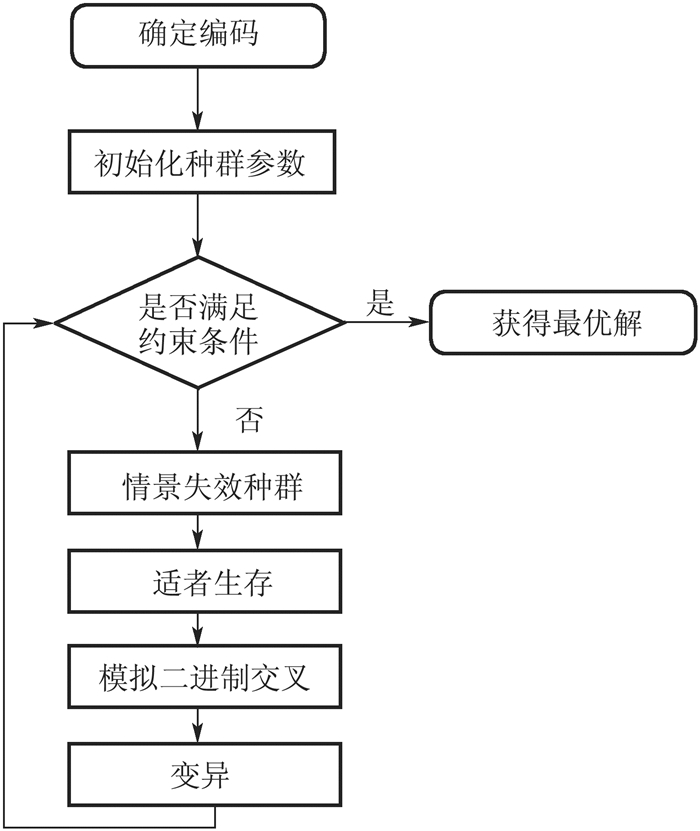
改进遗传算法流程图如图 3所示。
|
图 3 改进遗传算法流程图 |
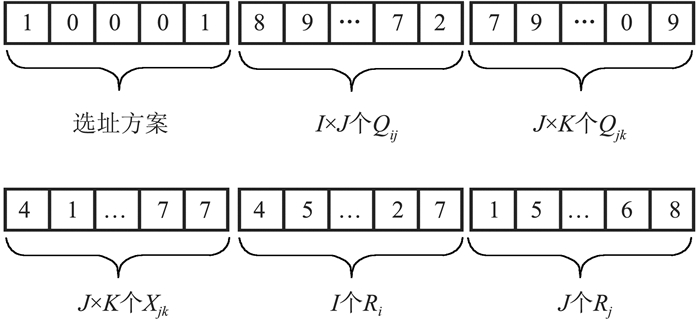
(1) 染色体的编码与初始化种群。为表达仓库选址和各节点的流量分配,以及各节点的弹性供应能力与弹性库存等信息,本文选用自然数串表达全部解空间,因此染色体的基因组成如图 4。在给定弹性系数值与需求量的前提下,各选址方案将依次选定失效情景, 产生初始化种群。在遗传算法解决过程之中,将根据以下步骤自动选址和求解供应量。
|
图 4 染色体基因组成 |
(2) 适应度的评估与选择。遗传算法采用优胜劣汰的方式对个体进行操作。在满足式(1)~式(11)约束条件情况下,利用最小化物流总成本目标函数计算染色体的适应度,来反映染色体被选中的概率。为避免遗漏,提高全局搜索能力,采用轮盘赌注策略进行选择,选择出适应度较大的作为父代。轮盘赌注选择的基本思想是要让个体被选的概率和适应度大小成正比例。假设群体大小为n,个体i的适应度为Fi,则个体被选中并遗传给下一代的概率为:
| $ P_{i}=F_{i} / \sum\limits_{i \in I} F_{i} $ |
(3) 交叉变异。交叉和变异是为了产生新个体,提升种群局部搜索能力。交叉主要是父代的基因遗传给子代,保持优良的适应度。自适应的模拟二进制交叉算子的过程:对实数编码的父代进行交叉操作,交换后位于交叉点两侧,使得父代中的染色体中模式信息在子代中得到保护。变异让基因突变以一定概率随机产生。
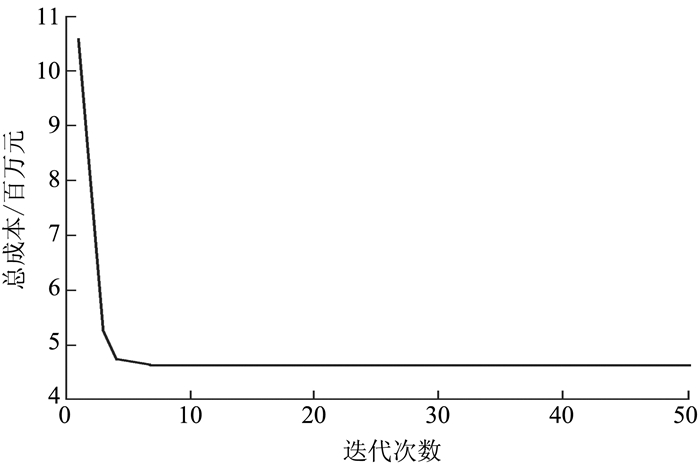
(4) 终止。若算法进行到预先设定的最大迭代数,中止算法,否则转向步骤1。迭代50次后目标函数结果如图 5所示。
|
图 5 GA最佳适应度曲线 |
S食品有限公司是国内最大的专业农产品生产企业之一。随着近年业务规模的不断扩张,在冷链物流与供应链方面存在一定的瓶颈,计划在G省重新进行冷链物流网络规划。公司目前在G省拥有两个生产工厂M1和M2,有6个冷藏仓库N1、N2、N3、N4、N5、N6,需求主要分布在L1、L2、L3、L4、L5…L21等21个区域。冷库点设立过多,产能过剩,造成物流总成本较高。企业要求的冷链物流网络弹性是0.6,各工厂的最大供应能力、失效概率、单位弹性供应能力成本如表 2所示。各冷藏仓库的固定费用、最大容量、失效概率及单位弹性备份成本如表 3所示。工厂到各冷藏仓库的距离如表 4所示。候选冷藏仓库到各需求地的距离如表 5所示。运费采用的是基于里程数的分段运费费率,单位运输费率如表 6所示。各个需求地的需求量如表 7所示。
| 表 2 各工厂的最大供应能力、失效概率、单位弹性供应能力成本 |
| 表 3 各冷藏仓库的固定费用、最大容量、失效概率及单位弹性备份成本 |
| 表 4 工厂到各冷藏仓库的距离 |
| 表 5 候选冷藏仓库到各需求地的距离 |
| 表 6 单位运输费率表 |
| 表 7 各需求地的需求量 |
考虑产品特殊性,运输过程中会产生一定货损,并且一旦发生供应中断会造成较大的缺货成本,因此对于物流网络的时效性以及弹性有较多要求。根据访谈数据,S公司目前因变质而导致的货损率达0.005%,参照国家最新出台的环境保护税税率0.01~0.10元/kg,结合相关研究成果的碳税税率数据[28, 32, 36-37],将税率价格设置为0.04元/kg,单位缺货损失成本为0.45元/kg。关于碳排放参数的范围,考虑冷链物流行业的作业能耗、转换系数以及杨建华等学者的研究[32],运输环节单位产品单位距离碳排放Ed在0.001 6~0.003 8kg CO2eq /(kg·km)随机产生,fi固定碳排放在500~1 500 kg CO2eq,vi变动碳排放为0.012~0.036 kg CO2eq/kg。
(二) 运行结果利用本文的模型和算法对案例求解,应用MATLAB软件进行编程,在个人计算机上运行25次,设立种群的个数为50,最大化迭代次数为50,交叉率为0.8,变异概率为0.2,经过50次的迭代以后得到较好的结果,算法收敛过程如图 3,求解结果如表 8。因此在R=0.6,α=0.04的情况之下,最终将N1、N4、N5作为冷藏仓库选址,优化后的总成本为4 987 738元。此时工厂M1的弹性供应能力为657 857kg,工厂M2的弹性供应能力为756 780kg,并且冷藏仓库N1、N4、N5的弹性储备能力分别为874 576kg、632 051kg和762 326kg。各项成本构成如表 9所示。同时为说明采用改进的遗传算法在有节点中断风险下的冷链物流网络规划优化问题的优越性,我们进行不同R值和α值的组合运算,挑选6种典型情境,分别是弹性系数高(R=0.8)、中(R=0.6)、低(R=0.4)和碳税税率低(α=0.04)、碳税税率高(α=0.08)的组合,对采用改进遗传算法和贪婪算法进行对比,为了能让算法重复结果,每次需要使用相同的随机数,因此我们对不同参数的问题设置了对应的固定随机数种子。两种算法求解结果见表 8,表 9为R=0.6,α=0.04时,两种算法的各项成本构成。为说明采用改进的遗传算法不同规模下的运行时间与运行效果,我们对原规模和增减20%规模下的需求进行运算,不同规模需求算法对比如表 10所示。
| 表 8 求解结果 |
| 表 9 各项成本构成 |
| 表 10 不同规模需求算法对比 |
为了说明弹性系数和碳税税率对冷链物流网络规划的影响,对弹性系数取值为0.4~1,对碳税税率取值为0.01~0.1[32]。
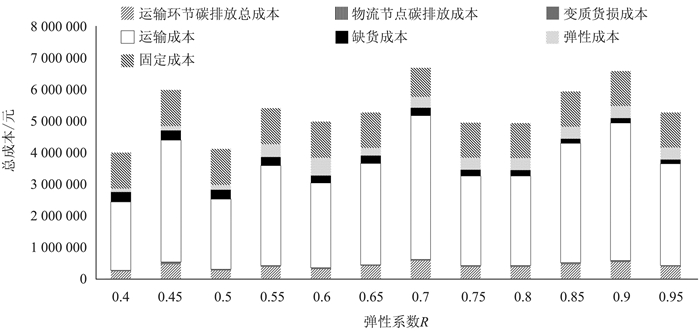
1. 弹性系数R灵敏度分析不同弹性系数下成本结构组成如图 6所示。通过各成本走势图发现:随着弹性系数的变化,其选址决策会发生相应的改变。但其带来的固定成本占总成本的比例差别不大,因此弹性系数变化和选址的失效中断的概率关系并不明显;而运输成本的波动,主要是由于选址变动以及流量再分配双重变动所致;随着弹性系数的增加,缺货成本主要呈下降趋势,这主要是由于企业面临节点中断风险时,可以动用弹性能力,满足市场需求,避免造成不良的影响。
|
图 6 不同弹性系数下成本结构组成图 |
从图 7可以看出,并不是弹性系数越小,或者弹性系数越大时总成本最小。在R为0.4和0.5的时候,冷链物流网络总成本达到最小。各个企业可以根据公司的现状和商品的性质(如缺货对市场的影响程度)来选择使总成本最低的弹性系数。
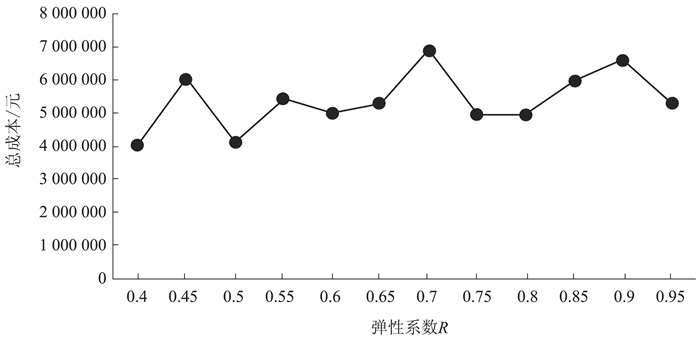
|
图 7 不同弹性系数的总成本 |
碳税税率的变化对总成本、碳排放成本、碳排放量的影响不同,不同碳税税率α下总成本及碳排放情况如表 11所示。从表 11中可以看出,在碳税价格为允许的变化区间内,碳税税率α变大,碳排放成本就增加,但是碳排放成本增加的比例小于碳税税率增加的比例。碳税税率α变大,对物流节点碳排放的影响比较小,对运输环节的碳排放成本影响比较大,运输环节的碳排放成本是碳排放总成本的主要来源,因此实施碳税政策可以有效降低碳排放量。但是总成本呈上升状,主要是由于碳排放量下降比例小于碳税上升比例,实施碳税政策给企业带来一定的成本压力,因此冷链物流网络规划时应提高运作效率,为企业减少成本。
| 表 11 不同碳税税率α下总成本及碳排放情况 |
本文在考虑节点中断风险的情境下,针对农产品冷链物流网络规划问题进行研究。主要研究结果为:一是构建了考虑多层级节点中断融入碳排放成本的冷链物流网络优化模型;二是设计了基于模拟二进制交叉算子的改进遗传算法,并用算例证明模型算法的有效可行,为企业的规划决策提供了方法和依据;三是通过对弹性系数和碳税税率的灵敏度分析发现,企业可以根据公司的现状、商品的性质来选择使总成本最低的弹性系数。同时,实施碳税政策给企业带来一定的成本压力,因此冷链物流网络规划时应提高运作效率,为企业减少成本。
本文的供应方式为单源供应,尚未考虑多源供应,未来研究可以对单源和多源供应进行对比,研究节点中断情景下的弹性系数要求是否存在差异。同时,本文的需求量是通过工厂历史数据整理的预估需求量,但是需求量是随着时间推移有所改变的,在将来的研究上可以考虑把需求不确定性加入到模型中。在算法上,可以考虑将目前运用于物流网络规划较多的粒子群算法、模拟退火法、蚁群算法在总成本与内存占用方面进行对比,找出各种算法在冷链物流网络规划模型的优劣势。
| [1] |
CHAABANE A, RAMUDHIN A, PAQUET M. Design of sustainable supply chains under the emission trading scheme[J]. International journal of production economics, 2012, 135(1): 37-49. DOI:10.1016/j.ijpe.2010.10.025 |
| [2] |
张喜才, 李海玲. 基于大数据的农产品现代冷链物流发展模式研究[J]. 科技管理研究, 2020, 40(7): 234-240. |
| [3] |
肖建华, 刘侠, 尚帅, 等. 基于节点失效和需求不确定的弹性供应链网络优化模型与算法[J]. 统计与决策, 2018, 34(17): 50-53. |
| [4] |
汪旭晖, 张其林. 基于物联网的生鲜农产品冷链物流体系构建: 框架、机理与路径[J]. 南京农业大学学报(社会科学版), 2016, 16(1): 31-41. |
| [5] |
兰伯特, 斯托克, 埃拉姆. 物流管理[M]. 张文杰, 叶龙, 刘秉镰, 译. 北京: 电子工业出版社, 2008.
|
| [6] |
罗娟娟. 基于复杂网络的生鲜农产品冷链物流网络抗毁性研究[D]. 杭州: 浙江工商大学, 2018.
|
| [7] |
BOGATAJ M, BOGATAJ L, VODOPIVEC R. Stability of perishable goods in cold logistic chains[J]. International journal of production economics, 2005, 93-94(Jan): 345-356. |
| [8] |
WANG M, ZHAO L. Cold chain investment and pricing decisions in a fresh food supply chain[J]. International transactions in operational research, 2018(4): 1-24. |
| [9] |
HSIAO Y H, CHEN M C, CHIN C L. Distribution planning for perishable foods in cold chains with quality concerns: formulation and solution procedure[J]. Trends in food science & technology, 2017, 61(3): 80-93. |
| [10] |
QIN G, TAO F, LI L. A vehicle routing optimization problem for cold chain logistics considering customer satisfaction and carbon emissions[J]. International journal of environmental research and public health, 2019, 16(4): 576-593. DOI:10.3390/ijerph16040576 |
| [11] |
梁海红. "互联网+"时代物流配送中心选址优化模型构建[J]. 统计与决策, 2016(22): 51-53. |
| [12] |
陈靖, 吴一帆. 考虑有限车辆载运能力的生鲜品集配策略研究[J]. 管理学报, 2018, 15(9): 1380-1392. DOI:10.3969/j.issn.1672-884x.2018.09.013 |
| [13] |
吴芳芸, 朱小林. 基于轴辐式理论的冷链物流网络优化模型[J]. 公路交通科技, 2019, 36(6): 144-150. |
| [14] |
袁群, 左弈. 基于改进混合遗传算法的冷链物流配送中心选址优化[J]. 上海交通大学学报, 2016, 50(11): 1795-1800. |
| [15] |
杨晓芳, 姚宇, 付强. 基于新鲜度的冷链物流配送多目标优化模型[J]. 计算机应用研究, 2016, 33(4): 1050-1053. DOI:10.3969/j.issn.1001-3695.2016.04.019 |
| [16] |
陈淑童, 王长军, 刘泳. 考虑时效与货损的多产品冷链物流配送中心选址与流量分配仿真[J]. 东华大学学报(自然科学版), 2017, 43(3): 436-442. DOI:10.3969/j.issn.1671-0444.2017.03.022 |
| [17] |
张文峰, 梁凯豪. 生鲜农产品冷链物流网络节点和配送的优化[J]. 系统工程, 2017, 35(1): 119-123. DOI:10.3969/j.issn.1001-2362.2017.01.080 |
| [18] |
杨华龙, 计莹峰, 刘斐斐. 生鲜农产品物流网络节点布局优化[J]. 大连海事大学学报, 2010, 36(3): 47-49. |
| [19] |
OSVAID A, STIRN LZ. A vehicle routing algorithm for the distribution of fresh vegetables and similar perishable food[J]. Journal of food engineering, 2008, 85(2): 285-295. DOI:10.1016/j.jfoodeng.2007.07.008 |
| [20] |
YU X. On-line ship route planning of cold-chain logistics distribution based on cloud computing[J]. Journal of coastal research, 2019, 93(spl): 1132-1137. |
| [21] |
李军涛, 路梦梦, 李都林, 等. 模糊时间窗多目标冷链物流路径规划[J]. 中国农业大学学报, 2019, 24(12): 128-135. DOI:10.11841/j.issn.1007-4333.2019.12.15 |
| [22] |
丁秋雷, 姜洋, 王文娟, 等. 鲜活农产品冷链物流配送的干扰管理模型研究[J]. 系统工程理论与实践, 2017, 37(9): 2320-2330. |
| [23] |
鲍春玲, 张世斌. 考虑碳排放的冷链物流联合配送路径优化[J]. 工业工程与管理, 2018, 23(5): 95-100. |
| [24] |
刘虹, 赵晶. 基于客户厌恶度的冷链物流配送网络优化[J]. 工业工程与管理, 2018, 23(2): 91-97. |
| [25] |
陈久梅, 周楠, 王勇. 生鲜农产品多隔室冷链配送车辆路径优化[J]. 系统工程, 2018, 36(8): 106-113. |
| [26] |
蔡浩原, 潘郁. 基于人工蜂群算法的鲜活农产品冷链物流配送路径优化[J]. 江苏农业科学, 2017, 45(15): 318-321. |
| [27] |
王维军, 罗伟. 基于改进智能水滴算法的冷链物流配送路径优化问题研究[J]. 工业工程, 2017, 20(2): 38-43. DOI:10.3969/j.issn.1007-7375.e16-2292 |
| [28] |
任腾, 陈玥, 向迎春, 等. 考虑客户满意度的低碳冷链车辆路径优化[J]. 计算机集成制造系统, 2020, 26(4): 1108-1117. |
| [29] |
马卫民, 李彬, 徐博, 等. 考虑节点中断和需求波动的可靠供应链网络设计问题[J]. 系统工程理论与实践, 2015, 35(8): 2025-2033. |
| [30] |
孟宏旭. 基于中断-应急的弹性供应链网络设计[J]. 物流技术, 2018, 37(12): 110-114. |
| [31] |
程发新, 李莉, 潘婷. 碳税政策下多目标再制造物流网络优化[J]. 工业工程与管理, 2017, 22(5): 135-141. |
| [32] |
杨建华, 郭继东, 马书刚. 碳税约束的城市冷链物流配送网络设计[J]. 工业工程, 2012, 15(5): 86-91. |
| [33] |
玄光南. 遗传算法与工程优化[M]. 北京: 清华大学出版社, 2004.
|
| [34] |
ZHANG X, DU K J, ZHAN Z H, et al. Cooperative coevolutionary bare-bones particle swarm optimization with function independent decomposition for large-scale supply chain network design with uncertainties[J]. IEEE transactions on cybernetics, 2019, 50(10): 4454-4468. |
| [35] |
付立, 窦明罡, 朱建凯, 等. 非支配排序遗传算法的改进[J]. 计算机与数字工程, 2011, 39(2): 11-15. |
| [36] |
陶帝豪, 刘蓉, 雷勇杰, 等. 基于绿色供应链的冷链物流配送路径优化[J]. 工业工程, 2019, 22(2): 89-95. |
| [37] |
王春阳, 杨斌, 朱小林. 基于低碳理念的多目标闭环供应链网络设计[J]. 工业工程, 2016, 19(3): 37-44. |
 2021, Vol. 23
2021, Vol. 23
