港口作为对外经济门户发展迅猛,在经历四代港口后,预计于2030年完成向第五代港口的转型。第五代港口即低碳港口,侧重于港口的生态功能和可持续发展的建设。目前,港口污染物的排放给沿江沿海城市带来巨大环境压力,严重影响港区空气质量和公众健康。为降低污染,我国提出了《公路水路交通运输节能环保“十三五”发展规划》《关于港口节能减排工作的指导意见》等指导纲领,而如广州、深圳等港口城市也随之出台了《广州港绿色港口建设指导意见(2014—2020年)》《深圳市绿色低碳港口建设五年行动方案(2016—2020)》等文件以控制港口污染。在针对港口污染排放的政策中,相较于碳税、碳交易等制约性措施,减排补贴政策因其激励作用,被各地政府广泛应用,因此,研究减排补贴政策在港口减排方面的应用有重要现实意义。
此外,在海上丝绸之路、粤港澳大湾区建设驱动下,港口投资主体愈发多元化,越来越多公有港口吸收私有资本以提高港口经济效益和服务水平,但公有港口在私有化的同时也会损失部分公共福利,加剧港口之间的竞争。因此,在国际化背景下公有港口是否需要私有化以及私有化水平如何才合适是政府急需思考的问题。鉴于此,本文考虑在政府减排补贴政策下,构建资本结构差异的港口竞争与合作模型,分析在港口竞争与合作时政府与港口的最优决策,以期为不同私有化水平的港口作出减排决策、吞吐量决策提供借鉴,为政府制定补贴策略、私有化策略提供参考。
一、文献综述关于港口减排的研究中,Zheng等[1]研究了不完全信息下的港口排放管制。Wang等[2]研究发现在珠三角设立排放控制区(ECA)会对港口的交通运输造成损失。Tseng等[3]对港务局及港口运营商进行访谈,发现碳税在实际运用中对港口贸易会造成负面影响。根据以上研究可以看出,碳税政策在促进港口减排的同时也具有一定局限性。Galinato等[4]研究发现, 相较碳税政策,减排补贴更能增加社会福利。曹细玉等[5]认为减排补贴比例变化对最优碳减排量、期望利润有较大的正面影响。因此,本文选择对港口减排补贴政策展开研究。
关于港口私有化的研究,许多学者发现政府选择港口私有化可以吸引更多的资本支持,提高港口竞争力。Pagano等[6]提出港口私有化可以提高港口效率和成本效用。Xiao等[7]研究发现港口所有权结构对港口吞吐量和定价有显著影响。Munim等[8]探讨了港口所有权结构转变导致的港口用户盈余和码头运营商利润现象。Choi等[9]研究发现, 在关税政策下,选择港口私有化会增加国家福利。以上研究表明港口私有化水平对社会福利、港口利润有着重要影响。而Lee等[10]研究发现港口所有权结构随出口公司竞争模式的不同而改变。Cui等[11]研究发现港口最优所有权结构随港口竞合模式的不同而改变。由此可见, 确定港口最优私有化水平是政府发展区域港口群急需解决的问题。
部分学者同时考虑了减排政策与私有化政策。例如,Meyer等[12]对比了国有企业与私有企业的碳排放水平,发现私有化会减少碳排放。Pal等[13]研究了企业古诺竞争时的碳税与私有化水平,发现最优私有化水平是部分私有化。Xu等[14]对比了古诺与伯特兰德竞争下企业的最优碳税和私有化水平,发现碳税在古诺竞争下更低,私有化水平在古诺模型下更高。Cui等[11]比较了古诺和伯特兰德竞争下,港口合作时的最优碳税和私有化水平,发现港口合作时最优私有化水平较低。以上的研究大多聚焦于古诺竞争、伯特兰德竞争模式下减排和私有化的关系。但是,在我国区域港口群中,完全私有的港口大多为小型港口;在吞吐量决策上,国有资本控股的港口有更大领导力和话语权,如山东的日照港与岚桥港。因此,本文采用斯塔克伯格博弈分析资本结构差异化港口之间的竞争与合作。
综上所述,现有的文献更多在碳交易、碳税背景下探讨减排政策对企业决策的影响。但是,港口减排成本高昂,相较于制约性措施,更需要减排补贴的“主动”激励作用,因此有必要在减排补贴背景下探讨港口决策。此外,我国港口市场发展使大量私有资本进入,私有化水平不同的港口的发展目标、运营模式有较大区别,研究港口的最优私有化水平对港口的发展定位有指导作用。因此,在新的经济形势与政策背景中,考虑减排补贴和私有化政策下港口竞合时,港口与政府最优决策是十分有必要的。本文首先构建私有港口与部分私有化的公有港口之间斯塔克伯格竞争与合作模型以及政府决策模型,求解政府最优补贴率与私有化决策、港口最优减排率与吞吐量,再对比竞争与合作模式下政府与港口最优决策差异,并分析私有化水平、港口服务差异化对最优决策的影响,最后得出相关的结论和建议。
二、问题描述与假设为了更好地描述问题,对模型涉及的参数进行说明,相关变量的符号及意义如表 1所示。
| 表 1 相关变量的符号及意义 |
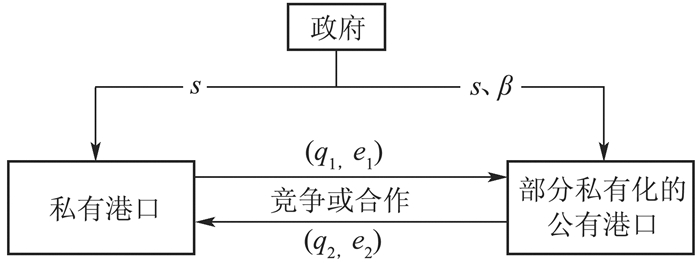
本文构建港口企业与政府两阶段决策模型。第一阶段,当地政府对港口减排补贴率以及部分私有化的公有港口的私有化水平进行决策,求解社会福利最大时的最优补贴率、私有化水平。第二阶段,在已知补贴率与私有化水平的基础上,构建私有港口与部分私有化的公有港口之间斯塔克伯格竞争与合作模型,求解两种情形下两港口的最优减排率、吞吐量。研究的问题框架如图 1所示。
|
图 1 问题框架图 |
设港口企业定价模型为:
| $ p_{1}=a-q_{1}-n q_{2} $ | (1) |
| $ p_{2}=a-q_{2}-n q_{1} $ | (2) |
其中,p1是私有港口单位吞吐量服务价格;p2是部分私有化的公有港口单位吞吐量服务价格。港口服务价格是关于港口自身吞吐量与竞争港口吞吐量的函数,由于港口效率、港区设备、港口场地等方面的不同,港口服务存在差异性,用系数n代表两港口服务差异化程度。其中,0 < n < 1,n越大则表示服务差异度越小,可替代性越大;当n=0时,则认为两港口装卸服务完全不同;当n=1时,则认为两港口装卸服务完全相同,可相互替代。
将港口装卸服务中托运人、船公司、货主等统称为港口消费者,设港口消费者的效用函数U[15]为:
| $ U\left(q_{1}, q_{2}\right)=a\left(q_{1}+q_{2}\right)-\frac{q_{1}^{2}+2 n q_{1} q_{2}+q_{2}^{2}}{2} $ | (3) |
由于消费者剩余取决于消费者效用与实际支付成本的差额,因此得到消费者剩余函数为:
| $ \mathrm{CS}=U\left(q_{1}, q_{2}\right)-q_{1} p_{1}-q_{2} p_{2}=\frac{q_{1}^{2}+2 n q_{1} q_{2}+q_{2}^{2}}{2} $ | (4) |
根据Subramaniam等[16]学者的研究,用减排量的二次方表示减排成本,并且设减排成本系数为1,得到减排成本函数为(eiqi)2/2。政府为了促进港口减排投资,提高减排量,对港口每单位减排量提供s补贴,则港口i的利润函数为:
| $ R_{i}=\left(p_{i}-c+s e_{i}\right) q_{i}-\frac{\left(e_{i} q_{i}\right)^{2}}{2} $ | (5) |
假设私有港口完全由私有资本构成,追求利润最大化,目标函数即其利润函数。部分私有化的公有港口资本结构较为复杂,包括国有资本、私有资本,运营目标多元化,既承担社会和公共责任(社会福利、就业、民生、社会影响力),又追求盈利目标,因此本文用消费者剩余表示公共目标,港口利润代表盈利目标,构建部分私有化的公有港口的综合收益函数为港口利润与消费者剩余的加权求和:
| $ G=\beta R_{2}+(1-\beta)\left(\mathrm{CS}+R_{2}\right) $ | (6) |
其中,系数β表示部分私有化的公有港口的私有化水平,即资本构成中私有资本比重,β∈[0, 1],β越大意味着部分私有化的公有港口的私有化水平越高。当β=0时,该港口为完全公有港口,此时社会公共目标与港口利润目标同等重要;当β=1时,该港口为仅以盈利为目标的完全私有港口。
根据Cui等[11]的研究,假设港口区域总碳排放量与其吞吐量大小相同;根据Poyaga-Theotoky[17]的理论,港口污染程度函数
| $ W=R_{1}+R_{2}+\mathrm{CS}-\mathrm{ED}-s\left(e_{1} q_{1}+e_{2} q_{2}\right) $ | (7) |
在竞争模型中,私有港口的决策目标是使利润收益最大化,部分私有化的公有港口决策目标是综合收益最大化。在合作模型中,私有港口与部分私有化的公有港口结合为整体,决策目标为共同收益最大化。港口与政府之间的两阶段博弈规则如下:①政府以社会福利最大化为目标决策部分私有化的公有港口的最优私有化水平、最优补贴率;②港口双方根据已知的私有化水平、补贴率决策其最优吞吐量、减排率;③竞争模式下的最优解以s上角标表示,合作模式下的最优解以c上角标表示。
(一) 斯塔克伯格竞争模型下港口与政府的最优决策 1. 港口减排率与吞吐量决策采用逆向求解法,首先考虑港口的最优减排率决策。令
| $ e_{1}=s / q_{1} $ | (8) |
| $ e_{2}=s / q_{2} $ | (9) |
由式(8)和式(9)可见,港口的最优减排率由其吞吐量与政府补贴率决定。两港口的总减排量相同,e1q1=e2q2=s。
同时,采用斯塔克伯格博弈求解港口最优吞吐量决策。由于部分私有化的公有港口受国有资本支持,在港口市场上有较大话语权,属于决策的领导方,令
| $ q_{1}= \frac{-(a-c)\left(2 n-2 \beta+\beta n^{2}-2\right)}{4 \beta-3 \beta n^{2}-n^{2}+4} $ | (10) |
| $ q_{2}=\frac{-(a-c)(n+\beta n-4)}{4 \beta-3 \beta n^{2}-n^{2}+4} $ | (11) |
将式(10)、式(11)代入式(8)、式(9)中,得到最优减排率:
| $ e_{1}=\frac{s\left(4 \beta-3 \beta n^{2}-n^{2}+4\right)}{(a-c)\left(-\beta n^{2}-2 n+2 \beta+2\right)} $ | (12) |
| $ e_{2}=\frac{s\left(4 \beta-3 \beta n^{2}-n^{2}+4\right)}{(a-c)(4-n-\beta n)} $ | (13) |
基于港口最优减排率、吞吐量决策,得到性质1:
| $ \left\{\begin{array}{l} \partial q_{1} / \partial \beta>0, \partial q_{2} / \partial \beta<0, \partial\left(q_{1}+q_{2}\right) / \partial \beta<0 \\ \partial e_{1} / \partial \beta<0, \partial e_{2} / \partial \beta>0 \\ q_{1}<q_{2}, e_{1}>e_{2}, \partial\left(q_{2}-q_{1}\right) / \partial \beta<0, \partial\left(e_{1}-e_{2}\right) / \partial \beta<0 \end{array}\right. $ | (14) |
从性质1的第1与第3点可以看出,由于国家政策、资金的扶持,部分私有化的公有港口相较私有港口而言拥有更大市场份额;但随着私有化水平提高,国有资本比重降低,其与私有港口之间逐渐趋向于完全竞争,私有港口吞吐量增加,部分私有化的公有港口吞吐量减少,两者市场份额差距缩小。
将式(10~13)代入式(1~5)中,得到港口在最优吞吐量与减排率决策下的定价函数以及目标收益函数为:
| $ p_{1}=\frac{(a+c)(2+2 \beta)-2 n(a-c)-n^{2}(c+a \beta+2 c \beta)}{4 \beta-3 \beta n^{2}-n^{2}+4} $ | (15) |
| $ p_{2}=\frac{(a-c)\left(n-\beta n+\beta n^{3}\right)+4 c+4 a \beta+(a-2 c-3 a \beta) n^{2}}{4 \beta-3 \beta n^{2}-n^{2}+4} $ | (16) |
| $ R_{1}=\frac{2(a-c)^{2}\left(\beta n^{2}+2 n-2 m-2\right)^{2}+s^{2}\left(3 \beta n^{2}-4 \beta+n^{2}-4\right)^{2}}{2\left(4 \beta-3 \beta n^{2}-n^{2}+4\right)^{2}} $ | (17) |
| $ R_{2}=\frac{2(a-c)^{2}(4-n-\beta n)\left[\beta\left(4-n-3 n^{2}+n^{3}\right)-n+n^{2}\right]+s^{2}\left(3 \beta n^{2}-4 \beta+n^{2}-4\right)^{2}}{2\left(4 m-3 \beta n^{2}-n^{2}+4\right)^{2}} $ | (18) |
| $ G=\frac{-(a-c)^{2}\left(\beta^{2} n^{2}-\beta^{2}-2 \beta n-2 n+5\right)+s^{2}\left(3 \beta n^{2}-4 \beta+n^{2}-4\right)}{6 \beta n^{2}-8 \beta+2 n^{2}-8} $ | (19) |
基于港口最优定价函数、目标收益函数,得到性质2:
| $ \left\{\begin{array}{l} \partial p_{1} / \partial \beta>0, \partial p_{2} / \partial \beta>0, p_{1}>p_{2} \\ \partial R_{1} / \partial \beta>0, \partial R_{2} / \partial \beta>0, \partial G / \partial \beta<0 \end{array}\right. $ | (20) |
从性质2的第1点可以看出,在港口竞争时,私有港口定价高于部分私有化的公有港口定价,这与实际情形相符,目前香港港单位集装箱装卸价格远高于深圳港、广州港,而且部分公有化的私有港口的私有化水平越高,两类港口的定价越高。因为当私有化水平提高时,部分私有化的公有港口吞吐量下降,港口提升服务价格以增加目标收益,而部分私有化的公有港口价格提升,私有港口也会随之加价。对于港口市场来说,公有港口私有化水平越高,货运人、承运方需要承担的服务成本更高。从性质2的第2点可以看出,提高公有港口私有化水平,两类港口的纯利润都会增加,部分私有化的公有港口综合收益会降低。即私有化水平越高,部分私有化的公有港口的社会福利性质逐渐减弱,营利性质逐渐提升。
2. 政府补贴率与私有化水平决策将式(10)~(13)代入社会福利函数(7)中,得到在港口最优决策下的社会福利W(n, β, s)为:
| $ \begin{array}{c} W(s, \beta, n)=\left\{-3 s^{2}\left(3 \beta n^{2}-4 \beta+n^{2}-4\right)^{2}+2 s(a-c)\left(3 n-2 \beta+\beta n+\beta n^{2}-6\right)\left(3 \beta n^{2}-4 \beta+n^{2}-4\right)+\right. \\ \left.(a-c)^{2}\left[\beta^{2}\left(n^{4}+2 n^{3}-5 n^{2}-2 n+4\right)+\beta\left(7 n^{3}-16 n^{2}-4 n+16\right)+n^{3}-3 n^{2}-6 n-4\right]\right\}\left(4 \beta-3 \beta n^{2}-n^{2}+4\right)^{-2} \end{array} $ | (21) |
依据社会福利最大化原则,求解港口竞争时的最优减排补贴率s,可证∂W2(s, β, n)/∂s2 < 0,即社会福利是关于补贴率的凹函数,存在最优补贴率使社会福利最大,令∂W(s, β, n)/∂s=0,求解得到:
| $ s=\frac{(a-c)\left(6+2 \beta-3 n-\beta n-\beta n^{2}\right)}{12 \beta-9 \beta n^{2}-3 n^{2}+12} $ | (22) |
将式(10)~(13)、式(22)代入环境污染程度函数ED,得到
| $ \mathrm{ED}=\frac{(a-c)^{2}\left(3 n-2 \beta+\beta n+\beta n^{2}-6\right)^{2}}{18\left(4 \beta-3 \beta n^{2}-n^{2}+4\right)^{2}} $ | (23) |
基于减排补贴率与环境污染程度函数,可以得到性质3:
| $ \partial s / \partial \beta<0, \partial \mathrm{ED} / \partial \beta<0 $ | (24) |
由式(8)、式(9)可知,环境污染程度函数可以化简为ED=q1+q2-2s。另由性质1可知,私有化会降低港口总吞吐量,而私有化同样会降低减排补贴率,因此港口私有化对环境污染的影响取决于私有化对吞吐量和减排补贴率两者之中谁有更强作用。由性质3可知,私有化水平对吞吐量的反向作用强于对补贴率的反向作用,即港口竞争时,公有港口私有化水平越高,环境污染越低。由此可见,政府私有化政策具有减少港口环境污染的效果。
将式(20)代入式(19),求解使社会福利最大的最优私有化水平。可证社会福利是关于私有化水平的凹函数,即存在最优私有化水平使得社会福利最大,令∂W/∂s=0,求解得到:
| $ \beta^{\mathrm{s}}=\frac{9 n^{2}-12}{-8 n^{3}+17 n^{2}+8 n-20} $ | (25) |
将最优私有化水平βs代入式(19)可以得到最优减排补贴率表达式为:
| $ s^{s}=\frac{(a-c)(5 n-6)}{8 n^{2}+4 n-16} $ | (26) |
再将βs、ss代入式(10)~(13),得到港口竞争时,两个港口的最优吞吐量与减排率分别为:
| $ \left\{\begin{array}{l} q_{1}^{\mathrm{s}}=\frac{(a-c)(7 n-8)}{8 n^{2}+4 n-16} \\ q_{2}^{\mathrm{s}}=\frac{(a-c)(4 n-5)}{4 n^{2}+2 n-8} \\ e_{1}^{\mathrm{s}}=\frac{5 n-6}{7 n-8} \\ e_{2}^{\mathrm{s}}=\frac{5 n-6}{8 n-10} \end{array}\right. $ | (27) |
合作时,私有港口与部分私有化的公有港口形成联盟,共享技术、设备资源,以联盟利益最大化为目标对最优减排率与吞吐量进行决策。此时两个港口同时决策,令∂(R1+G)/∂e1=0,∂(R1+G)/∂e2=0,∂(R1+G)/∂q1=0,∂(R1+G)/∂q2=0,联立得到:
| $ e_{1}=e_{2}=\frac{s(\beta+n+\beta n+1)}{a-c} $ | (28) |
| $ q_{1}=q_{2}=\frac{a-c}{\beta+n+\beta n+1} $ | (29) |
基于上述结果,可以得到性质4:
| $ \left\{\begin{array}{l} \partial q_{1} / \partial \beta<0, \partial q_{2} / \partial \beta<0 \\ \partial e_{1} / \partial \beta>0, \partial e_{2} / \partial \beta>0 \end{array}\right. $ | (30) |
从性质4可以看出,与竞争时不同,港口合作时,公有港口私有化水平增加,两港口的吞吐量都随之降低,港口群整体吞吐量下降,而减排率则会增加,即港口为了获得政府补贴,在排放量较小时,会增加减排率,政府应该调整补贴率以防止港口过度减排。
将式(28)、式(29)代入式(1)~(5)中,得到最优吞吐量与减排率决策下港口的定价函数以及目标收益函数为:
| $ p_{1}=p_{2}=\frac{a \beta+c}{\beta+1} $ | (31) |
| $ R_{1}=R_{2}=\frac{2 \beta(a-c)^{2}+s^{2}\left(2 \beta+n+1+\beta^{2}+2 \beta n+\beta^{2} n\right)^{2}}{2(1+\beta)(\beta+n+\beta n+1)^{2}} $ | (32) |
| $ G=\frac{(a-c)^{2}+s^{2}\left(2 \beta+n+1+\beta^{2}+2 \beta n+\beta^{2} n\right)}{2(1+\beta)(\beta+n+\beta n+1)} $ | (33) |
可以看出港口合作时,最优定价函数、目标收益函数与私有化水平的关系满足性质2。
2. 政府补贴率与私有化水平决策将式(28)、式(29)代入社会福利函数W中,得到合作时港口最优决策下社会福利函数为:
| $ W(n, \beta, s)=\frac{(a-c)^{2}\left[2 \beta^{2}\left(2 n^{4}+4 n^{3}-9 n^{2}-5 n+8\right)+9 \beta\left(3 n^{3}-6 n^{2}-4 n+8\right)+3\left(n^{3}-6 n+8\right)\right]}{3\left(4 \beta-3 \beta n^{2}-n^{2}+4\right)^{2}} $ | (34) |
W(n, β, s)关于s的一阶导数为∂W(n, β, s)/∂s=
| $ s=\frac{2(a-c)}{3(\beta+n+\beta n+1)} $ | (35) |
将式(28)、式(29)、式(35)代入环境污染函数ED中,得到:
| $ \mathrm{ED}=\frac{2(a-c)^{2}}{9(\beta+n+\beta n+1)^{2}} $ | (36) |
用港口合作时的环境污染函数以及政府补贴率对私有化水平求导,发现环境污染与减排补贴率与私有化水平同样为负相关,即港口合作时,政府提高公有港口私有化水平同样可以减少环境污染。
将式(28)代入式(27)中,求解社会福利最大时的港口最优私有化水平,可证社会福利是关于私有化水平的凹函数,即存在最优私有化水平使得社会福利最大,令∂W/∂s=0,求解得到:
| $ \beta^{\mathrm{c}}=\frac{2}{3 n+3} $ | (37) |
将式(37)代入式(35),得到港口合作时的最补贴率为
| $ q_{1}^{\mathrm{c}}=q_{2}^{\mathrm{c}}=\frac{3(a-c)}{3 n+5}, e_{1}^{\mathrm{c}}=e_{2}^{\mathrm{c}}=2 / 3 $ | (38) |
比较竞争与合作时港口最优吞吐量与减排率,得到命题1。
命题1:对于任意的0 < b < 1,恒存在以下关系:
| $ \left\{\begin{array}{l} q_{1}^{\mathrm{c}}>q_{1}^{\mathrm{s}}, \quad q_{2}^{\mathrm{s}}>q_{2}^{\mathrm{c}}, \quad\left(q_{1}+q_{2}\right)^{\mathrm{c}}>\left(q_{1}+q_{2}\right)^{\mathrm{s}} \\ e_{1}^{\mathrm{s}}>e_{1}^{\mathrm{c}}, \quad e_{2}^{\mathrm{c}}>e_{2}^{\mathrm{s}}, \quad\left(e_{1}+e_{2}\right)^{\mathrm{s}}>\left(e_{1}+e_{2}\right)^{\mathrm{c}} \end{array}\right. $ | (39) |
命题1表明,在吞吐量方面,港口合作时,私有港口吞吐量增加,部分私有化的公有港口吞吐量减少,即合作时,私有港口依靠部分私有化的公有港口所拥有的资源、技术和资金可以扩大自己的市场份额,部分私有化的公有港口市场份额相应减小。但是对于港口群总体而言,合作模式下港口群可以获得更大的吞吐量。在减排率方面,当港口竞争时,减排补贴政策对私有港口有更高的激励作用;在港口合作时,减排补贴政策对部分私有化的公有港口有更高的激励作用。此外,对比港口吞吐量和减排率,可以发现,当政府提供减排补贴后,港口吞吐量较低时,减排率相对较高,此时港口存在减排过度的风险。
(二) 港口目标收益比较将竞争与合作模式下港口与政府关于减排率、吞吐量、私有化水平、补贴率的最优决策分别代入式(4)、式(5)中,得到两港口的利润函数以及部分私有化的公有港口综合收益函数如下:
| $ \left\{\begin{array}{l} R_{1}^{\mathrm{s}}=\frac{(a-c)^{2}\left(123 n^{2}-284 n+164\right)}{32\left(2 n^{2}+n-4\right)^{2}} \\ R_{1}^{\mathrm{c}}=\frac{8(a-c)^{2}}{(3 n+5)^{2}} \end{array}\right. $ | (40) |
| $ \left\{\begin{array}{l} R_{2}^{\mathrm{s}}=\frac{(a-c)^{2}\left(16 n^{3}+69 n^{2}-236 n+156\right)}{32\left(2 n^{2}+n-4\right)^{2}} \\ R_{2}^{\mathrm{c}}=\frac{8(a-c)^{2}}{(3 n+5)^{2}} \end{array}\right. $ | (41) |
| $ \left\{\begin{array}{l} G^{s}=\frac{(a-c)^{2}\left(543 n^{4}-1384 n^{3}+205 n^{2}+1732 n-1108\right)}{16\left(7 n^{2}-10\right)\left(2 n^{2}+n-4\right)^{2}} \\ G^{c}=\frac{(a-c)^{2}(9 n+11)}{(3 n+5)^{2}} \end{array}\right. $ | (42) |
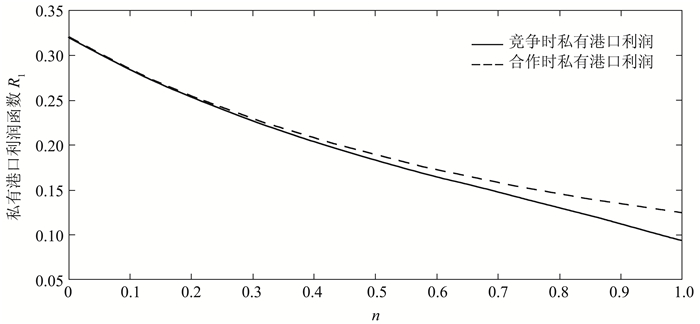
去掉公共部分(a-c)2后,对竞争与合作模式下私有港口的利润、综合收益对比,竞争与合作模式下私有港口与部分私有化的公有港口利润对比分别如图 2、图 3所示,竞争与合作模式下部分私有化的公有港口综合收益对比如图 4所示。
|
图 2 竞争与合作模式下私有港口利润对比 |
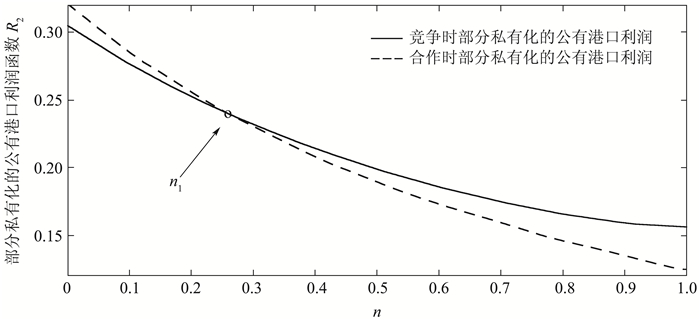
|
图 3 竞争与合作模式下部分私有化的公有港口利润对比 |
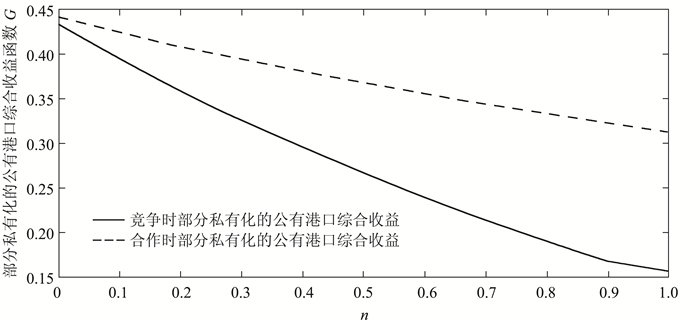
|
图 4 竞争与合作模式下部分私有化的公有港口综合收益对比 |
命题2:(1)竞争与合作模式下两港口利润对比:对于任意的0 < n < 1,恒有R1c>R1s;存在n1∈(0, 1),当0 < n < n1时,有R2c>R2s;当n1 < n < 1时,有R2s>R2c。
(2) 竞争与合作模式下,部分私有化的公有港口综合收益对比:对于任意的0 < n < 1,恒有Gc>Gs。
比较私有港口与部分私有化的公有港口在竞争与合作下的目标收益R1、G,可以看出当港口服务可替代程度较低时,各个港口的目标收益在竞争与合作模式下相差较小;但随着港口服务可替代程度的增加,两类港口在合作模式下的目标收益逐渐高于竞争时的目标收益,服务可替代程度越大,差额越大。即当港口服务可替代程度较小时,对港口目标收益的影响较小;然而当服务可替代程度较大时,两类港口的目标市场高度重叠,面临着严重的同质化竞争,此时采取合作模式可以减少港口之间的恶性竞争,实现港口规模经济,同时增加两港口的目标收益。
比较部分私有化的公有港口在竞争与合作下的纯利润R2,可以看出当港口服务可替代程度较小时,部分私有化的公有港口采取合作会获得更高的纯利润,但随着服务可替代程度的增加,部分私有化的公有港口在竞争时的纯利润逐渐高于合作时的纯利润。这说明,由于部分私有化的公有港口通常而言规模更大,受国有资本、地方政府支持,因此在激烈的竞争中,相较于私有港口有更大的竞争力,并且可以获得更高的利润。这点与深圳港和香港港的实际情况相符,随着深圳港港口集装箱码头的完善,服务质量与水平提高,与香港港之间的同质化竞争越发严重,而在竞争中香港港的吞吐量增长率持续下降,在2018年的世界港口排名中也落后于深圳港。
对比部分私有化的公有港口利润R2及其综合收益G,可以看出当服务可替代程度较小时,港口之间由竞争关系转变为合作关系会促使部分私有化的公有港口的纯利润与公共收益都增加;当港口服务可替代程度较大时,竞争关系向合作关系的转变会促使部分私有化的公有港口牺牲其纯利润,以获得更高的公共收益。这说明,在港口服务差异较大时,港口竞争缓和,此时选择合作,对于部分私有化的公有港口而言可以吸收私有港口更灵活的运营管理方式,提高港口服务效率,从而增加其纯利润和综合收益;在港口服务差异较小时,港口竞争激烈,部分私有化的公有港口更具备竞争优势,此时选择合作,对于部分私有化的港口而言需要共享其在资金、资源、信息以及货源方面的优势,导致其纯利润下降,但与此同时结成的港口联盟总吞吐量会得到提高,有利于社会公益性收益的增加,从而促使其综合收益提高。因此,对部分私有化的公有港口来说,港口服务可替代程度小时,合作是最好选择;在港口服务差异化大时,以纯利润为导向的最优选择是竞争,以综合收益为导向的最优选择是合作。
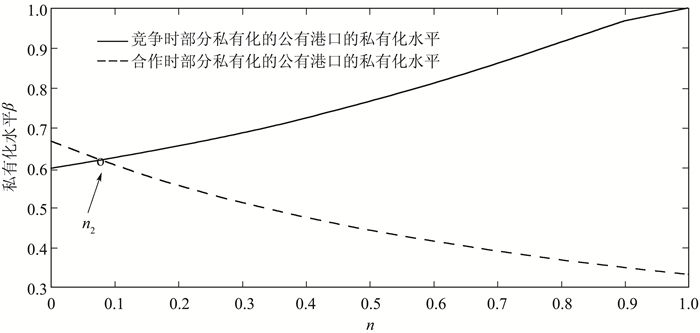
(三) 最优私有化水平比较去掉βs、βc表达式公共部分(a-c)2后,比较竞争与合作时部分私有化的公有港口的最优私有化水平,如图 5所示,得到命题3。
|
图 5 竞争与合作模式下部分私有化的公有港口的私有化水平对比 |
命题3:(1)在港口竞争时,对任意的0 < n < 1,有β∈(0.6, 1),且存在∂βs/∂n>0;
(2) 在港口合作时,对任意的0 < n < 1,有β∈(0.3, 0.7),且存在∂βc/∂n < 0;
(3) 对比港口竞争与合作时,存在n2∈(0, 1),当0 < n < n2时,有βc>βs;当n2 < n < 1时,有βs>βc。
命题3表明,在私有港口与部分私有化的公有港口竞争时,政府为了使社会福利达到最大,最优选择是高度私有化公有港口,并且随着服务可替代程度的增加,私有化水平增加,当两港口服务完全可替代时,部分私有化的公有港口转变为完全私有港口。在私有港口与部分私有化的公有港口合作时,政府最优选择是部分私有化的公有港口,并且随港口服务可替代度的增加,私有化水平降低,部分私有化的公有港口从较高私有化向较高公有化转变。
港口由竞争关系转变为合作,在港口服务可替代程度小于某一定值时,部分私有化的公有港口会小幅度增加私有化水平;在港口服务可替代程度高于某一定值时,部分私有化的公有港口会大幅度降低私有化水平,高度公有化。
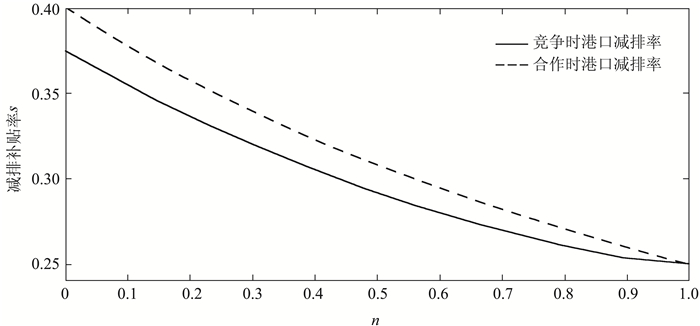
(四) 最优补贴率比较去掉ss、sc表达式公共部分(a-c)2后,比较港口竞争与合作情形下政府最优补贴率,如图 6所示,得到命题4。
|
图 6 竞争与合作模式下政府补贴率对比 |
命题4:对于任意的0 < n < 1,恒有sc>ss,且满足∂sc(ss)/∂n < 0。
命题4表明,港口合作时的减排补贴率,高于港口竞争时的补贴率。由命题1可知,在港口合作时,港口群的总吞吐量增加,环境污染越严重,越需要提供更高的减排补贴率以刺激港口增加减排率。此外,从图 6中还可以看出,当港口服务可替代程度较低时,无论港口是竞争或合作,政府提供的补贴率都较高;当港口服务可替代程度较高时,政府提供的补贴率都较低,因为服务可替代程度越高时,两港口之间的竞争越激烈,吞吐量整体减小,环境污染随之降低,此时政府不需要投入较高的补贴激励。
(五) 环境污染比较将不同模式下港口最优私有化水平代入式(20)、式(29)中,得到港口环境污染程度函数如下:
| $ \left\{\begin{array}{l} \mathrm{ED}^{\mathrm{s}}=\frac{(a-c)^{2}(5 n-6)^{2}}{32\left(2 n^{2}+n-4\right)^{2}} \\ \mathrm{ED}^{\mathrm{c}}=\frac{2(a-c)^{2}}{(3 n+5)^{2}} \end{array}\right. $ | (43) |
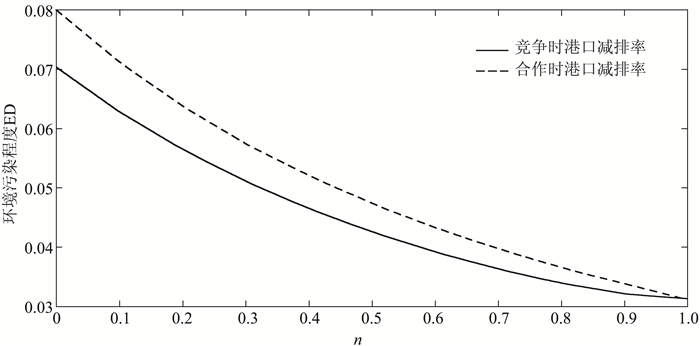
去掉公共部分(a-c)2后,对比竞争与合作模式下港口关于服务可替代程度的环境污染程度函数,如图 7所示,得到命题5。
|
图 7 竞争与合作模式下港口关于服务可替代程度的环境污染程度对比 |
命题5:对于任意的0 < n < 1,恒有EDc>EDs,且满足∂EDc(EDs)/∂n < 0。
命题5表明,港口在合作时的环境污染相较于竞争时更高。对比命题4可知,环境污染的变化与补贴率的变化一致,即在港口合作或者港口服务可替代程度较低时,港口群总吞吐量较高促使污染排放增加;在港口竞争或者服务可替代程度较高时,港口群总吞吐量较低,因此污染排放也相对较低。
五、结论与建议本文以私有港口与部分私有化的公有港口组成的混合垄断市场为研究对象,构建了两港口斯塔克伯格竞争与合作情形下,港口与政府的两阶段决策模型,比较两种情形下港口最优决策、政府最优决策、港口目标利润,研究了私有化水平、港口服务可替代程度对港口与政府决策的影响。研究得到如下结论与建议:
第一,就减排补贴政策而言,无论港口是处于竞争还是合作情形下,政府提供减排补贴都是促进港口增加减排力度的有效措施。但是,区域政府对减排补贴率的设置应该根据港口竞争或合作、港口服务可替代程度高或低等不同情形进行灵活调整。在港口合作时,港口总吞吐量相对增加,此时政府需要提高减排补贴率,促进港口减排力度;当港口之间服务可替代程度较低时,政府同样也需要进一步提高补贴率以限制港口排放。此外,政府还需要注意的是,当港口吞吐量较低时,实际产生的污染较小,此时为了防止港口减排过度不宜采用减排补贴激励政策,应该考虑碳税、碳交易等约束性政策。因此类似于广州港、深圳港等高吞吐量和高碳排放的港口适宜采用减排补贴政策;而对于一些内河港口,更适宜采取约束措施。
第二,就私有化政策而言,在一定范围内的私有化可以提高私有港口与部分私有化的公有港口的纯利润,使社会总福利增加。在港口竞争与合作的不同情形下,为了达到最大社会福利,政府对部分私有化的公有港口最优私有化水平有不同选择。竞争时,政府最优选择是高度私有化公有港口;而合作时,随着服务可替代程度的增加,政府对公有港口私有化水平的最优选择应该从较高私有化向较高公有化转变。在实际应用中,深圳港与香港港都是定位于面向集装箱服务的国际性枢纽港,存在激烈的竞争,深圳政府为了扩大竞争优势,不断招商引资,提高深圳港部分港区与码头的私有资本占比。而随着航运联盟的出现、港口群之间竞争的加剧,粤港澳大湾区港口群为了争取更多船舶挂靠,港口群内不同港口之间开始展开较频繁地合作,此时为了进一步提高社会福利,深圳政府应该考虑适当降低深圳港的私有资本占比,或者考虑推动深圳港开展其他类货品的装卸服务业务,以增加与香港港之间服务的差异性。
第三,就港口竞争与合作而言,当港口服务可替代程度较小时,合作与竞争对于私有港口没有较大区别,而部分私有化的公有港口有更高的合作意愿,此时部分私有化的公有港口可以通过给予私有港口一定的报酬或者资源扶持,激励其进行合作。当港口服务可替代程度较大时,私有港口与部分私有化的公有港口选择合作可以得到更高的目标收益。
| [1] |
ZHENG S Y, GE Y E, FU X W. Modeling collusion-proof port emission regulation of cargo-handling activities under incomplete information[J]. Transportation research part b, 2017, 104: 543-567. DOI:10.1016/j.trb.2017.04.015 |
| [2] |
Wang C X, Wang W, Huang R B. Supply chain enterprise operations and government carbon tax decisions considering carbon emissions[J]. Journal of cleaner production, 2017, 152: 271-280. DOI:10.1016/j.jclepro.2017.03.051 |
| [3] |
TSENG P H, PILCHER N. Exploring the viability of an emission tax policy for ships at berth in Taiwanese ports[J]. International journal of shipping and transport logistics, 2016, 8(6): 705-772. DOI:10.1504/IJSTL.2016.079289 |
| [4] |
GALINATO G I, YODER J K. An integrated tax-subsidy policy for carbon emission reduction[J]. Resource and energy economics, 2010, 32(3): 310-326. DOI:10.1016/j.reseneeco.2009.10.001 |
| [5] |
曹细玉, 张杰芳. 碳减排补贴与碳税下的供应链碳减排决策优化与协调[J]. 运筹与管理, 2018, 27(4): 57-61. |
| [6] |
PAGANO A M, WANG G W Y, ONESIMO V, et al. Impact of privatization on port efficiency and effectiveness: results from Panama and US ports[J]. Maritime policy & management, 2013, 40(2): 100-115. |
| [7] |
XIAO Y B, NG ADOLF K Y, YANG H J. An analysis of the dynamics of ownership, capacity investments and pricing structure of ports[J]. Transport reviews, 2012, 32(5): 629-652. DOI:10.1080/01441647.2012.709888 |
| [8] |
MUNIM Z H, SAEED N, LARSEN O I. "Tool port" to "landlord port": a game theory approach to analyse gains from governance model transformation[J]. Maritime policy & management, 2019, 46(1): 43-60. |
| [9] |
CHOI K, LIM S. Tariff protection and port privatization: an import-competing approach[J]. Maritime economics & logistics, 2018, 20(2): 228-252. DOI:10.1057/s41278-016-0004-1 |
| [10] |
LEE D J, LIM S, CHOI K. Port privatization under Cournot vs.Bertrand competition: a third-market approach[J]. Maritime policy & management, 2017, 44(6): 761-778. |
| [11] |
CUI, HAN, NOTTEBOOM, et al. Modelling emission control taxes in port areas and port privatization levels in port competition and co-operation sub-games[J]. Transportation research part D, 2017, 56: 110-128. DOI:10.1016/j.trd.2017.07.030 |
| [12] |
MEYER A, PAC G. Environmental performance of state-owned and privatized eastern European energy utilities[J]. Energy economics, 2013, 36(3): 205-214. |
| [13] |
PAL R, SAHA B. Pollution tax, partial privatization and environment[J]. Resource and energy economics, 2015, 40: 19-35. DOI:10.1016/j.reseneeco.2015.01.004 |
| [14] |
XU L, CHO S, LEE S H. Emission tax and optimal privatization in Cournot-bertrand comparison[J]. Economic modelling, 2016, 55: 73-82. DOI:10.1016/j.econmod.2016.02.008 |
| [15] |
张伟, 仲伟俊, 梅姝娥. 伯川德竞争下的混合寡头研发投入[J]. 系统管理学报, 2016, 25(4): 705-710. |
| [16] |
SUBRAMANIAM R, GUPTA S, TALLBOT B. Compliance strategies under permits for emissions[J]. Production and operations management, 2007, 16(6): 763-779. |
| [17] |
POYAGA-THEOTOKY J A. The organization of R&D and environmental policy[J]. Journal of economic behavior & organization, 2007, 62(1): 63-75. |
 2021, Vol. 23
2021, Vol. 23
