自20世纪70年代以来,能源在经济增长中的关键作用受到普遍的关注和重视。经济增长过程中环境问题的日益突出,当代面临的能源问题不只是如何为经济增长提供安全的能源供应,更在于如何控制传统能源大量燃烧伴随的温室气体排放。技术的进步增强了利用可再生能源的潜力,作为传统能源的替代品,可再生能源因其清洁、低碳、可持续的优势逐渐成为能源供应体系的重要组成部分。根据2019版《2050年世界与中国能源展望》的预测,清洁能源将逐渐代替煤炭,2050年清洁能源占比预计达到56%①。
① 数据来源:https://www.sohu.com/a/358633090_680938。
与传统能源不同,可再生能源利用须具备较好的地理条件,然而中国经济增长较快的地区发展可再生能源的地理条件往往并不优越,因此能源供应地区和能源需求地区常常在空间上呈现分离的格局。以中国电力产业为例,东部地区为中国经济增长较快的地区,电力需求也相应高于西部地区,而可再生能源电力生产主要集中在四川、贵州、内蒙古等西部地区,造成电力需求和电力产出空间分布不均衡。因此,中国建立了完善的跨省电网系统加强地区间电力生产和经济增长的联系。改革开放以来,电力短缺一度是制约中国经济发展的瓶颈,国家也长期实行“经济要发展,电力要先行”的战略;但近年来中国经济转型期间电力需求增长明显放缓,导致部分地区可再生电力项目集中投产的情况下出现较为严重的弃风、弃水现象。可再生能源和传统能源的电力投资须充分理解电力生产和经济增长间的动态关系,才可以避免电力产业发展中的电力不足和电力过剩两种极端情况,使电力生产与经济增长相匹配。目前,较少有研究测算地区间电力生产与经济增长的动态关系。本文主要提出并回答以下问题:中国各地区内传统能源、可再生能源电力生产与经济增长是如何相互影响的?地区间不同能源形式的电力生产与经济增长具有相互影响关系吗?近年来已经有学者围绕可再生能源与经济增长关系问题开展了研究[1],本文研究的问题也是能源与经济增长动态关系这一经典经济问题的延续。
与既有研究相比,本文主要贡献除了实证模型的创新,还包括以下几点:第一,在地区内和地区间层面考察了电力生产与经济增长的动态关系。中国已经建立了世界最大规模的电力输送系统,尤其是“西电东输”国家工程加强了跨省供电的能力,使地区间电力生产与经济增长联系更紧密。本文借助广义脉冲函数得出了“西电东输”主要地区间电力和经济增长相互的脉冲响应。第二,与大多实证研究选择电力消费变量不同,本文测算了电力生产与经济增长的相互影响。中国“西电东输”工程和较为完善的跨省电网系统使各地区的电力生产并不完全用于该地区内消费,电力生产和消费与经济增长存在不同的因果关系。电力输送中可能存在的偷电现象和不可避免的电力损失在电力消费数据中无法体现[2],所以使用电力生产变量能够更准确地反映电力生产消耗的能源。第三,本文将电力生产划分为可再生能源电力生产和传统能源电力生产。可再生能源电力生产主要包括水电、风电、太阳能光伏发电、生物质发电、地热发电等形式,传统能源电力生产则以火电生产代表。通过考察可再生能源、传统能源电力生产与经济增长的动态影响,也能够为中国电力生产结构调整提供支持。
二、文献回顾为了实现经济、能源、生态和谐发展的目标,各地区政府部门不仅要知道如何有效地控制传统能源消费比重,还必须考虑可再生能源的兴起是否会抑制经济增长,而测算传统能源、可再生能源电力产出与经济增长的动态关系为政府决策提供了有效的工具。能源与经济增长的关系主要围绕四种假说进行,即保护假说(经济增长单向影响能源)、增长假说(能源单向影响经济增长)、反馈假说(经济增长与能源相互影响)、中立假说(经济增长与能源无显著影响关系)。美国学者最早作了开拓性的研究,使用美国1947—1974年的年度数据,发现经济增长对能源消费的因果关系是单向的[3]。此后,大批学者检验了不同国家、不同时期的能源和经济增长的关系,然而研究结果不尽相同。目前,广泛使用的计量方法包括向量误差修正模型(VEC)和向量自回归模型(VAR)及它们的扩展模型、格兰杰因果检验、协整分析方法等。实证方法的不同,可能是导致研究结论差异的主要原因。
在能源消费与经济增长关系研究中,Zhang等[4]使用中国1960—2007年的数据通过向量自回归模型分析,结果显示经济增长具有对能源消费存在单向因果关系;Wang等[5]应用面板误差修正模型(PVEC)对中国28个省份1995—2007年的数据实证研究,发现能源消费与经济增长存在双向因果关系;也有学者使用自回归分布滞后模型(ARDL)发现中国能源消费对经济增长的因果关系是单向的[6]。近年的研究逐渐关注清洁能源、可再生能源消费与经济增长的关系。林美顺[7]使用联立方程模型发现中国提高清洁能源消费比例对经济增长存在正的内生效应和负的外生效应;Bao等[1]以中国各省为研究对象,使用面板模型分析了可再生能源消费与经济增长因果关系存在空间异质性,认为53%的省份可再生能源消费与经济增长不存在因果关系。
在整体电力消费与经济增长关系的研究中,由于中国拥有世界最大规模的电力生产系统,较多实证研究针对中国进行。例如,Yuan等[8]把1978—2004年中国用电量与实际GDP数据进行协整分析,发现用电量存在对GDP的单向因果关系。李强等[9]基于1990—2011年中国省际面板数据,使用VEC模型研究,结果显示短期内中国东、西部地区都存在经济增长到电力消费的单向因果关系,长期内西部地区经济增长与电力消费因果关系是双向的,东部地区只存在电力消费到经济增长的单向因果关系。Lin等[10]使用结构向量自回归模型(SVAR)研究,结果发现中国电力消费和经济增长出现不一致只是全球经济危机期间的暂时现象,并没有改变中国电力消费与经济增长的因果关系。Lin等[11]应用面板向量自回归模型(PVAR)发现电力消费与经济增长的关系存在区域异质性,大部分地区经济增长与电力消费因果关系是双向的。曹俊文等[12]使用对数平均迪氏指数分解法(LMDI)发现细分产业电耗强度不同是中国电力消费与经济增长相偏离的主要原因。
可再生能源电力消费与经济增长关系的实证研究对象从单一国家或地区转向多个国家或地区,研究结论差异明显。Apergis等[13]通过构建面板误差修正模型对多个国家进行研究发现:中美洲6个国家可再生能源消费与经济增长之间存在双向因果关系。随后,他们又对16个新兴市场经济体进行分析,发现经济增长对可再生能源电力消费存在短期单向因果关系和长期双向因果关系,传统能源电力消费与经济增长在短期和长期均存在双向因果关系[14]。Apergis等[15]又对世界水电消费量前列的巴西、加拿大、中国等10个国家1965—2012年的数据进行分析,发现1988年以前人均GDP对水电消费存在单向因果关系,1988年以后则存在双向因果关系。
变量选择和实证模型不同是现有实证研究结果差异的重要原因。变量选择方面,现有研究多从能源消费角度进行实证研究,生产角度的研究较少,故加入生产角度的实证研究可增加实证结果说服力。分析已有研究的实证模型,可以发现面板数据模型正在逐渐成为实证研究的主流,现有研究大多应用某一种面板模型建模,如面板向量自回归模型、面板误差修正模型等。这些模型都未考虑当期值的影响,不能识别投资和人力的结构性影响,而中国在固定资产的大力投入导致电力与经济增长短期不一致[10],故本文将面板模型与结构向量自回归模型结合起来。同时,已有研究大多忽略了能源价格对电力和经济增长的影响。已有学者发现了能源价格、清洁能源消费、人均GDP之间的协整关系[16],电力与经济增长关系的实证研究中能源价格是一个重要变量,对经济增长、能源都发挥了非线性的动态影响。国内研究中,已有学者应用全局向量自回归模型测算了中国省际能源消费对经济增长动态影响[17], 本文在此基础上进一步构建半参数结构全局向量自回归模型(SSGVAR)测算电力生产与经济增长的相互影响以满足上述各方面的计算要求。
三、模型构建、估计方法和数据说明 (一) 模型构建1.模型优势
本文使用的半参数结构全局向量自回归模型是全局向量自回归模型、结构向量自回归模型与半参数模型的结合,具有多个模型的优势。具体如下:
首先,全局向量自回归模型从向量自回归模型发展而来的,向量自回归模型是能源与经济增长因果关系的实证研究中常用的模型之一,对比向量自回归模型可以更清楚地看出全局向量自回归模型的优势。尽管向量自回归模型可以用于测算多个宏观经济变量间是否存在格兰杰因果关系,但是它的缺点也很明显。应用向量自回归模型计算多个经济体构成的面板数据时,由于存在维度限制往往很难进行计算。全局向量自回归模型的通过空间权重矩阵对外部经济体的变量进行加权求和,有效地避免了未知参数过多给模型估计带来的困难。
第二,半参数结构全局向量自回归模型不仅可以计算地区内部变量冲击的相互影响,而且可以计算地区间主要变量的影响和全局变量对所有地区变量的共同影响。具体计算方法通过广义脉冲响应函数完成,广义脉冲响应函数是早期主要用于分析向量自回归模型,以避免变量顺序对结果的干扰[18]。通过把广义脉冲响应函数用于半参数结构全局向量自回归模型,可以考察地区内部主要变量受到冲击后,该地区内和地区之间主要变量之间的脉冲响应,这样就可以从时间、空间两个维度考察变量间的影响关系,这也是向量自回归模型不具备的优势之一。对于全局向量,全局向量自回归模型也可计算出地区主要变量与全局变量间的脉冲响应关系,但半参数结构全局向量自回归模型更进一步结合非参数技术刻画了全局变量与其他变量的非线性关系,具体方法为应用半参数方法得出全局变量对主要变量的偏导图。
第三,全局向量自回归模型没有给出主要变量之间当期相关关系的确切形式,这些当期相关关系隐藏在误差项相关结构中无法解释,这一缺点可通过结合结构向量自回归模型来克服。通过将结构向量自回归模型与全局向量自回归进行结合,可以估计固定资产存量和劳动力对经济增长和电力产出的结构冲击。
2.建立模型
为了考察可再生能源、传统能源电力生产与经济增长的因果关系,本文在使用最为普遍的两要素生产函数基础上增加可再生能源电力生产和传统能源电力生产变量,构成生产模型如下:
| $ {Y_{it}} = f\left( {{\rm{R}}{{\rm{E}}_{it}},{\rm{NR}}{{\rm{E}}_{it}},{K_{it}},{L_{it}}} \right) $ | (1) |
其中,i表示省份;t表示时间;Yit表示省份i在时间t的实际生产总值,单位为亿元;RE表示可再生能源电力发电量;NRE表示传统能源电力发电量,单位均为亿千瓦时;K表示实际资本存量,单位为亿元;L表示劳动力资本,单位为千万人。
结合全局向量自回归、结构向量自回归模型和半参数模型的构建方法,本文构造每个省份的半参数结构向量自回归模型(SSVARX*)不仅包括式(1)的主要变量,还增加了全局变量和非参项。具体模型如下:
| $ \begin{array}{l} \Delta {Y_{it}} = {a_{1i}} + {b_{12i}}\Delta {\rm{R}}{{\rm{E}}_{it}} + {b_{13i}}\Delta {\rm{NR}}{{\rm{E}}_{it}} + {b_{14i}}\Delta {K_{it}} + {b_{15i}}\Delta {L_{it}} + {\beta _{1i}}\Delta {Y_{i,t - 1}} +\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\theta _{1i}}\Delta Y_{it}^* + {\vartheta _{1i}}\Delta Y_{i,t - 1}^* + {r_{1i}}{\rm{C}}{{\rm{A}}_t} + {\gamma _{1i}}{\rm{C}}{{\rm{A}}_{t - 1}} + {g_{1i}}\left( {{\rm{OI}}{{\rm{L}}_{it}}} \right) + {\varepsilon _{1it}} \end{array} $ | (2) |
| $ \begin{array}{l} \Delta {\rm{R}}{{\rm{E}}_{it}} = {a_{2i}} + {b_{21i}}\Delta {Y_{it}} + {b_{23i}}\Delta {\rm{NR}}{{\rm{E}}_{it}} + {b_{24i}}\Delta {K_{it}} + {b_{25i}}\Delta {L_{it}} + {\beta _{2i}}\Delta {\rm{R}}{{\rm{E}}_{i,t - 1}} + {\theta _{2i}}\Delta {\rm{RE}}_{it}^* + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\vartheta _{2i}}\Delta {\rm{RE}}_{i,t - 1}^* + {r_{2i}}{\rm{C}}{{\rm{A}}_t} + {\gamma _{2i}}{\rm{C}}{{\rm{A}}_{t - 1}} + {g_{2i}}\left( {{\rm{OI}}{{\rm{L}}_{it}}} \right) + {\varepsilon _{2it}} \end{array} $ | (3) |
| $ \begin{array}{l} \Delta {\rm{NR}}{{\rm{E}}_{it}} = {a_{3i}} + {b_{31i}}\Delta {Y_{it}} + {b_{32i}}\Delta {\rm{R}}{{\rm{E}}_{it}} + {b_{34i}}\Delta {K_{it}} + {b_{35i}}\Delta {L_{it}} + {\beta _{3i}}\Delta {\rm{NR}}{{\rm{E}}_{i,t - 1}} + {\theta _{3i}}\Delta {\rm{NRE}}_{it}^* + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\vartheta _{3i}}\Delta {\rm{NRE}}_{i,t - 1}^* + {r_{3i}}{\rm{C}}{{\rm{A}}_t} + {\gamma _{3i}}{\rm{C}}{{\rm{A}}_{t - 1}} + {g_{3i}}\left( {{\rm{OI}}{{\rm{L}}_{it}}} \right) + {\varepsilon _{3it}} \end{array} $ | (4) |
| $ \begin{array}{l} \Delta {K_{it}} = {a_{4i}} + {b_{41i}}\Delta {Y_{it}} + {b_{42i}}\Delta {\rm{R}}{{\rm{E}}_{it}} + {b_{43i}}\Delta {\rm{NR}}{{\rm{E}}_{it}} + {b_{45i}}\Delta {L_{it}} + {\beta _{4i}}\Delta {K_{i,t - 1}} + {\theta _{4i}}\Delta K_{it}^* + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\vartheta _{4i}}\Delta K_{i,t - 1}^* + {r_{4i}}{\rm{C}}{{\rm{A}}_t} + {\gamma _{4i}}{\rm{C}}{{\rm{A}}_{t - 1}} + {g_{4i}}\left( {{\rm{OI}}{{\rm{L}}_{it}}} \right) + {\varepsilon _{4it}} \end{array} $ | (5) |
| $ \begin{array}{l} \Delta {L_{it}} = {a_{5i}} + {b_{51i}}\Delta {Y_{it}} + {b_{52i}}\Delta {\rm{R}}{{\rm{E}}_{it}} + {b_{53i}}\Delta {\rm{NR}}{{\rm{E}}_{it}} + {b_{54i}}\Delta {K_{it}} + {\beta _{5i}}\Delta {L_{i,t - 1}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\theta _{5i}}\Delta L_{it}^* + {\vartheta _{5i}}\Delta L_{i,t - 1}^* +{r_{5i}}{\rm{C}}{{\rm{A}}_t} + {\gamma _{5i}}{\rm{C}}{{\rm{A}}_{t - 1}} + {g_{5i}}\left( {{\rm{OI}}{{\rm{L}}_{it}}} \right) + {\varepsilon _{5it}} \end{array} $ | (6) |
其中,Δ表示一阶差分;下标t-1表示时间滞后,根据施瓦兹准则和赤池准则选取滞后阶数,本文设定滞后期为1。ΔYit*表示i以外地区实际生产总值一阶差分的加权求和值,加权系数可通过空间邻近矩阵Wi计算得出,其他变量与此相同。式(2)~式(6)中,a1i、a2i、a3i、a4i、a5i为每个方程的个体效应项;bmni为i省的经济结构系数;m=1, 2, …, 5,为单个方程的因变量编号;n=1, 2, …, 5,为单个方程的自变量编号。根据经济理论分析,有的变量之间没有直接关系,则取相应的系数为0;βmi为时间滞后项的系数;θmi为空间滞后项的系数;ϑmi为时空间滞后项的系数;rmi为当期全局变量的系数;γ5i为全局变量时间滞后项的系数。ε为误差项。CA表示煤炭价格,用秦皇岛港动力煤Q5500现货离岸价表征,单位为元/吨,原数据为周数据,对每个月的周数据取均值可得月度数据。OIL表示油价,用布伦特现货原油价格表征,单位为美元/桶。OIL和CA为模型的全局向量,若把两个变量都作为非参项,则会因为维度诅咒使结果难以估计。分别把OIL和CA作为非参项带入模型计算,限于篇幅,本文仅描述OIL作为非参项的偏导图,故式(2)~式(6)中把OIL列为非参项。
将式(2)~式(6)改写为矩阵形式,则省份i的半参数结构向量自回归模型可表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{X}}_{it}} = {\mathit{\boldsymbol{a}}_i} + {\mathit{\boldsymbol{b}}_i}{X_{it}} + {\beta _i}{X_{i,t - 1}} + {\theta _i}X_{it}^* + {\vartheta _i}X_{i,t - 1}^* + {r_i}{\rm{C}}{{\rm{A}}_t} + {\gamma _i}{\rm{C}}{{\rm{A}}_{t - 1}} + {g_i}\left( {{\rm{OI}}{{\rm{L}}_{it}}} \right) + {\varepsilon _{it}}}\\ {{\mathit{\boldsymbol{X}}_{it}} = {{\left[ {\Delta {Y_{it}},\Delta {\rm{R}}{{\rm{E}}_{it}},\Delta {\rm{NR}}{{\rm{E}}_{it}},\Delta {K_{it}},\Delta {L_{it}}} \right]}^\prime },}\\ {\mathit{\boldsymbol{X}}_{it}^* = {{\left[ {\Delta Y_{it}^*,\Delta {\rm{RE}}_{it}^*,\Delta {\rm{NRE}}_{it}^*,\Delta K_{it}^*,\Delta L_{it}^*} \right]}^\prime },}\\ {{\mathit{\boldsymbol{a}}_i} = {{\left[ {{a_{1i}},{a_{2i}},{a_{3i}},{a_{4i}},{a_{5i}}} \right]}^\prime }} \end{array}} \right. $ | (7) |
其中,bi为5×5阶的经济结构系数矩阵,把结构约束设定为最典型的AB型。由于Xit与误差项εit相关,不能对式(7)直接进行估计。记Zit=[X′it, Xit*]′,经过移项,式(7)可重写为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{A}}_i}{Z_{it}} = {a_i} + {\varPi _i}{Z_{i,t - 1}} + {r_i}\Delta {\rm{C}}{{\rm{A}}_t} + {\gamma _i}{\rm{C}}{{\rm{A}}_{t - 1}} + {g_i}\left( {{\rm{OI}}{{\rm{L}}_{it}}} \right) + {\varepsilon _{it}}}\\ {{\mathit{\boldsymbol{A}}_i} = \left[ {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{b}}_i}, - {\theta _{it}}} \right],\quad {\varPi _i} = \left[ {{\beta _i},{\vartheta _i}} \right]} \end{array}} \right. $ | (8) |
其中,I为单位矩阵;Ai和Πi是ki×2ki的矩阵;ki为省份内部变量的个数;故本文中Ai和Πi为5×10阶的矩阵,且Ai是满秩矩阵。
计算需要给出空间权重矩阵,基于地理距离测度空间权重矩阵的方法在研究中较为常见, 其基本原则是随着两地地理距离的增加,空间相关性随之减少。本文选取两省省会城市间距离平方的倒数构建空间权重矩阵,如式(9)所示。
| $ \left\{ {\begin{array}{*{20}{l}} {{w_{ij}} = \frac{1}{{d_{ij}^2}},i \ne j}\\ {{w_{ij}} = 0,i = j} \end{array}} \right. $ | (9) |
其中,dij为省会城市间距离;wij为空间权重矩阵的元素。将各省份(自治区、直辖市)Xit结合在一起,得到一个k×1的向量Xt=(X′1t,X′2t,…,X′31t)′,k=
| $ {Z_{it}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{X}}_{it}}}\\ {\mathit{\boldsymbol{X}}_{it}^*} \end{array}} \right] = {\mathit{\boldsymbol{W}}_i}{\mathit{\boldsymbol{X}}_t},i = 1,2, \cdots ,31 $ | (10) |
将式(10)代入式(8),得到:
| $ {\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{W}}_i}{\mathit{\boldsymbol{X}}_t} = {a_i} + {\varPi _i}{\mathit{\boldsymbol{W}}_i}{\mathit{\boldsymbol{X}}_{t - 1}} + {\mathit{\boldsymbol{r}}_i}\Delta {\rm{CA}} + {\mathit{\boldsymbol{\gamma }}_i}\Delta {\rm{C}}{{\rm{A}}_{t - 1}} + {\mathit{\boldsymbol{g}}_i}\left( {\Delta {\rm{OI}}{{\rm{L}}_{it}}} \right) + {\varepsilon _{it}} $ | (11) |
显然,AiWi和ΠiWi是ki×k即5×105的矩阵。将全部省份(自治区、直辖市)的方程写为上下叠加的形式,得到半参数结构全局向量自回归模型:
| $ \left\{ \begin{array}{l} G{X_t} = a + {\mathit{\boldsymbol{H}}_1}{X_{t - 1}} + \mathit{\boldsymbol{r}}\Delta {\rm{C}}{{\rm{A}}_t} + \gamma {\rm{C}}{{\rm{A}}_{t - 1}} + g\left( {{\rm{OI}}{{\rm{L}}_t}} \right) + {\varepsilon _t}\\ \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{W}}_1}}\\ {{\mathit{\boldsymbol{A}}_2}{\mathit{\boldsymbol{W}}_2}}\\ \vdots \\ {{\mathit{\boldsymbol{A}}_{31}}{\mathit{\boldsymbol{W}}_{31}}} \end{array}} \right],\mathit{\boldsymbol{a}} = \left[ {\begin{array}{*{20}{c}} {{a_1}}\\ {{a_2}}\\ \vdots \\ {{a_{31}}} \end{array}} \right],{\mathit{\boldsymbol{H}}_1} = \left[ {\begin{array}{*{20}{c}} {{\varPi _1}{W_1}}\\ {{\varPi _2}{W_2}}\\ \vdots \\ {{\varPi _{31}}{W_{31}}} \end{array}} \right],\mathit{\boldsymbol{r}} = \left[ {\begin{array}{*{20}{c}} {{r_1}}\\ {{r_2}}\\ \vdots \\ {{r_{31}}} \end{array}} \right],\mathit{\boldsymbol{\gamma }} = \left[ {\begin{array}{*{20}{c}} {{\gamma _1}}\\ {{\gamma _2}}\\ \vdots \\ {{\gamma _{31}}} \end{array}} \right],\\ {\rm{OI}}{{\rm{L}}_t} = \left[ {\begin{array}{*{20}{c}} {{\rm{OI}}{{\rm{L}}_{1t}}}\\ {{\rm{OI}}{{\rm{L}}_{2t}}}\\ \vdots \\ {{\rm{OI}}{{\rm{L}}_{31t}}} \end{array}} \right], {\rm{C}}{{\rm{A}}_t} = \left[ {\begin{array}{*{20}{c}} {{\rm{C}}{{\rm{A}}_{1t}}}\\ {{\rm{C}}{{\rm{A}}_{2t}}}\\ \vdots \\ {{\rm{C}}{{\rm{A}}_{31t}}} \end{array}} \right],\mathit{\boldsymbol{g(}} \cdot \mathit{\boldsymbol{)}} = \left[ {\begin{array}{*{20}{c}} {{g_1}( \cdot )}\\ {{g_2}( \cdot )}\\ \vdots \\ {{g_{31}}( \cdot )} \end{array}} \right],{\varepsilon _t} = \left[ {\begin{array}{*{20}{c}} {{\varepsilon _{1t}}}\\ {{\varepsilon _{2t}}}\\ \vdots \\ {{\varepsilon _{31t}}} \end{array}} \right]。\end{array} \right. $ | (12) |
其中,G、H、g(·)为向量。
(二) 模型估计方法由于半参数结构全局向量自回归模型结合了多个模型,模型估计方法也较为复杂。模型的估计分两步,第一步是估计每组地区的半参数结构向量自回归模型的未知参数和非参数函数,第二步是在第一步估计的基础上再由权重矩阵计算出半参数结构全局向量自回归模型中的和,不需要对半参数结构全局向量自回归模型重新估计。
第i个省份半参数结构向量自回归模型估计方法如下:
以式(2)为例,由于ΔOIL为外生变量,与ε1it不相关,假定参数b12i、b13i、b14i、b15i、β1t、θ1it、ε1it、ϑ1t、ε1it、γ1t已知,由式(2)可知:
| $ {g_{1t}}\left( {\Delta {\rm{OI}}{{\rm{L}}_{it}}} \right) = E\left( {\begin{array}{*{20}{l}} {\Delta {Y_{it}} - \left( {{a_{1i}} + {b_{12i}}\Delta {\rm{R}}{{\rm{E}}_{it}} + {b_{13i}}\Delta {\rm{NR}}{{\rm{E}}_{it}} + {b_{14i}}\Delta {K_{it}} + {b_{15i}}\Delta {L_{it}} + } \right.}\\ {\left. {{\beta _{1i}}\Delta {Y_{i,t - 1}} + {\theta _{1i}}\Delta Y_{it}^* + {\vartheta _{1i}}\Delta Y_{i,t - 1}^* + {\mathit{\boldsymbol{r}}_{1i}}{\rm{C}}{{\rm{A}}_t} + {\gamma _{1i}}{\rm{C}}{{\rm{A}}_{t - 1}}} \right)} \end{array}/{\rm{OI}}{{\rm{L}}_{it}}} \right) $ | (13) |
将式(13)条件期望写成
| $ \begin{array}{l} {\widehat g_{1i}}\left( {{\rm{OI}}{{\rm{L}}_{it}}} \right) = {\widehat {\Delta Y}_{it}} - \left( {{a_{1i}} + {b_{12i}}{{\widehat {\Delta {\rm{RE}}}}_{it}} + {b_{13i}}{{\widehat {\Delta {\rm{NRE}}}}_{it}} + {b_{14i}}{{\widehat {\Delta K}}_{it}} + {b_{15i}}{{\widehat {\Delta L}}_{it}} + {\beta _{1i}}{{\widehat {\Delta Y}}_{i,t - 1}} + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{\theta _{1i}}\widehat {\Delta Y}_{it}^* + {\vartheta _{1i}}\widehat {\Delta Y_{i,t - 1}^*} + {r_{1i}}{{\widehat {{\rm{CA}}}}_t} + {\gamma _{1i}}{{\widehat {{\rm{CA}}}}_{t - 1}}} \right) \end{array} $ | (14) |
将式(14)和式(2)相减得到如下参数模型:
| $ \begin{array}{l} \Delta {Y_{it}} - {\widehat {\Delta Y}_{it}} = {b_{12i}}\left( {\Delta {\rm{R}}{{\rm{E}}_{it}} - {{\widehat {\Delta R{\rm{E}}}}_{it}}} \right) + {b_{13i}}\left( {\Delta {\rm{NR}}{{\rm{E}}_{it}} - {{\widehat {\Delta {\rm{NRE}}}}_{it}}} \right) + {b_{14i}}\left( {\Delta {K_{it}} - {{\widehat {\Delta K}}_{it}}} \right) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {b_{15i}}\left( {\Delta {L_{it}} - {{\widehat {\Delta L}}_{it}}} \right) + {\beta _{1i}}\left( {\Delta {Y_{i.t - 1}} - {{\widehat {\Delta Y}}_{i,t - 1}}} \right) + {\theta _{1it}}\left( {\Delta Y_{it}^* - \widehat {\Delta Y}{\kern 1pt} _{it}^*} \right) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\vartheta _{1i}}\left( {\Delta Y_{i,t - 1}^* - \widehat {\Delta Y}{\kern 1pt} _{i,t - 1}^*} \right){\kern 1pt} + {r_{1it}}\left( {{\rm{C}}{{\rm{A}}_t} - {{\widehat {{\rm{CA}}}}_t}} \right) + {\gamma _{1i}}\left( {{\rm{C}}{{\rm{A}}_{t - 1}} - {{\widehat {{\rm{CA}}}}_{t - 1}}} \right) \end{array} $ | (15) |
利用广义矩估计方法得到参数的估计
| $ {\hat g_{1i}} = {\hat g_{1i}}\left( {{{\hat a}_{1i}},{{\hat b}_{12i}},{{\hat b}_{13i}},{{\hat b}_{14i}},{{\hat b}_{15i}},{{\hat \beta }_{1i}},{{\hat \theta }_{1i}},{{\hat \vartheta }_{1i}},{{\hat r}_{1i}},{{\hat \gamma }_{1i}}} \right) $ | (16) |
本文使用了中国31个省(自治区、直辖市)(未包括港、澳、台地区)2005—2017年的月度面板数据进行实证测算,数据主要来自国家统计局官方资料。中国31个省(自治区、直辖市)的实际生产总值,取2000年为基期。为保证结果准确性,采用Eviews10.0的数据插值工具将实际生产总值季度值转化为月度值。使用永久库存法估计各省月度的实际资本存量,各省资本存量的初始值和折旧率,参考已有研究[19]的估计值,取2006年末各省资本存量为初始值,年度折旧率为10.96%,折算为月度折旧。
四、实证结果分析对31个省(自治区、直辖市)所有变量的ADF单位根检验,检验结果显示各地区变量均含有单位根I(1)过程。为了消除异方差的影响,模型对原数据取自然对数后采用一阶差分形式。检验各省(自治区、直辖市)可能存在的协整关系,发现它们均存在至少2个协整关系。为了保证地区内部变量对外部变量没有反作用,对存在协整关系的变量进行弱外生性检验,结果显示大部分地区外部变量满足弱外生性要求。最后,本文选取滞后阶p=1,q=1,得到半参数结构全局向量自回归模型估计结果。为计算主要变量当期值的影响需要结合结构向量自回归模型,每个地区包含5个主要地区内变量,所以需要对每个地区的半参数结构向量自回归模型施加15个约束条件才能有效识别结构模型,把结构约束设定为最典型的AB型。经典经济增长理论认为固定资本存量和人力资本存量是经济产出决定因素,故本文把与经济增长同期的资本增长率和劳动力增长率的系数设为非零项。电力产出为经济增长提供了能源供应,应用结构向量自回归模型考察电力消费与经济增长关系的研究中也把电力产出的当期值设为非零项[20]。为了验证经济增长是否刺激了当期电力产出的增长,本文把b21i和b31i也设为非零。大多经济增长模型中,都认为资本、劳动力、能源与经济增长有直接关系,而几乎未发现文献设定资本、劳动力、能源之间存在直接关系,故本文把相应结构系数设为零。最终,设定AB型矩阵为:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 1&{{b_{12i}}}&{{b_{13i}}}&{{b_{14i}}}&{{b_{15i}}}\\ {{b_{21i}}}&1&0&0&0\\ {{b_{31i}}}&0&1&0&0\\ 0&0&0&1&0\\ 0&0&0&0&1 \end{array}} \right],\mathit{\boldsymbol{B}} = I $ | (17) |
利用Eviews10.0软件估计参数结果表明,大部分地区资本、劳动力当期值增加导致生产总值增加,呈现正相关关系,这也符合经济增长模型。分析各个地区的结构系数发现,在不同省(自治区、直辖市)传统能源电力产出、可再生能源电力产出当期值与经济增长的结构系数存在一定差异,这可能是受地区产业结构、地理条件、跨省电力输送因素影响。
为了进一步讨论电力生产与经济增长的动态影响,绘制脉冲响应图作具体分析。
(一) 各省(自治区、直辖市)内部传统能源电力生产与经济增长受地理条件制约,中国水电、风电等可再生电力生产主要集中在西部地区,而经济增长较快省(自治区、直辖市)则大多为东部地区。本节计算结果选自31个省(自治区、直辖市)变量传统能源电力生产产出增长率(ΔNRE)受到正向冲击后对各省(自治区、直辖市)经济增长(ΔY)变量的响应图以及经济增长受到正向冲击后对各省(自治区、直辖市)变量的响应图。该部分结果由GVAR_Toolbox2.0和Eviews10.0联合计算得出。限于篇幅,选择北京、上海、广东、山东、四川、贵州、内蒙古7个省(自治区、直辖市)进行分析。所选地区中除山东外,其他地区为“西电东输”电力起点或输送目标地区,其中贵州、四川、内蒙古为“西电东输”工程南部通道、中部通道、北部通道的起点,广东、上海、北京则为3条通道对应的目标地区。此外,北京、广东、上海也是全国人均生产总值排名靠前、生产总值总量较大地区;贵州、四川、内蒙古则为可再生能源电力生产名次靠前的地区;山东则作为传统能源发电的代表省份,传统能源电力月度发电量在中国各省中长期保持第一。
给定北京等7个省(自治区、直辖市)实际生产总值增长率一个正向标准差冲击,计算各自传统能源电力产出增长率的脉冲响应。在提高各地区经济增长速度的情况下,绝大部分地区传统能源电力月度发电量立即表现正向响应,表明这些地区的经济增长增加了当地的电力需求,刺激了当地传统能源电力的供应。由于地区内可再生能源电力生产的替代效应和外地的电力输入,传统能源电力月度发电量增速在2个月后明显下降,北京下降幅度最明显,这表明健全的电网系统保证了北京电力供应的安全性,在北京电力需求陡升时可迅速由外地向北京输入电力。
给定北京等7个省(自治区、直辖市)传统能源电力产出增长率一个标准差正向冲击,计算各自地区经济增长率的脉冲响应。当传统能源电力增加时,各地区短期经济增长的响应呈现分散式特点,内蒙古、四川、山东作为能源大省(自治区)呈正向响应,北京、上海、广东作为经济强省(市)呈负向响应。影响经济增长对传统能源电力响应的因素主要有两类:一是产业结构决定的经济增长对电力的依赖性,二是电力供应方面的因素。北京、上海、广东作为我国经济发展水平较高的省(市)持续推进了产业结构调整,增加信息产业、金融业等低能耗第三产业在经济结构中的比重,降低了经济增长对电力的依赖。受到地理条件限制,京、沪、粤都不具备大规模可再生能源电力生产的条件(广东的核电产出不计入可再生电力产出),故排除可再生电力供应的因素。京、沪、粤三地经济增长主要动力来自对电力需求较低的第三产业,产业结构调整控制了电力需求上升,这是促成经济增长负向响应的主要因素。对于内蒙古、四川、贵州,则不能轻易排除该省(自治区)新能源电力对传统能源电力的替代作用,需要进一步考虑可再生能源电力与经济增长的影响关系。
(二) 各省(自治区、直辖市)内部可再生能源电力生产与经济增长计算各地区可再生能源电力生产产出增长率对经济增长正向冲击的响应,除上海、贵州外,其余地区可再生能源电力生产产出增长率均立即表现为正向响应,并在3个月后趋向平稳,表明这些地区经济增长仅在短期增加了对本地区新能源电力的需求。上海用于发电的可再生能源并不丰富,故很长时间内上海内部并未开发可再生能源发电产业,其电力供应主要来自传统能源电力和外部地区,因而上海本地区的新能源电力经济意义不大。贵州是我国新能源电力产出的大省,其产业结构中主导产业也包括新型建材、装备制造等高电耗产业,该省可再生能源电力生产产出增长率的负向响应似乎与增长理论相违。考虑到“西电东输”工程的南部通道的建设目标之一就是把贵州可再生能源电力输送至广东,省际电力输送可能是导致该结果的原因。
计算各地区经济增长对可再生能源电力生产产出增长率正向冲击的响应,短期内各地区经济增长的响应呈现与对传统能源电力响应类似的分散特征。广东经济增长对省内可再生能源电力生产产出增长率和传统能源电力生产产出增长率均呈现显著的负向响应,从产业结构调整角度分析,这显示了广东经济增长的“绿色”特征,即广东的产业结构调整使经济增长主要依靠低电耗产业,扩大电力生产反而降低了低电耗产业的投入,不利于整体产业的增长。
综上,从本地区电力生产与经济增长相互影响的分析来看,东部的经济强省(市)如北京、上海、广东经济增长与传统能源电力、新能源电力的相互响应大多表现为负向,仅广东经济增长与新能源电力存在相互的正向响应。但这并不能说明东部地区产业结构调整具有示范意义。因为至此的分析都没有考虑地区间电力传输的因素,东部地区相对“绿色”的经济增长是不是由于西部地区向其供应了低价的电力并承担了电力生产的环境成本呢?例如,贵州新能源电力与经济增长的相互影响、内蒙古经济增长对可再生能源电力生产产出增长率的负向响应都很难用产业结构调整解释,本文将进一步探讨。
(三) 地区间电力生产与经济增长在“西电东输”国家工程建设背景下,中国日渐完善的电力输送系统使各地区的电力生产不仅作用于本地区,也与其他地区经济增长存在关联。因此,在全局向量自回归模型框架下,采用广义脉冲响应分析方法分析不同省(自治区、直辖市)电力生产和经济增长之间的动态关系,本节内容包括了所选地区传统能源电力生产产出增长率、可再生能源电力生产产出增长率与经济增长的地区间响应关系。
给定北京、广东、上海实际生产总值增长率一个正标准差冲击下,山东传统能源电力月度发电量增长率的脉冲响应如图 1(a)所示。在北京、广东、上海实际生产总值增长率冲击下,山东传统能源电力产量增长率的响应在3个月后趋于平稳,分别稳定在1.6%、-1.9%、0.9%的水平上。对来自北京、上海经济增长的冲击,山东传统能源电力表现正向响应;对来自广东经济增长的冲击,山东传统能源电力表现为负向响应。可见,北京、上海的经济增长促进了山东传统能源电力生产,而广东经济增长对山东传统能源电力生产起到抑制作用。传统能源电力生产受到经济增长的反馈呈现为分散式,正向反馈与负向反馈均有出现,说明伴随经济结构转型和可再生能源产业兴起,部分呈负向反馈的地区对传统能源电力的依赖程度在减弱。给定山东传统能源电力生产增长率一个正标准差冲击,北京、广东、上海实际生产总值增长率脉冲响应如图 1(b)所示。北京、广东、上海经济增长在受到山东传统能源电力冲击6个月后均逐渐稳定,并保持正向响应,但在响应强度上存在差异。其中,北京实际生产总值增长率受冲击响应最显著(0.17%), 广东次之(0.11%), 上海响应程度最弱(0.08%)。可见,山东传统能源电力生产上升对东部主要省份的经济增长有促进作用,说明传统能源电力驱动仍是东部主要省份经济增长的主要驱动因素。
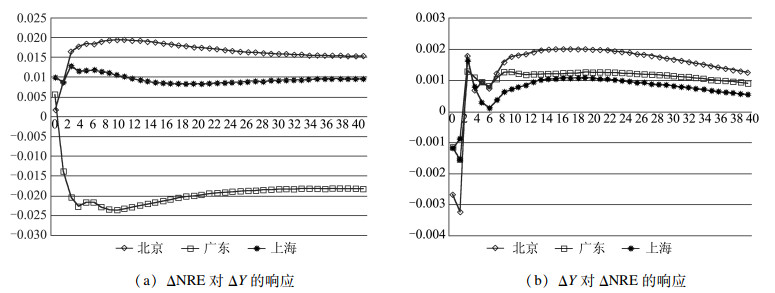
|
图 1 山东传统能源电力产出与京、粤、沪经济增长的相互响应 |
图 2、图 3给出了西部贵州、四川、内蒙古新能源电力产出增长率与东部北京、广东、上海经济增长相互冲击下的响应。给定贵州、四川、内蒙古新能源电力增长率一个正标准差的冲击,图 2(a)、(b)、(c)分别显示了北京、广东、上海实际生产总值增长率对贵州、四川、内蒙古新能源电力增长率冲击的响应。可以看出,东部地区经济增长对西部新能源电力生产具有长期的影响,不同的是,广东省经济增长冲击带来的脉冲响应为正,而北京、上海经济增长冲击带来的脉冲响应为负。由此可见,地区经济增长不仅对本地区可再生能源电力产出有影响,也会影响到其他地区。对比图 1,传统能源电力生产对这些地区经济增长的冲击与可再生能源电力的冲击呈现相反的长期响应,这表明地区在传统能源电力和可再生能源电力方向的消费倾向可能是决定响应正负的重要因素。
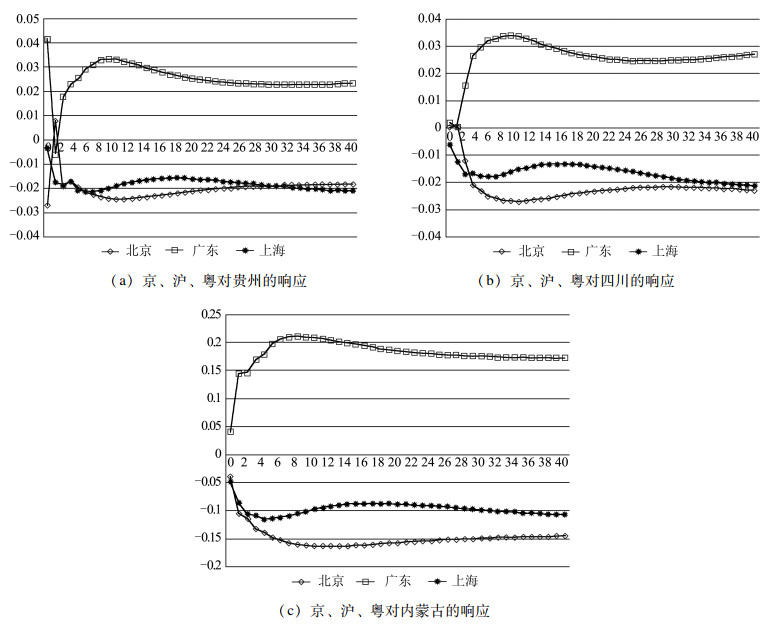
|
图 2 省际ΔRE对ΔY的响应 |
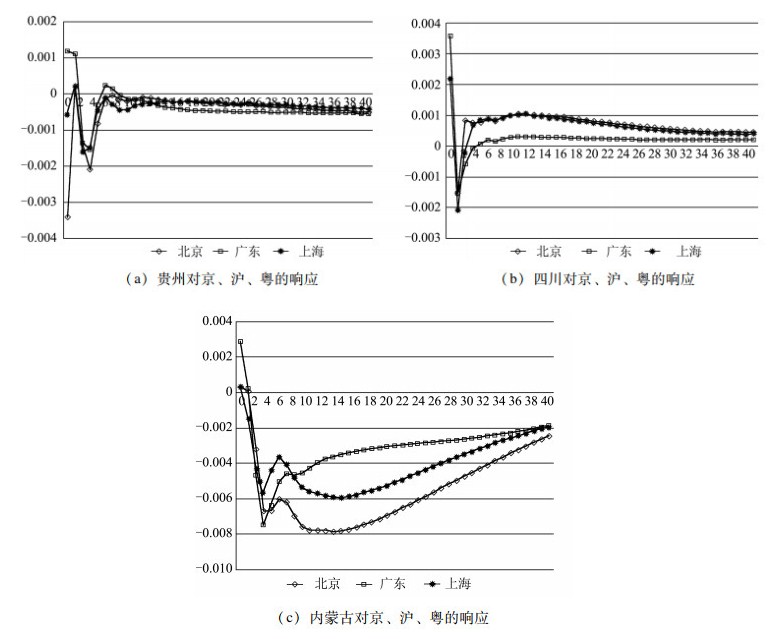
|
图 3 省际ΔY对ΔRE的响应 |
图 3(a)、(b)、(c)分别显示了贵州、四川、内蒙古新能源电力增长率对京、沪、粤实际生产总值增长率冲击的响应。贵州、四川新能源电力响应在经历3~6个月的短期振动后趋向于0,长期的变化区间分别在[-0.1%, 0]和[0, 0.1%]之间,影响不甚显著。内蒙古新能源电力响应在短期内达到最小负向影响后,逐渐趋向于0,但未表现出平稳的态势,其原因可能在于本文计算脉冲响应的时间周期较短,仅为40个月,在更长的时间周期内应能表现与贵州、四川类似的长期响应。这说明中国东部地区电力消费更主要依赖于传统能源电力而不是可再生能源电力,因此西部可再生能源电力受正向冲击后,东部地区生产总值长期响应不显著。
对比图 2和图 3,可以发现东部地区经济增长对西部新能源电力产出的影响远比西部地区新能源电力产出对东部地区经济增长的影响更显著。这印证了目前中国东部地区经济增长的主要电力能源基础仍是传统能源电力,但是,部分东部地区经济增长促进了西部可再生能源电力产出的增长。西部地区发展可再生电力产业除了要考虑地区自身电力需求外,东部地区的经济增长对传统能源电力和可再生能源电力的需求也是要考虑的因素之一。
(四) 能源价格对电力生产、经济增长的偏导图分析为了确定能源价格对经济增长、传统能源电力产出、可再生能源电力产出的非线性关系,运用局部线性估计方法,估算出主要变量经济增长、传统能源电力生产产出增长率与可再生能源电力生产产出增长率对油价(OIL)非参数拟合的偏导数,以散点图的形式表达。以广东省为例,拟合结果如图 4所示,横坐标表示原油价格,纵坐标分别表示经济增长、传统能源电力生产产出增长率、可再生能源电力生产产出增长率对油价的偏导数。其他地区偏导图结果大多与广东省类似,仅存在变化幅度上的差别,故未全部列出。需要指出的是,上海经济增长与油价偏导图近似为水平线,表示上海经济增长与油价的关系更接近线性关系,这可能是因为上海金融系统较为发达、产业结构倾向低能耗产业,对油价波动给经济增长带来的风险抵御能力较强。
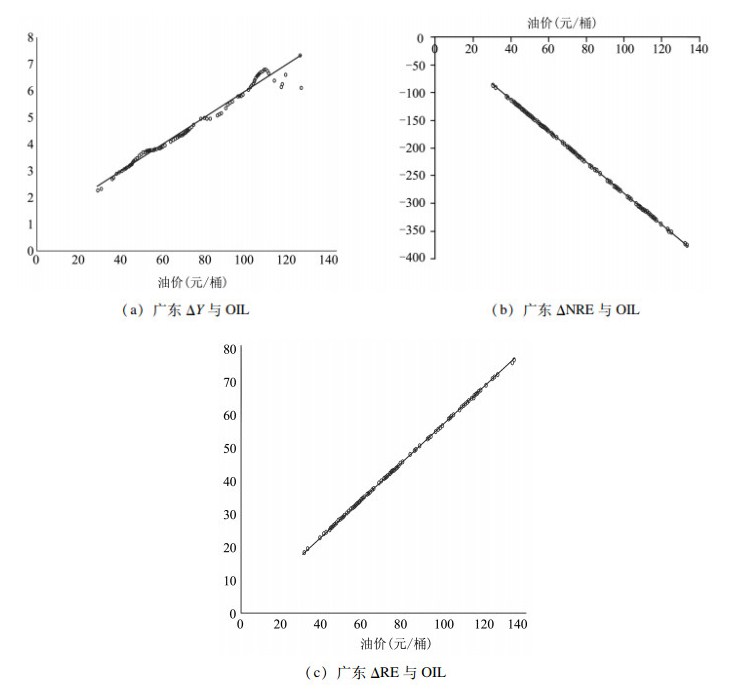
|
图 4 广东ΔY、ΔNRE与OIL的拟合曲线 |
图 4(a)中,经济增长的偏导数始终为正,可见广东经济增长的态势不会因能源价格波动出现转变,能源价格提高促进了广东的经济增长。由图 4(b)可知,当能源价格提高时,传统能源电力生产产出增长率偏导数变化随之下降,且偏导数数值为负数,说明油价提高抑制了广东省内的传统能源电力产出。图 4(c)中,广东可再生能源电力发电量产出增速随油价提高而增加,表明可再生能源电力生产对传统能源电力生产的替代作用,当能源价格提高抑制传统能源电力产出时,可再生能源电力产出填补了传统能源电力产出下降导致的供给不足。但是,从偏导数数值来看,传统能源电力生产产出增长率对能源价格偏导数的绝对值明显大于传统能源电力生产产出增长率对能源价格的偏导数,这是由于目前广东可再生能源电力生产规模还明显小于传统能源电力生产,可再生能源电力生产的替代效应尚显不足。
根据以上分析,能源价格上升阻碍经济增长的风险发生可能较小,但不能排除其对传统能源和可再生能源电力生产造成困难。由于目前可再生能源电力生产在总电力生产的占比较低,当能源价格上升时,可再生能源电力生产不足以替代传统能源电力生产,保障经济增长电力供应的任务仍主要由传统能源电力承担。这是我国当前电力生产结构中可再生能源电力生产规模不足带来的问题。
五、结论与政策建议 (一) 结论基于半参数结构全局向量自回归模型,借助广义脉冲响应函数分析,测算了中国31个省(自治区、直辖市)经济增长与传统能源电力生产、可再生能源电力生产的动态影响关系,考察了以“西电东输”国家工程为代表的省际电力生产与经济增长的关系,电力输送网络强化了东部地区经济增长与西部地区电力生产的联系。因此,一个地区的经济增长、电力生产不仅与该地区内的变量有关,还与外部地区主要变量存在影响关系。总结本文实证分析,得出以下结论:
第一,电力供应不足已经不是中国经济增长的主要瓶颈,电力供需的区域性不平衡逐渐成为各地区经济增长在电力方面的主要限制。
中国近年来总发电量持续增加已经极大缓解了电力供应不足对经济增长的限制,但经济规模较大的东部地区电力需求高,电力供应则主要分布在西部地区。原因一方面在于传统能源电力生产带来的环境污染使其在更注重环境效益的经济发达地区进行生产环境成本更高;另一方面在于西部地区可再生能源电力生产地理条件更为优越。
第二,东部经济发达地区经济增长更依赖于邻近地区传统能源电力生产,对西部地区可再生能源电力生产依赖性较弱。
电力供需存在区域不平衡状况下,东部地区是我国主要的电力需求地,西部地区可再生能源电力的发展不仅取决于本地区经济增长对电力的需求,也取决于东部经济发达地区经济增长。但从地区间经济增长对电力生产的响应结果来看,传统能源电力生产对东部经济发达地区经济增长有长期的正向促进作用,而可再生能源电力生产对东部地区经济增长在长期内没有显著影响。东部地区对传统能源电力消费的“锁定”导致了西部地区可再生能源电力投资增大而电力需求不足,进而出现弃水、弃风现象。因此,扩大西部地区可再生能源电力生产规模时,须注重引导东部地区扩大可再生能源电力的消费。
第三,传统能源电力生产与可再生能源电力生产存在相互替代的竞争关系,在省际层面这一竞争关系表现为经济增长对外地传统能源电力产出起正向促进作用的地区,对外部地区可再生能源电力产出影响较弱。
与北京、上海邻近的地区,如山东等传统能源电力产业规模大,且与北京、上海有长期的电力输送历史,形成的“锁定”现象阻碍了北京、上海经济增长对西部地区可再生能源电力生产的促进作用。广东邻近地区传统能源电力产业规模相对较小,“锁定”现象相对缓和,故广东经济增长对西部可再生能源电力产出的促进作用更显著。
第四,传统能源电力生产受能源价格波动影响较大,提高可再生能源电力生产比重是应对能源价格波动的主要措施。
(二) 政策建议本文的实证结果表明,当考虑资本增长和人力增长的当期影响时,地区内电力产出与经济增长相互影响较弱,但地区之间的电力生产与经济增长存在相互影响。对电力生产分类来看,地区之间的经济增长与传统能源电力生产相互影响强则与可再生能源相互影响弱。因此,如何突破东部地区对传统能源电力生产的“锁定”,改进经济增长对电力产出的保护机制是优化电力生产结构的关键。基于以上结论,围绕电力生产结构优化目标和区域性措施,提出以下政策建议:
第一,电力供应不应盲目扩大发电能力,而应注重产电能源的多样性,继续提高可再生能源发电的比重。长期来看,我国大多地区经济增长已经摆脱了电力短缺的限制,且伴随产业结构优化,未来经济增长对电力的需求几乎不会出现大幅度的上升,扩大发电能力无助于突破当前经济增长的瓶颈。我国当前电力生产仍以传统能源发电为主,该状况仍将维持较长时间,这也意味着煤炭、石油价格的剧烈上升会是我国电力供应主要风险。因此,提升可再生能源发电比重不仅是低碳经济的要求,也是应对能源价格陡升风险的重要预防手段。
第二,在传统能源电力生产占电力生产比重较大的情境下,可通过适当提高可再生能源电价刺激电力生产结构优化。具体地,对由西部输送至东部地区的可再生能源电力可适当提高电价,这样对西部则鼓励了可再生能源电力的生产,对东部则不会对其经济增长造成大的影响。西部可再生能源电力产出规模提高后,也减低了东部地区对传统能源电力的依赖程度。
| [1] |
BAO C, XU M. Cause and effect of renewable energy consumption on urbanization and economic growth in China's provinces and regions[J]. Journal of cleaner production, 2019(9): 483-493. |
| [2] |
ATEMS B, HOTALING C. The effect of renewable and nonrenewable electricity generation on economic growth[J]. Energy policy, 2018(1): 111-118. |
| [3] |
KRAFT J, KRAFT A. On the relation between energy and GNP[J]. The Journal of energy and development, 1978(3): 401-403. |
| [4] |
ZHANG X, CHENG X. Energy consumption, carbon emissions, and economic growth in China[J]. Ecological economics, 2009(10): 2706-2712. |
| [5] |
WANG S S, ZHOU D Q, ZHOU P, et al. CO2 emissions, energy consumption and economic growth in China:a panel data analysis[J]. Energy policy, 2011(9): 4870-4875. |
| [6] |
WANG Y, WANG Y C, ZHOU J, et al. Energy consumption and economic growth in China:a multivariate causality test[J]. Energy policy, 2011(7SI): 4399-4406. |
| [7] |
林美顺. 清洁能源消费、环境治理与中国经济可持续增长[J]. 数量经济技术经济研究, 2017(12): 3-21. |
| [8] |
YUAN J, ZHAO C, YU S, et al. Electricity consumption and economic growth in China:cointegration and co-feature analysis[J]. Energy economics, 2007(6): 1179-1191. |
| [9] |
李强, 王洪川, 胡鞍钢. 中国电力消费与经济增长——基于省际面板数据的因果分析[J]. 中国工业经济, 2013(9): 19-30. |
| [10] |
LIN B, LIU C. Why is electricity consumption inconsistent with economic growth in China?[J]. Energy policy, 2016(1): 310-316. |
| [11] |
LIN B, WANG Y. Inconsistency of economic growth and electricity consumption in China:a panel VAR approach[J]. JOURNAL OF CLEANER PRODUCTION, 2019(8): 144-156. |
| [12] |
曹俊文, 翟玉鹏. 中国电力消费强度的主导效应分析——基于结构效应与强度效应的视角[J]. 统计与信息论坛, 2017(2): 78-83. |
| [13] |
APERGIS N, PAYNE J E. The renewable energy consumption-growth nexus in Central America[J]. Applide energy, 2011(1): 343-347. |
| [14] |
APERGIS N, PAYNE J E. A Time varying coefficient approach to the renewable and non-renewable electricity consumption-growth nexus:evidence from a panel of emerging market economies[J]. Energy sources part b-economics planning and policy, 2014(1): 101-107. |
| [15] |
APERGIS N, CHANG T, GUPTA R, et al. Hydroelectricity consumption and economic growth nexus:Evidence from a panel of ten largest hydroelectricity consumers[J]. Renewable & sustainable energy reviews, 2016(9): 318-325. |
| [16] |
APERGIS N, PAYNE J E. Renewable energy, output, CO2 emissions, and fossil fuel prices in Central America:evidence from a nonlinear panel smooth transition vector error correction model[J]. Energy economics, 2014(3): 226-232. |
| [17] |
崔百胜, 朱麟. 基于内生增长理论与GVAR模型的能源消费控制目标下经济增长与碳减排研究[J]. 中国管理科学, 2016(1): 11-20. |
| [18] |
PESARAN H H, SHIN Y. Generalized impulse response analysis in linear multivariate models[J]. Economics letters, 1998(1): 17-29. |
| [19] |
单豪杰. 中国资本存量K的再估算:1952~2006年[J]. 数量经济技术经济研究, 2008(10): 17-31. |
| [20] |
NARAYAN PK, NARAYAN S, PRASAD A. A structural VAR analysis of electricity consumption and real GDP:evidence from the G7 countries[J]. Energy policy, 2008(7): 2765-2769. |
 2021, Vol. 23
2021, Vol. 23
