自2015年粮食补贴市场化改革以来,我国粮食市场化程度不断提升,市场风险呈日益增大趋势。如何更好地利用我国农产品期货市场来应对剧烈变化的国内外价格波动风险,已成为国家政策层面和微观经济主体均极为关注的重要议题。为此,中央一号文件连续四年(2016—2019年)要求以“保险+期货”试点来服务三农。中共中央、国务院印发的《乡村振兴战略规划(2018—2022年)》也同样明确要求发展农产品期货和期权市场,利用期货和期权来完善农业风险管理和预警体系。各界在这一风险管理政策框架的落地实施过程中展开了多方面探索,但是,对开放经济下农产品期货市场的风险溢出效应深入探讨尚有所欠缺。
一个无可回避的现实问题是,美国农产品期货市场在价格制定和风险溢出效应中发挥着引领作用,我国农产品期货的价格波动明显经常受到美国芝加哥期货交易所期货市场供求关系和极端风险变化的影响。特别是,由于大豆在我国所有农产品中市场化和国际化程度最高,因此其价格与美国大豆期货价格的关联性也最强。黄季焜等[1]很早就研究发现,在2005—2008年粮食危机和金融危机期间,我国政策干预并不能有效稳定国内大豆价格。2018年大豆成为中美贸易摩擦的首个农产品品种后,价格剧烈变化,再次揭示出市场中存在着极端风险溢出效应。可以认为,大豆市场的内外连接关系在很大程度上也预示着其他诸多农产品未来的风险变化模式,因此,研究中美大豆期货价格的风险关系特别是极端风险溢出不仅对当前的风险管理政策具有重要的参考意义,也是今后农业风险研究的一个理论探索方向。
在现有条件下,以下一系列问题需要进行剖析探索:作为国际大豆定价中心的美国大豆期货市场与我国大豆期货市场之间是否存在极端风险溢出效应?中美大豆期货市场间极端风险的传导方向和大小是什么?大豆补贴市场化改革后,国际期货市场对我国大豆期货市场风险溢出效应是否增强?我国大豆期货市场与国际期货市场之间的长短期极端风险溢出效应是否存在显著差异?面对国际期货市场的极端风险冲击,政策制定部门如何应对?
针对以上问题,本文拟在三个方面展开创新性实证研究。第一,从时变、非线性和不对称性尾部风险的角度对国际大豆期货市场与我国大豆期货市场之间的极端风险溢出状况进行较全面的研究。第二,将全样本以我国粮食干预政策改革时间为基本依据进行划分,着重探讨美国大豆期货市场对我国大豆期货市场极端风险溢出效应是否在市场化改革后增强。第三,将时变Copula-CoVaR模型与变分模态分解(VMD)模型相结合,首次从时间维度上研究我国大豆期货市场与国际大豆期货市场间极端风险溢出的长短期效应。
二、文献综述目前,关于国际农产品市场间的价格信息溢出效应主要从均值和波动溢出的角度开展研究,研究方法主要采用协整检验、格兰杰因果关系检验、向量自回归模型(VAR模型)以及多元GARCH模型。现有关于国际农产品期货市场间的风险溢出效应的研究也主要集中在大豆期货上[2]。首先,在均值溢出效应的研究中,周应恒等[3]、刘庆富等[4]和Chao等[5]发现价格在美国大豆期货市场中占主导地位,而夏天等[6]和Han等[7]的研究表明我国大豆期货市场并不是美国大豆期货市场的影子市场。其次,在波动溢出效应的研究中,国内外学者大多认为国内大豆期货的价格波动主要受美国大豆期货的影响[8-11]。其中,Liu等[9]和Jiang等[11]研究发现中国与美国大豆期货市场存在双向波动溢出,且中国对美国大豆期货市场风险溢出逐渐增强。而王振宇[12]发现中国大豆期货对美国期货市场的波动溢出效应更显著。王柏杰等[10]认为连续交易制度显著增强了中美期货市场的联动关系,并发现实施连续交易制度后,中美大豆期货市场波动溢出关系已由美国对中国的单项溢出转向双向溢出。赵一夫等[13]也指出在市场价格波动剧烈时,国际市场对国内市场的价格冲击增强。
另一些学者同时对我国多个品种的粮食市场与国际市场间的波动溢出效应进行了研究,发现粮食市场的开放程度会造成我国粮食市场与国际粮食市场的风险溢出效应存在显著差异性,其中,大豆在我国粮食市场与国际市场之间的波动溢出效应最强[14-16]。例如,肖小勇等[14]研究发现只有大豆的国际粮食价格对国内粮食价格存在波动溢出效应。李光泗等[15]发现粮食市场对外开放程度越高,市场间价格的协整程度越大,国际价格对中国粮食市场的波动溢出效应也越强。李光泗等[16]的研究进一步证实只有我国进口量大、市场开放程度高的大豆和玉米两个品种的国内市场与国际市场间存在双向波动溢出效应。Liu等[17]和Hernandez等[18]也证实中美大豆期货市场间存在双向的波动溢出效应。因此,随着农产品现货市场化程度和期货市场国际化程度加强,相比其他农产品,深入分析中美大豆期货市场风险溢出效应更加具有现实意义。
通过梳理发现,上述文献对国内外农产品市场之间的信息溢出关系进行了探讨,对国际大豆期货市场风险溢出的研究有重要的价值,但仍然存在一定的局限性。第一,现有研究主要集中在中美粮食市场之间的均值和波动溢出,而对极端风险情况缺乏探讨。由于均值和波动只能显示小范围的风险变化情况,因此不能准确刻画极端风险情况下境内外市场的风险溢出效应[19]。只有极少数学者从极端风险视角研究农产品期货市场的风险溢出问题。例如, Ke等[20]使用条件风险价值(CoVaR)方法研究我国农产品期货市场在国际市场的影响力;Jiang等[21]使用Cross-Quantilogram方法研究中美农产品期货市场在收益率分位数间的格兰杰因果关系。第二,从风险溢出的视角,现有的研究结论并不一致。其主要原因是研究大都基于静态的线性视角,运用BEKK-GARCH模型研究我国商品期货与国际期货市场之间的风险溢出效应。而现有的研究已表明大豆期货市场间的风险溢出效应具有明显的时变性和不对称性特征。基于静态视角研究市场间的风险传递效应,并不能很好地刻画风险溢出的非线性、不对称性和时变特征。第三,现有研究发现中美大豆期货市场存在信息溢出效应,但是关于中美大豆期货市场间的风险溢出效应定量的研究文献较少。
另外,已有研究表明,采用频域的方法来研究市场风险和市场风险溢出效应在时间维度上的长短期差异对深入了解市场风险、市场间的相关性和风险溢出效应具有重要意义。比如,一些学者研究了金融市场之间相依性的长短期差异[22-23]以及石油与金融市场间的长短期风险溢出效应[24-25];另一些学者[26-27]指出使用频域的方法可以提高市场风险预测的能力;但很少有学者对中美农产品期货市场间的长短期风险溢出效应进行研究。且已有研究表明VMD模型相比其他频域分解方法更有优点。比如,它不仅能解决经验模态分解(EMD)模态混叠问题,还能有效消除谱分析和小波分析中存在的虚假波动尺度问题[24, 28]。鉴于此,本文将采用VMD-GARCH-Copula-CoVaR模型来测度中美大豆期货市场间的长短期极端风险溢出效应,丰富和补充了中美农产品期货市场风险溢出问题的研究。
三、方法介绍和数据本文选用CoVaR这一指标来量化中美大豆期货市场间的极端风险溢出大小,并用ΔCoVaR作稳健型检验。首先,考虑到大豆期货收益率的分布通常表现出“尖峰厚尾”的特征以及金融时间序列波动的不对称性,为更精准地拟合中美大豆期货收益率序列的边缘分布,本文运用偏t-AR-GJR-GARCH(1, 1)分布模型来拟合。其次,借鉴周爱民等[29-30]研究经验,本文采用7种静态Copula函数和5种动态Copula函数对中美大豆之间的相依性进行估计,根据赤池信息准则(AIC准则)选出最优的Copula函数形式来刻画变量间的相依性①。最后,通过精准拟合的边缘分布和最优的Copula函数来获得更精确的Copula-CoVaR的计算结果。
① 7种静态Copula函数分别为: Gaussian,Student-t,Gumbel,Rotated Gumbel,SJC,Clayton,Rotated Clayton。5种动态Copula函数分别为: TVP-Gaussian,TVP-Student-t,TVP-Gumbel,TVP-Rotated Gumbel,TVP-SJC。
另外,借鉴Mensi等[24]的经验,本文为研究中美大豆期货市场间极端风险溢出效应在时间维度上差异性,使用Dragomiretskiy等[28]提出的VMD,通过对上述边缘分布拟合得到的标准化残差序列进行自适应分解成10个模态分量,每个模态分量均具有不同中心频率的有限带宽,使得每个模态的估计宽度之和为最小。然后,将变分模态分解得到的长(短)期模态分量进行概率积分变换成服从[0, 1]的均匀分布序列,再将其代入上述Copula模型中,从而求出刻画变量间的长(短)期相依性最优的Copula函数。最后,基于该最优的Copula函数,根据Copula-CoVaR模型得到CoVaR序列,该序列就是长(短)期CoVaR序列。详细的VMD方法介绍参见Dragomiretskiy等[28]和余方平等[31]的文章,本文不作详述。
具体模型及其估计方法如下:
(一) 边缘分布拟合根据AIC准则,中美大豆价格收益率的均值方程的最优滞后阶数均为1阶,因此,偏t-AR-GJR-GARCH的均值方程、方差方程和偏t分布密度函数分别如式(1)、式(2)和式(3)所示。
| $ {{r_t} = \mu + {\varphi _1}{r_{t - 1}} + {\varepsilon _t}} $ | (1) |
| $ {{\varepsilon _t} = \sqrt {{h_t}} \times {z_t},\quad {h_t} = \omega + \alpha \varepsilon _{t - 1}^2 + \beta {h_{t - 1}} + \gamma ({I_t}({\varepsilon _{t - 1}} < 0) \times \varepsilon _{t - 1}^2)} $ | (2) |
其中,rt为收益率;ht为残差εt的条件方差;下标t表示时间;zt为标准化残差;μ、φ、ω、α、β和γ均为常数,ω>0,α≥0,β≥0,α+β < 1;Ιt(·)为示性函数,即如果εt-1<0,则取值为1,否则为0。若待估参数r≠0,则说明存在杠杆效应。
| $ f({z_t};\lambda ,\eta ) = \left\{ {\begin{array}{*{20}{l}} {bc{{\left[ {1 + \frac{1}{{\lambda - 2}}{{\left( {\frac{{b{z_t} + a}}{{1 - \eta }}} \right)}^2}} \right]}^{ - (\lambda + 1)/2}},\quad {z_t} < - a/b}\\ {bc{{\left[ {1 + \frac{1}{{\lambda - 2}}{{\left( {\frac{{b{z_t} + a}}{{1 + \eta }}} \right)}^2}} \right]}^{ - (\lambda + 1)/2}},\quad {z_t} \ge - a/b} \end{array}} \right. $ | (3) |
其中,λ为偏t分布的自由度;η为对称性参数,且2 < λ < +∞,-1<η < 1;a、b、c为常数,且分别有:
将上述边缘分布拟合的标准化残差序列进行概率积分变换成服从[0, 1]的均匀分布序列,将两个序列的均匀分布序列u和v,代入Copula模型中进行参数估计,再根据AIC最小原则,求解出最优Copula模型。
其中,参考Patton[32]给出的定义,时变Copula函数允许静态Copula函数的相依参数随时间变化。首先,时变Gaussian和时变Student-t Copula函数的时变相依参数变化如下:
| $ {\rho _t} = \varLambda (\omega + \beta {\rho _{t - 1}} + \alpha \frac{1}{q}\sum\limits_{j = 1}^q {{\varPhi ^{ - 1}}} ({u_{t - j}}) \cdot {\varPhi ^{ - 1}}({v_{t - j}})) $ | (4) |
其中,Φ-1(x)是标准正态分布的分位数函数;q为常数;u和v表示不同变量的均匀分布序列;j表示第几期。为了使相关系数ρt
其次,时变Gumbel和Rotated Gumbel函数的时变相依参数变化如下:
| $ {\delta _t} = \omega + \beta {\delta _{t - 1}} + \alpha \frac{1}{q}\sum\limits_{j = 1}^q {{u_{t - j}} - {v_{t - j}}} $ | (5) |
其中,δ为相依参数。
最后,时变SJC Copula函数的时变相依参数变化如下:
| $ \begin{array}{*{20}{l}} {\tau _t^U = \Delta ({\omega _1} + {\beta _1}{\rho _{t - 1}} + {\alpha _1}\frac{1}{q}\sum\limits_{j = 1}^q | {u_{t - j}} - {v_{t - j}}|)}\\ {\tau _t^L = \Delta ({\omega _2} + {\beta _2}{\rho _{t - 1}} + {\alpha _2}\frac{1}{q}\sum\limits_{i = 1}^q | {u_{t - j}} - {v_{t - j}}|)} \end{array} $ | (6) |
其中,τtU和τtL为上下尾部时变相依参数;U表示上尾部;L表示下尾部;ρt-1为式(4)相依参数;且为了使τi∈(0, 1),令Δ(x)=(1+e-x)-1。
(三) 风险溢出测度CoVaR模型根据Adrian等[33]的最新定义,CoVaRαj/C(Xi)表示市场i处于极端风险事件C(Xi)中时,j市场的风险价值,称为条件风险价值,也简写成CoVaRαj。下行条件风险价值的数学表达式如下:
| $ P({X^j}|C({X^i}) \le {\rm{CoVaR}} _\alpha ^{j/C({X^i})}) = \alpha $ | (7) |
其中,α表示显著性水平;P()为概率函数。
具体而言,通过下列Copula-CoVaR模型即可求解出上下行条件风险价值。其中,下行条件风险价值可由式(8)求出,上行条件风险价值由式(9)求出。
| $ C({F_{r_t^j}}({\rm{CoVaR}}_{\beta ,t}^j),{F_{r_t^i}}({\rm{VaR}}_{\alpha ,t}^i)) = \alpha \beta $ | (8) |
| $ 1 - {F_{r_t^j}}({\rm{CoVaR}}_{\beta ,t}^j) - {F_{r_i^i}}({\rm{VaR}}_{\alpha ,t}^i) + C({F_{r_t^j}}({\rm{CoVaR}}_{\beta ,t}^j),{F_{r_t^i}}({\rm{VaR}}_{\alpha ,t}^i)) = (1 - \alpha )\beta $ | (9) |
其中,C()为最优Copula函数;Frtj和Frti分别为市场j和市场i的收益率rt的边缘分布函数;VaRαi为第i个市场在α水平下的无条件风险价值;α和β为显著性水平,令α=β=5%,通过式(8)计算下行条件风险值;令α=β=95%,通过式(9)计算上行条件风险值。
为比较市场之间的风险溢出强度,本文将CoVaRαj/C(Xi)进行标准化得到%CoVaRαj/C(Xi),当%CoVaRαj/C(Xi)>1,则表示市场间存在极端风险溢出。标准化公式如下:
| $ {\% {\rm{CoVaR}}_\alpha ^{j/i} = \frac{{({\rm{CoVaR}}_\alpha ^{j/{X^i} = VaR_\alpha ^i})}}{{{\rm{VaR}}_\alpha ^j}}} $ | (10) |
无条件风险价值由下式求出:
| $ {{\rm{VaR}}_\alpha ^i = {\mu _{i,t}} + {\sigma _{i,t}}t_{{\lambda _i},{\eta _i}}^{ - 1}(\alpha )} $ | (11) |
其中,tλi, ηi(α)为序列α的自由度为λi、对称性为ηi的偏t分布的边缘分布函数;σi, t为第i个市场的波动率;μi, t为收益率均值。
为考虑到模型的稳健性,本文同样使用GE-CoVaR来衡量市场i对j的溢出风险价值:
| $ \Delta {\rm{CoVaR}}_\alpha ^{j/i} = \frac{{({\rm{CoVaR}}_\alpha ^{j/{X^i} = {\rm{VaR}}_\alpha ^i} - {\rm{CoVaR}}_\alpha ^{j/{X^i} = {\rm{VaR}}_{50}^i})}}{{{\rm{CoVaR}}_\alpha ^{j/{X^i} = {\rm{VaR}}_{50}^i}}} $ | (12) |
其中,ΔCoVaRαj/i量化了在市场i处于极端情况下(Xi=VaRαi)和正常情况下(Xi=VaR50i)时,j市场所面临的条件风险价值之差。当ΔCoVaRαj/i>0,则表示市场间存在极端风险溢出。
(四) K-S检验为检验条件风险价值与无条件风险价值是否相等、上下行风险的溢出的不对称性以及中美期货市场间的风险溢出强弱,借鉴Reboredo等[34]的经验,本文选用Abadie[35]的K-S检验方法进行统计性检验。公式如下:
| $ {\rm{K}}{{\rm{S}}_{mn}} = {\left( {\frac{{mn}}{{m + n}}} \right)^{\frac{1}{\tau }}}{\rm{sup}}|{F_m}(x) - {G_n}(x)| $ | (13) |
其中,KS为检验统计量;m和n分别为两个序列的维度长度;τ为常数;F()和G()为累计分布函数;sup为上确界符号。
(五) 研究数据与描述性分析本文考察的中美期货市场大豆价格的样本时期均为2004年12月22日—2018年12月25日。其中,以大连商品交易所的豆一期货的主力合约的日收盘价代表中国大豆期货的价格,以芝加哥期货交易所的大豆连续合约的日收盘价代表美国大豆期货的价格,期货价格数据均来源Wind数据库。我国豆一期货以非转基因大豆为标的,主要作为食用大豆,来自国内自产。美国大豆期货均以转基因大豆为标的,主要出口我国。另外,考虑到中美大豆期货市场交易时区的不同,在研究美国大豆期货市场对我国大豆期货的风险溢出效应时,将美国大豆期货价格滞后一阶进行研究。首先对中美大豆期货收盘价格做对数处理,并令Rt为价格收益率,Pt为第t日期货收盘价格,则可以表示为:
| $ {R_t} = {\rm{ln}}({P_t}/{P_{t - 1}}) $ | (14) |
然后将处理好的中美大豆期货价格收益率进行描述性统计分析,结果如表 1所示。
| 表 1 中美大豆期货收益率的描述性统计 |
表 1中,标准差统计结果显示美国大豆市场收益率的波动大于我国期货市场收益率的波动,说明美国大豆市场风险高于我国大豆期货市场风险,佐证了研究国际期货市场对我国期货市场风险溢出的必要性。另外,偏度、峰度表明大豆期货收益率具有左偏和肥尾特征,且JB统计量表示不服从正态分布,这说明使用均值模型或多元GARCH模型并不能准确刻画中美大豆期货市场间的风险溢出效应。
四、实证分析 (一) 边缘分布估计表 2给出了我国大豆期货和美国大豆期货收益率的边缘分布的估计结果。
| 表 2 GARCH参数估计结果 |
由表 2可知:第一,豆一期货和美豆期货收益率均存在显著的1阶自相关性,且ARCH系数(β1)均显著,说明中美大豆期货市场均具有波动聚集效应,期货市场价格波动也具有较强的持续性。第二,表 2中的GARCH系数γ表示价格波动信息不对称性,其中豆一的系数不显著,而美豆的系数显著为负,说明我国大豆期货市场价格波动不存在信息不对称性特征,美国大豆期货市场价格波动存在信息不对称性特征,即坏消息对美国大豆的价格波动影响大于好消息的影响,造成中美大豆市场波动不对称的这种差异现象主要是由于豆一市场价格受我国价格支持政策的影响。第三,中美大豆的自由度参数估计结果均显著大于2,其中,中国大豆期货的自由度小于美国大豆期货的自由度,这说明美国大豆期货市场比中国大豆期货市场更具有“尖峰厚尾”特征,极端风险发生概率更大。最后, 使用K-S检验,结果均未能拒绝Skewed-Student-t分布的原假设,因此,上述模型较好地对大豆收益率的边缘分布进行了拟合。
(二) 变分模态分解为了分析比较中美大豆期货市场间依赖性和极端风险溢出效应在时间维度上的差异,沿用Mensi等[24]的经验,本文应用新型数据分解技术,即VMD模型,将中美大豆期货市场收益率的标准化残差均分解为10个不同时间尺度的变分模态分量,将波动较平稳且波动集聚较少的模态分量VMD1定义为长期收益率序列,将波动剧烈以及波动集聚明显的模态分量VMD10定义为短期收益率序列,从而获得具有不同中心频率有限带宽的短长期收益率序列。
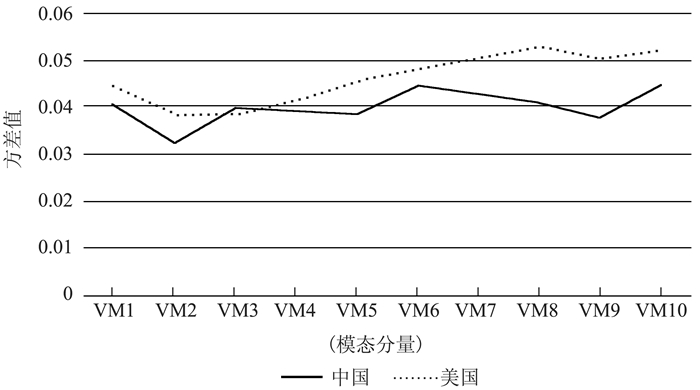
图 1为中美大豆期货市场的模态分量(VM)的方差图。从中可知,通过VMD分解得到中美大豆不同时间尺度的模态分量具有不同的方差,其值在0.03~0.06之间,且长短期中美大豆的模态分量的方差均表现出显著差异。这说明运用VMD方法可以有效分解出不同时间尺度的模态分量,使用该方法研究中美大豆期货市场间的极端风险溢出的长短期效应是合理的。
|
图 1 中美大豆期货市场的模态分量(VM)的方差图 |
为避免模型误设,本文根据AIC准则选择最优的Copula函数来刻画两变量间的联合分布。由于中美期货市场所处地区时间差异,本文在使用日数据原样本分析同一市场跨地区风险溢出情况时须分别对中国对美国的风险溢出时的相依性和美国对中国的风险溢出时的相依性进行估计。而对经过VMD模型分解得到的长短期时间序列不存在上述问题,因此不需要用滞后一期美国的时间序列来研究美国对中国的风险溢出相依性。依照AIC准则可知TVP-Student-t-Copula对原序列的拟合效果最好,TVP-Normal Copula对短期序列的拟合效果最好,TVP-SJC Copula对长期序列的拟合效果最好,最优Copula参数估计结果如表 3所示。
| 表 3 最优Copula参数估计结果 |
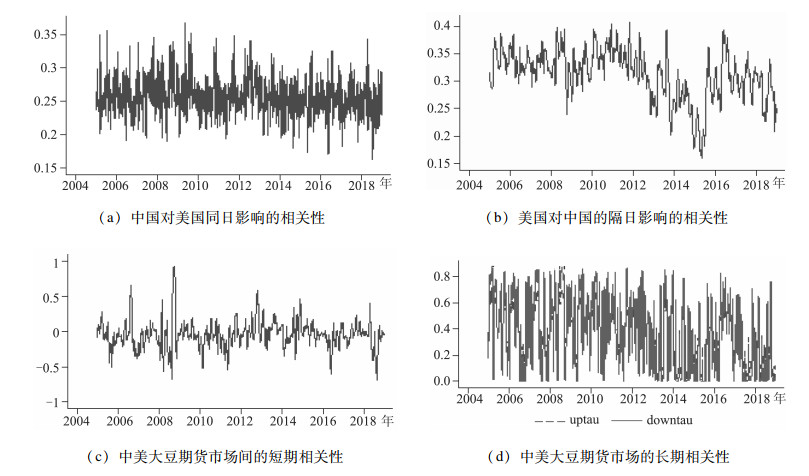
中美大豆期货市场动态相关性如图 2所示。可以看出,第一,我国大豆期货与美国大豆期货市场同日之间的相关性(见图 2(a))平均在0.25左右;而美国期货市场与我国大豆期货市场隔日之间的相关性(见图 2(b))在2010年以前大多数稳定在0.3以上,但2012年以后呈下降趋势,在2015年以后,隔夜相关性又显著增强。总体而言,相比隔夜相关性,中国大豆与美国大豆的同日相关性更稳定, 这主要是由于我国大豆期货市场在国际大豆市场仍然缺乏影响力。第二,中美大豆期货市场之间的长短期相关性(见图 2(c), 图 2(b))的波动存在显著差异,长期尾部相关性的波动较大,且表 2中的正态Copula(Normal-copula)也表明中美国的大豆短期尾部相关性为0,而SJC-copula表明长期相关性存在上下尾部相关性。这表明,相比短期相关性,长期中美大豆期货市场间的尾部相关性较强。这主要是由于短期相关性主要反映两个市场投资者情绪和交易噪音之间的信息传递,而长期相关性主要反映中美大豆市场供需等基本面和投资者预期之间的信息传递;且相比投资者情绪和交易噪音等短期因素,供需等基本面因素与投资者预期的变化对两市场之间的关联性影响更强,也更长期。第三,相比其他时期,中美大豆市场的长期相关性在2012—2015年间更多的处于0附件波动(见图 2(d))。这主要是由于国际大豆期货价格在这期间处于持续下跌走势,我国政府对大豆采取的临时收储等价格支持政策对我国大豆市场的稳定发挥了重要的作用,从而导致中美大豆期货市场的隔夜关联性和长期尾部关联性均呈现下降趋势。
|
图 2 中美大豆期货市场动态相关性图 注:图 2中的(a)、(b)、(c)子图中的相关系数为ρ,取值在[-1, 1]。图 2(d)中的相关系数中美大豆间的长期上下尾部相关系数为τ, 取值[0, 1],其中0表示无尾部相关性。uptau表示上尾τ;downtau表示下尾τ。 |
采用CoVaR来衡量当某一国大豆期货市场处于极端风险事件时,另一国大豆期货市场的极端风险水平,其中,5%分位数水平上的(条件)风险价值也叫(条件)下行风险价值,95%分位数水平上的风险价值叫(条件)上行风险价值。
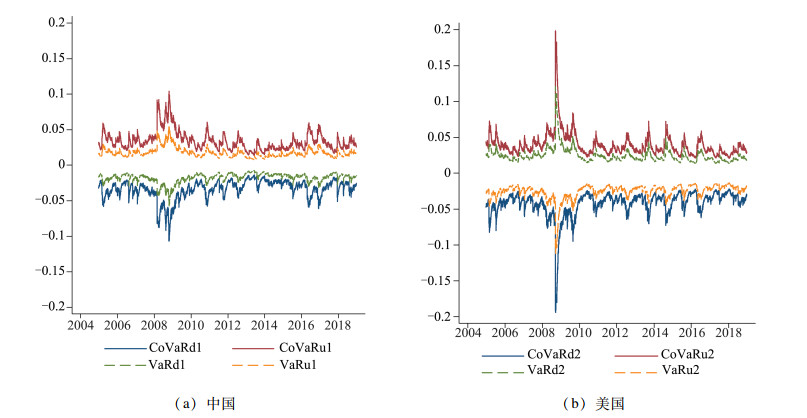
图 3(a)和图 3(b)分别给出了5%和95%的分位数水平下,美国对中国的条件风险价值和中国对美国的条件风险价值。首先,中美市场的CoVaR的绝对值均明显大于各市场的自身的风险价值(VaR)的绝对值,这表明市场之间存在极端风险溢出效应,也表明如果不考虑市场间极端风险溢出效应,对大豆期货市场的极端风险评估可能会被低估。从图 3进一步分析可知,金融危机期间(2008—2009年),国际和国内大豆期货的市场风险加剧,市场风险价值和条件风险价值均显著增强,境内外大豆期货市场关联性更加紧密,这与赵一夫等[13]发现中美大豆现货价格在此期间处于非平稳状态的结论是一致的。这表明,在国际大豆期货市场剧烈波动时,我国监管机构和市场参与者十分有必要采取相关措施缓解来自国际市场的市场间极端风险溢出。其次,从图 3可知,我国大豆期货市场的风险价值和条件风险价值的曲线峰值在2012—2014年间呈减缓的趋势,而美国大豆期货市场的风险价值和条件风险价值的曲线峰值在2012—2014年间呈上升趋势。这说明在2012年以后,我国政府对大豆等主要农产品采取的价格支持政策对我国大豆期货市场的价格波动起到了一定的稳定作用。最后,图 3表明我国大豆期货市场风险价值和条件风险价值在2015—2018年间的曲线峰值显著增强,与图 2中美国大豆期货与我国大豆期货市场隔日之间的关联性在该时期明显增强一致。这表明在政府对大豆市场干预减少的情况下我国市场风险增强,国际大豆期货市场对我国大豆期货市场的风险溢出效应也增强,也支持了柳苏芸等[36]认为2014年大豆目标价格改革以后,国内大豆价格出现了较大波动的结论。
|
图 3 不同分位数水平下中美大豆期货市场的上下行条件风险价值时间序列图 注:95%的条件风险价值和风险价值均在0水平线上方,而5%的条件风险价值和风险值在0水平线下方。其中,CoVaRd1和CoVaRd2分别表示在5%的分位数水平下中美大豆期货市场的条件风险价值;而CoVaRu1和CoVaRu2分别表示在95%的分位数水平下中美大豆期货市场的条件风险价值;VaRd1和VaRd2分别表示在5%的分位数水平下中美大豆期货市场的风险价值;而VaRu1和VaRu2分别表示在95%的分位数水平下中美大豆期货市场的条件风险价值。 |
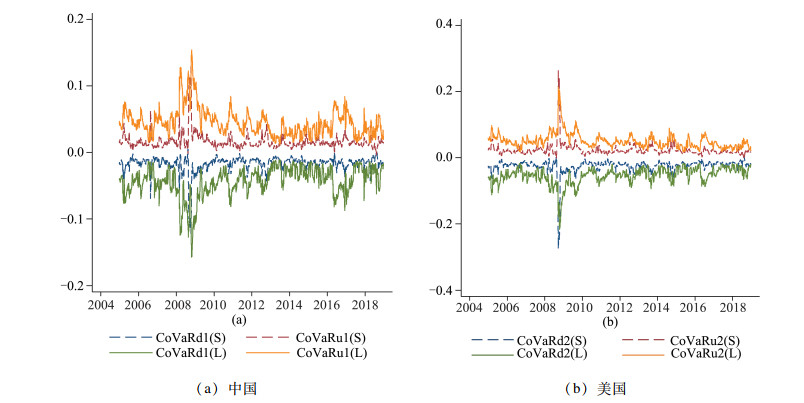
图 3为不考虑时间效应情况下的条件风险价值图,图 4为考虑时间效应情况下在5%和95%的分位数水平下长短期条件风险价值图。首先,由图 4可知,长短期条件风险价值存在显著差异,短期条件风险价值相对平缓,而长期的条件风险价值波动较大,且大多数情况下长期的条件风险价值均大于相应的短期的条件风险价值,这说明中美大豆期货市场长期极端风险溢出程度强于短期极端风险溢出。其次,结合图 3可知,只有在大豆期货市场处于极端情况下,短期条件风险价值才会显著增强,这表明在极端情况下大豆期货市场间短期风险溢出效应也会显著增强,尤其是在2008—2009年金融危机期间,短期风险价值接近长期条件风险价值,这也说明在重大极端风险事件发生时,国际极端风险在短期会快速传染到我国大豆期货市场。
|
图 4 不同分位数水平下中美大豆期货市场之间的上下行长短期极端风险溢出 注:95%的长期条件风险价值(CoVaR(L))和短期条件风险价值(CoVaR(S))在图中的0水平线上方区域,而5%的长期条件风险价值和短期条件风险值在0水平下方区域。其中,CoVaRd1(S)和CoVaRd2(S)分别表示在5%的分位数水平下中美大豆期货市场的条件风险价值;CoVaRu1(L)和CoVaRu2(S)分别表示在95%的分位数水平下中美大豆期货市场的条件风险价值。 |
表 4分别给出了中美大豆期货市场在5%和95%分位数水平下的风险价值和条件风险价值的描述性统计表的结果。其中,以5%分位数水平下的风险价值和条件风险价值表示下尾极端风险;以95%分位数水平下的风险价值和条件风险价值表示上尾极端风险。在不考虑时间效应的情况下,由表 4的均值可知:首先,美国市场的5%和95%分位数水平下的VaR分别为-0.025和0.024,而中国市场的5%和95%分位数水平下的VaR分别为-0.018和0.017。这说明美国大豆期货市场自身的极端风险大于我国大豆期货市场的自身的极端风险。其次,中美大豆期货市场的条件风险价值的绝对值均大于各自市场在同等分位数水平下的风险价值,中美大豆期货市场存在极端风险溢出效应。最后,在考虑时间效应的情况下,表 4也给出了5%和95%的显著水平下,两个市场的长短期条件风险价值。从均值来看,短期条件风险价值小于长期条件风险价值;从波动率来看,短期条件风险价值波动小于长期条件风险价值波动。这表明,总体而言,中美大豆期货市场间的极端风险溢出效应长期效应强于短期效应,这与图 4的分析结论一致。
| 表 4 中美大豆市场间的CoVaR统计描述性表 |
为更好地比较不同市场之间的风险溢出情况,将表 4的条件风险价值标准化得到表 5,表 5分别给出了中美大豆期货市场在5%和95%分位数水平下的标准化条件风险价值描述性统计值。
| 表 5 中美大豆期货市场间的标准化CoVaR描述性统计表 |
由表 5可知,在不考虑时间效应的情况下,首先,由统计表的最小值可以看出,中美大豆期货市场的条件风险价值均大于1,这说明中国大豆期货市场与美国大豆期货市场之间的极端风险双向溢出效应始终存在。其次,美国市场的上(下)行的标准化条件风险价值的均值、最小值和最大值均大于中国大豆市场的标准化上(下)行条件风险价值的均值、最小值和最大值,这说明,总体而言,美国对中国大豆期货市场的极端风险溢出强度强于中国对美国大豆期货市场的极端风险溢出强度。最后,中美大豆期货市场风险溢出效应存在上下行风险溢出效应不对称特征。美国对中国大豆期货市场的下行的标准化条件风险价值的均值、最小值和最大值均小于美国对中国大豆期货市场的上行的标准化条件风险价值的相应值,这说明,总体而言,美国对中国大豆期货市场上行的极端风险溢出效应强于美国对中国大豆期货市场的下行极端风险溢出效应。同理,表 5也表明中国对美国大豆期货市场下行风险溢出效应强于中国对美国期货市场上行风险溢出效应。
在考虑时间效应的情况下,首先,表 5表明中美大豆期货市场的短期标准化上下行条件风险价值的均值均小于1,这说明平均而言,中美大豆期货市场间的短期风险溢出效应并不显著。其次,表 5进一步表明,就均值、最小值和最大值而言,中美大豆间的标准化上下行长期条件风险价值始终大于1,且美国对中国大豆期货市场的长期标准化上(下)行条件风险价值均大于中国对美国大豆市场的长期标准化上(下)行条件风险价值,这支持了中美大豆期货市场长期存在双向极端风险溢出且美国大豆期货市场占主导地位的结论。最后,就均值、最小值和最大值而言,中美大豆期货市场之间的极端风险溢出长短期效应存在较大差异,总体而言,中美大豆期货市场之间的长期极端风险溢出效应强于短期极端风险溢出效应。
表 6的K-S统计检验结果均在1%的显著水平下拒绝了中美市场的条件风险价值与风险价值相等的原假设,进一步证实中美大豆期货市场之间的上尾部和下尾部的极端风险溢出效应均是双向的。
| 表 6 中美大豆期货市场极端风险溢出效应检验结果表 |
表 7中的K-S统计检验结果进一步证实中美大豆期货市场之间的日度和长期极端风险的标准化条件风险价值存在显著的上行和下行不对称性特征,即中国对美国大豆期货市场下行极端风险溢出强度强于中国对美国大豆期货上行极端风险的溢出强度,而美国对中国大豆期货市场的不对称性则相反,这主要是由于美国大豆期货市场本身的价格波动存在信息不对称特征,坏消息冲击大于好消息。而中美大豆期货市场之间短期标准化条件风险价值的对称性检验未能拒绝原假设,这表明短期标准化条件不对称性特征并不显著。总之,表 7表明中美大豆期货市场之间的日度和长期极端风险溢出效应存在显著的不对称性特征。
| 表 7 中美大豆期货市场条件风险价值不对称性检验结果表 |
为验证2012—2015年美国大豆期货市场对中国大豆期货市场的极端风险溢出与其他时期是否呈现统计意义上的差异,本文将样本分为三段,第一段为2004—2011年(粮食危机、金融危机期间和收储政策初期),第二阶段2012—2014年(收储政策后期),第三阶段为2015—2018年(大豆补贴市场化改革之后),并采用K-S统计检验美国对中国大豆的%CoVaR在这三阶段的是否存在显著差异,检验结果如表 8所示。
| 表 8 不同阶段下美国大豆期货市场对中国大豆风险溢出差异检验结果表 |
表 8的K-S统计检验结果均显著拒绝了原假设,表明美国大豆期货对中国大豆期货市场的风险溢出在这三阶段存在显著差异,其中,美国对中国大豆期货市场风险溢出效应在第一阶段(2004—2011年)最强,在第二阶段(2012—2014年)最弱。这表明中国大豆市场化补贴改革后,美国对中国大豆期货市场的风险溢出效应显著增强。美国对中国大豆风险溢出效应在第一阶段最强的主要原因是全球粮食危机与金融危机造成大豆市场风险急剧增强,这也说明2009年以前的政府政策在粮食和金融危机阶段并未有效地缓解国际大豆市场的冲击;而在第二阶段最弱的主要原因是由于国际大豆价格持续下跌,中国对大豆的相关干预政策确实在一定程度上缓解了美国大豆对中国大豆期货市场的极端风险溢出效应①。这与许祥云等[37]认为的市场化补贴改革之后,国际市场对中国大豆市场价格影响程度低于收储期的结论相反,不一致的主要原因是许祥云等的补贴改革后期研究样本较短,且政策实施与效果具有时滞性。
① 同样对中国对美国大豆的上下行极端风险在这三个时期的差异性进行比较分析,发现中国对美国的极端风险溢出强度在第一阶段(2004—2011年)最强,在第三阶段(2015—2018年)最弱,并不支持现有文献中关于中国期货市场在国际市场影响力逐渐增强的结论。限于篇幅有限,检验结果在此省略,如有需要可向作者索取。
表 9的K-S统计检验结果进一步表明中美大豆期货市场之间长短期极端风险溢出效应存在显著的差异,且短期极端风险溢出强度显著小于长期极端风险溢出强度。
| 表 9 中美大豆期货市场长短期风险溢出不对称检验结果表 |
本文进一步运用日度数据根据式(9)得到了在5%和95%分位数水平下的中美大豆极端风险溢出(ΔCoVaR)的大小。
表 10给出了根据式(9)计算中美大豆期货市场日度极端风险溢出值、长短期风险溢出值(ΔCoVaR)的描述性统计结果。由表 10结果可知:首先,中美大豆期货市场之间的日度极端风险溢出值和长期风险溢出值始终大于零,这说明在样本期内中美大豆期货市场之间始终存在日度极端风险溢出效应和长期极端风险溢出效应。而中美大豆期货市场之间的短期极端风险溢出的均值小于0,这说明平均而言短期极端风险溢出效应并不明显;但最大值大于0,且接近于长期风险溢出最大值,这说明短期极端风险溢出在中美大豆期货市场异常波动时期也会十分显著。其次,美国对中国大豆期货市场极端溢出风险的均值和最大值均大于中国对美国的极端风险溢出强度,这表明,总体而言,美国对中国大豆期货市场的极端风险溢出强度大于中国对美国的极端风险溢出强度。最后,平均而言,在日度数据频率层面上,中国对美国大豆期货市场的下行极端风险强于上行极端风险溢出强度,而美国对中国大豆期货市场的上行极端风险溢出强度强于下行极端风险溢出强度。
| 表 10 中美大豆极端风险溢出(ΔCoVaR)描述性统计表 |
由表 11可知,中美大豆期货市场之间的日度和长期极端风险的上行和下行溢出存在显著的不对称性特征,而中美大豆期货市场之间的短期极端风险在上行和下行溢出之间的不对称性特征并不显著。
| 表 11 中美大豆期货市场上下行极端风险不对称性检验表 |
表 12表明中美大豆期货市场之间极端风险溢出效应存在明显的长短期差异,且短期极端风险溢出强度小于长期极端风险溢出强度。
| 表 12 中美大豆期货市场长短期风险溢出不对称检验表 |
总之,通过上述分析可知,式(9)计算ΔCoVaR的实证结果均与通过VaR对CoVaR标准化的实证结果一致,这表明基于%CoVaR得到的对中美大豆期货市场间的极端风险溢出效应研究的实证结果是稳健的。
五、结论与政策建议本文基于VMD-GARCH-时变Copula-CoVaR模型来测度中国大豆期货市场与美国芝加哥期货交易所大豆期货市场间的极端风险溢出,得出三方面重要结论。第一,美国大豆期货市场对中国豆一期货市场的极端风险溢出最大,表明国际大豆期货市场极端风险是中国大豆期货市场风险管理中不可忽视的影响因素。第二,中美大豆期货市场间的极端风险溢出效应存在不对称性。尤其是美国大豆期货市场与中国大豆期货市场之间的长短期极端风险溢出效应存在显著差异,中美大豆期货市场之间的长期极端风险溢出效应更显著,而短期溢出效应在极端风险事件发生时急剧增强。这表明影响大豆现货供需的基本面因素和投资者预期对中美大豆期货市场风险溢出效应的影响程度更大、更长期,而在市场极端情况下,投资者情绪也会加剧中美大豆期货市场间的极端风险溢出效应。第三,中国收储政策降低了国际大豆期货市场对中国大豆期货市场的极端风险溢出效应,但大豆补贴市场化改革之后,国际大豆期货市场对中国大豆期货市场的极端风险溢出效应显著增强。
本文实证研究的主要建议有三点。首先,鉴于中美大豆期货市场存在显著的极端风险溢出效应,因此,在大豆期货市场国际化程度和大豆补贴市场化进程不断深化的背景下,有必要加强对输入型国际大豆期货市场极端风险的研究并建立预警体系。其次,由于国际期货市场对中国大豆期货市场极端风险溢出长短期效应和上下行极端风险溢出存在显著差异,因此有必要差异对待来自国际大豆期货市场的极端风险溢出,重点关注国际极端风险的长期溢出效应与上行风险溢出效应,从而实现有效的风险预警与管理。具体而言,对长期风险溢出效应的防范需要从调控大豆现货市场供需的基本面和引导投资者预期的角度出发;对于短期风险溢出效应,中国监管机构在国际大豆极端风险事件发生时及时采取有效措施就可以缓解国际大豆期货市场对中国大豆期货市场的短期影响;而对于上行风险溢出效应,中国大豆期货市场的空头投资者应注意防范国际大豆期货价格的暴涨引发的爆仓风险。最后,期货交易所应继续加强中国大豆期货市场的培育,推动中国大豆期货市场由量向质的转变。一方面,加强豆一期货市场的培育,防范中国豆一期货市场自身由于投机过度导致市场极端风险事件的发生。另一方面,监管者应该继续优化豆二期货合约,推动中国豆二期货市场成为对冲国际大豆期货市场极端风险的重要场所,同时也要防范国际大豆期货市场极端风险通过国内豆二期货市场输入中国大豆期货市场。
虽然采用的衡量系统性金融风险的CoVaR方法可以较好地衡量期货市场间的极端风险溢出状况,但其核心思想是基于市场波动而展开的损失概率研究,而危机发生前的市场波动往往较低,从而大大降低了CoVaR作为极端性风险预警指标的前瞻性[38]。另外,该指标的相关性变量的估计在危机前往往比危机后要较小,从而使得该指标更适合考察危机发生时的极端风险溢出效应。鉴于上述局限性,随着期货市场国际化进程的深化,未来研究应考虑如何构建具有前瞻性的国际期货市场间极端性风险溢出预警指标体系。
| [1] |
黄季焜, 杨军, 仇焕广, 等. 本轮粮食价格的大起大落:主要原因及未来走势[J]. 管理世界, 2009, 1(9): 80-86. |
| [2] |
刘建和, 王勇, 王玉斌. 沪铜期货还是伦铜期货的影子市场吗?[J]. 财经论丛:浙江财经学院学报, 2018, 232(4): 56-65. |
| [3] |
周应恒, 邹林刚. 中国大豆期货市场与国际大豆期货市场价格关系研究——基于VAR模型的实证分析[J]. 农业技术经济, 2007(1): 55-62. |
| [4] |
刘庆富, 华仁海. 基于非同步交易的国内外期货市场价格发现贡献度研究[J]. 统计研究, 2008, 25(12): 59-65. |
| [5] |
CHAO L, HAYES D J. Price discovery on the international soybean futures markets:a threshold co-integration approach[J]. Journal of futures markets, 2016, 37(1): 52-70. |
| [6] |
夏天, 程细玉. 国内外期货价格与国产现货价格动态关系的研究——基于DCE和CBOT大豆期货市场与国产大豆市场的实证分析[J]. 金融研究, 2006(2): 110-117. |
| [7] |
HAN L, LIANG R, TANG K. Cross-market soybean futures price discovery:does the Dalian commodity exchange affect the Chicago board of trade?[J]. Quantitative finance, 2013, 13(4): 613-626. |
| [8] |
华仁海, 刘庆富. 国内外期货市场之间的波动溢出效应研究[J]. 世界经济, 2007, 30(6): 66-76. |
| [9] |
LIU B, WANG Y, WANG J, et al. Is China the price taker in soybean futures?[J]. China agricultural economic review, 2015, 7(3): 389-404. DOI:10.1108/CAER-10-2014-0104 |
| [10] |
王柏杰, 李爱文. 夜盘交易与期货市场效率[J]. 证券市场导报, 2016(4): 63-70. |
| [11] |
JIANG H, TODOROVA N, ROCA E, et al. Dynamics of volatility transmission between the U.S. and the Chinese agricultural futures markets[J]. Applied economics, 2017, 49(34): 1-18. |
| [12] |
王振宇. 中美农产品价格波动特征及溢出效应研究——基于大豆期货数据的分析[J]. 农村经济, 2014(5): 100-103. |
| [13] |
赵一夫, 王宏磊. 基于MSVAR的中美大豆现货价格非线性空间传导特征研究[J]. 农业技术经济, 2017(10): 25-33. |
| [14] |
肖小勇, 李崇光, 李剑. 国际粮食价格对中国粮食价格的溢出效应分析[J]. 中国农村经济, 2014(2): 42-55. |
| [15] |
李光泗, 曹宝明, 马学琳. 中国粮食市场开放与国际粮食价格波动——基于粮食价格波动溢出效应的分析[J]. 中国农村经济, 2015(8): 44-52. |
| [16] |
李光泗, 王莉, 谢菁菁, 等. 进口快速增长背景下国内外粮食价格波动传递效应实证研究[J]. 农业经济问题, 2018(2): 94-103. |
| [17] |
LIU Q, AN Y. Information transmission in informationally linked markets:evidence from U.S. and Chinese commodity futures markets[J]. Journal of international money & finance, 2011, 30(5): 778-795. |
| [18] |
HERNANDEZ M A, IBARRA R, TRUPKIN D R. How far do shocks move across borders? Examining volatility transmission in major agricultural futures markets[J]. European review of agricultural economics, 2014, 41(2): 301-325. DOI:10.1093/erae/jbt020 |
| [19] |
郝毅, 梁琪, 李政. 境内外人民币外汇市场极端风险溢出研究[J]. 国际金融研究, 2017, 365(9): 76-85. |
| [20] |
KE Y M, LI C G, MCKENZIE A M, et al. Risk transmission between Chinese and U.S.agricultural commodity futures markets-a coVaR approach[J]. Sustainability, 2019, 11(239): 1-18. |
| [21] |
JIANG H, SU J J, TODOROVA N, et al. Spillovers and directional predictability with a cross-quantilogram analysis:the case of U.S. and Chinese agricultural futures[J]. Journal of futures markets, 2016, 36(12): 1231-1255. DOI:10.1002/fut.21779 |
| [22] |
SHAHZAD J, KUMAR R R, ALI S, et al. Interdependence between Greece and other European stock markets:a comparison of wavelet and VMD copula, and the portfolio implications[J]. Physica a statistical mechanics & its applications, 2016, 457: 8-33. |
| [23] |
SHAHZAD S J H, NOR S M, KUMAR R R, et al. Interdependence and contagion among industry-level U.S.credit markets:an application of wavelet and VMD based copula approaches[J]. Physica a statistical mechanics & its applications, 2016, 466: 310-324. |
| [24] |
MENSI W, HAMMOUDEH S, SHAHZAD S J H, et al. Oil and foreign exchange market tail dependence and risk spillovers for MENA, emerging and developed countries:VMD decomposition based copulas[J]. Energy economics, 2017, 67: 476-495. DOI:10.1016/j.eneco.2017.08.036 |
| [25] |
LI X F, WEI Y. The dependence and risk spillover between crude oil market and China stock market:new evidence from a variational mode decomposition-based copula method[J]. Energy economics, 2018, 74: 565-581. DOI:10.1016/j.eneco.2018.07.011 |
| [26] |
KAIJIAN HE G K F T, YINGCHAO ZOU, JIA LIU. Crude oil risk forecasting:new evidence from multiscale analysis approach[J]. Energy economics, 2018, 76: 574-583. DOI:10.1016/j.eneco.2018.10.001 |
| [27] |
JINCHAO LI S Z, QIANQIAN WU. Monthly crude oil spot price forecasting using variational mode decomposition[J]. Energy economics, 2019, 83: 240-253. DOI:10.1016/j.eneco.2019.07.009 |
| [28] |
DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE transactions on signal processing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675 |
| [29] |
周爱民, 韩菲. 股票市场和外汇市场间风险溢出效应研究——基于GARCH-时变Copula-CoVaR模型的分析[J]. 国际金融研究, 2017, 367(11): 56-66. |
| [30] |
周爱民, 韩菲. 股指期货与现货市场的风险溢出研究[J]. 财贸经济, 2017, 38(8): 52-65. |
| [31] |
余方平, 匡海波. 基于VMD-GRGC-FFT的BDI指数周期特性研究[J]. 管理评论, 2017, 29(4): 214-224. |
| [32] |
PATTON A J. Modelling asymmetric exchange rate dependence[J]. Int econ rev, 2006, 47(2): 527-556. |
| [33] |
ADRIAN T, BRUNNERMEIER M K. CoVaR[J]. Am econ rev, 2016, 106(7): 1705-1741. DOI:10.1257/aer.20120555 |
| [34] |
REBOREDO J C, UGOLINI A. Quantile dependence of oil price movements and stock returns[J]. Energ econ, 2016, 54(5): 33-49. |
| [35] |
ABADIE A. Bootstrap test for distributional treatment effects in instrumental variable models[J]. Publications of the American statistical association, 2002, 97(3): 284-292. |
| [36] |
柳苏芸, 韩一军, 石自忠, 等. 基于MS-VAR模型的我国大豆市场波动特征分析[J]. 华南理工大学学报(社会科学版), 2017, 19(2): 45-52. |
| [37] |
许祥云, 何恋恋, 高灵利. 农产品政策如何影响国际市场对国内期货市场的价格传递效应——以棉花和豆类产品的收储及补贴政策为例[J]. 世界经济研究, 2016(6): 55-68. |
| [38] |
杨子晖, 周颖刚. 全球系统性金融风险溢出与外部冲击[J]. 中国社会科学, 2018, 276(12): 70-91. |
 2020, Vol. 22
2020, Vol. 22

