2. 阳光学院 基础教研部, 福建 福州 350015
2. Department of Basic Teaching and Research, Yango University, Fuzhou 350015, Fujian, China
20世纪70年代以来,全球自然灾害频繁发生,如2008年中国汶川大地震、2010年海地大地震、2011年日本地震并引发海啸、2014年中国新疆和田大地震以及2016年中国南方特大洪水等,几乎每年世界都会发生多起巨灾事件。这些巨灾事件给人类带来了重大的人员伤亡和严重的经济损失。根据Sigma巨灾数据库统计的1970年到2017年间全球巨灾数据①可知,巨灾发生的年次数从1970年的100次,增加到2017年的301次,伴随的经济损失从16.01亿美元增长到337.29亿美元。由此可见,巨灾发生的频率与造成的经济损失呈现不断增长的趋势。作为世界上自然灾害最严重的国家之一,我国承受的巨灾风险不断加剧,保险业和政府部门的压力变大,保险业越来越难以支付日益庞大的保险赔付,亟须对巨灾风险进行管理。由于巨灾损失具有尖峰厚尾的特征,如何更准确地刻画实际的巨灾损失尾部特征,探寻更合适的分布形式,构建一套科学有效的巨灾损失估计模型,对巨灾风险的管理具有重大意义。
① 见网址:http://www.sigma-explorer.com/。
极值理论(Extreme Value Theory,EVT)能很好地衡量极端情况下的风险损失,用极值理论估计风险价值(value at risk,VaR),不仅能有效地拟合金融资产尖峰厚尾特征[1-2],而且该方法还有较好的统计特性,因此极值理论开始成为度量VaR的主流模型[3-4]。郝军章和崔玉杰[5]采用极值理论中的POT模型,对地震风险的VaR进行了度量。Copula函数可以描述多变量相关性的问题,在风险管理、资产定价等方面都得到了广泛的应用。Ganguli和Reddy[6]利用椭圆族Copula和阿基米德Copula研究印度在1900—2008年间的极端干旱风险。She和Xia[7]利用Gumbel Copula刻画中国黄土高原地区的干旱变量间的相关结构,并评估该地区潜在的干旱风险。Joyce等[8]利用Copula研究揭示了沿海城市流域低洼地区的潜在洪水风险与排水基础设施弹性之间的耦合关系,以评估洪水灾害及其可能的驱动力。巢文和邹辉文[9]利用藤Copula模型进行了巨灾风险的CVaR预测研究。李明等[10]利用Clayton Copula函数对长春干旱数据,构造了干旱历时和干旱程度的联合分布函数,进而计算了干旱历时和干旱程度在不同组合条件下的联合超越概率、联合重现期、同现重现期及条件重现期。
目前,应用Copula函数来研究灾害风险的文献往往忽视了损失变量的厚尾性。鉴于此,本文尝试利用极值理论中的POT模型估计巨灾损失变量的边缘分布,并用二元阿基米德Copula函数刻画巨灾损失变量间的相关结构,构建基于Copula-POT模型的巨灾损失评估模型,进而依此计算出巨灾损失的CVaR值。
二、模型构建利用Copula函数估算巨灾损失的CVaR值,需要解决两个主要问题:一是选择恰当的边缘分布拟合巨灾损失变量;二是选择合适的Copula函数对巨灾损失的相关特征进行刻画,从而得出巨灾损失的联合分布函数。
(一) 用POT模型构建边缘分布极值理论根据尾部区域行为提供了两种方式刻画观测数据的极值行为,一种是在给定区域内选最大值,称为块最值法(Block Maxima Method,BMM),另一种是选取超过门限水平的值,称为超阈值法(Peaks over Threshold,POT)。由于BMM在建模过程中只取模块中的最大值,而极值数据可能成串出现,这会造成大量有效数据信息丢失。为了更充分地利用数据信息,本文采用极值理论中的POT模型。POT模型最早是由Pickands[11]在极值理论的框架下引入的,POT模型将所有超出给定充分阈值的观测值作为观测样本,研究观测样本大于阈值的渐进分布,该渐进分布称为广义帕累托分布(GPD)。
对于一个具有相同分布函数F(x)的n个独立同分布的随机变量X1, X2, …, Xn给定一个阈值u,若Xi>u,则称它为超阈值(exceedance),将Xi-u称为超出量(excess)。不难得到:
| $ {F_u}(y) = P(X - u \le y|X > u),\quad y \ge 0 $ | (1) |
由数理统计知识和条件概率公式推导,可得用阈值u和Fu(y)表示的分布函数F(x)的表达式如下:
| $ {F_u}(y) = \frac{{P(u < X \le y + u)}}{{P(X > u)}} = \frac{{F(y + u) - F(u)}}{{1 - F(u)}} = \frac{{F(x) - F(u)}}{{1 - F(u)}},\quad x \ge 0 $ |
从而:
| $ F(x) = [1 - F(u)]{F_u}(x - u) + F(u),\quad x \ge u $ | (2) |
Pickands-Balkama-de Hann(简称PBdH)定理[12]:当u足够大时,Fu(x-u)可以用广义帕累托分布来近似。
| $ {F_u}(x - u) \approx {G_{\xi ,\sigma }}(x - u) = \left\{ {\begin{array}{*{20}{l}} {1 - {{\left( {1 + \xi \frac{{x - u}}{\sigma }} \right)}^{ - 1/\xi }},}&{\xi \ne 0}\\ {1 - {{\rm{e}}^{ - \frac{{x - u}}{\sigma }}},}&{\xi = 0} \end{array}} \right. $ | (3) |
式中,ξ和σ分别是形状(shape)参数和尺度(scale)参数。如果ξ>0,则分布具有厚尾性。
考虑对F(u)的一个合理的经验估计是(n-Nu)/n,其中n是样本总数,Nu为超出阈值的样本数,代入(2)式中,就得到厚尾分布在整个分布中的表达式:
| $ {F(x) = \left( {1 - \frac{{n - {N_u}}}{n}} \right){G_{\xi ,\sigma }}(x - u) + \frac{{n - {N_u}}}{n}} $ |
化简可得:
| $ {F(x) = 1 - \frac{{{N_u}}}{n}{{\left[ {1 + \frac{\xi }{\sigma }(x - u)} \right]}^{ - 1/\xi }},\quad x > u} $ | (4) |
Copula函数将联合分布函数和各自的边缘分布函数连接在一起,因此也称为连接函数,它通常用于探究随机变量之间的非线性关系。常见的Copula函数主要包括椭圆Copula函数和阿基米德Copula函数两大类。根据已有的研究可知,阿基米德Copula函数比其他类型的Copula函数在拟合尖峰厚尾的数据方面更具优势[13-14]。由于巨灾损失数据具有明显的尖峰厚尾特征,因此,本文选用阿基米德Copula函数来刻画巨灾损失变量之间的相关关系,其函数表达式为:
| $ C({u_1},{u_2}, \cdots ,{u_n}) = {\phi ^{ - 1}}(\phi ({u_1}) + \phi ({u_2}) + \cdots + \phi ({u_n})) $ |
式中ϕ(·)是阿基米德Copula函数的生成元,不同的生成元对应不同的Copula函数。常见的阿基米德Copula函数有Gumbel、Clayton和Frank Copula函数。如何从已有的Copula函数集合中选出最能准确刻画变量间相关结构的Copula函数,这需要对Copula函数进行检验和拟合度评价。选择的方法可以分为图形法和解析法两种,图形法常用的是Q-Q图法,而解析法里最常见的是KS检验、AD检验。本文将综合这两种方法从常用的三种阿基米德Copula函数中选出拟合效果最好的一种。
(三) CVaR的计算VaR是指在金融市场正常波动下,某一金融资产或证券组合在未来一段时间内,在给定的概率水平下发生的最大可能损失。在保险中VaR可理解为在给定置信水平p下,某风险产品可能的最大索赔额。从概率的角度来看,VaR是指在一定的持有期和置信水平下,投资组合损失函数的分布函数的分位点。VaR定义的数学表达式为:
| $ {\rm{Va}}{{\rm{R}}_\alpha } = {\rm{inf}}\{ l \in {\bf{R}}:p(L > l) \le 1 - \alpha \} = {\rm{inf}}\{ l \in {\bf{R}}:{F_L}(l) \ge \alpha \} $ |
其中,L为损失函数;α∈(0, 1)为显著性水平;FL为损失函数L的分布函数;p为概率;l为实数,R为实数集。特别是如果损失函数的分布函数连续,则VaRα(L)=
| $ {\rm{Va}}{{\rm{R}}^p} = {\rm{inf}}\{ l \in {\bf{R}}:p(X > l) \le p\} $ |
CVaR是条件VaR的值,设X、Y表示巨灾的两个损失变量,在Y=y的条件下,X的条件分布函数为F(x|Y=y),则置信水平为p的CVaR可如下定义:
| $ {\rm{CVa}}{{\rm{R}}^p} = {F^{ - 1}}(p|Y = y) $ |
式中F-1(· |Y=y)为F(·| Y=y)的反函数。由定义可知CVaR实际上就是条件分位点的值,它的含义是当解释变量Y=y时,在给定的置信水平下,另一损失变量X可能的最大损失值。
(四) 基于阿基米德Copula函数的CVaR估计当损失变量X、Y之间的相关关系由阿基米德Copula函数来刻画时,根据阿基米德Copula函数的定义,X、Y的联合分布函数为:
| $ F(x,y) = C({F_X}(x),{F_Y}(y)) = {\phi ^{ - 1}}[\phi ({F_X}(x)) + \phi ({F_Y}(y))] $ |
式中,FX(x)和FY(y)分别为X、Y的边缘分布函数;ϕ(·)为阿基米德Copula函数的生成元;ϕ-1(·)为ϕ(·)的反函数。
在Y=y的条件下,X的分布函数可以如下求出:
| $ F(x|y) = \frac{{\int_{ - \infty }^x {f(s,y)} {\rm{d}}s}}{{{f_Y}(y)}} = \frac{{\int_{ - \infty }^x {\frac{{{\partial ^2}F(s,y)}}{{\partial s\partial y}}} {\rm{d}}s}}{{{f_Y}(y)}} = \frac{{\frac{{\partial F(x,y)}}{{\partial y}}}}{{{f_Y}(y)}} $ | (5) |
(1) 当阿基米德Copula为Gumbel Copula时,由于
| $ {C_G}(u,v) = {\rm{exp}}( - {[{( - {\rm{ln}}u)^\theta } + {( - {\rm{ln}}v)^\theta }]^{1/\theta }}) $ |
所以
| $ F(x,y) = {\rm{exp}}( - {[{( - {\rm{ln}}{F_X}(x))^\theta } + {( - {\rm{ln}}{F_Y}(y))^\theta }]^{1/\theta }}) $ |
代入(5)式,得
| $ F(x|y) = \frac{{{\rm{exp}}( - {A^{1/\theta }}){A^{((1 - \theta )/\theta )}}{{( - {\rm{ln}}{F_Y}(y))}^{\theta - 1}}}}{{{F_Y}(y)}} $ | (6) |
其中,A=(-lnFX(x))θ+(-lnFY(y))θ。
(2) 当阿基米德Copula为Clayton Copula时,由于
| $ {C_{CL}}(u,v) = {({u^{ - \theta }} + {v^{ - \theta }} - 1)^{ - 1/\theta }} $ |
所以
| $ {F(x,y) = {{({{({F_X}(x))}^{ - \theta }} + {{({F_Y}(y))}^{ - \theta }} - 1)}^{ - 1/\theta }}} $ |
代入(5)式,得
| $ {F(x|y) = {{({F_X}(x))}^{ - \theta }} + {{({F_Y}(y))}^{ - \theta }} - 1{)^{ - (1 + \theta )/\theta }}{{({F_Y}(y))}^{ - \theta - 1}}} $ |
(3)当阿基米德Copula为Frank Copula时,由于
| $ {{C_F}(u,v) = - \frac{1}{\theta }{\rm{ln}}\left( {1 + \frac{{({{\rm{e}}^{ - \theta u}} - 1)({{\rm{e}}^{ - \theta v}} - 1)}}{{{{\rm{e}}^{ - \theta }} - 1}}} \right)} $ |
所以
| $ {F(x,y) = - \frac{1}{\theta }{\rm{ln}}\left( {1 + \frac{{({{\rm{e}}^{ - \theta {F_X}(x)}} - 1)({{\rm{e}}^{ - \theta {F_Y}(y)}} - 1)}}{{{{\rm{e}}^{ - \theta }} - 1}}} \right)} $ |
代入(5)式,得
| $ \begin{array}{l} F(x|y) = \frac{1}{{\frac{{1 + ({{\rm{e}}^{ - \theta {F_X}(x)}} - 1)({{\rm{e}}^{ - \theta {F_Y}(y)}} - 1)}}{{{{\rm{e}}^{ - \theta }} - 1}}}} \cdot \frac{{{{\rm{e}}^{ - \theta {F_Y}(y)}}({{\rm{e}}^{ - \theta {F_X}(x)}} - 1)}}{{{{\rm{e}}^{ - \theta }} - 1}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{{{\rm{e}}^{ - \theta {F_Y}(y)}}({{\rm{e}}^{ - \theta {F_X}(x)}} - 1)}}{{{{\rm{e}}^{ - \theta }} - 1 + ({{\rm{e}}^{ - \theta {F_X}(x)}} - 1)({{\rm{e}}^{ - \theta {F_Y}(y)}} - 1)}} \end{array} $ |
得到条件分布函数F(x|y)的表达式后,根据Clayton Copula和Frank Copula的情况,显然可以求出F(x|y)的反函数的解析解,进而就可以得到CVaR的值;而对于Gumbel Copula,由于其条件分布函数的反函数无法求出解析解,只能采用数值方法求其数值解。具体做法如下:记X的历史数据最小值为Xmin,最大值为Xmax;取足够大的正整数N,将区间[Xmin,Xmax]分为N个小区间,得到N+1个分点x(0),x(1), …,x(N),再利用(6)式得到F(x|y)在各个分点处的值,最后根据下式计算:
| $ {\rm{CVa}}{{\rm{R}}^p} = \mathop {{\rm{ argmin }}}\limits_{{x_{(j)}}} \{ |F({x_{(j)}}|y) - p|\} ,\quad (j = 0,1, \cdots ,N) $ |
本文的数据来源于达特茅斯学院洪水气象台提供的全球洪水档案①。这个数据库记载了1985年以来全球发生的4 000多件洪水事件,详细记录了每次洪水发生的时间、地点等多项指标。本文选取1985—2010年洪灾造成的经济损失②和受灾面积数据作为研究样本。由于损失数据单位为美元且时间跨度大,因此采用美国劳工部发布的CPI指数,将所有经济损失都调整到2010年的物价水平,以消除通货膨胀带来的影响。然后,提取有经济损失记录且损失超过100万美元的数据,共计872条。
① 见网址:http://www.dartmouth.edu/~floods/Archives/index.html。
② 本文中的经济损失是指洪灾造成的直接经济损失。事实上,巨灾间接经济损失与直接经济损失相比,在时间上有个滞后期,它的评估方法需要根据具体的损失对象加以确定,暂时还没有统一的方法和规范。因此,目前相关研究一般都是采用直接经济损失数据。
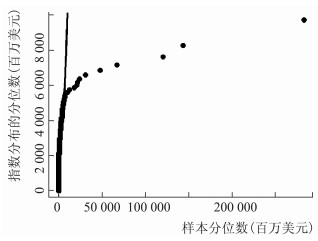
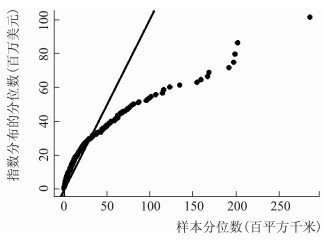
在构建POT模型之前,需要对洪水经济损失和受灾面积数据进行厚尾分布检验。从图 1和图 2中可以很明显看出,指数Q-Q图的尾部行为呈现上凸形状。这表明损失数据存在明显的“厚尾”特征。表 1列出了经济损失和受灾面积的描述性统计量,两个指标的峰度值分别为386.3和29.675,均大于3,因此可以判定洪水的经济损失和受灾面积数据具备厚尾特征,可以采用POT模型对边缘分布建模。
|
图 1 经济损失的指数Q-Q图 |
|
图 2 受灾面积的指数Q-Q图 |
| 表 1 经济损失和受灾面积的描述性统计表 |
如前所述,用GPD拟合Fu(x-u)要求有充分大的阈值。阈值的选择非常重要,不能过高也不能过低,需要权衡模型的方差和系统偏差。阈值过高会导致超过阈值的数据量较少,从而导致参数估计值方差很大;阈值过低则不能保证极值分布的收敛性,造成估计系统偏差很大。
目前阈值的选取有很多种方法,不同的方法得到的阈值存在较大的差异,并不存在十分精确有效的阈值确定方法。在实际应用中,常利用样本的平均剩余寿命图法和Hill图法[15]来选择阈值,本文拟采用Hill图法进行判断。
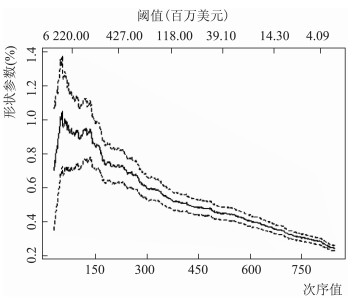
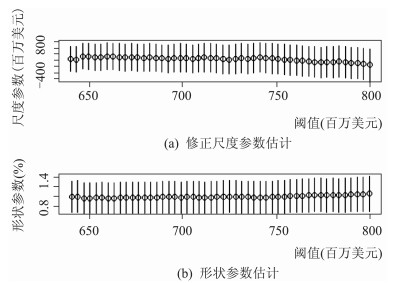
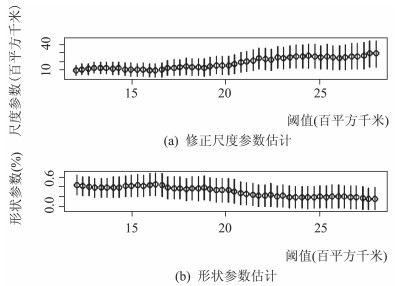
根据Hill图的选择标准,选取Hill图呈平稳的起始点的横坐标所对应的样本点作为阈值。如经济损失的Hill图,如图 3所示,在横坐标的次序值k≈135之前图形为曲线,波动较大;在次序值k≈165之后图形趋于稳定,则阈值应该取次序值k在135到165之间的u值。但由于k=165时,超过阈值的样本数据太多,此时虽然可观测的样本观察值变多,可以增加估计的精度,然而超出量Yi=Xi-u可能已经不再服从GPD分布。因此,选次序值k=135所对应的u值即720作为阈值。为了进一步判断是否合适,可以再做更细致的检查。具体而言,先选出一系列阈值,然后应用最大似然估计法得到每个阈值的参数估计值;如果在所选阈值的附近,所得到的参数估计值变化稳定,那就说明所选阈值是合适的。而后再进行经济损失的形状参数ξ和尺度参数σ的检验,如图 4所示。结果表明,ξ和σ在u=720附近各图形是稳定的,同时进一步证明阈值选取的合理性。同样的方法,根据图 5和图 6可判断受灾面积的阈值为u=20。
|
图 3 经济损失的Hill图 |
|
图 4 经济损失数据关于不同阈值的参数估计 |
|
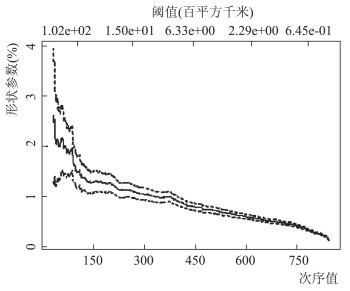
图 5 受灾面积的Hill图 |
|
图 6 受灾面积数据关于不同阈值的参数估计 |
当经济损失和受灾面积的最优阈值u确定以后,可以利用最大似然估计法得到参数ξ和σ的估计值。具体来说,根据(3)式,可以得到GPD的概率密度函数:
| $ {g_{\xi ,\sigma }}(y) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{\sigma }{{(1 + \xi \frac{y}{\sigma })}^{ - (1 + \frac{1}{\xi })}},}&{\xi \ne 0}\\ {\frac{1}{\sigma }{{\rm{e}}^{ - \frac{y}{\sigma }}},}&{\xi = 0} \end{array}} \right. $ | (7) |
相应的对数似然函数为:
| $ L(\xi ,\sigma |y) = \left\{ {\begin{array}{*{20}{l}} { - n{\rm{ln}}\sigma - (1 + \frac{\xi }{\sigma })\sum\limits_{i = 1}^n {{\rm{ln}}} (1 + \frac{\xi }{\sigma }{y_i}),}&{\xi \ne 0}\\ { - n{\rm{ln}}\sigma - \frac{1}{\sigma }\sum\limits_{i = 1}^n {{y_i}} ,}&{\xi = 0} \end{array}} \right. $ | (8) |
对该似然函数求极大值,便可得到参数ξ和σ的估计量。POT模型参数估计表如表 2所示:
| 表 2 POT模型参数估计表 |
利用估计结果,我们可以进一步得到拟合分布的诊断图。经济损失阈值超出量分析的诊断图和受灾面积阈值超出量分析的诊断图分别如图 7和图 8所示。
|
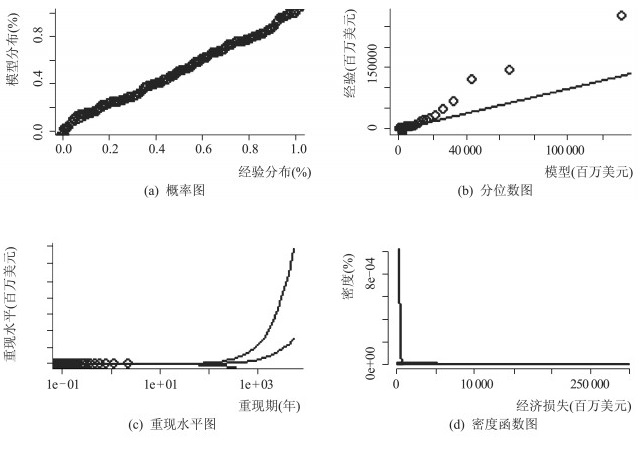
图 7 经济损失阈值超出量的诊断图 |
|
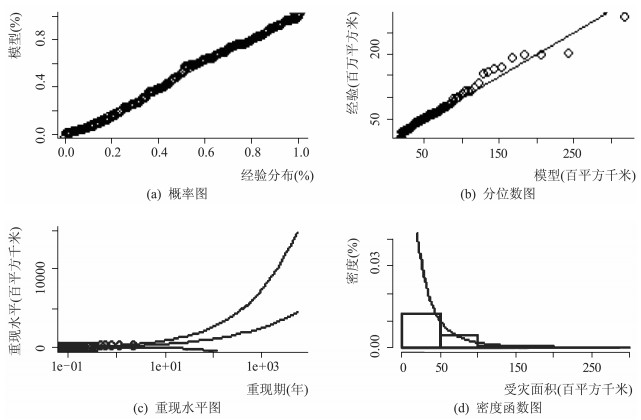
图 8 受灾面积阈值超出量的诊断图 |
以经济损失阈值超出量分析的诊断图为例进行分析。在图 7中,经济损失P-P图(probability plot)的所有点近似在一条直线上;Q-Q图(quantile plot)除了几个异常经济损失外,所有的点也基本都在一条直线上。从重现水平图(return level plot)看,所有的样本数据都落在指定分布的置信区间内部。另外,由于损失数据未做对数化处理,数量级上存在较大差异,因此密度曲线(density plot)的估计图与直方图的吻合效果不佳。用同样的方法对受灾面积阈值超出量分析的诊断图进行分析,也证明了运用POT模型及GPD分布拟合是合理的。
(三) Copula函数的参数估计及拟合检验将前面得到的阈值以及估计出的参数值代入GPD分布函数中,再由(4)式,得到尾估计,低于阈值的部分用经验分布。由于Copula函数的定义域是﹝0, 1﹞,因此,经过概率积分变换得到〔0, 1〕上的分布序列{Vi,Wi}。再将序列{Vi,Wi}当作Copula的观测值,对各Copula函数中的参数进行最大似然估计。由于不同的Copula函数所描述的是不一样的相关关系,因此针对所研究随机变量间的相关关系,如何选出最合适的Copula函数是非常重要的。为此,采用KS检验和AD检验对各Copula函数进行显著性检验。Copula函数的参数估计与KS、AD检验结果如表 3所示,三种Copula函数都可以通过这两种检验,但Gumbel Copula函数的p值在这两种检验法下都是最大的,因此采用Gumbel Copula函数来描述变量间相关关系最为合适。
| 表 3 Copula函数的参数估计与KS、AD检验结果 |
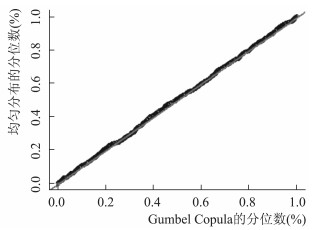
再采用Q-Q图法,可以从图 9直观地看到,Gumbel Copula拟合效果很好。
|
图 9 Gumbel Copula的Q-Q图 |
通过Gumbel Copula函数的相依结构,进而就可以得到损失变量X和Y的联合分布函数:
| $ F(x,y) = {\rm{exp}}\{ - {[{( - {\rm{ln}}{F_X}(x))^{1.2109}} + {( - {\rm{ln}}{F_Y}(y))^{1.2109}}]^{1/1.2109}}\} $ | (9) |
在已知损失变量Y=y的条件下,由前面得到的Gumbel Copula的条件分布函数,考察不同置信水平时的CVaR取值:
| $ F(x|y) = \frac{{{\rm{exp}}( - {A^{1/1.2109}}){A^{[(1 - 1.2109)/1.2109]}}{{( - {\rm{ln}}{F_Y}(y))}^{1.2109 - 1}}}}{{{F_Y}(y)}} $ |
其中,A=(-lnFX(x))1.2109+(-lnFY(y))1.2109。由于该条件分布函数的反函数无解析解,因此使用数值方法求CVaR。当受灾面积取历史数据的75%分位点(即y=13.247 6)时,不同置信水平下的CVaR值如表 4所示。
| 表 4 y=13.247 6时,不同置信水平下的CVaR值 |
表 4说明当受灾面积y=13.247 6时,发生一次洪灾时经济损失不超过395.8百万美元的概率是75%,不高于1 354.4百万美元的概率是90%,不超过10 996.9百万美元的概率是99%。
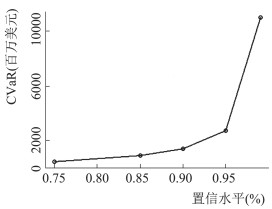
为了对CVaR的变化情况有更直观的了解,将CVaR值绘图,如图 10所示。可以看出,随着置信水平的提高,CVaR开始阶段缓慢增长,但是随着置信水平的进一步提升,CVaR呈现出指数级增长,尤其在置信水平0.97附近,CVaR出现跳跃,说明在此时CVaR对置信水平的变化极为敏感。这是由于巨灾损失具有厚尾特征,因此当置信水平很高时,即使很小的置信水平变化,也会使相应置信水平下的巨灾可能最大损失变化非常大。对于这个区间的巨额损失,保险公司的风险管理模式除了通过巨灾债券市场转移,还可以通过成立巨灾保险基金等方式,将巨灾风险转移到资本市场。
|
图 10 不同置信水平下的CVaR值 |
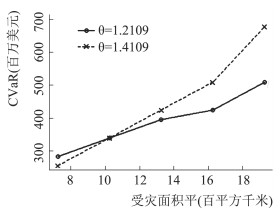
考察不同条件y时,CVaR值的变化情况。当置信水平p=0.75,分别在Copula参数θ=1.210 9和θ=1.410 9情况下,计算受灾面积y在8~20范围内的CVaR取值。从图 11可以看出,CVaR值随着y的增大而增大,并且CVaR值和y表现出一定的线性关系。也就是说,如果受灾面积越大,那么洪灾造成的经济损失也就越大,这与现实经验是相符的。另外,从图 11还可以看到,相较于θ=1.210 9,当θ=1.410 9时所对应的直线斜率更大,即变量间关系越紧密时,CVaR对y的变化越敏感。
|
图 11 不同受灾面积下的CVaR值 |
与上面类似的方法,还可以考察在给定经济损失变量X=x的条件下,关于变量Y的CVaR敏感度分析。由于结果相似,这里不再列出。
为凸显本文所建模型的优越性,以已有的洪水巨灾损失估计POT模型[16]和常用损失拟合分布正态-Copula模型、对数正态-Copula模型作为比较对象。以前述Gumbel Copula的参数估计结果为基础,利用R软件随机产生1 000组损失随机数用于模型的检验。表 5列出了几种模型在90%、95%和99%置信水平下的CVaR估计结果。如表 5可知:(1)POT-Copula模型的估计结果在三个不同置信水平下要比POT模型更接近失败次数的期望值。这说明综合考虑多种洪水巨灾损失风险,在一定受灾面积条件下给出的经济损失风险度量值,可以充分利用洪灾损失信息,从而有效地改进已有的洪水巨灾经济损失估计模型,但这对政府建立的巨灾损失数据库的准确性和全面性提出了更高的要求,才能保证模型估计的准确性。(2)正态-Copula模型则在三个置信水平下都低估了巨灾风险,所得到的CVaR估计失败次数明显超过期望失败次数;对数正态-Copula模型在较低的置信水平下与POT-Copula模型的估计效果无显著差异,但在较高置信水平下的估计效果则明显不如POT-Copula模型。这表明巨灾损失厚尾特征的准确刻画是估计巨灾损失的关键,而本文使用的POT模型对巨灾损失边缘分布的拟合效果要优于常用损失分布。
| 表 5 不同模型CVaR估计结果比较 |
巨灾事件发生次数少,但损失巨大,具有明显的尖峰厚尾特征,因此巨灾损失较一般风险难以估计。本文采用极值理论中的POT模型拟合了洪水经济损失和受灾面积的边缘分布,并利用二元阿基米德Copula函数刻画了巨灾损失变量之间的相依结构,从而得到巨灾损失的CVaR值。利用KS检验和AD检验从常用阿基米德Copula函数中进行拟合优度检验,结果表明Gumbel Copula拟合效果很好,可以很好地反映两者在极端情况下的相依结构。最后,利用数值方法计算出CVaR值并进行了敏感度分析,结果表明Copula函数的参数对CVaR的影响是十分显著的,相关系数越大,CVaR越敏感。这验证了本文利用Copula模型刻画巨灾变量间相关关系的必要性。
在进行巨灾衍生品定价时,有必要充分考虑巨灾损失变量之间的相关性,尤其在设定损失变量触发水平时,这样可以使巨灾衍生品定价更加贴合市场实际,满足投资者的需求,推动巨灾衍生品市场的发展。
| [1] |
周孝华, 张燕. 一种新的风险价值(VaR)计算方法及其应用研究[J]. 管理学报, 2008, 5(6): 819-823. DOI:10.3969/j.issn.1672-884X.2008.06.006 |
| [2] |
魏宇. 股票市场的极值风险测度及后验分析研究[J]. 管理科学学报, 2008, 11(1): 78-88. DOI:10.3321/j.issn:1007-9807.2008.01.009 |
| [3] |
姬新龙, 周孝华. 基于马尔科夫随机波动和极值理论的风险测度[J]. 中国管理科学, 2014, 22(10): 44-51. |
| [4] |
李锦成. 基于MCMC参数估计的POT极值理论度量影子银行与A股市场VaR-ES[J]. 中央财经大学学报, 2017(5): 39-49. |
| [5] |
郝军章, 崔玉杰. 基于POT模型的巨灾风险度量与保险模式研究——以地震风险为例[J]. 数理统计与管理, 2016, 35(1): 132-141. DOI:10.13860/j.cnki.sltj.20150213-002 |
| [6] |
GANGULI P, REDDY M J. Risk assessment of droughts in Gujarat using bivariate Copulas[J]. Water resources management, 2012, 26(11): 3301-3327. DOI:10.1007/s11269-012-0073-6 |
| [7] |
SHE D, XIA J. Copulas-based drought characteristics analysis and risk assessment across the loss plateau of China[J]. Water resources management, 2018, 32: 547-564. DOI:10.1007/s11269-017-1826-z |
| [8] |
JOYCE J, CHANG N B, HARJI R, et al. Coupling infrastructure resilience and flood risk assessment via copulas analyses for a coastal green-grey-blue drainage system under extreme weather events[J]. Environmental modelling and software, 2018, 100: 82-103. DOI:10.1016/j.envsoft.2017.11.008 |
| [9] |
巢文, 邹辉文. 基于藤Copula模型的巨灾风险条件VaR预测[J]. 系统科学与数学, 2017, 37(11): 2222-2231. |
| [10] |
李明, 张永清, 张莲芝. 基于Copula函数的长春市106年来的干旱特征分析[J]. 干旱区资源与环境, 2017, 31(6): 147-153. |
| [11] |
PICKANDS J. Statistical inference using extreme order statistics[J]. The annals of statistics, 1975, 3(1): 119-131. DOI:10.1214/aos/1176343003 |
| [12] |
EMBRECHTS P, HOING A, JURI A. Using Copula to bound the value at risk for functions of dependent risks[J]. Finance and stochastics, 2003, 7(2): 145-167. |
| [13] |
KUMAR P, SHOUKRI M M. Evaluating aortic stenosis using the Archimedean Copula methodology[J]. Journal of data science, 2008, 6(2): 173-187. |
| [14] |
韦艳华, 张世英. Copula理论及其在金融分析上的应用[M]. 北京: 清华大学出版社, 2008.
|
| [15] |
STUART C. An introduction to statistical modeling of extreme values[M]. New York: Springer-Verlag, 2001.
|
| [16] |
肖海清, 孟生旺. 极值理论及其在巨灾再保险定价中的应用[J]. 数理统计与管理, 2013, 32(2): 240-246. |
 2020, Vol. 22
2020, Vol. 22

