为了打破传统电网企业的垄断、提高输电效率、优化资源配置,构建一个公平、开放、有序、健康的电力市场体系,我国对电力市场进行了以市场化为主导的改革。中共中央、国务院2015年3月下发的《关于进一步深化电力体制改革的若干意见》(中发〔2015〕9号)(以下简称“9号文”)拉开了新一轮电力体制改革的序幕[1],提出了“输配电价逐步过渡到‘准许成本加合理收益’的原则”。“准许成本加合理收益”的原则本质上是投资回报率管制模式,但是投资回报率模式并不会改变电网企业垄断地位,这会导致政府和电网企业关于输电电价成本信息不对称。为了获得超额利润,电网企业有申报虚假成本的动机,这不仅不利于电网企业健康发展,而且会损害社会福利[2]。有效的政府监管机制是对投资回报率模式的弥补,研究在“准许成本加合理收益”的监管机制下,政府采取何种监管机制,才能有效地促进电网企业披露真实成本信息,保证电网企业申报真实成本,对于电力市场健康发展具有重要意义。
对于政府如何监管和规制电网企业的行为,相关学者进行了大量的研究(方德斌、刘文婷[3];杨先菊等[4];张慧峰等[5];蔡建刚,叶泽[6];李昂等[7]),但是,在目前的研究中均假设政府和电网企业为完全理性博弈主体[8-9]。而电网企业在申报成本的过程中,一方面由于政府和电网企业群体数量较少,另一方面电网企业存在为了短期利益而申报虚假成本的行为,政府在监管过程中也存在为了盲目促进电网企业发展而给予电网企业过高利润的现象,导致政府和电网企业均为有限理性的博弈主体,需要通过不断的学习来完善自身行为[10-11]。因而,政府和电网企业是以一种动态的方式来达到均衡过程和均衡结果,采用演化博弈模型来分析政府和电网企业的输电电价监管博弈均衡更加符合实际[12-13]。
本文的创新之处在于:一是考虑政府和电网企业均为有限理性的博弈主体,利用演化博弈方法,通过构建政府和电网企业输电监管博弈模型来分析政府和电网企业之间的博弈行为,并通过数值分析研究了政府和电网企业初始状态对演化博弈结果的影响;二是将电网企业成本分为虚假成本和真实成本两部分,将政府的惩罚力度与电网企业申报虚假成本比率相联系,使政府的监管机制更加合理。
二、文献综述采取何种输电监管机制既能提高输电效率,又能促进电力市场电价公平一直是国内外学者研究的焦点。目前,国际上主流的输电监管模式是投资回报率监管模式和价格上限监管模式。投资回报率监管模式也称成本加成模式,该模式可以保证电网企业得到足够的补偿,同时方便政府定价,但是这种模式也存在不足。例如:Averch和Johnson指出,在投资回报率管制模式下,被管制的企业为了获得超额利润,可能会过度使用资本,带来资源配置扭曲,产生“A-J效应”[14];张忠东[15]、赵会茹[16]等指出了投资回报率管制模式存在两个明显缺陷:企业缺乏降低成本的动机和存在受管制企业为了获得信息租金而虚报真实成本的现象。价格上限监管模式很好地克服了投资回报率监管模式的缺陷,但是价格上限监管模式是建立在一个合理的基价基础之上的,而我国目前没有一个合理的输电电价基价,价格上限监管模式并不适合我国。因此,为了促进电网企业健康发展,在投资回报率模式下,监管电网企业的电价申报行为就很有必要。
对于政府如何监管和规制电网企业的行为,相关学者进行了大量的研究。从政策激励角度出发,吴珊等在分析新电改的基础上,提出构建一个电网投资监管的激励与约束兼容机制[17];梁耀林等认为在输配电价监管模式下, 电网企业将合理优化电网投资和提高输配电服务水平, 促进电网的良性发展[18];张慧峰等提出了基于激励性管制的输配电价模型[5];蔡建刚、叶泽在激励相容机制基础上,建立了输配电企业价格管制模型[6];李昂等基于让·梯诺尔条件约束下的激励机制,提出了第三方企业监管的机制,以解决输电成本核算及申报过程中的信息不对称等问题[7];Silva等[19]、张少华等[20]、谢俊等[21]研究了激励相容的输电市场竞价机制问题;Roy从技术角度对输电电价定价模型进行了探讨[22]。
从政府规制角度出发,方德斌、刘文婷基于主从博弈,建立了电力市场政府和电网企业的博弈模型[3];蒋金良等运用演化博弈模型构建了电力监管模型[23];杨先菊等建立了政府与电网企业间两阶段微分博弈模型[4];宋宗耘等采用动态演化博弈模型分析了电力需求侧管理过程中政府-电网企业、政府-电力用户之间的博弈行为[25];曾鸣等利用仿真分析研究了输配电价与各影响因素之间的关系[24]。
博弈论模型是研究输电监管机制的一种有效方法[25],但是,目前的研究中均假设政府和电网企业为完全理性博弈主体[8-9],较少从有限理性角度研究政府和电网企业之间输电电价监管博弈均衡。因此笔者尝试假设政府和电网企业均为有限理性的博弈主体,构建政府和电网企业输电电价监管演化博弈模型,揭示政府和电网企业之间输电电价监管博弈均衡,并进一步分析政府监管成功率、电网企业“合理利润”比率、政府处罚力度和公众监督概率对政府和电网企业的输电电价监管演化稳定均衡的影响。
三、问题描述在电力改革背景下,政府出台了一系列的政策引导电网企业改革,因此政府对电网企业行为已经由是否监管问题转变为如何监管问题。因此,本文假设政府监管的策略集合为{主动监管,被动监管},其中, 主动监管指政府定期对电网企业进行监管的策略行为,被动监管是指电网企业被第三方举报申报虚报成本之后,政府采取监管措施的策略行为;假设电网企业的策略集合为{申报真实成本, 申报虚假成本}。
假设c11为电网企业输送一单位电量所付出的真实成本;假设θ为电网企业申报的虚假成本占真实成本的比率,则电网企业申报的虚假成本为c11(1+θ);假设在输电过程中没有电量损耗及回流等现象,也等于销售电量,即电网企业输电量为q;根据“9号文”提出的输电电价为“准许成本加合理收益”原则,假设α为政府设定的电网企业输送一单位电量的利润占成本的比例,则在申报真实成本和申报虚假成本两种情况下,电网企业的利润分别为αc11q和(α+θ+αθ)c11q;c21为政府主动监管付出的成本,c22为政府被动监管付出的成本,同时由于被动监管是在掌握第三方举报信息基础上进行,因此c21>c22>0;假设公众不存在恶意举报行为,c23为政府给予第三方举报者的奖励,则政府被动监管的总成本为c22+c23。
假设政府主动监管发现电网企业申报虚假成本的概率为p1,政府被动监管发现电网企业申报虚假成本的概率为p2,因为被动监管是在掌握第三方举报信息基础上进行,因此p2>p1>0;同时c21、c22、c23与p1、p2存在如下函数关系:p1=f(c21),p2=f(c22, c23),其中f′(c21)>0,f′(c22, c23)>0,f″(c21) < 0,f″(c22, c23) < 0,即政府的监管成本投入呈现边际效用递减规律;假设β为政府发现电网企业申报虚假成本后电网企业所受惩罚占电网企业申报虚假成本带来的额外收益的比例;ε为电网企业申报虚假成本所受的除罚金以外的损失(包括信誉损失等),则电网企业申报虚假成本可能遭受的损失为β(θ+αθ)c11q+ε,同时为了防止电网企业投机行为,有(θ+αθ)c11q < p1[(θ+αθ)βc11q+ε]和(θ+αθ)c11q < λp2[(θ+αθ)βc11q+ε]成立;假设π为政府发现电网企业申报虚假成本而得到的除罚金以外的收益(社会福利增加、促进社会公平等),则政府发现电网企业申报虚假成本的收益为π+β(θ+αθ)c11q;假设λ为第三方监督概率,即电网企业被第三方举报申报虚假成本的概率。
四、政府和电网企业演化博弈分析 (一) 模型构建根据演化博弈理论[26],假设在电网企业中,选择申报真实成本的群体和选择申报虚假成本的群体比例分别为x、1-x,政府选择主动监管和被动监管的概率分别为y、1-y,则政府和电网企业之间的演化博弈模型如表 2所示。
| 表 2 政府和电网企业演化博弈矩阵 |
电网企业选择申报真实成本的适应度为:
| $ {u_{11}} = \alpha {c_{11}}q $ | (1) |
电网企业选择申报虚假成本的适应度为:
| $ {u_{12}} = \left( {\theta + \alpha + \alpha \theta } \right){c_{11}}q - y{p_1}\left[ {\left( {\theta + \alpha \theta } \right)\beta {c_{11}}q + \varepsilon } \right] - \left( {1 - y} \right)\lambda {p_2}\left[ {\left( {\theta + \alpha \theta } \right)\beta {c_{11}}q + \varepsilon } \right] $ | (2) |
平均适应度为:
| $ {u_1} = x{u_{11}} + \left( {1 - x} \right){u_{12}} $ | (3) |
则电网企业的复制动态方程为:
| $ {U_1}\left( {x,y} \right) = \partial x/\partial y = x\left( {{u_{11}} - {u_1}} \right) = x\left( {1 - x} \right)\left[ {{\gamma _2} + \left( {{\gamma _1} - {\gamma _2}} \right)y} \right] = 0 $ | (4) |
式中,γ1=p1[(θ+αθ)βc11q+ε]-(θ+αθ)c11q,γ2=λp2[(θ+αθ)βc11q+ε]-(θ+αθ)c11q;γ1为在政府主动监管下,电网企业申报虚假成本的可能遭受的期望惩罚,γ2为在政府被动监管下,电网企业申报虚假成本的可能遭受的期望惩罚。同时因为(θ+αθ)c11q < p1[(θ+αθ)βc11q+ε]和(θ+αθ)c11q < λp2[(θ+αθ)βc11q+ε],所以γ1>0,γ2>0。由(4)式可得x1*=0,x2*=1,y*=γ2/(γ2-γ1)。对于式(4)求导:
| $ U_1^\prime \left( {x,y} \right) = \left( {1 - 2x} \right)\left[ {{\gamma _2} + \left( {{\gamma _1} - {\gamma _2}} \right)y} \right] $ | (5) |
根据Frideman[27]提出的方法,当U1(x*)=0,U′1(x*) < 0时,x1*为演化稳定策略(ESS)。因为γ1>0,γ2>0,所以y* < 0,或者y*>1,则y只存在y* < y或y*>y两种情况。
(1) 当y*>y时,因为U1(1)=0,U′1(1) < 0,即当电网企业在政府主动监管情况下申报虚假成本可能遭受的惩罚大于政府被动监管情况下申报虚假成本可能遭受的惩罚,电网企业最优策略是申报真实成本。
(2) 当y* < y时,因为U1(0)=0,U′1(0) < 0,即当电网企业在政府主动监管情况下申报虚假成本可能遭受的惩罚小于被动监管情况下可能遭受的惩罚,电网企业最优策略是申报虚假成本。
因此我们可以发现,为了促使电网企业申报真实成本,应该加大在主动监督时发现电网企业申报虚假成本时的惩罚,通过严厉的惩罚促使电网企业申报真实成本。
同理,政府选择主动监管的适应度、选择被动监管的适应度以及平均适应度分别为:
| $ {u_{21}} = \left( {1 - x} \right){p_1}\left[ {\left( {\theta + \alpha \theta } \right)\beta {c_{11}}q + {\rm{ \mathsf{ π} }}} \right] - {c_{21}} $ | (6) |
| $ {u_{22}} = \left( {1 - x} \right)\lambda {p_2}\left[ {\left( {\theta + \alpha \theta } \right)\beta {c_{11}}q + {\rm{ \mathsf{ π} }}} \right] - \lambda \left( {{c_{22}} + {c_{23}}} \right) $ | (7) |
| $ {u_2} = y{u_{21}} + \left( {1 - y} \right){u_{22}} $ | (8) |
则政府的复制动态方程为:
| $ {U_2}(x,y) = \partial x/\partial y = y\left( {{u_{21}} - {u_2}} \right) = y(1 - y)\left( { - {\delta _1} + {\delta _2} - {\delta _2}x} \right) = 0 $ | (9) |
式中δ1=c21-λ(c22+c23),δ2=(p1-λp2)[π+(θ+αθ)c11βq];δ1为政府主动监管期望成本与被动监管期望成本的差值,δ2为政府主动监管期望收益与被动监管期望收益的差值。由(9)式可得y1*=0,y2*=1和x*=(δ2-δ1)/δ2。对式(9)进行求导:
| $ U_2^\prime (x,y) = (1 - 2y)\left( { - {\delta _1} + {\delta _2} - {\delta _2}x} \right) $ | (10) |
现在讨论x*=(δ2-δ1)/δ2取值范围不同,即政府不同的策略行为。
(1) 当x=x*时,U2(y*)=0,U′2(y*)=0。对所有x轴水平都是稳定的,也就是当电网企业申报真实成本比率为x = x*时,所有政府主动监管和被动监管的概率是稳定的。
(2) 当x>x*时,因为当y2*=0时,U2(0)=0,U′2(0) < 0成立,即当电网企业申报虚假成本的可能性比较大时,政府的最优策略选择是被动监管。
(3) 当x < x*时,因为当y2*=1时,U2(1)=0,U′2(1) < 0成立,即当电网企业申报虚假成本的可能性比较小时,政府的最优策略选择是主动监管。
通过分析发现,只有当电网企业申报真实成本的概率足够大时(x>x*),政府才会选择主动监管,这也说明了政府主动监管比被动监管更有效。由式(4)和式(9)可以得到一个二维动力系统(Ι):
| $ \left\{ {\begin{array}{*{20}{l}} {{U_1}(x,y) = \partial x/\partial y = x\left( {{u_{11}} - {u_1}} \right) = x(1 - x)\left[ {{\gamma _2} + \left( {{\gamma _1} - {\gamma _2}} \right)y} \right]}\\ {{U_2}(x,y) = \partial x/\partial y = y\left( {{u_{21}} - {u_2}} \right) = y(1 - y)\left( { - {\delta _1} + {\delta _2} - {\delta _2}x} \right)} \end{array}} \right. $ | (11) |
命题1:系统(I)的纳什均衡点为(0, 0), (0, 1), (1, 0), (1, 1)。
证明:在系统(I)中,分别令U1(x, y)=0,U2(x, y)=0,求解可知,点(0, 0), (0, 1), (1, 0), (1, 1)为系统均衡点。
(二) 均衡及稳定点分析系统(I)的均衡点为(0, 0),(0, 1),(1, 0),(1, 1),当复制动态方程的雅克比(Jacobian)矩阵在上述不动点处的行列式大于零,迹小于零时,该点即为演化稳定均衡点(ESS)[22]。
系统(I)对应的雅克比矩阵为:
| $ \mathit{\boldsymbol{J}} = \left( {\begin{array}{*{20}{l}} {\partial {U_1}/\partial x}&{\partial {U_1}/\partial y}\\ {\partial {U_2}/\partial x}&{\partial {U_2}/\partial y} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\left( {1 - 2x} \right)\left[ {{\gamma _2} + \left( {{\gamma _1} - {\gamma _2}} \right)y} \right]}&{\left( {{\gamma _1} - {\gamma _2}} \right)x(1 - x)}\\ { - {\delta _2}y\left( {1 - y} \right)}&{(1 - 2y)\left( { - {\delta _1} + {\delta _2} - {\delta _2}x} \right)} \end{array}} \right) $ | (12) |
该矩阵对应的行列式和迹表达式分别为:
| $ \left\{ \begin{array}{l} \det .\mathit{\boldsymbol{J}} = (1 - 2x)(1 - 2y)\left( { - {\delta _1} + {\delta _2} - {\delta _2}x} \right)\left[ {{\gamma _2} + \left( {{\gamma _1} - {\gamma _2}} \right)y} \right] + {\delta _2}\left( {{\gamma _1} - {\gamma _2}} \right)xy(1 - x)(1 - y)\\ {\rm{tr}}.\mathit{\boldsymbol{J}} = (1 - 2x)\left[ {{\gamma _2} + \left( {{\gamma _1} - {\gamma _2}} \right)y} \right] + (1 - 2y)\left( { - {\delta _1} + {\delta _2} - {\delta _2}x} \right) \end{array} \right. $ | (13) |
将系统(I)的均衡点带入式(12),整理后得到矩阵行列式和迹表达式如表 3所示。
| 表 3 系统(I)的雅克布矩阵行列式和迹分析 |
同时,由各个点det.J和tr.J的表达式可知,δ1、δ2、γ1和γ2之间的关系会影响各个点det. J和tr. J值的大小,进而影响各个点的稳定性。下面从δ1、δ2、γ1和γ2之间的关系出发对各个点稳定性进行讨论。
命题2:当δ1 < 0,0 < γ1时,系统的演化稳定均衡点为C(1, 1)。
证明:根据演化博弈理论,当一个点满足det. J>0,tr. J < 0时,该点为演化稳定均衡点[27]。因此,当δ1 < 0 < γ1时,对于点C(1, 1),det. J>0,tr. J < 0,故点C(1, 1)为稳点演化均衡点。
由命题2可知,当政府主动监管期望成本小于被动监管期望成本,且政府主动监督相对期望成本小于在政府主动监管下电网企业申报虚假成本可能遭受的期望惩罚时,政府和电网企业演化稳定策略为{申报真实成本, 主动监管}。因此,此时为了促进电网申报真实成本,政府通过控制主动监管成本,同时加大在主动监管下发现电网企业申报虚假成本的惩罚力度。
命题3:当δ1>0时,系统的演化稳定均衡点为B(1, 0)。
证明同命题2证明,故略。
由命题3可知,当政府主动监管期望成本大于被动监管期望成本时,政府和电网企业演化稳定策略为{申报真实成本, 被动监管}。
命题4:系统的演化稳定均衡点不可能为点O(0, 0)和点A(0, 1)。
证明:对于点O(0, 0),det. J=(-δ1+δ2)γ2,tr. J=γ2-δ1+δ2, 因为γ2>0,当δ1>δ2时,det. J < 0;当δ1 < δ2时,tr. J>0。对于点A(0, 1),det. J=(δ1-δ2)γ1,tr. J=γ1+δ1-δ2,因为γ1>0,当δ1>δ2时,tr. J>0;当δ1 < δ2时,det. J < 0,故点O(0, 0)和点A(0, 1)不可能为系统演化稳定均衡点。
命题4表明,在目前的强监管机制下,电网企业不存在虚报成本的可能性。
由命题2至4可知,在目前的强监管机制下,电网企业最优的策略选择是申报真实成本,而政府的监管策略选择与主动监管和被动监管成本之间的关系有关。
五、结果讨论由前面的分析可以得知,当δ1 < 0 < γ1时,系统的演化稳定均衡点为C(1, 1);当δ1>0时,系统的演化稳定均衡点为B(1, 0)。在这两种情况下,由于监管力度能够有效地防止电网企业投机行为,因此电网企业最优的策略是选择申报真实成本,而政府的策略选择与政府主被动监管成本之间的关系有关。
(一) 政府监管成功率由δ1 < γ1可得:
| $ {c_{21}} - \lambda \left( {{c_{22}} + {c_{23}}} \right) < {p_1}\left[ {(\theta + \alpha \theta )\beta {c_{11}}q + \varepsilon } \right] - (\theta + \alpha \theta ){c_{11}}q $ | (14) |
同时因为(θ+αθ)c11q < p1[(θ+αθ)βc11q+ε], δ1 < 0,政府主动监管成功率应该满足如下约束:
| $ {p_1} > \frac{{(\theta + \alpha \theta ){c_{11}}q}}{{(\theta + \alpha \theta )\beta {c_{11}}q + \varepsilon }} $ | (15) |
当δ1>0时:
| $ {c_{21}} > \lambda \left( {{c_{22}} + {c_{23}}} \right) $ | (16) |
因为p1=f(c21),所以c21=f-1(p1),此时p1应该满足如下不等式:
| $ {f^{ - 1}}\left( {{p_1}} \right) > \lambda \left( {{c_{22}} + {c_{23}}} \right) $ | (17) |
从式(15)和式(17)中可以得到以下几点结论:
输电量越大的电网企业,政府主动监管力度应该越大。输电量越大的企业,申报虚假成本带来的收益越大,申报虚假成本的动机也就越大,因此政府应该针对不同规模的企业采取不同的监管力度。同时应该防止小企业“搭便车”的现象,保证每一个电网企业都受到合理监管。
电网企业申报成本越高,政府主动监管的力度应该越大。对于申报成本比较高的企业,政府应该警惕虚假成本;也应该分析电网企业成本构成,避免资本投入过度,造成电网行业不健康发展。
当电网企业申报虚假成本受到的除罚金以外的损失较高时,政府可以降低主动监督力度。政府可以通过建立良好的征信环境,通过外部的约束来防止电网企业申报虚假成本。
(二) 合理利润当δ1 < 0, 0 < γ1时,由式(14)同时考虑约束条件(θ+αθ)c11q<p1[(θ+αθ)βc11q+ε]和(θ+αθ)c11q<λp2[(θ+αθ)βc11q+ε],可得政府给予电网企业合理利润比率应该满足如下约束:
| $ \alpha > \max \left\{ {\frac{{{p_1}\varepsilon }}{{\theta {c_{11}}q\left( {{p_1}\beta - 1} \right)}} - 1,\frac{{\lambda {p_2}\varepsilon }}{{\theta {c_{11}}q\left( {{p_1}\beta - 1} \right)}} - 1} \right\} $ | (18) |
由式(18)可以得出以下几点结论:
政府主动监管成功率越高,政府可以给予电网企业的利润就越高。当政府主动监管成功率比较高时,由于政府监管有力,电网企业申报虚假成本的可能性较低,因此可以根据实际情况,给予电网企业更大的合理利润比例,促进电网企业发展。
政府发现电网企业申报虚假成本后电网企业所受惩罚越高,政府应该给予电网企业较低的利润率。如果一方面政府对于电网企业的惩罚较高,另一方面政府又给予电网企业较高的合理利润率,那么惩罚的效果将会大大减弱,因此在提高惩罚力度的同时,应该降低合理利润率。
电网企业申报成本越高,政府应该给予电网企业较低利润。对于申报的成本比较高的企业,申报的成本为虚假成本的可能性也就越大,此时政府给予的合理利润值也应该相对较小。
(三) 政府惩罚力度当δ1 < 0, 0 < γ1时,由式(14)同时考虑约束条件(θ+αθ)c11q<p1[(θ+αθ)βc11q+ε]和(θ+αθ)c11q < λp2[(θ+αθ)βc11q+ε],可得政府惩罚力度应该满足如下约束:
| $ \beta > \max \left\{ {\frac{{\left( {\theta + \alpha \theta } \right){c_{11}}q - \lambda {p_2}\varepsilon }}{{\lambda {p_2}(\theta + \alpha \theta ){c_{11}}q}},\frac{{(\theta + \alpha \theta ){c_{11}}q - {p_1}\varepsilon }}{{{p_1}(\theta + \alpha \theta ){c_{11}}q}}} \right\} $ | (19) |
由式(19)可以得出以下几点结论:
电网企业申报虚假成本比例越高,政府惩罚力度应该越大。只有通过较高的惩罚力度,才能有效抑制电网企业申报虚假成本。
对于规模越大的电网企业,政府的惩罚力度应该越大。电网企业规模越大,其申报虚假成本带来的利润也就越高,此时政府应该对其申报虚假成本给予较高的惩罚。
电网企业申报虚假成本受到的除罚金以外的处罚越高,政府可以给予电网企业较低的惩罚。当电网企业申报虚假成本受到的除罚金以外的惩罚越高时,由于外部环境和市场以及给予电网企业较高的惩罚,因此此时为了不阻碍电网企业正常发展,政府应该降低其惩罚力度。
(四) 第三方监督由前面分析可知,当δ1 < 0时,政府最优策略选择为主动监管,此时:
| $ \lambda > {c_{21}}/\left( {{c_{22}} + {c_{23}}} \right) $ | (20) |
当δ1>0时,政府最优策略选择为被动监管,此时:
| $ \lambda < {c_{21}}/\left( {{c_{22}} + {c_{23}}} \right) $ | (21) |
由式(20)和式(21)可以得知,当第三方监督概率比较高时(λ>c21/(c22+c23)),由于电网企业能够受到足够的第三方监督,此时政府可以选择被动监督;当第三方监督概率比较低时,社会对电网企业不能很好地监督电网企业行为,此时政府应该选择主动监督,防止电网企业申报虚假成本。
六、数值分析为了更好地研究政府和电网企业初始状态对模型稳定性的影响,同时研究公众监督概率情况下对政府和电网企业演化稳定性的影响,本文对政府和电网企业二维动态模型相关参数进行合理赋值,模拟系统收敛于理想演化稳定均衡路径,分析政策工具对博弈参与方演化稳定策略影响。
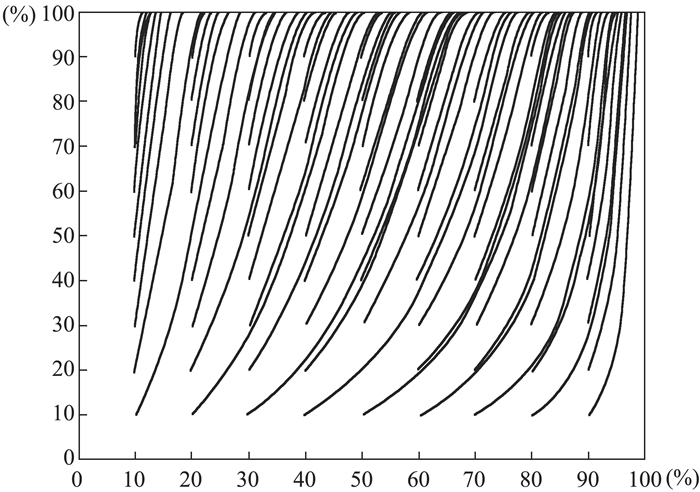
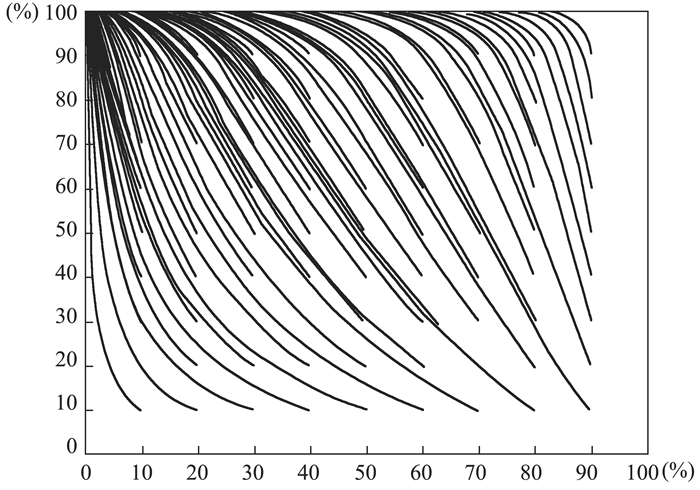
模型变量与参数赋值应该满足经济学假设和实际判断[28]。根据电网实际情况与相关学者研究经验,本文相关参数赋值如下:根据2017年《中国电力年鉴》中披露的成本信息,根据演化博弈模拟实际情况,令c11=200元/MWh,α=20%;假设q=1×108MWh,c21=2×106,根据c21≥c22,(θ+αθ)c11q < p1[(θ+αθ)βc11q+ε]和(θ+αθ)c11q < λp2[(θ+αθ)βc11q+ε],假设c22=1.5×106,c23=1×106;假设β=130%;根据实情况,假设ε=1.2×108,π=9.36×107,θ=1%。下面分别模拟政府主被动监督成功率、第三方监督概率较高情况(p1=60%, p2=80%, λ=80%)和政府主被动监督成功率、第三方监督概率较低情况(p1=10%, p2=20%, λ=10%)下,政府和电网企业演化状态,仿真结果分别见图 1、图 2。
|
图 1 政府主被动监督成功率、第三方监督概率较高情况 |
|
图 2 政府主被动监督成功率、第三方监督概率较低情况 |
由仿真结果可知,政府和电网企业最终达到的演化稳定状态与政府和电网企业初始状态无关,与政府主被动监督成功率、第三方监督概率有关。当政府监管成功率、第三方监督成功率较高时,政府会选择被动监督,电网企业会选择申报真实成本;反之政府会选择被动监督,电网企业会选择申报虚假成本。
七、结论本文在假设政府和电网企业均为有限理性的博弈主体基础上,运用演化博弈理论,构建了政府和电网企业输电电价监管演化博弈模型,揭示了政府和电网企业之间的输电电价监管演化博弈均衡,分析了政府监管成功率、电网企业“合理利润”比例、政府处罚力度和公众监督概率对政府和电网企业的输电演化稳定均衡的影响,在此基础上进行数值分析,分析了政府和电网企业初始状态对演化稳定均衡的影响。研究结果表明:在目前监管模式下,电网企业演化稳定策略为申报真实成本,政府监管策略与政府主动监管和被动监管成本之间相对大小关系有关;政府监管的成功率、“合理利润”比例、政府处罚力度和第三方监督概率存在临界值,政府和电网企业初始状态并不会影响演化博弈结果。具体包括以下几点:
政府发现电网企业申报虚假成本之后,采用按申报虚假成本比例惩罚更有效。当政府的监督机制能够保证电网企业申报虚假成本可能遭受的期望惩罚大于可能获得的期望收益时,电网企业演化博弈均衡策略为申报真实成本,而采用按照申报虚假成本比例惩罚,能够保证电网企业申报虚假成本的期望收益小于零。
政府应该厘清监管的成本结构,进而选择最优的监管方式。根据演化博弈结果,当政府主动监管期望成本小于被动监管期望成本时,政府和电网企业演化博弈均衡为{申报真实成本,主动监管};反之,政府和电网企业演化博弈均衡为{申报真实成本,被动监管}。
政府应该加强对申报成本较高和输电规模较大的电网企业的监管力度。申报成本较高的企业,申报虚假成本的可能性较大;同时输电规模越大的企业申报虚假成本获得的收益也越高。
完善第三方监管体系,可以有效地弥补政府监管的不足。政府应该促进电网企业之间相互监督,促进公众对电网企业的监督,降低政府和电网企业之间的信息不对称,进而保证电网企业披露真实成本信息。
但是由于研究能力的不足,本文还有一些待完善之处。例如本文假设公众不存在恶意举报的现象,但在实际中并非如此。公众的举报行为具有一定的投机性,政府如何建立有效的监管引导机制,避免公众恶意举报的行为,从而构建更加合理的监管体系,对于完善社会监管体系具有重要的意义。
| [1] |
中共中央办公厅.关于进一步深化电力体制改革若干意见(中发[2015]9号)[EB/OL].(2015-03-22).[2019-12-12].http://www.china-nengyuan.com/news/91900.html.
|
| [2] |
POPUTOAIA D, BOUZAROVSKI S. Regulating district heating in romania:legislative challenges and energy efficiency barriers[J]. Energy Policy, 2010, 38(7): 3820-3829. DOI:10.1016/j.enpol.2010.03.002 |
| [3] |
方德斌, 刘文婷. 不完全信息电力市场下政府监管者的目标函数模型研究[J]. 电力自动化设备, 2008, 28(7): 12-17. DOI:10.3969/j.issn.1006-6047.2008.07.003 |
| [4] |
杨先菊, 龚秀松, 赖明勇, 等. 基于Stackelberg微分博弈的销售电价规制模型及其分析[J]. 系统工程, 2009, 27(5): 77-81. DOI:10.3969/j.issn.1009-6744.2009.05.012 |
| [5] |
张慧峰, 吴兵建, 刘发全. 基于激励性管制的输配电价模型研究[J]. 能源技术经济, 2009, 21(2): 55-59. |
| [6] |
蔡建刚, 叶泽. 信息不对称条件下激励相容的输配电价模型研究[J]. 中国管理科学, 2014, 22(5): 91-97. |
| [7] |
李昂, 夏清, 钟海旺. 第三方输电成本监管方法探讨[J]. 电力系统自动化, 2016, 40(10): 1-7. DOI:10.7500/AEPS20160229001 |
| [8] |
LIANG X, MANDAYAM N B, POOR H V. Prospect theoretic analysis of energy exchange among microgrids[J]. IEEE Transactions on Smart Grid, 2017, 6(1): 63-72. |
| [9] |
FADLULLAH Z M, QUAN D M, KATO N, et al. GTES:an optimized game-theoretic demand-side management scheme for smart grid[J]. IEEE Systems Journal, 2014, 8(2): 588-597. DOI:10.1109/JSYST.2013.2260934 |
| [10] |
宋彪, 徐沙沙, 丁庆洋. "一带一路"倡议下企业合作及政府监管的机会主义行为演化博弈分析[J]. 管理评论, 2018(1): 118-126. |
| [11] |
WANG J, ZHI Z, BOTTERUD A. An evolutionary game approach to analyzing bidding strategies in electricity markets with elastic demand[J]. Energy, 2011, 36(5): 3459-3467. DOI:10.1016/j.energy.2011.03.050 |
| [12] |
杨虎涛. 两种不同的生态观——马克思生态经济思想与演化经济学稳态经济理论比较[J]. 武汉大学学报(哲学社会科学版), 2006(6): 735-740. |
| [13] |
SIMON H A. Rationality in psychology and economics[J]. Journal of Business, 1986, 59(4): S209-S224. |
| [14] |
AVERCH H A, JOHNSON L L. Behavior of the firm under regulatory constraint[J]. American Economic Review, 1961, 52(5): 1052-1069. |
| [15] |
张忠东. 成本加收益管制模式下电网企业输配电业务准许收益率的确定[J]. 电力技术经济, 2006, 18(2): 21-23. DOI:10.3969/j.issn.1674-8441.2006.02.008 |
| [16] |
赵会茹, 刘祎, 李春杰. 输配电价格管制中投资回报率水平的确定[J]. 电网技术, 2005, 29(21): 61-66. DOI:10.3321/j.issn:1000-3673.2005.21.013 |
| [17] |
吴珊, 段琪斐, 李成仁, 等. 电网投资监管的激励与约束兼容机制研究——兼析新电改以来监管政策推进与完善[J]. 价格理论与实践, 2019(4): 153-156. |
| [18] |
梁耀林, 郑俊健, 刘伟, 等. 输配电价监管模式下电网企业投资优化策略研究[J]. 智库时代, 2018(38): 94-95. |
| [19] |
SILVA C, WOLLENBERG B F, ZHENG C Z. Application of mechanism design to electric power markets (Republished)[J]. Power Systems IEEE Transactions on, 2001, 16(4): 862-869. |
| [20] |
张少华, 方勇, 李渝曾. 一种激励相容的发电市场竞价机制[J]. 电力系统自动化, 2003, 27(7): 27-31, 69. DOI:10.3321/j.issn:1000-1026.2003.07.006 |
| [21] |
谢俊, 陈星莺. 激励相容的输配分开电力市场竞价机制初探[J]. 电网技术, 2006, 30(8): 60-64. DOI:10.3321/j.issn:1000-3673.2006.08.012 |
| [22] |
ROY A, ABHYANKAR A R, PENTAYYA P, et al. Electricity transmission pricing: tracing based point-of-connection tariff for Indian power system[C].MONTREAL CANADA: Power Engineering Society General Meeting, IEEE, 2006: 2458.
|
| [23] |
蒋金良, 沈彦君. 基于演化博弈的电力需求侧管理监管分析[J]. 华南理工大学学报(社会科学版), 2012(5): 55-61. |
| [24] |
曾鸣, 怀文明, 叶嘉雯, 等. 输配电价监管下供电公司投资规模仿真模型研究[J]. 电力工程技术, 2019, 38(3): 1-7. |
| [25] |
宋宗耘, 张健, 郑泽东, 等. 电力需求侧管理政策激励过程的动态演化博弈分析[J]. 中国电力, 2019(10): 1-11. DOI:10.3969/j.issn.1007-3361.2019.10.001 |
| [26] |
赵昕, 朱连磊, 丁黎黎. 能源结构调整中政府、新能源产业和传统能源产业的演化博弈分析[J]. 武汉大学学报(哲学社会科学版), 2018(1): 145-156. |
| [27] |
FRIDEMAN D. Evolutionary games in economics[J]. Econometrica, 1991, 59(3): 637-666. DOI:10.2307/2938222 |
| [28] |
徐浩, 谭德庆, 张敬钦. 群体性突发事件非利益相关者羊群行为的演化博弈分析[J]. 管理评论, 2019(5): 254-266. |
 2020, Vol. 22
2020, Vol. 22

