2. 福建师范大学 经济学院, 福建 福州 350117
3. 福州大学 经济与管理学院, 福建 福州 350116
4. 福建工程学院 生态环境与城市建设学院, 福建 福州 350118
2. School of Economics, Fujian Normal University, Fuzhou, 350117, Fujian, China
3. School of Economics and Management, Fuzhou University, Fuzhou, 350116, Fujian, China
4. School of Ecological Environment and Urban Construction, Fujian University of Technology, Fuzhou, 350118, Fujian, China
随着经济总量的增长,资源、能源过度消耗,碳排放问题也日益突出。世界各国既对全球气候变暖带来的灾难表示忧心,又对全力实施碳减排存在顾虑。“碳生产率”是指单位二氧化碳排放所带来的经济产出,既要关注经济增长,又要致力于降低碳排放,体现了低碳发展的核心要求。据荷兰环境评估署的报告,中国的碳排放总量于2006年超过美国,成为世界第一大碳排放国[1]。提高碳生产率对于中国这样的碳排放大国来说,意义更加深远。
自2008年世界金融危机以来,外需爆炸式增长和外资大规模涌入的速度迅速放缓。同时,中国的人口红利逐渐消失,产业之间不平衡、不充分发展的矛盾日益突出。外部和内部问题的相互叠加迫使中国经济必须由高增长转向高质量发展。产业结构高级化是指通过产业结构调整实现产业重心由第一向第二和第三产业逐次转移的过程,它强调技术创新,注重科学技术与各产业的融合,是推动经济高质量发展的重要力量。
传统观念认为,产业结构高级化必然提升碳生产率,但其实两者不存在必然的正相关性。因为新技术在研发阶段具有经济产出不确定下投入确定增加的特点,这不利于碳生产率的提升,而在产业化阶段如果不注重清洁生产,也可能会产生更多的碳排放进而降低碳生产率。“互联网+”是信息技术与其他产业融合的典型模式,网上购物、网上订餐的兴起在方便人们生活的同时也因物流运输增加了碳排放,进而可能导致区域碳生产率的总体水平下降。不同的产业,经济产出不同,碳排放水平也各异,这使得在产业结构高级化进程中碳生产率也会发生改变。产业结构高级化能够提升碳生产率是包括低碳技术在内的多种因素共同作用的结果。在愈来愈大的碳减排压力下,中国必须调整产业结构,转变经济增长方式,确保产业结构高级化朝着提升碳生产率的方向持续、深入地推进。
二、文献综述Kaya等最早从经济学视角提出了碳生产率的概念,他们认为碳生产率是单位二氧化碳排放所产生的经济效益,用GDP与二氧化碳排放量之比表示[2]13。Enkvist、Beinhocker等认为碳生产率兼顾降低碳排放和促进经济增长两大发展目标,能够有效反映经济体的碳排放绩效[3, 4]。
影响碳生产率提升的因素很多。国外研究多结合特定行业或特定企业进行针对性分析。Kim等在研究影响韩国农业碳生产率的因素时发现,水稻种植面积、化肥使用量、猪存栏密度与碳生产率呈正相关关系,而奶牛养殖密度与碳生产率呈负相关关系。为了提升碳生产率,农业部门应减少含氮化肥使用密度,实现向高效能源消费结构的转变[5]。Hu等研究了澳大利亚建筑业的碳生产率,发现技术创新是促进碳生产率提升的关键因素,建筑市场规模、机械和设备存量与碳生产率之间存在弱相关性[6]。Nishitani等基于2011年139家上市制造业企业的截面数据,研究了日本制造企业低碳供应链管理对碳生产率的影响,发现低碳供应链管理超越企业内部组织形成跨组织环境控制力,比现有的环境管理体制能够更加有效地提升碳生产率[7]。Kim等研究了碳生产率和资本债务成本之间的关系,发现高排放企业通过能源管理制度创新可以取得较高的碳生产率,这样债权人可获得未来的现金激励,吸引资本市场参与者在考虑温室气体排放和能源绩效的前提下进行企业投资[8]。
相对于绝对碳减排而言,提升碳生产率更能体现发展中国家在碳排放约束下发展本国经济的意愿,这是包括中国在内的发展中国家低碳发展的核心。国内学者积极引入碳生产率的概念,进行了产业结构高级化对碳生产率影响的大量研究,结论大致分为三类。第一类观点认为产业结构高级化会促进碳生产率的提升。于雪霞运用LMDI方法研究了区域碳生产率变化规律及成因, 发现长期来看产业结构高级化对碳生产率提升的促进作用更加明显[9]。同样,范晓莉的研究也支持此类观点[10]。唐志鹏等使用混合地理加权回归分析了产业结构对碳生产率的影响,发现在所有影响碳生产率的因素中产业结构占据主导地位[11]。第二类观点认为产业结构高级化会抑制碳生产率的提升。程琳琳等运用空间杜宾模型分析农业碳生产率变动的主要影响因素时发现,农业结构升级对本地区农业碳生产率具有负向影响[12]。同样,王艳丽等使用工业行业动态面板数据研究了工业结构升级对碳生产率的影响,发现工业结构升级抑制了碳生产率的提升, 西部地区尤为显著[13]。第三类观点认为产业结构高级化对碳生产率的影响复杂。高文静等分别使用工业化和城镇化作为门限变量回归检验了工业化对工业碳生产率的影响,发现两种门限效应都存在,在门槛值上下工业化对碳生产率的影响分别为抑制和促进作用[14]。
从研究视角来看,国外对碳生产率影响因素的研究视角偏向微观,研究方法更加多样,而国内学者多从省级或行业的中观层面进行实证研究;从研究内容来看,大多数研究认为技术创新和制度创新是碳生产率提升的主要因素,国内学者侧重研究产业结构高级化对碳生产率的影响,适应当今中国经济高质量发展的新要求,但研究结论呈现多样化。
在前人研究的基础上,本文做了以下拓展:一方面,从二次非线性角度看待产业结构高级化对碳生产率的影响,拓宽了研究视角;另一方面,相邻地区间由于资源禀赋相近,碳生产率和产业结构也表现出一定的相似性,产业结构高级化对碳生产率的影响因空间特征而有所差异。本文使用2003—2016年中国30个省级行政区面板数据(港澳台、西藏地区除外),基于空间杜宾模型研究了产业结构高级化对碳生产率的非线性、空间影响,为产业结构高级化与碳生产率提升的同向发展提出针对性的政策建议。
三、产业结构高级化与碳生产率的空间相关性检验 (一) 指标测度本文采用付凌晖(2010)的做法构建产业结构高级化指数[15]。假设i省(区)t年产业结构向量为xit=(xi1t, xi2t, xi3t),向量中各元素分别为一、二、三次产业产值占该地区当年总产值的比例,三个坐标轴上的单位向量分别为x10=(1, 0, 0),x20=(0, 1, 0)和x30=(0, 0, 1)。xit与三个坐标轴的夹角分别为θ1t、θ2t和θ3t,三者之和表示三次产业调整幅度之和,体现的是i省(区)t年产业结构高级化水平,用Sit表示。Sit的测算公式如式(1)所示。
| $ \begin{array}{l} S_i^t = \theta _1^t + \theta _2^t + \theta _3^t = {\rm{arccos}}\left( {\frac{{\mathit{\boldsymbol{X}}_i^t \cdot \mathit{\boldsymbol{X}}_1^0}}{{{\rm{|}}\mathit{\boldsymbol{X}}_i^t{\rm{|}} \cdot {\rm{|}}\mathit{\boldsymbol{X}}_1^0{\rm{|}}}}} \right) + {\rm{arccos}}\left( {\frac{{\mathit{\boldsymbol{X}}_i^t \cdot \mathit{\boldsymbol{X}}_2^0}}{{{\rm{|}}\mathit{\boldsymbol{X}}_i^t{\rm{|}} \cdot {\rm{|}}\mathit{\boldsymbol{X}}_2^0{\rm{|}}}}} \right) + {\rm{arccos}}\left( {\frac{{\mathit{\boldsymbol{X}}_i^t \cdot \mathit{\boldsymbol{X}}_3^0}}{{{\rm{|}}\mathit{\boldsymbol{X}}_i^t{\rm{|}} \cdot {\rm{|}}\mathit{\boldsymbol{X}}_3^0{\rm{|}}}}} \right)\\ = {\rm{arccos}}\left( {\frac{{x_{i1}^t}}{{\sqrt {{{(x_{i1}^t)}^2} + {{(x_{i2}^t)}^2} + {{(x_{i3}^t)}^2}} }}} \right) + {\rm{arccos}}\left( {\frac{{x_{i2}^t}}{{\sqrt {{{(x_{i1}^t)}^2} + {{(x_{i2}^t)}^2} + {{(x_{i3}^t)}^2}} }}} \right)\\ \;\; + {\rm{arccos}}\left( {\frac{{x_{i3}^t}}{{\sqrt {{{(x_{i1}^t)}^2} + {{(x_{i2}^t)}^2} + {{(x_{i3}^t)}^2}} }}} \right)\\ \end{array} $ | (1) |
Sit值越大表明产业结构高级化水平越强。其实,基于上述方法构建的产业结构高级化指数测算的是三次产业结构调整幅度,从结构调整幅度越大得到产业结构越高级的结论存在一个假设前提:当今中国产业结构调整呈现向工业化和服务化快速迈进的趋势。如果中国处于从原始部落向农耕文明进化的时期,产业结构的调整是向着农业占比逐渐增大这个方向发展,此时产业结构调整幅度可能很大,但并不足以说明产业结构呈现高级化趋势。
碳生产率的测算采用Kaya等人(1997)的方法,用各省(区)总产值与二氧化碳排放量之比表示,其中各省(区)总产值来自各年《中国统计年鉴》,使用以2003年为基期的GDP指数进行平减,得到历年实际GDP。二氧化碳排放量的数据是根据各行业原煤、焦炭、原油、燃料油、汽油、煤油、柴油、液化石油气和天然气九种化石能源消耗量折算成每种能源的二氧化碳排放量,求和后得出各省(区)二氧化碳排放总量。
(二) 空间相关性检验空间相关性检验是识别产业结构高级化和碳生产率是否存在空间关联性的方法,分为全局相关性检验和局部相关性检验,前者测度整体的空间关联水平,后者测度相邻地区的局部关联水平。
1. 全局空间自相关检验全局空间自相关性常用全局莫兰指数(Global Moran' I)来衡量,该指数反映的是空间邻接地区属性值的相似程度,计算方法为:
| $ {\rm{Global}}\;{\rm{Moran}}'I = \frac{{\sum\nolimits_{i = 1}^n {\sum\nolimits_{i = 1,\;j \ne i}^n {{w_{ij}}({a_i} - a)({a_j} - a)} } }}{{{D^2}\sum\nolimits_{i = 1}^n {\sum\nolimits_{i = 1}^n {{w_{ij}}} } }} $ | (2) |
式中,ai、aj分别表示i、j省(区)的属性观测值;a表示属性的平均值;D2表示属性的方差;n为省(区)总数,此处取30;wij为空间权重矩阵中的任一元素。空间权重矩阵的确定方法有多种,二进制邻接矩阵是最常见的空间权重矩阵(叶阿忠等,2015)[16]7。本文使用该种权重矩阵,wij表示第i行第j列的元素,当区域i和j相邻接时,wij=1;否则wij=0,对角线上元素设定为0。在设定完空间权重矩阵后,Moran指数值就可以确定,通常介于-1到1之间。Moran指数的绝对值越大关联性越强:正值表示存在空间正相关,负值表示存在空间负相关,为零表示空间无关联性。
根据Moran指数分析各省(区)产业结构高级化和碳生产率的空间自相关性,检验结果见表 1。
| 表 1 产业结构高级化和碳生产率的全局自相关检验 |
由表 1可知,产业结构高级化的Moran指数值均大于0,呈现波动趋势。除2003和2011年以外,其他年份的Moran指数值均通过10%的显著性检验,说明产业结构高级化存在较显著的空间正相关性,一地区的产业结构高级化会通过空间溢出效应正向影响相邻地区的产业结构水平。碳生产率的Moran指数值同样大于0且呈现波动趋势,所有年份的Moran指数值均通过了1%的显著性检验,说明与产业结构高级化水平相比,碳生产率的空间正相关性更加显著。总之,无论产业结构高级化还是碳生产率,均存在显著的空间效应,忽略空间因素会导致模型估计结果的偏差。
2. 局部空间自相关检验全局Moran指数从总体上反映了中国碳生产率有无聚集性,但无法反映各省(区)具体的集聚水平和集聚类型(高值集聚还是低值集聚),因此需要反映空间联系的局部指标,Moran散点图就是此类指标。
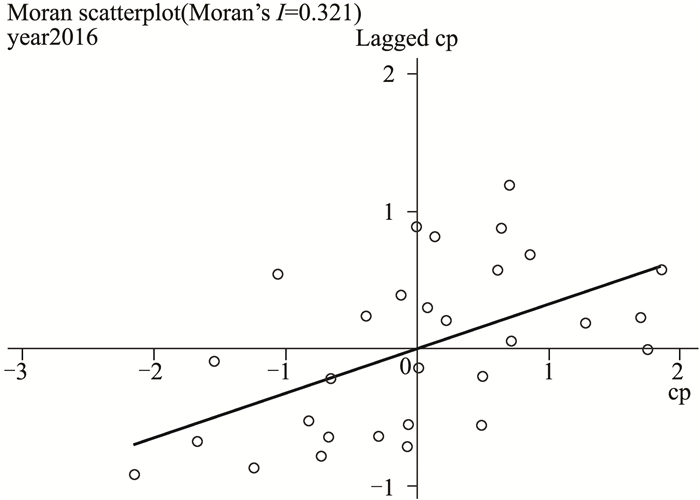
它以向量U为横坐标,以空间权重矩阵W和向量U的乘积(记为W×U)为纵坐标,将观测点分为四个象限,反映各省(区)的空间集聚水平和集聚类型,象限中的各项测点的值为(ui, ∑j=1nwijui),其中ui=ai-a,a表示区域i历年观测值的均值,其余符号含义与式(2)相同。横坐标表示观测省(区)与均值之间的离差,落于原点右侧的观测点为高值省(区),落于原点左侧的观测点为低值省(区)。纵坐标表示各省(区)观测值偏离程度的空间加权和,亦称“空间滞后”向量[17]8,落于原点上方的观测点为被高值区域包围的省(区),落于原点下方的观测点为被低值区域包围的省(区)。因此,Moran散点图有四个象限,分别对应于高值-高关联象限(简称高-高)、低值-高关联象限(简称低-高)、低值-低关联象限(简称低-低)和高值-低关联象限(简称高-低)。一、三象限分别表示高值省(区)被高值区域包围和低值省(区)被低值区域包围,呈现空间正相关;二、四象限分别表示低值省(区)被高值区域包围和高值省(区)被低值区域包围,呈现空间负相关。按照Moran散点图的绘制方法,分别绘制2003年和2016年碳生产率(用字母cp表示)的Moran散点图,见图 1和图 2(港澳台、西藏地区除外)。
|
图 1 2003年碳生产率的Moran散点图 |
|
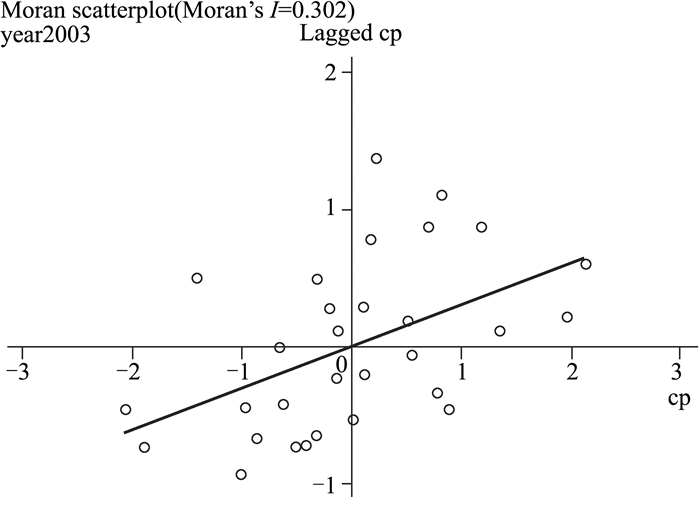
图 2 2016年碳生产率的Moran散点图 |
由以上两图可知,位于第一或三象限的省(区)数量保持在22至25个之间,说明2003—2016年间碳生产率呈现较强的空间正相关性。处于第一象限的省(区)具有自身碳生产率水平较高且周围被高碳生产率的邻接省(区)包围的特点,属于高-高集聚类型,此类型省(区)的数量在两个观测年份分别为10个和13个,保持稳定增长趋势;处于第三象限的省(区)具有自身碳生产率水平较低且周围被低碳生产率的邻接省(区)包围的特点,属于低-低集聚类型,此类型省(区)的数量在两个观测年份分别为12个和11个,有一定的下降趋势。两个象限数目增减对比发现,碳生产率的高质量空间正相关效应有所增强。对Moran散点图中30个省(区)的集聚类型进行统计,结果见表 2。
| 表 2 30个省(区)碳生产率集聚类型分布统计表 |
由表 2可知,2003—2016年,碳生产率的变动存在显著的空间俱乐部趋同效应,这与沈能等(2013)的结论是一致的[18]。具体而言:
一直处于高-高集聚的省(区)集中在东部沿海和部分中部地区,如上海、江苏、浙江、福建、广东、广西、江西、湖南等;长期处于低-低集聚的省(区)聚集在中西部和东北地区,包括黑龙江、吉林、辽宁、内蒙古、宁夏、陕西、甘肃、山西等。无论是高-高集聚还是低-低集聚,都说明了碳生产率呈现显著的空间正相关性。
2003—2016年,处于高-低集聚的北京和重庆全部演变为高-高集聚,说明高碳生产率地区通过空间溢出效应对邻接地区产生了明显的正向影响,实现了相邻地区碳生产率提升的协同发展。但是,处于低-高集聚的省(区)在考察期内集聚类型出现两极分化:天津和湖北在2016年演变为高-高集聚,而贵州和新疆在2016年则退化为低-低集聚,说明个别低碳生产率地区对邻接地区碳生产率的抑制作用较突出。
四、理论模型构建和数据说明 (一) 理论模型构建 1. 基本模型采用索洛增长模型,结合林伯强等人(2011)的研究[19],将模型设定为
| $ {Y_{it}} = {A_0}{{\rm{e}}^{{r_{1 \cdot s{s_{it}} + {r_2} \cdot v{s_{it}} + {r_3} \cdot {\rm{fd}}{i_{it}}}}}}{({\rm{k}}{{\rm{l}}_{it}})^\alpha }C_{it}^\beta $ | (3) |
式中,总产出Yit表示i省(区)t年的生产总值;ssit表示i省(区)t年的产业结构高级化水平;vsit表示i省(区)t年的低碳技术效率;fdiit表示i省(区)t年的外资利用水平;r1、r2和r3分别表示影响总技术水平的三个变量系数;klit表示i省(区)t年的资本劳动比,反映资本和劳动要素的相对使用情况,通常情况下资本和劳动之间存在高度相关性,用比值的方式可有效降低模型中的多重共线性问题;Cit表示i省(区)t年的二氧化碳排放量,反映经济增长所消耗的环境资源。
式(3)对Cit求偏导,得
| $ \frac{{\partial {Y_{it}}}}{{\partial {G_{it}}}} = \beta {A_0}{{\rm{e}}^{{r_{1 \cdot s{s_{it}} + {r_2} \cdot v{s_{it}} + {r_3} \cdot {\rm{fd}}{i_{it}}}}}}{({\rm{k}}{{\rm{l}}_{it}})^\alpha }C_{it}^{\beta - 1} $ | (4) |
由于实际经济活动及统计数据的非连续性,所以用差分替代微分,得
| $ \frac{{\Delta {Y_{it}}}}{{\Delta {C_{it}}}} = \frac{{\partial {Y_{it}}}}{{\partial {C_{it}}}} $ | (5) |
式(5)左边表示单位碳排放所引起的产出增加量,就是碳生产率cpit,因此式(4)变为
| $ {\rm{c}}{{\rm{p}}_{it}} = \beta {A_0}{e^{{r_{1 \cdot s{s_{it}} + {r_2} \cdot v{s_{it}} + {r_3} \cdot {\rm{fd}}{i_{it}}}}}}{({\rm{k}}{{\rm{l}}_{it}})^\alpha }C_{it}^{\beta - 1} $ | (6) |
对式(6)两边同时取对数,得:
| $ {\rm{lc}}{{\rm{p}}_{it}}{\rm{ = }}{\alpha _0} + {r_1} \cdot s{s_{it}} + {r_2} \cdot v{s_{it}} + {r_3} \cdot fd{i_{it}} + \alpha {\rm{lk}}{{\rm{l}}_{it}} $ | (7) |
其中α0=lnβ+lnA0,lcpit、lklit分别为ln(cpit)和ln(klit)的简写形式,此处在模型中加入产业结构高级化的平方项,反映两者间的非线性关系。综上,产业结构高级化对碳生产率影响的理论模型为
| $ {\rm{lc}}{{\rm{p}}_{it}} = {\alpha _0} + {r_1} \cdot {\rm{ }}s{s_{it}} + {r_4} \cdot ss_{it}^2 + {r_2} \cdot v{s_{it}} + {r_3} \cdot {\rm{fd}}{{\rm{i}}_{it}} + \alpha {\rm{lk}}{{\rm{l}}_{it}} $ | (8) |
其中r4表示产业结构高级化的平方对碳生产率的影响。理论模型中的被解释变量是碳生产率的对数lcpit,核心变量是产业结构高级化水平ssit,控制变量有低碳技术效率vsit、外资利用水平fdiit和资本劳动比的对数lklit。
2. 空间杜宾模型当产业结构高级化和碳生产率均存在显著的空间相关性时,根据传统计量回归会得出有偏或无效的估计,此时使用空间计量模型是最好的选择。Lesage等(2009)构建了一个同时体现空间滞后内生变量和外生变量的空间面板数据模型——空间杜宾模型(Spatial Durbin Model, 简称SDM)。SDM既考虑了因变量的空间相关性,又考虑了自变量的空间相关性[20]49。基于空间杜宾模型,产业结构高级化对碳生产率的影响最终表示为:
| $ {y_{it}} = \rho \sum\limits_{j = 1}^n {{w_{ij}}{y_{jt}} + \beta {x_{jt}} + \sum\limits_{j = 1}^n {\theta {w_{ij}}{x_{jt}} + {u_i} + {\varphi _t} + {\varepsilon _{it}}} } $ | (9) |
式中,yit为i省(区)在t年的碳生产率的对数值;xit表示各解释变量,包括产业结构升级水平ssit及其平方ssit2、低碳技术效率vsit、外资利用水平fdiit和资本劳动比的增长率lklit;wij是被解释变量和解释变量的空间权重矩阵中的元素,采用简单二进制邻接矩阵①;t表示年份;wijyjt是被解释变量的空间相关项矩阵,为内生变量,体现与i相邻的j地区碳生产率对i地区碳生产率的影响;βxit反映各解释变量对碳生产率的原本影响,β表示原效应系数;wijxjt是解释变量空间相关项矩阵,表示各解释变量的空间效应,体现了邻接地区各影响因素对i地区碳生产率的影响;ρ为被解释变量的空间相关项系数,反映邻接地区碳生产率对本地区碳生产率的影响方向和程度;θ表示解释变量的空间相关项系数,反映相邻地区各解释变量对本地区碳生产率的影响;μi表示个体效应;φt表示时间效应;εit表示空间自相关误差项。
①就一般意义而言,因变量的空间相关关系与自变量的空间相关关系可能相同也可能不同,此处认为两者的空间相关关系相同,统一采用邻接标准。
(二) 数据说明及描述性统计为简化描述,此处略去地区变量i和年份变量t。
lcp:碳生产率的对数,为被解释变量,表示碳生产率的增长率,此处取对数既为了与理论模型对应,又为了提升数据的平稳性。
ss:产业结构高级化指数,为核心变量,表示产业结构高级化水平。
vs:低碳技术效率,为控制变量,反映低碳技术水平对碳生产率的影响。DEA是目前测算技术效率的常见方法。Tsutsui等(2010)提出了一种包含径向和SBM两类距离函数的EBM模型[21],它使用混合距离函数,兼具径向DEA模型和SBM模型的优点,被认为是更切近现实的测算方法(师博等,2012[22];俞会新等,2018[23])。但是,EBM模型无法解决评价单元效率值为1时无法比较的问题,为此Tone Kauro提出超效率EBM模型。本文借助Maxdea ultra 7.0软件按照超效率EBM模型测算工业行业的低碳技术效率,测算过程借鉴韩清童(2017)的研究[24]。
低碳技术效率的投入变量包括:(1)资本投入,采用永续盘存法计算各省(区)历年的资本存量,单位为亿元;(2)劳动投入,采用各省(区)每年年末从业人员数,单位为万人;(3)人均水资源,单位为立方米/人;(4)土地面积,使用农用地和建设用地面积之和,单位为千公顷;(5)能源消费量,单位为万吨标煤。期望产出为各省(区)历年总产值数据,为了消除价格因素影响,使用以2003年为基期的GDP价格指数进行折减,单位为亿元。非期望产出包括:(1)碳排放量,单位为万吨,计算方法同碳生产率中二氧化碳排放量的计算方法;(2)废水排放量,单位为万吨;(3)固体废物排放量,单位为万吨;(4)废气中二氧化硫排放量,单位为万吨;(5)废气中烟(粉)尘排放量,单位为万吨。
fdi:外资利用水平,为控制变量。用各省(区)实际利用外商直接投资额与该地区生产总值之比表示,其中外商直接投资额使用当年的汇率换算成人民币。
lkl:资本劳动比的对数,为控制变量,表示资本劳动比的增长率。资本和劳动力的统计口径与低碳技术效率一致。此处取对数既为了与理论模型对应,又为了提升数据的平稳性。
上述变量的数据来自《中国统计年鉴》《中国能源统计年鉴》《中国互联网络发展状况统计报告》和各省(区)统计年鉴等。变量的描述性统计结果见表 3。
| 表 3 变量的描述性统计及平稳性检验结果 |
在进行实证分析前,需要对所有变量进行平稳性检验。对于面板数据,通过单位根检验来判断变量是否为平稳序列,LLC检验是面板单位根检验的常用方法。为节省篇幅,具体检验统计量值和p值汇报在表 3的最后两列。单位根检验的原假设是“存在单位根”,由表 3可知,所有变量的原序列均通过LLC检验,说明本文使用的数据具有“零阶单整”的特点:面板数据受过去扰动项的影响有限,是平稳过程,长期而言,能够达到其期望值的趋势。
此外,本文通过协整分析检验变量之间是否具有长期稳定的关系。通常用于协整检验的方法有两种:E-G两步法和Johansen协整检验法,但这两种方法都是针对时间序列数据。Persyn等(2008)创建了两组面板协整检验统计量,第一组为组间统计量Gτ、Gα,第二组为面板统计量Pτ、Pα[25]。对于组间统计量,拒绝原假设表明至少有一个截面单元存在协整关系;对于面板统计量,拒绝原假设表明面板数据整体存在协整关系。需要注意的是,在一些情况下,两组统计量可能会出现其中一个不能拒绝原假设的现象,对此Westerlund(2007)认为也是可以的[26]。因为本文的时间跨度是2003—2016年,仅包括14年的数据,为确保充分的观测点个数,仅对核心变量——产业结构高级化与碳生产率的关系进行协整检验,检验结果如表 4所示。
| 表 4 产业结构高级化与碳生产率的面板协整关系检验结果 |
由表 4可知,每组统计量中均有一个统计量的p值为0.000 0,因此可以认为产业结构高级化与碳生产率具有长期、稳定的协整关系。
五、空间计量模型的选择及结果分析 (一) 空间计量模型的选择空间计量模型的选择步骤如下:
利用Hausman检验判断固定效应和随机效应哪个更优。因为固定效应忽略个体性质的差异,能够专注研究核心变量对因变量的影响关系,所以很多情况下会根据研究情况适时地选择固定效应。本文的样本回归限于特定的30个省(区),无须以各省(区)的个体性质推断总体性质,因此选择固定效应模型效果更佳(熊灵等,2012)[27]。
根据LR的空间和时间检验确定是否应将模型扩展为时空双固定模型。本文中LR空间固定检验值为1 204.949 0,时间固定检验值为378.108 6,p值均为0,通过1%的显著性水平,说明模型存在空间效应和时间效应,应将模型扩展为时空双固定模型(杨恺钧等,2016)[28]。
使用Wald检验确定空间杜宾模型SDM是否可以简化为空间滞后模型SLM。本文中,Wald spatial lag和LR spatial lag值分别为43.745 4和41.842 1,p值均为0,说明在1%的显著性水平上拒绝了θ=0的原假设。同时,Wald spatial error和LR spatial error值分别为43.286 1和40.720 0,p值同样为0,在1%的显著性水平上拒绝了θ+ρβ=0的原假设,这说明时空双固定的空间杜宾模型更为适宜。此处将不同模型的估计结果一并汇报在表 5中。
| 表 5 不同模型回归结果比较 |
表 5中模型1、2、3分别为时间固定、空间固定和时空双固定的空间滞后模型,模型4为时空双固定的空间杜宾模型,其对数似然值(Log L)和拟合优度(R2)均高于空间滞后模型。不同模型中各变量系数正负基本一致,说明模型的估计结果具有稳健性。
(二) 直接效应和间接效应分析在不考虑空间相关项的时候,回归系数可以反映解释变量对被解释变量的影响,但是在存在空间滞后项的情况下,解释变量对被解释变量影响的表述变得非常复杂。Lesage等认为在空间计量回归中利用点估计得出的各解释变量的系数是有偏误的,他们通过求偏微分方程将解释变量系数估计值分解为直接效应和间接效应,这样解释变量对被解释变量的影响可以表述为直接效应、间接效应和总效应[20]34。表 6给出了空间杜宾模型估算的三种效应结果。
| 表 6 产业结构高级化对碳生产率的直接效应、间接效应和总效应 |
就目前而言,产业结构高级化显著提升了本地区的碳生产率增长率,但对邻接地区碳生产率增长率的提升作用有限。具体而言,产业结构高级化一次项的原效应系数和直接效应系数分别为-6.728 2和-7.054 9,均通过了1%的显著性检验,二次项的原效应系数和直接效应系数分别为1.337 3和1.454 4,均通过1%的显著性检验。在不考虑其他变量影响的情况下,当产业结构高级化水平的原效应为2.52(6.728 2/(2×1.337 3)≈2.52)或直接效应为2.43(7.054 9/(2×1.454 4)≈2.43)时,其对碳生产率增长率的影响出现“拐点”,结合产业结构高级化变量的描述性统计可知,产业结构高级化水平最小值为2.88,说明到目前为止所有地区的产业结构高级化均处于U型曲线的右端,即结构高级化有利于提升本地区的碳生产率增长率。此外,产业结构高级化一次项的空间相关项与间接效应系数均未通过10%的显著性检验,产业结构高级化二次项的空间相关项与间接效应系数分别为1.641 2和2.512 4,均通过5%的显著性检验。在不考虑其他变量影响的情况下,产业结构高级化与碳生产率增长率的空间关系也越过“拐点”,前者说明邻接地区产业结构高级化能够提升本地区碳生产率增长率,后者说明本地区产业结构高级化水平能够提升邻接地区碳生产率增长率。但是,与不考虑空间效应时相比,其显著性水平较低,说明产业结构高级化促进碳生产率增长率提升的空间溢出效应是一个局部现象,随着地理空间范围的扩大其溢出效应开始减弱。从总效应来看,产业结构高级化水平的一次项系数为-14.942 1,通过5%的显著性检验,而二次项系数为3.966 8且通过1%的显著性检验,再次印证了机理部分的分析,即产业结构高级化与碳生产率增长率的关系呈现U型关系。
低碳技术效率显著提升了本地区的碳生产率增长率,但通过空间溢出效应十分显著地降低了邻接地区的碳生产率增长率,这可能是由于邻接地区政府之间为争夺优势资源而导致的无序竞争。具体而言,低碳技术效率的原效应系数和直接效应系数分别为0.119 9和0.103 1,且通过了5%的显著性检验,说明低碳技术效率对本地区碳生产率增长率具有显著的促进作用。低碳技术效率的空间相关项和间接效应系数分别为-0.290 9和-0.333 2,均通过了1%的显著性检验。对比系数大小可知,邻接地区的低碳技术效率对本地区碳生产率增长率的抑制作用要较明显于本地区低碳技术效率对邻接地区碳生产率增长率的抑制。低碳技术效率对碳生产率增长率提升的总效应为负,但不显著,这是正向直接效应和负向间接效应叠加的结果,说明低碳技术效率对碳生产率增长率的正向促进作用还有待进一步提高。
外资利用水平显著提升了本地区的碳生产率增长率,且通过空间溢出效应提升了邻接地区的碳生产率增长率。具体而言,外资利用水平的原效应系数和直接效应系数分别为0.022 0和0.024 6,均通过了1%的显著性检验,说明本地区外资引入力度的增强会显著提升本地区的碳生产率增长率。外资利用水平的空间相关项和间接效应系数分别为0.039 3和0.057 2,通过了5%的显著性检验,前者说明邻接地区外资引入力度的增强会显著提升本地区的碳生产率增长率,后者说明本地区外资引入力度的提升会显著促进邻接地区碳生产率增长率,各地区在使用外资的过程中充分发挥了“技术溢出”对碳生产率增长率的正向促进作用。外资利用水平对碳生产率增长率影响的总效应系数为0.081 8且通过1%的显著性检验,这是直接效应和间接效应正向叠加的结果。
资本劳动比增长率的提升显著地降低了本地区的碳生产率增长率,且通过空间溢出效应十分显著地降低了邻接地区的碳生产率增长率。具体而言,资本劳动比增长率的原效应系数和直接效应系数分别为-0.189 4和-0.249 3,均通过了5%的显著性检验,说明资本劳动比增长率的上升会显著抑制本地区的碳生产率增长率。这是因为高排放产业的资本收益率高,本地区追加的资本会优先流入高排放产业,抑制了碳生产率增长率的提升。此外,资本劳动比增长率的空间相关项和间接效应系数分别为-0.878 9和-1.178 3,均通过了1%的显著性检验,前者说明邻接地区资本劳动比增长率的提升显著抑制了本地区的碳生产率增长率,后者说明本地区资本劳动比增长率的提升显著抑制了邻近地区的碳生产率增长率,且抑制作用更大。这是因为当邻近地区资本变得稀缺时,地方政府出于政绩和经济发展的考量,最先减少的是收益率较低的低排放产业的资本投入,进而无法充分发挥这些产业在碳减排上的促进作用,抑制了碳生产率增长率的上升。资本劳动比增长率对碳生产率增长率的影响总效应系数为-1.427 7,且通过1%的显著性检验,说明近年来资本投入提升对碳生产率增长率的促进作用已经不复存在,这与丁志国等(2011)的研究结论一致[29]。
(三) 稳健性检验本文使用信息化水平的对数lic来替代lkl进行模型的稳健性检验。信息化水平使用信息传输、软件和信息技术服务业城镇单位就业人员年底数,数据来源于《中国统计年鉴》。为提高数据的平稳性此处取对数,使用该变量的空间杜宾模型回归结果汇报在表 5的模型5中。
使用信息化水平替代资本劳动比后,从解释变量的原效应来看,产业结构高级化对碳生产率增长率的提升仍呈现一次项为负、二次项为正的U型关系,低碳技术效率能显著促进本地区碳生产率增长率提升,外资利用水平的影响不再显著,信息化水平增长率十分显著地促进了碳生产率增长率的提升。从解释变量的空间相关项来看,产业结构高级化水平的空间相关项对碳生产率增长率的影响仍是U型关系,且一次项的负向关系不显著;低碳技术效率和资本劳动比的空间相关项对碳生产率增长率的影响仍然为负;信息化水平增长率对邻接地区碳生产率增长率的提升作用不显著。从被解释变量的空间相关项来看,碳生产率增长率同样具有显著的空间正向溢出效应,即本地区碳生产率增长率的提升会十分显著地提升其他邻接地区的碳生产率增长率。
经过以上分析可知,除了替换的变量——信息化水平外,其余解释变量本身和其空间相关项对碳生产率增长率的影响均与前文分析结果一致,说明表 5中的模型估计结果具有稳健性。
六、结论与建议基于2003—2016年中国30个省(区)面板数据,运用空间杜宾模型定量研究了产业结构高级化对碳生产率的空间影响,得出的主要结论有:产业结构高级化与本地区和邻接地区碳生产率增长率之间均存在先抑制后促进的U型关系,但与前者的关系更加显著。此外,低碳技术效率能显著提升本地区的碳生产率增长率,但会显著抑制邻接地区的碳生产率增长率;外资利用水平提升了本地区和邻接地区的碳生产率增长率,空间正向溢出效应显著;资本劳动比的提升降低了本地区和邻接地区的碳生产率增长率,空间负向溢出效应显著。为此,特提出以下对策建议:
第一,加强区域间要素资源合作,持续推进产业结构高级化。当前,中国各地区产业结构高级化水平均处在U型关系的右侧,说明加速产业结构高级化能提升碳生产率。因此,各地区政府要积极建立双边或多边协商机制,形成区域经济联合体,以经济效率最大化为原则形成区域分工与协作,推动相邻区域间要素资源向二、三次产业的持续流动。
第二,坚持自主研发和地区合作并存,促进低碳技术效率提升。因为技术研发具有投入大量性和收益不确定性,研发成功者希望更多地占据技术产业化的高利润期,这抑制了低碳技术效率空间正向溢出效应的发挥。因此,对于低碳领域的核心技术,政府可对致力于自主研发的企业给予政策优惠和资金支持,为企业低碳技术创新活动的开展提供必要的便利条件。另一方面,对于基础性、前沿性技术和共性技术,相邻地区政府之间要探索建立地区间合作研发的模式,按照“成本共担、收益共享”的原则整合地区间优势资源,以合作代替恶性竞争,形成地区间低碳技术的研发合力。
第三,坚持高质量引进外资,提升资本使用效率。高质量利用外资就是根据国家产业政策发展方向,积极引导外商投资企业加入绿色制造、智能制造、服务型制造等重点行业,以提高税收等方式限制外资进入高耗能产业,鼓励国内企业与国外投资者在绿色产品和工艺上的合作,充分发挥外资企业在节能减排方面的“技术溢出”效应。另外,要进一步提升资本的使用效率,避免地方政府因引资而产生的恶性竞争行为,减少经济产出增长对资本的依赖。
| [1] | NETHERLANDS ENVIRONMENTAL ASSESSMENT AGENCY.China nowNo.1 in CO2 emissions, USA in second position[EB/OL]. (2007-09-20)[2018-10-12]. http://www.pbl.nl/en/dossiers/Climatechange/Chinanowno1inCO2emissionsUSAinsecondposition |
| [2] | KAYA Y, YOKOBORI K. Environment, energy and economy:strategies for sustainability[M]. NewYork: United nations university press, 1997. |
| [3] | ENKVIST P, NAUCLéR T, OPPENHEIM JM. Business strategies for climate change[J]. McKinsey quarterly, 2008,24(2): 24–37. |
| [4] | BEINHOCKER E, OPPENHEIM J, IRONS B, et al.The carbon productivity challenge: Curbing climate change and sustaining economic growth[R].McKinsey climate change special initiative report series, 2008. |
| [5] | KIM C G, KIM TH. Analysis of carbon productivity in Korea agriculture[J]. The Korean journal of agricultural economics, 2014,24(2): 21–34. |
| [6] | HU X, LIU C. Carbon productivity:a case study in the Australian construction industry[J]. Journal of cleaner production, 2016,112(9): 2354–2362. |
| [7] | NISHITANI K, KOKUBU K, KAJIWARA T. Does low-carbon supply chain management reduce greenhouse gas emissions more effectively than existing environmental initiatives?An empirical analysis of Japanese manufacturing firms[J]. Journal of management control, 2016,27(1): 33–60. DOI: 10.1007/s00187-015-0224-z |
| [8] | KIM S, JUNG Y. Carbon risk and the cost of debt[J]. Accounting research, 2017,42(2): 169–213. |
| [9] | 于雪霞. 区域碳生产率变化差异成因分析[J]. 中国人口·资源与环境, 2015, 25(S1): 344–349. |
| [10] | 范晓莉. 新型城镇化视角下中国碳生产率影响因素研究——基于VEC模型的动态关系分析[J]. 管理现代化, 2015, 35(1): 70–72. DOI: 10.3969/j.issn.1003-1154.2015.01.024 |
| [11] | 唐志鹏, 刘卫东, 宋涛. 基于混合地理加权回归的中国省域碳生产率影响因素分析[J]. 资源科学, 2017, 32(12): 2223–2232. |
| [12] | 程琳琳, 张俊飚, 田云, 等. 中国省域农业碳生产率的空间分异特征及依赖效应[J]. 资源科学, 2016, 38(2): 276–289. |
| [13] | 王艳丽, 王根济. 环境规制、工业结构变动与碳生产率增长——基于1998-2013年省级工业行业动态面板数据的实证检验[J]. 经济与管理, 2016, 30(6): 73–80. |
| [14] | 高文静, 柳亚琴, 潘明清. 工业化、城镇化对工业碳生产率的门槛效应分析[J]. 宏观经济研究, 2017, 12(4): 112–121. |
| [15] | 付凌晖. 中国产业结构高级化与经济增长关系的实证研究[J]. 统计研究, 2010, 27(8): 79–81. DOI: 10.3969/j.issn.1002-4565.2010.08.011 |
| [16] | 叶阿忠, 吴继贵, 陈生明, 等. 空间计量经济学[M]. 厦门: 厦门大学出版社, 2015. |
| [17] | ANSELIN L. The moran scatter plot as an ESDA tool to assess local instability inspatial association[M]. Morgantown: Research Institute of West Virginia University Press, 1993. |
| [18] | 沈能, 王艳, 王群伟. 集聚外部性与碳生产率空间趋同研究[J]. 中国人口·资源与环境, 2013, 23(12): 40–47. DOI: 10.3969/j.issn.1002-2104.2013.12.007 |
| [19] | 林伯强, 孙传旺. 如何在保障中国经济增长前提下完成碳减排目标[J]. 中国社会科学, 2011, 23(1): 64–76. |
| [20] | LESAGE J, PACE R K. Introduction to spatial econometrics[M]. New York: CRC Press, Taylor & Francis Group, 2009. |
| [21] | TSUTSUI M, TONE K. An epsilon-based measure of efficiency in DEA[J]. European Journal of Operational Research, 2010,207(5): 1554–1563. |
| [22] | 师博, 沈坤荣. 城市化、产业集聚与EBM能源效率[J]. 产业经济研究, 2012, 24(6): 10–16. DOI: 10.3969/j.issn.1671-9301.2012.06.002 |
| [23] | 俞会新, 林晓彤. 基于EBM超效率模型的京津冀环境污染治理投资效率分析[J]. 河北工业大学学报(社会科学版), 2018, 10(1): 9–16. |
| [24] | 韩清童.基于复杂网络与EBM模型的货运机场效率研究[D].大连: 大连海事大学, 2017. |
| [25] | PERSYN D, WESTERLUND J. Error-correction-based cointegration tests for panel data[J]. Stata Journal, 2008,8(2): 232–241. DOI: 10.1177/1536867X0800800205 |
| [26] | WESTERLUND J. Testing for error correction in panel data[J]. Oxford Bulletin of Economics & Statistics, 2007,69(6): 709–748. |
| [27] | 熊灵, 魏伟, 杨勇. 贸易开放对中国区域增长的空间效应研究:1987-2009[J]. 经济学, 2012, 11(3): 1037–1058. |
| [28] | 杨恺钧, 褚天威. 互联网发展、交通运输及进口贸易关系研究——基于中国省际面板数据空间计量分析[J]. 经济问题, 2016, 21(6): 95–100. |
| [29] | 丁志国, 赵宜凯, 赵晶. 直接影响与空间溢出效应:中国城市化进程对城乡收入差距的影响路径识别[J]. 数量经济技术研究, 2011, 25(9): 118–130. |
 2019, Vol. 21
2019, Vol. 21
