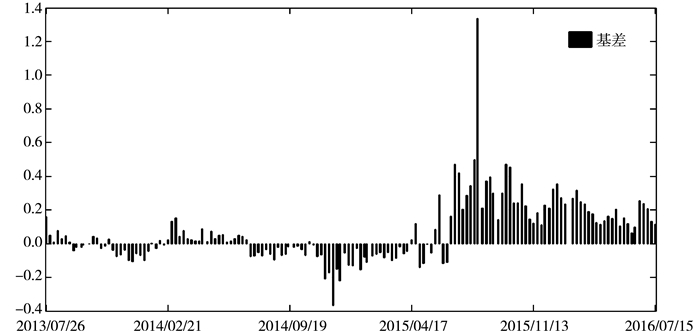
沪深300股指期货基差是沪深300现货指数和期货指数的差值,对资本市场的信息传递具有重要的作用,也是衡量套期保值效率、管理套利和投资策略的关键因素。通常在市场有效的条件下,股指期、现货之间的价差不存在系统性的大幅偏离现象,但在极端特殊的情形下,则可能会出现异常。如2015年我国股市崩盘过程中,就呈现出期指相对于股指大幅贴水、基差走强的状态(如图 1所示)。这种大幅贴水现象是资本市场运转中出现的重大问题,需要深入研究并予以解释。
|
图 1 我国沪深300股指期货周基差变化(2013/07/26—2016/07/15) |
在未来很长一段时期内,资本市场和理论界都应系统思考的是,股指期货基差由稳定转为走强的变化过程是否由我国投资者的情绪和非理性行为主导?投资者情绪对基差的非对称影响是否因处在不同市态而存在差异?我国资本市场的机构化程度提高是否有助于减轻投资者情绪对基差异常的作用?通过对这一系列问题的深入研究,可以全面分析投资者情绪因素对基差调整的作用,充分揭示我国股指期货市场的套期保值和定价效率,对市场投资策略制定及监管层的决策调整具有重要的参考意义。
二、文献评述 (一) 基差变化的影响因素研究和未及之处资本市场上存在诸多因素对基差走势产生影响,如市场流动性和波动性、无风险利率以及投资者结构等(Marcinkiewicz,2014)[1]。通常,流动性充足的市场便于套利者进行交易,因此国内外学者更多关注和研究的是流动性对基差的影响。在有关基差影响因素的文献中,大多支持流动性对基差的主导作用,如Lien等(2013)[2]发现流动性与基差的关系随时间发生改变,流动性对基差的影响是非对称的,且在基差为0的附近具有持续性。类似的结论也可以从Li和Guo(2017)[3]的文章中可以看出,基差对流动性存在非对称影响,说明流动性与基差之间存在因果关系。
随着国内外学者对投资者情绪以及行为偏差研究的不断深入,一些文献逐渐开始关注投资者情绪对证券市场的影响。投资者情绪反映的是投资者对市场未来的预期。由于投资者情绪难以直接度量,研究者通常利用单一或多个情绪因子构建投资者情绪指标。Baker和Stein(2004)[4]指出,在具有卖空约束的市场中,流动性可以作为投资者情绪指标。噪声交易者在情绪高涨时,更多地表现为非理性地买入行为,这种需求冲击会提高证券市场的流动性。流动性高的市场时常伴随较低的交易成本和股票的冲击成本,进一步推动股票价格的上涨,因此投资者产生乐观情绪往往伴随着良好的市场流动性和价格的非理性上涨。投资者情绪也是造成股票价格非理性波动的原因。国内外学者发现投资者情绪与市场波动率有显著关系,即投资者情绪越高,市场波动性越大。刘晨与安毅(2016)[5]的研究发现分级基金母基金收益率的波动率会随着投资者情绪增高而增大,但有更多学者侧重研究投资者情绪对股票市场或股指期货市场波动率的影响(Yang和Gao, 2014;Wang等, 2018)[6-7]。因此投资者情绪既可以通过非理性投资者的交易行为直接影响基差,也可以通过流动性和波动率间接影响基差走势。与以上学者的研究不同,郑振龙和林璟(2015)[8]发现流动性与沪深300股指期货定价偏差的关系并不显著,而投资者情绪才是我国沪深300股指期货定价偏差的主要作用因素。总体上看,国内外学者关于投资者情绪对基差影响的研究较为少见。此外,Zou和Sun(2012)[9]发现,投资者在不同市场态势下,交易行为受情绪的影响程度亦不同,不同市态下投资者情绪对股市收益及其波动存在不同的影响,他们的研究成果值得运用于投资者情绪与基差的关系研究。现在有必要全面考虑和深入研究在不同市态下,特别是我国资本市场由稳定状态向不稳定状态转移前后,投资者情绪对股指基差的影响是否发生了变化,发生了何种变化,以及具体产生哪些影响。
(二) 研究方法的改进国外对基差变化和相关影响因素的关系常用的分析方法是VAR模型及Granger因果检验法(Kadapakkam和Kumar,2012;Han和Pan,2016)[10-11]。在国内,关于噪声交易者对股票市场及期货市场套期保值效率的研究较为广泛,基于流动性或投资者情绪对基差非对称性影响的研究则十分罕见,且使用的方法常见于设定虚拟变量、利用非对称GARCH模型或分段回归模型分析。这些方法具有损失样本的缺点,无法有效衡量多个影响因素对基差调整的非对称影响。
据以上文献综述,本研究将从新的研究视角,把市场态势分为股市平稳阶段和股市动荡阶段,研究投资者情绪在不同市场态势下对基差的影响;也将首次使用分位数回归方法分析投资者情绪对基差的非对称影响;该方法相比于以往的处理手段能够消除极端值或异常值对参数估计造成的偏差,具备更加稳健的回归结果。
三、待检验假设与研究设计 (一) 待检验假设根据研究综述,可以整理出三方面的重要研究内容,以作进一步的分析假设。其一,投资者情绪既可以直接通过供求关系影响基差,也可以间接通过影响市场流动性和波动性对基差产生影响。投资者情绪较高时,套期保值和套利对投资者的吸引力不大,投资者倾向于对股指期货(高风险资产)进行单边投机。增强的市场流动性与波动性进一步缩小基差,容易形成期货升水。反之,当市场情绪较低时,投资者对指数走势的悲观判断会在股指期货的价格中有所反应,易推动股指期货贴水,基差走强。可以认为,投资者情绪是基差水平变动的影响因素之一,且基差随着投资者情绪指数的上涨而减小,随投资者情绪指数的下跌而增大。其二,在不同市场态势下,投资者的心理和行为会受到市场环境的影响,基差受情绪影响也会出现差别。这是因为市场态势能够体现在资本市场价格和波动特征中,市场的平稳与否都会影响投资者对于资本市场形势的判断(投资者会产生乐观或悲观的情绪),这种主观判断(某种市态下的投资者情绪)会带来与之相应的交易行为,并体现在股指期货的升贴水中,即股指期货基差中。综上所述,投资者在高涨或悲观的情绪作用下会因市场态势的不同产生不同的交易行为,因而对基差的影响也会存在差异。其三,现货市场的非对称做空机制使得期现反向套利往往遭受限制,这是投资者情绪对基差产生非对称效应的首要原因;其次,基差变动所受影响因素众多,期货升、贴水阶段投资者存在的心理和行为偏差,也会导致这些影响因素对基差的敏感性产生非对称变化。基于这三方面内容,本文提出三个待检验假设:
假设1:同一市态下,基差随着投资者情绪指数的上涨而减小,随投资者情绪指数的下跌而增大。
假设2:不同市态下投资者情绪对基差的影响表现不一。
假设3:投资者情绪对基差影响存在非对称效应。
(二) 变量构建 1. 投资者情绪指标(解释变量)的选取关于情绪指标的选取,国内资本市场中常直接采用央视看盘、好淡指数以及一些宏观经济指标(企业景气指数、消费者信心指数和经济学家信心指数等)。但这些指标数据的连续性和一致性较差,且数据编制的合理性有待通过实践进一步检验。在学术界,国内大部分学者使用情绪代理变量进行研究,如封闭式基金折溢价率、市盈率、新增开户数、IPO发行数量、IPO首日收益率以及一些市场流动性指标。鉴于流动性测算数据的难获取性,国内学者郑振龙和林璟(2015)[8]使用换手率和交易量作为流动性代理指标,在一定程度上可以代表投资者情绪的变化。本文将对这些情绪变量进行重新甄别和梳理,以便构筑模型。其一,IPO的发行数量与首日收益率受人为影响较多,而企业增加IPO发行数量是一个较为长期的过程,用来反映投资者情绪不甚合适。其二,我国于2015年4月开始全面放开A股市场“一人一户”限制,新增开户数作为投资者情绪指标也不再具有代表性,可使用新增参与交易的投资者数量替代。其三,鉴于Kumar和Lee(2006)[12]使用股票买卖额之差与总交易额的比率反映投资者情绪,实证表明这个指标比封闭式基金折溢价率更能代表投资者情绪对股价变化的解释力度,因此使用主动买入金额减去主动卖出的金额差值与总交易额的比率作为现货市场的主买率指标。由于主动买入和主动卖出数据的难获取性,使用沪深300板块的净流入金额作为主动买入金额和主动卖出金额的差值的代理变量,剔除股市熔断等极端情况,使用周内平均净流入金额作为现货市场主买率指标。其四,交易量和换手率可以反映投资者情绪的变化,并进一步影响期、现货市场的流动性,因此采用交易量与流通市值之比作为市场的换手率。
基于以上分析考虑,本文最终选取期末新增A股参与交易的投资者数量(num),以及封闭式基金折溢价率(prem)、市场换手率(turnover)、A股平均市盈率(PE)和现货市场主买率(buyrate)五个指标作为投资者情绪复合指数的原指标。
本文认为参考Huang等(2015)[13]提出的偏最小二乘法(PLS)得到的复合情绪指数比其他方法构建的复合情绪指数精确度更高,预测能力更强。使用全样本信息得到T×1阶复合情绪指数向量SPLS=(S1PLS,S2PLS,…,STPLS)′,SPLS是投资者情绪指标的线性组合,是复合情绪指标在PLS法下的表达式:
SPLS=XJNX′JTR(R′JTXJNX′JTR)-1R′JTR
其中,R表示T×1阶沪深300股指现货收益率向量;X是由单个投资者情绪原指标变量构成的T×N阶矩阵;N为选取的情绪原指标个数;矩阵
为研究投资者情绪对沪深300股指期现基差的影响,使用沪深300指数周度基差作为被解释变量,并且将t时刻的基差定义为:
Basist=ln(St)-ln(Ft)
其中,St、Ft分别为t时刻的沪深300指数价格和根据持仓量加权得到的期货价格。
3. 调节变量关于投资者结构(structure)数据,本文选自wind数据库中的季度数据,structure代表机构投资者持有沪深300成分股所占比例。这里还假定在一个季度内,投资者结构不发生改变。需要说明的是,尽管这种假设可能会导致序列相关性,但由于每天沪深300成分股的权重不同,因此相应的机构投资者持股比例并不是完全相同的; 而且分位数回归放宽了对误差项的假设条件,因此并不影响回归效果。
4. 控制变量(1) 市场利率(持有成本)。市场利率r能够影响市场资金的流向,并影响投资者投资现货市场和期货市场的成本。当市场利率升高时,融资成本增加会缩小期现套利空间,进一步对基差产生影响。为了与本文其他周度变量得到实时统一地匹配,这里使用国债回购周利率作为无风险利率。
(2) 套利成本。套利成本分为直接成本和间接成本。其中,股票市场的直接成本包括佣金和印花税,期货市场的直接成本只有佣金。虽然在2015年股灾期间,沪深300、上证50股指期货合约的非套期保值持仓的交易保证金和手续费均有不同程度的提高,但由于现货市场是“T+1”交易,因此套利交易的直接成本仍然固定,须主要考虑可变动的间接套利成本对基差调整的作用。间接交易成本主要包括冲击成本和等待成本。冲击成本不仅可以衡量交易成本中流动性溢价的部分,还能估测等待过程中价格向不利方向变化而带来的风险。在国外学者对冲击成本的研究中,有Harris(1990)[14]提出的基于市场分笔数据的统计类测算指标,也有基于计量模型方法的价格冲击模型(Hasbrouck,1991)[15]。由于这些方法所需的高频分笔数据较难获取且计算复杂,我们可以借鉴Almgren等(2005)[16]采用的冲击成本模型计算冲击成本。另外,沪深300期货分别与成分股、沪深300ETF套利的冲击成本不同,因此须分别计算沪深300股指期货、成分股及沪深300ETF的冲击成本(impact-F、impact-S和impact-ETF)。等待成本使用沪深300指数收益率的波动率(rsigma)和沪深300股指期货收益率的波动率(frsigma)表示。
(3) 均值回复特征(reversion)。市场上的套利机制使股指期货与现货之间具有长期均衡关系。如果基差处于无风险套利区间之外,大量的套利活动会造成均值回复现象。国内外学者(Jiang等, 2013;Monoyios和Sarno,2002;易蓉等,2010)[17-19]的各项研究均证明了股指期货基差呈现非线性的均值回复特征。在我国,由于股票现货市场存在卖空机制约束,这种均值回复具有更明显的非对称性。这里将参考Li和Linetsky(2014)[20]中的O-U均值回复模型,使用基差与均值之差再除以沪深300股指期货与现货指数的相对波动率对这种均值回复的特征进行解释。
(三) 分位数回归模型本文使用分位数回归模型检验投资者情绪对基差的影响,具体模型如下:
| $ {\rm{Basi}}{{\rm{s}}_t} = a + {\beta _1}S_t^{{\rm{PLS}}} + {\sum\nolimits_{j = 2}^n {{\beta _j}{\rm{Control}}} _{t - 1}} + {\varepsilon _t} $ | (1) |
其中,Basist表示第t周的沪深300期货基差;SPLS表示第t周复合投资者情绪指数。对控制变量Controlt-1进行滞后一阶处理能够避免回归模型的内生性问题。为了更好地比较不同因素对基差影响的效果,将对被解释变量以外的所有变量进行标准化处理,这样可以更方便地比较出各因素发生一单位变化对基差产生的具体影响。
稳健性检验使用控制函数法构建半参数分位数回归,具体模型如下:
| $ {\rm{Basi}}{{\rm{s}}_t} = a + {\beta _1}{\mathit{\boldsymbol{S}}}_t^{{\rm{PLS}}} + {\beta _2}{X_t} + {\sum\nolimits_{j = 3}^n {{\beta _j}{\rm{Control}}} _{t - 1}} + {\varepsilon _t} $ | (2) |
| $ {X_t} = {p_t} + {\theta _1}{\mathit{\boldsymbol{S}}}_t^{{\rm{PLS}}}{\theta _2}{Z_t} + \sum\nolimits_{j = 3}^n {{\theta _j}{\rm{Contro}}{{\rm{l}}_{t - 1}}} + {\delta _t} $ | (3) |
其中,Basist表示第t周的沪深300期货基差;SPLS表示第t周复合投资者情绪指数;Xt是内生解释变量;Zt是Xt的工具变量。对控制变量Controlt-1进行滞后一阶处理能够避免回归模型的内生性问题,可将Controlt-1视作外生解释变量。εt和δt是不可观测的实值随机变量。回归时首先对式(3)进行分位数回归,再将回归得到的残差项代入式(2)中进行分位数回归得到参数估计值。
四、样本数据与描述性统计 (一) 样本数据这里采用的样本数据为沪深300股指期货从2013年7月26日至2016年7月15日期间的日交易数据。其间,2014年中出现了股指期,现货市场的大幅上涨,随后2015年7月由股灾引发的价格暴跌,使得这段时期股指期、现货市场均出现了大幅度的波动,市场处于明显的动荡时期。市场更容易划分出平稳和动荡两个阶段,并且平稳与动荡的市场态势之间的特征也具有非常明显的差别,实证结果能够显著地体现两种不同市态下,投资者情绪对基差的不同作用。另外,从成交量来看,自2016年以来,股指期货成交量处于稳定且较低的水平,相比2013到2016年的样本数据区间有很大的缩量。由于投资者情绪与成交量呈现正相关关系,可以看出投资者情绪在2017年和2018年是非常悲观的,且情绪的波动并不大;因此以2013年7月26日至2016年7月15日作为样本数据进行实证研究是比较具有代表性的,能够更清晰地得到投资者情绪与基差的关系。由于投资者情绪代理变量大部分为周度数据,因此具体选取使用155周数据进行研究。另外,本文将在Pagan和Sossounov(2003)[21]关于牛、熊市的判别方法的基础上,使用周度数据计算第t周前后三个月的波动率区分市场态势。当t周及以后的波动率持续超过t周前波动率的20%,即认为股市进入动荡阶段。因此,市场被分成股市平稳阶段(2013年7月26日—2015年3月27日)和股市动荡阶段(2015年3月28日—2016年7月15日)。其中,被解释变量、解释变量、控制变量及调节变量数据均来自于wind数据库,然后使用R3.3.0进行分位数回归分析。
(二) 描述性统计与方差分析表 1是各个变量的具体说明与分市态的描述性统计。描述统计与方差分析显示,新增A股参与交易的投资者数量(num)、封闭式基金折溢价率(prem)、市场换手率(turnover)以及A股平均市盈率(PE)和现货市场主买率(buyrate)五个指标作为投资者情绪复合指数的原指标。除新增A股投资者数量和主买率指标外,其余指标在两个市态中都有显著差异,从方差分析结果易知,情绪复合指标在两个市态下存在显著差异。基差在这两个态势下的差别非常明显,在1%水平下显著,表明在两个市态下,股指期货升贴水程度不同,且在股市动荡态势下均值为0.2,呈现明显的贴水现象。调节变量和控制变量均在两种市态下呈现不同的显著程度,说明上述方法所划分的两个时间区间确实反映了不同的市场态势。
| 表 1 变量的描述性统计与方差分析 |
受篇幅所限,表 2只列出了具有代表性的分位点25%、50%和75%的回归结果。通常情况下,25%分位点代表期货市场升水,50%分位点表示基差处于0附近,75%分位点表示期货市场贴水。观察投资者情绪对基差的整体影响,在两个市场态势下,投资者情绪复合指数系数在所有分位点均为负,并且在股市动荡阶段的显著性最高,系数的绝对值最大;说明在其他控制变量不变的情况下,同样幅度的情绪变动在暴涨暴跌的市场中对基差的影响作用更强。这证实了假设1和假设2。
| 表 2 分位数模型回归结果 |
从分位数模型回归结果看出,投资者情绪对基差的影响具有非对称性,证实了假设3。这也说明了使用分位数回归模型的必要性和合理性。观察回归系数可知,在不同市场态势下,投资者情绪对基差的非对称影响效果亦不相同。股市在较为平稳的阶段,投资者情绪对期货升、贴水的影响相近。但在股市动荡期间,投资者情绪对基差的影响更大,作用更显著,且对基差的影响存在非对称效果,在贴水期间基差更容易受到投资者情绪的影响。这是由于市场在暴涨阶段往往伴随着投资者情绪高涨,会吸引大量的投机者频繁交易,在市场流动性提高的同时,价格预期也进一步被推高,形成更高的升水。而当市场处于暴跌阶段,现货市场的做空限制会引发投资者的恐慌心理,悲观的情绪会放大投资者的非理性行为,导致情绪对基差调整的作用更加显著。同时,正是由于做空机制的不完善,在市场出现异常下跌行情时,作为我国资本市场上为数不多的风险管理工具,股指期货被情绪悲观的投资者们过度使用,承接了大量来自现货市场的抛压。这一市场机制问题也是股市异常波动期间内股指期货持续深度贴水的重要成因之一。
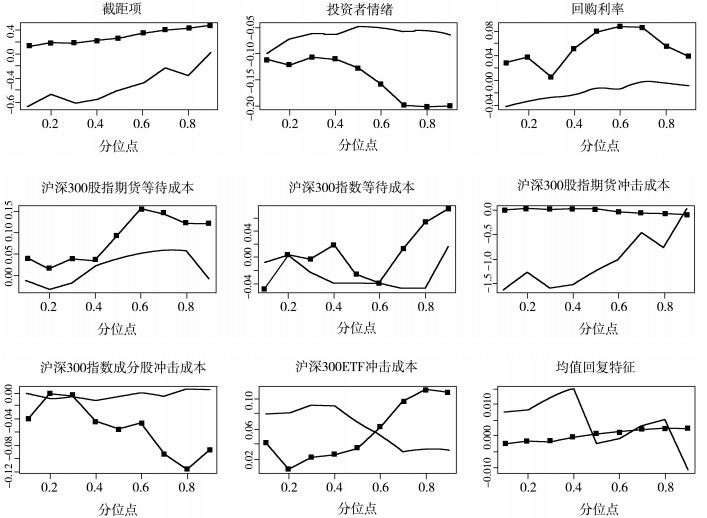
为了更直观地看出情绪指标对基差不同分位数的完整影响情况,图 2给出基差影响因素的分位数回归系数变化情况。显然可以看出,基差随着投资者情绪指数的上涨而减小,随投资者情绪指数的下跌而增大;且动荡市场态势各分位点系数均低于平稳态势,表明市场处于动荡态势下,投资者情绪对基差的影响更大。在平稳市场态势下,投资者情绪对基差的影响呈现较平稳的直线型,说明投资者情绪对基差不存在非对称影响。而市场处于动荡态势时,投资者情绪对基差的影响呈一条斜向下的曲线,投资者情绪对基差的影响存在非对称效应,且贴水期间基差更容易受到投资者情绪的影响。从分位数回归结果的显著性来看,套利成本也是影响基差的显著因素之一,而基差的均值回复特征不明显。虽然回购利率对基差影响在统计上不显著,但从图中可以看出两个市态下回购利率对基差的影响存在明显差别,这可以用持有成本理论来解释。在股市平稳的态势下,回购利率与基差呈现负相关关系,此时市场情绪较为稳定,融资成本的提高会引起基差走强。而在股市处于动荡态势时的情形恰恰相反,融资成本的提高更容易降低市场热度及收益率预期,引起基差进一步走弱。因此持有成本对基差也存在一定影响,但没有投资者情绪的作用明显。
|
注:图中带方形点的实线表示股市动荡态势下的分位数回归结果,实线表示平稳市态下的分位数回归结果;横轴表示基差水平的不同分位点,纵轴表示各变量的回归系数。 图 2 基差影响因素的分位数回归系数变化 |
通过检验流动性与沪深300期货基差的关系,可以避免因投资者情绪指标体系中含有流动性指标成分而否定投资者情绪对基差的影响。基于Li和Wu(2006)[22]、郦金梁等(2012)[23]、郑振龙和林璟(2015)[8]的研究分析,交易量作为流动性指标包含两个部分:流动性(期望交易量)和信息交易量。其中,信息交易量可以体现出投资者情绪。因此,可以采用Amihud(2002)[24]的一阶自回归方法,将沪深300股指期货与现货的交易量进行分解,以期望交易量代表市场流动性指标。同时,我们还可以借鉴李凤羽(2014)[25]关于稳健性检验的处理方法,使用五个单一投资者情绪指标分别代替投资者情绪指数,利用分位数回归模型重新拟合,以更清楚地说明投资者情绪对基差的主导作用以及各个投资者情绪源指标对基差的影响程度。最终的回归结果表明①:在多个分位点处,期货市场预期交易量的回归系数不显著,信息交易量的回归系数显著;现货市场的预期交易量和信息交易量的回归系数均显著。该结论与国外学者的研究相反,说明我国投资者情绪对基差的影响占据主导地位。另外,在多个分位点处,除新增开户数与封闭式基金折溢价率的回归系数不显著,其余投资者情绪源指标的回归系数均显著,这表明能够解释投资者情绪变化的流动性代理指标(换手率与主买率)和市盈率指标比新增开户数(新增A股参与交易的投资者数量)与封闭式基金折溢价率更能对基差变动作出解释,可以更有效地反映我国投资者情绪的变化。
①限于篇幅,本文略去投资者情绪指标的稳健性分析,相关表格留存待索。
2. 内生性分位数回归的稳健性分析。本文设定的模型中虽然引入了很多关键的控制变量进行回归分析,但仍可能忽略其他影响基差的因素,遗漏变量和测量误差所带来的内生性问题会导致模型估计结果有偏差且不一致。大部分国内学者使用分位数回归时通常使用基于工具变量的两阶段回归模型来解决,但估计得到的结果不一定是一致的(Terza等,2008)[26]。本文认为,可以在回归模型(1)的右侧引入滞后两期的基差值作为工具变量,基于工具变量分位数回归法可以相对有效地缓解模型的内生性问题。根据表 3的稳健性回归结果,投资者情绪在多个分位点处的回归系数仍然显著为负,并且投资者情绪系数大小及其显著性与表 2得到的结论相似,说明遗漏变量、测量误差等带来的内生性问题不会影响上面得出的结论。
| 表 3 基于工具变量的分位数回归估计结果 |
非理性的噪声交易容易造成市场价格与理论价格的持续偏离。Lee等(2012)[27]从不同类型投资者交易行为角度,实证得出不同投资者结构下的非理性行为对基差产生不同的影响。投资者情绪对基差的作用效果可能受到不同投资者结构的影响,市场中的机构投资者往往更具有投资理性(Valkanov,2006)[28],而个人投资者更容易产生非理性的投资行为(Verma等,2007)[29]。当市场个人投资者数量更多时,高涨的投资者情绪会扩大非理性购买行为,使基差持续扩张。由此,这里再提出假设4。
假设4:资本市场的机构化程度会改变投资者情绪对基差的影响。
为了检验假设4,我们可以在模型(1)中加入投资者情绪与投资者结构的交叉项。具体的检验结果见表 4。考虑到机构投资者的持股比例与股票市场行情密切相关,股指期货基差水平的变化会影响机构投资者的投资决策,进一步影响机构投资者的持股份额,股指期货基差水平与投资者结构之间可能存在因果关系而产生内生性,导致分位数回归结果是有偏或不一致的。本文借鉴Lee(2007)[30]和Chernozhukov(2015)[31]的研究,通过在模型右侧引入投资者结构的代理变量作为工具变量,采用控制函数的方法缓解内生性问题。所选取的代理变量参考张雄等(2010)[32]对于投资者结构的度量方法,即用交易量与持仓量之比来衡量。投资者结构可定义为投机行为和套期保值行为的相对程度,使用交易量与持仓量之比反映了投机行为与套期保值行为之间的较量。表 5为考虑投资者结构的分位数回归结果,与表 4得到的结论非常接近,可见所选取的工具变量是合适的。
| 表 4 考虑投资者结构的分位数回归结果 |
| 表 5 基于控制函数的分位数回归结果 |
通过观察回归结果中交叉项的系数可以发现,当股市处于平稳态势时,投资者情绪与投资者结构的交叉项的系数均为正数,与情绪对基差的作用相反,并且在10%的置信水平下显著。这证实了假设4,并且表明:在股市平稳的情况下,期货市场机构化程度越高,投资者情绪对基差的影响越小。这种积极影响在期货升水时更加显著。但是,需要注意另外两个重要结论:其一,在股市处于动荡的市场环境下,投资者情绪与投资者结构的交叉项前的系数并不显著,机构化程度的提高实际上并没有降低投资者情绪对基差的影响。这说明在股市平稳阶段,机构化程度的提高有助于市场稳定,但在动荡市场环境下,机构投资者的作用则不明显。其二,基于控制函数的分位数回归结果中,在股市动荡的环境下,尽管投资者情绪与投资者结构的交叉项前的系数存在较低的显著性,但投资者结构与基差呈负相关关系,且投资者结构前的系数的绝对值大于交叉项系数的绝对值,说明当考虑投资者情绪与投资者结构对基差的交互影响时,尽管机构投资者更具有理性投资行为,但机构投资者的交易行为在总体上并没有起到稳定市场的作用,在情绪的作用下甚至会推动股指期货的暴涨暴跌。而在市场处于平稳上升阶段时,投资者结构系数与交叉项前的系数均为正数,机构化程度的提高对于市场稳定起到非常显著的作用。总体而言,投资者结构确实是影响基差的重要因素,在股市平稳时,机构化程度的提高会减轻投资者情绪对基差的影响,但在股市动荡阶段机构投资者本身的交易行为并没有起到维护股市平稳运行的作用。
七、结论与启示本文基于分位数回归方法,对不同市态下的投资者结构、投资者情绪和股指期货基差的关系进行了系统研究,拓展了以往学者的研究边界和方法。具体研究发现投资者情绪对沪深300指数期货基差具有非对称影响。我国资本市场运行存在以下三方面问题:第一,投资者情绪对基差是负向影响,即基差随着投资者情绪指数的上涨而减小,随投资者情绪指数的下跌而增大,但存在非对称性。非对称性体现在:①不同市场态势下,投资者情绪对股指基差的负向影响程度不同。②股市动荡的市态下,当市场分别处于升水和贴水情形时,投资者情绪对基差的负向影响程度不同。当股指期货贴水时,基差更容易受到投资者情绪因素的作用。第二,在投资者情绪指标中,市盈率、换手率和主买率指标能够更有效地对基差变动作出解释。相比于流动性,投资者情绪是我国基差调整的主要影响因素。第三,市场机构化程度的提高不一定会减轻投资者情绪对基差的异常作用。在股市处于平稳状态时,投资者情绪对基差的影响会随着资本市场机构化程度的增加而减弱。然而,在股市动荡阶段,机构投资者受情绪引导产生的非理性交易行为甚至推动了我国股指期货暴涨暴跌。同理,在股市暴跌阶段,机构化发展并没有对市场的稳定起到预想中的作用。
我国期现基差变动中蕴含大量的投资者情绪因素,反映了我国资本市场投机氛围浓厚、市场效率低的现状,对认识资本市场运行和资本市场政策调整有三点重要启示。首先,期、现货市场较高的套利成本抑制了套利交易与套期保值的实现,使基差更容易受投资者情绪的影响,不利于基差水平的合理回归。其次,投资者情绪对基差的非对称影响主要归因于现货市场做多与做空机制的非对称性以及金融期货等风险管理工具的种类不足,这说明我国资本市场的做空机制有待完善,风险管理工具的种类有待丰富。最后,我国资本市场个人投资者占比较大,且存在机构散户化现象。一旦投资者出现整体的非理性行为,其交易策略制定及效果就会受到严重影响,并进一步增大资本市场的系统性风险。
| [1] | MARCINKIEWCZ E. Determinants of the Index Futures Basis: An Empirical Study of Warsaw Stock Exchange[C]//Proceedings of the 14th International Conference on Finance and Banking, Karvina: 7School Business Administration Karvina, 2014: 242-251. |
| [2] | LIEN D, LIM G, YANG L, et al. Dynamic dependence between liquidity and the S & P 500 index futures-cash basis[J]. Journal of futures markets, 2013,33(4): 327–342. DOI: 10.1002/fut.2013.33.issue-4 |
| [3] | LI P, GUO Y. Futures-cash basis and liquidity in security market[J]. Journal of management science, 2017,30(4): 151–160. |
| [4] | BAKER M, STEIN J C. Market liquidity as a sentiment indicator[J]. Journal of financial market, 2004(7): 271–299. |
| [5] | 刘晨, 安毅. 分级基金A类份额期权价值影响因素及度量[J]. 华南理工大学学报(社会科学版), 2016(4): 29–35. |
| [6] | YANG C, GAO B. The term structure of sentiment effect in stock index futures market[J]. North American journal of economics and finance, 2014(30): 171–182. |
| [7] | WANG X, YE Q, ZHAO F, et al. Investor sentiment and the Chinese index futures market:evidence from the internet search[J]. Journal of futures markets, 2018,38(4): 468–477. DOI: 10.1002/fut.v38.4 |
| [8] | 郑振龙, 林璟. 沪深300股指期货定价偏差与投资者情绪[J]. 数理统计与管理, 2015(6): 1129–1140. |
| [9] | ZOU H, SUN L. The Influence of Investor Sentiment on Stock Return and its Volatility under Different Market States[C]//International Conference on Business Intelligence & Financial Engineering?IEEE Computer Society, Lanzhou: IEEEE, 2012: 337-341. |
| [10] | KADAPAKKAM P R, KUMAR U. Impact of liquidity on the futures-cash basis:evidence from the indian market[J]. Journal of futures markets, 2012,33(3): 266–298. |
| [11] | HAN J, PAN Z. On the relation between liquidity and the futures-cash basis:evidence from a natural experiment[J]. Journal of financial markets, 2016(36): 115–131. |
| [12] | KUMAR A, LEE C M C. Retail investor sentiment and return comovements[J]. Journal of finance, 2006,61(5): 2451–2486. DOI: 10.1111/j.1540-6261.2006.01063.x |
| [13] | HUANG D, JIANG F, TU J, et al. Investor sentiment aligned:a powerful predictor of stock returns[J]. Review of financial studies, 2015,28(3): 791–837. DOI: 10.1093/rfs/hhu080 |
| [14] | HARRIS L. Liquidity, trading rules, and electronic trading system[C]//Monograph Series in Finance and Economic, New York: New York University Salomon Center, 1990. |
| [15] | HASBROUCK J. The Summary informativeness of stock trades:an econometric analysis[J]. Review of financial studies, 1991,4(3): 571–595. DOI: 10.1093/rfs/4.3.571 |
| [16] | ALMGREN R, THUM N, HAUPTMANN E. Directestimeation of equity market impact[J]. Risk, 2005,18: 57–62. |
| [17] | JIANG Y, WU W, YE W, et al. Nonlinear features and mean reversion mechanism research based on the basis of stock index futures[J]. Journal of University of Science & Technology of China, 2013,43(12): 989–996. |
| [18] | MONOYIOS M, SARNO L. Mean reversion in stock index futures markets:a nonlinear analysis[J]. Journal of futures markets, 2002,22(4): 285–314. DOI: 10.1002/(ISSN)1096-9934 |
| [19] | 易蓉, 张文, 陈冲, 等. 基于预期理论框架的农产品期货基差行为[J]. 系统工程理论与实践, 2010, 30(11): 1954–1959. DOI: 10.12011/1000-6788(2010)11-1954 |
| [20] | LI L, LINETSKY V. Time-changed ornstein-uhlenbeck processes and their applications in commodity derivative models[J]. Mathematical finance, 2014,24(2): 289–330. DOI: 10.1111/mafi.2014.24.issue-2 |
| [21] | PAGAN A R, SOSSOUNOV K A. A simple framework for analysing bull and bear markets[J]. Journal of applied econometrics, 2003,18(1): 23–46. |
| [22] | LI J, WU C. Daily return volatility, bid-ask spreads, and information flow:analyzing the information content of volume[J]. Journal of business, 2006,79(5): 2697–2739. DOI: 10.1086/jb.2006.79.issue-5 |
| [23] | 郦金梁, 雷曜, 李树憬. 市场深度、流动性和波动率——沪深300股票指数期货启动对现货市场的影响[J]. 金融研究, 2012(6): 124–138. |
| [24] | AMIHUD Y. Illiquidity and stock returns:cross-section and time-series effects[J]. Journal of financial markets, 2002,5(1): 31–56. DOI: 10.1016/S1386-4181(01)00024-6 |
| [25] | 李凤羽. 投资者情绪能够解释ETF的折溢价吗?——来自A股市场的经验证据[J]. 金融研究, 2014(2): 180–192. |
| [26] | TERZA J V, BASU A, RATHOUZ P J. Two-stage residual inclusion estimation:addressing endogeneity in health econometric modeling[J]. Journal of health economics, 2008,27(3): 531–543. |
| [27] | LEE H C, CHIEN C Y, LIAO T H. Commonality in trading activity and futures-cash basis:evidence from the taiwan futures and stock markets[J]. Journal of futures markets, 2012,32(10): 964–994. DOI: 10.1002/fut.2012.32.issue-10 |
| [28] | VALKANOV R. Measuring mutual fund performance with characteristic-based benchmarks (digest summary)[J]. Journal of finance, 2006,52(3): 1035–1058. |
| [29] | VERMA R, VERMA P. Noise trading and stock market volatility[J]. Journal of multinational financial management, 2007,17(3): 231–243. DOI: 10.1016/j.mulfin.2006.10.003 |
| [30] | LEE S. Endogeneity in quantile regression models:a control function approach[J]. Journal of econometrics, 2007,141(2): 1131–1158. DOI: 10.1016/j.jeconom.2007.01.014 |
| [31] | CHERNOZHUKOV V, FERNÁNDEZ-VAL I, KOWALSKI A E. Quantile regression with censoring and endogeneity[J]. Journal of econometrics, 2015,186(1): 201–221. |
| [32] | 张雄, 万迪昉, 杨光. 投资者结构与期限结构对期货市场效率的影响研究[J]. 证券市场导报, 2010(4): 35–40. |
 2019, Vol. 21
2019, Vol. 21
