2015年4月16日,上证50股指期货和中证500股指期货正式上市交易,这是继沪深300股指期货推出后,我国金融市场推出的第二批股指期货,不仅丰富了我国股指期货市场产品种类,而且为投资者提供了更多的投资途径。价格发现作为股指期货重要的市场功能之一,其功能是否正常发挥是监管层、投资者和学术界共同关注的问题。
然而,在上证50、中证500股指期货推出短短两个月之后,中国股市经历了连续大幅下跌,市场波动剧烈,以股指期货为首的金融衍生品市场受到诸多质疑。为抑制过度投机、维护市场稳定,中金所和上交所出台了多种限制期货等金融衍生品交易活动的政策措施,其中最主要的手段之一便是仓位限制。2015年9月7日,中金所推出了严格的政策措施,沪深300股、上证50股、中证500股指期货客户在单个产品、单日开仓交易量超过10手的构成“日内开仓交易量较大”的异常交易行为。
仓位限额包括限制开仓额度和限制持仓额度。限制仓位额度可能会抑制市场的异常波动,但会使该市场的参与率降低、市场交易活跃性降低。市场的交易越活跃,当信息变化时,投资者将首先在该市场做出反应并促成价格,因而提高了该市场的价格发现功能。学者们普遍发现市场交易活跃性会提高价格发现能力:Theissen(2002)[1]发现德国场内交易系统和电子交易系统的价格发现贡献度与市场交易活跃性成正比;Mizrach和Neely(2008)[2]发现美国国债市场的价格发现功能与市场交易活跃性正相关;Frijns等(2015)[3]用GMM方法回归分析了跨美国、加拿大市场上市交易股票的价格发现能力的影响因素,发现较高的交易活跃性提升市场的价格发现能力。同时,开平仓限额可能会使得期货投机者或套利交易者转向现货市场,增加现货市场的流动性和价格发现功能,从而间接降低期货市场的价格发现能力。
本文采用上证50股指期货和中证500股指期货上市后一年的1分钟高频数据,结合沪深300股指期货,探究我国股指期货市场相对现货市场的价格发现能力,并分析中金所推出的严格仓位限额对股指期货价格发现功能的影响。
二、文献回顾 (一) 价格发现贡献度衡量方法经过多年的研究发展,学术界形成了两种最常用的用以衡量市场价格发现贡献度的模型:Hasbrouck(1995)[4]的信息共享模型(information share,IS模型)和Gonzalo,Granger(1995)[5]的永久短暂模型(permanent transitory,PT模型)。如Tse(1999)[6]采用IS模型,发现道琼斯工业指数期货的价格发现贡献度大于现货;Booth等(1999)[7]采用PT模型研究了德国股市与衍生品市场之间的价格发现功能,发现指数和指数期货的价格发现贡献度大于期权;Mizrach和Neely(2006)[2]采用IS模型和PT模型研究美国国债市场的价格发现能力,发现国债期货在价格发现中占主导。
Baillie等(2002)[8]认为IS模型比PT模型更具有经济解释力,而且学术界一般倾向于使用IS模型作为主要的价格发现贡献度衡量模型。如Chang等(2013)[9]采用IS模型实证分析持仓限额对日元/美元、欧元/美元外汇期货的价格发现能力的影响,发现套期保值持仓量的上升对价格发现有负向作用,投机持仓量在一定的范围内促进价格发现过程;Boyd和Locke(2014)[10]采用IS模型研究期货和期权市场的价格发现功能,发现期货市场的价格发现能力强于期权市场;Bart等(2015)[11]采用IS模型和PT模型研究了跨加拿大和美国上市公司的价格发现能力,发现美国市场对信息的处理能力更强;Oztekin等(2017)[12]采用IS模型分析了美国电子交易期货和ETF市场的价格发现能力,发现期货市场在价格发现中占主导。
国内学者使用IS模型和PT模型对沪深300股指期货进行了大量研究,如严敏等(2009)[13]采用IS模型和PT模型分析沪深300股指期货的价格发现功能,结果表明现货的价格发现能力大于期货;何诚颖等(2011)[14]使用IS模型和PT模型实证分析沪深300指数期货价格发现能力,结果表明期货的价格发现能力更强;方匡南和蔡振忠(2012)[15]利用IS模型和PT模型计算期货价格发现的贡献度,结果表明现货市场在价格发现功能中的作用相对较大;陈莹等(2014)[16]采用IS模型和PT模型检验沪深300指数衍生证券的价格发现功能,结果表明股指期货的价格发现贡献度最大。
IS模型虽然应用广泛,但模型需要对协方差矩阵进行Cholesky分解,使得计算结果不唯一。Lien和Shrestha(2009)[17]发现了IS模型的缺陷,并提出修正的IS模型(modified information share, MIS模型)以改善IS模型。华仁海和刘庆富(2010)[18]采用MIS模型发现沪深300指数期货具有较强的价格发现能力;Liu和An(2011)[19]采用MIS模型研究美国与中国商品期货市场的价格发现能力,发现美国商品期货市场的价格发现能力更强;刘向丽和张雨萌(2012)[20]采用MIS模型发现期货市场在价格发现中起主导作用;Inani(2017)[21]采用MIS、IS和PT模型研究印度期货与股票市场的价格发现能力,结果表明期货市场发挥了价格发现的功能。
(二) 文献综述简析通过对国内外价格发现功能研究成果的分析发现,以往学者的研究有以下几点不足:首先,在研究模型方面,国内外学者大多采用传统IS模型和PT模型,MIS模型应用还不是很多;其次,以往的国内研究主要集中在沪深300股指期货的价格发现能力上,由于上证50股指期货和中证500股指期货的推出时间较晚,目前还鲜有研究;最后,关于仓位限额对价格发现能力影响的研究还相对较少。
针对以往研究的不足,本文从以下几个方面进行了研究改进:首先,采用1分钟高频数据作为本文的实验数据频率;其次,运用MIS模型和PT模型衡量上证50股指期货、沪深300股指期货和中证500股指期货相对现货的价格发现贡献度;最后,对比仓位限额推出前后的股指期货价格发现能力的变化。
三、研究模型与数据描述 (一) 研究模型1.向量误差修正模型
向量误差修正模型是IS模型和PT模型的基础,其最常用的形式为:
| $ \Delta {\mathit{\boldsymbol{y}}_\mathit{\boldsymbol{t}}} = \mathit{\boldsymbol{\alpha ec}}{\mathit{\boldsymbol{m}}_{\mathit{\boldsymbol{t}} - 1}} + \sum\limits_{i = 1}^{p - 1} {{\beta _i}\Delta {\mathit{\boldsymbol{y}}_{\mathit{\boldsymbol{t}} - \mathit{\boldsymbol{i}}}}} + {\mathit{\boldsymbol{\varepsilon }}_\mathit{\boldsymbol{t}}} $ | (1) |
其中,ecmt-1=ay1, t-1-by2, t-1+c是误差修正项;α为ecmt-1的短期调整系数矩阵;βi为差分项Δyt-1的系数,表示Δyt-1变动对Δyt的影响。
以期货和ETF为例,两者的向量误差修正模型可以表示为:
| $ r\_i{h_t} = {c_1} + {\alpha _1}ec{m_{t - 1}} + \sum\limits_{i = 1}^k {\beta _i^{1,1}r\_i{h_{t - i}}} + \sum\limits_{i = 1}^k {\beta _i^{1,2}r\_et{f_{t - i}} + {\varepsilon _{1,t}}} $ | (2) |
| $ r\_et{f_t} = {c_2} + {\alpha _2}ec{m_{t - 1}} + \sum\limits_{i = 1}^k {\beta _i^{2,1}r\_i{h_{t - i}}} + \sum\limits_{i = 1}^k {\beta _i^{2,2}r\_et{f_{t - i}} + {\varepsilon _{2,t}}} $ | (3) |
式(2)和式(3)中,r_iht, r_etft分别表示上证50股指期货和上证50ETF的对数价格的差分序列,即Δp_iht, Δp_etft;c1, c2表示常数项;α1, α2表示误差修正项调整系数;ecm表示误差修正项;βip, q(p=1, 2;q=1, 2)表示短期调整系数;ε1, t, ε2, t为残差序列。
2.价格发现贡献度模型
价格发现贡献度模型主要分为两种:信息共享模型(IS)和永久短暂模型(PT)。IS模型测度各市场的新息对共因子方差的贡献比例;PT模型认为误差修正机制仅是一个永久性的冲击,通过定义误差修正系数函数来衡量每个市场对共同因素的贡献。
(1) 信息共享模型(IS)。
Hasbrouck(1995)[1]将式(1)变换成移动平均形式:
| $ \Delta {\mathit{\boldsymbol{y}}_\mathit{\boldsymbol{t}}} = \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( \mathit{\boldsymbol{L}} \right){\mathit{\boldsymbol{\varepsilon }}_\mathit{\boldsymbol{t}}} $ | (4) |
和单整形式:
| $ {\mathit{\boldsymbol{y}}_\mathit{\boldsymbol{t}}} = {\mathit{\boldsymbol{y}}_0} + \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( 1 \right)\sum\limits_{\mathit{\boldsymbol{s}} = 1}^\mathit{\boldsymbol{t}} {{\mathit{\boldsymbol{\varepsilon }}_\mathit{\boldsymbol{s}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^ * }\left( \mathit{\boldsymbol{L}} \right){\mathit{\boldsymbol{\varepsilon }}_\mathit{\boldsymbol{t}}} $ | (5) |
其中,Ψ(L)是滞后算子L的矩阵多项式;Ψ(1)是影响矩阵,是移动平均系数的和;Ψ(1)εt是新息对每个市场价格的长期影响;Ψ*(L)εt为短期趋势。
Hasbrouck(1995)[1]认为序列之间存在严格的一对一协整关系,使得序列之间维持在均衡状态,也就是说每一对协整向量可以表示为(1:-1),意味着存在以下关系式:
| $ \mathop {{\mathit{\boldsymbol{\beta }}^{\rm{T}}}}\limits_{\left( {n - 1} \right) \times n} = \left[ {{\mathit{\boldsymbol{l}}_{\left( {n - 1} \right)}}: - {\mathit{\boldsymbol{I}}_{\left( {n - 1} \right)}}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{ - 1}&0& \cdots &0\\ 1&0&{ - 1}& \cdots &0\\ 1&0&0& \cdots &0\\ \vdots&\vdots&\vdots&\ddots&\vdots \\ 1&0&0& \cdots &{ - 1} \end{array}} \right] $ | (6) |
其中,l(n-1)为(n-1)阶单位列向量;I(n-1)为(n-1)×(n-1)阶单位矩阵。
同时,Engle和Granger(1987)[22]发现当不同序列存在协整关系时,满足以下条件:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\beta }}^{\bf{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( {\bf{1}} \right) = {\bf{0}},}&{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( {\bf{1}} \right)\mathit{\boldsymbol{\alpha }} = {\bf{0}}} \end{array} $ | (7) |
由式(7)可得,Ψ(1)存在相同的行向量。若令ψ=(ψ1, ψ2, …, ψn)为Ψ(1)的一行,l=(1, 1, …, 1)T,则式(5)可写为:
| $ {\mathit{\boldsymbol{y}}_\mathit{\boldsymbol{t}}} = {\mathit{\boldsymbol{y}}_0} + \mathit{\boldsymbol{\psi }}\left( {\sum\limits_{\mathit{\boldsymbol{s}} = 1}^\mathit{\boldsymbol{t}} {{\mathit{\boldsymbol{\varepsilon }}_\mathit{\boldsymbol{s}}}} } \right)\mathit{\boldsymbol{l}} + {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^ * }\left( \mathit{\boldsymbol{L}} \right){\mathit{\boldsymbol{\varepsilon }}_\mathit{\boldsymbol{t}}} $ | (8) |
ψεt是永久地融入了价格,故Hasbrouck将其定义为不同市场间的共同有效价格,方差为:
| $ Var\left( {\mathit{\boldsymbol{\psi }}{\mathit{\boldsymbol{\varepsilon }}_\mathit{\boldsymbol{t}}}} \right) = \mathit{\boldsymbol{\psi \boldsymbol{\varOmega} }}{\mathit{\boldsymbol{\psi }}^{\bf{T}}} $ | (9) |
在两市场的IS模型中,ψ=(ψ1, ψ2),Ω为残差向量εt=(ε1t, ε2t)'的协方差矩阵,即:
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = \left[ {\begin{array}{*{20}{c}} {\sigma _1^2}&{\rho {\sigma _1}{\sigma _2}}\\ {\rho {\sigma _1}{\sigma _2}}&{\sigma _2^2} \end{array}} \right] $ | (10) |
其中,σi(i=1, 2)为标准差;ρ为二者间的Pearson相关系数。
可得:
| $ \mathit{\boldsymbol{\psi \boldsymbol{\varOmega} }}{\mathit{\boldsymbol{\psi }}^{\bf{T}}} = \psi _1^2\sigma _1^2 + 2{\psi _1}{\psi _2}\rho {\sigma _1}{\sigma _2} + \psi _2^2\sigma _2^2 $ | (11) |
若ρ=0,即市场间的新息当期相互独立时,市场i在总方差Var(ψεt)所占的比重为:
| $ {S_i} = \frac{{\mathit{\boldsymbol{\psi }}_i^2\mathit{\boldsymbol{\sigma }}_i^2}}{{\mathit{\boldsymbol{\psi \boldsymbol{\varOmega} }}{\mathit{\boldsymbol{\psi }}^{\rm{T}}}}} $ | (12) |
若ρ≠0,则需要对Ω进行Cholesky分解用来消除新息间的当期相关,即:
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{F}}^{\rm{T}}} $ | (13) |
其中,
则,Var(ψεt)=ψΩψT=ψFFTψT=ψF(ψF)T,且:
| $ \mathit{\boldsymbol{\psi F}} = \left( {{\psi _1},{\psi _2}} \right)\left[ {\begin{array}{*{20}{c}} {{\sigma _1}}&0\\ {\rho {\sigma _2}}&{{\sigma _2}{{\left( {1 - {\rho ^2}} \right)}^{1/2}}} \end{array}} \right] = \left( {{\psi _1}{\sigma _1} + {\psi _2}\rho {\sigma _2},{\psi _2}{\sigma _2}{{\left( {1 - {\rho ^2}} \right)}^{1/2}}} \right) $ | (14) |
那么,市场i在总方差Var(ψεt)中所占的比重可表示为:
| $ {S_i} = \frac{{{{\left( {{{\left[ {\psi F} \right]}_j}} \right)}^2}}}{{\mathit{\boldsymbol{\psi \boldsymbol{\varOmega} }}{\mathit{\boldsymbol{\psi }}^{\rm{T}}}}} $ | (15) |
其中,[ψF]j是行向量ψF的第j(j=1, 2)个元素。
冲击因子结构为:εt=Fzt,E[zt]=0,E[ztztT]=I。
Baillie等(2002)[6]求得每个市场信息共享模型的上限与下限,如期货市场信息份额的上下限为:
| $ S_F^U = \frac{{{{\left( {\left| {{\alpha _2}} \right|{\sigma _1} + \left| {{\alpha _1}} \right|\rho {\sigma _2}} \right)}^2}}}{{{{\left( {\left| {{\alpha _2}} \right|{\sigma _1} + \left| {{\alpha _1}} \right|\rho {\sigma _2}} \right)}^2} + \left( {1 - {\rho ^2}} \right)\alpha _2^2\sigma _1^2}} = \frac{{{{\left( {\left| {{\alpha _2}} \right|{\sigma _1} + \left| {{\alpha _1}} \right|\rho {\sigma _2}} \right)}^2}}}{{\alpha _2^2\sigma _1^2 + 2\left| {{\alpha _1}} \right|\left| {{\alpha _2}} \right|\rho {\sigma _1}{\sigma _2} + \alpha _1^2\sigma _2^2}} $ | (16) |
| $ S_F^L = \frac{{\left( {1 - {\rho ^2}} \right)\alpha _2^2\sigma _1^2}}{{{{\left( {\left| {{\alpha _2}} \right|{\sigma _1} + \left| {{\alpha _1}} \right|\rho {\sigma _2}} \right)}^2} + \left( {1 - {\rho ^2}} \right)\alpha _2^2\sigma _1^2}} = \frac{{\left( {1 - {\rho ^2}} \right)\alpha _2^2\sigma _1^2}}{{\alpha _2^2\sigma _1^2 + 2\left| {{\alpha _1}} \right|\left| {{\alpha _2}} \right|\rho {\sigma _1}{\sigma _2} + \alpha _1^2\sigma _2^2}} $ | (17) |
其中,σi(i=1, 2)为标准差;αj(j=1, 2)为向量误差修正模型中的误差修正系数;ρ为两者间的Pearson相关系数。
(2) 改进的信息共享模型(MIS)。
IS模型的计算结果与研究变量的先后顺序有关,使得研究的结果可信度降低。虽然Baillie等(2002)[6]给出了价格发现贡献度的上下限,但当上下限相差很大时实证结果的精确性很难得到保障。针对IS模型的缺陷,Lien和Shrestha(2009)[15]给出了不依赖变量顺序的改进信息共享模型(MIS)。
若ρ=0,即市场间的新息当期相互独立时,Ω=diag(Ω11, Ω22, …, Ωnn),冲击因子结构为:
| $ Var\left( {\mathit{\boldsymbol{\psi }}{\mathit{\boldsymbol{\varepsilon }}_t}} \right) = \mathit{\boldsymbol{\psi \boldsymbol{\varOmega} }}{\mathit{\boldsymbol{\psi }}^{\rm{T}}} = E\left[ {\mathit{\boldsymbol{\psi }}{\mathit{\boldsymbol{\varepsilon }}_t}\mathit{\boldsymbol{\varepsilon }}_t^{\rm{T}}{\mathit{\boldsymbol{\psi }}^{\rm{T}}}} \right] = E\left[ {\mathit{\boldsymbol{\psi }}\hat F{z_t}z_t^{\rm{T}}{{\mathit{\boldsymbol{\hat F}}}^{\rm{T}}}{\mathit{\boldsymbol{\psi }}^{\rm{T}}}} \right] = \mathit{\boldsymbol{\hat \psi }}{{\mathit{\boldsymbol{\hat \psi }}}^{\rm{T}}} = \sum\limits_{i = 1}^n {\mathit{\boldsymbol{\hat \psi }}_i^2} $ | (18) |
其中,
那么,市场j的信息份额为:
| $ {S_j} = \frac{{\mathit{\boldsymbol{\hat \psi }}_j^2}}{{\sum\limits_{i = 1}^n {\mathit{\boldsymbol{\hat \psi }}_i^2} }} = \frac{{\mathit{\boldsymbol{\hat \psi }}_j^2}}{{\mathit{\boldsymbol{\hat \psi \boldsymbol{\varOmega} }}{{\mathit{\boldsymbol{\hat \psi }}}^{\rm{T}}}}} $ | (19) |
比较式(12)和式(19)可以发现,当市场之间的新息当期相互独立时,MIS模型和IS模型的公式相同。
若ρ≠0,即市场之间的新息存在当期相关时,MIS模型中的因子结构基于新息的相关矩阵Φ的因子分解,取代了IS模型中的协方差Ω矩阵Cholesky分解的下三角矩阵,从而使得模型与变量的顺序无关,市场j的信息份额为:
| $ S_j^ * = \frac{{\mathit{\boldsymbol{\psi }}_j^{ * 2}}}{{\mathit{\boldsymbol{\psi \boldsymbol{\varOmega} }}{\mathit{\boldsymbol{\psi }}^{\rm{T}}}}} $ | (20) |
F*、ψ*、Zt*、Sj*等都是针对前文中信息共享模型的改进表述,信息共享模型对应为F、ψ、Zt、Sj。其中:
F*=[GΛ-1/2G'V-1]-1;
G的列向量由新息的相关矩阵Φ的特征向量组成;
Λ为对角矩阵,对角元素为矩阵Φ的特征值;
V为对角矩阵,对角元素为矩阵Ω对角元素的标准差;
ψ*=(ψ1*, ψ2*, …, ψn*)=ψF*=(ψ1, ψ2, …, ψn)·[GΛ-1/2G'V-1]-1,ψj*为ψ*的第j个元素。
冲击因子结构为:εt=F*zt*,E[zt*]=0,E[zt*(zt*)T]=I。
(3) 永久短暂模型(PT)。
PT模型也是定量分析市场价格贡献度的一种方法。以现货和期货为例,当不同市场的价格序列存在协整关系并受某个公共因子Ct驱动时,有:
| $ {P_{j,t}} = {C_t} + {\varepsilon _{j,t}},j = 1,2 $ | (21) |
| $ {C_t} = {\lambda _1}{P_{1,t}} + {\lambda _2}{P_{2,t}} $ | (22) |
| $ {\lambda _1} + {\lambda _2} = 1 $ | (23) |
| $ \left( {{\alpha _1},{\alpha _2}} \right) \bot {\left( {{\lambda _1},{\lambda _2}} \right)^{\rm{T}}} $ | (24) |
式(21)中的εj, t代表各个市场自身的波动信息。式(24)表示向量(α1, α2)和向量(λ1, λ2)T正交,α1和α2分别为向量误差修正模型中的误差修正系数;λ1和λ2分别为现货市场的价格和期货市场的价格发现比例,即:
| $ \begin{array}{*{20}{c}} {{\lambda _1} = \frac{{ - {\alpha _2}}}{{{\alpha _1} - {\alpha _2}}},}&{{\lambda _2} = \frac{{{\alpha _1}}}{{{\alpha _1} - {\alpha _2}}}} \end{array} $ | (25) |
1.数据筛选和预处理
本文采用1分钟高频数据,全样本区间为2015/4/16—2016/4/15,共计246个交易日59 286条记录。为了对比出台仓位限额前后的股指期货价格发现能力,将全样本区间分为两个小样本区间,即严格的仓位限额出台前:2015/4/16—2015/9/2(区间一),共计98个交易日23 618条记录;严格的仓位限额出台后:2015/9/7—2016/4/15(区间二),共计148个交易日35 668条记录。
(1) 选取当月连续合约作为期货价格序列,这是因为当月合约代表了市场主力合约,成交量和流动性方面都要优于其他到期月份合约;选取交易日9: 30~11: 30以及13: 00~15: 00的价格数据,使得期货、指数和ETF市场数据能够同步对比。
(2) 对价格进行对数处理,即pj=ln(pk)(其中pk为原始价格序列;pj为对数价格序列)。
(3) 本文将期货、指数和ETF价格分别表示为p_ih(p_if、p_ic),p_sz和p_etf。
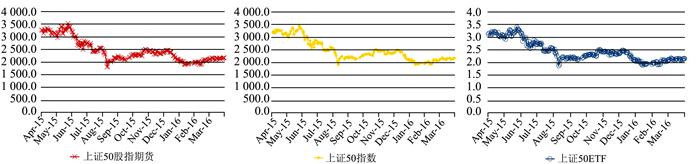
图 1~图 3分别为上证50股指期货和现货、沪深300期货和现货以及中证500股指期货和现货的价格走势。可以看出,股指期货、指数和ETF的价格呈现共变特征,价格走势相近,序列之间可能存在共同趋势项。区间对比发现,区间一的价格波动幅度相对区间二较大,说明仓位限额推出后市场波动有所降低。
|
图 1 上证50股指期货和现货的价格走势 |
|
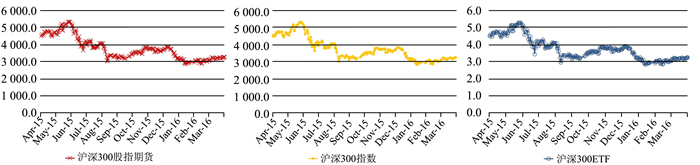
图 2 沪深300股指期货和现货的价格走势 |
|
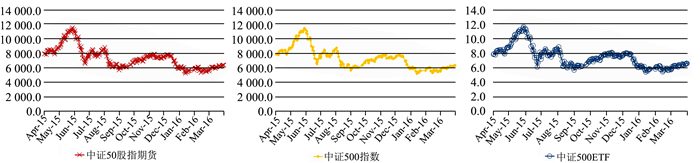
图 3 中证500股指期货和现货的价格走势 |
2.统计性描述
由表 1发现,区间一所有序列的均值都大于全样本区间和区间二,表明区间一中的价格处于相对较高水平。通过标准差的对比,发现各区间中期货的标准差都较大,表明期货的波动比ETF和指数的波动要大;所有序列的J-B统计量显著,拒绝服从正态分布的假设。
| 表 1 上证50期货和现货对数价格的统计性描述 |
由表 2发现,沪深300期货和现货的统计结果同表 1相近,也是区间一的均值最大,期货的标准差最大,J-B统计量显著性也相似。
| 表 2 沪深300期货和现货对数价格的统计性描述 |
表 3统计结果的对比分析与表 1和表 2相似,说明不同期货和现货在区间上的统计表现出一致性,基于不同指数的股指期货特征也表现出一致性。
| 表 3 中证500期货和现货对数价格的统计性描述 |
Hasbrouck(1995)[1]指出,为了准确估计高度相关的两种资产对价格发现的贡献,需要使用尽可能高频率的数据。1分钟数据相比日级别数据含有的信息更多,能够衡量期货市场日内和日间的价格发现功能;而日级别的数据只是采用日收盘价,难以衡量日内的价格发现功能。
(一) 不同数据频率的价格发现贡献度对比本文针对全样本区间,通过对1分钟、5分钟、15分钟、30分钟、60分钟和日数据进行对比,分析不同数据频率对实验结果的影响,如表 4所示。
| 表 4 不同数据频率的价格发现贡献度对比 |
从表 4可以看出,随着数据频率的升高,期货的价格发现贡献度逐渐升高,且与日内高频率数据计算的结果基本一致,而日级别数据计算的结果则与高频数据的结果相反。由此可以判定,日级别数据衡量的是日间的价格发现功能,而对日内间的价格发现功能无法衡量,从而无法从整体上衡量市场间的价格发现功能。
另外,从交易数据的完整性和可获取性方面,1分钟是数据频率的上限,故采用1分钟数据作为本文的实验数据频率。
(二) 上证50股指期货的价格发现贡献度在计算价格发现贡献度之前,本文对价格序列进行了平稳性检验、格兰杰因果检验和协整检验,结果表明对数价格序列是一阶单整序列,即I(1),序列间满足双向的格兰杰因果关系,序列之间普遍存在协整关系。
1.期货和指数
由MIS模型和PT模型计算出的上证50股指期货与上证50指数的价格发现贡献度如表 5所示。
| 表 5 上证50股指期货与指数的价格发现贡献度 |
从表 5可以看出,MIS模型和PT模型的结果一致:期货的价格发现度接近60%,大于指数的价格发现贡献度;严格的仓位限额推出后,期货的价格发现贡献度约降低了10%,但仍比指数的价格发现贡献度大。
2.期货和ETF
由MIS模型和PT模型计算出的上证50股指期货与上证50 ETF的价格发现贡献度如表 6所示。
| 表 6 上证50股指期货与ETF的价格发现贡献度 |
从表 6可以看出,MIS模型和PT模型的结果一致:期货的价格发现度接近70%,大于ETF的价格发现贡献度;严格的仓位限额推出后,期货的价格发现贡献度约降低了10%,仍在价格发现中占主导。
(三) 沪深300股指期货的价格发现贡献度1.期货和指数
由MIS模型和PT模型计算出的沪深300股指期货与沪深300指数的价格发现贡献度如表 7所示。
| 表 7 沪深300股指期货与指数的价格发现贡献度 |
从表 7可以看出,MIS模型和PT模型的结果一致:期货的价格发现度接近75%,大于指数的价格发现贡献度;严格的仓位限额推出后,期货的价格发现贡献度略微降低,仍为70%左右。
2.期货和ETF
由MIS模型和PT模型计算出的沪深300股指期货与沪深300 ETF的价格发现贡献度如表 8所示。
| 表 8 沪深300股指期货与ETF的价格发现贡献度 |
从表 8可以看出,MIS模型和PT模型的结果一致:期货的价格发现度接近75%,大于ETF的价格发现贡献度;严格的仓位限额推出后,期货的价格发现贡献度略微降低。
(四) 中证500股指期货的价格发现贡献度1.期货和指数
由MIS模型和PT模型计算出的中证500股指期货与中证500指数的价格发现贡献度如表 9所示。
| 表 9 中证500股指期货与指数的价格发现贡献度 |
从表 9可以看出,MIS模型和PT模型的结果一致:期货的价格发现度接近90%,明显大于指数的价格发现贡献度;严格的仓位限额推出后,期货的价格发现贡献度约降低了5%。
2.期货和ETF
由MIS模型和PT模型计算出的中证500股指期货与中证500 ETF的价格发现贡献度如表 10所示。
| 表 10 中证500股指期货与ETF的价格发现贡献度 |
从表 10可以看出,MIS模型和PT模型的结果一致:期货的价格发现度接近97%,明显大于ETF的价格发现贡献度;严格的仓位限额推出后,期货的价格发现贡献度略微降低。
五、结论本文采用1分钟高频数据,采用改进的信息贡献模型和永久短暂模型量化上证50股指期货、沪深300股指期货和中证500股指期货价格发现贡献度以及股指期货市场间的价格发现贡献度,并分析仓位限额对期货价格发现能力的影响。研究结论如下:
(1) 上证50股指期货、沪深300股指期货和中证500股指期货的价格发现贡献度均大于现货的价格发现贡献度,在价格发现过程中占主导地位,较好地发挥了价格发现功能。
(2) 期货仓位限额推出后,上证50股指期货、沪深300股指期货和中证500股指期货的价格发现贡献度相对现货的价格发现贡献度均有不同程度的降低,说明仓位限额降低了期货的价格发现能力,而且对上证50股指期货的价格发现能力影响最大。
综上可见,本文的研究具有一定的现实意义。首先,期货市场由于其准入门槛低、高杠杆、T+0交易和交易成本低等特点,使其交易相对活跃,对市场信息的反应最显著,在价格引导方面起到了主导作用,股指期货的价格先于指数和ETF市场价格变化,当三者的价格出现偏离时,指数和ETF的价格将会向股指期货价格方向调整,股指期货市场可作为现货市场的先行指标,为现货投资者判断市场运行方向提供参考;其次,仓位限额的推出降低了市场波动,维护了市场稳定,但是期货的交易量呈现了较大幅度的下跌,期货市场的价格发现能力显著降低,不利于整个金融市场的长远健康发展,监管层应适时放宽股指期货交易仓位的限制。因此,适度、审慎地使用政府干预手段对我国期货市场的健康发展具有重要的现实意义。
| [1] | THEISSEN E. Price discovery in floor and screen trading systems[J]. Journal of Empirical Finance, 2002,9(4): 455–474. DOI: 10.1016/S0927-5398(02)00005-1 |
| [2] | MIZRACH B, NEELY C J. Information shares in the US treasury market[J]. Journal of Banking & Finance, 2008,32(7): 1221–1233. |
| [3] | FRIJNS B, GILBERT A, TOURANI-RAD A. The determinants of price discovery:Evidence from US-Canadian cross-listed shares[J]. Journal of Banking & Finance, 2015,59(11): 457–468. |
| [4] | HASBROUCK J. One security, many markets:Determining the contributions to price discovery[J]. The Journal of Finance, 1995,50(4): 1175–1199. DOI: 10.1111/j.1540-6261.1995.tb04054.x |
| [5] | GONZALO J, GRANGER C. Estimation of common long-memory components in cointegrated systems[J]. Journal of Business & Economic Statistics, 1995,13(1): 27–35. |
| [6] | TSE Y. Price discovery and volatility spillovers in the DJIA index and futures markets[J]. Journal of Futures Markets, 1999,19(8): 911–930. DOI: 10.1002/(ISSN)1096-9934 |
| [7] | BOOTH G G, SO R W, TSE Y. Price discovery in the German equity index derivatives markets[J]. Journal of Futures Markets, 1999,19(6): 619–643. DOI: 10.1002/(ISSN)1096-9934 |
| [8] | BAILLIE R T, BOOTH G G, TSE Y, et al. Price discovery and common factor models[J]. Journal of Financial Markets, 2002,5(3): 309–321. DOI: 10.1016/S1386-4181(02)00027-7 |
| [9] | CHANG Y K, CHEN Y L, CHOU R K, et al. The effectiveness of position limits:Evidence from the foreign exchange futures markets[J]. Journal of Banking & Finance, 2013,37(11): 4501–4509. |
| [10] | BOYD N, LOCKE P. Price discovery in futures and options markets[J]. Journal of Futures Markets, 2014,34(9): 853–867. DOI: 10.1002/fut.v34.9 |
| [11] | BART F, IVAN I, ALIREZA T. Macroeconomic news announcements and price discovery:Evidence from Canadian-U.S.cross-listed firms[J]. Journal of Empirical Finance, 2015,32: 35–48. DOI: 10.1016/j.jempfin.2014.05.001 |
| [12] | OZTEKIN A S, MISHRA S, JAIN P K, et al. Price discovery and liquidity characteristics for US electronic futures and ETF markets[J]. The Journal of Trading, 2017,12(2): 59–72. DOI: 10.3905/jot.2017.12.2.059 |
| [13] | 严敏, 巴曙松, 吴博. 我国股指期货市场的价格发现与波动溢出效应[J]. 系统工程, 2009(10): 32–38. |
| [14] | 何诚颖, 张龙斌, 陈薇. 基于高频数据的沪深300指数期货价格发现能力研究[J]. 数量经济技术经济研究, 2011(5): 139–151. |
| [15] | 方匡南, 蔡振忠. 我国股指期货价格发现功能研究[J]. 统计研究, 2012(5): 73–78. DOI: 10.3969/j.issn.1002-4565.2012.05.010 |
| [16] | 陈莹, 武志伟, 王杨. 沪深300指数衍生证券的多市场交易与价格发现[J]. 管理科学学报, 2014(12): 75–84. |
| [17] | LIEN D, SHRESTHA K. A new information share measure[J]. Journal of Futures Markets, 2009,29(4): 377–395. DOI: 10.1002/fut.v29:4 |
| [18] | 华仁海, 刘庆富. 股指期货与股指现货市场间的价格发现能力探究[J]. 数量经济技术经济研究, 2010(10): 90–100. |
| [19] | LIU Q, AN Y. Information transmission in informationally linked markets:Evidence from US and Chinese commodity futures markets[J]. Journal of International Money & Finance, 2011,30(5): 778–795. |
| [20] | 刘向丽, 张雨萌. 基于向量误差修正模型的股指期货价格发现功能研究[J]. 管理评论, 2012(2): 71–77. DOI: 10.3969/j.issn.2095-3410.2012.02.011 |
| [21] | INANI S K. Price discovery in Indian stock index futures market:New evidence based on intraday data[J]. International Journal of Indian Culture and Business Management, 2017,14(1): 23–43. DOI: 10.1504/IJICBM.2017.080758 |
| [22] | ENGLE R F, GRANGER C W J. Co-integration and error correction:Representation, estimation, and testing[J]. Econometrica:journal of the Econometric Society, 1987: 251–276. |
 2018, Vol. 20
2018, Vol. 20

 ,
,