随着电子商务和电子支付的极大普及,网络购物行为已经成为市场中绝大多数消费者的首选之一。根据中国互联网信息中心(China Internet Network Information Center, CNNIC)发布的最新统计数据,截至2017年6月,我国网络购物用户规模达到5.14亿人。其中年度人均交易次数超过每周一次(62次),人均年度购物金额接近1万元(男性为10 025元,女性为8 559元)。这使得以网络零售为主的新型经济体系——平台经济成为未来经济发展的一个核心和重点。
不同于传统零售店有限的空间展位,网络零售店铺可以将所有产品“摆放”出来供顾客挑选。但是,网络零售店的店主也需要产品导购或网络“咨客”向潜在用户介绍并推荐产品,避免因潜在消费者在平台上众多可替代产品搜索和选择过程中迷失而放弃购买该产品。因此,如何吸引潜在消费者的注意力,即“眼球”,成为平台经济下产品供应方的热点关注问题。
在各种网上销售的市场策略中,朋友推荐是其中最为有效、最为高效的营销实践之一。本文所指的朋友推荐是指产品的供应方邀请一些有“号召力/影响力”的用户向其朋友或粉丝推荐产品。通过这些有影响力的用户的推荐和推动,引发产品口碑传播和产品购买的网络效应。鉴于朋友推荐这种“自发”的营销方式,产品供应方能够以近似“零成本”的代价迅速将产品迅速推送给市场中的潜在消费者。并且,信息发送方和接收方之间的“朋友”或“粉丝”关系,使得推荐的效果(产品的购买转化率)要远远高于传统的广告营销。因而,用户推荐成为当前最为成功的网络营销模式。例如,实践中的微信营销、微博营销、Twitter营销、“粉丝”营销等,都是这种网络营销的成功应用。
因此,如何从众多潜在顾客中挑选出来最有影响力的产品“代言人”/“推手”成为产品供应方的网络营销效果的关键。进而,如何评价产品“代言人” /“推手”的投资回报率也成为实际应用中企业非常关心的问题之一。
本文就是在此经济环境和市场需求推动下,通过对实践中的经验法则进行检验和对比,提出最优产品“代言人” /“推手”的搜索和评价方法。
二、国内外研究现状网络营销中的“朋友推荐”是市场营销领域中线上口碑营销(online word-of-mouth marketing)的通俗叫法[1]。其中,最具影响力的“代言人”则是潜在顾客关系网络(social network)中的意见领袖(opinion leader),即那些在信息扩散中能够影响舆情走向的关键节点。
如前所述,随着网络营销的蓬勃发展,潜在顾客关系网络中的意见领袖的搜索算法或评价方法成为包括复杂网络分析、信息扩散、口碑营销等多交叉领域的共同研究重点。例如,Shriver S K等[2]实证分析了信息传播中意见领袖的影响力,Bapna R等[3]实证研究了容易受到口碑信息影响的消费者特征,Zang J等[4]分析了不同特征的网络结构对口碑转播和意见领袖的影响力的影响,Li F等[5]则是在社会关系网络分析的基础上提出了识别意见领袖的评价指标体系。
国内学者对于意见领袖的识别主要是基于复杂网络分析中的几个节点中心度指标[6-7]。表 1给出了近几年代表性工作的评述。
| 表 1 关系网络中意见领袖/关键节点的识别算法 |
从表 1中数据可以看出,网络节点中心度指标——节点度中心性(Point Centrality)、接近中心性(Closeness Centrality)和中间中心性(Betweenness Centrality)指标都是较为认可的重要节点的评价指标。具体来说,节点的点度中心性描述的是节点的度指标,接近中心性描述的是每个节点到其他节点的最短路的平均值,而中间中心性描述的是节点位于其他两个节点之间最短路的次数。并且,网络用户之间的关系网络多采用无标度网络(Scale-Free Network)生成算法得到,而口碑扩散则多应用病毒式营销的SIR模型。
从这些研究信息扩散中关键节点的评价方法或选择策略中可以发现,前人关注的“关键节点”都是信息扩散中的源头节点。但是在实践中,更多广为流传的信息往往是由一些“草根”用户所发布的,即一个非常普通的信息源头。而通过回溯信息扩散的过程和路径,可以发现一些重要节点的加入和转发行为使得信息扩散的范围和速度出现阶跃式变化。例如,根据新浪微博给出的多个热点话题“某艺人吸毒”“某艺人嫖娼被抓”事件的回溯就可以发现,话题的疯狂扩散是由几个关键节点(“橙V”用户)转发所造成的。这表明,在信息扩散的中间过程中,存在的若干关键节点起到了非常重要的作用。因此,对于在网络中随机出现的信息而言,哪些节点能够通过转发/推荐的形式有效地促进信息的扩散是被领域专家所低估的一个重要基础性问题。
本文即是在此实践先行的研究问题基础上,采用计算机仿真的研究方法,探索这些重要的“二次”推荐用户节点的识别方法和算法。
三、线上社交网络上信息扩散实践 (一) 线上社交网络的复杂网络分析根据前人的研究成果分析,无论是对社交网络采取滚雪球式的网络重建,还是对信息扩散实例的回溯,都基本确定了线上社交网络的无标度特性,即其为无标度网络。并且,无论是对国外流行的微博系统——Twitter[16],国内流行的微博系统——新浪微博[11, 17],还是专业性的社交平台——知乎[15],小世界特性(Small-World)也是一个被普遍认同的网络特征(无标度是另外一个普遍特征)。因此,无论数据获取的方法如何,或者研究的实际网络平台对象如何,都能够确定研究的社交网络平台为一个典型的小世界网络。
在此文献分析基础上,本文选取小世界网络作为研究口碑信息扩散的网络平台。鉴于小世界网络生成算法中Watts-Strogatz算法的权威性,本文也将采用该算法生成一个小世界网络,并在此网络上分析信息扩散的过程和结果[18]。
(二) 信息扩散过程模型分析在社交网络上信息扩散的实例和模型研究中,病毒式的信息扩散模型是其中最为广泛采用和验证的模型[19]。
病毒式信息扩散模型,即SIR模型,定义了网络中节点的状态和状态转移规律。具体来说,SIR模型假定初始时所有节点都没有获得信息,即类比病毒传染中没有被感染病毒的“易感染(Susceptible)”状态——S状态。整个信息扩散过程如下:
(1) 从所有S状态节点集合中随机选中一个节点,作为本次信息扩散的唯一源头节点。将此节点的状态更新为“已感染(Infected)”状态——I状态。
(2) 从I状态集合中,随机选中一个节点A。并从该节点的相连节点集合中,随机选中一个邻居节点B:
① 状态转移规则一:如果节点B的状态为S,则节点B的状态转移为I,节点A的状态不变(状态I)。这表示节点A将信息传递给节点B,即类比病毒传播中的节点A将病毒传染给节点B。此状态转移可以描述为:
| $ {I_A} + {S_B} \to {I_A} + {I_B} $ | (1) |
② 状态转移规则二:如果节点B的状态为I,则节点B的状态不变,节点A的状态转移为“免疫(Removed)”状态——R状态。这表示节点A发现邻居已经获取了信息,因而失去了继续传播信息的兴趣,即类比病毒传播中的节点A从病毒中恢复,并永久免疫。此状态转移可以描述为:
| $ {I_A} + {I_B} \to {R_A} + {I_B} $ | (2) |
③ 状态转移规则三:如果节点B的状态为R,则节点B的状态不变,节点A的状态转移为“免疫(Removed)”状态——R状态。类似状态转移规则二,此规则表示节点A发现邻居已经获取了信息,因而失去了继续传播信息的兴趣。此状态转移可以描述为:
| $ {I_A} + {R_B} \to {R_A} + {R_B} $ | (3) |
(3) 重复上述信息扩散过程,直到网络中不存在状态为I的节点。
当SIR模型的信息扩散平台为同质或规则网络时,信息扩散的过程和结果也可以采用平均场理论(Mean Field Theory)建模和分析[20]:
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}S}}{{{\rm{d}}t}} = - S \cdot I\\ \frac{{{\rm{d}}I}}{{{\rm{d}}t}} = S \cdot I - I \cdot \left( {I + R} \right)\\ \frac{{{\rm{d}}R}}{{{\rm{d}}t}} = I \cdot \left( {I + R} \right) \end{array} \right. $ | (4) |
当定义S、I、R分别为网络中节点的比例,即S+I+R=1时[21],则
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}I}}{{{\rm{d}}S}} = - \frac{{S - \left( {1 - S} \right)}}{S} \Rightarrow {\rm{d}}I = - \left( {2 - \frac{1}{S}} \right){\rm{d}}S \Rightarrow I\left| {} \right._0^\infty = - 2 \cdot S\left| {} \right._0^\infty + \ln \left( S \right)\left| {} \right._0^\infty \\ {I_\infty } = 0, {I_0} \approx 0, {S_0} \approx 1 \Rightarrow \ln \left( {{S_\infty }} \right) = 2 \cdot \left( {{S_\infty } - 1} \right) = - 2 \cdot {R_\infty }\\ \Rightarrow {S_\infty } = {{\rm{e}}^{ - 2 \cdot {R_\infty }}} \Rightarrow {R_\infty } = 0.796 \end{array} \right. $ | (5) |
式(5)表明:信息扩散的最终结果为网络中79.6%的节点都将获得信息(状态R),而剩下的20.4%的节点则没有获得信息(状态S)。
但是当社交网络为异质网络时,即网络中节点的点度分布非均匀分布、随机分布等对称分布时,信息扩散的过程和结果则难以用平均场理论进行分析[20]。此时,唯一的分析方法就是计算机仿真分析[1]。
(二) 信息扩散中“推手”节点的实践分析如前文所述,在口碑信息扩散的实践中,关键节点的作用已经为业界所推崇。但是,对信息扩散过程中起到重要推动作用的节点,如何选择和如何评价还处于粗放状态,基本借鉴了对信息扩散源头节点的分析思路。
以新浪微博发布的最新统计数据为例(http://data.weibo.com),在新浪微博中注册的化妆品类账号(节点)约有39万个,这表明潜在消费者的产品选择变得非常困难。而其中,如果产品的供应商选择名人明星帮助产品推广,总能够获得较大的信息扩散效果。例如,新浪微博平台上2016年7月6日开始的“倩碧”产品推广,在商家上线产品的当天,就邀请两位明星进行产品推广。
在7月22日,商家再次邀请这两位明星进行推广。整个产品推广/信息扩散活动,一共吸引了两位明星的3 061万粉丝,吸引了86万粉丝点赞,7万粉丝的信息转发。从图 1给出的统计数据可以清楚地看出,明星的推动作用非常明显。
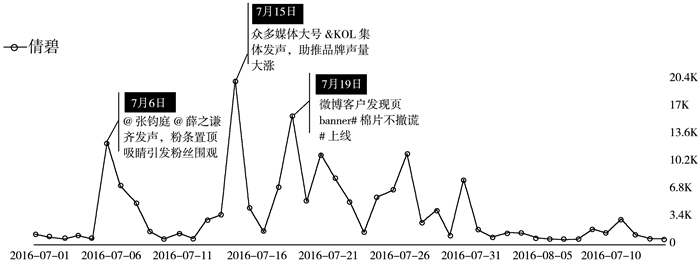
|
图 1 “倩碧”产品的网络推广轨迹 |
新浪微博平台上的另一款产品——“兰蔻”产品的推广活动也较为相似,产品于2016年12月16日上线后,3天之后邀请3位名人推动产品营销,使得产品话题曝光达4 527万次。
这些信息扩散成功案例,可以总结出两点实践中的经验规律:产品供应商发布产品信息后,在非常短的时间间隔之后,就启动一些重要节点展开信息的推广活动;产品供应商通常选择名人明星作为重要节点帮助推送信息。
这表明在实践应用中,企业(源头节点)通常发布信息后,通常非常迅速地跟进,且简单地挑选网络中点度(Degree/Point Centrality)最大的节点推动信息扩散。
(三) 社交网络上信息扩散模型小结如上文分析所示,本文将以无标度网络再现实际社交网络,并以病毒扩散的SIR模型作为信息扩散的扩散模型。
对于信息扩散中重要推手节点的选择,本文将根据前人的研究成果,并结合实际应用中的经验,对比测试包括节点的点度中心性、接近中心性和中间中心性在内的多种选择方法的各自特点和效果。
四、信息扩散过程的仿真分析在前期工作基础上,本文在多智能体建模与仿真平台Netlogo 6.01上,代码实现了无标度网络上的信息扩散仿真模型。其中,小世界网络Watts-Strogatz算法中的参数为:节点总数N=6 400,节点平均度k=4,节点之间链接的重连概率p=0.20;二次“推动”节点的作用时间Tp=5。
(一) 信息扩散过程和结果分析当考虑信息扩散中二次“推动”节点的作用时,对标准SIR模型中的第2步进行调整,即并非从I状态集合中随机选择一个节点A进行信息扩散,而是从S状态集合中有意识地选择一个节点进行信息扩散。具体信息扩散过程如下:
① 从所有S状态节点集合中随机选中一个节点,作为本次信息扩散的唯一源头节点。将此节点的状态更新为“已感染(Infected)”状态——I状态,并将仿真时钟T设置为0,即初始状态。
② 如果仿真时钟T值小于Tp,则遵循标准SIR模型中信息扩散的规则和过程,即从I状态集合中,随机选中一个节点A。并从节点A的相连节点集合中,随机选中一个邻居节点B。如果节点B的状态为S状态,则节点B状态更新为I状态,节点A状态不变;如果节点B的状态为I或R状态,则节点B的状态不变,节点A的状态更新为R状态。并且,将仿真时钟T向前推进一个单位,即T=T+1。
③ 如果仿真仿真时钟T值等于Tp,则启动信息扩散的二次推动。此时,按照一定规则,从所有S状态节点集合中选择一个节点作为信息扩散的二次推动“推手”节点,将其更新为状态I。并且,将仿真时钟T向前推进一个单位,即T=T+1。
④ 如果仿真时钟T值大于Tp,则恢复标准SIR模型中信息扩散的规则和过程。并且,将仿真时钟T向前推进一个单位,即T=T+1。
⑤ 重复上述信息扩散过程,直到网络中不存在状态为I的节点。
图 2给出了实践中常采用的二次“推手”节点的选择策略——点度最大的节点,并定义Tp=5时的单次仿真过程和结果。
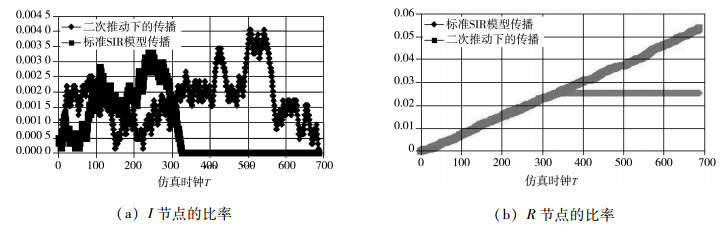
|
图 2 单次仿真的过程数据 |
图 2同时给出了标准SIR模型的单次仿真结果。对比两次仿真的结果可以看出,虽然标准SIR模型下信息扩散的速度更快,即图 2(a)中I节点的比率更早降低为0(仿真时钟T=325),但是,二次推动下的信息扩散网络覆盖率更大(=0.537 5),即图 2(b)中R节点的比率终值更大。这个结果可以看出二次推动策略下“推手”节点的作用。
重复500次仿真,得到二次推动下信息扩散最终结果如表 2所示。
| 表 2 仿真结果统计值 |
从表 2中数据可以看出,在节点度指标最大的节点推动下,信息在网络中的扩散更加广泛,是没有其作用下的2.49倍(=0.062 0/0.024 9)。
(二) 二次“推手”节点的选择根据前人的研究,本文继续对比测试了两种不同的节点选择策略下的信息扩散。具体包括节点接近中心性指标最大的S节点和中间中心性指标最大的S节点两种不同策略。
如表 3所示,在相同的网络下,点度最大的节点对信息扩散的影响最佳:信息扩散的速度更快,且信息扩散的范围更广。这表明实践中的选择具有相当的科学性和合理性。
| 表 3 不同“推手”节点作用下的效果对比 |
根据小世界网络Watts-Strogatz算法的描述,当算法中节点之间连线重连概率p越接近0,网络越接近于规则网络;当重连概率p越接近1,生成的网络越接近于E-R随机网络。
表 4给出了在网络节点数N=6 400,节点平均度k=4不变前提下,重连概率p值对信息扩散的影响。
| 表 4 不同“推手”节点作用下的效果对比 |
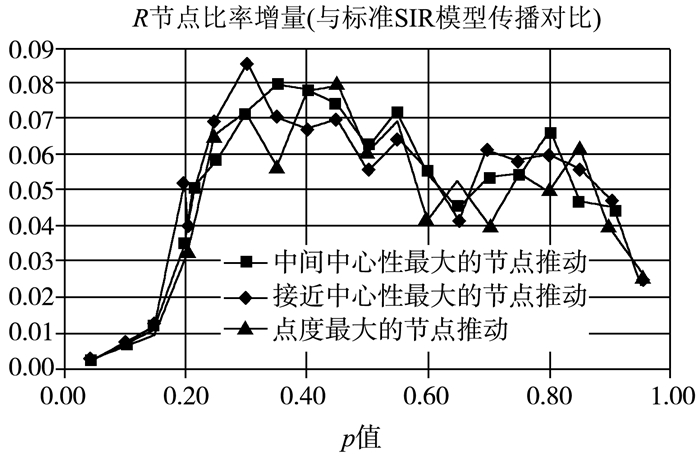
将表 4中的数据用折线图的形式展示出来,可以清楚地对比出二次推动节点的影响力。具体如图 3所示。
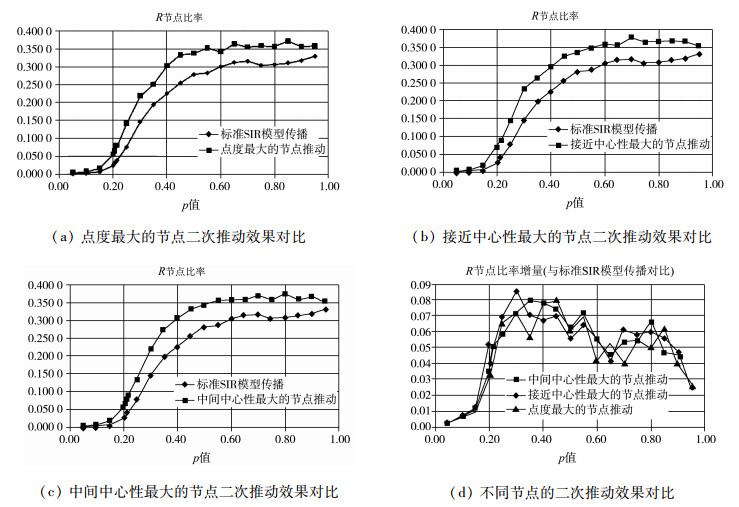
|
图 3 不同二次推动节点的影响力对比 |
从图 3中数据可以看出:
(1) 三种不同类型的节点对于信息扩散有明显的推动作用。
(2) 随着p值的增大,网络直径原来越小,并逐步稳定在14,相应的信息扩散的最终结果也逐步稳定在0.35。
(3) 当p值接近于0和p值接近于1时,节点的二次推动效果都不明显;而当p值趋近于0.5时,节点的二次推动效果非常明显。
(4) 从图 3(d)可以看出,三种不同节点的影响力基本相同,并没有一种节点具有明显的优势。
另外,对比信息扩散的总时长,具体如图 4所示。
|
图 4 不同二次推动节点的信息扩散总时长对比 |
从图 4可以看出,在二次推动节点的作用下,信息扩散的时间都有显著增加但三种不同节点的时间对比基本也无明显差异。
(四) 二次推动节点的作用时间Tp的影响在信息扩散模型中,二次推动节点的作用时间Tp也对信息扩散的效果产生影响。简单来说,如果时间Tp趋近于0,则问题转化为信息扩散中源头节点的选择问题。而当时间Tp较大时,由于信息扩散已经基本稳定,此时节点对信息扩散的影响将被削弱。时间Tp对信息扩散效果的影响如表 5所示。
| 表 5 时间Tp对信息扩散效果的影响 |
将表 5的数据以图的形式展示出来(见图 5),可以看出时间Tp与信息扩散两个效果指标之间的趋势特征:
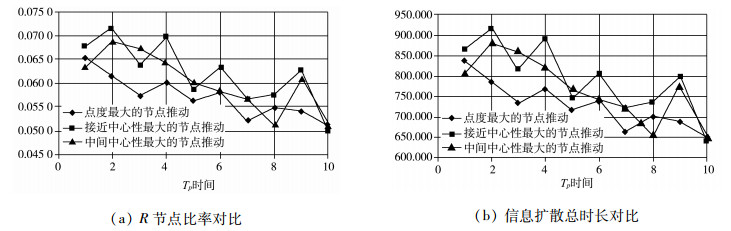
|
图 5 不同时间Tp下的信息扩散对比 |
(1) 随着二次推动的时间推移,其效果在显著下降。
(2) 在三种不同的节点选择下,接近中心性的信息扩散推动效果更好。但同时,信息扩散的时间也最长。
(五) 仿真结果小结通过上面所示的信息扩散仿真和参数分析,本文可以得到以下结论:
(1) 信息扩散过程中,“推手”节点能够显著地提高信息扩散的节点覆盖率,并增加了信息扩散的时间。如图 2所示,“推手”节点能够使得信息扩散的节点覆盖率指标增加1倍以上。
(2) 当信息扩散的网络平台为一个典型的小世界网络时,“推手”节点的影响力非常明显。而当网络趋近于规则网络或随机网络时,其影响力都将下降。同时,三种不同的“推手”节点选择策略,其对信息扩散的促进效果基本相同。因此,实践中采用点度最大的节点作为“推手”节点具有非常高的有效性。如图 3和图 4所示,三种不同的“推手”选择策略其在信息扩散的节点覆盖率指标和时间长度指标上都没有明显的差异性。
(3)“推手”节点的作用时间越早,其对信息扩散的影响就越明显。同时,在相同的时间节点上,接近中心性指标最大的节点在信息扩散中的影响力具有一定优势,要略好于其他两种不同的节点选择策略。如图 5所示,接近中心性指标最大的节点在节点覆盖率指标上能够大于其他两种方法的结果。
根据以上分析,我们可以综合得到最佳的二次“推手”节点的选择策略是接近中心性指标最大的节点。这一点与前期的分析结论较为吻合[15]。同时,为了提高信息扩散的效果,二次“推手”节点的推动时间点越早越好。
最后,表 6给出了不同参数设置情景下,接近中心性指标最大的节点选择策略的信息扩散效果(与标准SIR模型结果的对比)。
| 表 6 接近中心性指标最大的节点对信息扩散效果的影响 |
本文通过对社交网络平台上信息扩散过程中的“推手”节点的选择问题进行研究。通过对比三种不同的节点选择方法,确定了对信息扩散起到最佳效果的节点为接近度中心性指标最大的节点。并且,确定了“推手”节点的影响力随着时间推移而逐渐衰减的特性。鉴于“推手”节点的选择是产品供应方展开产品推广的重要和普遍问题,本研究结论对于企业实践有着直接的指导作用。
| [1] | LI F, DU T C. The effectiveness of word of mouth in offline and online social networks[J]. Expert Systems With Applications, 2017,88: 338–351. DOI: 10.1016/j.eswa.2017.07.004 |
| [2] | SHRIVER S K, NAIR H S, HOFSTETTER R. Social ties and user-generated content:Evidence from an online social network[J]. Management Science, 2013,59(6): 1425–1443. DOI: 10.1287/mnsc.1110.1648 |
| [3] | BAPNA R, UMYAROV A. Do your online friends make you pay? A randomized field experiment on peer influence in online social networks[J]. Management Science, 2015,61(8): 1902–1920. DOI: 10.1287/mnsc.2014.2081 |
| [4] | ZANG J, LIU Y, CHEN Y. Social learning in networks of friends versus strangers[J]. Marketing Science, 2015,34(4): 573–589. DOI: 10.1287/mksc.2015.0902 |
| [5] | LI F, DU T C. Listen to me-evaluating the influence of micro-blogs[J]. Decision Support Systems, 2014,62: 119–130. DOI: 10.1016/j.dss.2014.03.008 |
| [6] | 任晓龙, 吕琳媛. 网络重要节点排序方法综述[J]. 科学通报, 2014(13): 1175–1197. |
| [7] | 刘建国, 任卓明, 郭强, 等. 复杂网络中节点重要性排序的研究进展[J]. 物理学报, 2013(17): 178901. DOI: 10.7498/aps.62.178901 |
| [8] | 韩忠明, 陈炎, 李梦琪, 等. 一种有效的基于三角结构的复杂网络节点影响力度量模型[J]. 物理学报, 2016(16): 168901. DOI: 10.7498/aps.65.168901 |
| [9] | 苏臻, 高超, 李向华. 节点中心性对复杂网络传播模式的影响分析[J]. 物理学报, 2017(12): 120201. DOI: 10.7498/aps.66.120201 |
| [10] | 任卓明, 刘建国, 邵凤, 等. 复杂网络中最小K-核节点的传播能力分析[J]. 物理学报, 2017(10): 108902. |
| [11] | 苑卫国, 刘云, 程军军, 等. 微博双向"关注"网络节点中心性及传播影响力的分析[J]. 物理学报, 2013(3): 038901. |
| [12] | 赵之滢, 于海, 朱志良, 等. 基于网络社团结构的节点传播影响力分析[J]. 计算机学报, 2014(4): 753–766. |
| [13] | 肖卫东, 谭文堂, 葛斌, 等. 网络节点重要度的快速评估方法[J]. 系统工程理论与实践, 2013(7): 1898–1904. DOI: 10.3969/j.issn.1000-6788.2013.07.033 |
| [14] | 苏长明, 陈端兵, 傅彦. 复杂网络中初始节点对传染病传播的影响分析[J]. 计算机科学, 2011(11): 144–147. DOI: 10.3969/j.issn.1002-137X.2011.11.033 |
| [15] | 魏莹, 刘冠, 李锋. 线上社交网络上信息扩散中"隐形"关键节点的识别及影响力评价[J]. 情报科学, 2018(3): 138–143. |
| [16] | JAVA A, SONG X, FININ T, et al. Why we Twitter: Understanding microblogging usage and communities[C]. In Proceedings of International Conference on Knowledge Discovery and Data Mining. USA: San Jose, 2007: 56-65. |
| [17] | FU F, LIU L, WANG L. Empirical analysis of online social networks in the age of web 2.0[J]. Physica A, 2008,387(2-3): 675–684. DOI: 10.1016/j.physa.2007.10.006 |
| [18] | WATTS D J, STROGATZ S H. Collective dynamics of"Small-World"networks[J]. Nature, 1998,393: 440–442. DOI: 10.1038/30918 |
| [19] | DOMENICO M D, LIMA A, MOUGEL P, et al. The anatomy of a scientific rumor[J]. Scientific Reports, 2013,3: 2980. DOI: 10.1038/srep02980 |
| [20] | MORENO Y, NEKOVEE M, PACHECO A F. Dynamics of rumor spreading in complex networks[J]. Physical Review E, 2004,69(6): 066130. DOI: 10.1103/PhysRevE.69.066130 |
| [21] | 李锋, 林宁, 庄东. 迭代产品病毒式线上口碑营销下的库存优化[J]. 华南理工大学学报(社会科学版), 2017(6): 55–67. |
 2018, Vol. 20
2018, Vol. 20
