食品价格是我国物价运行系统的重要组成部分,在居民消费价格指数(CPI)长期保持较高的权重①。食品价格是几次物价较大波动的主因,也因此成为宏观通胀监测、调控与治理的着力点之一。厘清物价传导机制,特别是食品的传导机制,是理解和把握我国通货膨胀形成机理并进行有效调控的关键。物价传导路径、传导机制的识别与判断,是通胀调控手段和方式选择的重要依据。
① 2016年以前,食品类在CPI的权重长期保持超过30%。2016年CPI例行调整降低了食品权重,但仍然保持在18%左右(如2016年9月,CPI同比上涨1.9%,其中食品价格上涨3.2%,非食品价格上涨1.6%,简单测算食品类的权重为18.75%)。调整后的CPI,食品与烟酒合并统计,但仍保留“食品”和“非食品”的统计指数,可见食品类价格在物价系统的重要性。
学术界和统计部门对物价传导机制进行了较为丰富的研究,但大多以整体物价传导机制为主,对分类商品价格研究尚较少。这些研究多以PPI和CPI作为研究对象,PPI和CPI分别反映了生产领域和消费领域的物价变动和趋势,是价格链首尾两端的代表性物价指数。如国家统计局课题组[1]和刘敏等[2]等实证研究发现样本期内PPI和CPI传导较为顺畅,上下游产品市场竞争格局不同导致其价格传导变动幅度不一致。贺力平等[3]发现PPI不传导至CPI,但CPI传导至PPI,需求因素对通货膨胀的影响大于供给因素。徐伟康[4]则发现CPI和PPI是彼此的格兰杰原因,两者之间存在双向传导。张成思[5]检验更长的价格链,包括RMPI、PPI、CGPI和CPI,发现PPI向CPI传导,但CPI通过RMPI再传导至PPI。近期,孙坚强等[6]认为价格预期和产业链是物价传导的基础,并实证研究发现PPI和CPI之间存在相互传导且分别呈现明显的线性与非线性特征。
对食品物价传导问题的研究主要集中在探讨食品与非食品的价格传导。如崔冶[7]采用VAR模型实证发现食品价格与非食品价格存在传递作用,食品价格上涨对非食品价格产生同向冲击。苏楗芳和臧楠[8]采用两区制门槛协整模型的实证研究也发现,食品和非食品价格存在协整,两者之间具有双向的格兰杰因果。过新伟和张孝岩[9]分析发现食品价格的传导比非食品价格传导更顺畅,非食品存在显著的价格倒逼机制。亦有少数研究针对具体食品的物价传导进行分析,如针对猪肉[10]、生产农产品(西红柿)[11]、粮食价格[12]等。
我国居民消费的食品价格网络相对复杂,消费端包括13类食品①,向上游可追溯至农林牧渔初级生产或食品加工生产,初级生产、加工生产和消费3个价格的环节价格传导路径和机制较为复杂。综合所述,目前尚无系统地探讨我国食品价格的传导机制的研究,因此,本文尝试进行有益的补充。我们根据居民消费支出分类目录(2013年)和工业品价格调查目录(2015年)以及食品的上下游产业链关系,系统梳理我国居民日常消费13类食品的3个基本价格环节,并归纳出两个基本物价传导路径,即“路径1:农林牧渔初级生产→消费者消费”和“路径2:农林牧渔初级生产→食品加工生产→消费者消费”。
① 参考居民消费支出分类目录(2013年)。
在实证检验方法上,早期研究多采用相关分析或者线性回归[2]以及线性模型(VAR/VEC)基础上的格兰杰因果检验[3],近期研究注意到线性模型的局限[13-15]并尝试使用非线性检验,如TVAL和Tn统计量[16, 17]等。但是,仅仅单一使用线性或者非线性统计量容易导致信息遗漏[6],如线性检验忽略了物价变量之间的非线性关系,反之亦然。因此,我们尝试拓展结合线性和非线性的格兰杰因果检验,进行两阶段的检验。我们选取“农业生产资料指数”“PPI食品”和“CPI食品”分别代表初级生产、加工生产和消费的3个价格环节,先建立VEC模型进行线性格兰杰因果检验,再进一步检验建立的VEC模型是否仍存在非线性信息残余,如果存在则进一步根据VEC的残差进行TVAL/Tn非线性格兰杰因果检验,最后结合线性和非线性的检验结果综合分析物价传导特征。这种两阶段的检验方法很大程度上克服了信息遗漏问题。我们发现路径1传导顺畅,但路径2传导受阻;同时发现上游农林牧渔业生产环节与中游加工生产环节存在单向的需求反馈传导,与下游消费环节存在双向的成本传递和需求反馈传导,中游加工生产环节与下游消费环节存在单向的成本传递传导,成本传递和需求反馈均在中游出现阻滞。
本文主要边际贡献为系统地梳理了我国居民消费食品的基本传导路径;并拓展结合线性和非线性格兰杰因果检验的两阶段检验,为食品价格的传导机制和特征提供实证证据,进一步补充关于物价传导的研究文献。接下来的结构安排为,第二节分析食品价格的传导路径和传导基础,第三节进行实证分析,最后总结全文。
二、食品价格的传导路径与传导基础 (一) 传导路径根据居民消费支出分类目录(2013年),我国居民的食品消费(代码0101)包括13小类,分别为:谷物、薯类、豆类、食用油和食用油脂、蔬菜及食用菌、畜肉类、禽肉类、水产类、蛋类、奶类、甘鲜瓜果类、糖果糕点类和其他食品。进一步根据工业统计报表制度(2015年)的工业品价格调查目录,分析13类食品消费品对应的上游加工业。工业品价格调查产品目录中,与食品相关的目录包括农副食品加工产品(代码13000000)和食品(代码14000000)。农副食品加工产品包括8个小类:谷物磨制产品(大米、小米、高粱米、玉米、小麦粉等),饲料加工(配合饲料、混合饲料等),植物油加工产品,糖制品,屠宰及肉类加工产品(畜禽屠宰产品、肉制品及副产品加工产品等),水产品加工产品,蔬菜、水果和坚果加工产品(速冻蔬菜、净菜、腌菜等),其他农副食品加工产品(淀粉及淀粉制品、豆制品、蛋制品等)。食品包括7个小类:焙烤食品(糕点、面包等),糖果、巧克力及蜜饯制品(糖果等),方便食品(米面制品如挂面和米粉丝等、速冻食品、方便面等),液体乳及乳制品,罐头,调味品、发酵制品,其他食品。显然,食品商品不管是否需要加工,其始端上游为农林牧渔初级产品。
对13类食品分别向上追溯分析其上游产业链,可以发现价格路径包括两条:“路径1,农林牧渔初级产品→食品消费”,即农林牧渔初级产品未经加工(或生产种植者简单加工处理)直接进入流通领域,再到消费者(家庭、饭店等),例如新鲜蔬菜、生鲜薯、豆等;“路径2,农林牧渔初级产品→食品加工→食品消费”,即农林牧渔初级产品经过专门加工再进入流通领域,再到消费者,例如奶制品。路径1不进入PPI的统计范畴,路径2进入PPI的统计范畴。例如,蔬菜和食用菌(010105)的两条价格传导路径如图 1所示。更详细的13类食品的基本传导路径如表 1所示。
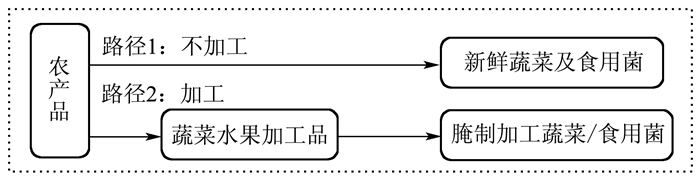
|
图 1 蔬菜和食用菌(010105)的传导路径 |
| 表 1 食品的基本传导路径汇总 |
表 1显示,全部食品都存在路径2的传导路径,7类食品同时存在路径1和路径2的传导路径(薯类、豆类、蔬菜和食用菌、水产品、蛋类、奶类、干鲜瓜果类),其余6类食品仅存在路径2的传导路径。进一步分析,可以综合为以下4种情况:第一,路径1和路径2并存,但路径1发挥主要作用,包括蔬菜和食用菌、蛋类、干鲜瓜果类3类食品。如蔬菜和食用菌在采摘后经过简单处理,多数直接进入收购/批发或者零售环节,经超市、集市和餐厅直接到达消费者,小部分被加工为如“腌制加工蔬菜”再到达消费者。第二,路径1和路径2并存,但路径2发挥较大作用,包括薯类、豆类、水产品、奶类4类食品。如奶类,生奶消费较少,液体乳和固体乳(包括奶粉)消费较多。“牧产品的生奶→‘液体乳及乳制品’加工出厂→‘液体乳及固体乳’消费”是主要的传导路径。第三,仅存在路径2,但加工成本占比低,包括谷物、畜肉类、禽肉类3类食品。如农产品的稻谷、小麦等成熟收割后,进入收购储粮环节,再加工为“谷物磨制品”,最后成为消费的“谷物、大米、小麦(粉)”等。大米和小麦粉等的主要成本是上游初级农产品,中间环节的加工成本在总成本中占比较低。第四,仅存在路径2,但加工成本占比高,包括食用油、糖果糕点和其他食品3类食品。如食用油,压榨加工成本是重要的生产成本。可以看出,对于第一、第三种情况,上游农林牧渔初级生产对价格系统影响较大,食品加工影响较弱;但第二、第四种情况则相对复杂,对于加工成本占比高的食品,加工环节对价格系统影响较大。
(二) 传导基础“产业链”和“价格预期”是物价传导的基础[6]。“产业链”是经济基础,根据产业链传导机制[2, 18],上游农林牧渔产品价格变动,作为成本项沿着生产链向下传递,加工环节和消费环节的食品价格相应发生变动,物价呈现成本推动的变化,即成本传递。下游食品价格变动,需求信息沿着生产链向上传递,加工食品价格和农林牧渔产品价格相应变动,物价呈现需求拉动的变化,即需求反馈。这两种价格传导也常解释为成本推动或者价格倒逼[3, 14]。“价格预期”是价格传导的实现基础。经济主体具有前瞻决策的特点,厂商和消费者根据预测的未来价格进行对应的生产和消费决策。影响成本或者需求的经济事件发生后,厂商和消费者获得消息并形成新的预期,并以此预期重新决策形成新的供给和需求关系,从而形成新的价格(包括价格不变)。“产业链”和“价格预期”的综合作用,特别是价格预期的复杂非线性过程,使得物价传导并非简单线性比例地自上而下或者自下而上传递,而是同时呈现线性和非线性的传导特征。因此,单一地采用线性模型或者非线性模型都难以正确且全面地理解物价传导特征。
三、实证分析 (一) 数据样本我国农业统计调查经过多年的改革和完善,已形成较为完整的统计体系。农业生产环节的价格指数包括“农业生产资料指数”和“农产品生产价格指数”,前者主要反映农业生产中投入物质资料价格的变动状况,后者主要反映农产品生产者出售农产品的价格变动情况。直观理解,前者反映生产的投入环节,后者反映生产的产出环节。“农产品生产价格指数”于2003年开始发布季度数据,“农业生产资料指数”则于1994年开始发布月度数据。因此,我们选择“农业生产资料指数”月度同比数据作为上游初级生产的代表价格,记为F_SC。如前文所述,PPI和CPI的统计调查目录广泛包含了各类食品,因此分别选择PPI和CPI的食品分类指数作为中游加工生产和下游消费的价格代表,分别选取其月度同比数据,记为F_PPI和F_CPI。考虑到我国CPI统计制度于2001年作了重大改革,价格指数的统计、公布和使用以居民消费价格指数为主,改变以往以商品零售价格指数为主的做法,因此样本时间范围选择为2001年1月至2016年9月,共189个月。各个时间序列的平稳性检验结果如表 2。结果显示,3个价格序列均为非平稳数据,特别是3个时间序列的PP检验在5%显著水平均不能拒绝单位根原假设。3个时间序列一阶差分后均为平稳,ADF和PP检验均在1%的显著水平拒绝单位根原假设,KPSS检验在5%显著水平不拒绝平稳性原假设。因此,3个价格序列均为一阶单整过程Ⅰ(1)。
| 表 2 各个时间序列的平稳性检验结果 |
对于非平稳时间序列,是否存在协整是后续模型选择的关键。我们采用协整检验判断3个价格序列的协整关系[19]。根据AIC和SC信息准则确定协整检验VAR模型的滞后阶数为4个月,根据Pantula规则[20]选择检验的备选模型为模型3,即假设协整方程和VAR有截距无趋势。Pantula规则选择结果如表 3所示。结果显示,在5%或1%的显著水平上,价格序列之间存在3个协整关系,即3个阶段的食品价格两两之间存在长期均衡关系。
| 表 3 协整检验根据Pantula规则的选择结果 |
上述检验显示,食品价格时间序列非平稳但存在协整关系。因此我们建立误差修正模型(VECM)进行第一阶段的检验,即线性格兰杰因果检验[19, 21]。VECM模型如下:
| $\Delta {Y_t} = \sum\nolimits_{j = 1}^{k - 1} {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_j}\Delta {Y_{t - j}}} + \alpha \beta '{Y_{t - k}} + \mu + {\varepsilon _t}$ | (1) |
其中,Yt=(F_SCt, F_PPIt,F_CPIt)′为价格向量,∑j=1k-1ΓjΔYt-j和αβ′Yt-k分别为VAR项和误差修正项,μ为常数,εt为白噪音误差项,Δ表示一阶差分。参数矩阵Γj反映对滞后项的短期响应,β′为协整向量,β′Yt-k反映协整向量对长期均衡的偏离程度,而参数向量α则反映偏离后对均衡的回复速度。模型的滞后阶数、截距和趋势等选择,根据上述Pantula规则选择结果。格兰杰因果检验结果如表 4所示。
| 表 4 食品价格的线性格兰杰因果检验结果 |
结果显示,在5%的显著水平下,拒绝“F_PPI不是F_CPI的线性格兰杰原因”和“F_CPI不是F_SC的线性格兰杰原因”的原假设。线性检验表明,中游加工环节的食品价格(F_PPI)对下游消费环节的食品价格(F_CPI)存在传导,下游消费环节的食品价格(F_CPI)对上游初级生产环节的食品价格(F_SC)存在传导,我们将在下文展开讨论。线性检验结果的简要图示如图 2。

|
图 2 食品价格的线性格兰杰因果检验图示 |
接下来进行第二阶段的检验,我们检验上述VECM是否存在尚未被解释的非线性信息残余,如果存在则进一步进行非线性格兰杰因果检验。
对F_SC、F_PPI和F_CPI三个方程的残差进行BDS检验①。BDS检验常用于检验时间序列的非线性特征,其原假设为残差服从独立同分布。拒绝原假设则说明残差存在非线性信息。对于时间序列{Xt}, t=1, 2,…, n, m阶领先向量定义为Xtm={Xt, Xt+1,…,Xt+m-1},关联积分(correlation integrals)定义为:
① BROCK W, DECHERT W, SKEINKMAN J. A Test for Independence Based upon the Correlation Dimension [R]. Working Paper, 1987.
| $c\left( {m,n,\varepsilon } \right) = \frac{2}{{\left( {n - m + 1} \right)\left( {n - m} \right)}}\sum\nolimits_{s = 1}^{n - m + 1} {\sum\nolimits_{t = s + 1}^{n - m + 1} {\prod\nolimits_{j = 0}^{m - 1} {\left( {{\mathit{\boldsymbol{X}}_{s + j}},{\mathit{\boldsymbol{X}}_{t + j}}} \right)} } } $ | (2) |
其中,Iε为示性函数:
| ${I_\varepsilon }\left( {x,y} \right) = \left\{ {\begin{array}{*{20}{c}} {1,}&{\left| {x - y} \right| < \varepsilon }\\ 0&{其他} \end{array}} \right.$ | (3) |
如果时间序列{xt}t=1n独立同分布,则BDS统计量满足:
| $\sqrt {n - m - 1} \frac{{c\left( {m,n,\varepsilon } \right) - c{{\left( {1,n - m - 1,\varepsilon } \right)}^m}}}{{\sigma \left( {m,n,\varepsilon } \right)}}\xrightarrow{a}N\left( {0,1} \right)$ | (4) |
其中,σ(m, n, ε)为[c(m, n, ε)-c(1, n-m-1, ε)m]的渐近标准差。VECM模型3个方程残差的BDS检验结果如表 5所示。出于稳健目的,表格报告了m=, 2, 3…, 6的结果。结果显示,在5%的显著水平,F_PPI和F_CPI方程的残差拒绝BDS的原假设,特别是F_PPI的方程残差。实证表明VECM存在显著的非线性信息残余。
| 表 5 VECM模型残差的BDS检验结果 |
因此,进一步根据VECM三个方程的残差检验食品价格之间的非线性传导特征。我们采用TVAL统计量[16]和Tn统计量[17],这是检验时间序列非线性关系的常用非参数统计量。考虑两个严平稳且弱相关的时间序列Xt和Yt,滞后Lx和Ly的向量分别为Xt-LxLx≡(Xt-Lx, Xt-Lx+1,…, Xt-1),Lx=1, 2,…,t=Lx+1, Lx+2,…和Yt-LyLy≡(Yt-Ly, Yt-Ly+1, …,Yt-1),Ly=1, 2,…,t=Ly+1,Ly+2,…。对于给定的m,Lx和Ly≥1以及e>0,如果
| $\begin{gathered} \mathit{Pr}\left( {\left\| {\mathit{\boldsymbol{X}}_t^m - \mathit{\boldsymbol{X}}_s^m} \right\| < e\left\| {\;\;\left\| {\mathit{\boldsymbol{X}}_{t - Lx}^{Lx} - \mathit{\boldsymbol{X}}_{s - Lx}^{Lx}} \right\| < e,\left\| {\mathit{\boldsymbol{Y}}_{t - Ly}^{Ly} - \mathit{\boldsymbol{X}}_{s - Ly}^{Ly}} \right\| < e} \right.} \right) \hfill \\ = \mathit{Pr}\left( {\left\| {\mathit{\boldsymbol{X}}_t^m - \mathit{\boldsymbol{X}}_s^m} \right\| < e\left| {\;\;} \right.\left\| {\mathit{\boldsymbol{X}}_{t - Lx}^{Lx} - \mathit{\boldsymbol{X}}_{s - Lx}^{Lx}} \right\| < e,} \right) \hfill \\ \end{gathered} $ | (5) |
成立,则表示Y不是X的严格格兰杰因。其中,Pr(·)表示概率,‖·‖表示最大范数(maximum norm)。上式可以重新表述为:
| $\frac{{C1\left( {m + Lx,Ly,e} \right)}}{{C2\left( {Lx,Ly,e} \right)}} = \frac{{C3\left( {m + Lx,e} \right)}}{{C4\left( {Lx,e} \right)}}$ | (6) |
其中C1(·), ·i=1, 2, 3, 4为关联积分估计量[16]。对于给定的m,Lx和Ly≥1以及e>0,以及Y不是X的严格格兰杰因的条件,TVAL统计量服从渐进正态分布,
| $\sqrt n \left( {\frac{{C1\left( {m + Lx,Ly,e} \right)}}{{C2\left( {Lx,Ly,e} \right)}} - \frac{{C3\left( {m + Lx,e} \right)}}{{C4\left( {Lx,e} \right)}}} \right)\xrightarrow{a}N\left( {0,{\sigma ^2}\left( {m,Lx,Ly,e} \right)} \right)$ | (7) |
Tn统计量进一步克服了TVAL统计量可能产生的过度拒绝[17]。“Y不是X的严格格兰杰因”原假设表示为:
| $E\left[ {\left( {\frac{{{f_{{x_t},{y_t},{x_{t + 1}}}}\left( {{X_t},{Y_t},{X_{t + 1}}} \right)}}{{{f_{{x_t},{y_t}}}\left( {{X_t},{Y_t}} \right)}} - \frac{{{f_{{x_t},{x_{t + 1}}}}\left( {{X_t},{X_{t + 1}}} \right)}}{{{f_{{x_t}}}\left( {{X_t},{Y_t}} \right)}}} \right) \times g\left( {{X_t},{Y_t},{X_{t + 1}}} \right)} \right] = 0$ | (8) |
其中,f(·)为联合密度函数,g(·)为恒正的权重函数。简化定义q为:
| $q = E\left[ {{f_{{x_t}{y_t},{x_{t + 1}}}}\left( {{X_t},{Y_t},{X_{t + 1}}} \right){f_{{x_t}}}\left( {{X_t}} \right) - {f_{{x_t},{y_t}}}\left( {{X_t},{Y_t} \cdot } \right){f_{{x_t},{x_{t + 1}}}}\left( {{X_t},{X_{t + 1}}} \right)} \right]$ | (9) |
不妨
| $Tn\left( {{e_n}} \right) = \frac{{n - 1}}{{n\left( {n - 2} \right)}}\sum\nolimits_{i = 1}^n {\left[ {{{\hat f}_{{x_t}{y_t},{x_{t + 1}}}}\left( {{X_t},{Y_t},{X_{t + 1}}} \right){{\hat f}_{xt}}\left( {{X_t}} \right) - {{\hat f}_{{x_t}{y_t}}}\left( {{X_t},{Y_t} \cdot } \right){{\hat f}_{{x_t}{x_{t + 1}}}}\left( {{X_t},{X_{t + 1}}} \right)} \right]} $ | (10) |
记Sn为Tn(en)渐进方差的估计,在原假设条件下,Tn收敛于正态分布:
| $\sqrt n \frac{{\left[ {Tn\left( {{e_n}} \right) - q} \right]}}{{{S_n}}}\xrightarrow{d}N\left( {0,1} \right)$ | (11) |
根据Hiemstra和Jones蒙特卡罗数值结果的建议①,设定领先阶数m=1,设定滞后阶数Lx=Ly为1至8阶[17]。非线性格兰杰因果检验结果如表 6所示。
| 表 6 VECM模型残差的非线性格兰杰因果检验结果 |
① HIEMSTRA C, JONES J. Monte Carlo Results for A Modified Version of the Baek and Brock Nonlinear Granger Causality test [R]. Working Paper, 1993.
结果显示,在5%的显著水平,TVAL检验和Tn检验同时拒绝了“F_SC不是F_CPI的非线性格兰杰原因”以及“F_PPI不是F_CPI的非线性格兰杰原因”的原假设,上游初级生产环节和中游加工环节的食品价格对下游消费环节的食品价格存在传导;TVAL检验和Tn检验同时拒绝了“F_PPI不是F_SC的非线性格兰杰原因”以及“F_CPI不是F_SC的非线性格兰杰原因”的原假设,中游加工环节和下游消费环节的食品价格对上游初级生产环节的食品价格存在传导。非线性格兰杰因果检验结果的简要图示如图 3。图 3同时合并了线性检验的结果,实线为线性检验结果,虚线为非线性检验结果,箭头表示传导方向。
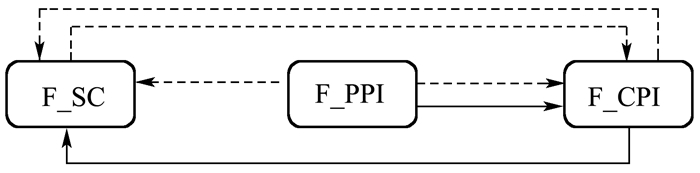
|
图 3 食品价格的线性(实线)和非线性(虚线)格兰杰因果检验 |
综合线性和非线性格兰杰因果检验的实证结果,发现我国食品价格的传导呈现如下特点:
第一,上游农林牧渔初级生产环节与中游食品加工生产环节仅存在单向的需求反馈传导。上游初级生产向中游加工生产传递成本受阻,但对加工环节的需求反馈作出价格响应,需求反馈传导顺畅。表 4、表 6和图 3显示,加工生产环节食品价格向上游初级生产环节存在显著的传导,反之不显著。存在这种单向反馈传导的可能原因包括:①农林牧渔业生产者与食品加工商的交易通常是批量交易,且常常在生产前就已签署约定数量和价格的订单合同。自2000年以来,订单农业包括“农户+科研、种子机构”“农户+农业龙头企业”“农户+专业批发市场”“农户+协会”“农业+经销商”等模式得到很大的鼓励和发展。订单合同周期一般覆盖了较长的生产周期。订单契约性和期货性的抑制,很大程度使得上游生产价格变动向下传递受阻。②农林牧渔生产事关民生,世界各国包括我国在内,通常采取包括政策收购、生产补助、价格干预等经济手段和行政手段来避免价格过低而“谷贱伤农”,并保护环境资源等。价格政策干预,特别是价格保护,也在一定程度上“吸收”和抑制上游价格变动向中游加工的成本传递。③加工环节的食品价格变动,向上游反映了市场需求变化。由于农林牧渔生产周期长,很大程度上依赖自然资源,难以灵活调整生产品种和规模,中短期内供给价格弹性小。对于市场需求变化,初级生产环节难以及时调整供给,价格上则会迅速调整以适应需求冲击。
第二,上游农林牧渔初级生产环节与下游消费环节存在双向的成本传递和需求反馈传导。表 4、表 6和图 3显示,上游农林牧渔生产环节的价格变动显著传递到下游的消费环节,消费环节价格变动的需求信息也显著反馈传递到上游生产环节。原因可能包括:①食品为民生消费必需品,需求弹性小,当生产领域受到如自然灾害等冲击时,消费价格迅速作出响应,特别是生产周期相对较短的农产品,如生鲜蔬菜等。②在整个市场体系中,食品消费者尽管数量众多但通常是分散独立的零散购买者,难以形成规模优势和垄断力量。因此,食品消费者通常在价格链中议价能力低,主要表现为价格接受者,上游成本上涨容易传递给消费者。从图 3同时可以看到,中游食品加工成本也传递到消费者。③如第一点所述,大部分农林牧渔初级生产的供给弹性小,当消费领域受到如食品安全事件等需求冲击时,生产价格作出相应的响应。从图 3同时可以看到,农林牧渔初级生产对中游加工需求变化也作出价格响应。
第三,中游加工生产环节与下游消费环节仅存在单向的成本传递传导。食品加工环节向消费环节传递成本变动,但对消费环节的需求变动没有作出价格上的响应。表 4、表 6和图 3显示,加工环节食品价格向消费环节的食品价格存在显著的传导,但反之不显著。原因可能包括:①如上文所述,消费者的低议价能力以及食品需求的弹性缺乏,加工成本容易向消费者传递,特别是对于存在传导路径2且加工成本较高的食品,如奶类、食用油等。②从加工食品的市场结构来看,加工食品的产品差别程度较小(依赖原料食品的自然属性),且多数食品加工行业的进出壁垒相对较小,因此,加工食品的供给弹性相对初级生产的供给弹性较大。消费环节的需求变动,除了被价格干预如储备吞吐等“吸收”和抑制一部分,往往容易被加工行业的供给调整所“吸收”。因此,加工环节对下游消费需求变化往往不存在价格响应。
综合前面分析,上游农林牧渔初级生产向中游加工生产环节传递成本受阻,但向下游消费环节传递成本顺畅;上游农林牧渔初级生产对中游、下游的需求信息作出价格反应,但中游食品加工生产对下游的需求信息没有作出价格反应,即需求的价格反馈传导在下游消费与中游食品加工之间受阻。
第四,食品价格传导路径1顺畅,但传导路径2阻滞。图 3显示,上游农林牧渔生产到下游居民消费的直接路径1传导顺畅,自上而下的成本传递和自下而上的需求反馈均存在显著的传导。但上游农林牧渔初级生产到中游加工生产,再到居民消费的加工传导路径2传导阻滞,成本传递在上中游之间受阻,需求反馈在下中游之间受阻。这与价格干预的非对称和加工环节的市场结构有关。当食品价格下降导致种植饲养等生产积极性低迷时,政府常常采取生产补贴(如种子补贴、渔业捕捞油价补贴、仔猪补贴等)刺激生产积极性,主要干预上游生产环节;当食品价格上扬导致需求高涨时,则常常采取储备投放(如投放储备冻肉)等抑制需求,主要干预下游消费环节。中间环节的加工生产则通常较少受到直接干预。
第五,食品价格传导的非线性传导特征相对线性传导特征更为明显。实证结果显示,仅“F_PPI-F_CPI”和“F_CPI-F_SC”两个方向存在线性传导特征,但“F_SC-F_CPI” “F_CPI-F_SC”“F_PPI-F_SC”和“F_PPI-F_CPI”4个方向存在非线传导特征。“产业链”和“价格预期”是物价传导的两个作用基础,特别是后者为物价传导的实现基础,价格预期传导的3个过程——“消息传播过程”“预期形成过程”和“经济决策过程”均存在高度复杂非线性,因此物价传导更易出现非成比例上下变化的非线性特征[6]。
四、结论与讨论本文在梳理我国居民13类食品消费品的价格传导路径的基础上,采用线性和非线性格兰杰因果检验相结合的两阶段检验方法探讨我国食品的传导机制。主要研究结论包括:我国居民的消费食品存在两条基本的价格传导路径,即“路径1:农林牧渔初级生产→消费者消费”和“路径2:农林牧渔初级生产→食品加工生产→消费者消费”,前者不进入PPI的统计范畴,后者进入PPI的统计范畴。实证研究显示,食品传导路径1顺畅,但传导路径2受阻,这与食品价格干预的非对称性和加工环节的市场结构有关。不同传导路径情况,上游和下游对价格变动的影响和传递价格的能力明显不同。因此建议在价格稳定调控中,根据不同传导路径和传导情况,有针对性地选择价格环节采取调控措施。
农林牧渔业初级生产环节与加工生产环节存在单向的需求反馈传导,与消费环节存在双向的成本传递和需求反馈传导,加工生产环节与消费环节存在单向的成本传递传导。实证表明,农林牧渔初级生产向加工生产传递成本受阻,但向消费环节传递成本顺畅;前者与生产订单的契约性和期货性以及农业价格保护有关;后者与食品的需求弹性缺乏和消费者议价力低有关。实证研究同时表明,上游农林牧渔初级生产环节对中游、下游的需求信息作出价格反应,主要与农林牧渔初级生产供给缺乏弹性有关;但中游食品加工对下游需求信息没有作出价格反应,与中游食品加工的市场结构有关。
| [1] | 国家统计局课题组. 我国新一轮通货膨胀的主要特点及成因[J]. 统计研究, 2005(4): 3–9. |
| [2] | 刘敏, 张燕丽, 杨延斌. PPI与CPI关系探析[J]. 统计研究, 2005(2): 24–28. |
| [3] | 贺力平, 樊纲, 胡嘉妮. 消费者价格指数与生产者价格指数:谁带动谁?[J]. 经济研究, 2008(11): 16–26. |
| [4] | 徐伟康. 对《消费者价格指数与生产者价格指数:谁带动谁?》一文的质疑[J]. 经济研究, 2010(5): 139–148. |
| [5] | 张成思. 长期均衡、价格倒逼与货币驱动——我国上中下游价格传导机制研究[J]. 经济研究, 2010(6): 42–52. |
| [6] | 孙坚强, 崔小梅, 蔡玉梅. PPI和CPI的非线性传导:产业链与价格预期机制[J]. 经济研究, 2016(10): 54–68. |
| [7] | 崔冶. 中国食品与非食品间的价格传导机制:理论和实证分析[J]. 上海金融, 2011(10): 23–26. |
| [8] | 苏楗芳, 臧楠. 食品与非食品价格的长期均衡关系与短期非线性调整——基于两区制门槛协整模型的实证研究[J]. 财经研究, 2011, 37(2): 112–123. |
| [9] | 过新伟, 张孝岩. 基于CPI "篮子商品"的价格传导机制研究——对非食品渠道和食品渠道的考察[J]. 财经研究, 2012(3): 27–38. |
| [10] | 王芳, 陈俊安. 中国养猪业价格波动的传导机制分析[J]. 中国农村经济, 2009(7): 31–41. |
| [11] | 董晓霞, 许世卫, 李哲敏, 等. 完全竞争条件下的中国生鲜农产品市场价格传导——以西红柿为例[J]. 中国农村经济, 2011(2): 22–32. |
| [12] | 娄峰, 张涛. 中国粮食价格变动的传导机制研究——基于动态随机一般均衡(DSGE)模型的实证分析[J]. 数量经济技术经济研究, 2012(7): 92–103. |
| [13] | 杨子晖, 赵永亮, 柳建华. CPI与PPI传导机制的非线性研究:正向传导还是反向倒逼[J]. 经济研究, 2013(3): 83–95. |
| [14] | KYRTSOU C, LABYS W C. Evidence for Chaotic Dependence Between US Inflation and Commodity Prices[J]. Journal of Macroeconomics, 2005,28(1): 256–266. |
| [15] | NISHIYAMA Y, HITOMI K, KAWASAKI Y, et al. A Consistent Nonparametric Test for Nonlinear Causality-specification in Time Series Regression[J]. Journal of Econometrics, 2011,165(1): 112–127. DOI: 10.1016/j.jeconom.2011.05.010 |
| [16] | HIEMSTRA C, JONES JD. Testing for Linear and Nonlinear Granger Causality in the Stock Price-volume Relation[J]. The Journal of Finance, 1994,49(5): 1639–1664. |
| [17] | DIKS C, PANCHENKO V. A New Statistic and Practical Guidelines for Nonparametric Granger Causality Testing[J]. Journal of Economic Dynamics and Control, 2006,30(9-10): 1647–1669. DOI: 10.1016/j.jedc.2005.08.008 |
| [18] | CLARK TE. Do Producer Prices Lead Consumer Prices?[J]. Federal Reserve Bank of Kansas City Economic Review, 1995,80(Third Quarter): 25–39. |
| [19] | JOHANSEN S, JUSELIUS K. Maximum Likelihood Estimation and Inference on Co-integration-with Applications to the Demand for Money[J]. Oxford Bulletin of Economics and statistics, 1990,52(2): 169–210. |
| [20] | JOHANSEN S. Determination of Co-integration Rank in the Presence of a Linear Trend[J]. Oxford Bulletin of Economics and Statistics, 1992,54(3): 383–397. DOI: 10.1111/obes.1992.54.issue-3 |
| [21] | GRANGER CW. Investigating Causal Relations by Econometric Models and Cross-spectral Methods[J]. Econometrica, 1969,37(3): 424–438. DOI: 10.2307/1912791 |
 2018, Vol. 20
2018, Vol. 20
