近年来,我国物流业发展迅速,2015年全国社会物流总额219.2万亿元,“十二五”期间年均增长速度8.7%[1]。作为促进国民经济发展的“加速剂”,物流业对经济发展的支撑作用日益明显。2015年3月国家发展改革委、外交部、商务部联合发布《推动共建丝绸之路经济带和21世纪海上丝绸之路的愿景与行动》,明确提出基础设施互联互通是“一带一路”建设的优先领域,这既给物流业的发展带来新的机遇,也对物流业提出更高的发展要求。物流业属于能源消耗大户,面临巨大的碳减排压力,要实现可持续发展,必须转变发展方式,通过节能减排,实现绿色发展。鉴于此,研究碳排放约束下海上丝绸之路(以下简称海丝路)沿线地区物流业运行效率具有重要的现实意义。
一、文献综述数据包络分析(data envelopment analysis,DEA)方法被广泛运用于物流业效率评价中,该方法在处理多投入、多产出的同质决策单元时具有很强的适用性。孟鑫(2015)[2]应用DEA方法对长江经济带11个地区的物流业效率进行评价,研究结果表明长江经济带上游地区的物流业效率低于下游地区,并从企业和政府两个视角提出促进该区域物流业发展的政策建议。张雪青(2016)[3]以“一带一路”沿线17个地区的物流业为研究对象,从综合技术效率、纯技术效率以及规模效率三个方面分析这些地区物流业在2009—2013年间的效率变化,指出“一带一路”沿线地区的物流业投入产出失衡,未实现有效协同发展。林珊和温惠英(2014)[4]将DEA与层次分析法结合,测算我国10家物流企业运输效率。碳减排方面,毕志雯(2011)[5]以低碳作为物流业转型发展的核心,采用SBM(slack based measure)方向性距离函数,结合序列DEA以及Meta-frontier方法,将二氧化碳作为非期望产出,研究我国30个地区的物流业效率,分析表明忽视非期望产出的效率评价方式会高估物流业效率,我国东部与中部地区物流业“低碳型”效率要高于西部地区。唐建荣和卢玲珠(2013)[6]认为外部环境和随机因素对区域物流效率具有重要影响。王维国和马越越(2012)[7]在考虑非期望产出条件下,研究我国区域物流业效率变化及其影响因素,指出我国物流业普遍存在着技术不环保现象,多数地区物流业所处的外部环境水平较低。
目前关于物流业效率的研究取得一定成果,且已有学者开始关注物流业的节能减排问题。但既有文献对物流业效率进行评价时,普遍将决策单元视为“黑箱”,鲜有学者深入物流业内部运行过程,探究整个运行过程中各阶段的情况。而物流业的运行是包含着从初始各类资源的投入,到产生货物的空间转移,直至最终实现服务价值的连续过程。其中,前一过程可认为是服务生产阶段,即投入劳动力、资本、能源等各类资源要素,为物流活动提供支撑并获得货运量;后一过程则为创造效益阶段,反映出物流业通过各类物流活动所创造出来的经济价值。若忽视从初始投入到最终产出的中间过程,则无法精准分析各地物流业的运行效率,使得相应的效率改进措施对现实的指导意义不大[8]。因此,本文根据物流业运行特点,将其运行过程分为服务生产阶段与创造效益阶段,同时考虑碳排放对物流业服务生产阶段效率的影响,将二氧化碳排放量作为服务生产阶段的非期望产出,采用基于非期望产出的网络SBM模型,并结合视窗分析,以海丝路沿线地区物流业作为决策单元,研究这些地区物流业在2011—2015年间的运行效率,以期为海丝路沿线地区物流业发展提供相关政策建议,助力“一带一路”倡议顺利实施。
二、研究方法DEA是一种非参数的数学模型,可以用来评价若干决策单元(decision making unit, DMU)的相对效率。但传统的DEA模型将决策单元视为一个“黑箱”,忽略内部运营过程,无法准确评价决策单元效率。因此,本文参考Tone和Tsutsui(2009)[9]提出的网络SBM模型,分解物流业的运行过程,再根据Kao(2014)[10]和Liu,et al.(2015)[11]对非期望产出的处理方法,结合视窗分析,构建一个适用于物流业运行效率评价的NSBM(network slack based measure)模型。
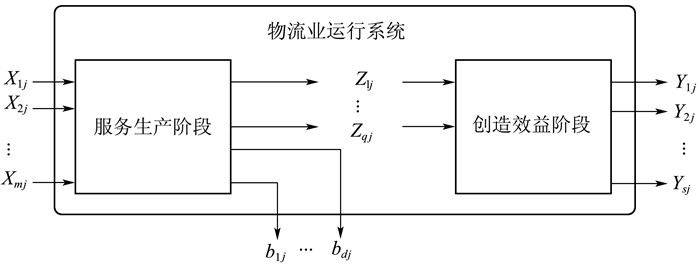
(一) NSBM模型设有n个同质的决策单元DMU,记为DMUj(j=1,2,…,n)。在本文中,DMUj代表第j个地区物流业。每个地区物流业运行过程都由两个阶段组成,第一个阶段为服务生产阶段,第二个阶段为创造效益阶段。对于第j个地区物流业而言,Xj=(X1j,X2j,…,Xmj)T表示物流业运行系统的初始投入,即服务生产阶段的投入,服务生产阶段的产出由两部分构成,第一部分为期望产出,记为Zj=(Z1j,Z2j,…,Zqj)T,第二部分为非期望产出,记为bj=(b1j,b2j,…,bdj)T。将服务生产阶段的期望产出作为创造效益阶段投入,并将创造效益阶段产出记为Yj=(Y1j,Y2j,…,Ysj)T,也是物流业运行系统的最终产出。物流业运行系统可用图 1来表示。
|
图 1 物流业两阶段运行系统构成 |
用λj,μj分别表示服务生产阶段与创造效益阶段的决策变量,即乘数;k表示第k个被评价的地区,si-,sr+,fp+,fp-分别表示各投入产出的松弛变量值。构建一个基于规模报酬可变,包含非期望产出NSBM模型如下:
| $ {{E}_{k}}=\text{min}\frac{1-\frac{1}{m+q}\left( \sum\limits_{i=1}^{m}{\frac{s_{i}^{-}}{{{X}_{ik}}}+\sum\limits_{p=1}^{q}{\frac{f_{p}^{-}}{{{Z}_{pk}}}}} \right)}{1+\frac{1}{q+s}\left( \sum\limits_{p=1}^{q}{\frac{f_{p}^{+}}{{{Z}_{pk}}}+\sum\limits_{r=1}^{s}{\frac{s_{r}^{+}}{{{Y}_{rk}}}}} \right)} $ | (1) |
| $ \begin{align} &\text{s}\text{.t}\text{.}\ \ \ \ \ \sum\limits_{j=1}^{n}{{{\lambda }_{j}}{{X}_{ij}}+s_{i}^{-}={{X}_{ik}}}\ \ \ \left( i=1, 2, \ldots, m \right)\text{ } \\ &\ \ \ \ \ \ \ \ \ \sum\limits_{j=1}^{n}{{{\lambda }_{j}}{{Z}_{pj}}-f_{p}^{+}={{Z}_{pk}}}\ \ \ \ \left( p=1, 2, \ldots, q \right)\text{ } \\ &\ \ \ \ \ \ \ \ \ \sum\limits_{j=1}^{n}{{{\lambda }_{j}}{{b}_{gj}}={{b}_{gk}}}\ \ \ \ \ \ \ \ \ \ \ \left( g=1, 2, \ldots, d \right)\text{ } \\ &\ \ \ \ \ \ \ \ \ \sum\limits_{j=1}^{n}{{{\lambda }_{j}}=1} \\ &\ \ \ \ \ \ \ \ \ \sum\limits_{j=1}^{n}{{{\mu }_{j}}{{Z}_{pj}}+f_{p}^{-}={{Z}_{pk}}}\ \ \left( p=1, 2, \ldots q \right)\text{ } \\ &\ \ \ \ \ \ \ \ \sum\limits_{j=1}^{n}{{{\mu }_{j}}{{Y}_{rj}}-s_{r}^{+}={{Y}_{rk}}}\ \ \ \ \ \ \ \left( r=1, 2, \ldots, s \right)\text{ } \\ &\ \ \ \ \ \ \ \ \sum\limits_{j=1}^{n}{{{\mu }_{j}}=1} \\ &\ \ \ \ \ \ \ \ {{\lambda }_{j}}, {{\mu }_{j}}\ge 0\ \ \ \ \left( j=1, \ldots, n \right);\text{ }s_{i}^{-}\ge 0\text{ }\left( i=1, 2, \ldots, m \right)\text{ } \\ &\ \ \ \ \ \ \ \ f_{p}^{+}, f_{p}^{-}\ge 0\ \ \ \left( p=1, \ldots, q \right);\text{ }s_{r}^{+}\ge 0\ \left( r=1, 2, \ldots, s \right) \\ \end{align} $ |
假设λj*, μj*, si-*, sr+*, fp+*, fp-*为模型(1)的最优解,则第k个地区物流业的运行总效率(Ek)、服务生产阶段效率(Ek1)、创造效益阶段效率(Ek2)可分别由下列各式求得:
| $ {{E}_{k}}=\frac{1-\frac{1}{m+q}\left( \sum\limits_{i=1}^{m}{\frac{s_{i}^{-*}}{{{X}_{ik}}}+\sum\limits_{p=1}^{q}{\frac{f_{p}^{-*}}{{{Z}_{pk}}}}} \right)}{1+\frac{1}{q+s}\left( \sum\limits_{p=1}^{q}{\frac{f_{p}^{+*}}{{{Z}_{pk}}}+\sum\limits_{r=1}^{s}{\frac{s_{r}^{+*}}{{{Y}_{rk}}}}} \right)} $ | (2) |
| $ E_{k}^{1}=\frac{1-\frac{1}{m}\sum\limits_{i=1}^{m}{\frac{s_{i}^{-*}}{{{X}_{ik}}}}}{1+\frac{1}{q}\sum\limits_{p=1}^{q}{\frac{f_{p}^{+*}}{{{Z}_{pk}}}}} $ | (3) |
| $ E_{k}^{2}=\frac{1-\frac{1}{q}\sum\limits_{p=1}^{q}{\frac{f_{p}^{-*}}{{{Z}_{pk}}}}}{1+\frac{1}{s}\sum\limits_{r=1}^{s}{\frac{s_{r}^{+*}}{{{Y}_{rk}}}}} $ | (4) |
DEA视窗分析最早由Charnes和Cooper提出[12]。DEA视窗分析所采用的数据为面板数据而非截面数据,将不同时期的同一决策单元视为不同的受评单元来评价,同时将多个时期数据按受评单位跨越的时间段归为一个视窗,且每个视窗的期数均相同。物流业运行效率在一定程度上会受行业内节能减排技术的创新程度以及新能源应用推广的影响。然而技术创新与新能源利用并非在某一时间点就可以体现出效果,其对效率的影响主要表现在连续、动态的运行周期中,因此,DEA视窗分析同时考虑时间因素与投入因素的积累效应。利用DEA视窗分析,不仅可以将某个地区的物流业运行效率同其他海丝路沿线地区进行比较,同时也可以实现同一地区不同时期之间的运行效率比较,能更为准确地分析海丝路沿线地区的物流业运行效率,有利于研究不同时期多个地区物流业运行效率的动态变化。
假设需要评价N个决策单元在M个时期内的相对效率,设视窗宽度为K,则每个视窗内有N×K个观测值。考虑到DEA视窗分析要求每个视窗内决策单元所处环境基本不变,参照Charnes,et al.(1984)[13]、Cullinane,et al.(2004)[14]以及陈浩等(2013)[15]的研究,本文选取的视窗宽度K=3。以3年为一个视窗计算海丝路沿线地区物流业运行效率,选取观察期为2011—2015年,因此第一个视窗为2011—2013年,第二个视窗为2012—2014年,第三个视窗为2013—2015年,每个地区物流业有3个视窗,本文对海丝路沿线11个地区进行研究,因此每个视窗内的决策单元个数为33个。
三、变量选择与数据来源 (一) 变量选取目前,我国《国民经济行业分类与代码》中没有物流业,对物流业的界定比较模糊。考虑到近年来,交通运输、仓储、邮政业增加值占物流业增加值均超过80%①,这一指标能够反映区域物流的发展状况,因此本文所指的物流业是指包括交通运输、仓储、邮政业的综合现代物流业。
① 根据2012—2016年《中国第三产业统计年鉴》计算整理得到。
1. 初始投入变量劳动力投入:劳动力是物流业运行最基本的投入要素之一,本文选取的劳动力即物流业年末就业人数,包括物流业的城镇单位年末就业人数以及城镇私营和个体年末就业人数。
资本投入:根据柯布-道格拉斯生产函数,除劳动力以外,资本也是基本投入要素。目前,国内学者多采用永续盘存法估算资本存量,但该方法涉及累计折旧率以及基期资本存量的选取,且计算得到的结果不一。刘秉镰(2009)[16]指出DEA研究的是决策单元相对效率,只要保持样本的相对一致性,计算结果就不会有太大偏差。因此,本文依据其做法,以物流业固定资产投资额代替资本存量作为资本投入。
能源投入:物流业在运行过程中会消耗煤油、柴油、天然气、电力等各类能源,本文将物流业消耗的各类型能源统一折算为标准煤作为物流业的能源投入。
2. 中间变量期望产出:虽然货运量与货物周转量均可反映区域物流的活跃程度,但是货物周转量包括了距离因素,在一定程度上会造成转口贸易较活跃地区物流效率的失真,相比较而言,货运量更加切实地反映区域物流规模,因此本文选取货运量作为期望产出变量。
非期望产出:能源消耗会产生大量CO2,本文将物流业CO2排放量作为非期望产出变量。CO2排放量参考宋震(2016)[17]的计算方法,根据物流业主要能源消耗的CO2排放系数(表 1)和地区份供电平均CO2排放系数(表 2),结合各地区综合能源平衡表中不同类型能源消耗量,计算得到相应地区物流业CO2排放量。
| 表 1 物流业主要能源消耗CO2排放系数 |
| 表 2 各地区供电平均CO2排放系数 |
行业增加值:物流业增加值可以刻画物流业在一定时期内通过物流活动为社会提供最终成果的货币表现,因此,可作为创造效益阶段产出变量,也是物流业运行系统的最终产出变量,用来衡量物流业整体运行状况。
(二) 样本选择与数据来源本文以海丝路沿线地区物流业作为决策单元,根据2015年《“一带一路”环球行动报告》界定的范围[18]5-6,选择海丝路沿线省份(自治区、直辖市)具体包括:广东、广西、福建、浙江、江苏、上海、河北、天津、山东、辽宁以及海南。所有投入产出变量数据来源于2012—2016年《中国第三产业统计年鉴》《中国能源统计年鉴》以及海丝路沿线各地区统计年鉴。
四、实证分析根据视窗NSBM模型求解得到海丝路沿线地区物流业在不同视窗内的运行效率,某地区物流业在某一年的运行效率为该地区在重叠的视窗内运行效率的均值。以上海为例,其物流业运行效率的计算结果如表 3所示,其余10个地区物流业运行效率的计算与此类似。表 3直观地显示出上海市物流业在2011—2015年物流业运行总效率及各阶段效率的动态变化过程。从表 3可知,在2011—2013年间,上海物流业运行总效率全距为0.091,效率波动不大,呈现缓慢上升趋势,历年效率均值在0.91以上,一直处于较高水平。从两阶段来看,上海物流业服务生产阶段表现较优秀,除2013年无效外,其余年份均为有效状态;创造效益阶段三个视窗内效率均为递增状态,因此整体也呈现出递增趋势。
| 表 3 上海市物流业2011—2015年三个视窗的运行总效率及分阶段效率 |
为充分了解海丝路沿线地区物流业运行总效率及服务生产阶段与创造效益阶段效率的动态变化过程,依据视窗NSBM模型计算得到不同时间点上各地区物流业效率均值,各地区物流业效率的历年均值以及所有地区物流业在2011—2015年期间效率均值,并对各地区物流业效率历年均值进行排名,结果如表 4、表 5以及表 6所示。
| 表 4 海丝路沿线地区物流业2011—2015年运行总效率 |
| 表 5 海丝路沿线地区物流业2011—2015年服务生产阶段效率 |
| 表 6 海丝路沿线地区物流业2011—2015年创造效益阶段效率 |
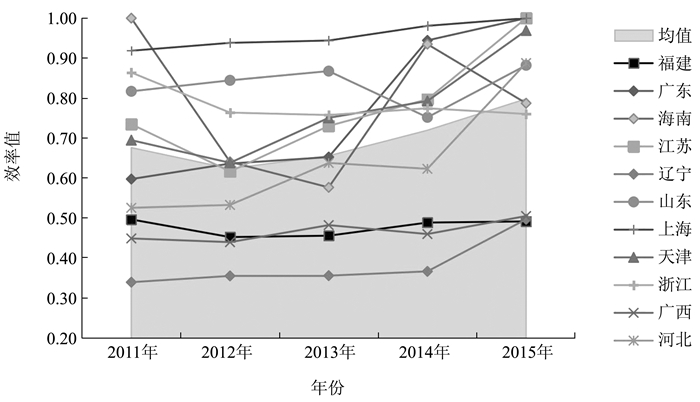
表 4和图 2显示出海丝路沿线地区物流业2011—2015年间的运行总效率。由表 4可知,海丝路沿线11个地区物流业在2011—2015年间效率整体均值为0.694,总体表现欠佳。结合图 2可知,上海、山东、海南物流业运行总效率较高,其中上海除2011年之外,其余年份物流运行总效率均为最高;福建、广西和辽宁物流业运行总效率相对较低,其中辽宁除2015年之外,其余年份物流业运行总效率均为最小,但整体呈现出缓慢上升趋势。结合表 5和表 6,进一步从服务生产阶段与创造效益阶段进行分析,可知导致它们运行总效率差异的原因有所不同。
|
图 2 海丝路沿线地区物流业2011—2015年运行总效率 |
物流业运行总效率排名前两位的分别为上海和山东,历年效率均值都在0.83以上,但上海和山东在生产阶段和创造效益阶段的表现有所不同。上海物流业在服务生产阶段历年效率均值高达0.993,创造效益阶段历年效率均值同样高达0.925,由此导致其运行总效率历年均值高达0.956,排名第一。山东物流业在服务生产阶段历年效率均值虽高达0.964,但创造效益阶段历年效率均值为0.586,导致其运行总效率历年均值为0.832,低于上海物流业运行总效率水平,排名第二。
福建、广西和辽宁物流业运行总效率排名靠后,历年效率均值不足0.48,但导致它们运行总效率较低的原因有所不同。福建和辽宁物流业运行总效率较低,是由于它们在服务生产阶段和创造效益阶段效率都相对较低。以辽宁为例,辽宁物流业在服务生产阶段历年效率均值为0.692(排名第十),在创造效益阶段效率历年均值为0.309(排名第十),最终导致辽宁物流业运行总效率排名最末。广西物流业在服务生产阶段始终处于有效状态,效率值为1,而在创造效益阶段其历年效率均值仅0.304,为样本最小值,导致广西物流业运行总效率排名第十。
由此可见,海丝路沿线地区物流业运行总效率受服务生产阶段和创造效益阶段效率共同影响,单一阶段的高效率并不一定导致运行总效率较高。
(二) 两阶段运行效率分析为进一步分析物流业服务生产阶段和创造效益阶段对运行总效率的影响程度,根据视窗NSBM模型计算结果,以运行总效率为因变量,以服务生产阶段效率和创造效益阶段效率为自变量,构建回归模型,利用Eviews8.0进行估计,结果如下:
| $ {{E}_{k}}=-0.202+0.615E_{k}^{1}+0.588E_{k}^{2} $ | (5) |
| $ \begin{align} &t-Value=\left( 21.717 \right)\left( 18.674 \right) \\ &p-Value=\left( 0.000 \right)\left( 0.000 \right) \\ &\overline{{{R}^{2}}}=0.945F-Value=448.862p-Value=0.000 \\ \end{align} $ |
从回归结果看,模型有较高的拟合优度,且回归方程在1%显著性水平上通过F检验,各阶段效率系数t检验结果也是显著的,由此可知,运行总效率与两阶段效率密切相关。这表明,海丝路沿线地区物流业运行总效率确实受到服务生产阶段和创造效益阶段效率的共同影响。因此,可以从服务生产和创造效益两方面入手,研究如何提升海丝路沿线地区物流业运行效率。
1. 服务生产阶段效率分析海丝路沿线地区物流业2011—2015年间服务生产阶段效率如表 5所示。观察期内,这些地区物流业服务生产阶段效率保持在较高水平,整体均值为0.805。然而随着时间的推移,这些地区物流业服务生产阶段效率出现微小波动,2012年服务生产效率有所降低,之后呈现上升趋势。服务生产阶段效率排名前四地区包括广西、上海、山东、海南,历年效率均值都在0.91以上;辽宁和福建物流业服务生产阶段表现相对较差,历年效率均值不足0.70。
广西物流业在服务生产阶段排名第一位,观察期内效率值始终为1,这意味着在现有投入水平下,相比而言广西已实现最佳产出。分析其原因,一方面是广西对物流业节能减排的重视,“十二五”期间广西深入开展“车、船、路、港”千家企业低碳交通运输专项行动和万家企业节能低碳行动,大力发展多式联运、甩挂运输等高效运输组织模式,鼓励淘汰老旧高能耗货车、船舶和作业机械,推广应用节能环保车船,有效促进了物流行业节能减排。到“十二五”期末,营运车辆、营运船舶单位运输周转量能耗和港口生产单位吞吐量综合能耗较“十一五”期末分别累计下降6.0%、8.5%和8.8%①。另一方面,广西物流业资源配置较为合理,观察期内,其每万个从业人数可产出0.41亿吨货运量,在所有样本中排名第二,每10亿元固定资产投资可产出0.14亿吨货运量,排名第四,每万吨标准煤能耗可产出1.90亿吨货运量,排名第一。广西结合建设海丝路枢纽门户等国内外发展新趋势,将防城港、钦州港、北海港实施整合,三港统一调度,各联检部门与港口信息共享,实现了统一规划、统一建设、统一管理、统一运营的“四统一”,有效促进了港口之间的协调发展,达到了整体提升的效果。“十二五”期间,广西通过打通大通道关键缺失段,实现了高速公路、铁路与港口的直接连通,推进多式联运中各种运输方式的无缝对接,有效提升了港口服务生产能力。
① 数据源自《广西节能减排降碳和能源消费总量控制“十三五”规划》。
辽宁和福建等省份物流业在服务生产阶段效率值较低,排名比较靠后。一方面是因为较高的碳排放对其服务生产效率有一定负面影响,另一方面较高的投入要素冗余,导致其物流业服务生产效率偏低。根据计算获得的松弛变量来看,辽宁和福建物流业的能源投入冗余程度较为严重,观察期内两省份能源投入平均冗余率分别为12.55%和17.63%。近年来,随着我国对物流业重视,物流业迎来快速发展时期,受国家各项利好政策刺激,这些省份纷纷加大在物流领域的投入,但并未转化为有效产出,物流业粗放的发展方式对环境造成一定影响,因此导致这些省份服务生产效率偏低。
2. 创造效益阶段效率分析海丝路沿线地区物流业2011—2015年创造效益阶段效率如表 6所示。由表 6可知,在观察期内,虽然2012年创造效益阶段效率有所降低,但总体呈现上升趋势,整体均值为0.682。这些地区物流业现在乃至未来一段时间内仍有较大上升空间,这一点可以从2015年创造效益阶段效率均值仅0.775的表现上得到印证。与服务生产阶段有所不同,在创造效益阶段,天津、江苏则表现较为突出。由此可见各地区物流业在服务生产阶段和创造效益阶段的效率差异较大,反映出海丝路沿线地区物流业在各阶段发展的不平衡性。
天津物流业在创造效益阶段表现较为优秀,历年效率均值高达0.952,在11个地区中排名第一位,这主要得益于在同等货物周转量水平下,天津物流业创造了更多经济价值,获取效益的水平更高。近年来,天津市根据物流需求变化,适时扩展和强化公路、航空、港区铁路运输网络,积极有序地推进航空物流区、海港、无水港等基础设施建设,建成了一批投资多元、功能集成、特色鲜明的物流园区和物流基地。天津市依托港口航运优势,利用三大海陆联运通道,加强了与俄罗斯、蒙古两国的物流业合作;积极推进京津冀交通与物流一体化发展,在甩挂运输、铁路快运班列、港口投资、机场运营方面实现协同发展战略合作。此外,天津市积极推动物流综合信息服务平台建设,有效促进了物流企业与生产、商贸、批发零售等企业的数据共用、资源共享和信息互通。这些措施均有益于天津市通过物流活动为社会创造更多经济价值,获得较高的创造效益阶段效率,同时也值得创造效益阶段效率较低地区借鉴和学习。
此外,辽宁、广西等地区物流业在创造效益阶段效率值较低,排名比较靠后。这些地区单位货运量所产出的物流业增加值相对较低,与天津、上海相比仍存在很大差距,“量大利薄”导致在现有投入水平下产出不足。因此,这些地区在物流规模提升的同时,其效益创造水平仍有待提高。
五、结论与启示 (一) 研究结论本文采用视窗NSBM模型,考虑碳排放约束下,全面分析海丝路沿线地区物流业在2011—2015年的运行效率,得到以下结论:
海丝路沿线地区物流业运行总效率受服务生产阶段效率和创造效益阶段效率的共同影响。单一阶段的高效率并不一定能保证运行总效率也处于较高水平,如广西物流业。只有服务生产阶段和创造效益阶段同时表现优异,如上海物流业,才能全面提升物流业总运行水平。此外,不同地区物流业在服务生产阶段和创造效益阶段表现各有差异,因此在制定相关政策时应有所侧重。
碳排放水平对海丝路沿线地区物流业发展有一定负面影响。从实证分析结果来看,辽宁和福建等地区物流业服务生产效率偏低与其比较高的碳排放水平有关。在绿色发展理念下,将CO2排放量作为服务生产阶段非期望产出变量,从经济和环境两个维度综合考虑物流业运行状况,更加符合实际情况,有助于物流业的可持续发展。
(二) 政策启示 1. 服务生产阶段效率提升措施针对服务生产阶段效率较低的海丝路沿线地区,诸如辽宁、福建,在重视创造效益的同时,需要转变物流业发展方式,整合物流资源,进一步提升服务生产效率,才能在“一带一路”建设中获得更长足发展。具体包括:
第一,合理规划各类物流资源投入,提升现有物流资源利用率。政府应科学规划、合理配置已有物流资源,不能盲目加大对物流基础设施投资。海丝路沿线地区应重点整合港口资源,一方面可加强同区域内不同港口之间的协作,另一方面需要不断完善港口的集疏运系统,大力发展多式联运,提高一体化衔接水平和多式联运全程服务能力,推进联运服务“一单制”,以提升服务生产阶段效率。
第二,引导物流业节能减排,改善能源结构。从实证分析结果可知,碳排放水平对服务生产阶段效率有一定负面影响。因此,需要重视物流业节能减排。一方面,政府可制定物流业污染物排放标准,出台低碳物流的相关法律法规,落实节能减排目标责任制,在物流企业之间建立碳排放交换机制,将低碳理念融入企业经营和政府管理中。另一方面,需要改善物流业能源结构,构建低碳能源系统,推广应用节能和清洁能源运输工具,减轻物流运作的环境负担。以绿色发展引导效率提升,为推动“一带一路”建设作出应有贡献。
2. 创造效益阶段效率提升措施针对创造效益阶段效率较低的海丝路沿线地区,诸如辽宁、广西,在既有碳排放约束下,应采取措施降低物流成本,提高物流业经济效益,实现降本增效,提升创造效益阶段效率。
第一,创新物流服务模式,推动产业转型升级。服务创新是物流业发展的不竭动力。海丝路沿线地区可深入推进甩挂运输发展,推动站场、车辆、信息等甩挂资源的共享利用;依托“一带一路”倡议,加快建设中欧班列国内节点,实施快递向外工程,在重点口岸城市建设国际快件处理中心,以支持跨境电商物流发展。以创新为驱动,将潜在物流需求转化为实际经济效益,从而提升海丝路沿线地区物流业创造效益阶段效率。
第二,构建多级互通信息网络,优化物流发展软环境。海丝路沿线地区可分步骤、分区域、分层次建设物流信息资源共享的物流信息化体系,增进物流服务精准化和智能化。具体可拓展信息技术在企业应用的深度和广度,逐步实现物流作业的信息化、专业化、自动化、高效化;鼓励物流园区通过与入驻企业信息系统互连或其他数据采集方式,逐步实现物流信息资源的集中与整合;加快物流公共信息资源交易平台建设,实现客户、承运商、政府机构、中介服务机构平台的互通互联。通过为物流业发展提供良好的软环境,进一步提升物流业经济效益水平。
| [1] | 何黎明. 我国物流业"十二五"发展回顾与"十三五"展望[J]. 中国流通经济, 2016, 21(3): 5–9. |
| [2] | 孟鑫. 基于DEA模型的长江经济带物流产业效率分析[J]. 企业经济, 2015(12): 108–113. |
| [3] | 张雪青. "一带一路"区域物流协同发展分析[J]. 统计与决策, 2016(8): 108–110. |
| [4] | 林珊, 温惠英. 基于AHP-DEA两阶段模型的物流公司绩效评价研究[J]. 华南理工大学学报(社会科学版), 2014(4): 50–55. |
| [5] | 毕志雯. 低碳约束下我国物流产业技术效率动态评价——基于Meta-Frontier和序列SBM-DEA的分析[D]. 天津: 南开大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10055-1011111484.htm |
| [6] | 唐建荣, 卢玲珠. 低碳约束下的物流效率分析——以东部十省份为例[J]. 中国流通经济, 2013(1): 40–47. |
| [7] | 王维国, 马越越. 中国区域物流产业效率——基于三阶段DEA模型的Malmquist-Luenberger指数方法[J]. 系统工程, 2012(3): 66–75. |
| [8] | 石晓. 网络DEA理论方法与应用研究[D]. 合肥: 中国科学技术大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10358-1016107335.htm |
| [9] | TONE K, TSUTSUI M. Network DEA:A Slacks-based Measure Approach[J]. European Journal of Operational Research, 2009,197(1): 243–252. DOI: 10.1016/j.ejor.2008.05.027 |
| [10] | KAO C. Efficiency Decomposition in Network Data Envelopment Analysis with Slacks-based Measures[J]. European Journal of Operational Research, 2014,192(3): 949–962. |
| [11] | LIU W, ZHOU Z, Ma C, et al. Two-stage DEA Models with Undesirable Input-intermediate-outputs[J]. Omega, 2015,56: 74–87. DOI: 10.1016/j.omega.2015.03.009 |
| [12] | CHARNES A, COOPER W W. Preface to Topics in Data Envelopment Analysis[J]. Annals of Operations Research, 1984,2(1): 59–94. DOI: 10.1007/BF01874733 |
| [13] | CHARNES A, CLARK C T, COOPER W W, et al. A Developmental Study of Data Envelopment Analysis in Measuring the Efficiency of Maintenance Units in the U.S.Air forces[J]. Annals of Operations Research, 1984,2(1): 95–112. DOI: 10.1007/BF01874734 |
| [14] | CULLINANE K, SONG D W, JI P, et al. An Application of DEA Windows Analysis to Container Port Production Efficiency[J]. Review of Network Economics, 2004,3(2): 184–206. |
| [15] | 陈浩, 王晓红, 张宝生. 基于视窗分析模型的我国高校科研效率评价[J]. 科研管理, 2013(7): 101–111. |
| [16] | 刘秉镰, 李清彬. 中国城市全要素生产率的动态实证分析:1990-2006——基于DEA模型的Malmquist指数方法[J]. 南开经济研究, 2009(3): 139–152. |
| [17] | 宋震, 丛林. 环境约束下中国交通运输业能源效率研究[J]. 交通运输系统工程与信息, 2016(4): 39–45. |
| [18] | 杨善民. "一带一路"环球行动报告(2015)[M]. 北京: 社会科学文献出版社, 2015. |
 2018, Vol. 20
2018, Vol. 20
