2. 北京工商大学 经济学院, 北京 100048
2. School of Economics, Beijing Technology and Business University, Beijing, 100048, China
疫苗是人们预防和抵抗传染病的有效武器,其重要性不言而喻。而疫苗需求的预测是保证疫苗充足储备与供应的前提条件。疫苗可以预防传染性和感染性疾病,在人群中形成免疫屏障,降低传染给他人的机会,其他人可以从某人接种中获得显著收益,具有正外部性属性。因此,疫苗接种的社会总收益高于接种个体的收益。对于正外部性产品,竞争性市场往往会供给不足,同时由于接种疫苗对个人有益,而个人并不清楚其最佳收益所在,所以很难达到最佳需求量。故而了解疫苗的接种偏好和需求对于提高疫苗接种率和人群健康水平具有重要意义(朱大伟,郭娜等,2016)。[1]目前,预防接种疫苗供应的剧烈波动不能被客观科学地预测,如何预测疫苗需求量使其既满足实际需要,又不造成浪费,至关重要(姜晓飞等,2013)。[2]
对于疫苗需求的研究,国内外学者主要采用调研或建立数理模型来进行相关预测。Whittington,et al.(2008)[3]通过调研访谈等形式在泰国曼谷等三个城市发放2000多份调查问卷,建立回归模型对家庭的艾滋病疫苗需求展开预测。Amarasinghe,et al.(2010)[4]将2007年的麻疹疫苗覆盖率作为基准参考,通过类比假设的方式对登革热疫苗在亚洲和美洲等地区的接种率进行预测。阮玉华、郭欣等(2001)[5]通过调研方式,收集接种肾综合征出血热灭活疫苗的人群样本,并且利用需求弹性理论来进行疫苗接种价格降低可能性的探讨,得出原定价不同时,疫苗价格降低可能性不同的相关结论。曹雷、王华庆等(2012)[6]通过抽样调查分析儿童接种国家扩大免疫规划疫苗的情况,得出东中部地区疫苗接种率高于西部地区,低接种率地区主要集中在中西部。朱大伟等(2013)[7]通过随机效用理论,建立相关模型,分析数据得出在农村地区个体层面上,对乙肝疫苗接种有显著影响的因素有年龄、受教育程度、职业、家庭人均年收入和认知水平,从而对疫苗需求进行分析。Nunes,et al.(2013)[8]将疫苗供求关系、健康影响评估和财政分析相互关联,从而建立完整的疟疾疫苗系统模型,对疟疾疫苗的需求进行预测。熊文等(2016)[9]则根据知识溢出理论构建大规模传染病空间扩散模型,并运用VBA计算机技术对大规模传染病例进行预测、预警研究。
综合国内外对于疫苗需求预测的相关研究,有的是在一定时间段内预测,有的是在特定的地点进行调研,或者就是针对特定疾病疫苗的预测,都未能考虑到疫情不同阶段下人们对于疫苗需求的选择。而当人们陷入大规模传染疫情灾难时,疫情的预警程度不同,人们对于疫苗的选择和需求差异会比较明显,而这也是在疫情从开始到爆发时,政府、疫苗生产者和卫生组织所需要参考的重要依据。
而疫苗的需求,从经济学角度看,就是一种特殊商品的需求。对于商品需求,无论内容[10, 11]还是方法[12, 13]都有着丰富的研究,而疫苗需求更符合短生命周期产品的需求特征。[14]任何一种疫情的爆发,都需要一种全新疫苗,其需求特征都是不可复制的。因此,对于这种特殊的短生命周期产品,我们要把握其共通性,并从类似的产品入手。为此,本文第二部分将从疫苗产品面临的共通特性出发展开需求调研;第三部分以调研数据为支撑构建一个疫苗需求预测分析框架;第四部分则以H1N1为疫情程度背景,对于不同预警下疫苗需求进行预测分析,从而展示疫苗需求的具体预测过程;最后是相关结论与总结。
二、调研情况及样本有效性分析 (一) 问卷基本情况介绍本研究假设了同H1N1类似的大规模传染病在我国爆发的事件(事实上,假设任何传染病爆发情景都一样,无非是反映疫情对人们的危机程度),并按程度分为9种预警情景:① 你所处的省份爆发,尚未波及其他省(自治区、直辖市);② 在全国部分省份爆发,你所处的省份及邻近省份还未出现病例;③ 在全国范围爆发,邻近省份已经出现,你所处省份还未出现病例;④ 在全国范围爆发,你所处的省份已出现10个以下病例,而你所处城市还未出现;⑤ 在全国范围爆发,你所处的省份已出现10个以下病例,而你所处城市也已经出现;⑥ 在全国范围爆发,你所处的省份已达500个病例;⑦ 在全国范围爆发,你所处的省份已达1000个病例;⑧ 在全国范围爆发,你所处的省份已达3000个病例;⑨ 在全国范围爆发,你所处的省份已出现5000个及以上病例。
在这些情景下,如果已有疫苗发布,人们就需要对是否接受疫苗作出抉择。根据需求理论,产品需求取决于消费者的购买欲望与购买能力。购买欲望反映了人们的偏好,体现了人们对产品的认知与判断;而购买能力则与价格水平紧密相连。因此对于疫苗产品这种特殊的需求,人们是否选择疫苗主要取决于两方面因素:一方面是疫苗本身的特质,产品是否真能起到应有的防护作用,这种作用效果有多大;使用后会不会存在风险性,是否有副作用。另一方面是人们的经济承受能力,人们愿意花多少钱接受疫苗。
为此,我们的问卷调研分成了三个区块,在有效性方面,设置“80% ~ 100%”“50% ~ 80%”“50%以下”及“不接受”等4种层级选项;在风险性方面,设置“0.01% ~ 0.05%” “0.05% ~ 0.10%”“0.1%以上”及“不接受”等4种层级选项;在定价方面,设置“免费”“50元以下”“50 ~ 100元”“100 ~ 200元”“200 ~ 500元”“500 ~ 1000元”及“1000元以上”等7种层级选项。进而从疫苗有效性、风险性及定价三方面去调查人们在不同预警情景下是否接受疫苗的决策行为。
(二) 样本有效性分析本研究的调研全权委托问卷网(苏州爱调言网络科技有限公司)进行。整个调研包括样本3000份,由于本文涉及省市级层面的空间区位选择,需要全面掌握全国各省(自治区、直辖市)的情况,通过网络调研方式向30个省(自治区、直辖市)均匀发布(由于无法达到调查需求样本,故不含西藏及港澳台地区)。根据网络调研的随机性,问卷回收无法达到精确一致,各省(自治区、直辖市)的样本数存在差异,但每个省(自治区、直辖市)回收问卷保证基本在100份左右,最多的新疆达到113份,最少的山东、重庆为93份。我们的调研样本遍布全国30个省(自治区、直辖市),分布合理且有很强的代表意义。
然而样本选择与分布的合理,并不能说明调研的结果就是合理的,被调研者是否认真答题也是非常重要的影响因素。一直以来,对于调查问卷填写的可信度问题都是困扰调查结果有效性程度的主要难题。但对于本研究来说,却设计了一个可行的可判定的标准,或者说是方法。
1. 问题条件的严格累进性从这9种情景可以看到,除了第一种情景在传染病爆发初期且是传染源地,与后面几种情景不好判定强弱,人们可能存在选择困难外,问题2 ~ 9存在严格的累进性,每一个问题情景都是上一个情景的恶化。于是,对于问题2 ~ 9,如果人们都是认真地回答,其选择应该存在一种严格的累进性。
这里我们定义选择的严格累进性,由于选项存在由低到高的程度差异,当人们在低约束条件情况下选择程度较低的选项时,随着条件约束的加强,从理性的角度人们必定会选择程度更高的选项,至少不会低于前一个较低约束条件下所做出的选择。因此,根据问题条件的严格累进性原则,我们可以对所有调查问卷进行判定,从而筛选有效的样本,以使整个研究结论更加准确。
2. 样本有效性判定利用严格累进性原理对样本有效性进行判定,我们需要对不同程度的问题选项进行赋值,按照选项的程度高低情况,程度低的赋予较小的值,程度高的赋予较大的值。在本研究中,核心问题选项在4 ~ 7个不等,因此分别赋值为1-4或者1-7。
很明显,根据严格累进性原则,如果某一问卷是认真回答的,对于问题2(Q2) ~问题9(Q9) 的选择必定存在以下性质:无论Q2的选项程度有多高,其后面的问题Q3 ~ Q9的选项都不会低于Q2的程度。比如Q2的选项为2,那么Q3 ~ Q9的选项必定大于等于2,也即是说如果用Q3 ~ Q9中的选项减去Q2的选项,其差值必定大于等于0。
为此,我们构造了问题严格累进差值,即高程度的问题选项值与低一个程度的问题选项值之差(如问题3的选项减去问题2的选项,即Q3-Q2),以此来对样本的可信度进行判定。如果差值为正就表示样本合理,若出现负值则不合理,该样本就淘汰。
按照这种办法,我们对回收的3000份问卷进行了计算,并从有效性、风险性、成本三分类样本及总体样本角度统计了所有严格累进差值的负值个数、各问题差值的均值等相关情况,具体见表 1。
| 表 1 问题条件严格累进下总体样本差值均值及分解 |
从表 1可以看到,无论是有效性、风险性、成本三方面样本,还是总体样本,问题严格累进差值都为正,没有负值存在。由此可以判定,对于所有问卷,人们在回答所有问题的时候都基本遵循了自身的理性判断,所有问卷都是符合调研标准的。
另外,对于每一个问题差值的均值都大于0,从有效性、风险性、成本三方面样本及总体样本看,问题差值的均值都呈现出逐步上升的过程。这表明随着传染病扩散的越来越严重,人们越来越愿意接受疫苗,对疫苗有效性的容忍度越来越高,对疫苗风险性的承受能力越来越强,愿意支付的费用也不断提高。
同时,由于总体样本由有效性、风险性、成本三方面样本组成,其差值当然也可以分解为有效性、风险性、成本三方面差值。可以明显看到,总体样本方面的差值的增加主要来源于成本方面,其次是风险性,然后是有效性。也即是说,随着传染病扩散程度的越来越严重,人们更容易在费用上放松要求,从而作出选择上的改变。
三、疫苗需求预测分析框架为了展示利用疫情情景调研数据进行疫苗需求量预测的过程,我们需要选择一个已经出现过的疫情进行案例尝试。而2009年H1N1是迄今为止波及范围广泛、持续时间很长,且有充足的时间、空间数据支撑的案例。当然由于数据源自对公开媒体的收集整理,其准确性存疑。但本文并不是要对某个特殊的疫情进行预测,因为每个疫情都是独特的,探索特殊是缺乏价值的,而是要探索如何利用人们对不同风险情景疫苗需求偏好这种共通的特性展开疫苗需求预测。事实上,H1N1数据仅仅只是作为反映疫情危机程度的背景数据。因此,采用H1N1数据是可行的,具体预测分析框架如下。
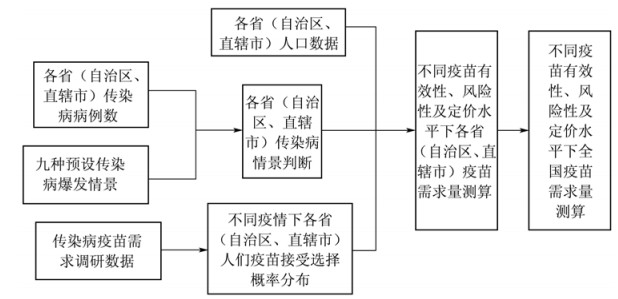
(一) 疫苗需求预测过程通过对不同疫情情景下疫苗有效性、风险性及定价水平差异的疫苗接受情况的调研,我们获得了人们选择接受疫苗的基础数据。以此数据为基础结合各省(自治区、直辖市)传染病疫情的具体情况,就可以展开我国疫苗需求量的估计。为此,我们设计了相应的计算过程,如图 1。
|
图 1 我国疫苗需求量测算过程 |
首先,需要对各省(自治区、直辖市)传染病情景进行判断。根据调研问卷我们将疫情按程度分为9种预警情景。以2009年H1N1为例,从公开数据可以发现,疫情爆发的前两个月(5月、6月),对于各省(自治区、直辖市)的疫情发展情况每天都有相应的数据更新,根据各省(自治区、直辖市)每天的数据,我们就可以对每个省(自治区、直辖市)处于9种情景中的哪一个进行具体的判断。
其次,我们以传染病疫苗需求调研数据为基础,可以计算出不同疫情下各省(自治区、直辖市)人们疫苗接受选择概率分布。
第三,根据我们对各省(自治区、直辖市)的情景判断,以各省(自治区、直辖市)人们疫苗接受选择概率分布为基础,结合各省(自治区、直辖市)人口数据,进一步计算出每个省(自治区、直辖市)在不同疫苗有效性、风险性及定价水平下的疫苗需求量。
最后,将各省(自治区、直辖市)疫苗需求量数据汇总,即可得到全国疫苗的理论需求量。
(二) 疫苗接受比例计算标准通过网络调研,3000个被调研对象都根据9种疫情情景对有效性、风险性及定价水平进行了疫苗接受的选择。有效性、风险性分别有4个选项,定价水平有7个选项,这样就会有112(即4×4×7) 种组合选项,从而形成概率分布。于是,根据调研数据我们便可计算出每个省(自治区、直辖市)的疫苗选择的概率分布情况。由于30个省(自治区、直辖市)都有各自的疫苗选择概率分布情况,数据量过大不在文中详述,在此仅以北京为例介绍情景1的疫苗选择的概率分布,见表 2。
| 表 2 不同疫苗有效性、风险性及定价水平下北京市接受疫苗概率分布(情景1) |
表中展示了112种选项的概率分布情况,很明显北京的人们更倾向于选择有效性高、风险性低的组合,如1_ 1(即有效性在80% ~ 100%、风险性在0.01% ~ 0.05%的组合),特别是此组合的低价区间(100 ~ 200元、50 ~ 100元、50元以下及免费分别达到0.0918、0.0510、0.0204、0.0714);完全不接受疫苗的人还是较少的,无论有效性选择4(不接受),还是风险性选择4(不接受),其比例都较少甚至为0。
当然,仅仅依靠112种选项的概率分布是无法对需求量进行评估的,我们还需要在此基础上进行一些特别的计算。由于我们设置的是单项选择,因此在人们接受一种更严格的条件时,那么对于宽松的条件当然也是接受的。对于定价条件来说,每个人都会选择一个接受疫苗的价格,当定价超过他选择的价格,也即是超过了他的经济承受范围,那么在计算这个定价标准的疫苗接受人数时,就不应该将这个人包括在内。比如,当某人选择接受1000元以上的定价水平时,他同时也会接受500 ~ 1000元、200 ~ 500元、100 ~ 200元、50 ~ 100元、50元以下及免费等定价水平。于是,当我们定价在500 ~ 1000元之间时,此时选择接受疫苗的人数就应包括选择1000元以上及500 ~ 1000元两个概率区间的人们,也即是说应该计算这两个定价水平的累计概率。根据此方法,我们给出了不同定价水平下接受疫苗的累计百分比计算标准,具体见表 3。
| 表 3 不同定价水平下接受疫苗累计百分比计算标准 |
这样解释:我们现在对A、B、C、D、E、F、G七个人进行调研,问他们愿意付多少钱接受疫苗。他们分别选择1000元以上、500 ~ 1000元、200 ~ 500元、100 ~ 200元、50 ~ 100元、50元以下及免费,每人各选择了一项。也即是说,这7个选项,每个选项有1个人。
现在我们问,当免费时,有多少人愿意接受疫苗?很显然,免费的定价标准对于任何人都没有限制,只要他愿意接受疫苗就能接受疫苗。所以这里应该是7人,选择这7个选项的人都应该包括在内。
当定价为50元以下时,有多少人愿意接受疫苗?很明显,相对于免费,定价50元以下,已经是有价格了,对于个人来说就是有花费了。那么选择免费时才接受疫苗的人不应该包括在内。而对于1000元以上的定价,都选择接受疫苗的人,免费的时候,他当然愿意接受疫苗。难道在大规模传染病来临时,因为定价为免费,这些愿意掏1000元以上接受疫苗的人,因为定价太低甚至免费,而愿意冒传染病的风险?同理,选择50元以下、50 ~ 100元、100 ~ 200元、200 ~ 500元、500 ~ 1000元的人,因为定价50元以下都在他们的经济承受范围内,所以计算的时候他们都应该包括在内。
每个人都会选择一个接受疫苗的价格,当定价超过他选择的价格,也即是超过了他的经济承受范围。因此,在计算这个定价标准的疫苗接受人数时,就不应该将这个人包括在内。
同样,当选择接受50% ~ 80%有效性时,同时也就接受了80% ~ 100%有效性;当选择接受0.05% ~ 0.10%风险性时,同时也就接受了0.01% ~ 0.05%风险性。于是,当我们的疫苗有效性在50% ~ 80%时,此时选择接受疫苗的人数就应包括选择50% ~ 80%有效性及80% ~ 100%有效性两个概率区间的人们,也即是说应该计算这两个有效性水平的累计概率。对于风险性也是同样的道理。根据此方法,我们又给出了不同有效性、风险性组合下接受疫苗的累计百分比计算标准,具体见表 4。
| 表 4 不同疫苗有效性、风险性组合下接受疫苗累计百分比计算标准 |
依据表 3与表 4给出的累计百分比的计算标准,我们对9种情景30个省(自治区、直辖市)的疫苗接受百分比进行了计算,同样是数据量过大的缘故,本文仅介绍北京的情况。
表 5给出了北京的人们在情景1条件下对于不同疫苗有效性、风险性及定价水平的接受百分比。此表结果正是在表 2的北京人们疫苗选择概率分布表基础上,按照表 3与表 4的计算标准,进行交叉累计计算出来的。
| 表 5 不同疫苗有效性、风险性及定价水平下北京市接受疫苗百分比(情景1) |
从表 5可以看到,在情景1时,也即是疫情从北京发起尚未波及其他地区的情况,在疫苗有效性最高、风险性最低且免费的情况下(即有效性与风险性组合1_ 1中免费的情况),北京人民将有88.78%愿意接受疫苗,随着定价的升高接受数量开始降低,特别定价超过200以后迅速下降到27.55%,到1000元以上时仅剩6.12%,表明在疫情初期价格对疫苗接受与否发挥了巨大的影响。对于风险性变化带来的影响,我们可选免费且有效性最高的状况来分析。随着风险的提高,有效性与风险性组合由1_ 1,到1_ 2,再到1_ 3,北京人民愿意接受的比例由88.78%迅速下降为41.84%,再至6.12%,表明疫情初期风险性在是否接受疫苗的决策过程中起到重要的作用。同理我们也可以通过有效性与风险性组合由1_ 1,到2_ 1,再到3_ 1的变化分析有效性降低同样对是否接受疫苗带来了巨大的影响。
当然,随着情景的变化,北京人民的选择也会发生变化,而其他省(自治区、直辖市)的选择也与北京有着差异,这里的研究主要为全国需求量的预测做支撑,在此就不一一论述。
四、预测结果分析有了详尽的各种情景下30省(自治区、直辖市)不同疫苗有效性、风险性及定价水平下接受疫苗百分比数据作为支撑,结合分省区的疫情数据及各省的人口状况,我们便可以进行疫苗需求量的理论值预测。根据前面的传染病疫苗需求预测框架,本文将以2009年我国H1N1疫情为例,研究我国的疫苗理论需求量的估计。由于人们在疫情风险下的偏好总是一致的,通过此分析可为以后我国类似疫情发生时应急产品特别是疫苗需求作出前期判估,从而为相关医药产能建设提供决策支持,以应对未来应急之需。
(一) 数据来源与预处理本研究各地市人口数据源自2010中国统计年鉴,各省H1N1每日病例数据则根据各大官方媒体报道收集整理。由于公开报道的数据并不是每天都有,且有部分数据还会出现冲突现象,需要做相应的矫正处理。另外,本研究的疫苗需求分析需要尽可能详细的各时间段各省(自治区、直辖市)的病例数据,对于缺少的某些天的数据,就需要利用插值法进行相应的补充。若数据缺失严重而无法支持分析,则不采用相应时间的数据。具体方法如下:
(1) 如果需要补充的几天,该地区病例数没有发生变化,就采用原数据。如2009年5月16日和19日报道的北京病例均为1,17、18两日数据则循例补充为1。
(2) 如果需要补充的几天,该地区病例数发生了变化,则采取均匀插值。如2009年6月5日、9日报道的上海病例数分别为7和11,6、7、8三日数据则分别补充为8、9、10。
(3) 全国总计数据,需要补充的,不是根据总计数据的差额进行插值处理,而是根据各地区的数据进行插值补充后,对补充的各地数据求和计算所得。
(4) 由于2009年7月5日后报道频度减少,无法对各地区进行大规模插值处理,插值的准确度也大受影响。故此后,仅选用了一些数据相对完整的时间段进行分析,如8月份仅选用5、10、28日,9月仅选用27日,等等。
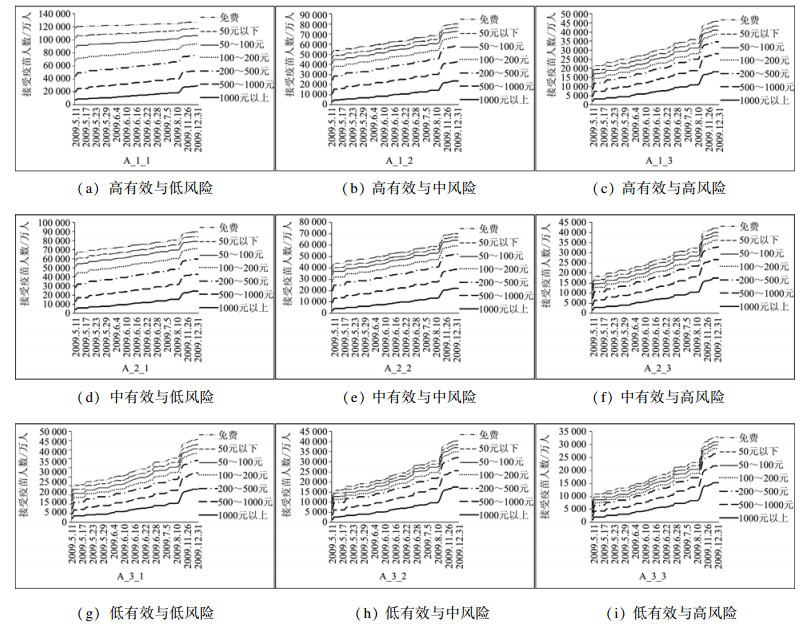
(二) 预测结果分析按照疫苗需求预测分析框架,根据2009年我国H1N1疫情各时期状况,我们对疫情演变过程中的疫苗需求量进行了测算,具体结果见图 2。图中又分为9个小图,分别表示了不同有效性与风险性的组合。而每个小图又展示7种定价标准,详细描绘了不同有效性、风险性及定价差异情景下,随着疫情的不断加重,我国疫苗需求量的变化态势。在此必须说明的是,这里的预测结果是在我国所有人都对疫苗的有效性、风险性及价格知情的前提下,根据疫情状况作出的选择,本文没有考虑信息不对称的情况。
|
图 2 各种疫苗风险性、有效性及定价差异下我国疫苗的需求量变化 |
从图中可以看到,对于所有情景组合,随着疫情的不断加重,疫苗的需求量均呈现出不断上升的趋势。对于低风险、高有效性的情况(见图 2a),疫苗需求量是所有有效性、风险性组合中最高的,并随疫情的加重而增加,但增加速度较为平缓。疫苗价格对需求影响非常大,价格每上升一个区间,都会带来需求的大幅下降;在疫情初期各价格区间接受疫苗的比例大致相当;随着疫情的加重,高价格区间的比例不断提高,表明人们受价格的影响在降低。
风险性的上升与有效性的下降,对于疫苗需求量都会产生非常大的影响。从图 2a到图 2c(或从图 2a到图 2g),我们可以看到,风险性的上升或有效性的下降,带来了疫苗需求量的大幅度的下降,特别是对于疫情早期下降幅度非常之大。这也表明在疫情早期人们对于有效性与风险性非常敏感,而随着疫情威胁的加大,这种敏感性在不断下降。另外,较之于有效性,人们对于风险性的敏感度更大,从图 2b与图 2d比较可以看到,风险性的升高带来的降幅更大。
对于疫苗价格来说,伴随着风险性的上升或有效性的下降,中低价区间的价格敏感性在下降,高价区间的价格敏感性在增强。从图 2b到图 2i(特别是图 2i)可看到,中低价区的价格变化带来的需求量增减幅度较小,而高价区的价格变化带来的需求量增减幅度非常大。特别是在疫情最严重的时期尤为明显,人们对于中低价敏感性减弱的同时,也更愿意在疫苗上花费更多的钱。
五、结论与讨论在问卷调查的基础上,提出了传染病疫苗需求量预测分析方法,并以2009年H1N1疫情为基准,对我国大规模传染病疫苗理论需求量进行了分情景预测,从而进一步分析疫苗风险性、有效性及定价差异三方面其疫苗需求量的影响。
以问卷调查为基础的需求量预测方法,为传染病疫苗需求预测提供了新的选择。通过对各种疫情情景的合理设置,以获取不同情景下人们对于疫苗需求的决策选择,从而对未知传染病爆发时疫苗需求量判断提供可行的预测分析支持。
在问卷调查中,通过对问题条件的严格累进性设计,可以对样本的有效性判定提供支持,增强问卷的可信度。从严格累进性的差值也发现,随着传染病扩散程度的越来越严重,人们更容易在费用上放松要求,从而作出选择上的改变。
疫苗风险性、有效性及定价差异对疫苗需求量有着重要的影响。风险性的上升、有效性的下降及价格的提高,均会带来需求量的下降。但随着疫情的加重,这种影响会减弱。特别是到疫情非常严重的时期,人们会愿意接受更低的有效性、更高的风险及价格。
较之有效性,人们更敏感于风险性;较之于中低价格,人们也更敏感于高价格。而这种敏感性的差异也随着有效性的降低或风险性的增加,而变得越来越大。
另外,由于没有考虑信息的不对称性,本文的预测只能是理论上的需求量。当然,进一步考察信息不对称的影响也是进一步深入研究的方向。
| [1] | 朱大伟, 郭娜, 王建, 等. 离散选择实验在疫苗接种偏好及需求研究中的应用[J]. 中国卫生经济, 2016(2): 5–7. |
| [2] | 姜晓飞, 曹玲生. 国内外国家免疫规划疫苗需求量预测方法综述[J]. 中国疫苗和免疫, 2013(3): 279–284. |
| [3] | WHITTINGTON D, SURARATDECHA C, POULOS C, et al. Household demand for preventive HIV/AIDS vaccines in Thailand:do husbands' and wives' preferences differ?[J]. Value in Health, 2008,11(11): 965–974. |
| [4] | AMARASINGHE A, WICHMANN O, MARGOLIS H S, et al. Potential dengue vaccine demand in disease endemic and non-endemic countries[J]. Procedia in Vaccinology, 2010,2(1): 113–117. DOI: 10.1016/j.provac.2010.03.021 |
| [5] | 阮玉华, 郭欣, 傅继华, 等. 利用需求弹性理论探讨肾综合征出血热灭活疫苗接种价格[J]. 中国计划免疫, 2001(2): 109–111. |
| [6] | 曹雷, 王华庆, 郑景山, 等. 中国扩大国家免疫规划疫苗接种率调查分析[J]. 中国疫苗和免疫, 2012(5): 419–478. |
| [7] | 朱大伟, 郭娜, KNUTR W, 等. 基于随机效用理论的农村地区成人乙肝疫苗需求研究[J]. 中国卫生经济, 2013(3): 61–63. |
| [8] | NUNES J K, CARDENAS V, LOUCQ C, et al. Modeling the public health impact of malaria vaccines for developers and policymakers[J]. Bmc Infectious Diseases, 2013,13(1): 1–15. DOI: 10.1186/1471-2334-13-1 |
| [9] | 熊文, 宋劲松, 周清杰. 大规模传染病应急管理模型构建[J/OL]. (2016-07-19)[2016-08-09] http://www.cnki.net/kcms/detail/21.1234.R.20160719.0920.010.html. |
| [10] | 王海涛, 任震. 灰色系统理论在电力需求滚动预测中的应用[J]. 华南理工大学学报(自然科学版), 2001(9): 37–39. |
| [11] | 胡郁葱, 陈海伟, 欧阳剑, 等. 新城土地利用空间分布模拟与交通需求预测[J]. 华南理工大学学报(自然科学版), 2014(12): 27–34. DOI: 10.3969/j.issn.1000-565X.2014.12.005 |
| [12] | 黄阜民, 谢乐军, 刘研平, 等. 月电量需求预测的组合时序模型算法[J]. 华南理工大学学报(自然科学版), 1997(8): 72–76. |
| [13] | 黄爱华, 蒲洪彬, 李伟光, 等. 基于人工免疫机理和LS-SVM的顾客需求重要度预测[J]. 华南理工大学学报(自然科学版), 2013(1): 89–94. |
| [14] | 姬长虹, 丁锡海. 基于改进Bass模型的短生命周期产品的需求预测[J]. 科学技术与工程, 2010(10): 2577–2580. DOI: 10.3969/j.issn.1671-1815.2010.10.072 |
 2017, Vol. 19
2017, Vol. 19
