面对激烈的市场竞争环境,产品的升级换代成为企业延续和扩大市场份额的营销理念和手段。以苹果公司为例,自2007年以来,公司每年都会推出一款新的iPhone手机。而其竞争对手三星公司,手机产品的更新换代更加频繁。迭代产品不同于新产品,其带来的运营管理难题远远不是一句“顾客重复性购买”可以描述的。对于制造商而言,一方面升级换代后的“新”产品,其产品的生产和库存管理完全独立于原“旧”产品,需要重新定义。而另一方面,“新”产品与“旧”产品共同分享一个相同的细分市场,其产品销售无法独立,甚至是受制于原“旧”产品的销售。对于市场中潜在消费者而言,升级换代后的“新”产品继承了原“旧”产品的口碑,消费者的认可程度等同或高于原“旧”产品,两个产品互补合作共同使用各种资源。同时,“新”产品上市后许多潜在消费者放弃“旧”产品而转向购买“新”产品,两个产品相互竞争,争夺各种资源。从运营管理视角上看,迭代产品之间存在较强的相关关系:“新”产品延续了“旧”产品的销售轨迹,并挤压了“旧”产品的销售空间;“新”“旧”产品的需求时间变化高度非线性。特别是当企业之间的竞争加速了产品升级换代,迭代产品的需求变化更加复杂,随之的产品运营管理变得更加具有挑战性。
反观当前运营管理领域中对此问题的研究进展,由于迭代产品需求变化的复杂非线性天性,数学建模分析方法难以对其实现有效的刻画和描述,进而难以展开深入而系统的分析。本文正是鉴于当前网络(社交)营销风潮下产品升级换代的普遍性和频繁性启动的研究趋势,在更适合此类问题研究的多智能体建模研究方法论支撑下,分析网络营销情景下迭代产品的需求变化、风险控制和库存管理。通过本项研究,我们期望回答以下问题:“新”产品的上市,对原“旧”产品的市场需求影响有多大?口碑营销对产品需求有什么影响?网络口碑营销策略下,企业如何控制成本,实现利润最大化?由于本项研究瞄准当前社会迫切需要解决的普适性问题,并引入更适合问题求解的研究方法,研究工作的理论价值和现实意义非常明显。
二、国内外研究现状虽然现实世界中产品的升级换代变得越来越频繁,但是运营管理领域对迭代产品需求函数的分析还主要停留在20世纪80年代的工作基础上,即对经典的Norton-Bass模型进行扩展。[1]代表性工作包括:胡知能等人在Norton-Bass模型上考虑免费赠送产品这种企业营销手段对迭代产品需求的影响[2];Li等人应用排队论思想,将潜在顾客细分为新顾客、竞争对手的顾客以及老顾客等三个源头,并以迭代产品之间的差异作为顾客购买决策时的重要依据[3];Ke等人Norton-Bass模型基础上考虑了市场中“高端”用户,即企业首先推出“高端”产品满足“高端”用户需求,然后再推出平民化产品满足大众需求[4]。另外,Liao和Seifert考虑了顾客的重复购买以及顾客的流失[5];Stremersch等人考虑了老顾客的重复购买,并验证了迭代产品需求曲线的重复性[6]。除此之外,一些专家将迭代产品简化为两个相互影响的“独立”产品。例如,Li和Graves将迭代产品看作是两个可替换产品,顾客的选择则引用了离散选择函数。[7]
这些模型能够较好的拟合20世纪七八十年代“高技术”产品的需求变化,但是由于无法预见到Web 2.0时代口碑营销的特点,已经完全不能解释当前新兴经济体下产品需求曲线。具体来说,忽略了竞争的市场环境下,可替代产品的存在导致潜在顾客的流失;忽略了口碑营销中顾客对于口碑传播的热情逐步衰减,而最终不再参与口碑营销;忽略了顾客之间关系数量和强度的差异性。而这些特点是被实证研究所证实普遍存在的特点。例如,Centola以1 500多人为实验对象,证明了顾客之间的关系网络对口碑传播产生决定性影响[8],Domenico等人以Twitter平台上45万用户组成的社交网络为例,证实网络用户传播信息后会短时间“失去”传播的兴趣[9]。
因此,本文以信息传播领域中广泛认可的SIR模型为基准模型[10, 11],额外考虑了因市场竞争导致市场萎缩,迭代产品上市导致参与口碑营销的顾客数量减少等因素,使得模型能够更加真实地再现口碑营销的过程和结果。同时,采用智能体建模分析方法,以经典的“小世界网络(small-world network)”为实例,分析当市场中顾客关系网络表现为“小世界”特性,即小世界网络[12],网络特征对口碑营销的影响。进而,为了刻画口碑营销对企业运营决策的影响,本文以经典的单周期库存问题——报童问题为背景,分析口碑营销不确定性和随机性作用下的最优订货量决策。相比于前人的工作,本文采用智能体建模分析方法,可以更加细致地描述消费者的决策过程和决策模型,因而能够更加真实再现口碑营销的过程和结果;以迭代产品的库存管理为研究问题,研究问题和研究结果更加具有实践性。
三、迭代产品的报童问题口碑营销下迭代产品的报童问题求解涉及以下三个方面:口碑传播的建模、顾客社交网络的建模、报童问题的建模。下面将分别从以下方面进行描述:
(一) 研究问题本文研究迭代产品的销售和库存管理问题如下所述:一企业在社交网络平台通过口碑营销方式直销某产品,如针对女性市场的化妆品、游戏玩家的游戏手柄等。在产品上市的初期(第一阶段),该产品具有独占性,即市场中消费者受到口碑营销的影响而购买产品。随着时间的推移,产品的良好销售记录引发了类似可替代产品的出现,从而导致潜在顾客的分流(第二阶段)。此时,为了应对其他企业的跟随行为,企业主动推出升级产品吸引顾客(对于该产品而言,升级产品也是一种替代产品)。由于产品的销售周期非常短,企业必须在销售尚未开始时决定产品的订购量,并不再补货。在整个销售过程,企业只能通过库存满足市场需求。因此,在已知单位产品的成本和利润的前提下,企业应该如何制定最优的库存水平。
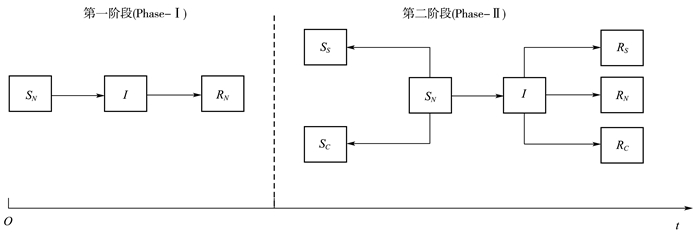
(二) 迭代产品的口碑传播以口碑营销中经典的SIR模型为基本模型,根据研究问题的描述将其扩展成为两阶段口碑营销模型。具体来说,定义市场中消费者的状态集合包括:SN——尚未购买产品的潜在顾客,I——已经购买产品且主动传播产品口碑的顾客,RN——已经购买产品但逐步失去口碑传播兴趣的顾客,RC——已经购买产品但因竞争产品出现导致失去口碑传播兴趣的顾客,RS——已经购买产品但因为迭代产品出现导致失去口碑传播兴趣的顾客,SC——尚未购买产品但因竞争产品出现而流失的顾客,SS——尚未购买产品但因迭代产品的出现而流失的顾客。
两阶段模型下消费者的状态转移如图 1所示:
|
图 1 迭代产品口碑传播的两阶段状态转移示意 |
如图 1所示,状态集合之间的转移可以详细描述为:
| $ {\rm{Phase}} - Ⅰ:\left\{ \begin{array}{l} {S_N}\left( i \right) + I\left( j \right)\mathop \to \limits^\lambda I\left( i \right) + I\left( j \right)\\ I\left( i \right) + I\left( j \right)\mathop \to \limits^{{\beta _N}} I\left( i \right) + {R_N}\left( j \right)\\ {R_N}\left( i \right) + I\left( j \right)\mathop \to \limits^{{\beta _N}} {R_N}\left( i \right) + {R_N}\left( j \right) \end{array} ;\\ \right.{\rm{Phase}} - Ⅱ:\left\{ \begin{array}{l} {S_N}\left( i \right)\mathop \to \limits^{{\alpha _C}} {S_C}\left( i \right),{S_N}\left( i \right)\mathop \to \limits^{{\alpha _S}} {S_S}\left( i \right)\\ {S_C}\left( i \right) + I\left( j \right)\mathop \to \limits^{{\beta _N}} {S_C}\left( i \right) + {R_N}\left( j \right)\\ {S_S}\left( i \right) + I\left( j \right)\mathop \to \limits^{{\beta _N}} {S_S}\left( i \right) + {R_N}\left( j \right)\\ {S_N}\left( i \right) + I\left( j \right)\mathop \to \limits^\lambda I\left( i \right) + I\left( j \right)\\ I\left( i \right) + I\left( j \right)\mathop \to \limits^{{\beta _N}} I\left( i \right) + {R_N}\left( j \right)\\ {R_N}\left( i \right) + I\left( j \right)\mathop \to \limits^{{\beta _N}} {R_N}\left( i \right) + {R_N}\left( j \right)\\ {R_C}\left( i \right) + I\left( j \right)\mathop \to \limits^{{\beta _N}} {R_C}\left( i \right) + {R_N}\left( j \right)\\ {R_S}\left( i \right) + I\left( j \right)\mathop \to \limits^{{\beta _N}} {R_S}\left( i \right) + {R_N}\left( j \right)\\ I\left( i \right)\mathop \to \limits^{{\beta _C}} {R_C}\left( i \right),I\left( i \right)\mathop \to \limits^{{\beta _S}} {R_S}\left( i \right) \end{array} \right. $ | (1) |
式(1)中,
当口碑营销状态转移是在一个节点规模巨大且同质的网络环境下展开,上述两阶段的口碑营销过程也可以用平均场理论(mean-field theory)表述为:
| $ {\rm{Phase}}-Ⅰ:\left\{ \begin{array}{l} {S_N}{|_0} = \frac{{\left( {N-1} \right)}}{N}, I{|_0} = \frac{1}{N}, {R_N}{|_0} = 0\\ \frac{{{\rm{d}}{S_N}}}{{{\rm{d}}t}} =-\lambda \cdot {S_N} \cdot I\\ \frac{{{\rm{d}}I}}{{{\rm{d}}t}} = \lambda \cdot {S_N} \cdot I - {\beta _N} \cdot I \cdot \left( {I + {R_N}} \right) = \lambda \cdot {S_N} \cdot I - {\beta _N} \cdot I \cdot \left( {1 - {S_N}} \right)\\ \frac{{{\rm{d}}{R_N}}}{{{\rm{d}}t}} = {\beta _N} \cdot I \cdot \left( {I + {R_N}} \right) = {\beta _N} \cdot I \cdot \left( {1 - {S_N}} \right)\\ {S_N} + I + {R_N} = 1 \end{array} \right. $ | (2) |
式(2)中,N为市场中所有消费者的总数。
| $ {\rm{Phase}}-Ⅱ:\left\{ \begin{array}{l} \frac{{{\rm{d}}{S_C}}}{{{\rm{d}}t}} = {\alpha _C} \cdot {S_N},\frac{{{\rm{d}}{S_S}}}{{{\rm{d}}t}} = {\alpha _S} \cdot {S_N}\\ \frac{{{\rm{d}}{S_N}}}{{{\rm{d}}t}} =-\lambda \cdot {S_N} \cdot I-{\alpha _S} \cdot {S_N} - {\alpha _C} \cdot {S_N}\\ \frac{{{\rm{d}}I}}{{{\rm{d}}t}} = \lambda \cdot {S_N} \cdot I - {\beta _N} \cdot I \cdot \left( {1 - {S_N}} \right) - {\beta _S} \cdot I - {\beta _C} \cdot I\\ \frac{{{\rm{d}}{R_N}}}{{{\rm{d}}t}} = {\beta _N} \cdot I\cdot(1-S_N)\\\frac{{{\rm{d}}{R_C}}}{{{\rm{d}}t}} = {\beta _C} \cdot I,\frac{{{\rm{d}}{R_S}}}{{{\rm{d}}t}} = {\beta _S} \cdot I\\ {S_C} + {S_S} + {S_N} + I + {R_N} + {R_C} + {R_S} = 1\\ I\left( \infty \right) = 0, {S_N}\left( \infty \right) = 0\\ {S_S}\left( \infty \right) + {S_C}\left( \infty \right) + {R_N}\left( \infty \right) + {R_S}\left( \infty \right) + {R_C}\left( \infty \right) = 1 \end{array} \right. $ | (3) |
如果口碑营销过程保持式(2)所述的形式,可以计算得到稳定状态时各状态节点比例如下:
| $ \begin{array}{l} \frac{{{\rm{d}}{S_N}}}{{{\rm{d}}I}} = \frac{{-\lambda \cdot {S_N} \cdot I}}{{\lambda \cdot {S_N} \cdot I-{\beta _N} \cdot I \cdot \left( {1-{S_N}} \right)}} = \frac{{ - \lambda \cdot {S_N}}}{{\lambda \cdot {S_N} - {\beta _N} \cdot \left( {1 - {S_N}} \right)}}\\ \Rightarrow {\rm{d}}I = - \left( {1 + \frac{{{\beta _N}}}{\lambda }} \right) \cdot {\rm{d}}{S_N} + \frac{{{\beta _N}}}{\lambda } \cdot \frac{{{\rm{d}}{S_N}}}{{{S_N}}} \Rightarrow I|_0^\infty =\\ - \left( {1 + \frac{{{\beta _N}}}{\lambda }} \right) \cdot {S_N}|_0^\infty + \frac{{{\beta _N}}}{\lambda } \cdot ln\left( {{S_N}} \right)|_0^\infty \end{array} $ | (4) |
因
所以
但是,当口碑营销进入第二阶段,即式(3)所示的状态转移,系统的状态转移过于复杂而无法得到最终的稳定解。并且,由于各状态变量第一阶段结束时并未达到稳定状态,而第二阶段各状态变量的终态SS(∞), SC(∞), RN(∞), RS(∞), RC(∞)受到第一阶段结束时各状态,即第二阶段起始时各状态数值的影响,根据式(2)无法推导出最终数值。更重要的是,由于社交网络中各个节点的连接情况(节点的平均度指标)也并非同质,式(1)描述的状态转移过程无法采用数学分析方法得到最终结果。这就造成了当前口碑营销过程的数学分析瓶颈。
为了解决这一问题,本文作者引入智能体建模方法,将式(2)和式(3)重新描述为式(5)和式(6)所示的离散状态转移下的差分方程组。
| $ {\rm{Phase}}- Ⅰ:\left\{ \begin{array}{l} {S_N}\left( 0 \right) = \frac{{\left( {N- 1} \right)}}{N}, I\left( 0 \right) = \frac{1}{N}, {R_N}\left( 0 \right) = 0\\ {S_N}\left( {t + 1} \right)- {S_N}\left( t \right) = - \lambda \cdot {S_N}\left( t \right) \cdot I\left( t \right)\\ I\left( {t + 1} \right) - I\left( t \right) = \lambda \cdot {S_N}\left( t \right) \cdot I\left( t \right) - {\beta _N} \cdot I\left( t \right) \cdot \left[{N-{S_N}\left( t \right)} \right]\\ {R_N}\left( {t + 1} \right) - {R_N}\left( t \right) = {\beta _N} \cdot I\left( t \right) \cdot \left[{N-{S_N}\left( t \right)} \right]\\ {S_N}\left( t \right) + I\left( t \right) + {R_N}\left( t \right) = N \end{array} \right. $ | (5) |
| $ {\rm{Phase}}- Ⅱ:\left\{ \begin{array}{l} {S_C}\left( {t + 1} \right)- {S_C}\left( t \right) = {\alpha _C} \cdot {S_N}\left( t \right)\\ {S_S}\left( {t + 1} \right)- {S_S}\left( t \right) = {\alpha _S} \cdot {S_N}\left( t \right)\\ {S_N}\left( {t + 1} \right) - {S_N}\left( t \right) = - \lambda \cdot {S_N}\left( t \right) \cdot I\left( t \right) - \left( {{\alpha _S} + {\alpha _C}} \right) \cdot {S_N}\left( t \right)\\ I\left( {t + 1} \right) - I\left( t \right) = \lambda \cdot {S_N}\left( t \right) \cdot I\left( t \right) - {\beta _N} \cdot I\left( t \right) \\\cdot \left[{N-{S_N}\left( t \right)} \right] - \left[{{\beta _S} + {\beta _C}} \right] \cdot I\left( t \right)\\ {R_N}\left( {t + 1} \right) - {R_N}\left( t \right) = {\beta _N} \cdot I\left( t \right) \cdot \left[{N-{S_N}\left( t \right)} \right]\\ {R_C}\left( {t + 1} \right) -{R_C}\left( t \right) = {\beta _C} \cdot I\left( t \right)\\ {R_S}\left( {t + 1} \right) -{R_S}\left( t \right) = {\beta _S} \cdot I\left( t \right)\\ {S_C}\left( t \right) + {S_S}\left( t \right) + {S_N}\left( t \right) + I\left( t \right) + {R_N}\left( t \right) + {R_S}\left( t \right) + {R_C}\left( t \right) = N\\ {S_N}\left( \infty \right) = I\left( \infty \right) = 0 \end{array} \right. $ | (6) |
进而,根据式(5)和式(6)所描述的状态转移模型下,定义智能体建模方法下口碑营销过程如下:
a) 初始化。
a.1) 设定市场上所有顾客的状态都为SN,即产品的潜在顾客。
a.2) 企业根据一定策略从所有潜在顾客中选择一位顾客,设定该顾客为口碑传播/营销的源头,即将其状态修订为I。
b) 第一阶段:从I节点集合中随机选择一个I节点ni,并从节点ni的相连节点中随机选择一个节点nj。
b.1) 如果节点nj状态为SN,那么节点nj状态转移为I的可能性/概率为λ。此时,生成一个随机数x,如果λ≥x,表明节点nj状态变化为I,否则节点nj状态保持为SN不变。
b.2) 如果节点nj状态不是SN,即状态为I或者RN,那么节点ni状态转移为RN的可能性/概率为βN。此时,生成一个随机数x,如果βN≥x,表明节点ni状态变化为RN,否则节点ni状态保持为I不变。
c) 重复步骤b),直到企业引入升级产品,状态空间发生变化。
d) 企业根据市场需求变化,引入升级产品。同时,市场中出现竞争企业的可替代产品。
e) 第二阶段:从节点集合中随机选择一个节点ni。
e.1) 如果节点ni状态为SN,那么节点ni状态转移为SS或SC的可能性/概率分别为αS和αC。此时,生成一个随机数x,如果αS≥x,表明节点ni状态变化为SS;如果αS+αC≥x>αS,表明节点ni状态变化为SC;否则节点ni状态保持为SN不变。
e.2) 如果节点ni状态为RN,那么节点ni状态转移为RS或RC的可能性/概率分别为βS和βC。此时,生成一个随机数x,如果βS≥x,表明节点ni状态变化为RS;如果βS+βC≥x>βS,表明节点ni状态变化为RC;否则节点ni状态保持为RN不变。
e.3) 如果节点ni状态为I,从节点ni的相连节点中随机选择一个节点nj。如果节点nj状态为SN,那么节点nj状态转移为I的可能性/概率为λ。此时,生成一个随机数x,如果λ≥x,表明节点nj状态变化为I,否则节点nj状态保持为SN不变。如果节点nj状态不是为SN,即状态SC, SS, I, RN, RS, RC,那么节点ni状态转移为RN的可能性/概率为βN。此时,生成一个随机数x,如果βN≥x,表明节点ni状态变化为RN,否则节点ni状态保持为I不变。
f) 重复步骤e),直到网络中不存在I节点,即所有节点状态皆为SC, SS, RN, RS, RC。
通过上述口碑营销过程,最终状态为RN的节点数量即是原产品的市场需求量。
(三) 顾客社交网络的建模前人的研究工作表明,现实世界中消费者之间的社交网络通常满足复杂网络分析中的“小世界”特性。[12]相比于同质性较强的随机网络而言,小世界网络的平均距离(average path length)较短,且平均聚类系数(average clustering coefficient)较大。网络节点的平均距离较短,表明口碑营销更容易影响到所有人——“无死角”。而节点的平均聚类系数较大,则表明顾客之间存在着小团体,营销速度较快,并且,节点的度分布并非均匀分布,而是正态分布。也就是说,网络中有少数节点具有较高的度,即有些节点为“明星”节点。相比于其他节点而言,这些“明星”节点能够影响更多的“粉丝”节点。
本文以Watts和Strogatz提出的小世界网络WS构造模型为研究问题中的顾客社交网络构造算法,通过设定WS模型的参数来生成具有小世界网络特性的社交网络。
(四) 报童问题的建模以一个单周期报童问题为基本模型,即企业在整个产品销售期间无法补货,仅通过产品库存来满足市场需求。模型中,每销售出一件产品,企业将获得单位利润p;而当产品滞销时,企业将损失单位成本c。不同于基本模型,本文假定产品的市场需求并非外生变量,而是在企业口碑营销策略下的销售量。而企业的决策包括以下三点:一是口碑营销初始节点的选择;二是产品的最优订货量决策;三是升级产品上市时间的选择。
其中,口碑营销初始节点的选择,我们采用两个应用较为广泛的评价指标:一是Rfinal——口碑营销结束后,网络中RN节点的数量占比,即口碑营销的网络覆盖率。从口碑营销的角度来说,该指标值越大越好。二是Tfinal——口碑营销结束的时刻,即口碑营销的时长。该指标反映了口碑营销的速度,因此取值越小越好。
本文假定当产品销售达到峰值时,出现竞争企业的可替代产品。此时,企业立即推出升级产品避免市场份额的减少。
而企业的报童问题最有订货量满足下面目标函数:
| $ \max \pi = \int_0^Q {\left[{p \cdot x-c \cdot \left( {Q-x} \right)} \right] \cdot f\left( x \right){\rm{d}}x} + \int_Q^{ + \infty } {p \cdot Q \cdot f\left( x \right){\rm{d}}x} $ | (7) |
在前期工作基础上,本文在Netlogo平台上实现口碑营销的多智能体仿真模型[13, 14]。模型中,主要的参数设置如表 1所示:
| 表 1 仿真模型中的参数设置 |
采用小世界网络的生成算法——WS算法,设置如表 1中所示的算法参数,计算得到一个网络实例。[12]该网络的网络属性指标如表 2所示:
| 表 2 小世界网络基本参数表 |
算法生成的小世界网络与节点和平均度相同的E-R随机网络相比:小世界网络的平均聚类系数远远大于E-R随机网络,而平均路径长度则差别不大。
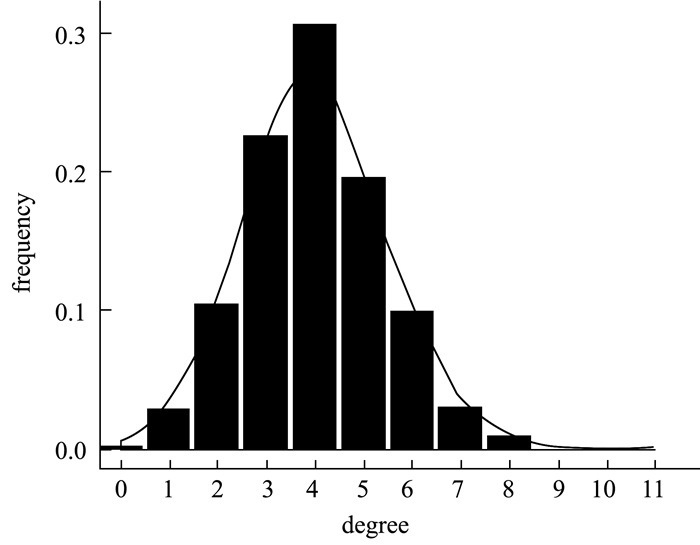
从图 2所示的节点度分布也可以直观看出,所生成的小世界网络的节点度服从近似的泊松分布(Poisson distribution),大部分节点的度指标接近与平均点度。结合平均聚类系数、平均路径长度以及度分布三个指标,可以确定生成的小世界网络符合小世界网络的定义,即为一个小世界网络。
|
图 2 网络节点度的分布图 |
以生成的小世界网络为信息传播的平台,设定第二阶段顾客流失的概率为0(αC=αS=βC=βS=0),并定义信息传播概率λ和停止传播概率βN分别为1(λ=βN=1.0),口碑传播模型退化为一个标准的SIR模型。并且,假定口碑传播的初始节点为随机选择的源头节点,重复口碑传播实验。
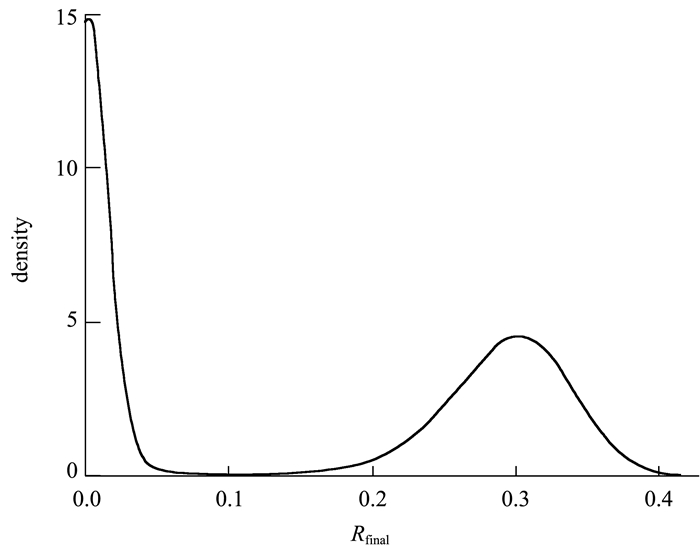
口碑传播重复100 000次后,统计仿真结束后状态为RN的节点占总节点数的比例,即RN|∞,Rfinal。统计结果如图 3所示。
|
图 3 口碑转播RN的稳态值Rfinal仿真统计结果 |
口碑传播结果呈现明显的双峰特性,一个峰值出现在近似为0.0的附近,而一个峰值出现在0.3的附近。此结果表明,即使在完全相同的社会关系网络下,口碑传播的结果也会出现显著性差异。一种情况是口碑未能在网络中传播开去就消亡了,另一种情况则是传播能够覆盖部分顾客/节点(40.56%左右的网络覆盖率)。
此结果与论文[10]中给出的结果一致,但是与公式(4)计算结果差异较大。
| $ \lambda = 1.0, {\beta _N} = 1.0 \Rightarrow {R_N}{|_\infty } = 1- \exp \left[{-\left( {1 + \frac{\lambda }{{{\beta _N}}}} \right) \cdot {R_N}{|_\infty }} \right]\\ = 1 - \exp \left[{-2 \cdot {R_N}{|_\infty }} \right] \Rightarrow {R_N}{|_\infty } \approx 0.796 $ | (8) |
此结果一方面验证了本文所构建的口碑传播的正确性,而另一方面表明了平均场理论在实际网络传播的结果分析上存在较大地偏差。而这也从侧面进一步验证了仿真方法研究口碑传播的适用性和正确性。
(三) 两阶段口碑传播的源头节点选择鉴于口碑传播的目的是希望口碑信息传播的越快(Tfinal值越小)和越广(Rfinal值越大),本文测试了几种较为通用的源头节点选择策略。
为了测试源头节点选择策略的适用性,作者以表 1中网络构造参数随机生成30个相同规模的小世界网络,并用每种选取策略在30个网络中分别重复1 000次仿真。统计结果如表 3所示。
| 表 3 源头节点选择的结果评价(95%置信区间) |
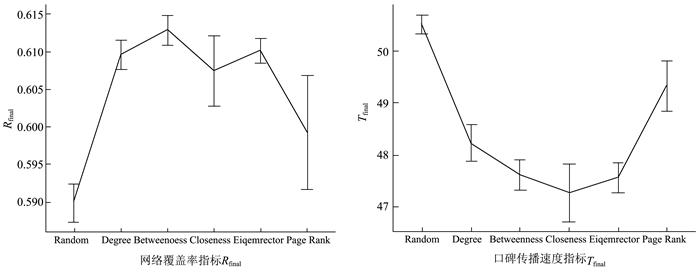
在所测试的六种源头节点选择策略中,随机选择策略的表现最差,即网络覆盖率最小,且传播过程更长。相比之下,复杂网络分析中的四种中心性评价策略表现都比较好,超过了经典PageRank算法得到的源头节点。具体来说,最大中介中心性指标选择的源头节点网络覆盖率指标最佳,而最大接近中心性指标选择的源头节点传播速度最快。
从图 4所示的数据对比中,可以发现:虽然最大接近中心性指标的传播速度更快,但是其传播速度的变化/离散程度更大。而相比之下,最大中介中心性指标的结果更加稳定。
|
图 4 六种源头节点选择策略的效果对比(95%的置信区间) |
综合考虑下,本文在后续分析中,以最大中介中心性指标计算得到的节点最为口碑传播的源头节点。
(四) 报童问题最优订货量求解以最大中介中心性指标选择的节点为源头节点,重复仿真250(=M)次,以平均值作为对最优订货量和收益的估计。为了验证此最优订货量和收益的正确性和可行性,重复40组实验。
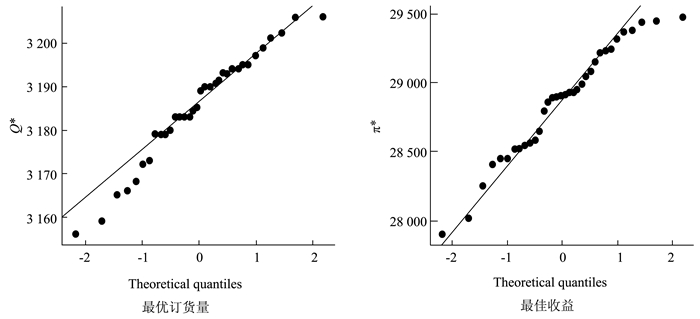
从图 5所示40组数据的百分数—百分数图(quantile-quantile plot)可以看出,40组数据在理论线(图中直线)上下随机散落,这较为直观地体现出40组数据服从正态分布,即表明仿真结果通过了检验。另外,对40组数据进行K-S检验,计算得到P-Value=0.5205,远远大于显著性水平。这进一步表明数据服从正态分布。
|
图 5 40组仿真实验结果的Q-Q图 |
此时,最优订货量和最优收益为:
| $ {Q^*} = 3193, {\pi ^*} = 28\;872.64 $ | (9) |
考虑95%的置信区间,最优订货量和最优收益取值范围为:
| $ {Q^*}~\left[{3185, 3201} \right], {\pi ^*}~\left[{28\;724.45, 29\;020.82} \right] $ | (10) |
值得注意的是,如果企业在订货量决策中未能考虑顾客的流失,即αC=αS=βC=βS=0,企业将面对的是一个标准的SIR传播模型。在此口碑传播市场模型下,仿真计算得到“最优”订货量为4 521(期望收益为43 920.92)。而实际情况是,当企业设定订货量为4 521时,其必定因为多订货而承担13 280的损失,即收益减少46%。
五、灵敏度分析由于口碑传播的网络覆盖率和传播速度受到传播模型中参数的影响,因而企业的最优决策还受到产品单位成本和利润的影响。下面分别就这些参数进行单因素参数分析。
(一) 顾客间传播概率λ在式(1)所示口碑传播模型中,当顾客间传播概率λ越大,潜在顾客在接触中更容易/更快速地被“传染”。因此,可以认为顾客间传播概率λ的增加有利于企业通过订货而获得更多利润。
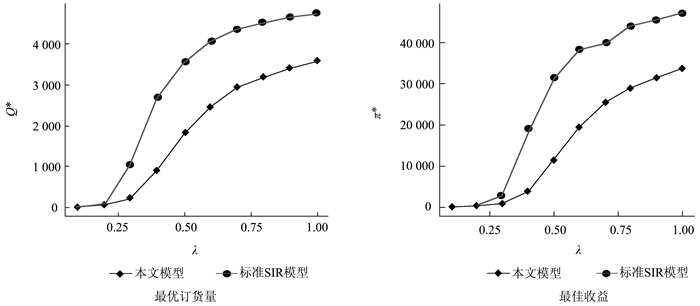
图 6给出了口碑传播中顾客间概率λ变化下的企业最优决策问题。同时,图中对比了标准SIR模型下的企业最优决策问题。
|
图 6 顾客间传播概率λ对企业决策的影响 |
从图 6可以看出,传播概率λ对企业最优订货量和最佳收益的影响呈现出“S”型。在传播概率较小时(λ≤0.20),企业的最优订货量和最佳收益变化不大。而随着传播概率的逐渐增加(0.20 < λ≤0.70),企业的最优订货量和最佳收益增加较为迅速。但是,当传播概率较大时,企业的最优订货量和最佳收益变化又逐步减慢。另外,标准SIR模型与本文提出的两阶段口碑模型对企业影响较为一致。
根据图 6数据显示,可以得出结论:企业应该考虑各种营销措施以提高顾客间的传播概率λ。一方面,口碑传播能够更迅速地转化为产品销售;另一方面,能够迅速占领市场,避免后续的顾客流失。
(二) 顾客停止传播概率βN顾客停止传播概率βN直接影响了主动传播口碑的节点数量,即当停止传播概率βN越小,市场中状态为I的节点数量越多;反之,则状态为I的节点数量越小。但是,当市场中状态为I的节点数量越多时,状态为I的节点与状态为非SN的节点接触的可能性就越大,而发生状态转移的可能性也就越大。因此,状态转移的过程和结果是这两个对立因素共同作用的结果。
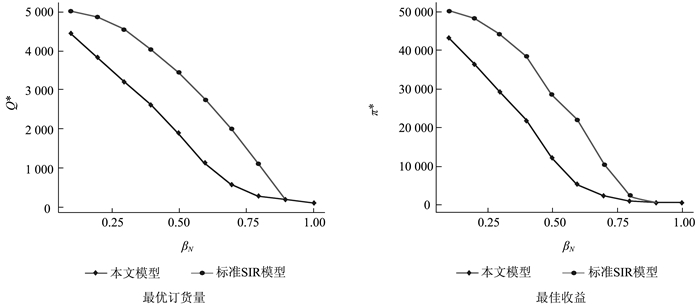
从图 7可以看出,当顾客间停播概率βN较小时,口碑传播地更加充分,因此口碑传播网络覆盖率更大,即市场需求更大;反之,则市场需求更小。而对比两个模型的仿真结果可以看出,当顾客间停播概率βN适中时,两个模型结果差异较大;而顾客间停播概率βN取值两端时,两个模型的结果差异较小。
|
图 7 顾客间停播概率βN对企业决策的影响 |
根据图 7数据显示,当口碑传播兴趣保持较为一般水平时,竞争企业和替代产品对产品的销售产生较大影响,在决策过程中不容忽视。
(三) 潜在顾客流失概率αS, αC替代产品(含升级产品)的上市,导致产品市场的萎缩。因此,产品市场需求“总量”随着潜在顾客流失概率αS, αC的增加而降低。
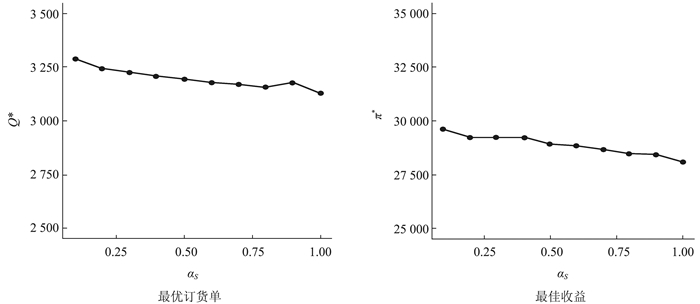
如图 8所示,在设定顾客流失概率αS=αC前提下,企业的最优订货量和收益受到顾客流失影响相对较小。这一方面表明在基准模型中顾客间传播概率λ(=0.80)取值较大时,潜在顾客流失数量较小;另一方面则表明第二阶段剩余的潜在顾客数量较小。
|
图 8 潜在顾客流失概率αS(=αC)对企业决策的影响 |
根据图 8数据显示,潜在顾客流失对企业的最优决策影响较小。企业的一个积极应对措施是提高顾客间传播概率λ,从而减少第二阶段中潜在顾客的总体数量。
(四) 顾客停止传播概率βS, βC顾客停止传播概率βS, βC的增加,将一定程度上减少传播口碑的顾客数量。因此,潜在顾客的流失将增加。
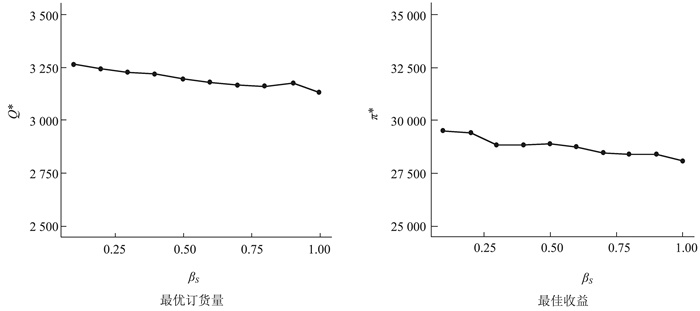
从图 9数据可以看出,顾客停止传播概率βS, βC与潜在顾客流失概率αS, αC对企业的运营影响较为类似。一方面,由于参与口碑传播的顾客减少导致了口碑传播的网络覆盖率降低;另一方面,其对企业的运营影响较小。
|
图 9 顾客停止传播概率β2(βC)对企业决策的影响 |
产品单位利润p和单位成本c两者共同反映了产品的盈利能力。因此,不同的(p/c)取值,对应的产品具有较大区别,而企业的运营也应有明显差异。例如,(p/c)较低的产品利润较薄,如微波炉、电视机等产品;而(p/c)较大的产品则多为技术创新的产品,如苹果公司的iPhone手机。产品的单位利润p和单位成本c对于产品需求不产生影响,但是对企业的收益产生显著影响。下面仿真了不同产品单位利润p和单位成本c对企业运营的影响。
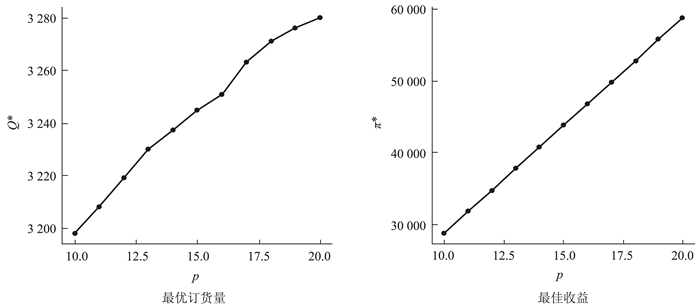
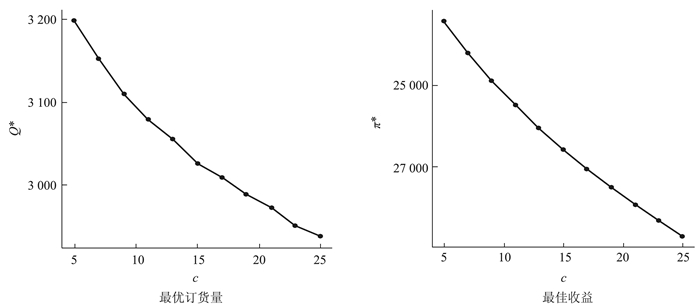
从图 10和图 11可以看出,产品单位利润p和单位成本c对企业决策的影响较为简单和直观。随着产品利润的增加,企业将显著增加产品的订货量,并获得更多收益;而随着产品成本的增加,企业将减少产品订货量。
|
图 10 产品单位利润p对企业决策的影响 |
|
图 11 产品单位成本c对企业决策的影响 |
本文采用多智能体建模方法,仿真分析了包括迭代产品在内的可替代产品进入市场对该产品的市场销售和利润的影响。数据结果表明,迭代产品的上市对原产品的运营和绩效产生非常显著的影响。如果企业忽视了替代产品的竞争,必然遭受重大利益损失。而企业的对策除了传统意义上的提高单位产品利润和降低单位产品成本以外,更多的应是关注如何加速产品的购买行为,以及在可替代产品上市之前完成主要市场销售计划。通过各种营销努力,能够削弱可替代产品上市引发的潜在顾客流失现象和问题。
| [1] | NORTON J A, BASS F M. A Diffusion Theory Model of Adoption and Substitution for Successive Generations of High-Technology Products[J]. Management Science, 1987,33(9): 1069–1086. DOI: 10.1287/mnsc.33.9.1069 |
| [2] | 胡知能, 邓欢, 张弛, 等. 基于Norton-Bass模型的多代创新产品扩散研究[J]. 管理工程学报, 2012(4): 127–136. |
| [3] | LI H, ARMBRUSTER D, KEMPF K G. A Population-Growth Model for Multiple Generations of Technology Products[J]. Manufacturing & Service Operations Management, 2013,15(3): 343–360. |
| [4] | KE T T, SHEN Z J M, LI S. How Inventory Cost Influences Introduction Timing of Product-Line Extensions[J]. Production and Operations Management, 2013,22(5): 1214–1231. |
| [5] | LIAO S, SEIFERT R W. On The Optimal Frequency of Multiple Generation Product Introductions[J]. European Journal of Operational Research, 2015,245(3): 805–814. DOI: 10.1016/j.ejor.2015.03.041 |
| [6] | STREMERSCH S, MULLER E, PERES R. Does New Product Growth Accelerate Across Technology Generations?[J]. Marketing Letters, 2010,21(2): 103–120. DOI: 10.1007/s11002-009-9095-0 |
| [7] | LI H, GRAVES S C. Pricing Decisions During Inter-Generational Product Transition[J]. Production and Operations Management, 2012,21(1): 14–28. DOI: 10.1111/poms.2011.21.issue-1 |
| [8] | CENTRAL D. The Spread of Behavior in an Online Social Network Experiment[J]. Science, 2010,329(5996): 1194. DOI: 10.1126/science.1185231 |
| [9] | DOMENICO M D, LIMA A, MOUGEL P, et al. The Anatomy of a Scientific Rumor[J]. Scientific Reports, 2013,3(10): 2980. |
| [10] | ZANETTE D H. Dynamics of Rumor Propagation on Small-World Networks[J]. Physical Review E, 2002,65(4): 041908. DOI: 10.1103/PhysRevE.65.041908 |
| [11] | MORENO Y, NEKOVEE M, PACHECO A F. Dynamics of Rumor Spreading in Complex Networks[J]. Physical Review E, 2004,69(6): 066130. DOI: 10.1103/PhysRevE.69.066130 |
| [12] | WATTS D J, STROGATZ S H. Collective Dynamics of "Small-World" Networks[J]. Nature, 1998,393: 440–442. DOI: 10.1038/30918 |
| [13] | 李锋, 庄东. 社会网络的多层次特性对口碑营销影响的综合评价[J]. 华南理工大学学报(社会科学版), 2016(5): 1–8. |
| [14] | 李锋, 魏莹. 企业横向竞争对供应链整体绩效影响[J]. 华南理工大学学报(社会科学版), 2015(1): 15–21. |
 2017, Vol. 19
2017, Vol. 19
