2. 华南理工大学 金融工程研究中心, 广东 广州 510006
2. Research Center of Financial Engineering, South China University of Technology, Guangzhou 510006, Guangdong, China
风险价值度(value at risk, VaR)是指在一定的置信水平与持有期内,某一金融资产或资产组合在未来资产价格波动下所面临的最大损失额。VaR以单个数字的形式把已知金融资产组合的可能损失与发生概率结合起来衡量资产组合面临的整体风险,有利于金融机构及监管当局进行风险控制。目前VaR已成为国际上风险管理中广泛应用的重要工具之一。
近年来随着市场环境的剧烈变化以及风险种类的多样化,流动性风险显示出越来越大的破坏力。从LTCM的失败到2008年危害全球经济的金融危机,流动性风险加剧了市场损失。因此,市场开始重视流动性风险的管理和控制。仅仅考虑市场风险的VaR没有把流动性风险涵盖在内,会导致其大多数时候低估整体风险。国外学者在研究中尝试把流动性风险纳入成熟的VaR度量模型之中,提出VaR度量的改进模型。如Bangia等人(2001)[1]3-13从外生流动性风险方面入手,用价差来衡量外生流动性,提出将流动性风险纳入VaR计算的BDSS模型。Angelidis和Benos(2006)[2]通过考察雅典订单驱动市场的买卖价差行为,建立了包含价差变量的流动性调整VaR模型(Liquidity adjusted VaR, 简称La_VaR)。在中国学者的研究中,杜海涛(2002)[3]直接采用价格与成交量结合的非流动性指标,即L=(Ph-Pl)/(Pl×V)来度量流动性给交易带来的成本,从而度量流动性风险。宋逢明和谭慧(2004)[4]则考虑通过持有期来反映流动性风险,把投资者的偏好通过效用函数引入La_VaR的计算当中,综合反映内生流动性风险与外生流动性风险。武磊(2009)[5]则使用流动性调整的收益率LaR=R-C去衡量La_VaR,其中C=R/V,R为收益率,V为成交量。林辉(2010)[6]在Bangia等人(1999)[1]的基础上,通过建立GARCH模型,估计中间价格和价差回报序列的期望与标准差,构建条件异方差的时变价差La_VaR模型。而刘向丽和常云博(2015)[7]在武磊(2009)[5]的基础上提出一种度量流动性成本的方法,即C=(Ph-Pl)/(Pm×V),C为每交易一单位资产造成的价格波动,V为成交量,令L=R-XC/2为流动性调整的收益率,X为交易头寸,然后用GARCH模型来拟合L序列的均值和标准差从而计算La_VaR,并运用沪深300股指期货主力合约的5分钟高频数据去做实证研究,较为合理准确地衡量包括流动性风险的整体风险。
综合现有考虑流动性风险的VaR研究,本文认为刘向丽和常云博(2015)[7]提出的流动性调整收益率的方法综合考虑了流动性风险的外生性和内生性并结合价格和成交量两个指标,是比较准确的衡量方法,但关于收益率的流动性调整,还要考虑更多的市场流动性特征。尤其是日内交易,金融市场的不对称流动性以及其不对称的程度大小,将产生不对称的流动性风险,对VaR的计算产生影响。
金融市场的流动性具有不对称性,不对称性是指卖方与买方之间的不对称性。Huang和Wang(2010)[8]认为市场参与费用导致的交易间不协调促使流动性供求的不对称性的产生。交易者在市场中要不断调整持有的头寸以达到最优,但是买卖双方对于交易的渴望度是不对称的,从而导致内部订单不平衡,当这种不平衡以及对流动性的需求过于偏向某一方时,就会产生流动性极端不对称情况,如Xiang和Zhu(2014)[9]提及的卖方(买方)循环。相比于市场流动性不对称程度较轻的情况,在卖方循环和买方循环中,买卖双方对于流动性的需求更大,更倾向于交易。由此可以看出流动性不对称程度的大小的确会影响买卖双方的流动性风险。关于买卖双方间的不对称流动性,Avramov(2006)[10]等人运用卖方成交量比例(交易流)去刻画买卖双方间的不对称流动性,而Xiang和Zhu(2014)[9]则引入卖方深度比例(报价流)去描述不对称流动性。流动性不对称性的存在,导致卖方与买方之间的流动性风险是不同的,因此在考虑VaR模型中流动性风险的衡量时应该把这种不对称性考虑进去。
近年来,随着计算机网络技术的飞速发展,市场上的交易速度和交易频率得到很大的提高,几乎每时每刻都可以进行交易,对风险管理的频率也逐步提高,传统以日为频率来计算风险的方法无法再适应市场的需求和发展。例如,邵锡栋等人(2009)[11]认为使用日数据会损失部分日内信息,因而本文采用高频数据进行研究。
基于以上的考虑,本文通过研究买卖双方间的流动性不对称性,及其不对称的程度大小,对已有的流动性调整收益率方法进行扩展,提出日内不对称流动性调整VaR计算方法,并以中国股指期货市场为研究对象,采用沪深300股指期货5分钟高频数据,计算不同头寸下的不对称流动性调整VaR。
本文结构安排如下:第二部分对不对称流动性进行说明,分析市场的不对称流动性及其程度大小所产生的影响,并基于这种影响提出不对称流动性调整收益率模型以及不对称流动性调整VaR计算方法,第三部分为不对称流动性调整VaR的计算,第四部分进行不同VaR模型的比较与回测检验,第五部分对全文进行总结。
二、不对称流动性调整VaR计算方法 (一) 不对称流动性指标本文通过计算Xiang和Zhu(2014)[9]提出的卖方深度比例,买方深度比例,卖方渴望度以及买方渴望度4个指标来反映买卖双方间不对称流动性。其计算公式如下:
| $ \begin{array}{l} 卖方深度比例{\rm{ = }}\frac{卖1量}{卖1量+买1量} \\ 买方深度比例{\rm{ = }}1-卖方深度比例 \\ 卖方渴望度{\rm{ = }}\frac{卖1价-卖价}{卖1价-买1价}\\ 买方渴望度{\rm{ = }}\frac{买价-买1价}{卖1价-买1价} \end{array} $ |
其中,买价(卖价)指买方(卖方)发起交易中的成交价,买方(卖方)渴望度反映买方(卖方)渴望交易的程度。
同时为反映流动性不对称程度的大小对于流动性风险的影响,本文采用Xiang和Zhu(2014)[9]提出的卖方(买方)循环概念,即连续3个或3个以上卖方(买方)发起交易,并分别计算以上提出的4个指标;以下根据买卖双方力量不对称程度的加深,依次展示4个指标计算后的结果,如表 1所示。
| 表 1 卖方(买方)循环统计 |
由表 1可知,随着买卖双方力量不对称极端程度的加深,不对称程度极端情况下,卖方(买方)发起交易具有更大的交易渴望度,更大的买(卖)方深度比例。出现更大的交易渴望度说明在倾向于卖方或买方的极端情况下,买卖双方更急于交易,因此渴望度上升。而在卖方循环中,其买方深度比例大于处在同样极端情况下买方循环的卖方深度比例,说明卖方更易成交,买卖双方间存在不对称流动性,流动性不对称性更倾向于买方,买方面临更大的流动性风险。而且随着买卖双方力量不对称极端情况的加深,买卖双方之间的卖方深度比例的差距越来越大,说明买卖双方间的流动性不对称性的程度也在加剧,买卖双方之间的供求愈加不平衡,因此买卖双方间的流动性不对称程度的大小也会影响买卖双方的流动性风险。流动性的不对称性及其程度大小会影响买卖双方在交易时所面临的流动性成本,因此在考虑流动性成本时,应加入考虑不对称流动性及其程度大小的影响。
(二) 不对称流动性调整收益率模型根据前文分析,本文通过考虑买卖双方间的不对称流动性以及流动性不对称程度的大小对于流动性成本的影响,对刘向丽和常云博(2015)[7]提出的流动性调整收益率进行扩展。因为买卖双方间的不对称流动性使买卖双方面临不同的流动性风险,因此买卖双方的流动性成本应分开计算,形成两个流动性调整收益率序列,即卖方流动性调整收益率序列和买方流动性调整收益率序列。
模型构造思想如下:假设待交易的头寸为X,IS为主卖量,WS为委卖量,IB为主买量,WB为委买量,R为未调整的收益率,V为成交量,Pm为中间价,Ph为最高价,Pl为最低价,spread为相对价差。
假设交易方为买方,
(1) 当X-IS<0时,买方面临的流动性成本为0,即Cb=0,买方的流动性调整收益率为Lb=R。
(2) 当0<X-IS<WS时,IS部分对应的流动性成本为0,X超过IS的部分对应的流动性成本为
(3) 当X-IS>WS时,WS部分对应的流动性成本为
以此类推,当交易方为卖方,
(1) 当X-IB<0时,Ls=R。
(2) 当0<X-IB<WB时,
(3) 当X-IB>WB时,
用R减去上述不对称流动性调整收益率Ls或Lb,分别得到卖方或买方的流动性成本,记为Cs和Cb。该流动性成本用于计算后文的VaR(C),其中C=Cs或Cb。
(三) 不对称流动性调整VaR模型假设事先确定的置信水平为α,持有资产头寸为X,则在一段时间内,投资者可能承受的最低收益率为:
| $ {L_{{\rm{low}}}} = \mu-{z_\alpha } \cdot \sigma $ |
其中,μ为流动性调整收益率的均值,σ为流动性调整收益率的标准差,zα为正态分布下的α分位数,流动性调整收益率的均值和标准差根据构建的GARCH模型进行估计,则按收益率表示的买卖双方不对称流动性调整VaR(Asy_La_VaR)为:
| $ \begin{array}{l} {\rm{Asy\_La\_VaR}}s = {\mu _{\rm{s}}}-{z_\alpha }\cdot{\sigma _{\rm{s}}}(卖方)\\ {\rm{Asy\_La\_VaR}}b = {\mu _{\rm{b}}}-{z_\alpha }\cdot{\sigma _{\rm{b}}}(买方) \end{array} $ |
假设初始资产为W0,则按资产价值表示的不对称流动性调整VaR为:
| $ \begin{array}{l} {\rm{Asy\_La\_VaR}}s = {W_0}\cdot(-{\mu _{\rm{s}}} + {z_\alpha }\cdot{\sigma _{\rm{s}}})(卖方)\\ {\rm{Asy\_La\_VaR}}b = {W_0}\cdot(-{\mu _{\rm{b}}} + {z_\alpha }\cdot{\sigma _{\rm{b}}})(买方) \end{array} $ |
这样可得到在一定置信水平α下,投资者在一段时间内可能承受的最大损失。
三、中国股指期货市场的不对称流动性调整VaR计算 (一) 数据处理说明2015年8月份后的市场无论在成交量还是报价量上,与8月份之前相比发生了较大的变化,为保证所使用数据的平稳性以及回测检验的准确性,本文采用沪深300股指期货主力合约2010年4月19日至2015年4月30日每日的分笔数据,并对数据进行以下的处理:
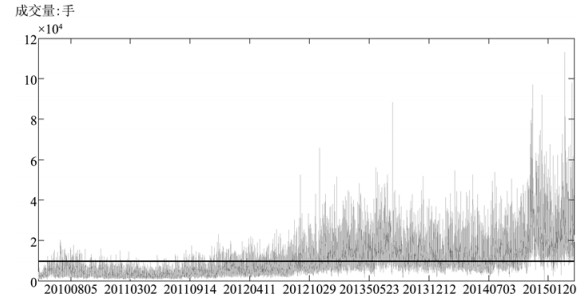
(1) 先将每日的分笔数据处理成5分钟高频数据,根据所选用数据区间5分钟成交量的均值:9 766份股指期货合约(如图 1水平线所示),本文选用5分钟成交量均值1/10的头寸即X=1 000,并根据之前提出的模型计算扩展的流动性调整收益率序列,得到未经流动性调整的收益率,买方流动性调整收益率和卖方流动性调整收益率3个序列,分别包含65 922个数据。
|
注:图中显示的是2010年4月19日至2015年4月30日每5分钟作为一个时间间隔的成交量。 图 1 5分钟成交量 |
(2) 为对后文构建的模型进行回测检验,本文将数据分为样本内数据和样本外数据两个部分。样本内数据包含64 000个数据,用于构建模型;样本外数据包含1 922个数据,用于对模型进行回测检验。
(二) 数据特征说明及ADF检验对生成的未经流动性调整的原收益率序列R、买方流动性调整收益率序列Lb和卖方流动性调整收益率序列Ls进行描述性统计,得到表 2。Lb序列和Ls序列具有相同的统计特征,同为右偏尖峰分布。JB统计量显示Lb和Ls序列均不服从正态分布。
| 表 2 五分钟收益率序列的描述性特征说明 |
对Lb和Ls序列(样本内64 000个数据)进行ADF检验,其ADF统计值的p值皆为0.000,远小于1%,因此在1%的置信度下拒绝存在单位根的原假设,Lb和Ls序列是平稳的。
(三) 序列相关性检验及ARCH效应检验观察流动性调整收益率Lb和Ls序列滞后36阶的序列相关图,从各阶的p值来看,拒绝各阶无自相关的原假设。从自相关图和偏相关图来看,当滞后阶数为1阶时的序列相关性最为明显,因此对这两个序列分别构造滞后阶数为1阶的自相关AR(1)模型,构造结果如下:
| $ \begin{array}{l} {L_{{\rm{b}}, t}} =-1.94 \times {10^{-6}}-0.021\;848\cdot{L_{{\rm{b}}, t - 1}}{\rm{ }}\\ {L_{{\rm{s}}, t}} = - 1.83 \times {10^{ - 6}} - 0.021\;848\cdot{L_{{\rm{s}}, t - 1}} \end{array} $ |
对两个自回归方程的残差图进行观察,发现两个残差图中,部分时间残差的波动很大,部分时间残差的波动又相对较小,说明残差可能存在条件异方差性。对残差进行ARCH-LM检验。Lb和Ls序列各自的20阶ARCH-LM检验统计值的p值为0.000,说明到20阶时,方程残差依然存在ARCH效应。两个自回归方程的残差存在高阶ARCH效应,应对Lb和Ls序列构造GARCH模型。
(四) GARCH模型构建根据AIC和SC准则,服从t分布的GARCH(2, 1)模型是最合适的GARCH模型。关于t分布的选择,在王吉培和旷志平(2009)[12]研究中认为t分布符合金融时间序列有偏分布和长记忆性的特征,适用于VaR的计算。故本文分别对Lb和Ls序列样本内64 000个数据构建服从t分布的GARCH(2, 1)模型,构造结果如下:
| $ \begin{array}{l} {L_{b, t}} = \begin{array}{*{20}{c}} {-1.68 \times {{10}^{-5}}}\\ {\left( {-3.59} \right)} \end{array} - \begin{array}{*{20}{c}} {0.044{\rm{ }}689}\\ {\left( { - 12.26} \right)} \end{array}\cdot{L_{b, t - 1}} + {\varepsilon _{b, t}}\\ {\sigma _{b, t}}^2 = \begin{array}{*{20}{c}} {3.14 \times {{10}^{ - 8}}}\\ {\left( {14.59} \right)} \end{array} + \begin{array}{*{20}{c}} {0.068{\rm{ }}485}\\ {\left( {11.78} \right)} \end{array}\cdot{\varepsilon _{b, t - 1}}^2 - \begin{array}{*{20}{c}} {0.020{\rm{ }}742}\\ {\left( { - 3.53} \right)} \end{array}\cdot{\varepsilon _{b, t - 2}}^2 + \begin{array}{*{20}{c}} {0.947{\rm{ }}347}\\ {\left( {537.12} \right)} \end{array}\cdot{\sigma _{b, t - 1}}^2\\ {L_{s, t}} = \begin{array}{*{20}{c}} { - 1.68 \times {{10}^{ - 5}}}\\ {\left( { - 3.59} \right)} \end{array} - \begin{array}{*{20}{c}} {0.044{\rm{ }}684}\\ {\left( { - 12.26} \right)} \end{array}\cdot{L_{s, t - 1}} + {\varepsilon _{s, t}}{\rm{ }}\\ {\sigma _{s, t}}^2 = \begin{array}{*{20}{c}} {3.14 \times {{10}^{ - 8}}}\\ {\left( {14.60} \right)} \end{array} + \begin{array}{*{20}{c}} {0.068{\rm{ }}296}\\ {\left( {11.77} \right)} \end{array}\cdot{\varepsilon _{s, t - 1}}^2 - \begin{array}{*{20}{c}} {0.020765}\\ {\left( { - 3.54} \right)} \end{array}\cdot{\varepsilon _{s, t - 2}}^2 + \begin{array}{*{20}{c}} {0.947{\rm{ }}491}\\ {\left( {538.16} \right)} \end{array}\cdot{\sigma _{s, t - 1}}^2\\ (括号内的数字是每一个系数所对应的t统计量) \end{array} $ |
由GARCH模型均值方程和标准差方程各项变量系数的t统计量可知,方程各项系数均在1%的水平上显著。接下来对Lb和Ls序列各自GARCH模型的残差项进行ARCH-LM检验。
检验结果表明,在1阶时两个模型的残差已经消除ARCH效应,说明构造的模型已经不存在条件异方差性,该模型可以很好地拟合流动性调整收益率Lb和Ls序列。
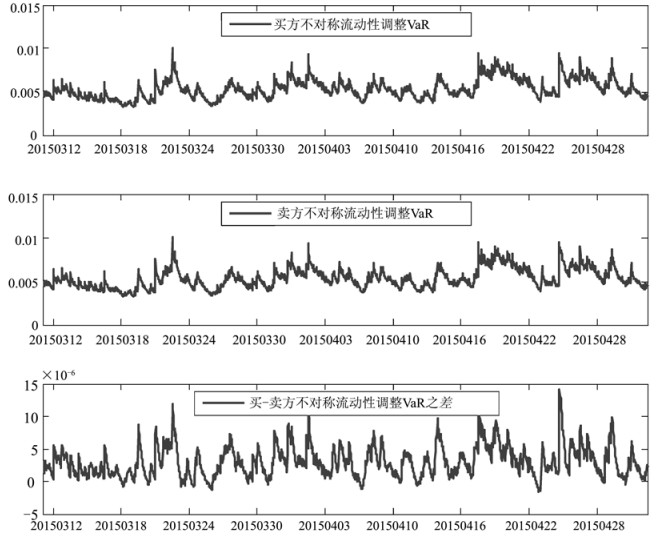
(五) 不对称流动性调整VaR计算结果基于前文得到的GARCH模型,由此来估计样本外收益率数据的条件均值和条件方差(样本外数据共有1 922个,时间跨度从2015年3月11日至2015年4月30日)。根据Asy_La_VaR的计算公式可以得到Ltb和Lts序列两组样本外数据按收益率表示的Asy_La_VaR计算结果(一般而言,Asy_La_VaR计算结果为负,但这里取Asy_La_VaR的绝对值,表示要交易的头寸在一定置信水平下可能发生的最大损失所占的百分比),同时对买卖双方按收益率表示的VaR结果进行比较,由买方不对称流动性调整VaR与卖方不对称流动性调整VaR(按收益率表示)的差来表示,结果如图 2所示。
|
图 2 买(卖)方不对称流动性调整VaR及其比较 |
在武磊(2009)[5]以及刘向丽和常云博(2015)[7]关于流动性调整收益率的研究中,流动性风险的衡量对于买卖双方来说是没有区别的。但由图 2可以看出,市场在大多数时候,买方不对称流动性调整VaR都大于卖方不对称流动性调整VaR,说明买方所面临的流动性风险要大于卖方所面临的流动性风险。因此,买卖双方间存在不对称流动性,考虑买卖双方间的不对称流动性以及这种不对称性程度的大小,将买卖双方所面临的流动性风险分开计算是必要的。
四、VaR模型比较与回测检验 (一) VaR模型计算结果比较传统VaR的计算没有涵盖流动性风险的衡量,而本文所计算的不对称流动性调整VaR(Asy_La_VaR)综合考虑流动性风险与市场风险。本文将Asy_La_VaR大于传统VaR的部分称为额外风险,额外风险占传统VaR的百分比所衡量的是整体风险被传统VaR所低估的程度,记为:
| $ lr(X) = \frac{{{\rm{Asy\_La\_VaR-VaR}}}}{{{\rm{VaR}}}} $ |
不同的交易头寸所面临的风险是不同的,为比较不同的VaR模型以及头寸大小对不对称流动性调整VaR计算的影响,本文假设投资者事先交易的股指期货合约头寸规模为500、1 000、3 000和5 000份4种情况,分别计算传统VaR低估风险的程度。当X=V(成交量)的时候,额外风险衡量的是整个市场的风险被低估的程度。
根据表 3和表 4的统计结果,随着头寸X的增大,买卖双方面临的流动性风险增加,传统VaR低估风险的程度也增加。当X=V时,买方风险最高低估的程度达24.704%,卖方风险最高低估的程度达28.958%。说明当缺少流动性风险的考虑时,整个市场面临的总风险最大可以被低估近1/5,传统的VaR衡量不能很好地衡量市场所面临的整体风险,因此在传统VaR衡量中纳入流动性风险的考虑是非常必要的。
| 表 3 买方额外风险占市场风险的比例的描述性统计 |
| 表 4 卖方额外风险占市场风险比例的描述性统计 |
根据前文的理论分析,传统的VaR计算,简单相加法(VaR+VaR(C))以及本文计算的不对称流动性调整VaR,这三者之间的关系应为:
| $ {\rm{VaR}} < {\rm{Asy\_La\_VaR}} < {\rm{VaR + VaR}}\left( {\rm{C}} \right) $ |
为比较这三者的关系,按相同的方法计算传统VaR和VaR(C),并将其与不对称流动性调整VaR进行比较,同时为说明根据本文的模型所计算的Asy_La_VaR结果优于根据刘向丽和常云博(2015)[7]的模型所计算的La_VaR,将Asy_La_VaR和La_VaR进行比较。除此之外,本文考虑到实际市场情况下,不可能永远只进行单向买或卖的交易,故本文将买卖双方不对称流动性调整VaR的均值(Asy_La_VaRbs)和传统VaR,简单相加法以及La_VaR进行比较,结果如表 5所示。
| 表 5 传统VaR、简单相加法、La_VaR与Asy_La_VaR的比较 |
根据表 5的比较结果,可以得出3个结论:
(1) Asy_La_VaR总是大于传统VaR的,这说明传统的VaR衡量会低估整体风险。
(2) 简单相加的VaR总是大于Asy_La_VaR的,说明简单将两种风险相加会高估整体风险。
(3) La_VaR总是大于Asy_La_VaR,说明La_VaR在没有考虑到买卖双方间的不对称流动性情况下高估了买卖双方的流动性风险,本文计算的Asy_La_VaR相比于La_VaR更为准确合理地衡量了整体风险。
(二) 回测检验 1. Kupiec检验模型的准确性要通过回测检验进行确定。本文进行回测所采用的统计量是由Kupiec(1995)[13]提出的LR统计量,计算公式如下:
| $ LR =- 2{\rm{ln}}\left[{{{\left( {1-\alpha } \right)}^{T-N}}\cdot{\alpha ^N}} \right] + 2{\rm{ln}}\left[{{{\left( {1-N/T} \right)}^{T-N}}\cdot{{\left( {N/T} \right)}^N}} \right] $ |
其中,T代表研究时间段内交易数据的个数,N代表模型预测失败的实际个数,即实际收益率小于所计算VaR值的次数。如果模型预测的结果是准确的,N/T理论上应等于事先确定的置信度α,如果两者差距较大的话,说明模型预测失败。失败概率计为p=N/T,原假设为p=α,根据LR值的结果,确定是否拒绝原假设。
根据表 6,在不同的头寸下,买卖双方的不对称流动性调整VaR均能通过Kupiec检验,说明不应该拒绝原假设,本文的模型构建结果可信。相比之下,当交易头寸规模增大的时候,La_VaR模型的失败次数增多,在头寸达到5 000时,未能通过Kupiec检验,说明本文的Asy_La_VaR模型比La_VaR模型更为合理。
| 表 6 Kupiec检验结果 |
Kupiec检验只是检验VaR模型的有效性,并没有对VaR模型估计的精度进行一个评估。
所估计VaR值越大,VaR模型失败率越小,但VaR模型高估了风险。因此在保证VaR模型有效性的同时,要对VaR模型精度进行评估,否则VaR模型可能高估或低估风险。
为检验VaR模型精确度,本文构造非异常情况下的均方误差(MSE),计算公式如下:
| $ {\rm{MES}}{|_{r >-{\rm{VaR}}}} = \left. {\sum\limits_{t = 1}^N {\sqrt {\frac{{{{({r_t} + {\rm{Va}}{{\rm{R}}_t})}^2}}}{N}} } } \right|{r_t} >-{\rm{Va}}{{\rm{R}}_t} $ |
MSE代表偏离程度,MSE的值越小,表明VaR模型的精度越好。
根据表 7,虽然传统VaR模型的MSE最小,但其估计没有考虑流动性风险。相对而言,本文估计的Asy_La_VaR相较与简单相加法和La_VaR,其MSE最小,说明本文估计的Asy_La_VaR模型精度最好。
| 表 7 不同VaR模型MSE计算结果 |
本文基于武磊(2009)[5]、刘向丽和常云博(2015)[7]的研究,对他们提出的流动性调整收益率进行扩展,考虑了买卖双方间的不对称流动性及其不对称程度大小,分别衡量了买卖双方的流动性成本,提出一种把流动性风险纳入VaR衡量的方法。根据本文的研究,主要得出以下结论:
(1) 买卖双方之间存在不对称流动性,不对称流动性的存在使买卖双方面临不同的流动性风险。
(2) 随着买卖双方力量不对称极端情况的加深,买卖双方间的流动性不对称性的程度也在加剧,买卖双方之间的供求愈加不平衡,买卖双方间的流动性不对称程度的大小影响买卖双方的流动性风险。
(3) 根据买卖双方不对称流动性调整VaR的计算结果,市场在大多数时候,买方不对称流动性调整VaR都大于卖方不对称流动性调整VaR,说明买方面临更大的流动性风险。
(4) 传统VaR的计算会低估整体风险。而简单相加的方法,没有考虑两种风险之间的相关性,产生对整体风险的高估。La_VaR总是大于Asy_La_VaR,Asy_La_VaR比La_VaR更为准确合理地衡量了整体风险。而根据Kupiec检验的结果,Asy_La_VaR模型的确较La_VaR模型更为合理。
(5) 根据MSE计算结果,说明本文估计的Asy_La_VaR模型精度最好。
| [1] | BANGIA A, DIEBOLD F X, SCHUERMANN T, et al. Modeling Liquidity Risk, with Implications for Traditional Market Risk Measurement and Management[M] Risk Management:The State of the Art. Springer US, 2001. |
| [2] | ANGELIDIS T, BENOS A. Liquidity Adjusted Value-at-risk Based on the Components of the Bid-ask Spread[J]. Applied Financial Economics, 2006,16(11): 835–851. DOI: 10.1080/09603100500426440 |
| [3] | 杜海涛. 中国股市流动性风险测度研究[J]. 证券市场导报, 2002(11): 38–43. DOI: 10.3969/j.issn.1005-1589.2002.11.008 |
| [4] | 宋逢明, 谭慧. VaR模型中流动性风险的度量[J]. 数量经济技术经济研究, 2004, 21(6): 114–123. |
| [5] | 武磊. 在VaR模型中嵌入流动性风险: 基于流动性调整收益率的方法[C]. 第九届中国经济学年会论文集, 2009: 1-28. |
| [6] | 林辉. 条件异方差La-VaR模型及其对金融危机的实证研究[J]. 统计与决策, 2010(17): 132–135. |
| [7] | 刘向丽, 常云博. 中国沪深300股指期货风险度量——基于流动性调整的收益率方法的研究[J]. 系统工程理论与实践, 2015(7): 1760–1769. DOI: 10.12011/1000-6788(2015)7-1760 |
| [8] | HUANG J, WANG J. Liquidity and Market Crashes[J]. Review of Financial Studies, 2010,22(7): 2407–2443. |
| [9] | XIANG J, ZHU X. Intraday Asymmetric Liquidity and Asymmetric Volatility in FTSE-100 futures market[J]. Journal of Empirical Finance, 2014,25(1): 134–148. |
| [10] | AVRAMOV D, CHORDIA T, GOYAL A. The Impact of Trades on Daily Volatility[J]. Review of Financial Studies, 2006,19(4): 1241–1277. DOI: 10.1093/rfs/hhj027 |
| [11] | 邵锡栋, 连玉君, 黄性芳. 交易间隔、超高频波动率与VaR——利用日内信息预测金融市场风险[J]. 统计研究, 2009, 26(1): 96–102. |
| [12] | 王吉培, 旷志平. 偏态t分布下FIGARCH模型的动态VaR计算[J]. 统计与信息论坛, 2009, 24(5): 75–79. |
| [13] | KUPIEC P H. Techniques for Verifying the Accuracy of Risk Measurement Models[J]. Journal of Derivatives, 1995,3(2): 73–84. DOI: 10.3905/jod.1995.407942 |
 2017, Vol. 19
2017, Vol. 19
