股票指数的预测问题一直以来都是学界和业界十分关注的话题,指数平滑预测法[1]、ARMA (自回归移动平均模型)[2]和ARCH (自回归条件异方差模型)[3]等传统的时间序列分析法被学者广泛研究。然而,这些模型具有较强的使用限制,只有满足特定的条件时才能使用。为了克服这一问题,以时间序列驱动的各类人工智能预测模型,特别是人工神经网络模型逐步成为研究的热点。
1988年,White首次利用神经网络来预测股票每日报酬率,然而预测效果并不理想。White认为神经网络陷入局部极小值而无法跳出,影响了预测效果。[4]Kimoto等利用神经网络对东京证交所股价加权平均指数进行预测,指出神经网络模型对报酬率的预测效果优于TOPIX加权平均指数方法。[5]为了进一步提高神经网络模型的预测能力,许多学者又对人工智能技术进行了改进,比如说,Hassan等把HMM、ANN和GA进行结合对金融市场的行为进行预测,他们认为,改进后的模型对金融市场的预测与传统人工智能技术相比更加精确。[6]Wang等提出WDBP神经网络来预测上证综合指数,其结果表明WDBP神经网络与传统的BP神经网络相比具有更强的预测能力。[7]常松等利用小波包理论将价格波动序列最优地分解为一系列子波动并运用神经网络对子波动进行预测,实证结果表明小波包与神经网络结合起来对股票价格的预测效果比单独的神经网络更好。[8]徐少华等提出一种基于混沌遗传与带有动态惯性因子的粒子群优化相结合的学习方法来优化神经网络的训练问题,以提高神经网络的训练精度。实证结果表明该改进算法提供了PNN网络的训练精度。[9]杨一等提出一种基于输出敏感度方差重要性的结构优化算法来解决RBF神经网络的结构设计问题。结果表明该算法可根据研究对象自适应地调整RBF的网络结构,提高其泛化能力。[10]
由于传统人工神经网络存在结构上的缺陷,比如说,学习速度慢、学习率难以确定、易过度训练等,学者们对人工神经网络的有效性产生质疑。为了克服神经网络模型的结构缺陷,Huang等人提出极限学习机(Extreme Learning Machine,ELM)的概念。[11]ELM算法是一种十分简单快速的单隐层神经网络训练算法,在网络参数的确定过程中隐层节点参数(内权和偏置值)随机设置,且其在网络学习过程中不再改变,而网络外权通过最小化误差的原理计算得出。ELM的学习机制使其只需进行一次运算即可输出权值,与需要进行多次迭代的前馈型神经网络相比大幅度地减少了学习时间、提高了学习效率,近年受到了广泛的关注。
ELM算法的运算机制使该算法同样存在结构上的不足,比如说:隐层输出矩阵易发生奇异,部分隐层节点不起作用。为了进一步改善ELM算法的不足,学者提出了一系列改进方案,比如说:Lan等提出了CS-ELM算法,该算法对ELM算法的隐层节点参数进行筛选,去除显著性较弱的隐层节点来实现网络结构的优化。[12]Wang等提出EELM算法,运用对角占优的方法来优化隐层节点参数,进而保证了隐层输出矩阵的非奇异性,提高了极限学习机的稳定性。[13]Toh等通过添加正则项的方式避免了隐层矩阵奇异和接近奇异情况的发生,有效地提高了ELM算法的学习能力。[14]Huang等提出EI-ELM算法来优化隐层节点参数,简化了ELM算法的复杂度,提高了其优化效率。[15]高光勇等提出CC-ELM算法,运用复合混沌和混沌变尺度算法对极限学习机的参数进行搜索和优化,提高了ELM算法的泛化性能。同时,通过算例指出CC-ELM算法与同类型算法相比更加有效。[16]
然而,上述改进算法均未同时考虑隐层节点数目和参数两方面。为了克服这一问题,本文提出双层DE-ELM预测模型。该模型使用双层差分进化算法(DE)与极限学习机(ELM)结合,利用差分进化(DE)算法对极限学习机(ELM)的网络隐层节点数目、隐层内权和偏置值进行优化。最后,本文利用双层DE-ELM预测模型对上证综合指数和标准普尔500指数的日度数据和月度数据进行预测,以讨论双层DE-ELM预测模型的应用价值。
一、 模型介绍股票市场具有复杂性、非线性、多变性等特点,随着ETF和股指期货等金融工具的出现,股指对股票市场的重要性越发重要,投资者可以利用股指的衍生品进行套利或套保,对股指走势进行预测就显得越发重要。但股指同样具有走势难预测、方向难确定、影响因素多等方面的特点,导致对其进行预测具有很多的困难。
本文利用时间序列的方法,以股指过去n天/月的历史收盘价作为模型的输入,以第n+1天/月的收盘价作为输出函数进行一步预测。股票价格走势与近期的历史信息有关,本文着重考虑单个因素(股价)对自身短中期预测的影响,不考虑其他因素。
(一) 极限学习机(ELM)Huang等依据摩尔-彭罗斯(MP)广义逆矩阵理论[17]提出了极限学习机(ELM)算法。[11]该算法的特点是在网络参数的确定过程中,内权和偏置值随机选取且无需进行二次调节,而网络外权通过最小化损失函数得到。这种机制使得ELM算法在网络参数确定过程中无需进行任何迭代步骤,只需一次计算即可得出最优网络参数。这样的处理机制大大降低了运算时间,与需要多次迭代的前馈型神经网络相比具有巨大的优势。
神经网络算法在股指预测方面获得了较好的成果,而ELM算法作为神经网络的一种改进算法,其在金融领域的应用较少。而ELM算法的低迭代次数、运行时间短和高精度的特点使其比神经网络更加适合金融市场的复杂性、非线性和多变性,所以我们在这里尝试使用ELM算法作为模型的一部分。
针对学习样本(xj, tj),j=1, 2, …, N,具有L个隐层节点的ELM输出函数表达式为:
| $ {o_j} = \sum\limits_{i = 1}^L {{\beta _i}G({w_i}, {x_j}, {b_i}), j = 1, 2, } \cdots, N $ | (1) |
式(1)中,oj代表第j个学习样本对应的网络输出值,wi=[w1i, w2i, …, wmi]代表连接网络输入层节点与第i个隐层节点的内权,βi=[βi1, βi2, …, βin]T代表连接第i个隐层节点与网络输出层节点的输出外权,G(wi, xj, bi)表示第i个隐层对应于样本xj的隐层节点输出,i=1, 2, …, L,j=1, 2, …, N。针对加法型的隐层节点,其表达式为:
| $ G({w_i}, {x_j}, {b_i}) = g({w_i} \bullet {x_j} + {b_i}) $ | (2) |
其中,g(·)为激活函数,wi·xj代表内权向量wi和样本xj的内积。
考虑N个互异的数据样本(xj,tj),1≤j≤N,Huang提出,理论上具有L个隐层节点的ELM算法能以零误差逼近这N个互异的数据样本,即存在wi,bi,βi,i=1, 2, …, L,使得
| $ {o_j} = \sum\limits_{i = 1}^L {{\beta _i}g({w_i} \bullet {x_j} + {b_i}_i) = {t_j}, j = 1, 2, } \cdots, N $ | (3) |
然而,过多的隐层节点易使网络矩阵出现奇异,进而影响ELM算法的预测能力。多数情况下,为了保证ELM学习样本外的预测能力,隐层节点数目远小于学习样本个数。这就使得ELM算法难以实现以零误差逼近学习样本,也就是说,学习样本的网络输出和实际输出之间将会出现误差。若以损失函数E来表示该误差,可表示为下式(4):
| $ E(S, \beta ) = \sum\limits_{j = 1}^N {||{o_j}-{t_j}||} $ | (4) |
式(4)中,S=(wi, bi, i=1, 2, …, L),可见S包含了隐层节点内权及隐层节点偏置值,||.||代表欧氏距离。Huang等指出极限学习机的训练目标就是寻找最优的S和β,使得网络输出值与对应实际值之间的误差最小[11],表示为下式(5):
| $ \min \;E(S, \beta ) = \mathop {\min }\limits_{{w_i}, {b_i}, \beta } ||H({w_1}, \cdots, {w_L}, {b_1}, \cdots, {b_L}, {x_1}, \cdots {x_N})\beta-T|| $ | (5) |
其中,
| $ \begin{array}{l} H({w_1}, \cdots, {w_L}, {b_1}, \cdots, {b_L}, {x_1}, \cdots {x_N})\\ = {\left[{\begin{array}{*{20}{c}} {g({w_1}{x_1} + {b_1})}& \cdots &{g({w_L}{x_1} + {b_L})}\\ \vdots &{}& \vdots \\ {g({w_1}{x_N} + {b_1})}& \cdots &{g({w_L}{x_N} + {b_L})} \end{array}} \right]_{N \times L}}, \\ \beta = {\left( {\begin{array}{*{20}{c}} {\beta _1^T}\\ \vdots \\ {\beta _L^T} \end{array}} \right)_{L \times n}}, T = {\left( {\begin{array}{*{20}{c}} {t_1^T}\\ \vdots \\ {t_N^T} \end{array}} \right)_{N \times n}} \end{array} $ | (6) |
同时,Huang等提出当网络的激活函数即g(x)无限可微时,隐层节点内权(w)和隐层节点偏置值(b)可随机赋值。[18]在w和b随机赋值后,矩阵H为一常数矩阵,极限学习机的网络训练过程可视为求解Hβ=T的最小二乘解β*。根据MP广义逆矩阵理论,其计算式如下:
| $ {\beta ^*} = {H^ + }T $ | (7) |
其中,H+是矩阵H的MP广义逆。计算出β后极限学习机的网络训练过程也就完成了。得出ELM算法的参数之后,我们即可利用式(3)对股指收盘价进行一步预测。
(二) 差分进化算法(DE)类似于遗传算法,差分进化(DE)算法是一种比较新的基于群体的随机优化算法,具有较强的自适应全局优化搜索能力。[19]它具有运算速度快、不易陷入局部最优、鲁棒性好等优点。该算法主要用于解决实参数优化问题,它对非线性和不可微的连续空间问题的求解较其他搜索启发式算法具有明显的优势。
二、 双层DE-ELM预测模型通常情况下,隐层节点数目根据输入输出变量的维度和样本数量事先设定,属于经验设定的范畴,只有合适的隐层节点数目才能够使ELM的优秀机制出来。同时,ELM算法的学习机制决定隐层节点内权和偏置值是随机取值的,这就导致隐层节点不具有学习和自我调节的能力。如果隐层节点参数取值不合理,就会导致部分隐层节点在极限学习机网络中不具有或仅有很少的作用,甚至导致极限学习机的网络矩阵出现奇异,使ELM算法的预测效果大打折扣。
为了克服这个问题,本文尝试使ELM算法与双层DE算法进行结合,利用双层DE算法通过优胜劣汰的自然选择机制解决隐层节点数目、内权及偏置值的赋值问题,避免对ELM算法本身学习机制的破坏。
(一) 双层DE-ELM预测模型组成部分双层DE-ELM包含两层DE算法:外层DE算法对隐含层节点数目进行优化,内层DE算法对隐含层节点参数进行优化。
1. 外层DE算法根据以往的研究发现,隐层节点数目在合适的范围内算法具有较好的表现,而在这个范围之外,算法的精度将会受到严重影响。当输入输出变量维度和样本数量过大时,范围的确定是十分困难的,所以我们利用DE算法通过自然选择机制来确定合适的隐层节点数目。
外层DE算法以隐层节点数目作为进化个体,以个体在内层DE算法的最优结果作为个体适应度,按照DE算法的进化机制进行进化,确定合适的隐层节点数目。具体流程详见(二)。
2. 内层DE算法内层DE算法以ELM的隐层节点内权和偏置值作为进化个体,以ELM预测误差的倒数作为适应度函数,通过自然选择机制优化内权和偏置值。
1) 编码表示和初始化种群
个体为ELM网络的隐层内权w和偏置值b,个体定义为:
| $ y = [{w_1}, \cdots, {w_L}, {b_1}, \cdots, {b_L}] $ | (8) |
上式中,L为隐层节点数目(外层DE算法的进化个体),wi=[w1i, w2i, …, wmi], i=1, 2, …L,个体的长度为(m+1)·L。对个体进行定义后,接下来介绍如何产生初始种群:
| $ y_{ij}^0 = {l_j} + rand \bullet ({u_j}-{l_j}), j = 1, 2, \cdots, NP $ | (9) |
其中,i表示个体在种群中的序号,j表示个体的维度,NP为种群规模,lj表示第j维的下界,uj表示第j维的上界,rand代表[0, 1]区间的随机数。由于ELM的隐层内权和偏置值均在[-1, 1]内随机设置[11],故lj设为-1,uj设为1。
2) 适应度的度量
个体的适应度包含两种:学习样本的拟合效果和检验样本的预测效果。为了防止双层DE-ELM预测模型陷入过度学习,我们对学习样本进行了细分,选择内部检验样本的预测效果作为衡量个体适应度的方法。接下来将会详细介绍适应度的度量过程。
此处把学习样本分为两部分:内部学习样本和内部检验样本,见下图 1。

|
图 1 样本数据分类 |
首先,利用内部学习样本对ELM算法部分进行学习。针对内部学习样本(xstudyj, tstudyj),j=1, 2, …, N,具有L个隐层节点的输出函数表达式为:
| $ ostud{y_j} = \sum\limits_{i = 1}^L {{\beta _i}g} ({w_i} \bullet xstud{y_j} + {b_i}), j = 1, 2, \cdots, N $ | (10) |
上式中,ostudyj代表网络输出值。这样,ELM算法的损失函数转变成式(11):
| $ \min E(y, \beta ) = \mathop {\min }\limits_\beta ||H({w_1}, \cdots, {w_L}, {b_1}, \cdots, {b_L}, xstud{y_1}, \cdots xstud{y_N})\beta-Tstudy||, $ | (11) |
其中,
| $ \begin{array}{l} H({w_1}, \cdots, {w_L}, {b_1}, \cdots, {b_L}, xstud{y_1}, \cdots xstud{y_N}) = \\ {\left[\begin{array}{l} \begin{array}{*{20}{c}} {g({w_1}xstud{y_1} + {b_1})}& \cdots &{g({w_L}xstud{y_1} + {b_L})} \end{array}\\ \begin{array}{*{20}{c}} {g({w_1}xstud{y_N} + {b_1})}& \cdots &{g({w_L}xstud{y_N} + {b_L})} \end{array} \end{array} \right]_{N \times L}}, \\ Tstudy = {\left( {\begin{array}{*{20}{c}} {tstudy_1^T}\\ \cdots \\ {tstudy_N^T} \end{array}} \right)_{N \times n}} \end{array} $ | (12) |
通过求解式(11)即可得出最小二乘解β*。最后,把预测模型的个体和其对应的β*作为参数,利用内部检验样本通过式(13)计算样本外的预测误差。以该预测误差的倒数作为个体的适应度度量。
| $ Etest = ||H({w_1}, \cdots, {w_L}, {b_1}, \cdots, {b_L}, xtes{t_1}, \cdots xtes{t_{N1}}){\beta ^*}-Ttest|| $ | (13) |
其中,xtest代表内部检验样本的输入,Ttest代表内部检验样本的输出,N1代表内部检验样本数量。
3) 变异算子
变异算子是指个体通过种群中的其他个体而产生变异的操作,是对个体基因实现多样化的操作。变异算子要求对种群中的所有个体yiG(G代表迭代次数)进行变异操作,具体形式见下式:
| $ v_i^{G + 1} = y_{r1}^G + F \bullet (y_{r2}^G-y_{r3}^G) $ | (14) |
其中,viG+1代表第G次迭代时通过变异操作产生的与第i个父代个体对应的变异个体,r1、r2和r3为{1, 2, …, NP}中随机选取的互不相同的数值,F为服从[-2, 2]均匀分布中产生的随机数。
4) 交叉算子
交叉算子是在保留父代个体部分信息的前提下,进而实现新个体基因多样化的操作,具体形式如下式:
| $ u_{ij}^{G + 1} = \left\{ \begin{array}{l} y_{ij}^G, rand(j) \le CR或j = randn(i)\\ v_{ij}^{G + 1}, rand(j) > CR且j \ne randn(i) \end{array} \right. $ | (15) |
其中,i=1, 2, …, NP,j=1, 2, …, (m+1)·L,CR∈[0, 1],rand(j)为[0, 1]区间上的随机数,randn(i)为{1, 2, …, (m+1)·L}中的随机数。交叉操作保证新个体uiG+1至少保留父代个体yiG中的一维信息。
5) 选择操作
采用贪婪策略,只有当新个体uiG+1比父代个体yiG拥有更高的适应度时才会用uiG+1代替父代个体yiG。否则,父代个体yiG将被保留至下一代。贪婪策略保证了种群在进化过程中不会出现种群退化的现象,具体见下式:
| $ y_i^{G + 1} = \left\{ \begin{array}{l} u_i^{G + 1}, u_i^{G + 1}比y_i^G适应度更高\\ y_i^G, y_i^G比u_i^{G + 1}适应度更高 \end{array} \right. $ | (16) |
以上主要介绍了双层DE-ELM预测模型的组成部分,下面给出该模型的主要流程。
1. 外层DE算法流程1) 初始化种群及种群个体适应度评价
初始化产生NP1个个体(个体代表隐层节点数目)作为初始种群,并对其适应度进行计算。适应度评价方法:对每个个体分别运行内层DE算法,以内层DE算法的最小误差的倒数作为外层DE算法个体的适应度。
2) 迭代(for G1=1:1:maxgen1)
(1) 执行变异算子,产生NP1个新个体。注:外层DE只包含一个参数,不进行交叉操作。
(2) 计算NP1个新个体的适应度。
(3) 执行选择操作,选择父代和子代中适应度最大的NP1个个体作为新种群。
(4) 若G1==maxgen1,进入步骤3;否则回到步骤2.1,并设置G1←G1+1。
3) 迭代终止
此时种群中适应度最大的个体包含了双层DE-ELM预测模型的最优隐层节点数目和隐层节点对应的参数(参数通过内层DE算法求出)。
2. 内层DE算法流程1) 初始化种群及种群个体适应度评价
初始化产生NP2个个体作为初始种群,并对其适应度进行计算。
2) 迭代(for G2=1:1:maxgen2)
(1) 执行变异算子,产生NP2个变异个体。
(2) 执行交叉算子,产生NP2个新个体。
(3) 计算NP2个新个体的适应度。
(4) 执行选择操作,产生第G2+1代的种群,记录新种群个体适应度。
(5) 若G2=maxgen2,进入步骤3;否则回到步骤2.1,并设置G2←G2+1。
3) 计算最终代个体适应度
此时种群中适应度最大的个体为外层DE算法中个体所对应的最优隐层节点参数。
三、 实证分析我国上海证券交易所起步较早,而上证综合指数包含我国上海证券交易所的所有上市股票信息,能够反映我国上海股市的整体情况,所以本文采用上证综合指数作为样本来检验模型效果。同时,为了验证双层DE-ELM预测模型对不同市场的适应程度,我们同时选取国际上具有较高影响力的标准普尔500指数(S & P500)进行研究。本文采用上证综合指数和标准普尔500指数在2001年1月1日至2014年9月30日间的日收盘价和月收盘价数据,数据来源于WIND数据库。随机选取样本中的80%作为学习样本,剩余20%作为检验样本。之后,进一步对学习样本进行细分,随机选取学习样本中的80%作为内部学习样本,剩余20%为内部检验样本。即本文的数据被分为三部分:64%的内部学习样本、16%的内部检验样本和20%的检验样本。
首先,我们要确定双层DE-ELM预测模型的输入和输出,本文采用指数的十阶滞后项作为历史信息(输入),利用历史信息对指数进行一步预测(输出),即xi=[xi1, xi2, …, xim]T∈Rm中m=10;ti=[ti1, ti2, …, tin]T∈Rn中n=1。其次,为了验证双层DE-ELM预测模型的有效性,本文利用DE-ELM模型、BP神经网络[8]模型、ELM[11]模型与其进行对比分析。接下来进行参数设置。双层DE-ELM预测模型的激活函数选用Sigmoidal函数,外层种群个数设置为10个,迭代次数为10代,内层种群个数设置为50个,迭代次数为50代。DE-ELM预测模型在短期预测(日度数据)时隐层节点为200个,在中期预测(月度数据)时隐层节点设置为20个,其余参数与双层DE-ELM预测模型一致。ELM模型的隐层节点数目与DE-ELM模型一致。BP神经网络迭代次数为1000代,其余参数与双层DE-ELM预测模型一致。
为了直观地判断三个模型之间拟合能力和预测能力的差别,我们给出双层DE-ELM预测模型和对比模型对上证综合指数的短期拟合预测结果与真实数据的对比曲线(图 2)。其中,图 2a表示上证综合指数日度数据的真实值,图 2b为双层DE-ELM预测模型的短期拟合和预测效果图,图 2c为DE-ELM模型的效果图,图 2d为ELM模型的效果图,图 2e为BP神经网络模型的效果图。
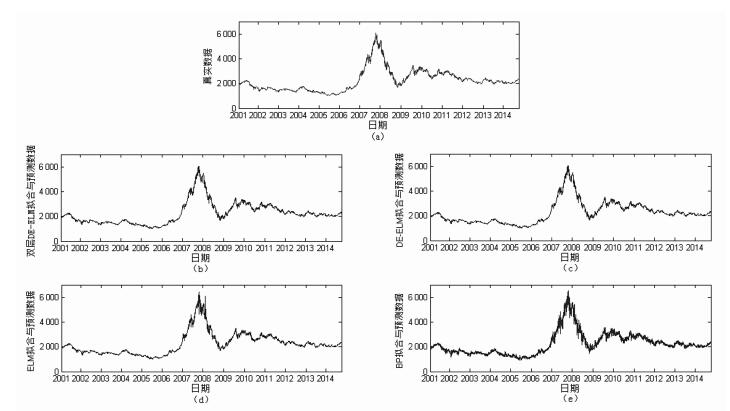
|
图 2 上证综指短期拟合预测曲线图 |
从图 2中可得出如下结果:在对上证综合指数的短期预测中,双层DE-ELM预测模型和DE-ELM预测模型的拟合与预测结果最贴近真实数据;ELM模型的拟合与预测效果次之,仅在个别时点发生较大偏离;BP神经网络模型效果最差,在真实值附近波动。由图可以看出,双层DE-ELM预测模型与DE-ELM预测模型的效果近似,这是由于时间窗口过长,掩盖了大部分细节所导致的。
为了保证试验的科学性和有效性,本文利用三个模型对上证综合指数和标准普尔500指数分别进行短期和中期预测30次,结果见表 1~表 4。
| 表 1 上证综合指数短期预测对比分析(检验样本) |
| 表 2 上证综合指数中期预测对比分析(检验样本) |
| 表 3 S & P 500短期预测对比分析(检验样本) |
| 表 4 S & P 500中期预测对比分析(检验样本) |
其中,均方根误差RMSE (root mean square error)、平均绝对值误差MAE (mean absolute error)和平均绝对误差率MAPE (mean absolute percentage error)为极小型指标,即每一种指标的数值越低,表示其预测效果越好。而方向正确率DS (directional symmetry)为极大型指标。接下来,我们对表 1~表 4的结果进行详细分析。
RMSE、MAE所代表的含义近似,二者可同时分析。从RMSE的角度来看,双层DE-ELM预测模型的整体效果最优,DE-ELM预测模型效果其次,BP神经网络效果最差。从MAE的角度来看将会得到同样的结果。也就是说,从RMSE和MAE检测指标的角度来看,双层DE-ELM预测模型的效果最优。
MAPE代表预测误差绝对值与真实值比值的均值,代表了平均预测误差率。双层DE-ELM预测模型在该检测指标上表现良好,对上证综合指数的短期预测中,预测误差率最大值仅为1.24%,最小只有1.05%,表现出该模型强大的预测能力。从表 1~表 4中可以看出在该检测指标下,双层DE-ELM预测模型优于DE-ELM预测模型,更优于另外两种预测模型。
DS是实际应用中最为重要的检测指标,其代表了对趋势预测的正确率。该指标越大表示对趋势的预测正确率越高,也代表利用该模型进行投资时取得超额收益的几率越大。针对DS指标,双层DE-ELM预测模型表现十分优秀,在对上证综合指数的短期预测中,预测准确率最低为50.30%,最大值甚至高达73.09%。而ELM预测模型与BP神经网络预测模型的该项指标均值几乎接近50%,表示该两种对比模型对指数的趋势并未完成较好的学习,对趋势的判断率等同于掷硬币,加大了投资风险。
综上所述,在对上证综合指数和标准普尔500指数的短期预测和中期预测中,预测效果从高到低分别是双层DE-ELM预测模型、DE-ELM预测模型、ELM预测模型、BP神经网络预测模型。
除了预测精度之外,预测稳定性同样是预测模型的一个重要指标。因为ELM预测模型与BP神经网络预测模型对趋势的判断近乎于掷硬币,导致其检测指标DS波动较小,所以预测稳定性我们主要从RMSE、MAE和MAPE的角度分析。从表 1可看出双层DE-ELM预测模型与ELM预测模型的三个检测指标波动范围最小,具有最强的稳定性;DE-ELM预测模型其次;BP神经网络的波动较大,稳定性最差。表 2~表 4的结果与表 1相同,在这里不再重复。
值得一提的是,双层DE-ELM预测模型对中期预测的趋势判断正确率比短期预测时更高。在短期内,投资者易受突发信息的影响而产生不稳定的情绪,进而导致指数偏离正常的轨迹,短期内价格趋势不稳定。随着时间段的加长,投资者的不稳定情绪对指数轨迹的影响逐渐变小,能够形成较为稳定的价格趋势。这就产生了中期趋势比短期趋势更加稳定、更易预测的情况。同时,三个预测模型的短期预测误差均小于中期预测的误差,这包含两部分原因:(1)涨跌幅限制和流动性的影响。短期内股票指数波动较小,而中期内股票指数波动较大。(2)影响指数的因素众多,模型中只包含指数的收盘价信息。随着预测区间的加长,其余因素的影响逐步加强,使得指数价格发生较大偏离,进而使模型的预测效果逐步降低,所以本文未进行指数的长期预测检验。
双层DE-ELM预测模型融合了差分进化(DE)算法和极限学习机(ELM)模型的优点,既保留了ELM模型优秀的学习样本拟合能力,又利用DE算法通过机器学习的方法确定了最优隐层节点数目、优化了ELM模型的网络输入内权和偏置值的产生方式。这种结合方式克服了DE-ELM模型的缺点,提高了其预测能力。
结束语不同于修改ELM模型形式的改进方法,本文提出的双层DE-ELM预测模型使ELM模型嵌入在双层差分进化(DE)算法中。利用人工智能技术优化ELM网络的隐层节点数目、内权与偏置值,尽可能地排除人为主观因素,既保留了强大的学习能力,又提升了预测能力,并利用该模型对上证综合指数和标准普尔500指数进行短期预测和中期预测。实证结果表明:双层DE-ELM预测模型具有较高的预测精度,对数据的依赖性较弱,具有较强的适应性。本研究可辅助投资者进行风险规避和资产决策,为量化投资提供一种参考工具。在之后的工作中,可尝试在模型中加入更多影响股票市场的因素,比如股票交易额、换手率等,使其更加满足中长期预测的需求。
| [1] | de Faria E L, Albuquerque Marcelo P, Gonzalez J L, Cavalcante J T P, Albuquerque Marcio P. Predicting the Brazilian stock market through neural networks and adaptive exponential smoothing methods[J]. Expert Systems with Applications, 2009,36(10): 12506–12509. DOI: 10.1016/j.eswa.2009.04.032 |
| [2] | Minakhi Rout, Babita Majhi, Ritanjali Majhi, Ganapati Panda. Forecasting of currency exchange rates using an adaptive ARMA model with differential evolution based training[J]. Journal of King Saud University-Computer and Information Sciences, 2014,26(1): 7–18. DOI: 10.1016/j.jksuci.2013.01.002 |
| [3] | Robert D Brooks, Robert W Faff, Michael D McKenzie, Heather Mitchell. A multi-country study of power ARCH models and national stock market returns[J]. Journal of International Money and Finance, 2000,19(3): 377–397. DOI: 10.1016/S0261-5606(00)00011-5 |
| [4] | White H. Economic prediction using neural networks:the case of IBM daily stock returns[J]. Neural Networks, IEEE International Conference on, 1988,2(6): 451–458. |
| [5] | Kimoto T, Asakawa K, Yoda M, et al. Stock Market Prediction System with Modular Neural Networks[J]. International Joint Conference on, 1990(1): 1–6. |
| [6] | Hassan M R, Nath B, Kirley M. A fusion model of HMM, ANN and GA for stock market forecasting[J]. Expert Systems with Applications, 2007,33: 171–180. DOI: 10.1016/j.eswa.2006.04.007 |
| [7] | Wang J-Z, Wang J-J, Zhang Z-G, Guo S-P. Forecasting stock indices with back propagation neural network[J]. Expert Systems with Applications, 2011,38: 14346–14355. |
| [8] | 常松, 何建敏. 基于小波包和神经网络的股票价格预测模型[J]. 中国管理科学, 2001(5): 8–15. |
| [9] | 徐少华, 何新贵. 一种基于混沌遗传与粒子群混合优化的过程神经网络训练算法[J]. 控制与决策, 2013(9): 1393–1398. |
| [10] | 杨一, 高社生, 胡高歌. 基于敏感度方差重要性的RBF神经网络结构优化算法[J]. 控制与决策, 2015(8): 1393–1398. |
| [11] | Huang G B, Zhu Q Y, Siew C K. Extreme learning machine:Theory and applications[J]. Neurocomputing, 2006,70: 489–501. DOI: 10.1016/j.neucom.2005.12.126 |
| [12] | Lan Y, Soh Y C, Huang G B. Constructive hidden nodes selection of extreme learning machine for regression[J]. Neurocomputing, 2010,73: 3193–3199. |
| [13] | Wang Y G, Gao F L, Yuan Y B. A study on effectiveness of extreme learning machine[J]. Neurocomputing, 2011,74: 2483–2490. DOI: 10.1016/j.neucom.2010.11.030 |
| [14] | Toh K A. Deterministic neural classification[J]. NeuralComputation, 2008,72(6): 1565–1595. |
| [15] | Huang G B, Chen L. Enhanced random search based incremental extreme learning machine[J]. Neurocomputing, 2008,71: 3460–3468. DOI: 10.1016/j.neucom.2007.10.008 |
| [16] | 高光勇, 蒋国平. 采用优化极限学习机的多变量混沌时间序列预测[J]. 物理学报, 2012(4): 37–45. |
| [17] | Rumelhart D E, Hinton G E, Williams R J. Learning representation by back-propagation errors[J]. Nature, 1986,323(9): 533–536. |
| [18] | Huang G B, Siew C K. Extreme learning machine with randomly assigned RBF kernels[J]. International Journal of Information Technology, 2005,11(1): 16–24. |
| [19] | Mohamed A W, Sabry H Z. Constrained optimization based on modified differential evolution algorithm[J]. Information Sciences, 2012,194(1): 171–208. |
 2016, Vol. 18
2016, Vol. 18
