2. 华南师范大学 经济与管理学院,广东 广州 510006
3. 贵州大学 理学院,贵州 贵阳 550025
2. School of Economics and Management, South China Normal University, Guangzhou 51006, Guangdong, China
3. College of Science, Guizhou University, Guiyang 550025, Guizhou, China
技术创新对于一国经济持续增长有重要作用已被广泛接受。有研究将美国上世纪末经济低通胀下的高速增长归因于技术创新特别是信息科技的突破,并认为风险投资对富有前景的技术创新活动的支持是美国技术进步的主要原因之一。Kortum和Lerner[1]指出,是否拥有一套完整良好的风险投资机制甚至能关系到其一国经济的可持续发展。
伴随着风险投资在全球范围内的蓬勃发展,学术界关于风险投资这一新兴领域的研究也不断深化,已有的研究主要集中于探讨风险投资组合策略[2-4]、风险投资是否影响创业企业成功上市[5]、IPO折价率[6]、IPO择机[7]、IPO后股票长期表现[8-9]、采用股权激励及撤换CEO[10],以及风险投资回报率的影响因素。[11]由于风险投资的对象主要是处于初创和成长阶段的中小企业,其未来的成长具有极大的不确定性,因而防范和规避投资风险成为风险投资家决策中最为关心的问题。学者们研究发现,在现实中风险投资家广泛地采用组合投资策略,以防范单个风险投资失败对整体利益的影响。基于分散风险的思想,Gorman和Sahlman[12],提出了风险投资组合理论(VCP:venture capital portfolio)。VCP已成为当前风险投资研究的重要领域之一。
为防范被风险企业“套牢”的风险,风险投资家还常采用分阶段投资策略,以降低风险提高风险投资整体的投资价值。分阶段投资(staged financing)策略被风险投资家们广泛地运用于风险投资契约中。分阶段投资是指,风险投资家在开始阶段只注入部分资金,以后再根据项目的进展情况决定下一阶段的最佳投资量,或者停止注资,在每一阶段所投入的资本足够让公司过渡到它发展的下一个阶段,目的是为了防范“套牢”(hold-up)问题的出现。[13-14]“套牢”风险产生的原因在于,创业者的人力资本是初创企业成功必不可缺的因素,且这种资本不可转让,创业者有可能以退出风险企业为要挟在中途否决协议,以便要求更多的收益,从而威胁到风险投资家的利益。实施分阶段投资策略可让风险投资家保留放弃前景暗淡项目的权利,从而在高度不确定环境下保护自己的利益。[15]另一方面创新企业由于创业家独特的人力资本使项目增值,分阶段投资可从制度上降低创业家从项目中撤出宝贵人力资本的可能,从而较好地解决了风险投资家与创业家之间的不对称信息问题并控制了投资风险。
鉴于风险投资高风险的特征,进行分段投资和组合投资已成为风险投资家惯用的规避投资风险手段。迄今为止,对风险投资组合的研究大多偏重实证方面,已有的少数理论研究也存在着对风险投资特性结合研究不够的问题;虽然很多专家和学者对分阶段风险投资问题进行了深入研究,但重点集中在对单个企业的研究上,关于风险资本多阶段投资组合决策问题的研究成果并不多见,研究结论的应用范围受到限制。本文将基于风险投资的合理特征假设和绝对离差风险测度,构造出多阶段风险投资组合的约束条件,以最大化最终期望价值为目标,提出一种新的多阶段风险投资组合优化模型。
二、 多阶段风险投资问题描述及研究假设风险投资家在投资期初进行投资决策。考虑如下的风险投资决策情景:投资期初总募集资金S0,经过考察,风险投资家筛选出了n家满足投资标准的风险企业,拟选择对这n家风险企业进行T轮分阶段投资。募集资金S0不能满足对n家风险企业全部投资的要求,因而风险投资家需在资金有限和风险约束下,对n家风险企业进行多阶段风险投资决策,以制定最优投资决策,实现投资组合终期收益最大化。
为简化决策问题,我们提出以下研究假设:
风险投资家与风险基金投资人达成了最大募集资金额协议,投资期间全部投资额不能超出金额S0;协议还规定,风险投资中各个阶段投资所需资金均可在阶段初募集到位。因此本文不考虑资金时间价值问题。
风险投资家与风险基金投资人之间存在着最佳激励机制,它能够促使风险投资家全力以赴为风险基金价值最大化工作。因此本文不考虑两者之间的委托代理问题。
为防范被风险企业“套牢”的风险,风险投资家采用分阶段投资策略,并形成投资对象路径依赖。假设对全部风险企业的T期投资区间完全一致,即同时从最初阶段开始投资,且都持续T个阶段;在第1阶段初,风险投资家可从初始的n家风险企业中,选择m(0 < m≤n)家风险企业进行投资;在第2阶段初,风险投资家只能从第一阶段的m家风险企业中选择p(0≤p≤m)家风险企业进行投资;同样,在第3阶段初,风险投资家也只能从第二阶段的p家风险企业中选择部分进行投资;以此类推,直至第t阶段结束为止。投资对象路径依赖意味着,风险投资家在风险投资第一阶段开始后,后阶段各期的投资对象不能选择全部n家风险企业之外的其他企业进行投资,也不能选择之前各期放弃的风险企业再进行投资。即风险投资家不会投资于以前阶段(t=1阶段除外)未投资过的风险企业。
风险投资家经过研究和分析,筛选出了满足其投资标准的风险企业n家,且风险投资家与风险企业协商已经确定了未来各阶段对风险企业的拟投资金额。如对第i家风险企业家在未来第t阶段确定的投资额为sit,t=1, 2, …, T。
所有的风险投资均在阶段初投入风险企业,可以在每个阶段末计算出相应的资产价值,但是在风险投资的中间阶段不能变现这些资产价值,仅只能在投资的T阶段期末可以计算或变现价值。
风险投资家拥有出色的研究能力,能够运用合适方法预测出风险企业K种情形下的发生概率以及相应的收益情况。
考虑到风险企业既可能获得风险投资的资金投入,也可能会被风险投资家放弃投资。将风险企业j在第t阶段时第k种情形发生的概率表示为ptj(kt),有
由于风险投资家和风险企业已经商定好了对每个风险企业各个阶段的投资金额,因此风险投资家实际的决策是面对单个风险企业,仅需要作出投资或不投资决策。当风险投资公司决定本阶段投资于该风险企业,决策变量则取值1,表示投资;否则取值0,表示不投资。现在风险投资家面临的是n个企业T个阶段的投资决策问题时,故可令风险投资家的投资决策变量为xtj,当xtj=1时,表示风险投资家将对风险企业i进行投资;反之,则xtj=0。其中i=1, 2, 3, …, n; t=1, 2, 3, …, T。由此可知,本文所描述的风险投资问题本质上是一个动态风险投资0-1规划问题。在构建决策模型之前,首先讨论投资资金约束、风险约束和目标函数三方面的问题。
(一) 投资资金约束 1. 风险投资家的阶段资金约束在第t阶段,风险投资家与第j个风险企业事先协商的投资金额为st, j,相应的决策变量为xt, j,所以可得出在第t阶段,对全部n个风险企业的投资资金即为:
| $ \sum\limits_{j = 1}^n {{s_{tj}} \bullet {x_{tj}} = {s_t}}, 其中t = 1, 2 \cdots, T $ | (1) |
则对全部T个阶段,风险投资家全部的投资资金为
| $ {s_1} + {s_2} + \cdots {s_t} + \cdots + {s_T} \le {S_0}, t = 1, 2, \cdots T $ | (2) |
根据投资对象路径依赖假设,即风险投资家如果在前期选择不投资某家风险企业,则后期也不会选择投资该企业,则有:
| $ {x_{tj}} \le {x_{t-1, j}}, t = 2, 3, \cdots, T;j = 1, 2, \cdots n $ | (3) |
对于风险投资家而言,其投资风险企业的收益来源于投入风险企业的资金不断增值。对于风险投资家来说,在第t阶段末,所实现的全部投资价值等于在第t-1阶段末的资产价值与在第t阶段期初投入风险企业的本金之和在本阶段所创造的价值。以第j家风险企业为例,设在第t阶段之前,也即在第t-1阶段末已经获得的资金投入的总价值为Zt-1, j,同时风险企业在第t阶段初获得的风险投资资金为stj·xtj,那么,在第t阶段初,可视作风险投资家对第j家风险企业实际投入资金(Zt-1, j+stj·xtj)。
考虑到风险投资家在每阶段会对之前阶段投资的风险企业,在本阶段做出继续投资或不再继续投资的选择,因此,投资过程将会出现以下两种情形:
第一,在第t阶段,风险投资家继续对第j家风险企业进行投资,则在第t阶段末,对第j家风险企业投资在第k种情况出现时获得的实际总价值可以表示为(Zt-1, j+stj·xtj)·(1+Rtj(kt)),其中,Rtj(kt)为第t阶段末,风险投资家投资第j家风险企业时,在第k种情况下所获得的实际收益率。
第二,在第t阶段,风险投资家放弃对第j家风险企业进行投资,则意味着本阶段不再有资金投入第j家风险企业,而之前投入到该家风险企业的所有资金价值Zt-1, j,在第k种情况出现时将以一个较低的收益率R′tj(kt)增长。在第t阶段末第j家风险企业在第k种情况出现时的实际总价值可以表示为:Zt-1, j·(1+R′tj(kt))。
综合上述两种情形,在第t阶段末,风险投资家投资第j家风险企业在第k种情况出现时的所有资金总价值可表示为:
| $ \begin{array}{l} {Z_{tj}}({k_t}) = ({Z_{t- 1, j}} + {s_{tj}} \bullet {x_{tj}})[(1 + {R_{tj}}({k_t})) \bullet {x_{tj}} + \\ (1 + {{R'}_{tj}}({k_t}))(1-{x_{tj}})] \end{array} $ | (4) |
其中t=2, …, T;k=1, …, K。
当第1阶段时,风险投资家投资第j家风险企业在第k种情况出现时的所有资金总价值可表示为:
| $ {Z_{1j}}({k_t}) = {s_{1j}} \bullet {x_{1j}} \bullet (1 + {R_{1j}}({k_t})), j = 1, \cdots, n;k = 1, \cdots, K $ | (5) |
在第t阶段末,风险投资家投资的全部m家风险企业在第k种情形发生时的所有资金总价值为:
| $ {Z_t}({k_t}) = \sum\limits_{j = 1}^n {{Z_{tj}}({k_t}) = } \sum\limits_{j = 1}^n {{Z_{tj}}({k_t}) = ({Z_{t- 1, j}} + {s_{tj}} \bullet {x_{tj}})[(1 + {R_{tj}}({k_t})) \bullet {x_{tj}} + } (1 \\+ {{R'}_{tj}}({k_t}))(1-{x_{tj}})] $ | (6) |
其中t=2, …, T;k=1, …, K。
在第1阶段末,风险投资家对风险企业的全部投资在第k种情形发生时的所有资金总价值为:
| $ {Z_t}({k_t}) = \sum\limits_{j = 1}^n {{Z_{tj}}({k_t}) = } \sum\limits_{j = 1}^n {_{{s_{1j}}} \bullet (1 + {R_{tj}}({k_t})} \bullet {x_{tj}}, t = 2, \cdots, T;k = 1, \cdots, K $ | (7) |
在风险投资实践中,阶段投资收益均是不能在阶段期末及时兑现的,这意味着风险投资每个阶段初的可用于投资的资金额不等于上阶段末全部资产资金,这是构建多阶段风险投资组合与证券多阶段投资组合相区别的一个最大问题。为了便于构建模型,假设全部的投资均只能在T期末才能收回。由于t-1阶段末的风险投资资产价值不能在当期末迅速变现为现金以进行t阶段投资,因此能够投入t阶段的资金只能是尚未进行风险投资的风险投资基金中剩余资金的一部分。
本部分讨论风险投资组合各阶段的风险控制问题。不考虑累积至t-1期末的资产价值在第t期的投资风险,仅考虑各期投入的新资金的风险控制问题。
在第t阶段末,在第k种情况下风险投资家当期初投入资金所构建的风险投资组合的期望价值,可表示为:
| $ {v_t}({k_t}) = \sum\limits_{j = 1}^n {{V_{tj}}({k_t})} = \sum\limits_{j = 1}^n {{s_{tj}} \bullet {x_{tj}} \bullet (1 + {R_{tj}}({k_t})), t = 1, \cdots, T;k = 1, \cdots K} $ | (8) |
我们采用Yu et al.[16]提出的绝对离差控制投资组合的风险方法。设πt为第t阶段的风险投资组合的最低预定义资产价值,即当新投入资金stj.xtj形成的风险投资组合在第t期的期望价值Vt(kt)低于πt时,风险投资家将不再进行任何形式的投资。同时,以BRt表示风险投资组合在第t阶段的破产临界点。
BRt的概率为:P(BRt)=P(Vt(kt)≤πt|Vi(kt)>πi, i=1, …, T-1)
设需要控制的临界状态发生在P(BRt)≤αt,根据切比雪夫不等式,有:
| $ \begin{array}{l} P(B{R_t}) = P({V_t}({k_t})) \le {\pi _t}|{V_i}({k_t}) \ge {\pi _i}, i = 1, \\ \cdots, t-1 \le P({V_t}({k_t}) \le {\pi _t}) \le \\ P(|{V_t}({k_t})-E({V_t}({k_t}))| \ge E({V_t}({k_t})-{\pi _t})\\ \le \frac{{E(|{V_t}({k_t}) - E({V_t}({k_t}))|)}}{{E({V_t}({k_t})) - {\pi _t}}} \le {\alpha _t} \end{array} $ |
参照Yu et al.(2010),提出如下风险投资组合绝对离差约束条件:
| $ \begin{array}{l} E(|{V_t}({k_t})-E({V_t}({k_t}))|) = \\ E(|\sum\limits_{j = 1}^n {{R_{tj}}({k_t}) \bullet {s_{tj}}{x_{tj}}-\sum\limits_{j = 1}^n {E({R_{tj}}({k_t})) \bullet {s_{tj}}{x_{tj}}} } |)\\ \le n \bullet \mathop {\max }\limits_{1 \le j \le n} E(|{R_{tj}}({k_t}) \bullet {s_{tj}}{x_{tj}}-{r_{tj}} \bullet {s_{tj}}{x_{tj}}|) \end{array} $ |
因而有,
在此,给A一个确定的αt界限,来具体限定在第t阶段风险投资组合的风险大小,则:
| $ \frac{{E(|{V_t}({k_t})-E({V_t}({k_t}))|)}}{{E({V_t}({k_t}))-{\pi _t}}} \le \frac{{n\;\mathop {\max }\limits_{1 \le j \le n} E(|{R_{tj}}({k_t}) \bullet {s_{tj}}{x_{tj}}-{r_{tj}} \bullet {s_{tj}}{x_{tj}}|)}}{{E({V_t}({k_t})) - {\pi _t}}} \equiv {\alpha _t} \equiv n{\varepsilon _t} $ |
其中,εt为风险投资家在第t阶段,能承受当期风险投资组合的最大风险水平。
进而可以转换为:
| $ \mathop {\max }\limits_{1 \le j \le n} E(|{R_{tj}}({k_t})- {r_{tj}}|{s_{tj}}{x_{tj}}) \le {\varepsilon _t}[E({V_t}({k_t}))-{\pi _t}], t = 1, \cdots, T $ | (9) |
由资金约束和风险约束对Zt(kt)和Vt(kt)的描述可知,Zt(kt)表示的是风险投资家在第t阶段末,第k种情形下所有投资资金在当期增值后的价值,而Vt(kt)则表示的是在第t阶段末,第k种情形下当期所投资的资金增值后的价值。两者的关系可表示为:
| $ \begin{array}{l} {Z_t}({k_t}) = \sum\limits_{j = 1}^n {{Z_{tj}}({k_t}) = \sum\limits_{j = 1}^n \begin{array}{l} ({Z_{t- 1, j}} + {s_{tj}} \bullet {x_{tj}})\\ [(1 + {R_{tj}}({k_t})) \bullet {x_{tj}} + (1 + {{R'}_{tj}}({k_t})(1- {x_{tj}})) \end{array} } \\ = \sum\limits_{j = 1}^n \begin{array}{l} {Z_{t- 1, j}} \bullet [1 + {R_{tj}}({k_t})) \bullet {x_{tj}} + (1 + {{R'}_{tj}}({k_t})\\ (1-{x_{tj}})] + \sum\limits_{j = 1}^n {{s_{tj}}} \bullet {s_{tj}}(1 + {R_{tj}}({k_t})) \end{array} \end{array} $ | (10) |
其中,当t=1时,则有Z1(kt)=V1(kt),表明在第1阶段末,风险投资家对已投风险企业的资金总价值就是等于风险投资家在第1阶段的投资组合的期望价值。
(四) 一般模型的建立风险投资家的决策是:在初期投资风险企业构建相应的风险投资组合,并在风险投资的后续阶段,不断优化并分配资金到风险投资组合中,同时,始终控制每阶段的风险投资组合风险以及投资过程的价值组合风险在一定的风险阈值之内,以求在整个投资阶段结束时,能获得尽可能多的投资收益。即在一定风险承受范围内,风险投资家追求在第T(T>1)阶段末,ZT的最大化。
针对上述问题,可构建如下多阶段风险投资组合规划模型:
| $ \begin{array}{l} \max E({Z_T}({k_T}))\\ s.t.\left\{ \begin{array}{l} {x_{tj}} = \left\{ \begin{array}{l} 0, ABC\\ 1, ABC \end{array} \right., t = 1, \cdots, T;j = 1, \cdots, n\\ {x_{tj}} \le {x_{t- 1, j}}, t = 2, \cdots, T;j = 1, \cdots, n\\ \sum\limits_{j = 1}^n {{s_{tj}} \bullet {x_{tj}} = {s_t}, t = 1, \cdots, T} \\ {s_1} + {s_2} + \cdots {s_t} + \cdots + {s_T} \le {S_0}, t = 1, 2, \cdots T\\ {r_{tj}} = \sum\limits_{{k_t} = 1}^K {{R_{tj}}({k_t}) \bullet {p_{tj}}({k_t}), t = 1, \cdots, T;j = 1, \cdots, n} \\ {Z_t}({k_t}) = \sum\limits_{j = 1}^n {{Z_{tj}}({k_t}) = } \sum\limits_{j = 1}^n {{Z_{tj}}({k_t}) = ({Z_{t- 1, j}} + {s_{tj}} \bullet {x_{tj}})[(1 + {R_{tj}}({k_t})) \bullet {x_{tj}} + } \\ (1 + {{R'}_{tj}}({k_t}))(1-{x_{tj}})], t = 2, \cdots, T;{k_t} = 1, \cdots, K\\ {v_t}({k_t}) = \sum\limits_{j = 1}^n {{s_{tj}} \bullet {x_{tj}} \bullet (1 + {R_{tj}}({k_t})), t = 1, \cdots, T;{k_t} = 1, \cdots K} \\ \mathop {\max }\limits_{1 \le j \le n} E(|{R_{tj}}({k_t}) = {r_{tj}}|{s_{tj}} \bullet {x_{tj}}) \le {\varepsilon _t}[E({V_t}({k_t}))-{\pi _t}, t = 1, \cdots, T;{k_t} = 1, \cdots K]\\ {y_{tj}} = {Z_{t -1, j}} + {s_{tj}} \bullet {x_{tj}}, t = 2, \cdots, T;j = 1, \cdots, n\\ {y_{1j}} = {s_{1j}} \bullet {x_{1j}}, j = 1, \cdots, n \end{array} \right. \end{array} $ |
该规划模型本质上是一个多阶段非线性0-1规划模型,模型的解析解难以获得。因此,本文拟通过一个数值算例的求解和分析来说明模型的应用。
四、 数值算例设风险投资家经过调研,在众多可供选择的风险企业中,筛选出12个符合其投资标准的风险企业。风险投资家与风险企业已经协商好对风险企业各期的具体投资金额。风险投资家专业团队已经预测了风险企业在各种情形下的投资收益率及其概率分布,
包括对风险企业投资之后在放弃阶段的收益率及其概率分布。由于篇幅所限,数据不在此列出。风险投资家筹集资金3亿元,对这些风险企业分4个阶段进行投资。由于资金有限,风险投资家考虑将有限的资金在各风险企业中进行最优分配,使得风险投资组合在获得满意的收益率同时,所承担的风险最小。
假设风险投资家的最低期望值(πt)为每阶段投资资金的90%,同时,在考虑风险投资家的最大风险承受水平时,我们认为风险投资家对每个阶段的最大风险承受水平是一致的。因而,在接下来的应用中,我们将考虑四种情况下的最大风险承受水平,即分别为0.10、0.11、0.12、0.13。通过改变风险投资家对投资组合的风险承受水平,来调节风险阈值,利用多阶段风险投资的一般模型,来求出最优化的投资组合。
此外,我们在应用中还考虑风险投资家风险偏好为风险中性的投资情形,即风险投资家在投资决策中不考虑风险约束问题,仅追求资金约束下的期末价值最大化。此时模型仅需在模型中去掉风险约束。
在matlab7.12环境下,利用bintprog函数来对多阶段风险投资的一般模型进行编程求解,根据风险投资家不同的风险承受水平及最低期望值,得出最优的风险投资组合结果,如表 1所示。
| 表 1 不同风险承受水平下的多阶段投资组合最优结果 |
在表 1中,共有五组最优的风险投资组合,其中前四组是根据风险投资家不同的风险偏好而得到的投资组合,最后一组是风险投资家在不考虑任何风险约束的情况下,仅以总资金作为约束条件而得到的投资组合。从表 1中,我们可以得出:
第一,在不同风险约束条件下,会有有不同的风险投资组合,也就是说,风险投资家可以根据自己不同的风险偏好,通过多阶段风险投资的一般模型来筛选出不同的优化风险投资组合。
第二,在同一风险水平下,发现每阶段的风险投资组合出现了不同的变化,这种变化符合多阶段风险投资的一般模型的假设,即在风险投资的过程中,风险投资家在第1阶段会从众多风险企业中,挑选一部分风险企业进行投资,而在之后的阶段,风险投资家只能对投资组合中的风险企业做出是否继续投资的抉择,不能再挑选其他风险企业进行投资。
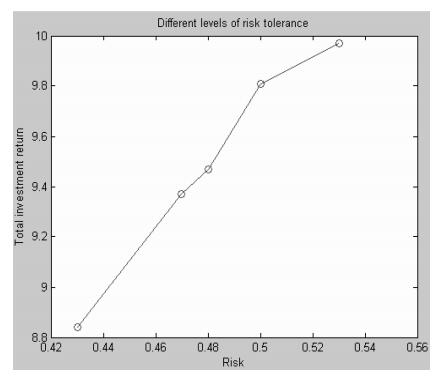
同时,根据表 1的结果,并参照已知的数据可以计算出每阶段最优的风险投资组合的投资额、组合风险和最优总投资额以及总投资收益和总投资风险,分别见表 2、表 3以及图 1。
| 表 2 每阶段最优的投资额、组合风险及总投资额 |
| 表 3 最优的总投资收益及总投资风险 |
|
图 1 不同风险承受水平下最优的总收益及其风险值 |
对表和图的分析可以得出:一是随着风险投资家的风险承受水平的增大,风险投资家能接受具有更高风险、高收益的投资组合;反之,随着风险投资家的风险承受水平的减小,风险投资家在选择投资组合时,变得更加谨慎,容易接受风险相对较小的投资组合。二是在较低的风险水平下,每阶段投资的风险金额相对比较平均,并且在前三个阶段对风险投资组合投入的金额都相对较多,而在第4阶段投资额相对较少。查询原始数据,可以发现在第4阶段,每家风险企业与风险投资家签订的投资金额是四个阶段中最高的,风险与收益也是最大的。因而,说明在较低风险水平下,多阶段风险投资的一般模型给出的投资组合是最优的。
| [1] | Kortum S, Lerner J. Assessing the Contribution of Venture Capital to Innovation[J]. RAND Journal of Economics, 2000,31: 674–692. DOI: 10.2307/2696354 |
| [2] | André F Gygax, Anna Griffiths. Do venture capitalists imitate portfolio size?[J]. Financial Markets and Portfolio Management, 2007,21(1): 69–94. DOI: 10.1007/s11408-006-0040-4 |
| [3] | Christensen J L. The Development of Geographical Specialization of Venture Capital[J]. European Planning Studies, 2007,15(6): 817–833. DOI: 10.1080/09654310701232137 |
| [4] | Yang Y, Narayanan V K, Zahra S. Developing the selection and valuation capabilities through learning:The case of corporate venture capital[J]. Journal of Business Venturing, 2009,24(3): 261–273. DOI: 10.1016/j.jbusvent.2008.05.001 |
| [5] | Bottazzi L, Da Rin M, Hellmann T. Who are the active investors?Evidence from venture capital[J]. Journal of Financial Economics, 2008,89(3): 488–512. DOI: 10.1016/j.jfineco.2007.09.003 |
| [6] | Barry C, Muscarella C, Peavy J, Vetsuypens M. The role of venture capital in the creation of public companies:evidence from the going-public process[J]. Journal of Financial Economics, 1990(27): 447–472. |
| [7] | Lerner J. The syndication of venture capital investments[J]. Financial Management, 1994(23 Autumn): 16–27. |
| [8] | Brav A, Gompers P A. Myth or reality?the long-run underperformance of initial public offerings:evidence from venture and nonventure capital-backed companies[J]. Journal of Finance, 1997(52): 1791–1821. |
| [9] | 张学勇, 廖理. 风险投资背景与公司IPO:市场表现与内在机理[J]. 经济研究, 2011(6): 118–132. |
| [10] | Hellmann T, Puri M. Venture capital and the professionalization of start-up firms:empirical evidence[J]. Journal of Finance, 2002(57): 69–97. |
| [11] | 钱苹, 张帏. 我国创业投资的回报率及其影响因素[J]. 经济研究, 2007(5): 78–90. |
| [12] | Gorman M, Sahlman W A. What do venture capitalists do?[J]. Journal of Business Venturing, 1989(4): 231–248. |
| [13] | Gompers P A. Optimal Investment, Monitoring and the Staging of Venture Capital Optimal Investment, Monitoring, and the Staging of Venture Capital[J]. Journal of Finance, 1995(5): 1461–1489. |
| [14] | Inderst R, Mueller H M, Munnich F. Financing a Portfolio of Projects the Role of Venture Capital[J]. Review of Financial Studies, 2007,20(4): 1289–1325. DOI: 10.1093/rfs/hhl038 |
| [15] | Sahlman Wa. The Structure and Governance of Venture Capital Organizations[J]. Journal of Financial Economics, 1990,27(2): 473–521. DOI: 10.1016/0304-405X(90)90065-8 |
| [16] | Yu M, Takahashi S, Inoue H, Wang S. Dynamic portfolio optimization with risk control for absolute deviation model[J]. European Journal of Operational Research, 2010,201: 349–364. DOI: 10.1016/j.ejor.2009.03.009 |
 2016, Vol. 18
2016, Vol. 18
