分级基金是一种根据收益分解成低风险的A类份额和高风险的B类份额的基金,分级A获得约定收益,分级B获取剩余收益。2007年,我国第一支主动投资型分级基金(国投瑞银瑞福分级基金)出现后,该类市场发展十分迅速,截至2015年1月30日,已成立的分级基金有100多只,基金市值超过千亿。从市场实践看,分级基金已经逐步对我国资本市场的运行和稳定、投资者投资结构和收益分布产生重要影响。
2014年下半年开始,我国股票市场迎来罕见的快速上涨行情,分级B备受市场关注,其杠杆性质使得分级B的溢价率持续走高。由于分级A和分级B可以与母基金按照约定的比例相互转换,母基金与分级A和分级B之间形成折溢价套利机制,使得A+B的价格围绕母基金净值波动。因此当分级B溢价时,分级A大多数处于折价状态。具体而言,在牛市中,分级B易形成较大的溢价,投机者的溢价套利行为会使分级A的价格遭到压制,如果此时购买分级A相当于为牛市中的股票购买一份看跌期权,具有一定的股市避险作用。而在熊市中,当母基金净值下跌,分级A的净值仍按照约定的收益逐日增加,分级B净值则在快速减少,分级B的下折概率增大。当触发下折时,分级A通过折算机制获得额外的收益,即分级A的期权价值;若分级B没有下折,分级A就不进行折算,无法获得额外收益,则期权价值为0。在2015年6-7月的我国股市崩盘过程中,分级B接连重挫,濒临下折,分级A的期权性质和避险功能开始突出显现出来,受到各类投资者的广泛重视。因此,我们极有必要深入分析研究分级A的期权价值及其影响因素。
一、 文献综述我国很多学者认为分级A除具有固定收益外,还具有期权价值与配对转换价值。例如,马刚(2014)指出A、B份额的互动性质可以使分级A衍生出配对转换价值及看跌期权价值,并在理论上指出A类份额在接近下折时是一种看跌期权。[1]方正证券分级A专题报告(2015)中也指出分级A具有丰厚的期权价值与配对转换价值。[2]其中,为保证分级A的低风险,分级A每年都会获得约定的收益,具有固定收益性质。当分级B下跌到一定程度触发下折时,分级A的市价与净值之间的差值形成了期权价值。分级A可以与分级B合并转换为母基金的权利是其配对转换价值,具体而言,当分级B出现流动性不足、难以在二级市场上卖出时,往往通过购买分级A转换为母基金。需求的增加使分级A的价格升高,形成了配对转换价值。分级A具有的三种价值中,期权价值是分级A能否正确定价的关键因素,也是最难以评估的。从文献看,关于分级A定价方法的研究成果十分有限,没有跟上市场创新的步伐,研究方法值得商榷,有诸多需要改进之处。
我国学者对分级基金的定价研究中,普遍使用的方法是Black-Scholes模型及蒙特卡洛模拟法。马亦舟(2012)分别使用了Black-Scholes模型与蒙特卡洛模拟法对国泰估值优势(LOF)进行定价,但其认为无论采用哪种方式都无法对优先份额(低风险的A类份额)的市场价格进行有效拟合。[3]尹航(2013)使用蒙特卡洛模拟法给出分级基金的理论定价,并说明Black-Scholes模型的使用范围仅限于可以进行期权解析的分级基金。[4]这两篇文献均给出分级基金A类份额和B类份额的定价方法,但由于Black-Scholes模型一般用于标准欧式期权定价,且折算机制的存在使基金的现金流具有路径依赖的特征,该定价方法仅适用于具有固定运作期、不具有折算机制的分级基金。我国学者(杨倩君,2014)对永续型分级基金的定价研究中,更侧重于分级B类份额的定价,对分级A类份额的定价仅考虑其固收性质。[5]王静明(2013)则以申万深成分级基金为对象,认为永续型分级基金A类份额的内在价值等于债券价值加配对转换价值[6],没有考虑其期权价值,也没有给出具体的定价公式。随着分级基金A类份额期权价值的发现,分级A的定价不能仅考虑固定收益及配对转换价值。在考虑分级A期权价值的前提下,我国尚无关于分级A类份额的期权价值评估及其定价的学术研究文献,仅有方正证券的专题报告中提出了分级A期权价值的计算方法。因此,在对分级A类份额定价之前,应从学术研究的视角,采用更为严谨的方法对分级A的期权价值加以评估。另一方面,需要注意的是,我国2014年以来发行的分级基金最常见的是融资型分级基金,其中绝大多数是永续型基金,且具有折算机制,因此已经无法简单地使用Black-Scholes模型对分级A内含的美式看跌期权加以定价。为此,必须寻找合理的方法对分级A的期权价值进行研究。
从分级基金的设计机制看,分级A具有显著的二元看跌期权价值。所谓二元期权又称为固定收益期权,是基于一种标的资产在到期时收盘价是高于还是低于执行价格的结果,决定是否获取约定的固定收益的期权。到期时,如果标的资产价格符合事先约定的启动条件,二元期权的购买者可以获得一个固定收益,反之则损失固定的期权费。因此,研究分级A的期权价值可从二元期权角度予以展开。这也是方正证券(2015)对分级A所具有的期权价值进行研究的思路。不过,方正证券的研究中存在一个值得商榷的问题,即其假定在约定收益为6%、波动率为25%的条件下计算分级A的期权价值。[2]本文认为,母基金的预期收益率及波动率是影响分级A下折时间的重要因素,也是分级A期权价值准确度量的前提,应采用合适的模型对母基金的收益率及波动率进行预测,而不能简单地对这两个变量进行假定。Stentoft(2005)[7],Hsieh and Ritchken(2005)[8]使用GARCH模型研究期权定价问题,估计期权标的资产的收益波动率,认为GARCH模型可以提高期权定价模型的精准度。吴恒煜等(2014)[9]对中国大陆和香港权证定价的实证研究中,考虑到股票收益率在GARCH模型下的非正态性,以及收益率标准差序列的非对称特征,使用Levy过程修正下的GJR-GARCH模型对股票权证加以定价,通过对GARCH模型的改进得到更优的股票权证定价方法。分级基金的母基金可以看作分级A内含期权的标的资产,可根据母基金的收益率序列特征使用改进后的GARCH模型,进一步优化分级A期权价值的度量方法。为综合考虑母基金收益率序列的非对称性及滞后效应,采用ARMA-GJR-GARCH模型预测母基金收益率及其波动率。
分级A的二元看跌期权价值往往会受到分级基金折价率、下折时间、上折、母基金净值距离下折的距离、母基金的波动率、AB份额比例、约定收益率、贴现率的影响。其中,母基金的波动率又直接影响了分级基金触发上折与下折的概率,进一步影响分级A的期权价值。因此分级A期权价值度量的合理与否,取决于母基金的波动率预测是否准确。李进芳(2014)构建了市场情绪指数[10],建立了带信息多期交易的情绪资产定价模型,表明投资者情绪是影响资产价格的重要因素,正向情绪会向上加剧股票价格的过度反应,负向情绪导致股价的过度下跌。这也提示,市场情绪具有对资产价格助涨助跌的作用,会直接影响到母基金的预期收益率及波动率,进而影响分级A的期权价值。
通过以上的文献梳理,我们可以再借助Uygur和Tas(2004)关于市场情绪对股票市场收益率与波动率的影响研究[11],将市场情绪指标引入到波动率模型,建立一个全新的模型,以更精准地度量分级A的二元期权价值。
二、 分级基金期权价值的形成和计算方法分级基金的下折条款以及分级A折价交易现象是分级A具有二元期权价值的本质原因。由于分级B的杠杆性质,受到投资者的普遍关注,其较大的交易量使得分级B常出现溢价交易,而分级A处于折价交易状态。另一方面,分级B每年都会给分级A约定的收益,即使母基金净值没有发生亏损,分级B也最终会触发下折,给折价的分级A带来额外的收益,这个收益便是分级A内含的期权价值。下折条款中约定:B类份额净值下降到0.25及以下时发生下折,A类份额在维持AB份额固定比例的前提下,净值归1,份额折为原先的1/4,其余3/4转化为母基金份额派发给持有人。因此价格与净值之间这部分折价的3/4便是分级A的期权价值。假设分级A的份额数为n,净值为1(其中约定收益带来的利息为固定收益,不考虑在期权价值内),分级A的价格为φ(φ<1),那么分级A的折价率为1-φ。当触发下折时,分级A净值归1,份数折算为n/4,另外的3n/4转化为母基金,因此分级A的下折收益为3n/4(1-φ)。若将下折日看成期权到期日,那么3n/4(1-φ)便是二元期权约定的固定收益。
配对转换条款是指母基金与分级A和分级B之间可以配对转换,即可以将持有的母基金申请转换为约定比例的A类份额和B类份额,或将持有的A类份额和B类份额以约定的比例转换为母基金。当母基金大幅溢价时,可以实现溢价套利;当母基金大幅折价时,可以实现折价套利。假设AB份额比为a,分级A的交易价格为PA,分级B的交易价格为PB,母基金净值用S表示,基于无套利定价原则,A和B的交易价格应围绕母基金净值波动。假设没有交易成本和冲击成本,分级A、分级B的交易价格以及母基金净值的关系如下:
| $a{{P}_{A}}+{{P}_{B}}=\left( a+1 \right)\times S$ | (1) |
由于分级B的杠杆性质,市场行情被看好时,其交易活跃度高。当交易热度促使PB上涨时,另一方PA便下降,因此分级A普遍处于折价交易状态。当市场上出现暴跌,分级B净值下跌时,分级A的期权价值便可以实现。分级A虽只有在达到下折这个特定条件时才可以获得固定的收益,但由于配对转换机制的存在,分级B濒临下折时,投资者可以通过购买分级A,与分级B合并转换成母基金的方式放弃对分级B的持有,需求的增加会抬高分级A的价格。配对转换收益便是已经实现的期权价值,此时期权的内涵价值增加,时间价值减少,通过提前行权便可以获取一定的期权收益。当分级B濒临下折时,分级A的固定收益相比于期权价值可以忽略不计,此时分级A是一个特殊的二元美式看跌期权。下面给出分级A在到期日的价值为:
| $V\left( S\left( T \right),T \right)=\left\{ \begin{matrix} 3n/4\left( 1-\varphi \right) & {{S}_{B}}\left( T \right)<0.25且\varphi <1 \\ 0 & {{S}_{B}}\left( T \right)\ge 0.25或\varphi \ge 1~ \\ \end{matrix} \right.$ | (2) |
其中SB(T)是到期日分级B的净值,其值由母基金净值和分级A的净值计算得出,T为发生下折的时间。分级A作为二元看跌期权的特殊之处:一是由于分级B每年都会给分级A支付固定的成本(分级A的约定收益率),使得分级B最终总会触发下折,比普通的二元期权行权的概率更大;二是期权的到期日T是未知的,到期时的期权价值却是一定的,即3n/4(1-φ)。折溢价率决定期权价值是否为正,下折时间影响期权价值的大小;三是分级A的期权价值影响因素颇多,如:折价率、下折时间、上折、母基金净值距离下折的距离、母基金的波动率、AB份额的比例、约定收益率和贴现率等均会对二元期权价值产生不同的影响。从计算公式来看,折价率是分级A期权价值的构成基础,在交易时刻,只有折价交易才能保证下折时的期权价值为正。分级基金触发下折的时间越长,分级A的期权价值就会随时间缩水。当母基金触发上折时,分级B净值重新归1,更容易触发下折;通常,母基金净值距离下折的距离越大,触发下折的时间就会越长。但是,母基金距离下折的距离并非与期权价值呈完全的负相关关系。当母基金距离下折的距离较大,且接近上折阈值时,期权价值反而会变大,这是由于上折后的分级B更容易触发下折;母基金的波动率越大,越容易在短时间内达到下折阈值,或增加触发上折的几率,进一步触发下折;约定收益率越大,分级B每年支付给分级A的固定成本越大,越容易触发下折,期权价值增加。但也存在着相反的情况,当约定收益率较大时,分级A的需求会增加,折价率会减少,由于折价率对期权价值的影响更大,期权价值便会相应减少;AB比越大,分级B的杠杆越大,这等同于母基金的波动率越大,期权价值越大。
三、 基本模型及实证检验期权定价模型的假设条件之一是:金融资产的收益率服从对数正态分布,但实际上金融资产收益率却呈现尖峰厚尾的特征,Rockenbach(2004),Xiao(2010)和Thavaneswaran(2013)[12-14]均在分数布朗运动环境下研究期权定价方法。因此我们在实证分析时,也将假定期权标的资产服从分数布朗运动,在此基础上再根据二元期权定价方法分析分级A期权价值的影响因素。
这里首先假定二元期权的标的资产服从分数布朗运动[15],以便得到风险资产价格的变化轨迹。假设风险资产{S(t),t≥0}满足随机微分方程:
| $dS\left( t \right)=\mu \left( t \right)S\left( t \right)dt+\sigma \left( t \right)S\left( t \right)d{{B}_{H}}\left( t \right)$ | (3) |
其中,{BH(t),t ≥0}是概率空间(Ω,F,FtH,P)上的分数布朗运动,是满足以下条件的连续高斯过程。
1. BH(0)=EBH(t)=0
2. E[BH(t)BH(s)]=$\frac{1}{2}$(|t|2H+|s|2H-|t-s|2H) t, s>0
3. 当H=$\frac{1}{2}$,是标准布朗运动,0<H<$\frac{1}{2}$,具有反持续性,当$\frac{1}{2}$<H<1,序列是趋势增强的,具有持续性。
假设μ等于μ(t)的期望收益率,等于无风险利率,使用Wick积分[16]得到:
| $\begin{align} & S\left( t \right)=S\left( 0 \right)exp\{\mu t-\int_{0}^{t}{H}{{\sigma }^{2}}\left( s \right){{s}^{2H-1}}ds+ \\ & \int_{0}^{t}{\sigma }\left( s \right)d{{B}_{t}}^{(H)}\left( s \right)\}\text{ }S\left( 0 \right)={{S}_{0}}>0 \\ \end{align}$ | (4) |
根据风险中性理论得到t时刻分级A的期权价值为:
| $V\left( S\left( t \right),t \right)=3/4{{e}^{-r(T-t)}}n\left( 1-\varphi \right)$ | (5) |
为了求出分级A的期权价值,我们的目标是确定T折时间T。首先根据分数布朗运动模型通过蒙特卡洛模拟获取母基金净值波动路径,进而计算出分级B的净值路径。当母基金净值达到1.5以上时触发上折,路径从1重新开始;当分级B净值达到0.25以下时触发下折,则路径停止。以沪深300分级基金为例,在2015年7月31日这一天,对未来母基金净值走势进行上万次的模拟,得到平均下折时间,进而得到这一天分级A的期权价值。
考虑到分级A属于固定收益类产品,且分级A获取下折收益的时间一般超过一年,故使用1年期上海银行间同业拆放利率(Shibor)作为无风险利率。使用GARCH族模型模拟预测的收益率序列及条件方差序列对分级A进行定价,建立母基金对数收益率方程:
| ${{r}_{t}}=\ln \left( S\left( t \right) \right)-\ln \left( S\left( t-1 \right) \right)$ | (6) |
以信诚沪深300分级基金为例。在2015年7月31日这一天,沪深300A的折价率较高,6月下旬股市暴跌使得近期市场情绪低迷,此时分级A是股市较为理想的套保工具。使用2013年8月28日到2015年7月31日的历史母基金净值,得到一组母基金的收益率序列。该收益序列呈现峰度过大和偏度为负,且JB指标强烈拒绝了正态性的假设,呈现明显的波动率簇性,这是由于股票市场上负面消息的影响要大于正面消息的影响;另一方面,市场情绪会加速负面消息的影响程度,同时影响母基金收益率变化,进而改变下折时间和分级A的期权价值。Glosten(1993)开发的GJR-GARCH模型[17-18]能够很好地处理资产收益率序列的有偏分布,因此使用ARMA(2,2)-GJR-GARCH(1,1)模型并将市场情绪考虑在内,得到沪深300A的条件方差序列:
| $\begin{align} & {{r}_{t}}={{\gamma }_{0}}+{{\gamma }_{1}}AR\left( 1 \right)+{{\gamma }_{2}}AR\left( 2 \right)+{{\gamma }_{3}}MA\left( 1 \right)+ \\ & {{\gamma }_{4}}MA\left( 2 \right)+{{\gamma }_{5}}MS{{I}_{t}}+{{\varepsilon }_{t}}~{{\varepsilon }_{t}}\sim N(0,{{\sigma }_{t}}^{2}) \\ \end{align}$ | (7) |
| $\begin{align} & {{\sigma }_{t}}^{2}={{\alpha }_{0}}+(\alpha +\delta {{I}_{t-1}}){{\varepsilon }_{t-1}}^{2}+\beta {{\sigma }_{t-1}}^{2}+ \\ & {{\theta }_{1}}{{(MS{{I}_{t-1}})}^{2}}{{D}_{t-1}}+{{\theta }_{2}}{{(MS{{I}_{t-1}})}^{2}}(1-{{D}_{t-1}}) \\ \end{align}$ | (8) |
其中,MSI表示市场情绪,当市场不存在情绪时,MSI值为0,当MSI>0时,表示存在正的市场情绪,当MSI<0时,表示存在负的市场情绪;It、Dt是虚拟变量,当εt-1≥0时,It=0,当εt-1<0时,It=1,表示股票市场上负向冲击大于正向冲击;当存在正向市场情绪,即MSI≥0时,Dt=1,当存在负向市场情绪,MSI<0时,Dt=0;由于正向情绪与负向情绪对波动率的影响不同,因此分别设置不同的两个参数θ1和θ2来表示正向情绪影响和负向情绪影响程度。
为了得到市场情绪对期权价值的影响关系,我们首先考虑当市场情绪为零的情形,使用不含市场情绪的ARMA(2,2)-GJR-GARCH(1,1)模型得到的估计结果为:
| ${{\sigma }_{t}}^{2}=3.12\times {{10}^{-7}}+(0.079-0.029{{I}_{t-1}}){{\varepsilon }_{t-1}}^{2}+0.94{{\sigma }_{t-1}}^{2}$ | (9) |
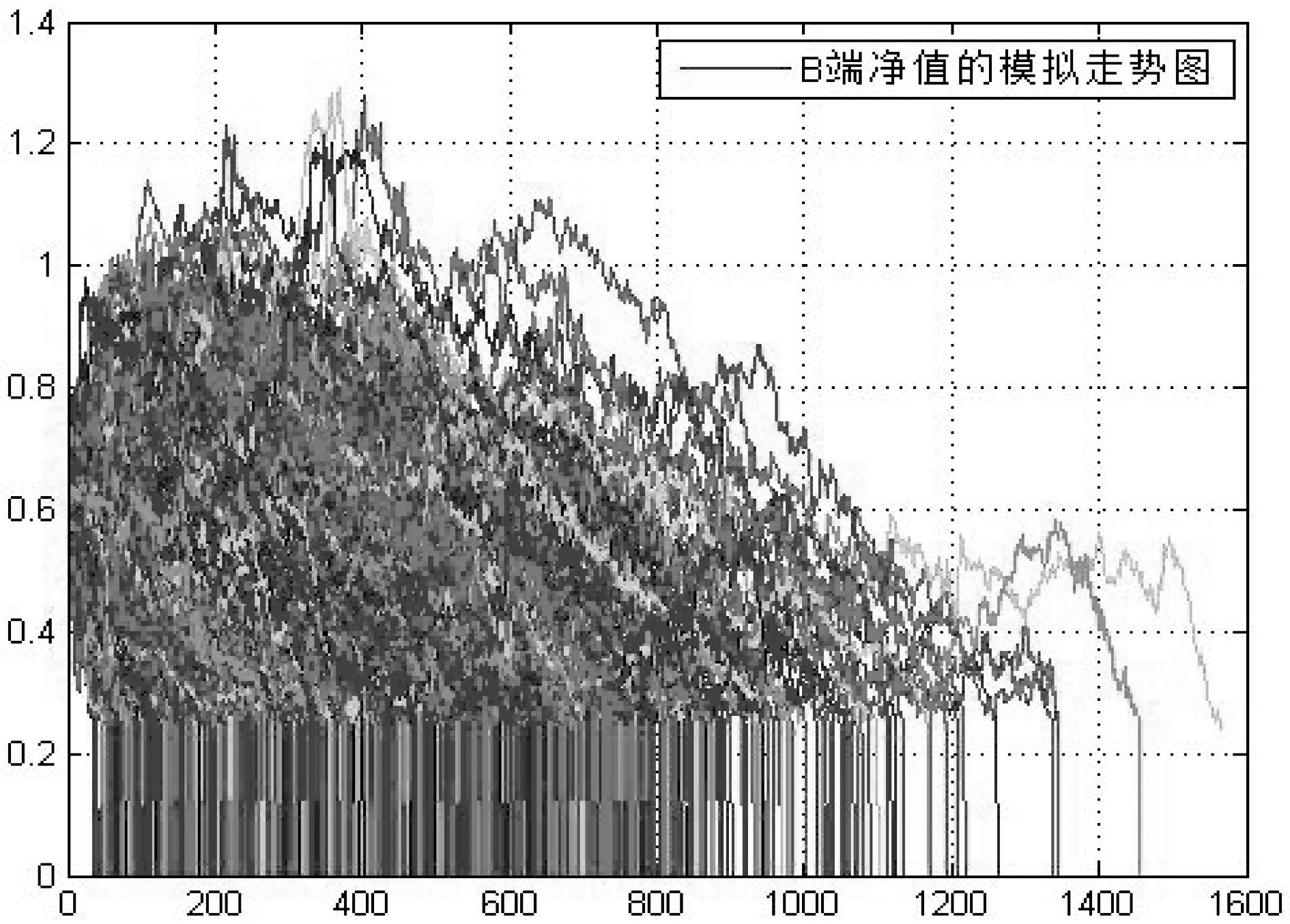
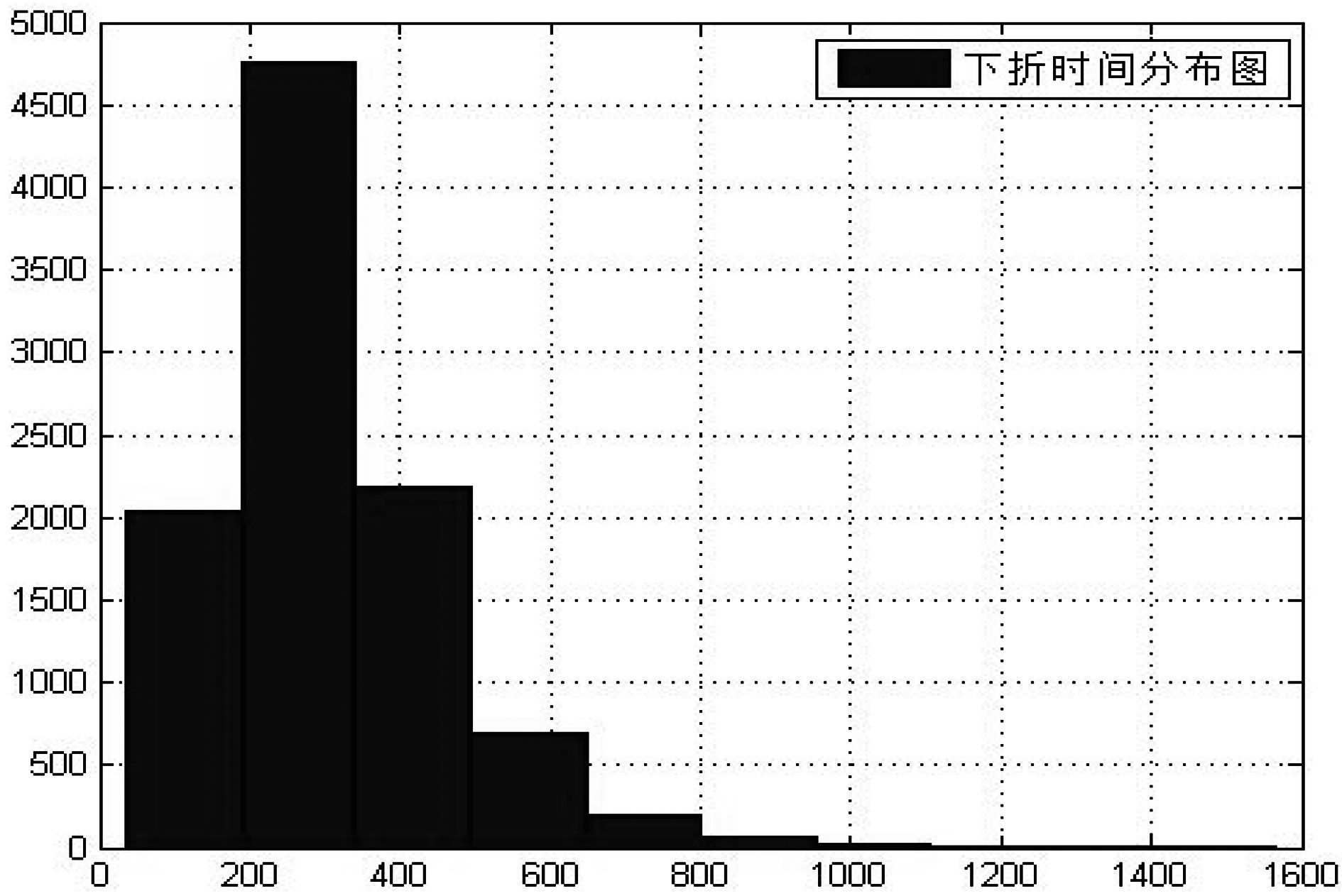
首先使用沪深300分级基金的母基金历史收益率得到其Hurst指数为0.568 8,表明母基金的收益率具有微弱的持续性。然后根据预测的收益率序列及条件方差序列使用蒙特卡洛进行10 000次的模拟得到沪深300分级B的净值路径图,模拟结果显示沪深300分级B的平均下折时间为306.06天。由于一年的交易日为244天,所以平均下折时间为1.25年左右,代入(5)式得到一单位沪深300A在2015年7月31日这一天的期权价值为:
| $\begin{align} & V\left( S\left( t \right),t \right)=3/4{{e}^{-r(T-t)}}n\left( 1-\varphi \right)= \\ & 3/4{{e}^{-0.000\text{ }18\times 306.06}}\times \left( 1-0.885 \right)=0.0816 \\ \end{align}$ | (10) |
由上述计算结果可知,一单位的沪深300A在2015年7月31日的二元看跌期权价值为0.081 6,分级B净值模拟路径图及下折时间分布图见图 1和图 2。
|
注:横坐标表示下折天数,纵坐标表示分级B净值。 图 1 分级B净值模拟路径图 |
|
注:横坐标表示下折天数,纵坐标表示频数。 图 2 分级基金下折时间分布图 |
类似地,可以考虑市场情绪对期权价值的影响。考虑到市场情绪指标体系构建的复杂性以及市场情绪会影响市场涨跌走势,采用沪深300指数涨跌比例构建分级基金的市场情绪指标。考虑前10日沪深300指数的收盘价,当收盘价的上涨天数大于下跌天数时,当日MSI=上涨天数/下跌天数×前10日沪深300指数收益率的标准差,上涨天数越多,市场情绪越乐观,母基金的收益率越高;当收盘价的下跌天数大于上涨天数时,当日MSI=(-1)×下跌天数/上涨天数×前10日沪深300指数收益率的标准差,下跌天数越多,市场情绪越悲观,母基金的收益率越低。MSI指标同时还满足,母基金的波动率随情绪波动的增大而增大。将MSI指标代入到ARMA(2,2)-GJR-GARCH(1,1)模型中,估计结果为:
| $\begin{align} & {{\sigma }_{t}}^{2}=3.07\times {{10}^{-7}}-(0.101-0.067{{I}_{t-1}}){{\varepsilon }_{t-1}}^{2}+ \\ & 0.173{{\sigma }_{t-1}}^{2}+0.002{{(MS{{I}_{t-1}})}^{2}}{{D}_{t-1}}+ \\ & 0.002{{(MS{{I}_{t-1}})}^{2}}~(1-{{D}_{t-1}}) \\ \end{align}$ |
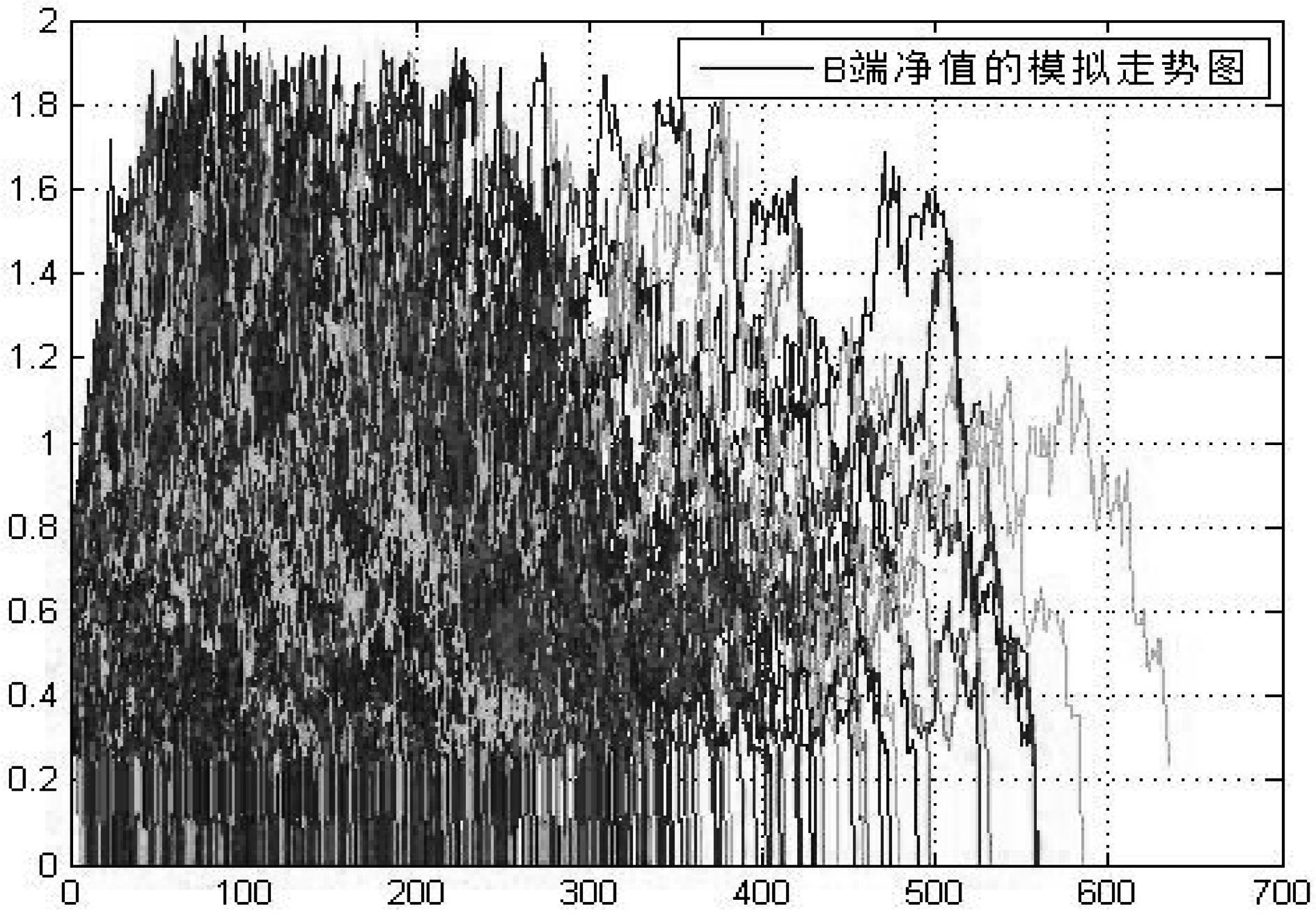
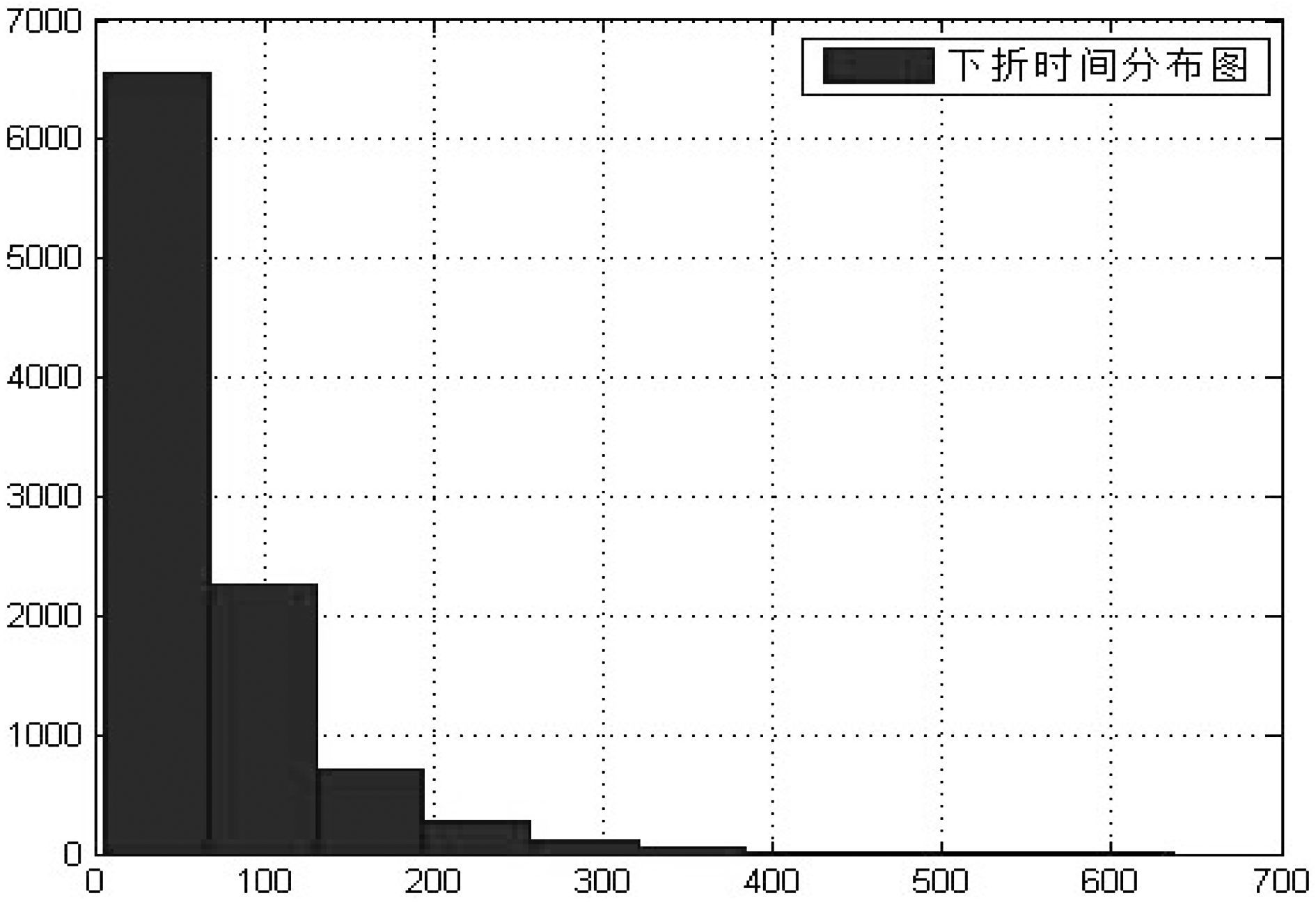
在考虑市场情绪的条件下,使用蒙特卡洛进行10 000次的模拟得到沪深300分级B净值路径图,其中沪深300分级B的平均下折时间为68.48天,平均下折时间近0.28年左右,代入(5)式得到一单位沪深300A在2015年7月31日这一天的期权价值为:
| $\begin{align} & V\left( S\left( t \right),t \right)=3/4{{e}^{-r(T-t)}}n\left( 1-\varphi \right)= \\ & 3/4{{e}^{-0.000\text{ }18\times 68.48}}\times \left( 1-0.885 \right)=0.0852 \\ \end{align}$ | (11) |
由上述实证结果可知,若考虑市场情绪的影响,一单位的沪深300A在2015年7月31日这一天的二元期权价值为0.085 2。分级B净值模拟路径图及下折时间分布见图 3和图 4。
|
注:横坐标表示下折天数,纵坐标表示分级B净值。 图 3 考虑市场情绪因素的分级B净值模拟路径图 |
|
注:横坐标表示下折天数,纵坐标表示频数。 图 4 考虑市场情绪因素的分级基金下折时间分布图 |
从实证结果看出,当不考虑市场情绪时,沪深300B的平均下折时间为306.06天,对应沪深300分级A的期权价值为0.081 6;当考虑市场情绪时,沪深300B的平均下折时间为68.48天,对应沪深300分级A的期权价值为0.085 2。由于2015年7月的整体市场情绪以负向为主,预测的母基金收益率多为负值,沪深300B更容易触发下折。通过实证结果可以看出:市场上的负向情绪会加速分级B的下折,缩短下折时间,对应的沪深300A的期权价值会增大。
类似的,本文还论证了其他10种分级A的期权价值受市场情绪的影响情况,表 1给出了分级A的期权价值与市场情绪之间的关系。
| 表 1 分级A的期权价值与市场情绪之间的关系 |
通过实证结果可知,除传统的影响因素以外,市场情绪对分级A的期权价值具有不可忽略的影响。当市场存在负向情绪时,分级B可能更容易触发下折。股票市场上消息的负向冲击影响要大于正向冲击影响,而市场情绪会加速负向冲击的作用。负向情绪会加速分级B下折,缩短下折时间,加快实现分级A的期权价值。在实证结果中,除国企改分级基金下折时间相同以外(易方达国企改革基金成立时间较晚,实证数据较少),考虑市场情绪的下折时间均小于不考虑市场情绪的下折时间。在本研究数据所取时间之后的一个月内(即截止至2015年8月31日),很多分级基金出现下折,考虑市场情绪的下折时间更接近实际的下折时间,可以进一步肯定市场情绪对分级A期权价值的影响作用。
现将分级A二元看跌期权价值及其影响因素之间的关系总结如下(见表 2):
| 表 2 分级A的期权价值与其影响因素之间的关系 |
从市场实际情况来看,如果选择实证中的分级A进行投资,从2015年7月31日到触发下折,获得的收益远远高于持有期间的固定收益,这肯定了其内含期权价值的重要研究意义。分级A作为一种投资工具,其期权价值会给投资者带来可观的收益。考虑市场情绪的模型能够更加准确的度量分级A的期权价值,有助于投资者更好地实现分级A的价值投资及避险功能。
| [1] | 马刚. 分级基金上市份额的折溢价问题研究[J]. 证券市场导报, 2014(8): 64–70. |
| [2] | 楼华锋, 高子剑.分级基金A专题报告——她的美还未曾被发现[EB/OL].(2015-03-05)[2015-06-12]. http://yanbao.stock.hexun.com/dzqt583362.shtml. |
| [3] | 马亦舟.中国分级基金设计与定价方法研究[D].上海: 上海交通大学上海高级金融学院, 2012. |
| [4] | 尹航.我国分级基金的发展与估值分析[D].上海: 复旦大学经济学院, 2013. |
| [5] | 杨倩君.中国分级基金定价方法研究[D].上海: 复旦大学经济学院, 2014. |
| [6] | 王静明.基于申万深成分级基金的永续性股债分级基金定价的研究[D].上海:上海交通大学上海高级金融学院,2013. |
| [7] | Stentoft L. Pricing American options when the underlying asset follows GARCH processes[J]. Journal of Empirical Finance, 2005(12): 576–611. |
| [8] | Hsieh K C, Ritchken P. An empirical comparison of GARCH option pricing models[J]. Review of Derivatives Research, 2005,8(3): 129–150. |
| [9] | 吴恒煜, 马俊伟, 朱福敏, 等. 基于Levy过程修正GJR-GARCH模型的权证定价——对中国大陆和香港权证的实证研究[J]. 系统工程理论与实践, 2014(12): 3009–3021. |
| [10] | 李进芳.带信息的情绪资产定价研究[D].广州: 华南理工大学经济与贸易学院, 2014. |
| [11] | Uygur U, Tas O. The impacts investor sentiment on returns and conditional volatility of international stock market[J]. Qual Quant, 2004,48(3): 1165–1179. |
| [12] | Rockenbach B. The behavioral relevance of mental accounting for the pricing of financial options[J]. Journal of Economic Behavior and Organization, 2004,53(4): 513–527. DOI: 10.1016/S0167-2681(03)00097-0 |
| [13] | Xiao W L, Zhang W G, Zhang X L, Wang Y L. Pricing currency options in a fractional Brownian motion with jumps[J]. Economic Modeling, 2010,27(5): 935–942. DOI: 10.1016/j.econmod.2010.05.010 |
| [14] | Thavaneswaran A, Appadoo S S, Frank J. Binary option pricing using fuzzy numbers[J]. Applied Mathematics Letters, 2013(26): 65–72. |
| [15] | Guerra J, Nualart D. Stochastic differential equations driven by fractional Brownian Motion and Standard Brownian Motion[J]. Stochastic Analysis and Applications, 2008,26(5): 1053–1075. DOI: 10.1080/07362990802286483 |
| [16] | 张翠娥, 徐云. 随机利率下服从O-U过程的二元期权定价[J]. 数学理论与应用, 2012(3): 27–31. |
| [17] | Glosten L R, Jagannathan R, Runkle D K. On the relation between the expected value and the volatility and the volatility of the nominal excess returns on stocks[J]. Journal of Financial, 1993,48(5): 1779–1801. |
| [18] | Monfared S A, Enke D. Volatility forecasting using a hybrid GJR-GARCH neural network model[J]. Procedia Computer Science, 2014(36): 246–253. |
 2016, Vol. 18
2016, Vol. 18
