A robust crater detection algorithm and optical navigation for lunar landers
-
摘要: 针对月球探测器环形山检测方法受光照影响、鲁棒性差的问题，本文提出一种基于极大熵阈值三值化的鲁棒环形山检测算法。采用不同滤波核对图像进行去噪平滑，然后对处理后的图像进行极大熵阈值分割、将图像信息三值化，去除图像对光源的敏感性，同时最大程度保留图像信息；提出一种归一化多指标约束环形山匹配和拟合方法完成环形山提取，将环形山提取算法应用于光学导航中进行打靶实验验证算法实时性表现。仿真结果表明: 与传统基于形态学或自适应边缘检测的方法相比，本文方法在较大尺度条件下提取出连续、光滑的环形山边缘，有效环形山数量提升35%以上，同时实时性更好、计算消耗降低40%；基于鲁棒环形山提取的光学导航算法实时性更好。Abstract: Traditional crater detection algorithms (CDAs) are photosensitive and have poor robustness. To solve this problem, a new CDA based on maximum entropy threshold ternary segmentation is proposed and used in optical navigation. This method uses different filter kernel functions to eliminate noise and thereby smooth an image. Furthermore, the processed image is segmented by the maximum entropy threshold, and the image information is trivalued to remove the photosensitivity of the image while retaining the image information to the greatest extent. A normalized multi-indicator constrained crater matching and a ellipse fitting method are proposed for complete crater extraction. This CDA method is applied to optical navigation Monte Carlo experiments and verify the real-time algorithm. Simulation results show that compared with traditional methods based on morphology or adaptive edge detection, the proposed CDA can extract continuous and smooth crater edges on a large scale, increasing the number of effective craters by more than 35% while reducing the calculation cost by 40%. The optical navigation algorithm based on robust crater detection algorithm has better real-time performance.
-
针对月球(阿波罗[1-2]，嫦娥[3-6])、火星(天问-1[7]，好奇号[8]、机遇号[9])、小行星(隼鸟号[10])等天体，世界各国已经开展了一系列成功的探测任务。通常来说，具有更高科学研究价值的地区其地形也往往越复杂，着陆探测的难度也越大。因此，作为探测任务的基础之一，环形山检测算法(crater detection algorithm, CDA)对导航系统和障碍规避系统十分重要。“嫦娥”4号探测器是第1个降落在月球背面的探测器[11-12]。与以往的月球着陆探测器相比，其着陆地区缺乏高精度的地形数据，着陆风险更大。
对未来的月球探测或行星探测任务而言，往往无法事先制备目标天体的高精度数字高程图(digital e-map, DEM)，因此需要开发鲁棒性强、实时性优的环形山检测方法，以满足高精度和高可靠性的探测需求，为光学导航、障碍感知与规避系统提供支撑。
现有的环形山检测算法有很多，一些算法注重环形山有效检测的检测率，另一些理论更注重算法的速度和实时性。依处理信息不同可将算法分为基于DEM的环形山检测和基于光学信息的环形山检测。文献[13-15]将机器学习和卷积神经网络等人工智能方法应用到DEM分析中进行环形山检测；文献[16]采用转移学习的方法也获得了具有一定泛化性的环形山检测结果；文献[17]采用多层神经网络构建出了可达人类水平的环形山检测方法，该方法需要同时对探测到的DEM数据和红外成像数据进行分析；文献[18]提出了一种基于CNN的环形山检测方法，这种方法需要在任务前确定目标地区的检测概率。一些传统理论也被用于环形山检测中[19]，如霍夫变换、小波分析、Canny边缘检测[20]、级联决策森林[21]、形态学分析[22]、光照方向和图像纹理分析等[23-24]。文献[25]采用霍夫变换和Canny边缘检测的方法对高精度月面图像进行处理，计算量较大；文献[26]直接根据环形山的曲线特征进行匹配以实现行星着陆导航，取得了很高的导航精度。不同的环形山检测方法有不同的缺点，基于学习的方法需要合适的数据集训练；基于霍夫变换、形态学分析的方法对光照很敏感，适应性较差[27-28]。
本文提出一种基于极大熵阈值分割(maximum entropy threshold segmentation, METS) 三值化的鲁棒环形山检测算法(METS-CDA)，最大程度保留图像信息条件下将图像分为亮区、暗区和周围环境3个部分，极大程度地降低环形山检测的计算量，避免光照方向不同对环形山提取信息产生干扰；同时提出了一种多指标约束体系实现环形山的匹配和拟合，实现算法的鲁棒性和实时性。
1. 基于极大熵阈值的环形山边缘检测
在滤波去除图像噪声后，计算出最大限度保留图像信息的三值化判别阈值，采用极大熵阈值法对图像亮区、暗区和周围环境区域进行分割，显著降低环形山提取计算量，增强环形山提取的鲁棒性，降低太阳光照方向对算法的影响。
月面图像的信息熵H为：
$$ H=-\sum\limits_{i=0}^{255} p_i \log p_i $$ (1) 式中pi为图像中各个像素值i出现的概率密度。
选定三值化阈值α、β (β>α)对图像进行处理，将图像分为亮区、暗区和周围环境，三值化后各区域对应的概率分布为：
$$ P_1(\alpha)=\sum\limits_{i=0}^\alpha p_i, P_2(\alpha, \beta)=\sum\limits_{i=\alpha+1}^\beta p_i, P_3(\beta)=\sum\limits_{i=\beta+1}^{255} p_i $$ (2) 概率分布满足关系：
$$ P_1(\alpha)+P_2(\alpha, \beta)+P_3(\beta)=1 $$ (3) 对应信息熵分别为：
$$ \left\{\begin{array}{l} H_1(\alpha)=-\sum\limits_{i=0}^\alpha \frac{p_i}{P_1(\alpha)} \log \frac{p_i}{P_1(\alpha)} \\ H_2(\alpha, \beta)=-\sum\limits_{i=\alpha+1}^\beta \frac{p_i}{P_2(\alpha, \beta)} \log \frac{p_i}{P_2(\alpha, \beta)} \\ H_3(\beta)=-\sum\limits_{i=\beta+1}^{255} \frac{p_i}{P_3(\beta)} \log \frac{p_i}{P_3(\beta)} \end{array}\right. $$ (4) 可计算出分割后的图像总熵：
$$ H(\alpha, \beta)=H_1(\alpha)+H_2(\alpha, \beta)+H_3(\beta) $$ (5) 问题转化为选取恰当的分割阈值α, β使图像三值化后的总熵H(α, β)最大。
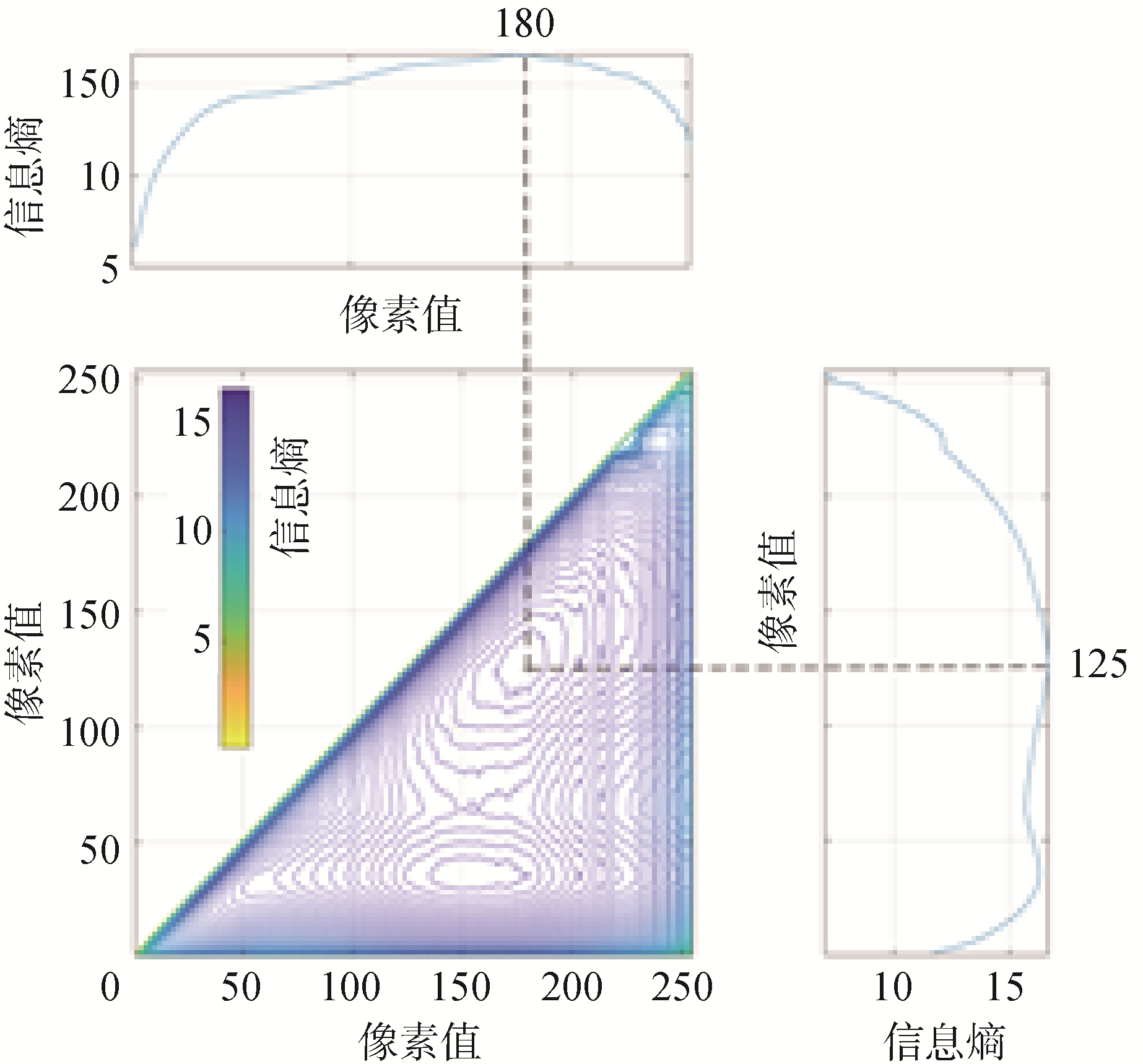
$$ [\alpha, \beta]=\underset{\alpha, \beta \in[0, 255]}{\operatorname{argmax}} H(\alpha, \beta) $$ (6) 以月面图像图 1为例，选取不同分割阈值后计算图像分割后的总熵，总熵分布如图 2所示。三值化后，Canny边缘检测中强弱阈值(τl, τh)的选取不再影响图像边缘检测结果，无论边缘检测的强弱阈值如何选择，三值化后的图像均可以提取出清晰、连续法的环形山边缘，且提取出的边缘不与周围环境粘连，有助于环形山边缘提取和椭圆拟合。
图 1 月面图像Fig. 1 Lunar image
下载:
全尺寸图片
图 2 分割后图像总熵分布Fig. 2 Distribution of segmented image entropy下载:
全尺寸图片
2. 归一化多约束环形山匹配和拟合
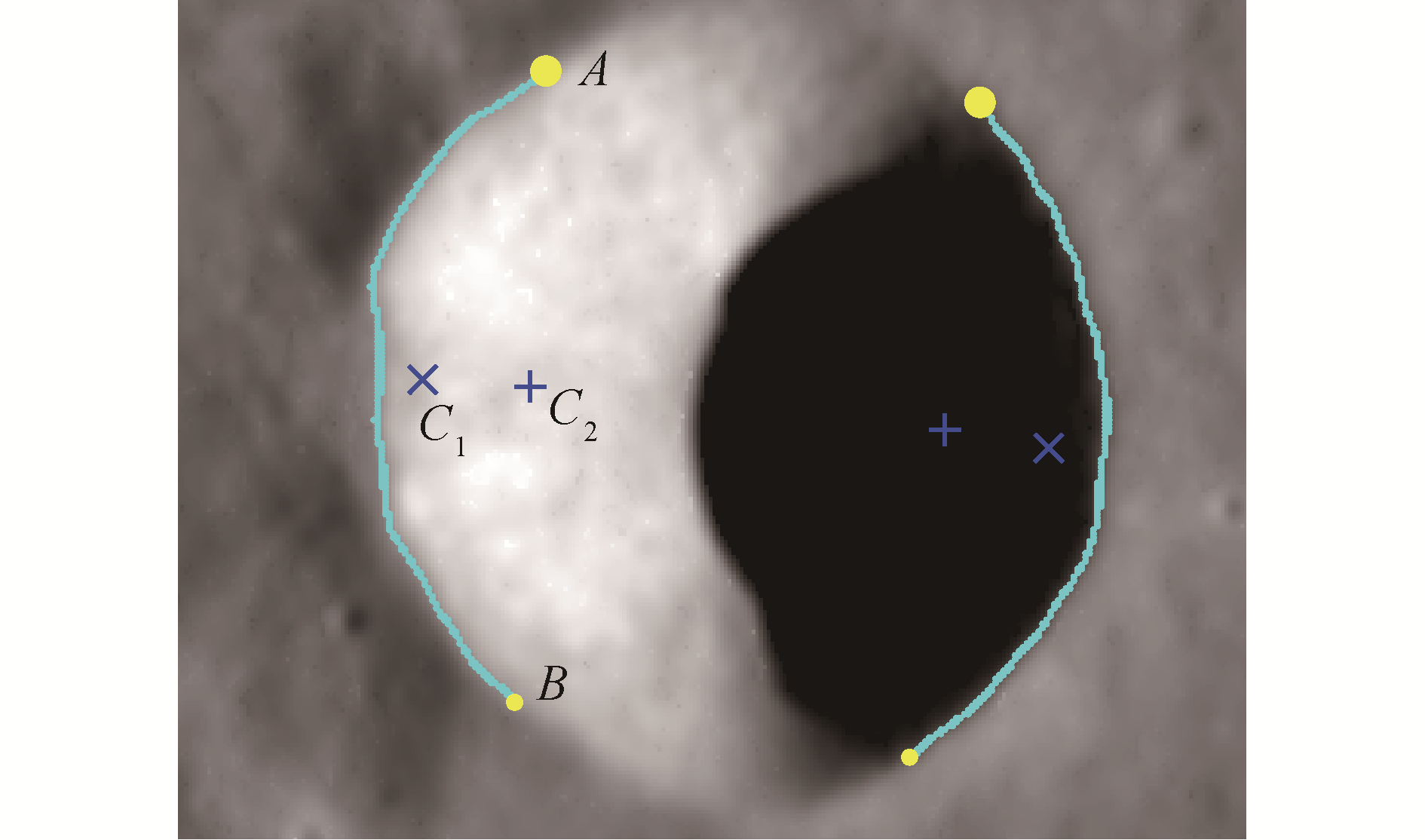
在图像三值化和环形山边缘检测后，属于同一环形山的明、暗边缘断开，因此需要对属于同一环形山的边缘进行配对。传统环形山边缘配对方法在图像尺寸大、环形山多的大尺度检测环境下表现不够好，因此需要采用具有更强约束力的多个匹配约束构成多参数约束矩阵实现适应大尺度条件的环形山边缘匹配。匹配前，用一组特征点对环形山明、暗边缘进行表，如图 3所示。
图 3 图环形山边缘特征点Fig. 3 Feature points of crater edge下载:
全尺寸图片
一侧环形山边缘vi可由4个特征点表征，分别为端点A和B，几何中心C1，边缘中点C2。环形山的方向向量r表示为：
$$ \boldsymbol{r}=\overrightarrow{C_1 C_2} $$ (7) 综合考虑环形山半边缘长度、距离、方向、形状、明暗等约束，构建归一化多参数约束Ji评估任意2个半边缘vi和vj。Ji=1表示2个环形山匹配最佳，Ji=0表示2个环形山半边缘完全无法匹配。综合考虑的约束如下。
1) 归一化长度相似性约束J1(vi, vj)。
归属于同一环形山的2个半边缘长度不会相差特别大。约束值越大，2个环形山匹配越好。
$$ J_1\left(v_i, v_j\right)=1-\frac{\left|l_i-l_j\right|}{l_i+l_j}, \quad J_1 \in(0, 1) . $$ (8) 式中li, lj为待匹配的环形山长度。
2) 明暗亮度约束J2(vi, vj)。
太阳光照射下，半边缘几何中心C1处的亮度不同，通常处于明、暗不同区域。用几何中心处的灰度值lexi评估环形山匹配效果。J2(vi, vj)=1表示匹配成功。
$$ J_2\left(v_i, v_j\right)= \begin{cases}1, & \operatorname{lex}_i \neq \operatorname{lex}_j \\ 0, & \operatorname{lex}_i=\operatorname{lex}_j\end{cases} $$ (9) 3) 归一化方向约束J3(vi, vj)。
属于同一环形山的2个半边缘应当方向相反，方向向量成钝角。J3(vi, vj)越大，匹配性越好。
$$ J_3\left(v_i, v_j\right)=\frac{\left|\boldsymbol{r}_i\right|\left|r_j\right|-\boldsymbol{r}_{\boldsymbol{i}} \cdot \boldsymbol{r}_j}{2\left|\boldsymbol{r}_i\right|\left|\boldsymbol{r}_j\right|} \quad J_3 \in(0, 1) $$ (10) 4) 归一化距离约束J4(vi, vj)，J5(vi, vj)。
属于同一环形山的两半边缘不会相距过远。采用两半边缘长度的几何均值$\sqrt{l_i l_j}$分别评估两者之间的水平距离约束J4(vi, vj)和竖直方向约束J5(vi, vj)。
$$ \begin{aligned} & J_4\left(v_i, v_j\right)= \begin{cases}1 & \left|\boldsymbol{r}_1 \cdot \boldsymbol{s}\right|<\eta_1 \sqrt{l_i l_j} \\ 0 & \left|\boldsymbol{r}_1 \cdot \boldsymbol{s}\right| \geqslant \eta_1 \sqrt{l_i l_j}\end{cases} \\ & J_5\left(v_i, v_j\right)= \begin{cases}1 & \left|\boldsymbol{r}_1 \times \boldsymbol{s}\right|<\eta_2 \sqrt{l_i l_j} \\ 0 & \left|\boldsymbol{r}_1 \times \boldsymbol{s}\right| \geqslant \eta_2 \sqrt{l_i l_j}\end{cases} \end{aligned} $$ (11) 式中：s是太阳光方向向量，ηk为尺度参数。实际探测中，两半边缘几何中心间的距离小于环形山周长的一半，且两半边缘长度的几何均值也小于环形山周长的一半。结合工程实际情况，可将取值范围设定在2.5左右。
5) 归一化形状约束J6(vi, vj)。
当仅考虑Ji(i=1, 2, …, 5)5种约束时，匹配结果有2类，按形状可分为“X型”和“O型”。“O型”结果为环形山准确匹配结果而“X型”通常为巨石、月丘带来的误匹配。为规避它们的影响，引入太阳光照方向构建形状约束：
$$ \begin{gathered} J_6\left(v_i, v_j\right)=\frac{\left|\overrightarrow{C_{2 i} C_{2 j}}\right|-\left(\operatorname{lex}_i-\operatorname{lex}_j\right) \overrightarrow{C_{2 i} C_{2 j}} \cdot s}{2\left|\overrightarrow{C_{2 i} C_{2 j}}\right|}, \\ J_6 \in(0, 1) \end{gathered} $$ (12) 计算多参数约束J(vi, vj)：
$$ J\left(v_i, v_j\right)=J^{i, j}=\prod\limits_k J_k\left(v_i, v_j\right) \quad k=1, 2, \cdots, 6 . $$ (13) 与传统环形山边缘匹配的离散性判据相比，以上归一化约束可以连续地表达两半边缘之间的匹配性，且可以计算出具有综合性、全面性的半边缘匹配度，有助于匹配过程各环形山边缘之间横向对比。对n个提取出的明显的半边缘，构建多约束相似性矩阵D：
$$ \boldsymbol{D}=\left[\begin{array}{cccc} J\left(v_1, v_1\right) & J\left(v_1, v_2\right) & \cdots & J\left(v_1, v_n\right) \\ J\left(v_2, v_1\right) & J\left(v_2, v_2\right) & \cdots & J\left(v_2, v_n\right) \\ \vdots & \vdots & \ddots & \vdots \\ J\left(v_n, v_1\right) & J\left(v_n, v_2\right) & \cdots & J\left(v_n, v_n\right) \end{array}\right] $$ (14) 式中D是一个对称阵，主对角线元素恒为零，表征任意2个半边缘之间的相似性，对矩阵D进行处理可以完成环形山边缘的匹配。首先，选取出D中最大的元素Jmax(1)；删去D中Jmax(1)所处位置的所有行列元素，形成的新矩阵命名为D1；然后在新矩阵D1中选取出新的最大值Jmax(2)，删去Jmax(2)所在行列所有元素；重复上述过程直到选取出的元素Jmax(m)∈Dm－1低于设定的匹配阈值ε。半边缘匹配完成后，进行环形山拟合。
将月面环形山建模为椭圆：
$$ F(X)=\boldsymbol{X}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{X}+\boldsymbol{b}^{\mathrm{T}} \boldsymbol{X}+\boldsymbol{c}=0 $$ (15) 式中：X为两半边缘灰度坐标集。采用最小二乘法(least-squares method, LSM)计算式中的参数A、b和c。拟合后的椭圆中心坐标Xo为:
$$ \boldsymbol{X}_o=\left[\begin{array}{ll} x_o & y_o \end{array}\right]^{\mathrm{T}}=-\frac{1}{2} \boldsymbol{A}^{-1} \boldsymbol{b} $$ (16) 3. 基于鲁棒CDA的VINS组合导航
3.1 月球探测器运动学模型
采用四元数对姿态微分方程进行更新：
$$ \dot{\boldsymbol{q}}=\frac{1}{2} \boldsymbol{q} \otimes \boldsymbol{\omega}_{n b}^b $$ (17) 式中ωnbb为飞行器本体系相对导航系的角速度在本体系下的投影：
$$ \boldsymbol{\omega}_{n b}^b=\boldsymbol{\omega}_{i b}^b-\boldsymbol{\omega}_{i n}^b=\boldsymbol{\omega}_{i b}^b-\boldsymbol{C}_n^b\left(\boldsymbol{\omega}_{i f}^n+\boldsymbol{\omega}_{f n}^n\right) $$ (18) 式中：ωibb为本体系相对惯性系的角速度在本体系下的投影；ωinb为导航系相对惯性系的角速度在本体系下的投影；ωifn为由于月球自转导致的月面固连坐标系相对惯性系的角速度在导航系下的投影；ωfnn为由于飞行器飞行位置变化导致的导航系相对固连系的角速度在导航系下的投影。
导航系下的月球探测器速度更新为：
$$ \boldsymbol{v}_n=C_f^n \boldsymbol{v}_f=C_f^n \dot{\boldsymbol{r}}_f=C_f^n \boldsymbol{C}_i^f\left(\dot{\boldsymbol{r}}_i-\boldsymbol{\omega}_{i f}^i \times \boldsymbol{r}_i\right) $$ (19) 对式(19)求导，并考虑$\dot{\boldsymbol{\omega}}_{i f}^i$，可得:
$$ \begin{gathered} \dot{\boldsymbol{v}}_n=\frac{\mathrm{d}}{\mathrm{d} t}\left(\boldsymbol{C}_i^n\left(\dot{\boldsymbol{r}}_i-\boldsymbol{\omega}_{i f}^i \times \boldsymbol{r}_i\right)\right)= \\ \boldsymbol{C}_i^n\left[\boldsymbol{\omega}_{n i}^i \times\right]\left(\dot{\boldsymbol{r}}_i-\boldsymbol{\omega}_{i f}^i \times \boldsymbol{r}_i\right)-\boldsymbol{C}_i^n\left(\ddot{\boldsymbol{r}}_i-\boldsymbol{\omega}_{i f}^i \times \dot{\boldsymbol{r}}_i\right) \end{gathered} $$ (20) 参考牛顿第二定律:
$$ \ddot{\boldsymbol{r}}_i=\frac{\boldsymbol{F}}{m}+\boldsymbol{G}_i=\boldsymbol{f}_i+\boldsymbol{G}_i $$ (21) 月面重力加速度矢量为：
$$ \boldsymbol{g}_i=\boldsymbol{G}_i-\boldsymbol{\omega}_{i f}^i \times\left(\boldsymbol{\omega}_{i f}^i \times \boldsymbol{r}_i\right) $$ (22) 联立式(20)~(22)，可得月球探测器下降着陆过程中的速度更新方程：
$$ \dot{\boldsymbol{v}}_n=\boldsymbol{f}_n-\left(2 \boldsymbol{\omega}_{i f}^n+\boldsymbol{\omega}_{f n}^n\right) \times \boldsymbol{v}_n+\boldsymbol{g}_n $$ (23) 式中fn为导航系下的比力。
飞行器对应地理系位置更新方程为：
$$ \left[\begin{array}{c} L \\ \lambda \\ h \end{array}\right]=\left[\begin{array}{ccc} 0 & \left(R_M+h\right)^{-1} & 0 \\ \left(R_N+h\right)^{-1} \sec L & 0 & 0 \\ 0 & 0 & 1 \end{array}\right] \boldsymbol{v}_n $$ (24) 3.2 基于环形山检测的光学导航
提取出环形山后，根据环形山成像像素齐次坐标Puv、环形山中心的地理系齐次坐标Pf和相机系坐标PC之间关系可计算出飞行器(相机)位姿信息：
$$ \left\{\begin{array}{l} \boldsymbol{P}^{u v}=\left[\begin{array}{lll} u & v & 1 \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{P}^f=\left[\begin{array}{llll} X^f & Y^f & Z^f & 1 \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{P}^C=\left[\begin{array}{lll} X^C & Y^C & Z^C \end{array}\right]^{\mathrm{T}} \end{array}\right. $$ (25) 飞行器本体坐标系到固连坐标系转移矩阵为Cbf，飞行器在地理系下位置为T:
$$ \boldsymbol{C}_f^b=\left[\begin{array}{lll} c_{11} & c_{12} & c_{13} \\ c_{21} & c_{22} & c_{23} \\ c_{31} & c_{32} & c_{33} \end{array}\right]=\left[\begin{array}{l} \boldsymbol{c}_1^T \\ \boldsymbol{c}_2^T \\ \boldsymbol{c}_3^T \end{array}\right] $$ (26) $$ \boldsymbol{T}=\left[\begin{array}{lll} X_C & Y_C & Z_C \end{array}\right]^{\mathrm{T}} $$ (27) 式中f为焦距，环形山j成像模型为：
$$ U_j=\frac{u_j}{f}=\frac{X_j^C}{Z_j^C}, \quad V_j=\frac{v_j}{f}=\frac{Y_j^C}{Z_j^C} $$ (28) 飞行器位姿与成像关系为：
$$ \left[\begin{array}{c} X_j^C \\ Y_j^C \\ Z_j^C \end{array}\right]=\left[\begin{array}{lll} c_{11} & c_{12} & c_{13} \\ c_{21} & c_{22} & c_{23} \\ c_{31} & c_{32} & c_{33} \end{array}\right]\left[\begin{array}{l} X_j^f \\ Y_j^f \\ Z_j^f \end{array}\right]+\left[\begin{array}{c} X_C \\ Y_C \\ Z_C \end{array}\right] $$ (29) 基于鲁棒环形山提取的飞行器光学导航求解即求取式(26)、(27)，考虑求解的两类约束。对于探测到的任一环形山j，联立式(28)、(29)，可构建2个探测约束：
$$ \left\{\begin{array}{l} U_j=\frac{c_{11} X_j^f+c_{12} Y_j^f+c_{13} Z_j^f+X_C}{c_{31} X_j^f+c_{32} Y_j^f+c_{33} Z_j^f+Z_C} \\ V_j=\frac{c_{21} X_j^f+c_{22} Y_j^f+c_{23} Z_j^f+Y_C}{c_{31} X_j^f+c_{32} Y_j^f+c_{33} Z_j^f+Z_C} \end{array}\right. $$ (30) 第二类约束为转移矩阵约束：
$$ \left(\boldsymbol{C}_b^f\right)^{\mathrm{T}} \boldsymbol{C}_b^f=\boldsymbol{I} $$ (31) 至少检测到4个环形山时，联立两类约束，采用高斯牛顿法可进行求解。
3.3 光学/惯性组合导航滤波模型
由于月球探测器下降时间较短，重力变化较小，且月球自转在此过程中可忽略不计。故舍弃小量，惯性导航系统姿态误差传递方程为：
$$ \dot{\phi}=\delta \boldsymbol{\omega}_{i f}^n+\delta \boldsymbol{\omega}_{f n}^n-\left(\boldsymbol{\omega}_{i f}^n+\boldsymbol{\omega}_{f n}^n\right) \times \phi+\boldsymbol{\varepsilon}^n \approx \boldsymbol{\varepsilon}^n $$ (32) 式中：ϕ为误差角；εn为陀螺零偏。
惯性导航系统速度误差传递方程为：
$$ \delta \dot{\boldsymbol{v}}_n=\delta \dot{\boldsymbol{f}}_n-\delta\left(\left(2 \boldsymbol{\omega}_{i f}^n+\boldsymbol{\omega}_{f n}^n\right) \times \boldsymbol{v}^n\right)+\delta \boldsymbol{g}^n \approx \delta \dot{\boldsymbol{f}}_n $$ (33) 式中：$\delta \boldsymbol{f}^n=\boldsymbol{f}^n \times \phi+$∇n, ∇n为加计零偏。
惯性导航系统位置误差传递方程由式(24)微分得到。选取状态变量X为15×1的向量，由9维姿态偏差ϕ、速度偏差δvn、位置偏差δp和6维惯导偏差$\boldsymbol{\varepsilon}^n, $∇n组成。量测方程为：
$$ \boldsymbol{Z}=\boldsymbol{H} \boldsymbol{X}+\boldsymbol{V}=\left[\begin{array}{lll} \boldsymbol{I}_{3 \times 3} & \vdots & 0_{3 \times 12} \end{array}\right] \boldsymbol{X}+\boldsymbol{V} $$ (34) 式中V为量测白噪声。
4. 仿真分析
环形山检测是基于特征地形的光学导航和障碍规避的基础。为检验提出方法的可行性和可靠性，验证其在环形山检测过程中具有鲁棒性和实时性，构建了数值仿真实验和基于月面沙盘的半实物仿真试验，并将算法应用于光学导航进行验证。
数值仿真实验结果表明，相比于传统方法，本文提出算法提取有效环形山数量更多、计算消耗更低、实时性更好；半实物仿真试验验证表明提出的方法不受光照因素影响，在不同光照环境下具有鲁棒性。
4.1 基于月面图像的数值仿真验证
采用“嫦娥”2号探测器拍摄的分辨率7 m、尺寸9 638×12 472月面图像作为仿真数据提取图像中的环形山。文献[24]标记图中1 337个显著环形山作为真值数据。设定匹配阈值ε=0.5，算法共提取出1 170座有效环形山，检测结果如表 1所示。
表 1 真值和环形山结果Table 1 Ground truth and detection results数据 检测数 环形山数量 d < 70 m 70 m < d < 700 m d>700 m 真值 1 337 96 1 204 37 检出数 1 170 77 1 056 37 检出率/% 87.5 80.2 87.7 100 注：d为检出环形山直径。 提取出的所有环形山被标记在月面原始图像中，如图 4所示。提取出的1 170个环形山没有假阳性(false positive)误匹配。对于不同尺寸的环形山，提出算法有不同检出效率。环形山直径越大，检出率越高，这是因为相较于大型环形山来说，小环形山的明暗变化不够明显，易被大环形山遮挡；同时，环形山之间的重叠更容易影响小环形山的检测。即便如此，提出算法的检测性能仍明显高于传统方法。
图 4 环形山检测结果Fig. 4 Crater detection result下载:
全尺寸图片
进一步说明匹配阈值选取方式，对检测后不同状态的环形山进行计数完成环形山检测算法评估，检出环形山状态包括：真阳性nTP(true positive)，对应成功检出的环形山；假阳性nFP(false positive)，对应错误检出的环形山；假阴性nFN(false negative)，对应未检出的环形山。统计出nTP、nFP、nFN值后，计算质量参数，包括检出率D(detection percentage)，质量百分比Q(quality percentage)，分化因子B(branching factor)和精确度P(precision)：
$$ D=100 \% \times n_{\mathrm{TP}}\left(n_{\mathrm{TP}}+n_{\mathrm{FN}}\right)^{-1} $$ (35) $$ Q=100 \% \times n_{\mathrm{TP}}\left(n_{\mathrm{TP}}+n_{\mathrm{FP}}+n_{\mathrm{FN}}\right)^{-1} $$ (36) $$ B=n_{\mathrm{FP}} n_{\mathrm{TP}}^{-1} $$ (37) $$ P=100 \% \times n_{\mathrm{TP}}\left(n_{\mathrm{TP}}+n_{\mathrm{FP}}\right)^{-1} $$ (38) 参数D、B和Q反映算法性能，P反映提出算法的可靠性。与传统方法相比，本文综合评估了所有质量参数，并采用了一种定量评估的方式选取最优匹配阈值ε。选取0.1~0.9的不同匹配阈值进行环形山检测，同时计算出所有对应的质量参数，如表 2所示，标记出所有单项最优值。
表 2 环形山检测数量和对应质量参数Table 2 Detected crater numbers and quality factor匹配阈值ε 环形山检测数 质量参数 检测结果 D/% Q/% B P/% TP FP FN 0.1 1 430 89.8 76.7 0.19 84.0 1 201 229 136 0.2 1 276 89.7 84.8 0.06 94.0 1 199 77 138 0.3 1 264 89.7 85.5 0.05 94.9 1 199 65 138 0.4 1 230 88.6 85.6 0.04 96.3 1 184 46 153 0.5 1 170 87.5 87.5 0 100 1 170 0 167 0.6 1 074 80.3 80.3 0 100 1 074 0 263 0.7 962 72.0 72.0 0 100 962 0 375 0.8 909 68.0 68.0 0 100 909 0 428 0.9 209 15.6 15.6 0 100 209 0 1128 当ε=0.1时，检出环形山数量最多，参数D最优；当ε=0.5时，环形山检测质量最好，参数Q、B、P最优，对应参数D与最优值区别不大；当ε>0.5时，环形山检测鲁棒性逐渐加强，参数B和P最优，但参数Q显著下降。
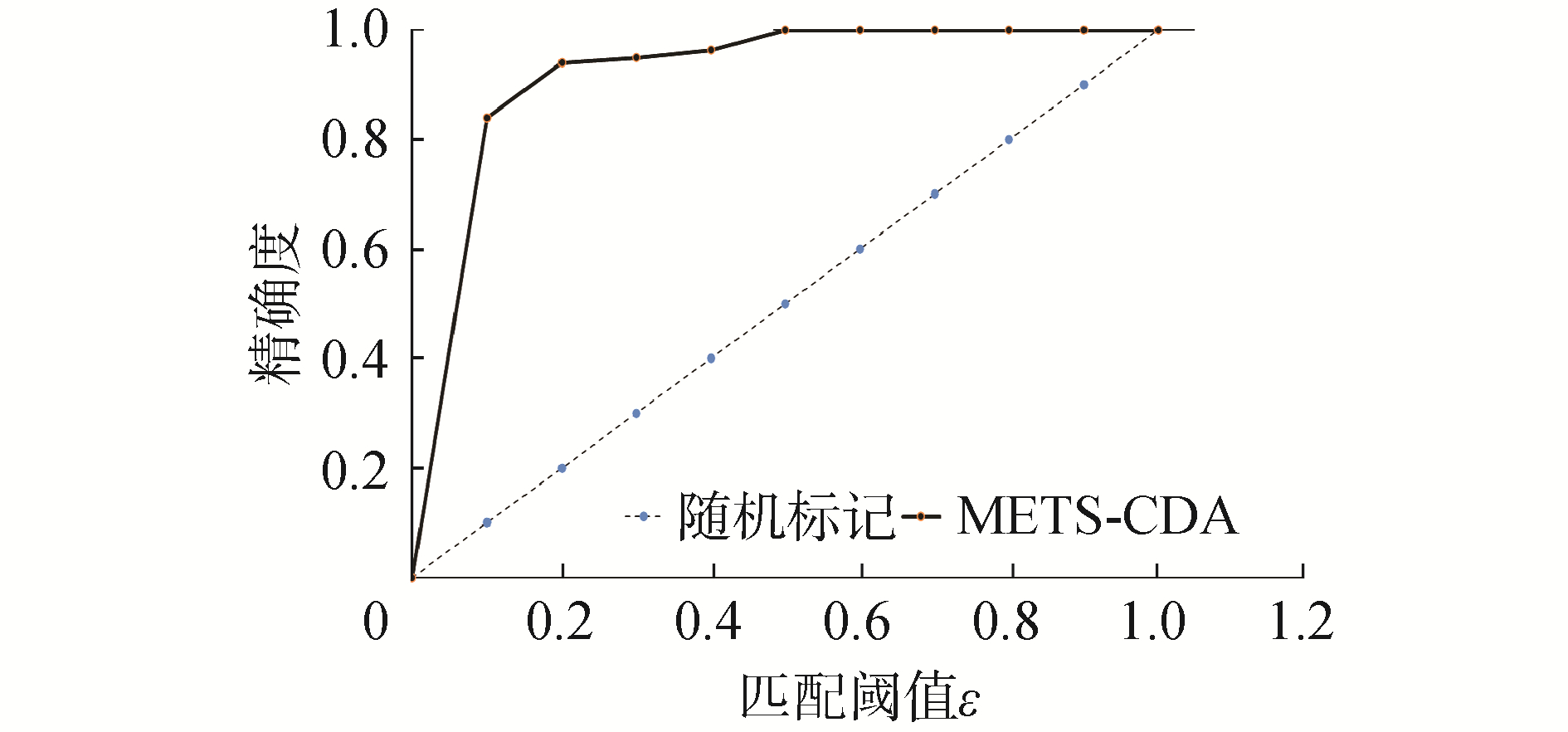
参考表 2检测精确度，绘制检测百分比曲线，如图 5所示。分析得出：
图 5 检测精确度百分比曲线Fig. 5 Detection precision percentage curve下载:
全尺寸图片
1) 当匹配阈值ε=0.1时，提取结果并不可靠，提取数量甚至大于参考真值。主要原因是匹配标准过松使不属于同一环形山的2个半边缘产生误匹配；
2) 随着匹配阈值增加，匹配要求逐渐增强，提取出环形山的数量逐渐下降，nTP和nFP也随之下降；
3) 随着匹配阈值增加，nFN增加，这是由于匹配要求增强使属于同一环形山，但相似性不大、或明暗特征不明显的2个半边缘无法匹配成功；
4) 为使算法综合特性最好，需要选取恰当的匹配阈值。当ε=0.5时，参数Q、B和P表现均为最优，D虽不为最优但与最优值89.8%相差不大，说明ε=0.5是算法潜在的最优取值；
5) 设计质量评估参数E综合评估各质量参数
$$ E=D+Q+(1-B)+P $$ (39) 当ε=0.5时，对应E=3.75最大，说明0.5确实为最优阈值；
6) 计算检测百分比曲线的曲线下面积(area under curve, AUC)Sauc，Sauc=0.919 2，远远大于随机猜测Sauc=0.5，说明提出算法有效性非常好。
将提出算法与其他理论的方法进行对比，评估提取效果，评估结果如表 3所示。
表 3 与其他环形山检测算法对比Table 3 Comparison with other CDA理论 检出
环形山数量质量参数 D/% Q/% B 提出方法 1 170 87.5 87.5 0 自适应边缘检测 979 64.6 60.0 0.12 霍夫变换 917 45.8 38.5 0.42 纹理分析 1 047 59.2 52.5 0.22 与基于自适应边缘检测的方法(自适应CDA)相比，本文提出METS-CDA算法提取有效环形山数量nTP提升35%以上。
将提出算法进一步分解为图像预处理、图像三值化、边缘强弱阈值选取，边缘检测、边缘匹配和椭圆拟合6个检测步骤，进一步评估算法的时效性。选取检测性能与本文算法最接近、检测步骤最相近的自适应环形山检测算法进行对比，统计各步骤所用时间，如表 4所示。
表 4 与其他环形山检测算法检测时间对比Table 4 Crater detection time comparison with other CDA检测步骤 本文理论/ms 自适应CDA/ms 图像预处理 395 364 图像三值化 257 0 边缘强弱阈值选取 0 1 112 边缘检测 353 664 边缘匹配 701 842 椭圆拟合 25 15 总时间 1 831 3 057 与自适应环形山检测方法相比，本文提出算法的算力消耗大大降低。二者图像预处理的时间几乎相同；而本文算法在图像三值化后直接完成边缘检测，节省了大量计算时间；此外，由于三值化后的环形山边缘提取结果更连续、杂散干扰较少、且单边缘包含的点更多，故边缘匹配时长略低而椭圆拟合时长略高。总体而言，本文提出算法计算效率更高，总体计算效率提升40%以上。
4.2 基于月面沙盘的半实物试验验证
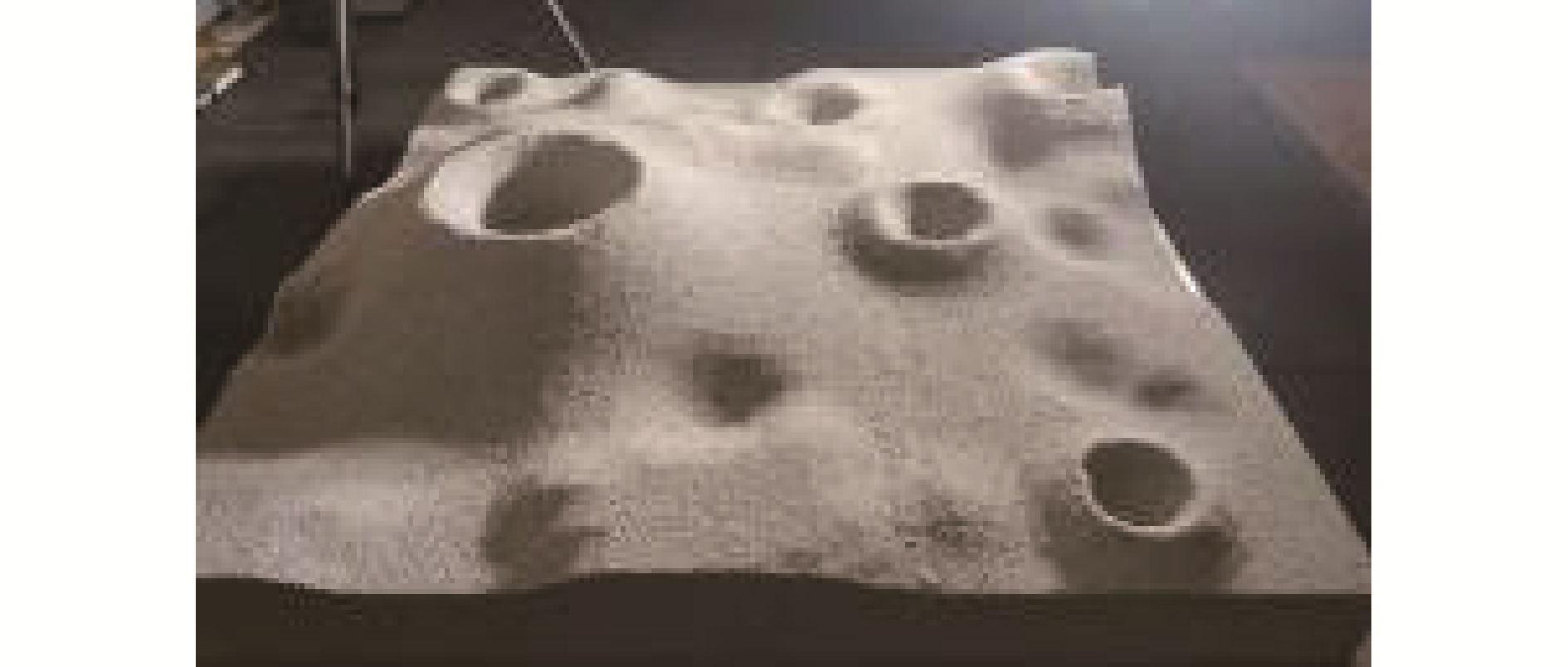
试验采用尺寸为2 m×2 m的仿真月面沙盘进行多光照条件下的环形山检测。实验系统包含月面沙盘、MT9V034摄像头、平行光源和数据交换机。图 6为实验使用的沙盘。
图 6 月面沙盘Fig. 6 Lunar sand table下载:
全尺寸图片
构建半实物仿真试验环境，如图 7所示，各器件参数见表 5。平行光源分别设置在沙盘两侧，照射高度1 m，模拟太阳直射方向。对采集图像进行高斯滤波处理后，规避沙盘周围试验场地影响，提取出不同方向光照条件下的环形山检测结果进行对比分析。
图 7 半实物仿真试验环境Fig. 7 Partial physical simulation environment下载:
全尺寸图片
表 5 实验各组成部分参数Table 5 Parameters of experiment实验设备 参数 沙盘 尺寸 2 m×2 m 环形山数量 8 最大环形山深度 0.30 m 平行光源 5 600 K×2 摄像头 45 fps@1 280×960, 60 fps@1 280×720
80 fps@640×480, 160 fps@320×240数据交换机 Jetson TX2 图 8为不同光照条件下月面沙盘采集图像，三值化结果及对应环形山检测结果，对检测到的环形山进行编号。分析得出：
图 8 不同光照条件下检测结果Fig. 8 Detection results under different illumination directions下载:
全尺寸图片
1) 2组实验均检出7个环形山。1号~6号环形山2组实验均检出，它们在光照条件下产生的明暗特征与周围环境区别明显。但2次拟合出的环形山形状有区别，尺寸和扁率不同;
2) 由于2号环形山较高，7号和8号环形山在2组实验中分别被2号环形山阴影掩盖，受到了地形影响，虽未同时检出但不影响算法的可靠性；
3) 提出的算法可在不同光照条件下进行有效环形山提取，不受光照方向影响，说明算法具有较强的鲁棒性。
4.3 基于CDA的光学导航方法对比仿真
飞行器导航相机焦距f=0.008 m，在图 5中随机选取960×1 247像素的图窗进行导航仿真实验。图窗中环形山数量较多，而导航解算最少只需要4个有效环形山检测结果，因此不需完成全图窗的环形山检测就可进行导航解算。为保证选取的4个有效环形山具有优良的几何因子，实验采取从四角到中心的搜索方式进行环形山检测。
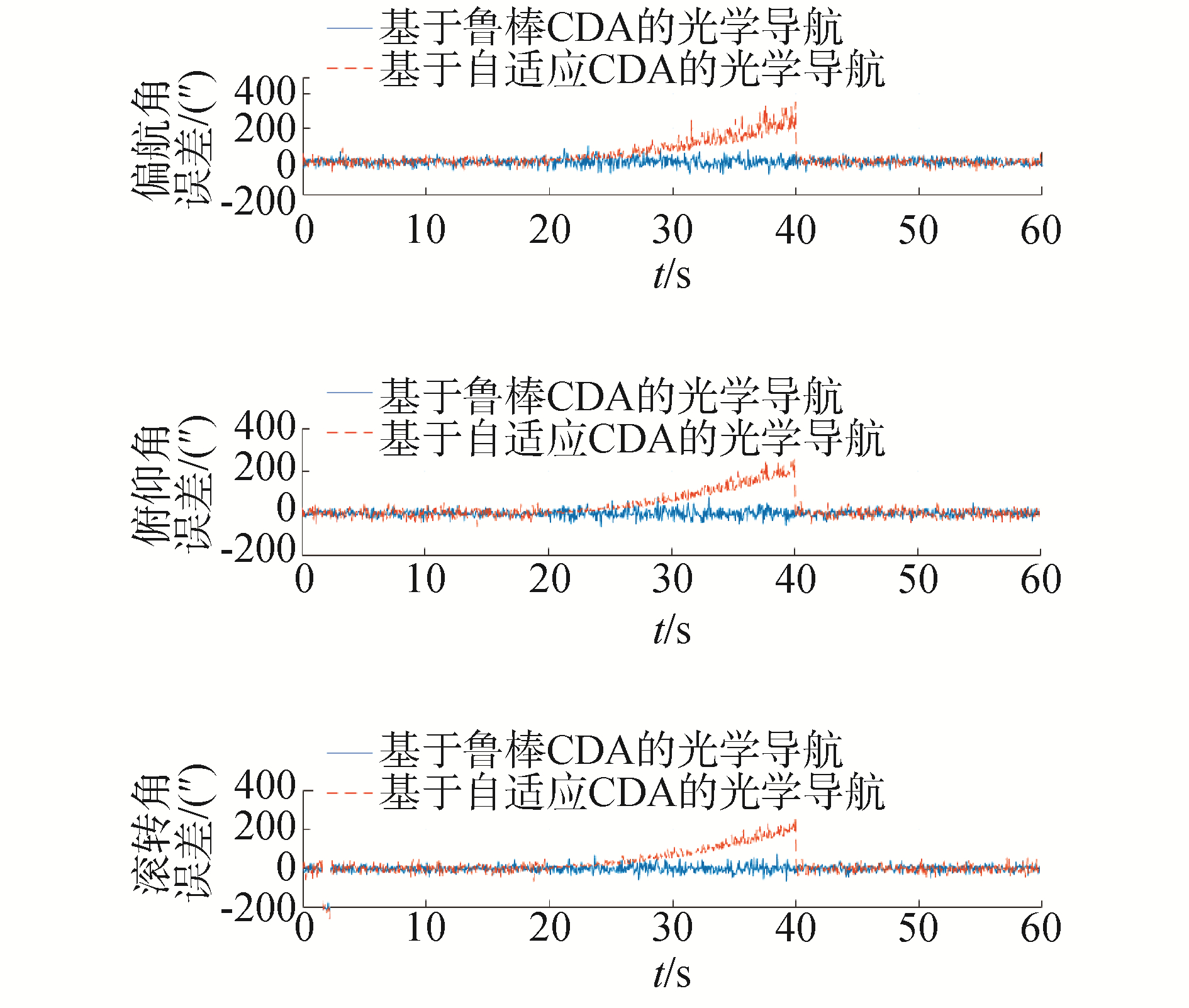
对基于鲁棒环形山检测(METS-CDA)和基于自适应环形山检测(adaptive CDA)算法的月球探测器光学导航进行对比仿真，结果如图 9所示。可以看出，当月面图像拍摄质量较好，视野中有丰富环形山作为导航地标特征时，基于自适应环形山检测的光学导航精度与基于鲁棒环形山检测的光学导航精度相近；当月面图像拍摄区域无明显环形山或者图像拍摄质量较差时，基于自适应环形山检测的光学导航方法出现发散，而提出的鲁棒环形山检测方法仍能提取出可用的环形山信息用于光学导航，姿态估计仍然收敛，说明提出的算法具有较强的鲁棒性。
图 9 不同光学导航精度对比Fig. 9 Accuracy comparison of visual navigation methods based on METS-CDA and adaptive CDA下载:
全尺寸图片
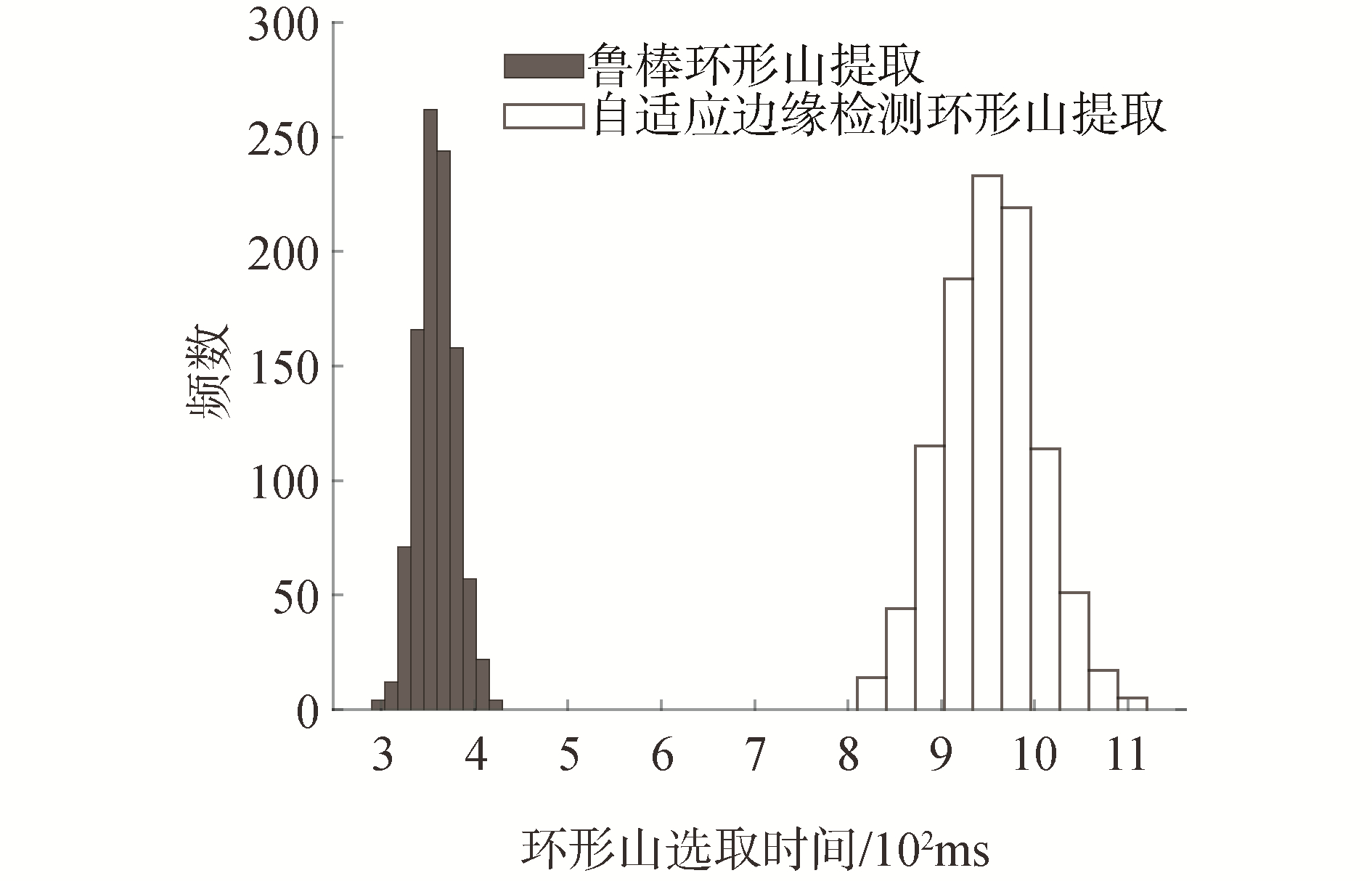
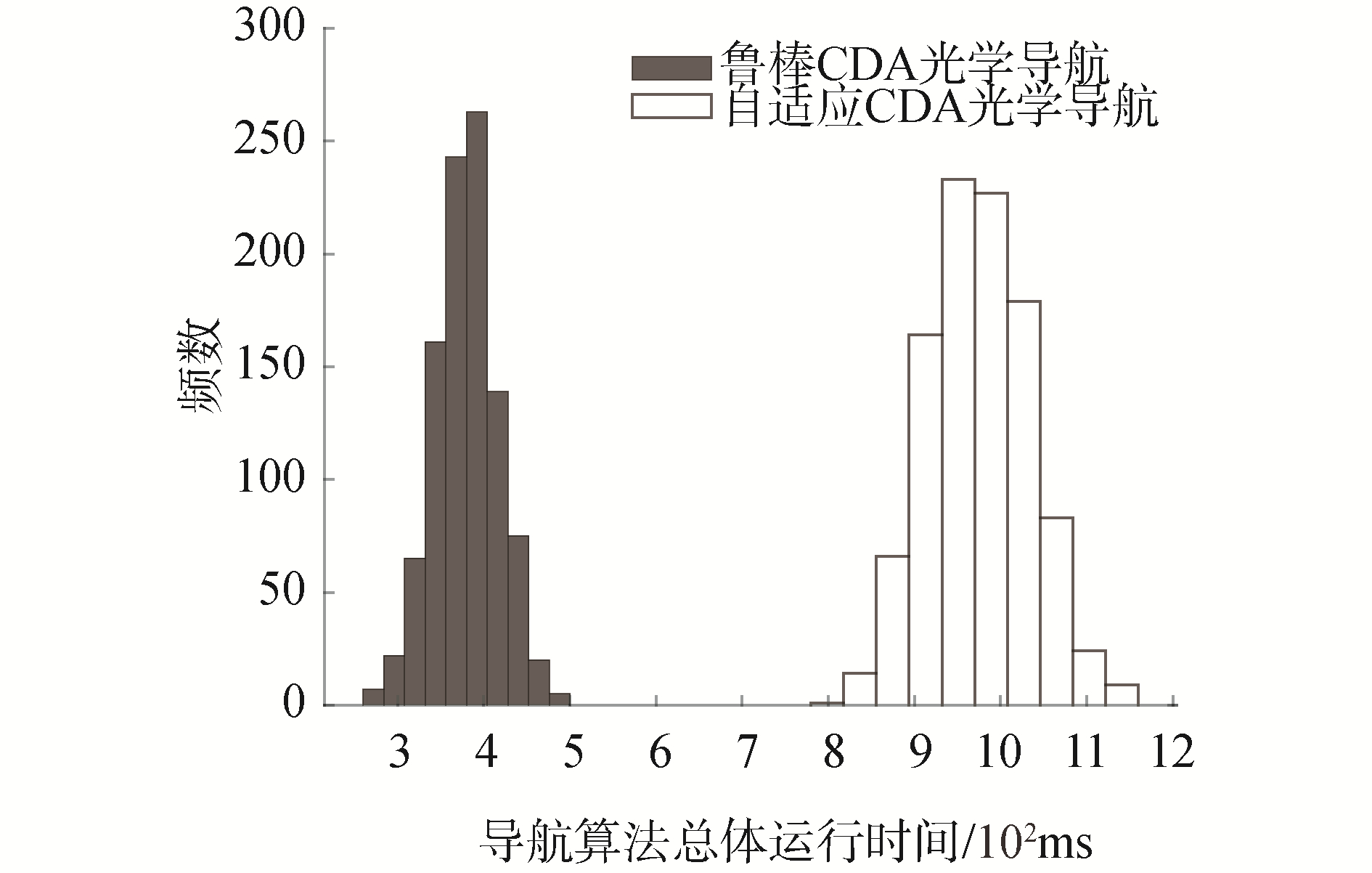
分别采用本文提出的鲁棒CDA方法和自适应CDA方法，进行1 000次蒙特卡罗打靶实验。完成环形山检测后，计算飞行器位置和姿态，统计2种算法环形山提取时间和导航解算时间。
图 10 提取环形山时间对比Fig. 10 CDA time of two methods下载:
全尺寸图片
图 11 环形山检测光学导航时间对比Fig. 11 Navigation time of two methods下载:
全尺寸图片
鲁棒环形山提取时间要显著低于自适应边缘检测环形山提取时间，方差更小、运行更稳定，这是因为前者提取出的环形山边缘更连续、清晰，利于环形山边缘匹配和椭圆拟合；而自适应边缘检测由于要对图像梯度检测进行强弱阈值选取，其基础运行时间就高于第一种算法。2种基于环形山检测的光学导航算法运行时间分布与环形山选取时间分布几乎相同，说明提取出有效环形山后，导航计算时间差异不大。总体来说，基于鲁棒环形山提取的光学导航计算实时性更优良。
5. 结论
1) 与传统方法相比，环形山提取算法提取出有效环形山数量提升35%以上、计算消耗降低40%；环形山提取过程不受不同光照因素影响，具有鲁棒性。
2) 以提出算法为基础的光学导航实时性更好、精度高，极端条件下不发散，可以满足月球探测任务障碍检测与规避系统、光学导航系统的可靠性和实时性需求。
-
图 1 月面图像
Fig. 1 Lunar image
下载:
全尺寸图片
图 2 分割后图像总熵分布
Fig. 2 Distribution of segmented image entropy
下载:
全尺寸图片
图 3 图环形山边缘特征点
Fig. 3 Feature points of crater edge
下载:
全尺寸图片
图 4 环形山检测结果
Fig. 4 Crater detection result
下载:
全尺寸图片
图 5 检测精确度百分比曲线
Fig. 5 Detection precision percentage curve
下载:
全尺寸图片
图 6 月面沙盘
Fig. 6 Lunar sand table
下载:
全尺寸图片
图 7 半实物仿真试验环境
Fig. 7 Partial physical simulation environment
下载:
全尺寸图片
图 8 不同光照条件下检测结果
Fig. 8 Detection results under different illumination directions
下载:
全尺寸图片
图 9 不同光学导航精度对比
Fig. 9 Accuracy comparison of visual navigation methods based on METS-CDA and adaptive CDA
下载:
全尺寸图片
图 10 提取环形山时间对比
Fig. 10 CDA time of two methods
下载:
全尺寸图片
图 11 环形山检测光学导航时间对比
Fig. 11 Navigation time of two methods
下载:
全尺寸图片
表 1 真值和环形山结果
Table 1 Ground truth and detection results
数据 检测数 环形山数量 d < 70 m 70 m < d < 700 m d>700 m 真值 1 337 96 1 204 37 检出数 1 170 77 1 056 37 检出率/% 87.5 80.2 87.7 100 注：d为检出环形山直径。 表 2 环形山检测数量和对应质量参数
Table 2 Detected crater numbers and quality factor
匹配阈值ε 环形山检测数 质量参数 检测结果 D/% Q/% B P/% TP FP FN 0.1 1 430 89.8 76.7 0.19 84.0 1 201 229 136 0.2 1 276 89.7 84.8 0.06 94.0 1 199 77 138 0.3 1 264 89.7 85.5 0.05 94.9 1 199 65 138 0.4 1 230 88.6 85.6 0.04 96.3 1 184 46 153 0.5 1 170 87.5 87.5 0 100 1 170 0 167 0.6 1 074 80.3 80.3 0 100 1 074 0 263 0.7 962 72.0 72.0 0 100 962 0 375 0.8 909 68.0 68.0 0 100 909 0 428 0.9 209 15.6 15.6 0 100 209 0 1128 表 3 与其他环形山检测算法对比
Table 3 Comparison with other CDA
理论 检出
环形山数量质量参数 D/% Q/% B 提出方法 1 170 87.5 87.5 0 自适应边缘检测 979 64.6 60.0 0.12 霍夫变换 917 45.8 38.5 0.42 纹理分析 1 047 59.2 52.5 0.22 表 4 与其他环形山检测算法检测时间对比
Table 4 Crater detection time comparison with other CDA
检测步骤 本文理论/ms 自适应CDA/ms 图像预处理 395 364 图像三值化 257 0 边缘强弱阈值选取 0 1 112 边缘检测 353 664 边缘匹配 701 842 椭圆拟合 25 15 总时间 1 831 3 057 表 5 实验各组成部分参数
Table 5 Parameters of experiment
实验设备 参数 沙盘 尺寸 2 m×2 m 环形山数量 8 最大环形山深度 0.30 m 平行光源 5 600 K×2 摄像头 45 fps@1 280×960, 60 fps@1 280×720
80 fps@640×480, 160 fps@320×240数据交换机 Jetson TX2 -
[1] DICKEY J O, BENDER P L, FALLER J E, et al. Lunar laser ranging: a continuing legacy of the Apollo program[J]. Science, 1994, 265(5171): 482-490. doi: 10.1126/science.265.5171.482 [2] KLUMPP A R. Apollo lunar descent guidance[J]. Automatica, 1974, 10(2): 133-146. doi: 10.1016/0005-1098(74)90019-3 [3] OUYANG Ziyuan, LI Chunlai, ZOU Yongliao, et al. Primary scientific results of Chang'E-1 lunar mission[J]. Science China earth sciences, 2010, 53(11): 1565-1581. doi: 10.1007/s11430-010-4056-2 [4] 吴伟仁, 王琼, 唐玉华, 等. "嫦娥4号"月球背面软着陆任务设计[J]. 深空探测学报, 2017, 4(2): 111-117. WU Weiren, WANG Qiong, TANG Yuhua, et al. Design of Chang'E-4 lunar farside soft-landing mission[J]. Journal of deep space exploration, 2017, 4(2): 111-117. [5] XU Weiming, YU Hongxuan, JIANG Hao, et al. Navigation doppler lidar sensor for precision landing of China's Chang'E-5 lunar lander[J]. Applied optics, 2020, 59(27): 8167. doi: 10.1364/AO.398382 [6] ZHAO Baochang, YANG Jianfeng, WEN Desheng, et al. Overall scheme and on-orbit images of Chang'E-2 lunar satellite CCD stereo camera[J]. Science China technological sciences, 2011, 54(9): 2237-2242. doi: 10.1007/s11431-011-4519-5 [7] LIU Kai, HAO Xinjun, LI Yiren, et al. Mars orbiter magnetometer of China's first Mars mission Tianwen-1[J]. Earth and planetary physics, 2020, 4(4): 384-389. doi: 10.26464/epp2020058 [8] HASSLER D M, ZEITLIN C, WIMMER-SCHWEINGRUBER R F, et al. Mars' surface radiation environment measured with the Mars Science Laboratory's Curiosity rover[J]. Science, 2014, 343(6169): 1244797. doi: 10.1126/science.1244797 [9] MORRIS R V, KLINGELHÖFER G, SCHRÖDER C, et al. Mössbauer mineralogy of rock, soil, and dust at Meridiani Planum, Mars: opportunity's journey across sulfate-rich outcrop, basaltic sand and dust, and hematite lag deposits[J]. Journal of geophysical research: planets, 2006, 111(E12S15): 1-27. [10] GLASSMEIER K H, BOEHNHARDT H, KOSCHNY D, et al. The Rosetta mission: flying towards the origin of the solar system[J]. Space science reviews, 2007, 128(1): 1-21. [11] HUANG Jun, XIAO Zhiyong, FLAHAUT J, et al. Geological characteristics of von Kármán crater, northwestern south pole-aitken basin: Chang'E-4 landing site region[J]. Journal of geophysical research: planets, 2018, 123(7): 1684-1700. doi: 10.1029/2018JE005577 [12] YE Peijian, SUN Zezhou, ZHANG He, et al. An overview of the mission and technical characteristics of Change'4 Lunar Probe[J]. Science China technological sciences, 2017, 60(5): 658-667. doi: 10.1007/s11431-016-9034-6 [13] STEPINSKI T F, DING W, VILALTA R. Detecting impact craters in planetary images using machine learning[J]. Intelligent data analysis for real life applications theory & practice, 2012, 8: 1-13. [14] DELATTE D M, CRITES S T, GUTTENBERG N, et al. Automated crater detection algorithms from a machine learning perspective in the convolutional neural network era[J]. Advances in space research, 2019, 64(8): 1615-1628. doi: 10.1016/j.asr.2019.07.017 [15] SILBURT A, ALI-DIB M, ZHU Chenchong, et al. Lunar crater identification via deep learning[J]. Icarus, 2019, 317: 27-38. doi: 10.1016/j.icarus.2018.06.022 [16] WANG Hao, JIANG Jie, ZHANG Guangjun. CraterIDNet: an end-to-end fully convolutional neural network for crater detection and identification in remotely sensed planetary images[J]. Remote sensing, 2018, 10(7): 1067. doi: 10.3390/rs10071067 [17] LEE C, HOGAN J. Automated crater detection with human level performance[J]. Computers & geosciences, 2021, 147: 104645. [18] LEE H, CHOI H L, JUNG D, et al. Deep neural network-based landmark selection method for optical navigation on lunar highlands[J]. IEEE access, 2020, 8: 99010-99023. doi: 10.1109/ACCESS.2020.2996403 [19] WU Peng, MU Rongjun, DENG Yanpeng. Review of intelligent bionic vision navigation[C]//Proc SPIE 10605, LIDAR Imaging Detection and Target Recognition, 2017, 2017, 10605: 898-905. [20] SAHEBA S M, UPADHYAYA T K, SHARMA R K. Lunar surface crater topology generation using adaptive edge detection algorithm[J]. IET image processing, 2016, 10(9): 657-661. doi: 10.1049/iet-ipr.2015.0232 [21] YAN Yunfeng, QI Donglian, LI Chaoyong. Vision-based crater and rock detection using a cascade decision forest[J]. IET computer vision, 2019, 13(6): 549-555. doi: 10.1049/iet-cvi.2018.5600 [22] CHEN Min, LIU Danyang, QIAN Kejian, et al. Lunar crater detection based on terrain analysis and mathematical morphology methods using digital elevation models[J]. IEEE transactions on geoscience and remote sensing, 2018, 56(7): 3681-3692. doi: 10.1109/TGRS.2018.2806371 [23] TIAN Yang, YU Meng, YAO Meibao, et al. Crater edge-based flexible autonomous navigation for planetary landing[J]. Journal of navigation, 2019, 72(3): 649-668. doi: 10.1017/S0373463318000966 [24] WU Peng, MU Rongjun, DENG Yanpeng. Robust crater detection algorithm based on maximum entropy threshold segmentation[J]. International journal of aerospace engineering, 2022, 4872248: 1-15. [25] GALLOWAY M J, PAXMAN J, BENEDIX G, et al. Auomated crater detection and counting using the hough transform and canny edge detection[C]//Workshop on Issues in Crater Studies and the Dating of Planetary Surfaces, 2015, 1841: 9024. [26] CUI Pingyuan, GAO Xizhen, ZHU Shengying, et al. Visual navigation based on curve matching for planetary landing in unknown environments[J]. Acta astronautica, 2020, 170: 261-274. doi: 10.1016/j.actaastro.2020.01.023 [27] ZHENG L, HU W D, LIU C. Large crater identification method based on deep learning[J]. Journal of BeiHang University of Aeronautics and Astronautics, 2020, 327(5): 159-169. [28] MU Rongjun, WU Peng, DENG Yanpeng, et al. Optical navigation method and error analysis for the descending landing phase in planetary exploration[J]. Aerospace, 2022, 9(9): 496-522. doi: 10.3390/aerospace9090496
