船舶动力定位非线性模型预测控制

张泉; 郭晨

doi:10.11990/jheu.202110026

船舶动力定位非线性模型预测控制

doi: 10.11990/jheu.202110026

张泉,
郭晨^,

大连海事大学船舶电气工程学院, 辽宁大连 116026

基金项目:

国家自然科学基金项目 51879027;

国家自然科学基金项目 51579024;

中央高校基本科研业务费 3132019318.

详细信息

作者简介:
张泉, 男, 讲师, 博士研究生;

郭晨, 男, 教授, 博士生导师.

通讯作者:
郭晨, E-mail: guoc@dlmu.edu.cn.

中图分类号: TP273, U664.82
出版历程
- 收稿日期: 2021-10-12
- 网络出版日期: 2023-09-20

Nonlinear model predictive control for the dynamic positioning system of ships

ZHANG Quan,
GUO Chen^,

College of Marine Electrical Engineering, Dalian Maritime University, Dalian 116026, China

摘要

摘要: 针对受船舶运动状态和推力饱和约束影响的动力定位控制问题，本文提出了一种非线性模型预测控制方法。依据多面体描述理论建立了船舶动力定位多面体描述偏差模型，针对上述模型采用线性矩阵不等式设计非线性模型预测控制器中的终端要素，并证明了闭环系统的稳定性。仿真结果表明: 设计的控制器能在满足约束条件和受环境干扰条件下快速控制船舶稳定在计划航向和计划船位，验证了控制器的有效性和本质鲁棒性。
- 动力定位 /
- 模型预测控制 /
- 约束满足问题 /
- 运动控制 /
- 多面体描述系统 /
- 线性矩阵不等式 /
- 终端约束 /
- 渐进稳定性
Abstract: This paper proposes a nonlinear model predictive control method for solving the problems of maintaining the planned position of a dynamically positioned ship constrained by the thrust and motion states. First, a polyhedron description deviation model for the dynamically positioned ship is established based on the polyhedron theory. Second, for the above model, the terminal ingredients in the nonlinear model prediction controller are designed using linear matrix inequalities, and the stability of the closed-loop system is verified. The simulation results show that the designed controller can swiftly stabilize the ship in the planned heading and position under the conditions of meeting constraint requirements and being affected by environmental disturbances, thus verifying the effectiveness and inherent robustness of the controller.
- dynamic positioning /
- model predictive control /
- constraint satisfaction problem /
- motion control /
- polyhedron description system /
- linear matrix inequality /
- terminal constraints /
- asymptotic stability

HTML全文

动力定位(dynamic positioning, DP)是指船舶不借助锚泊而单独利用其自身安装的推进器，实现船位、航向或预设航迹的自动保持。DP是船舶进行海洋资源开发时利用的重要技术手段，因此DP控制系统的设计一直备受关注，诸多控制算法被应用在DP控制系统的设计中，如反步法控制^[1]、动态面控制^[2]、滑模控制^[3-4]、自抗扰控制^[5-6]、鲁棒控制^[7-8]、智能控制^[9-10]等。但这些控制器在设计阶段大多忽略了2个问题：1)船舶推进系统存在推力饱和以及推力变化率饱和约束，无法提供任意大小的推力及力矩；2)船舶进行DP作业时极有可能要求船舶保持低速航行，即对船舶运动状态进行约束。一旦忽略了上述问题，控制效果将难以达到预期，甚至可能无法保证闭环系统的稳定性，最终导致船舶控制失效。

模型预测控制(model predictive control, MPC)由于可以显式处理约束条件、优化控制作用而备受人们关注。在DP领域中，挪威厂商Konsberg首次在DP系统中应用了MPC算法^[11]。同年，文献[12]利用精确反馈线性化方法将移动式海上平台动力定位数学模型中的非线性问题和已知扰动做线性化处理，并结合线性MPC控制算法对平台进行控制。文献[13]提出了一种基于拉盖尔函数的线性MPC算法，该算法可提高DP控制系统的实时性。相比于线性MPC控制器，非线性MPC控制器(nonlinear model predictive control, NMPC)能够更好地处理非线性系统，控制效果更佳。文献[14]针对DP作业的非线性阶段和线性阶段分别设计了NMPC控制器和MPC控制器，并设计了切换函数实现不同作业阶段的控制器切换。上述工作对MPC在DP领域的应用做出了较深入的研究，但在保证系统稳定性方面鲜有讨论，仍需要进一步研究。文献[15]中已经指出，选择合适的终端要素可以确保系统稳定性，但构造终端要素目前尚未有统一的方法。基于上述分析，本文针对DP控制问题，提出了一种NMPC控制方法。引入多面体描述系统和线性矩阵不等式(linear matrix inequalities, LMI)理论设计NMPC控制器中的预测模型和终端要素，通过性能指标递减法理论证明了闭环系统的稳定性。

1. 船舶运动数学模型

船舶在动力定位时船速较低，为方便问题研究，此时可认为船舶所受阻尼是线性的，所受的科里奥利向心力近似为0。假设船舶关于艏艉线左右对称，则在不计风、浪、流等环境影响下，只考虑三自由度运动的船舶动力定位数学模型可表示为^[11]：

$$ \left\{\begin{array}{l} \dot{\eta}=R(\psi) v \\ M \dot{v}+D v=\tau \end{array}\right. $$

(1)

式中：$\boldsymbol{\eta}=\left[\begin{array}{lll} x & y & \psi \end{array}\right]^{\mathrm{T}}$为位置状态向量; x、y为大地坐标系下的船舶纵向和横向位置; Ψ为船舶航向；$\boldsymbol{v}=\left[\begin{array}{lll} u & v & r \end{array}\right]^{\mathrm{T}}$为速度状态向量; u、v、r分别为船体坐标系下的纵向速度、横向速度和首摇角速度；R (ψ)为大地坐标系和船体坐标系之间的旋转变换矩阵；M为船舶惯性矩阵；D为线性阻尼系数矩阵；$\boldsymbol{\tau}=\left[\begin{array}{lll} \boldsymbol{\tau}_x & \boldsymbol{\tau}_y & \boldsymbol{\tau}_N \end{array}\right]^{\mathrm{T}}$为控制输入变量矩阵，表示推进器的纵向、横向合力及合力矩指令。R(ψ)、M和D矩阵的结构形式为：

$$ \boldsymbol{R}(\psi)=\left[\begin{array}{ccc} \cos \psi & -\sin \psi & 0 \\ \sin \psi & \cos \psi & 0 \\ 0 & 0 & 1 \end{array}\right] $$

(2)

$$ \boldsymbol{M}=\left[\begin{array}{ccc} m-X_{\dot u} & 0 & 0 \\ 0 & m-Y_{\dot{v}} & -Y_{\dot{r}} \\ 0 & -N_{\dot{v}} & I_z-N_{\dot{r}} \end{array}\right] $$

(3)

$$ \boldsymbol{D}=\left[\begin{array}{ccc} -X_u & 0 & 0 \\ 0 & -Y_v & -Y_r \\ 0 & -N_v & -N_r \end{array}\right] $$

(4)

式中：m为船舶质量；$X_{\dot{u}} 、Y_{\dot{v}} 、Y_{\dot{r}} 、N_{\dot{v}} 、N_{\dot{r}}$为惯性类船体水动力导数；I_Z为船舶转动惯量；X_u、Y_v、Y_r、N_v、N_r为粘性类船体水动力导数。

2. 船舶动力定位NMPC控制器设计

2.1 模型预测控制原理

考虑非线性系统：

$$ \boldsymbol{x}(k+1)=f(\boldsymbol{x}(k), \boldsymbol{u}(k)) $$

(5)

式中：x(k)为k时刻状态变量; u(k)为k时刻输入变量; f(·)为非线性函数且f(0, 0)=0。在k时刻从系统状态x(k)出发的MPC问题可以表示为：

$$ \left\{\begin{array}{l} \min\limits_{\boldsymbol{u}(k+i)} J_N(\boldsymbol{x}(k), \boldsymbol{u}(k+i))=\sum\limits_{i=0}^{N-1} l(\boldsymbol{x}(k+i), \\ \boldsymbol{u}(k+i))+F(\boldsymbol{x}(k+N)) \\ \text { s.t. } \quad \boldsymbol{x}(k+i+1)=f(\boldsymbol{x}(k+i), \boldsymbol{u}(k+i)) \\ \boldsymbol{u}(k+i) \in \boldsymbol{\varOmega}_u, \boldsymbol{x}(k+i) \in \boldsymbol{\varOmega}_x \\ \boldsymbol{x}(k+N) \in \boldsymbol{\varOmega}, \boldsymbol{u}_F(\boldsymbol{x}(k+N)) \in \boldsymbol{\varOmega}_u \end{array}\right. $$

(6)

式中：N为预测时域；i=0, 1, …, N-1; F(·)为终端惩罚项；l(·, ·)为非线性性能函数，l(·, ·)≥0当且仅当l(0, 0)=0；Ω_u和Ω_x分别为输入变量和状态变量约束集；Ω为终端约束集；u_F(·)为终端控制律。每一采样时刻根据当前状态x(k)在线求解式(6)，得到控制输入序列$\left[\begin{array}{lll} u(0) & u(1) & \cdots \end{array}\right]^{\mathrm{T}}$，并将序列中的第1个元素u(0)作为实际控制输入量作用在被控系统上，在下一采样时刻重复上述过程。文献[15]指出，当终端要素(终端惩罚项、终端约束集和终端控制律)满足A₁~A₄条件时，闭环系统渐近稳定：

条件A₁终端约束集Ω是状态约束空间的子集，并且是一个包含原点的闭集；

条件A₂对于所有的x∈Ω，终端控制律 u_F(x)均满足输入约束，并且当 x=0时，u_F(x)=0；

条件A₃当x∈Ω时，u_F(x)能控制系统状态轨迹一直保持在终端约束集中；

条件A₄当k>0时，设计的终端惩罚项F(x)应使得J_N^*(k+1)≤J_N^*(k)，J_N^*(k+1)和J_N^*(k)分别表示k+1时刻和k时刻时的最优性能指标值。

2.2 控制目标和NMPC控制器设计

本文的控制目标是在满足推进器推力约束、推力变化率约束以及船舶速度状态自身约束的条件下，控制船舶从当前位置状态$\left[\begin{array}{lll}x & y & \psi\end{array}\right]^{\mathrm{T}}$移动至期望位置状态$\left[\begin{array}{lll}x_r & y_r & \psi_r\end{array}\right]^{\mathrm{T}}$，并且能够稳定在该船位和航向上。为方便后续的稳定性分析，将式(1)整理成微分方程组形式，并根据控制目标对该模型做出适当调整，得到基于状态偏差的数学运动模型：

$$ \left\{\begin{array}{l} \dot{\tilde{x}}=\tilde{u} \cos \left(\tilde{\psi}+\psi_r\right)-\tilde{v} \sin \left(\tilde{\psi}+\psi_r\right) \\ \dot{\tilde{y}}=\tilde{u} \sin \left(\tilde{\psi}+\psi_r\right)+\tilde{v} \cos \left(\tilde{\psi}+\psi_r\right) \\ \dot{\tilde{\psi}}=\tilde{r} \\ \dot{\tilde{u}}=\frac{X_u}{m-X_{\dot{u}}} \cdot \tilde{u}+\frac{1}{m-X_{\dot{u}}} \cdot \tau_x \\ \dot{\tilde{v}}=\frac{\left[Y_v\left(I_z-N_{\dot{r}}\right)+N_v Y_{\dot{r}}\right] \cdot \tilde{v}+\left[Y_r\left(I_z-N_{\dot{r}}\right)+N_r Y_{\dot{r}}\right] \cdot \tilde{r}}{\left(m-Y_{\dot{v}}\right)\left(I_z-N_{\dot{r}}\right)-N_{\dot{v}} Y_{\dot{r}}}+\frac{\left(I_z-N_{\dot{r}}\right) \cdot \tau_y+Y_{\dot{r}} \cdot \tau_N}{\left(m-Y_{\dot{v}}\right)\left(I_z-N_{\dot{r}}\right)-N_{\dot{v}} Y_{\dot{r}}} \\ \dot{\tilde{r}}=\frac{\left[N_v\left(m-Y_{\dot{v}}\right)+Y_v N_{\dot{v}}\right] \cdot \tilde{v}+\left[N_r\left(m-Y_{\dot{v}}\right)+Y_r N_{\dot{v}}\right] \cdot \tilde{r}}{\left(m-Y_{\dot{v}}\right)\left(I_z-N_{\dot{r}}\right)-N_{\dot{v}} Y_{\dot{r}}}+\frac{N_{\dot{v}} \cdot \tau_y+\left(m-Y_{\dot{v}}\right) \cdot \tau_N}{\left(m-Y_{\dot{v}}\right)\left(I_z-N_{\dot{r}}\right)-N_{\dot{v}} Y_{\dot{r}}} \end{array}\right. $$

(7)

式中: $\tilde{x}=x-x_r, \tilde{y} 、\tilde{\psi} 、\tilde{u} 、\tilde{v} 、\tilde{r}$的含义同上。将状态偏差量定义为$\boldsymbol{\xi}=\left[\begin{array}{llllll}\tilde{x} & \tilde{y} & \tilde{\psi} & \tilde{u} & \tilde{v} & \tilde{r}\end{array}\right]^{\mathrm{T}}$，式(7)也可以表达为$\dot{\boldsymbol{\xi}}=f(\boldsymbol{\xi}, \boldsymbol{\tau})$。

在考虑控制目标、状态和输入约束以及确保系统稳定性的情况下，MPC性能指标函数设计为：

$$ \left\{\begin{array}{l} \min\limits_{\boldsymbol{\tau}(k+i)} J_N(\boldsymbol{\xi}(k), \boldsymbol{\tau}(k+i))=\sum\limits_{i=0}^{N-1}\left(\|\overline{\boldsymbol{\xi}}(k+i)\|_{\boldsymbol Q}^2+\right. \\ \left.\qquad\|\boldsymbol{\tau}(k+i)\|_{\boldsymbol{R}}^2\right)+\boldsymbol{F}(\overline{\boldsymbol{\xi}}(k+N)) \\ \text { s.t. } \overline{\boldsymbol{\xi}}(k+i+1)=g(\boldsymbol{\xi}(k+i), \boldsymbol{\tau}(k+i)) \\ \boldsymbol{\tau}_{\min } \leqslant \boldsymbol{\tau}(k+i) \leqslant \boldsymbol{\tau}_{\max } \\ \Delta \boldsymbol{\tau}_{\min } \leqslant \boldsymbol{\tau}(k+i+1)-\boldsymbol{\tau}(k+i) \leqslant \Delta \boldsymbol{\tau}_{\max } \\ u_{\min } \leqslant \tilde{u}(k+i) \leqslant u_{\max } \\ v_{\min } \leqslant \tilde{v}(k+i) \leqslant v_{\max } \\ r_{\min } \leqslant \tilde{r}(k+i) \leqslant r_{\max } \\ \overline{\boldsymbol{\xi}}(k+N) \in \boldsymbol{\varOmega} \\ \Delta \boldsymbol{\tau}_{\min } \leqslant \boldsymbol{u}_F(\overline{\boldsymbol{\xi}}(k+N))-\boldsymbol{\tau}(k+N-1) \leqslant \Delta \boldsymbol{\tau}_{\max } \end{array}\right. $$

(8)

式中：$j=1, 2, \cdots, N ; i=0, 1, \cdots, N-1 ; \| \overline{\boldsymbol{\xi}}(k+i)\| _{\boldsymbol{Q}}^{2}$和$\|\boldsymbol{\tau}(k+i)\|_{\boldsymbol{R}}^2$分别是向量ξ(k+i)和向量 τ(k+i)的2范数，定义为$\overline{\boldsymbol{\xi}}^{\mathrm{T}}(k+i) \boldsymbol{Q} \overline{\boldsymbol{\xi}}(k+i)$和$\boldsymbol{\tau}^{\mathrm{T}}(k+i) \boldsymbol{R} \boldsymbol{\tau}(k+i)$，矩阵Q和R为权重矩阵，二者均是正定的对角矩阵；ξ(k+i)为基于 ξ(k)预测的第k+i时刻的状态，g(·)是连续函数$\dot{\boldsymbol{\xi}}=f(\boldsymbol{\xi}, \boldsymbol{\tau})$的离散化形式；$F(\overline{\boldsymbol{\xi}}(k+N))$、Ω和$\boldsymbol{u}_F(\overline{\boldsymbol{\xi}}(k+N))$的定义与2.1节相同；τ_min、τ_max表示推进器能输出的最小和最大推力及推力力矩，且τ_min=-τ_max；Δτ_min和Δτ_max表示推力及推力力矩的最小和最大变化率，且Δτ_min=-Δτ_max；第4~6个公式分别表示船舶纵向、横向移动速度偏差和艏摇角速度偏差的约束范围，且u_min=-u_max，v_min=-v_max，r_min=-r_max；最后一个公式表示第N时刻的控制变量$\boldsymbol{u}_F(\overline{\boldsymbol{\xi}}(k+N))$与前一时刻的控制变量τ(K+N-1)之间的差值也应满足推力变化率的约束^[16]。

3. NMPC算法稳定性分析

设计终端要素是保证系统稳定性的重要步骤。目前，对于终端要素还没有统一的设计方法。本文将终端要素的具体形式定义为：终端惩罚项$F(\overline{\boldsymbol{\xi}})=\overline{\boldsymbol{\xi}}^{\mathrm{T}} \boldsymbol{P} \overline{\boldsymbol{\xi}}$；终端约束集$\boldsymbol{\varOmega}:=\left\{\overline{\boldsymbol{\xi}} \in R^6 \mid \overline{\boldsymbol{\xi}}^{\mathrm{T}} \boldsymbol{P} \overline{\boldsymbol{\xi}} \leqslant \alpha\right\}$；终端控制律$\boldsymbol{u}_F(\overline{\boldsymbol{\xi}})=\boldsymbol{H} \overline{\boldsymbol{\xi}} $。其中，P是终端惩罚权重矩阵，该矩阵是正定矩阵；α是正标量；H是状态反馈矩阵。只要找到合适的P、α和H，使得终端要素满足2.1节中的A₁~A₄条件，就能保证闭环系统的稳定性。为此，本节建立式(7)的多面体描述系统，并基于该系统确定P、α和H。

3.1 船舶多面体描述系统

多面体描述系统广泛用于描述存在不确定性的非线性系统，它是由一系列线性系统构成的集合，且该集合能够包裹原非线性系统。将式(7)在平衡点 ξ=0附近线性化，其Jacobian矩阵

$$ \begin{gathered} {\left[\begin{array}{cc} \frac{\partial f(\boldsymbol{x}, \boldsymbol{\tau})}{\partial \boldsymbol{\xi}} & \frac{\partial f(\boldsymbol{\xi}, \boldsymbol{\tau})}{\partial \boldsymbol{\tau}} \end{array}\right]=} \\ {\left[\begin{array}{ccccccccc} 0 & 0 & a_{13} & a_{14} & a_{15} & 0 & 0 & 0 & 0 \\ 0 & 0 & a_{23} & a_{24} & a_{25} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & a_{44} & 0 & 0 & a_{47} & 0 & 0 \\ 0 & 0 & 0 & 0 & a_{55} & a_{56} & 0 & a_{58} & a_{59} \\ 0 & 0 & 0 & 0 & a_{65} & a_{66} & 0 & a_{68} & a_{69} \end{array}\right]} \end{gathered} $$

Jacobian矩阵中的a₁₃、a₂₃、a₁₄、a₂₄、a₁₅、a₂₅会随着系统状态的变化而变化，表达式为：

$$ \left\{\begin{array}{l} a_{13}=\left(-\tilde{u} \cos \psi_r+\tilde{v} \sin \psi_r\right) \sin \tilde{\psi}-\left(\tilde{u} \sin \psi_r+\tilde{v} \cos \psi_r\right) \cos \tilde{\psi} \\ a_{24}=\sin \left(\tilde{\psi}+\psi_r\right) \\ a_{23}=\left(\tilde{u} \cos \psi_r-\tilde{v} \sin \psi_r\right) \cos \tilde{\psi}-\left(\tilde{u} \sin \psi_r+\tilde{v} \cos \psi_r\right) \sin \tilde{\psi} \\ a_{15}=-\sin \left(\tilde{\psi}+\psi_r\right) \\ a_{14}=\cos \left(\tilde{\psi}+\psi_r\right) \\ a_{25}=\cos \left(\tilde{\psi}+\psi_r\right) \end{array}\right. $$

(9)

而Jacobian矩阵中的其余元素均为常数，受篇幅限制不再逐个列出。

对式(7)建立多面体描述系统时，可根据上述参数的最大值和最小值来确定多面体的顶点。式(7)的多面体描述集合Π定义为：

$$ \boldsymbol{\varPi}:=\operatorname{Co}\left\{\left[\begin{array}{ll} \boldsymbol{A}_1 & \boldsymbol{B}_1 \end{array}\right] \quad\left[\begin{array}{ll} \boldsymbol{A}_2 & \boldsymbol{B}_2 \end{array}\right] \quad \cdots \quad\left[\begin{array}{ll} \boldsymbol{A}_q & \boldsymbol{B}_q \end{array}\right]\right\} $$

(10)

式中: A_i∈R^6×6为第i个顶点的系统矩阵; B_i∈R^6×3为第i个顶点的输入矩阵; q表示顶点个数。符号Co代表凸包，其意义为所有包含顶点[A_i B_i]的凸集的交集。故描述式(7)的离散多面体系统为：

$$ \boldsymbol{\xi}(k+1) \subseteq \boldsymbol{\varPi}_0\left[\begin{array}{l} \boldsymbol{\xi}(k) \\ \boldsymbol{\tau}(k) \end{array}\right], \boldsymbol{\varPi}_0:=\left[\begin{array}{ll} \boldsymbol{A} & \boldsymbol{B} \end{array}\right] \in \boldsymbol{\varPi} $$

(11)

式中[A B]为实际的系统矩阵和输入矩阵，它将基于式(10)取值：

$$ \left[\begin{array}{ll} \boldsymbol{A} & \boldsymbol{B} \end{array}\right]=\sum\limits_{i=1}^q \lambda_i\left[\begin{array}{ll} \boldsymbol{A}_i & \boldsymbol{B}_i \end{array}\right] $$

(12)

式中λ_i≥0且$\sum\limits_{i=1}^q \lambda_i=1$。从式(12)可以看出，式(11)所示的多面体描述系统包含了非线性系统式(7)的所有可能模型，因此该多面体描述系统可以用来代替式(7)。

3.2 终端要素的设计方法

定理1^[17] 对于式(11)所示的多面体描述系统，如果存在正定对称矩阵X∈R^6×6和矩阵 Y∈R^3×6，对所有的i=(1, 2, …, q)满足矩阵不等式：

$$ \left[\begin{array}{cccc} \boldsymbol{X} & * & * & * \\ \boldsymbol{A}_i \boldsymbol{X}+\boldsymbol{B}_i \boldsymbol{Y} & \boldsymbol{X} & * & * \\ \boldsymbol{Q}^{\frac{1}{2}} \boldsymbol{X} & {\mathbf{0}} & \boldsymbol{I} & * \\ \boldsymbol{R}^{\frac{1}{2}} \boldsymbol{Y} & {\mathbf{0}} & {\mathbf{0}} & \boldsymbol{I} \end{array}\right] \geqslant 0 $$

(13)

则在终端控制律$\boldsymbol{u}_F(\overline{\boldsymbol{\xi}})=\boldsymbol{H} \overline{\boldsymbol{\xi}}=\boldsymbol{Y} \boldsymbol{X}^{-1} \overline{\boldsymbol{\xi}}$的作用下，对于任意$\overline{\boldsymbol{\xi}} \in \boldsymbol{\varOmega}$，终端惩罚项F(ξ)满足条件A₄，终端控制律 u_F (ξ)满足条件A₃。其中，P=X^-1；I是适当维数的单位矩阵；*表示沿对角线对称位置的各块矩阵的转置。

证明对于任意的λ_i≥0，$\sum\limits_{i=1}^q \lambda_i=1$，i=(1, 2，…，q)，由式(13)可得：

$$ \left[\begin{array}{cccc} \boldsymbol{X} & * & * & * \\ \sum\limits_{i=1}^q \lambda_i\left(\boldsymbol{A}_i \boldsymbol{X}+\boldsymbol{B}_i \boldsymbol{Y}\right) & \boldsymbol{X} & * & * \\ \boldsymbol{Q}^{\frac{1}{2}} \boldsymbol{X} & {\mathbf{0}} & \boldsymbol{I} & * \\ \boldsymbol{R}^{\frac{1}{2}} \boldsymbol{Y} & {\mathbf{0}} & {\mathbf{0}} & \boldsymbol{I} \end{array}\right] \geqslant 0 $$

(14)

根据Schur补性质可知，式(14)等价于矩阵不等式：

$$ \begin{gathered} \boldsymbol{X}-\left(\sum\limits_{i=1}^q \lambda_i\left(\boldsymbol{A}_i \boldsymbol{X}+\boldsymbol{B}_i \boldsymbol{Y}\right)\right)^{\mathrm{T}} \boldsymbol{X}^{-1} \times \\ \left(\sum\limits_{i=1}^q \lambda_i\left(\boldsymbol{A}_i \boldsymbol{X}+\boldsymbol{B}_i \boldsymbol{Y}\right)\right)-\boldsymbol{X}^{\mathrm{T}} \boldsymbol{Q} \boldsymbol{X}-\boldsymbol{Y}^{\mathrm{T}} \boldsymbol{R} \boldsymbol{Y} \geqslant 0 \end{gathered} $$

(15)

将式(15)分别左乘P^T和右乘P，可得：

$$ \begin{gathered} \boldsymbol{P}-\left(\sum\limits_{i=1}^q \lambda_i\left(\boldsymbol{A}_i+\boldsymbol{B}_i \boldsymbol{H}\right)\right)^{\mathrm{T}} \boldsymbol{P}\left(\sum\limits_{i=1}^q \lambda_i\left(\boldsymbol{A}_i+\boldsymbol{B}_i \boldsymbol{H}\right)\right)- \\ \boldsymbol{Q}-\boldsymbol{H}^{\mathrm{T}} \boldsymbol{R} \boldsymbol{H}=\boldsymbol{S} \geqslant 0 \end{gathered} $$

(16)

k+1时刻和k时刻的最优性能指标值J_N^*(k+1)、J_N^*(k)可分别表示为：

$$ \begin{gathered} J_N^*(k+1)=\sum\limits_{i=0}^{N-2}\left(\left\|\boldsymbol{\xi}^*(k+i+1 \mid k)\right\|_{\boldsymbol{Q}}^2+\right. \\ \left.\left\|\boldsymbol{\tau}^*(k+i+1 \mid k)\right\|_{\boldsymbol{R}}^2\right)+ \\ \left\|\boldsymbol{\xi}^*(k+N \mid k)\right\|_{\boldsymbol{Q}}^2+\left\|\boldsymbol{H} \boldsymbol{\xi}^*(k+N \mid k)\right\|_{\boldsymbol{R}}^2+ \\ \left\|\sum\limits_{i=1}^q \lambda_i\left(\boldsymbol{A}_i+\boldsymbol{B}_i \boldsymbol{H}\right) \boldsymbol{\xi}^*(k+N \mid k)\right\|_{\boldsymbol{P}}^2 \end{gathered} $$

(17)

$$ \begin{gathered} J_N^*(k)=\sum\limits_{i=0}^{N-1}\left(\left\|\boldsymbol{\xi}^*(k+i \mid k)\right\|_{\boldsymbol{Q}}^2+\right. \\ \left.\left\|\boldsymbol{\tau}^*(k+i \mid k)\right\|_{\boldsymbol{R}}^2\right)+\left\|\boldsymbol{\xi}^*(k+N \mid k)\right\|_{\boldsymbol{P}}^2 \end{gathered} $$

(18)

式中：τ^*(k+i|k)表示在k时刻预测系统在未来k+i时刻的最优控制作用; ξ^*(k+i+1|k)表示与 τ^*(k+i|k)相对应的最优系统状态。式(17)与式(18)相减可得：

$$ \begin{gathered} J_N^*(k+1)-J_N^*(k)=-\left\|\boldsymbol{\xi}^*(k \mid k)\right\|_Q^2- \\ \left\|\boldsymbol{\tau}^*(k \mid k)\right\|_{\boldsymbol{R}}^2-\left\|\boldsymbol{\xi}^*(k+N \mid k)\right\|_S^2 \end{gathered} $$

(19)

由于Q、R和S均为正定矩阵，故J_N^*(k+1)-J_N^*(k)≤0，条件A₄成立。

当ξ(k)∈Ω时，

$$ \begin{gathered} \overline{\boldsymbol{\xi}}^{\mathrm{T}}(k+1) \boldsymbol{P} \overline{\boldsymbol{\xi}}(k+1)-\overline{\boldsymbol{\xi}}^{\mathrm{T}}(k) \boldsymbol{P} \overline{\boldsymbol{\xi}}(k)= \\ \overline{\boldsymbol{\xi}}^{\mathrm{T}}(k)\left(-\boldsymbol{Q}-\boldsymbol{H}^{\mathrm{T}} \boldsymbol{R} \boldsymbol{H}-\boldsymbol{S}\right) \overline{\boldsymbol{\xi}}(k) \leqslant 0 \end{gathered} $$

(20)

故$\overline{\boldsymbol{\xi}}^{\mathrm{T}}(k+1) \boldsymbol{P} \overline{\boldsymbol{\xi}}(k+1) \leqslant \overline{\boldsymbol{\xi}}^{\mathrm{T}}(k) \boldsymbol{P} \overline{\boldsymbol{\xi}}(k) \leqslant \alpha$，条件A₃成立。定理1证明完毕。

定理2 对于式(11)所示的多面体描述系统，如果存在正定对称矩阵X∈ R^6×6和矩阵 Y∈R^3×6，满足下述矩阵不等式:

$$ {\left[\begin{array}{cc} \frac{\boldsymbol{\tau}_{\max , j}^2}{\alpha} & \boldsymbol{e}_{\tau j}^{\mathrm{T}} \boldsymbol{Y} \\ * & \boldsymbol{X} \end{array}\right] \geqslant 0} $$

(21)

$$ {\left[\begin{array}{cc} \frac{\overline{\boldsymbol{\xi}}_{\max , i}^2}{\alpha} & \boldsymbol{e}_{\xi i}^{\mathrm{T}} \boldsymbol{X} \\ * & \boldsymbol{X} \end{array}\right] \geqslant 0} $$

(22)

则当ξ∈Ω时，终端控制律$\boldsymbol{u}_F(\overline{\boldsymbol{\xi}})=\boldsymbol{H} \overline{\boldsymbol{\xi}}$满足式(8)中的第2项约束条件，即符合条件A₂。ξ满足式(8)中的第4~6个约束条件，即符合条件A₁。其中，τ_{max, j}表示控制输入向量τ的第j个分量的最大值，j=1, 2, 3；ξ_{max, i}表示状态ξ的第i个分量的最大值，i=1, 2, …, 6；e_τj和e_ξi分别为控制输入空间R³的第j个标准向量基和状态空间R⁶的第i个标准向量基^[17]。

定理2的证明详见文献[17]，本文不再赘述。综上可知，只要求解出符合定理1~2的矩阵X和Y，就可以确定终端惩罚项的权重矩阵P和终端控制律中的反馈矩阵H。

正常数α的大小会影响到Ω的容量，一般而言Ω的容量越大，系统可行解的范围越大。本文设计的Ω是一个高维椭球域，其容量大小与椭球各维度的长短半轴之积成正比，即$\boldsymbol{\Omega} \propto(\operatorname{det}(\boldsymbol{P} / \alpha))^{-\frac{1}{2}}$，det(·)表示相应矩阵的行列式。根据文献[18]可知，上述正比关系等价于$\boldsymbol{\Omega} \propto \log \operatorname{det}(\boldsymbol{P} / \alpha)^{-1}$，log det(·)表示对数行列式函数。因此可结合定理1~2中提出的矩阵不等式，可通过求解下述优化问题寻找使Ω容量最大的α：

$$ \begin{gathered} -\min\limits_{\alpha, \boldsymbol{X}, \boldsymbol{Y}} \log \operatorname{det}\left(\boldsymbol{X}_0\right) \\ \text { s. t. } \alpha>0, \boldsymbol{X}_0=\alpha \boldsymbol{X}, \boldsymbol{Y}_0=\alpha \boldsymbol{Y} \end{gathered} $$

(23)

$$ \begin{gathered} {\left[\begin{array}{cccc} \boldsymbol{X}_0 & * & * & * \\ \boldsymbol{A}_i \boldsymbol{X}_0+\boldsymbol{B}_i \boldsymbol{Y}_0 & \boldsymbol{X}_0 & * & * \\ \boldsymbol{Q}^{\frac{1}{2}} \boldsymbol{X}_0 & \mathbf{0} & \boldsymbol{\alpha} \boldsymbol{I} & * \\ \boldsymbol{R}^{\frac{1}{2}} \boldsymbol{Y}_0 & \mathbf{0} & \mathbf{0} & \alpha \boldsymbol{I} \end{array}\right] \geqslant {\mathbf{0}}} \\ {\left[\begin{array}{cc} \boldsymbol{\tau}_{\max , j}^2 & \boldsymbol{e}_j^{\mathrm{T}} \boldsymbol{Y}_0 \\ * & \boldsymbol{X}_0 \end{array}\right] \geqslant 0} \\ {\left[\begin{array}{cc} \overline{\boldsymbol{\xi}}_{j, \max }^2 & \boldsymbol{e}_j^{\mathrm{T}} \boldsymbol{X}_0 \\ * & \boldsymbol{X}_0 \end{array}\right] \geqslant 0} \end{gathered} $$

文献[19]指出当X₀为正定矩阵时，log det(X₀)是凸函数。因此，可利用凸优化求解器和LMI工具箱对式(23)进行求解，得到α、X和Y，进而确定3个终端要素的具体表达形式。

4. 数字仿真算例及结果分析

为验证设计的船舶动力定位NMPC控制器的性能，对一艘供给船(船长76.2 m，满载排水量4 591 t)在Matlab环境下进行仿真。该船的水动力参数详见文献[20]。

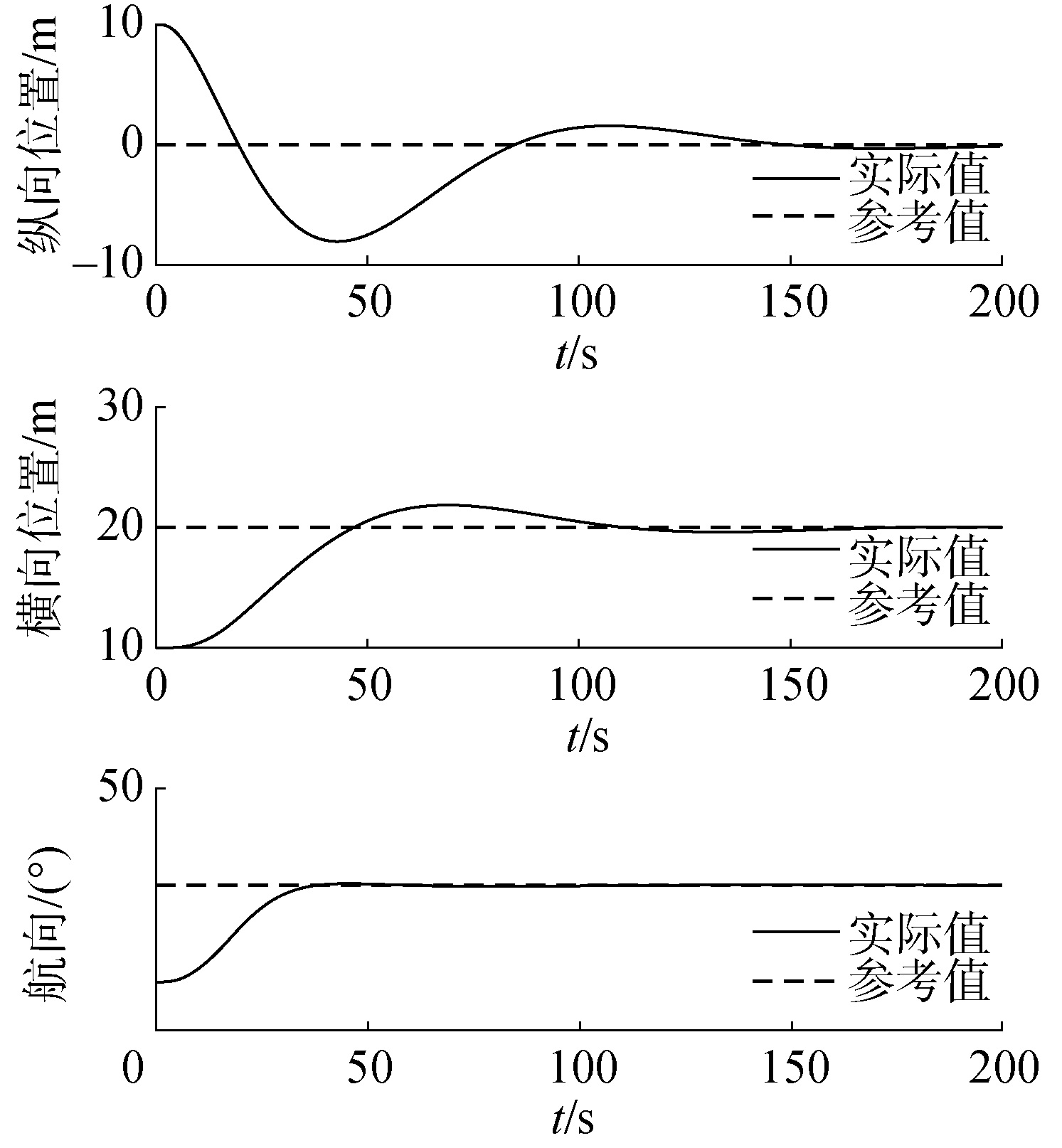
在仿真中，设置船舶推力和力矩的约束范围是[±1 000 kN ±300 kN ±7 620 kN·m]^T，单位时间内推力和力矩变化量的大小为各自幅值的20%。船舶速度状态[u v r]^T的约束范围是[±1.5 m/s ±1 m/s ±1(°)/s]^T。船舶初始位置状态为[10 m 10 m 10°]^T，初始速度状态为[0 m/s 0 m/s 0°/s]^T，期望的位置状态为[0 m 20 m 30°]^T。基于上述约束条件和初始条件，可计算出多面体描述系统式(11)的32个顶点矩阵。

NMPC控制器参数设置如下：预测时域N=50，采样时间h=0.5 s，权重矩阵 Q=diag {5×10⁹, 1×10¹⁰, 5×10¹², 1, 1, 1}，权重矩阵 R=diag{1, 1, 0.001}。利用YALMIP工具箱离线求解式(23)可得α=2.02×10²⁰，P= diag{5×10⁸, 1×10¹⁰, 5.1×10¹², 9×10¹⁹, 2×10²⁰, 6.6×10²³}。

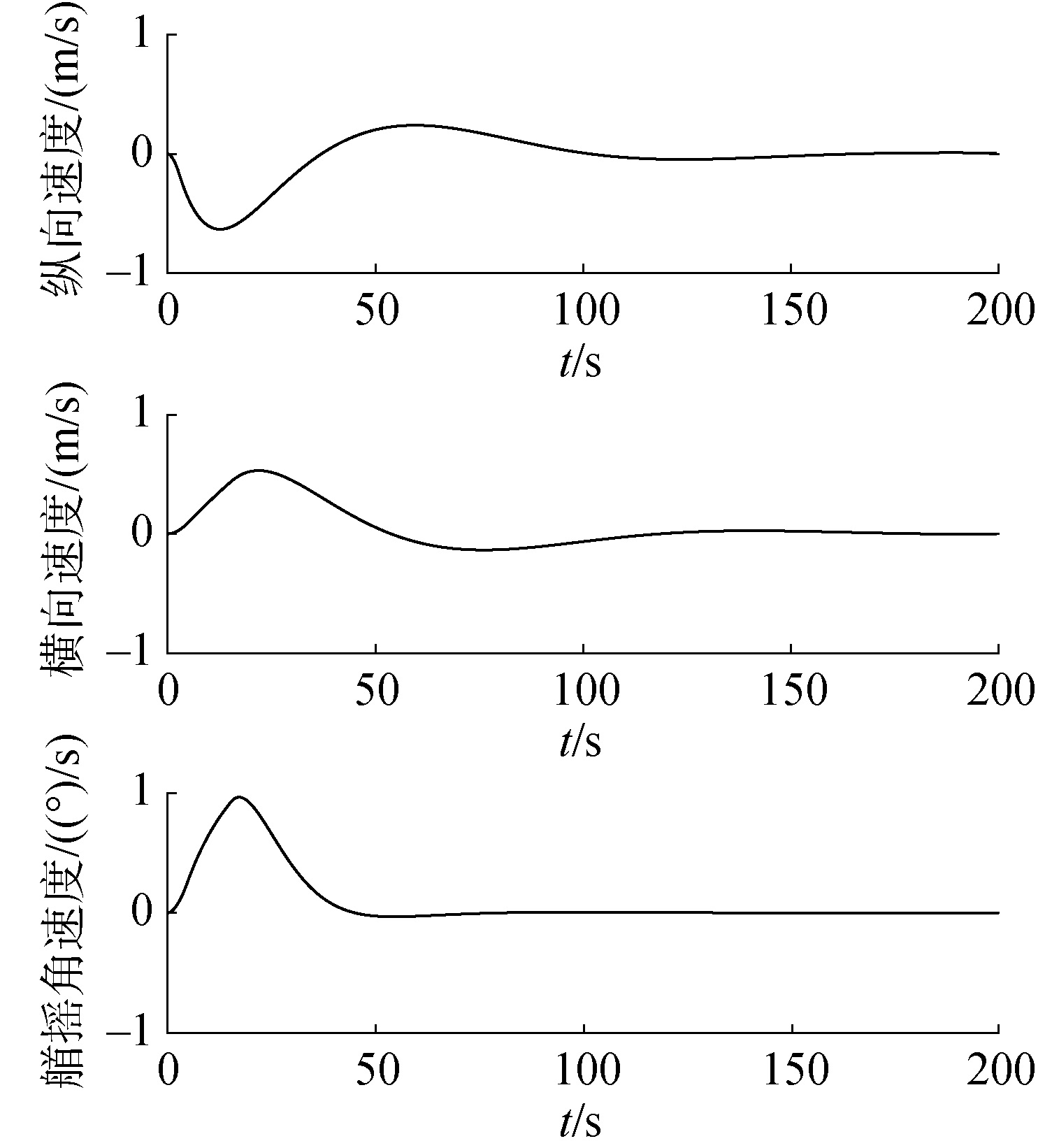
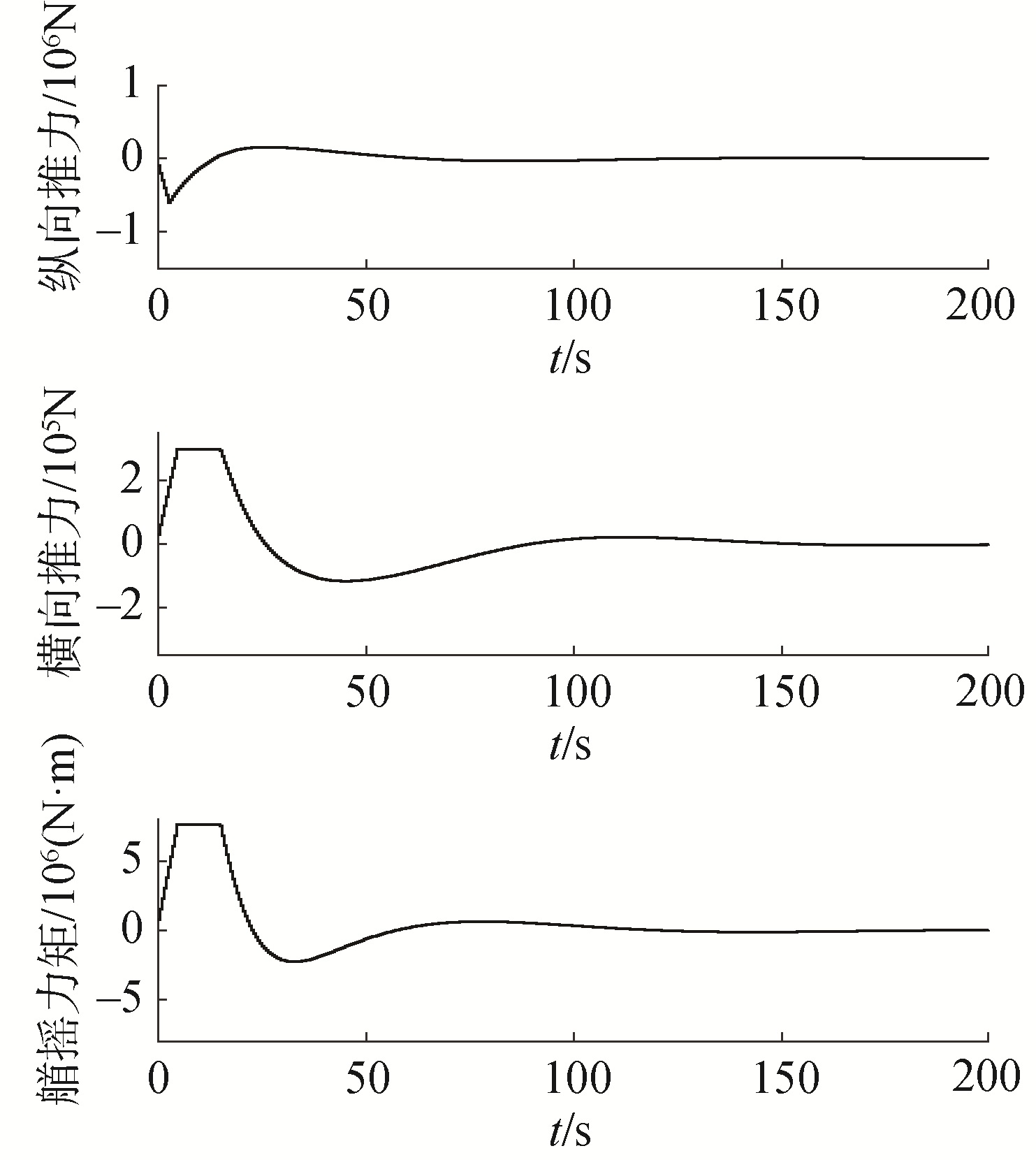
图 1~2是船舶不受外界扰动时的位置状态和速度状态时间响应曲线。总体来看，本文设计的NMPC控制器能够控制船舶以较快的速度到达期望位置并稳定在期望状态上，稳定时间大约为140 s，这表明了系统的稳定性。此外，从图 1中还可以看出航向ψ快速稳定在参考值上且没有超调，稳定时间约为40 s。这是因为船舶在实际进行动力定位时，一般都会优先稳定住航向后再控制船舶的其他状态，故本文将航向ψ的权重设置的较大。图 3是船舶推力与力矩的响应曲线，从图中可以看出推力及力矩的大小未超出设定范围，并且在控制期间内推力及力矩变化平缓，符合海洋工程实践需求。

图 1 无外界扰动时船舶位置和航向响应曲线

Fig. 1 Position and course curves with no disturbance

下载: 全尺寸图片

图 2 无外界扰动时船舶速度状态u、v、r响应曲线

Fig. 2 u, v, r curves with no disturbance

下载: 全尺寸图片

图 3 无外界扰动时船舶推力及力矩响应曲线

Fig. 3 Control input curves with no disturbance

下载: 全尺寸图片

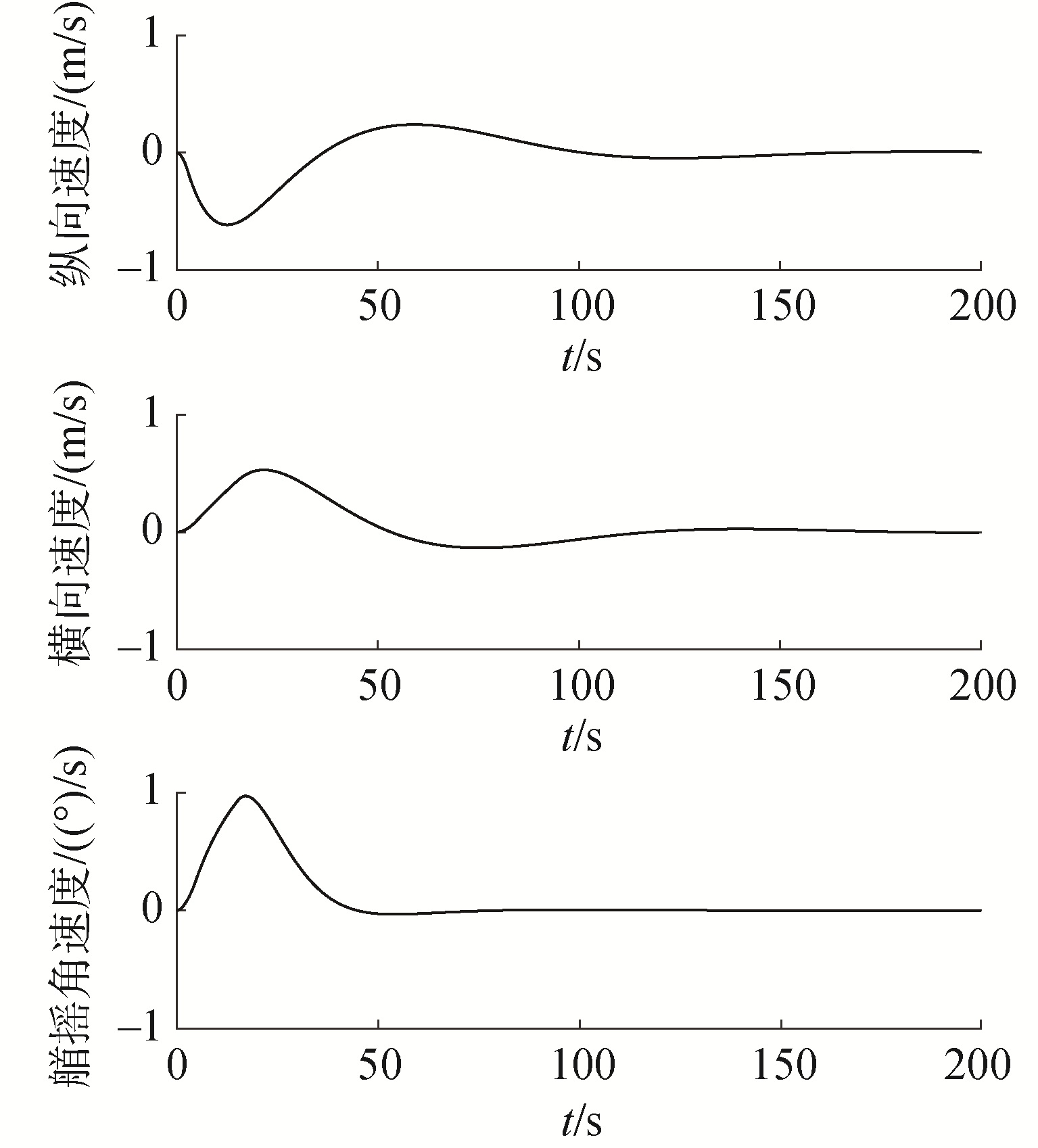
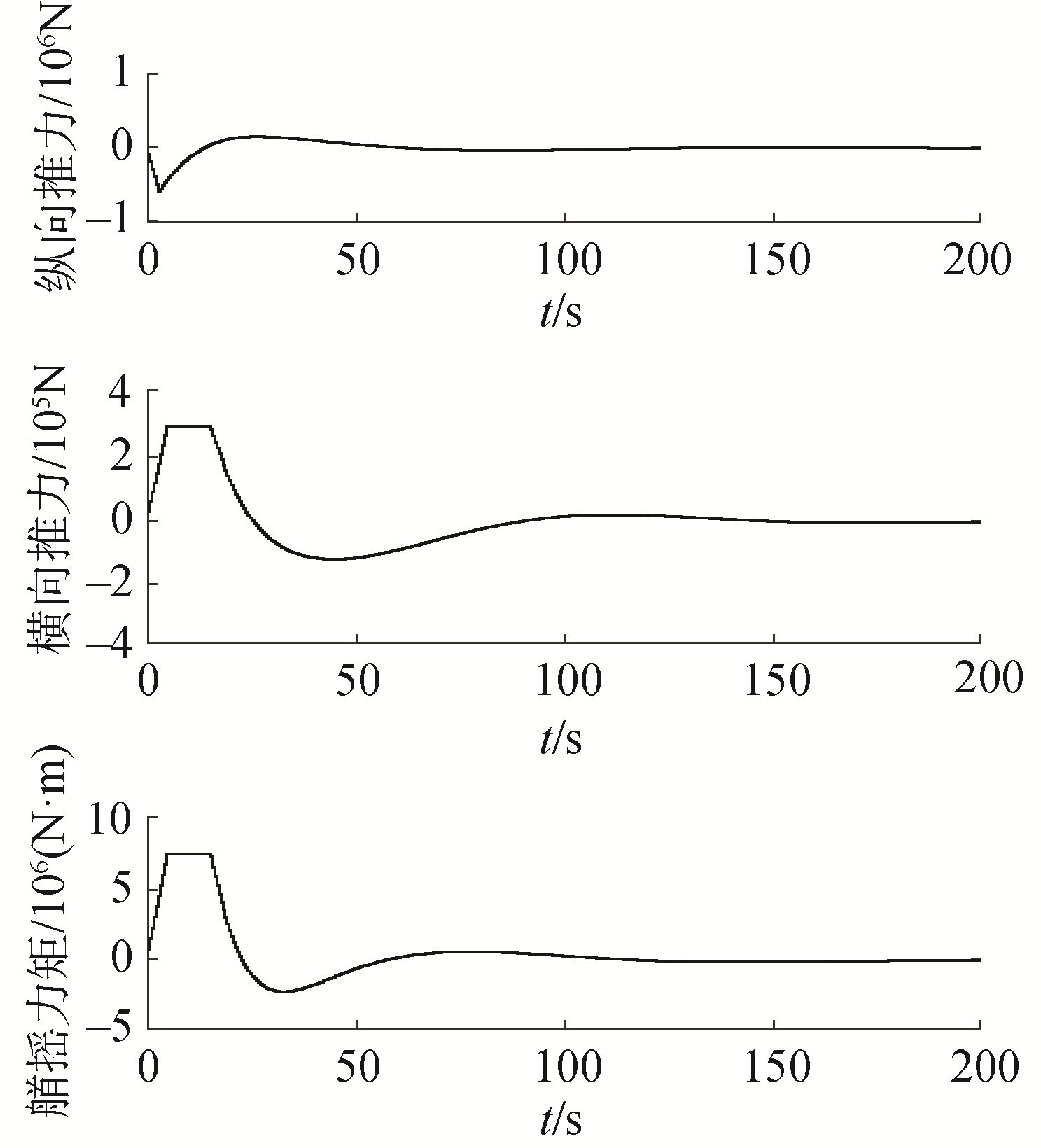
图 4~6是船舶受定常扰动时的位置状态、速度状态和推力与推力力矩的响应曲线。定常扰动大小为d=[1×10⁴ N 3×10³ N 7×10⁴ N·m]^T，分别表示船舶纵向、横向和艏摇方向上的扰动力及扰动力矩。从图 4~6中可以看出，即使船舶受到一定扰动，NMPC控制器依然能够控制船舶达到稳定状态，稳定时间大约为160 s。与无扰动时相比，稳定时间没有显著增加，船舶最终稳定的位置状态与参考状态存在一定偏差，但偏差极小。这说明本文设计的NMPC控制器具有一定的本质鲁棒性。

图 4 有扰动下船舶位置和航向响应曲线

Fig. 4 Position and course curves with disturbances

下载: 全尺寸图片

图 5 有扰动下船舶速度状态u、v、r响应曲线

Fig. 5 u, v, r curves with disturbances

下载: 全尺寸图片

图 6 有扰动下船舶推力及力矩响应曲线

Fig. 6 Control input curves with disturbances

下载: 全尺寸图片

5. 结论

1) 本文提出的NMPC方法能够在较短时间范围内将船舶准确地控制在期望状态上，同时满足实际作业中对船舶运动状态和推力的限制要求；

2) 在动力定位过程中存在干扰时，本文提出的控制器亦能表现出良好的控制性能，具备本质鲁棒性。

本文建立多面体描述系统时顶点矩阵较多，这导致求解LMI矩阵时计算量较大，有时甚至无法求出合适的解。后续将研究如何简化LMI矩阵的求解问题。

图 1 无外界扰动时船舶位置和航向响应曲线

Fig. 1 Position and course curves with no disturbance

下载: 全尺寸图片

图 2 无外界扰动时船舶速度状态u、v、r响应曲线

Fig. 2 u, v, r curves with no disturbance

下载: 全尺寸图片

图 3 无外界扰动时船舶推力及力矩响应曲线

Fig. 3 Control input curves with no disturbance

下载: 全尺寸图片

图 4 有扰动下船舶位置和航向响应曲线

Fig. 4 Position and course curves with disturbances

下载: 全尺寸图片

图 5 有扰动下船舶速度状态u、v、r响应曲线

Fig. 5 u, v, r curves with disturbances

下载: 全尺寸图片

图 6 有扰动下船舶推力及力矩响应曲线

Fig. 6 Control input curves with disturbances

下载: 全尺寸图片

参考文献(20)

[1]	张玉芳, 刘长德. 基于扰动观测器的船舶动力定位反步控制[J]. 船舶工程, 2020, 42(12): 79-84, 92. ZHANG Yufang, LIU Changde. Backstepping control of ship dynamic positioning based on disturbance observer[J]. Ship engineering, 2020, 42(12): 79-84, 92.
[2]	杜佳璐, 杨杨, 胡鑫, 等. 基于动态面控制的船舶动力定位控制律设计[J]. 交通运输工程学报, 2014, 14(5): 36-42, 50. DU Jialu, YANG Yang, HU Xin, et al. Control law design of dynamic positioning for ship based on dynamic surface control[J]. Journal of traffic and transportation engineering, 2014, 14(5): 36-42, 50.
[3]	关克平, 张新放. 滑模控制船舶动力定位控制系统研究[J]. 舰船科学技术, 2018, 40(5): 61-65. GUAN Keping, ZHANG Xinfang. Research on sliding mode control ship dynamic positioning control system[J]. Ship science and technology, 2018, 40(5): 61-65.
[4]	CHIN C S, LIO C S. Sliding-mode control of STENA DRILLMAX drillship with environmental disturbances for dynamic positioning[C]//Proceedings of the 11th International Conference on Modelling, Identification and Control (ICMIC2019). Singapore: Springer, 2020: 99-111.
[5]	赵大威, 边信黔, 丁福光. 非线性船舶动力定位控制器设计[J]. 哈尔滨工程大学学报, 2011, 32(1): 57-61. http://heuxb.hrbeu.edu.cn/#/digest?ArticleID=671 ZHAO Dawei, BIAN Xinqian, DING Fuguang. Design of nonlinear ship dynamic positioning controller[J]. Journal of Harbin Engineering University, 2011, 32(1): 57-61. http://heuxb.hrbeu.edu.cn/#/digest?ArticleID=671
[6]	和红磊, 王玉龙. 半潜式海洋平台动力定位的动态面自抗扰控制[J]. 舰船科学技术, 2017, 39(19): 70-74, 83. HE Honglei, WANG Yulong. Dynamic active disturbance rejection control for dynamic positioning of semi-submersible offshore platform[J]. Ship science and technology, 2017, 39(19): 70-74, 83.
[7]	HASSANI V, SØRENSEN A J, PASCOAL A M. Robust dynamic positioning of offshore vessels using mixed-μ synthesis part Ⅰ: a control system design methodology[J]. IFAC proceedings volumes, 2012, 45(8): 177-182. doi: 10.3182/20120531-2-NO-4020.00042
[8]	HASSANI V, SØRENSEN A J, PASCOAL A M. Robust dynamic positioning of offshore vessels using mixed-μ synthesis part Ⅱ: simulation and experimental results[J]. IFAC proceedings volumes, 2012, 45(8): 183-188. doi: 10.3182/20120531-2-NO-4020.00043
[9]	黄羽韬, 徐海祥, 余文曌, 等. 动力定位自适应变论域模糊PID控制器设计[J]. 武汉理工大学学报(交通科学与工程版), 2020, 44(2): 311-315. HUANG Yutao, XU Haixiang, YU Wenzhao, et al. Design of adaptive variable universe fuzzy PID controller for dynamic positioning[J]. Journal of Wuhan university of technology (transportation science & engineering), 2020, 44(2): 311-315.
[10]	刘辉. 遗传算法控制在船舶动力智能定位系统中的研究与实现[J]. 舰船科学技术, 2016, 38(18): 52-54. LIU Hui. Research and implementation of genetic algorithm control in ship dynamic intelligent positioning system[J]. Ship science and technology, 2016, 38(18): 52-54.
[11]	边信黔, 付明玉, 王元慧. 船舶动力定位[M]. 北京: 科学出版社, 2011.
[12]	AMIN J, MEHRA R, ARAMBEL P. Coordinated dynamic positioning of a multi-platform mobile offshore base using nonlinear model predictive control[C]//Proceedings of the 11th International Offshore and Polar Engineering Conference, Stavanger, Norway, 2001: 206-211.
[13]	唐洁. 船舶动力定位控制及推力分配优化研究[D]. 大连: 大连海事大学, 2018. TANG Jie. Research on ship dynamic positioning control and thrust distribution optimization[D]. Dalian: Dalian Maritime University, 2018.
[14]	SOTNIKOVA M V, VEREMEY E I. Dynamic positioning based on nonlinear MPC[J]. IFAC proceedings volumes, 2013, 46(33): 37-42. doi: 10.3182/20130918-4-JP-3022.00058
[15]	席裕庚. 预测控制[M]. 2版. 北京: 国防工业出版社, 2013.
[16]	YU Shuyou, QU Ting, XU Fang, et al. Stability of finite horizon model predictive control with incremental input constraints[J]. Automatica, 2017, 79: 265-272. doi: 10.1016/j.automatica.2017.01.040
[17]	刘洋. 基于模型预测控制的移动机器人路径跟踪控制[D]. 长春: 吉林大学, 2016. LIU Yang. Path tracking control of mobile robot based on model predictive control[D]. Changchun: Jilin University, 2016.
[18]	BOYD S P. Linear matrix inequalities in system and control theory[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1994.
[19]	BOYD S P, VANDENBERGHE L. Convex optimization[M]. Cambridge, UK: Cambridge, 2004.
[20]	FOSSEN T I, SAGATUN S I, SØRENSEN A J. Identification of dynamically positioned ships[J]. Control engineering practice, 1996, 4(3): 369-376 doi: 10.1016/0967-0661(96)00014-7

点击查看大图

图(6)

摘要

船舶动力定位非线性模型预测控制

doi: 10.11990/jheu.202110026

作者简介: 张泉, 男, 讲师, 博士研究生; 郭晨, 男, 教授, 博士生导师.

通讯作者: 郭晨, E-mail: guoc@dlmu.edu.cn.

出版历程

Nonlinear model predictive control for the dynamic positioning system of ships

1. 船舶运动数学模型

2. 船舶动力定位NMPC控制器设计

2.1 模型预测控制原理

2.2 控制目标和NMPC控制器设计

3. NMPC算法稳定性分析

3.1 船舶多面体描述系统

3.2 终端要素的设计方法

4. 数字仿真算例及结果分析

5. 结论

出版历程

目录

作者简介:
张泉, 男, 讲师, 博士研究生;

郭晨, 男, 教授, 博士生导师.

通讯作者:
郭晨, E-mail: guoc@dlmu.edu.cn.