Nonlinear sound field under the bubble softening effect
-
摘要: 为研究气泡的存在对介质中非线性声场的影响，本文利用波动方程和Rayleigh-Plesset方程建立的有限差分和有限体积模型，分别求解了在单频波和双频波激励下含气泡水介质中任意时刻的声压分布。计算表明：在非线性条件下，沿声波传播方向长度为半波长的介质内存在共振频移，即介质发生了软化；含气泡水介质的非线性共振频移与振源的振幅有关，在一定范围内，频移随着振幅的增大而增大；并证明了介质中的软化是由气泡平均体积增大而引起的。本研究为提高参量阵声发射和接收效率等提供了一种思路。Abstract: This work aims to study the influence of the presence of bubbles on nonlinear sound fields in media. The finite difference and finite volume models established by the wave and Rayleigh-Plesset equations are used to solve the sound pressure distribution in a medium containing bubble water at any time under the excitation of single-and dual-frequency waves, respectively. Calculation shows that under nonlinear conditions, a resonance frequency shift with a length of half a wavelength along the direction of sound wave propagation occurs in the medium; that is, the medium softens. The nonlinear resonance frequency shift in the medium containing bubble water is related to the amplitude of the vibration source. Within a certain range, the frequency shift increases with the increase in amplitude. The softening of the medium is proven to be caused by an increase in the average volume of bubbles. The work presented in this paper provides new ideas for improving the acoustic transmission and reception efficiency of parametric arrays.
-
声波在含气泡的水介质中传播，由于气体的物理特性与液体有明显的不同，且气泡受声波激励会产生大量散射，所以含气泡水介质中会产生许多非线性声学现象[1-4]。之前的很多研究都是将这种混合介质等效成一种特殊的均匀介质，忽略了气泡之间的相互作用[5-7]。而当水中的气泡含量超过0.001%时，则需要考虑气泡间的相互作用，这种方法称为多重散射法[8-10]。在考虑气泡多重散射效应后，满足一定条件时，在介质中可以观察到介质的共振频率随激励振幅变化的现象，这种现象与颗粒介质中的软化性质相似。岩石、土壤等颗粒介质中的软化已在其他领域有广为人知的意义，它是指介质的共振频率随着压力振幅的增大而降低的现象[11-12]。声波在介质中传播，若声波振幅响应随激励频率的变化出现极大值，则此时声波的频率即为介质的共振频率。对于含气泡的水介质中的这种现象，为了区别于固体颗粒介质中的软化行为，可以将其称为声学软化，对它进行研究，有助于更好地理解声波与气泡的非线性作用规律以及气泡在声场中的非线性动力学行为。
Lauterborn[13]研究了单个气泡在声场中的动力学行为，分析了压力对气泡共振的影响，并得出气泡共振存在位移并取决于压力振幅的结论。Omta[14]研究了信号通过含气泡液体后的频谱，第1次证明了含气泡液体的共振频率会随压力振幅的变化而变化。Sojahrood[15]通过实验验证了气泡液体中的声速和衰减与压力有关。Matsumoto等[16]也观察到了含有气泡液体的共振随压力振幅变化的现象。Jean-Baptiste Doc等[17]在对含气泡的水介质进行研究时，发现了该介质中存在与砂岩或裂化材料等相似的软硬化效应：当增加激励振幅时，可以观察到与入射波有关的向下或向上的共振频移。Tejedor Sastre等[18]建立了一个数值模型，结合了有限体积法和有限差分法，对气泡液体中的非线性超声驻波进行了研究，求解了一维谐振腔中声压与气泡振动相互作用的微分系统。此外他们又研究了由液体和气泡组成的非线性双相介质中一维空腔的非线性共振，证明了信号的压力振幅会改变空腔的共振频率[19]。
María等仅对一维介质中的软化现象进行了研究，且侧重于激励频率为200 kHz时介质中的软化现象。本文将对声学软化现象的研究扩展到了三维介质，并考虑其他频率激励时的情况，综合分析了在单频波和双频波激励时含气泡水介质中的软化现象，计算了声波与气泡相互作用时三维介质中的非线性声场。本文研究了多种不同频率激励时介质中的软化现象，充分证明了含气泡水介质中的确存在声学软化行为，即存在非线性共振频移，且这是一种普遍存在的现象。本文的计算结果证明了非线性共振频移与振源的振幅有关，在一定范围内频移随着振幅的增大而增大。又分别研究了在单频和双频声波激励下，气泡体积对软化效应的影响，验证了介质中的软化是由气泡平均体积增大而引起的。本文的内容可以作为提高参量阵声发射和接收效率的理论基础，为进一步实现噪声控制等技术提供思路。
1. 数学模型
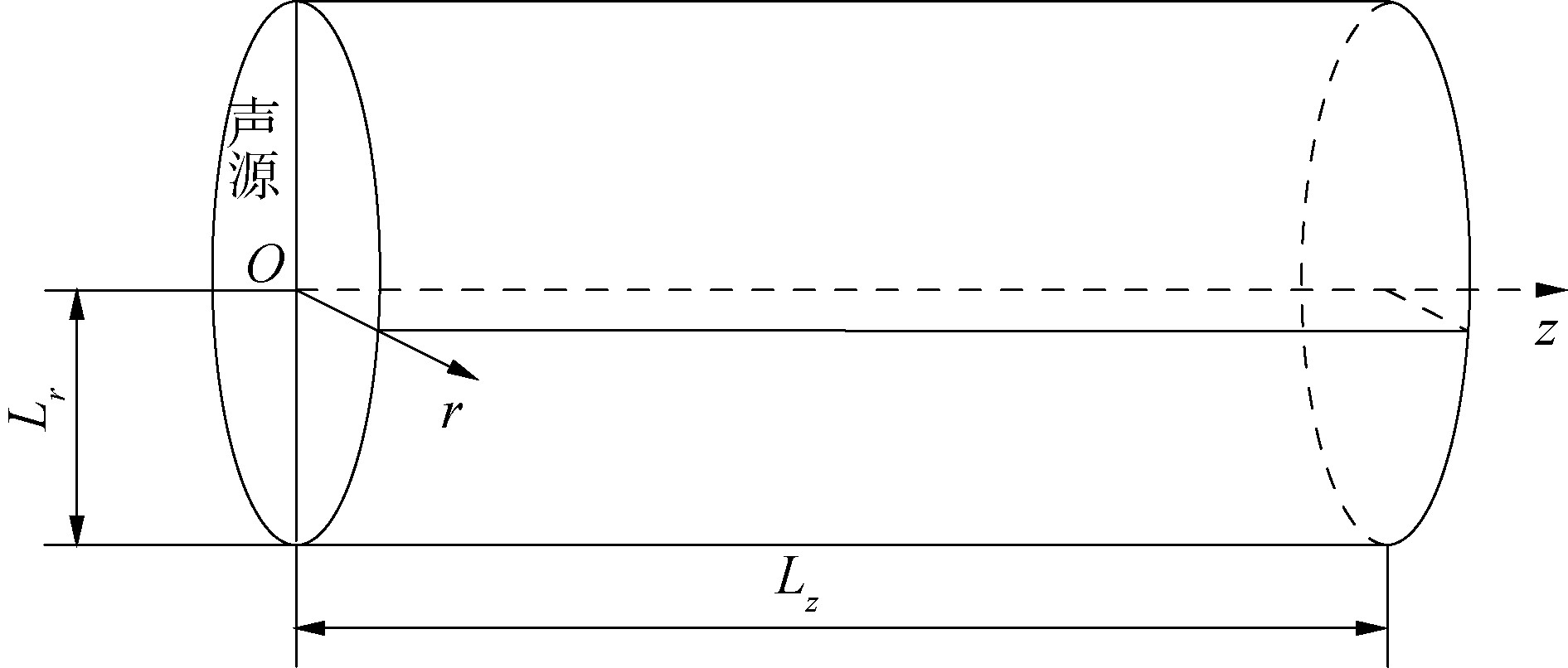
三维介质都具有一定的形状。在这里假设一个充满含气泡水介质的圆柱形空腔, 该空腔在三维空间$(x, y, z)$中围绕$z$轴对称, 使用柱坐标系$(r, z)$来表示。该圆柱空间在$r$方向上半径长度为$L_{r}$且在$z$方向上长度为$L_{z}$。其中, $r$方向是垂直于声波传播的方向, $z$方向是沿声波传播的方向。如图1所示。
图 1 三维圆柱形空腔Fig. 1 Three-dimensional cylindrical cavity
下载:
全尺寸图片
气泡体积变化$v(r, z, t)=V(r, z, t)-v_{0 g}$, 其中, $V(r, z, t)$是某一空间位置上气泡当前的体积, $v_{0 g}$是气泡的初始体积。表示[20]:
$$ \begin{gathered} \frac{\partial^{2} p}{\partial r^{2}}+\frac{1}{r} \frac{\partial p}{\partial r}+\frac{\partial^{2} p}{\partial z^{2}}-\frac{1}{c_{0 l}^{2}} \frac{\partial^{2} p}{\partial t^{2}}=-\rho_{o l} N_{g} \frac{\partial^{2} v}{\partial t^{2}} \\ 0<r<L_{r}, 0<z<L_{z}, 0<t<T_{t} \\ \end{gathered} $$ (1) $$ \begin{gathered} \frac{\partial^2 v}{\partial t^2}+\delta \omega_{0 g} \frac{\partial v}{\partial t}+\omega_{0 g}^2 v+\eta p=a v^2+ \\ b\left(2 v \frac{\partial^2 v}{\partial t^2}+\left(\frac{\partial v}{\partial t}\right)^2\right) \\ 0 \leqslant r \leqslant L_r, 0 \leqslant z \leqslant L_z, 0<t<T_t \end{gathered} $$ (2) 式(1) 为波动方程; 式(2) 为Rayleigh-Plesset方程。式中: $c_{0 l}$为液体中的声速; $\rho_{0 l}$为平衡时液体的密度; $N_{g}$为单位体积介质中气泡的数目。$\delta=$ $4 v_{l} /\left(\omega_{0 g} R_{0 g}^{2}\right)$是粘性阻尼系数, 其中$v_{l}$为液体的粘滞系数; $\omega_{0 g}=\sqrt{3 \gamma_{g} p_{0 g} / \rho_{0 l} R_{0 g}^{2}}$为气泡的共振频率; $\gamma_{g}$为气体的比热比, $p_{0 g}=\rho_{0 g} c_{0 g}^{2} / \gamma_{g}$为气体的压强; $\rho_{0 g}$为气体在平衡状态时的密度; $c_{0 g}$为气体中的声速。$\begin{aligned} & a=\left(\gamma_{g}+1\right) \omega_{0 g}^{2} /\left(2 v_{0 g}\right) \text { 以及 } b=1 /\left(6 v_{0 g}\right), \eta=4 \pi R_{0 g} / \rho_{0 l} \text { 。 } \end{aligned}$
假设在开始时气泡处于静止状态，施加初始条件：
$$ \left\{\begin{array}{l} p(r, z, 0)=0, v(r, z, 0)=0 \\ \frac{\partial p}{\partial t}(r, z, 0)=0, \frac{\partial v}{\partial t}(r, z, 0)=0 \\ 0 \leqslant r \leqslant L_{r}, 0 \leqslant z \leqslant L_{z} \end{array}\right. $$ (3) 式中$L_{r}$和$L_{z}$都是常数。将声源$s(t)$放置在$z=0$平面处, 即图1中的左侧圆柱底面。使用轴对称条件获得问题的三维解:
$$ p(r, 0, t)=s(t), 0<r<L_r, 0 \leqslant t \leqslant T_t $$ (4) $$ \frac{\partial p}{\partial r}(0, z, t)=0, 0 \leqslant z \leqslant L_z, 0<t \leqslant T_t $$ (5) 对于刚性边界条件的圆柱形空腔, 在$z=L_{z}$处施加自由壁条件, 在$r=L_{r}$处施加刚性壁条件:
$$ p\left(r, L_z, t\right)=0, 0 \leqslant r \leqslant L_r, 0 \leqslant t \leqslant T_t $$ (6) $$ \frac{\partial p\left(L_r, z, t\right)}{\partial r}=0, 0 \leqslant r \leqslant L_r, 0 \leqslant t \leqslant T_t $$ (7) 2. 数值计算方法
Tejedor Sastre等[21]在考虑不同边界条件的情况下，利用含气泡液体的频散特性，对不同腔体中的复杂模态进行了数值模拟实验，对于理解超声在含气泡液体中的行为、声化学过程和非线性频率混合的应用具有重要意义。本文采用文献[21]中提出的三维刚性壁圆柱形空腔中的声场数值模型，对由式(1)和式(2)组成的耦合系统进行计算。
2.1 时间近似和空间近似
总时间$T_{t}$被分成$R-1$个持续时间为$\tau$的间隔。每个时间点由$t_{k}(k=2, 3, \cdots, R-1)$表示。时域离散结果如图2所示。
图 2 时间离散化Fig. 2 Time discretization下载:
全尺寸图片
则时间导数可以近似为：
$$ \left\{\begin{array}{l} \frac{\partial^{2} p_{k}}{\partial t^{2}} \approx \frac{p_{k+1}-2 p_{k}+p_{k-1}}{\tau^{2}} \\ \frac{\partial^{2} v_{k}}{\partial t^{2}} \approx \frac{v_{k+1}-2 v_{k}+v_{k-1}}{\tau^{2}} \\ \frac{\partial p_{k}}{\partial t} \approx \frac{p_{k}-p_{k-1}}{\tau} \\ \frac{\partial v_{k}}{\partial t} \approx \frac{v_{k}-v_{k-1}}{\tau} \end{array}\right. $$ (8) 对于一阶导数, 误差是$O(\tau)$; 对于二阶导数, 误差是$O\left(\tau^{2}\right)$。
由于圆柱腔是围绕z轴对称的，对称位置处的声压相等，所以只要求出某一个切面(如图1中虚线所示平面)上的声压分布，即可得知整个圆柱腔内的声压。
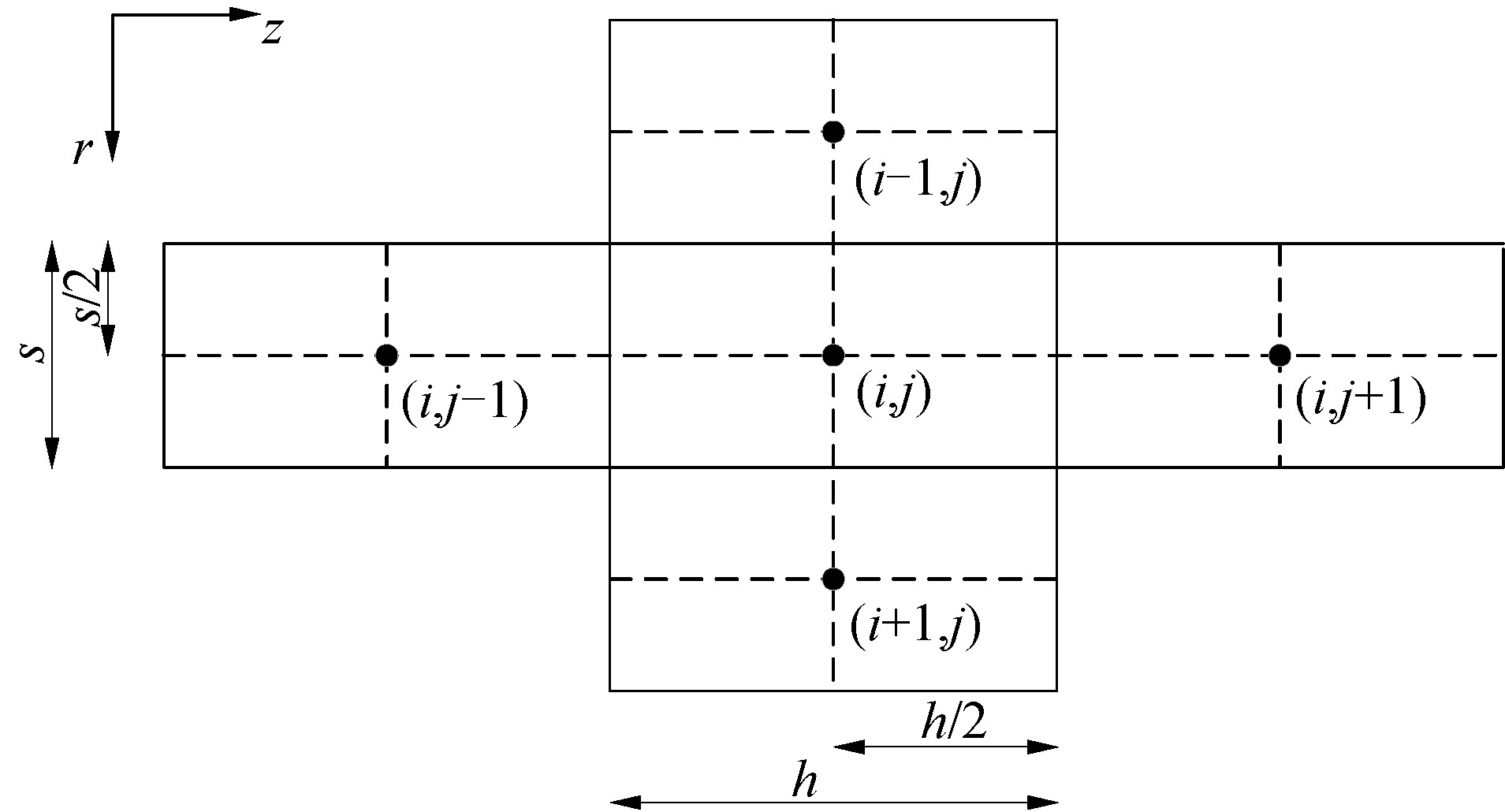
将图1中的平面划分为$N \times M$个大小为$V_{c}$的控制模块, 每个模块在$r$方向的尺寸为$h, z$方向的尺寸为$s_{\circ}$用$r_{i}(i=1, 2, \cdots, N)$和$z_{j}(j=1, 2, \cdots, M)$表示每个控制模块的中心点, 如图3所示。
图 3 空间离散化Fig. 3 Spatial discretization下载:
全尺寸图片
由此得到空间的近似公式:
$$ \frac{\partial^2 p_i}{\partial r^2}+\frac{1}{r} \frac{\partial p_i}{\partial r}=i s p_{i+1}+(1-2 i) s p_i+(i-1) s p_{i-1} $$ (9) $$ \begin{gathered} \frac{\partial^{2} p_{j}}{\partial z^{2}} \approx \frac{h^{2}}{2}(2 i-1)\left(\frac{p_{j+1}-p_{j}}{s}-\frac{p_{j}-p_{j-1}}{s}\right)= \\ \frac{h^{2}}{2}(2 i-1)\left(\frac{p_{j+1}-2 p_{j}+p_{j-1}}{s}\right) \end{gathered} $$ (10) 这些方程的误差是O(h, s)。
2.2 离散方程
将近似公式(9) 和(10) 应用于式(1) 和(2), 就得到了任意空间模块$V_{c}$和任意时间$t_{k}(k=2, 3, \cdots$, $R-1)$的方程式:
$$ \begin{gathered} p_{i, j, k+1}=\left\{\tau^2 s^2\left(A p_{i+1, j, k}+B p_{i-1, j, k}\right)+\right. \\ \frac{\tau^2 h^2}{2}\left(C p_{i, j+1, k}+D p_{i, j-1, k}\right)+ \\ {\left[-E \tau^2 s^2-\frac{F \tau^2 h^2}{2}+\frac{h^2 s^2(2 i-1)}{c_{0 l}^2}\right] p_{i, j, k}-} \\ \frac{h^2 s^2(2 i-1)}{2 c_{0 l}^2} p_{i, j, k-1}+\frac{\rho_{0 l} N_g h^2 s^2(2 i-1)}{2} \times \\ \left.\left(-2 v_{i, j, k}+v_{i, j, k-1}\right)+\frac{\rho_{0 l} N_g h^2 s^2(2 i-1)}{2} v_{i, j, k+1}\right\} \times \\ {\left[\frac{h^2 s^2(2 i-1)}{2 c_{0 l}^2}\right]^{-1}} \end{gathered} $$ (11) $$ \begin{gathered} v_{i, j, k+1}=\left(\left(1-\delta \omega_{0 g} \tau-b v_{i, j, k-1}\right) v_{i, j, k-1}+\right. \\ \left(-2+\delta \omega_{0 g} \tau+\omega_{0 g}^2 \tau^2\right) v_{i, j, k}+\eta \tau^2 p_{i, j, k}+ \\ \left.\left(-a \tau^2+3 b\right) v_{i, j, k}^2\right) /\left(2 b v_{i, j, k}-1\right) \end{gathered} $$ (12) 式中$A 、B 、C 、D 、E 、F$取不同的值, 这取决于空腔的几何形状以及$V_{c}$是否位于空腔的边界上。
2.3 特定参数
对于刚性壁圆柱腔，当Vc的位置不同时，式(11)中参数取值为：
1) 当$i=1, j=1$时: $A=i, B=0, C=2 i-1, D=$ $2(2 i-1) s(t) / p_{i, j-1, k}, E=i, F=3(2 i-1)$;
2) 当$i=1, j=M$时: $A=i, B=0, C=0, D=2 i-$ $1, E=i, F=3(2 i-1)$;
3) 当$i=1, j=2, \cdots, M-1$时: $A=i, B=0, C=$ $2 i-1, D=2 i-1, E=i, F=2(2 i-1)$;
4) 当$i=N, j=1$时: $A=0, B=i-1, C=2 i-1$, $D=2(2 i-1) s(t) / p_{i, j-1, k}, E=i-1, F=3(2 i-1)$;
5) 当$i=N, j=M$时: $A=0, B=i-1, C=0, D=$ $2 i-1, E=i-1, F=3(2 i-1)$;
6) 当$i=N, j=2, 3, \cdots, M-1$时: $A=0, B=i-1, C=$ $2 i-1, D=2(2 i-1), E=i-1, F=2(2 i-1)$;
7) 当$i=2, \cdots, N-1, j=1$时: $A=i, B=i-1, C=2 i-$ $1, D=2(2 i-1) s(t) / p_{i, j-1, k}, E=2 i-1, F=3(2 i-1)$;
8) 当$i=2, \cdots, N-1, j=M$时: $A=i, B=i-1, C=0$, $D=2(2 i-1), E=2 i-1, F=3(2 i-1)$;
9) 当$i=2, \cdots, N-1, j=2, \cdots, M-1$时: $A=i, B=i-$ $1, C=2 i-1, D=2(2 i-1), E=2 i-1, F=2(2 i-1)$。
由此得到的方程组成的系统能够求解每个时间步长内所取平面上的声压分布和气泡体积，进而推断出整个圆柱腔中的声压和气泡体积变化。
3. 数值仿真
气泡的存在会使介质的性质发生变化，含气泡水介质中的非线性声传播是一个很吸引人的问题。在对岩石的非线性弹性共振行为进行研究时，已经观察到共振峰随着驱动水平的增加而向下移动的现象，即非线性共振频移。表明此时由弹性颗粒之间相互接触并进行机械运动导致的非线性摩擦比大量均匀介质中产生的摩擦具有更高的水平级[22]。在含气泡的水介质中，气泡之间没有直接接触，但是它们存在许多其他方面的相互作用。
本文对不同声波激励下介质中的软化现象进行了研究，探讨了气泡体积对介质软化的影响以及发生软化时介质中的声场。其中，在双频波激励时，将二者产生的和频声波作为研究对象。根据轴对称条件可知, 任意平行于$z$轴的平面上声压分布相同。由于声源均匀分布在$z=0$平面上且该平面上任意点处声压值相同, 所以在任意平行于$z$轴的平面上, 某点处的声压只取决于该点在$z$方向上的坐标, 即该平面上任意一条表达式为$r=a(a$为常数, $\left.0 \leqslant a \leqslant L_{r}\right)$的直线上的声压分布与$z$轴上的声压分布相同。因此, 可以用声压在$z$轴上的分布来代表整个空腔中的声压分布。
为了使仿真结果更有说服性, 本文为气泡体积$R_{0 g}$选取了4个值, 分别为$4.5 \times 10^{-6} \mathrm{~m}^{3} 、5 \times 10^{-6} \mathrm{~m}^{3}$、$8 \times 10^{-6} \mathrm{~m}^{3}$和$10^{-5} \mathrm{~m}^{3}$, 而单位体积的介质中气泡数目保持$N_{g}=2 \times 10^{11} \mathrm{~m}^{-3}$不变。
3.1 参数设置
3.1.1 激励频率的选取
在本文的仿真中, 激励信号均采用连续信号形式, 且激励源位于整个$z=0$平面上。水中的声速为$c_{0 l}=1500 \mathrm{~m} / \mathrm{s}$, 密度为$\rho_{0 l}=1000 \mathrm{~kg} / \mathrm{m}^{3}$, 运动粘滞系数$v_{l}=1.43 \times 10^{-6} \mathrm{~m}^{2} / \mathrm{s}$。气体声速$c_{0 g}=340 \mathrm{~m} / \mathrm{s}$, 密度$\rho_{0 g}=1.29 \mathrm{~kg} / \mathrm{m}^{3}$, 气体比热比为$\gamma_{g}=1.4$。
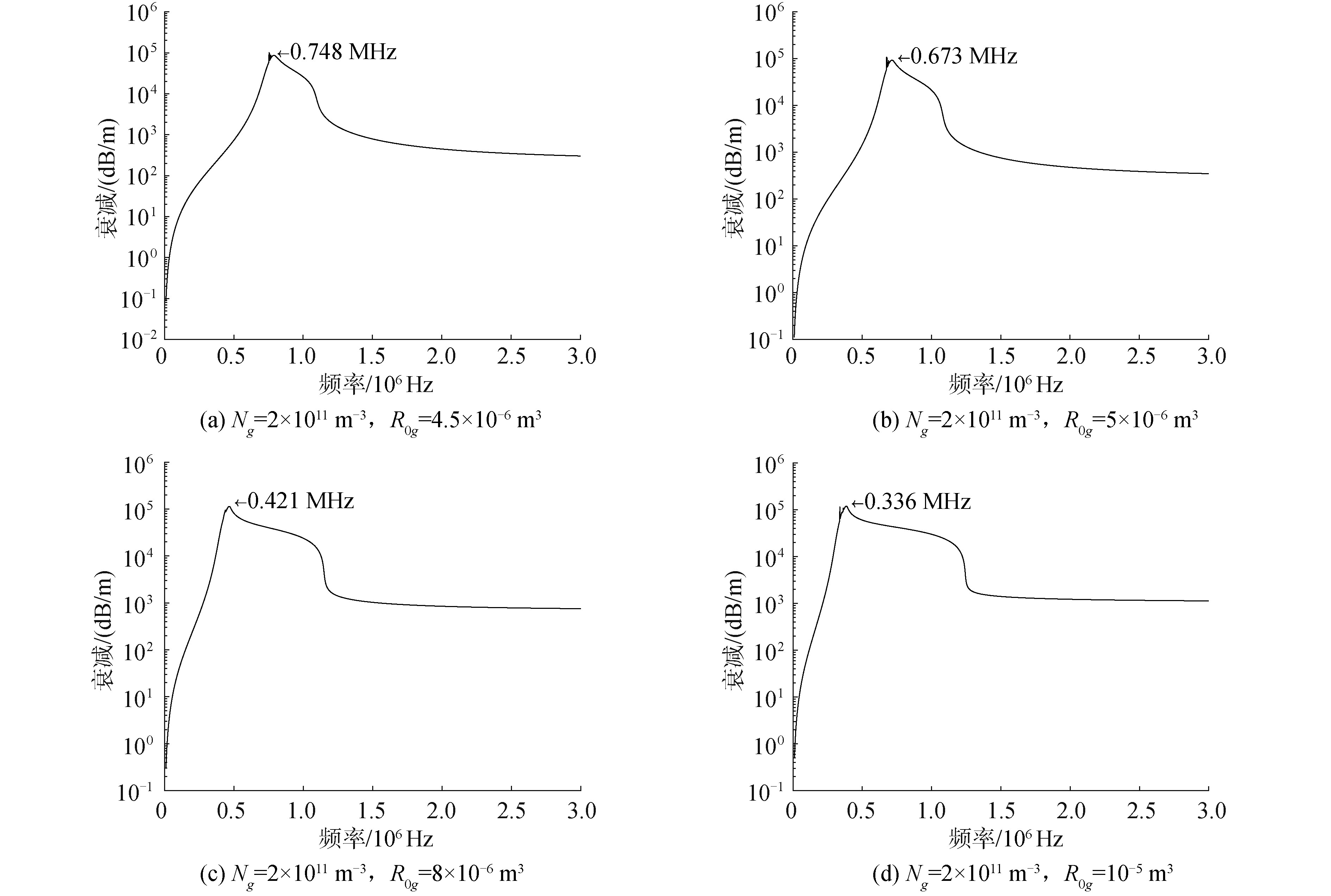
为了在介质中获得较低的衰减, 激励信号的频率应低于单个气泡的共振频率。单位体积介质中的气泡数目$N_{g}$为$2 \times 10^{11} \mathrm{~m}^{-3}$并保持不变, 气泡半径不同时, 含气泡液体中声波的衰减如图4所示。
图 4 介质中的衰减Fig. 4 Attenuation in the medium下载:
全尺寸图片
由图4可知, 当气泡半径$R_{0 g}$为$4.5 \times 10^{-6} \mathrm{~m}^{3}$时, 气泡的共振频率为$f_{0 g}=\omega_{0 g} /(2 \pi)=0.748 \mathrm{MHz}$; 当气泡半径$R_{0 g}$为$5 \times 10^{-6} \mathrm{~m}^{3}$时, 共振频率$f_{0 g}=0.673 \mathrm{MHz}$; 当$R_{0 g}$为$8 \times 10^{-6} \mathrm{~m}^{3}$时, 共振频率$f_{0 g}=0.421 \mathrm{MHz}$; 当$R_{0 g}$为$10^{-5} \mathrm{~m}^{3}$时, $f_{0 g}=0.336 \mathrm{MHz}_{\text {。 }}$
本文分别用单频声源和双频声源作为激励声源，将单频声源发出的基波以及双频声源产生的和频波作为研究对象进行仿真计算。为了获得较强的非线性效应和较高的系统响应，并综合考虑衰减、频散等因素，在双频激励时，2个声源的参数设置如表1所示。
表 1 双频激励时声源发射频率Table 1 The emission frequency of the sound source when dual-frequency excitationkHz 和频频率 声源发射频率 f1 f2 50 20 30 60 25 35 80 30 50 100 30 70 150 70 80 160 70 90 180 80 100 200 90 110 当单频声激励时，令声源发射的频率等于双频激励时2列声波产生的和频频率，即单频声源频率为表1中第1列的数值。
3.1.2 介质中的声速
由于气泡与水的密度、阻抗及压缩率等有很大的差异，所以含气泡水介质的声学特性与纯水介质有显著的不同，对声波的传播产生很大的影响。因此, 声波在含气泡水介质中的声速不能用$c_{0 l}=1500 \mathrm{~m} / \mathrm{s}$来表示, 而应该将波动方程和Rayleigh-Plesset方程进行数值耦合重新计算。
图 5 $N_{g}=2 \times 10^{11} / \mathrm{m}^{3}, R_{0 g}=4.5 \times 10^{-6} \mathrm{~m}^{3}$时介质中的声速Fig. 5 The speed of sound in the medium when $N_{g}=2 \times 10^{11} / \mathrm{m}^{3}, R_{0 g}=4.5 \times 10^{-6} \mathrm{~m}^{3}$下载:
全尺寸图片
按照上述方法, 可以得到含有不同半径气泡的介质中的声速。在研究含气泡水介质中的软化现象时, 为了验证该现象广泛存在于不同激励条件下, 应该对同一气泡参数下不同长度介质中的软化现象进行研究, 因此选取气泡体积$R_{0 g}=4.5 \times 10^{-6} \mathrm{~m}^{3}$, 单位体积介质中气泡数目$N_{g}=2 \times 10^{11} / \mathrm{m}^{3}$, 介质的共振频率为$150 \sim 200 \mathrm{kHz}$; 在研究气泡体积对介质软化的影响时, 为确保仿真结果更有说服性, 对于每一个长度的介质, 均应改变介质中的气泡半径并对计算结果进行对比, 因此选取的气泡参数为$R_{0 g}$在$4.5 \times 10^{-6} \sim 10^{-5} \mathrm{~m}^{3}$, 介质共振频率为$50 \sim 100 \mathrm{kHz}$。根据上述分析, 含气泡水介质中不同激励频率下的声速计算如表2所示。
表 2 $N_{g}=2 \times 10^{11} / \bf{m}^{3}$时介质中的声速Table 2 The speed of sound in the medium when $N_{g}=2 \times 10^{11} / \mathrm{m}^{3}$激励频率/kHz 声速/(m/s) R0g=4.5×10-6 m3 R0g=5×10-6 m3 R0g=8×10-6 m3 R0g=10-5 m3 50 1 023.21 934.28 546.27 404.66 60 1 022.53 933.23 545.06 402.57 80 1 021.08 931.72 541.62 397.15 100 1 019.67 929.51 537.16 391.43 150 1 013.72 — — — 160 1 011.96 — — — 180 1 088.77 — — — 200 1 004.38 — — — 表2~3中气泡体积分别为$3.82 \times 10^{-16} \mathrm{~m}^{3}$、$5.23 \times 10^{-16} \mathrm{~m}^{3} 、2.14 \times 10^{-15} \mathrm{~m}^{3}$以及$4.19 \times 10^{-15} \mathrm{~m}^{3}$。结果表明, 当气泡密度和气泡体积均相同时, 激励频率越高, 介质中的声速越小; 在气泡密度相同的前提下, 当激励频率相同时, 气泡体积越大, 介质中的声速越小。
3.1.3 介质长度的选取
共振意味着振幅响应随着频率的变化会出现极大值，而在正弦信号中，极大值也是最大值。气泡的存在改变了介质中的声速，由声波波长表达式λ=c/f可知，声信号的波长也会随之发生变化。
在本文的研究背景下, 应保证单频声波发射的源信号以及双频声波产生的和频信号能够在声场中发生共振, 即作为激励信号的声波频率等于介质中的线性共振频率$f_{L}$。驻波场是共振的一种特殊情况。本文通过设置介质长度, 使激励声波可以在介质中形成驻波。为了使单频声波在介质中产生驻波共振, 将介质在声波传播方向的长度设置为$L_{z}=n \lambda_{f} / 2, n$为整数, 即在声波传播方向上, 介质的长度为半波长的整数倍, 其中$\lambda_{f}$是激励声波的波长; 为了计算简便, 将垂直于声波传播方向的长度设置为$L_{r}=n \lambda_{f} / 4$。当双频声波激励时, 则将介质参数设置为$L_{z}=n \lambda_{h} / 2, L_{r}=n \lambda_{h} / 4, n$为整数。其中$\lambda_{h}$是2个信号在线性条件下产生的和频声波的波长。
随着声波传播距离的增加，由于波阵面的扩张、不均匀粒子的散射等，声波在传播过程中会产生衰减，使声压幅值降低；同时，由于介质本身对声能的吸收，声场中的声能也会降低。为了减少声能的损耗、使声波有足够的能量激励气泡，并使声波能够在介质中发生共振，在计算过程中将介质长度设置为半个波长，因此取n=1。根据3.1.1节中设置的激励频率，以及3.1.2节中计算得到的声速，介质长度设置如表3所示。
表 3 $N_{g}=2 \times 10^{11} / \bf{m}^{3}$时介质的长度Table 3 The length of the medium when $N_{g}=2 \times 10^{11} / \mathrm{m}^{3}$激励频率/kHz 介质长度/m R0g=4.5×10-6 m3 R0g=5×10-6 m3 R0g=8×10-6 m3 R0g=10-5 m3 50 0.010 23 0.009 34 0.005 47 0.004 04 60 0.008 52 0.007 78 0.004 54 0.003 35 80 0.006 38 0.005 82 0.003 38 0.002 48 100 0.005 09 0.004 65 0.002 69 0.001 96 150 0.003 38 — — — 160 0.003 17 — — — 180 0.002 80 — — — 200 0.002 51 — — — 上述计算表明，为了保证声波在介质中发生共振，当气泡体积和单位介质中的气泡数目一定时，对于每一个激励频率，都需要相应长度的介质与之匹配，激励频率的变化意味着介质长度的变化。激励频率越高，共振时所需要的介质长度越短；而当气泡密度和激励频率一定时，气泡体积越小，共振时所需要的介质长度越长。
3.2 含气泡水介质中的软化现象
对不同声波激励时介质中的非线性共振频率进行计算, 取气泡半径$R_{0 g}$为$4.5 \times 10^{-6} \mathrm{~m}^{3}$, 单位介质中气泡数目$N_{g}$为$2 \times 10^{11} / \mathrm{m}^{3}$, 改变介质的长度以使不同频率的声波能在介质中发生驻波共振, 即令介质中线性共振频率从$150 \mathrm{kHz}$变化到$200 \mathrm{kHz}$。
3.2.1 单频激励
本文所使用的单频连续信号的表达形式为$s(t)=p_{1} \sin \left(\omega_{1} t\right)$, 其中$\omega_{1}=2 \pi f_{1}$。$p_{1}$为振幅, $f_{1}$是信号频率。
使激励频率$f_{1}$以线性时该介质的共振频率$f_{L}$为中心进行扫频, 通过傅里叶变换从各个频率分量中提取出$f_{1}$分量并读取幅值, 记为$p_{f}$。记录$p_{f}$随$f_{1}$的变化情况并绘制曲线, 找到其中的最大值所对应的频率, 即为此时介质的非线性共振频率, 记为$f_{N}$。
在计算过程中，为保持差分方程组的解是收敛且稳定的，应满足Courant稳定性条件[23]:
$$ c \Delta t \leqslant \frac{1}{\sqrt{\frac{1}{(\Delta x)^{2}}+\frac{1}{(\Delta y)^{2}}+\frac{1}{(\Delta z)^{2}}}} $$ (13) 式中: $\Delta t$为时间离散间隔; $\Delta x 、\Delta y 、\Delta z$为空间离散间隔。
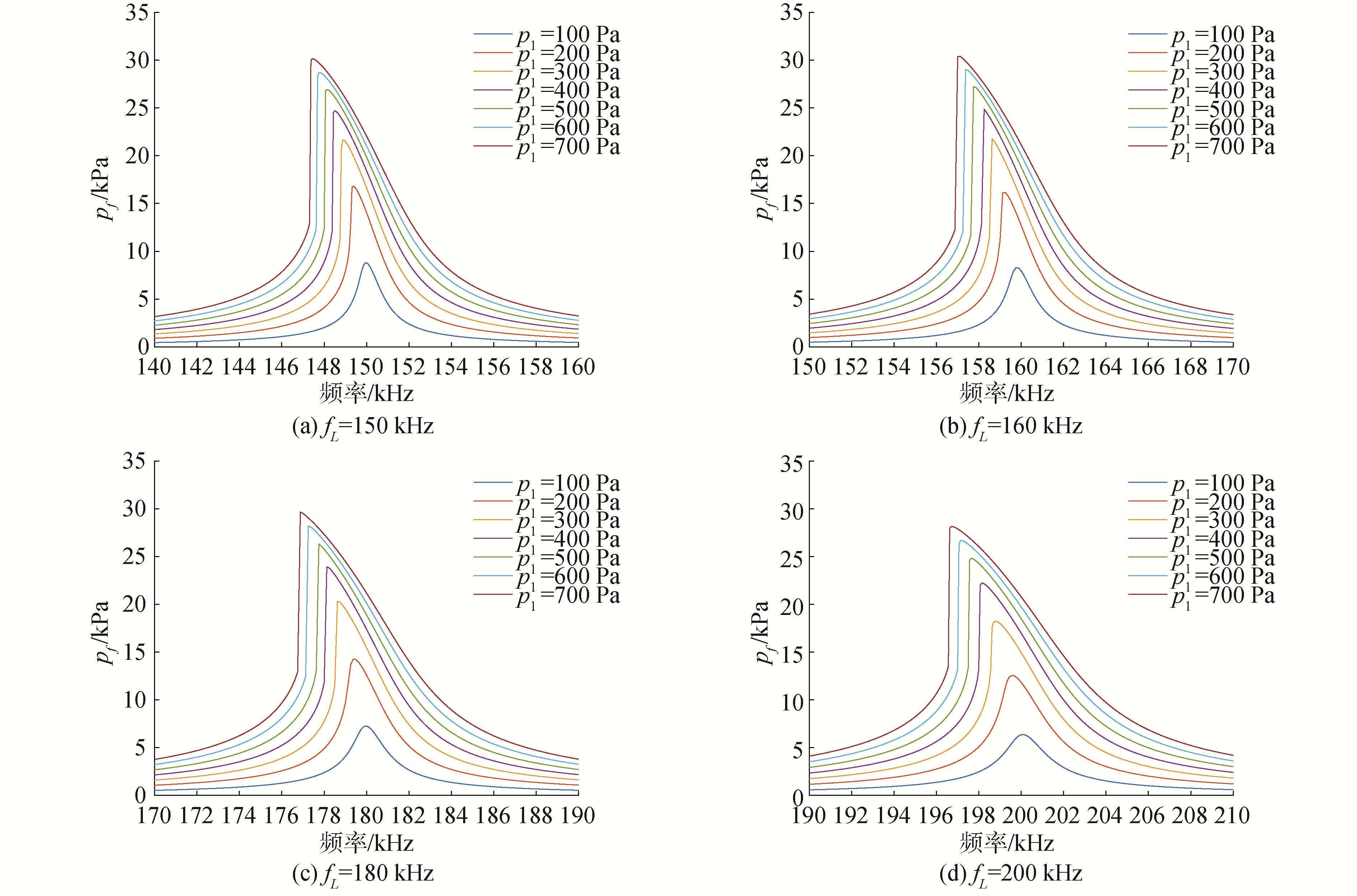
在每组计算过程中, 均使激励振幅从$p_{1}=100 \mathrm{~Pa}$变化到$p_{1}=700 \mathrm{~Pa}$, 间隔为$\Delta p=100 \mathrm{~Pa}$, 所得到的结果如图6所示。
图 6 $N_{g}=2 \times 10^{11} / \mathrm{m}^{3}, R_{0 g}=4.5 \times 10^{-6} \mathrm{~m}^{3}$时单频声波激励下介质中的软化Fig. 6 Softening in the medium under single-frequency acoustic excitation when $N_{g}=2 \times 10^{11} / \mathrm{m}^{3}, R_{0 g}=4.5 \times 10^{-6} \mathrm{~m}^{3}$下载:
全尺寸图片
图6展示了在单频声波激励时，不同长度的介质中共振频率随激励振幅的变化情况。在单频声波的激励下，随着激励振幅的增加，介质的共振频率有向下移动的趋势，这说明此时含气泡水介质中发生了声学软化。含气泡水介质的共振明显依赖于压力振幅，具有与岩石等粒状介质相似的软化性质。在低振幅时，介质的共振曲线具有对称性，且未出现共振频移现象；当振源振幅增加时，介质的共振频率逐渐降低，即存在非线性频移。且激励振幅越高，非线性频移量越大，即介质的软化效应越强。
同时，当介质发生非线性共振时，介质中测得的f1分量的振幅增强，说明当介质发生软化时，声波与气泡之间的相互作用增强，气泡受到激励产生较强的非线性效应，使介质中的振幅响应增大。
3.2.2 双频激励
本节数值仿真中所使用的激励信号表达形式为$s(t)=p_{1} \sin \left(\omega_{1} t\right)+p_{2} \sin \left(\omega_{2} t\right)$, 即双频连续波。$p_{1}$和$p_{2}$为振幅, $f_{1}$和$f_{2}$是信号频率, 其中$\omega_{1}=2 \pi f_{1}, \omega_{2}=2 \pi f_{2}$。与单频波激励时相同, 分别进行4组仿真计算, 在每组计算过程中, 介质长度保持不变, 使激励声源产生的和频声波的频率$f_{h}$以线性时该介质的共振频率$f_{h L}$为中心进行扫频。在扫频过程中, 保持$f_{1}$不变, 使$f_{2}$围绕表1和表2中相应的数值变化。
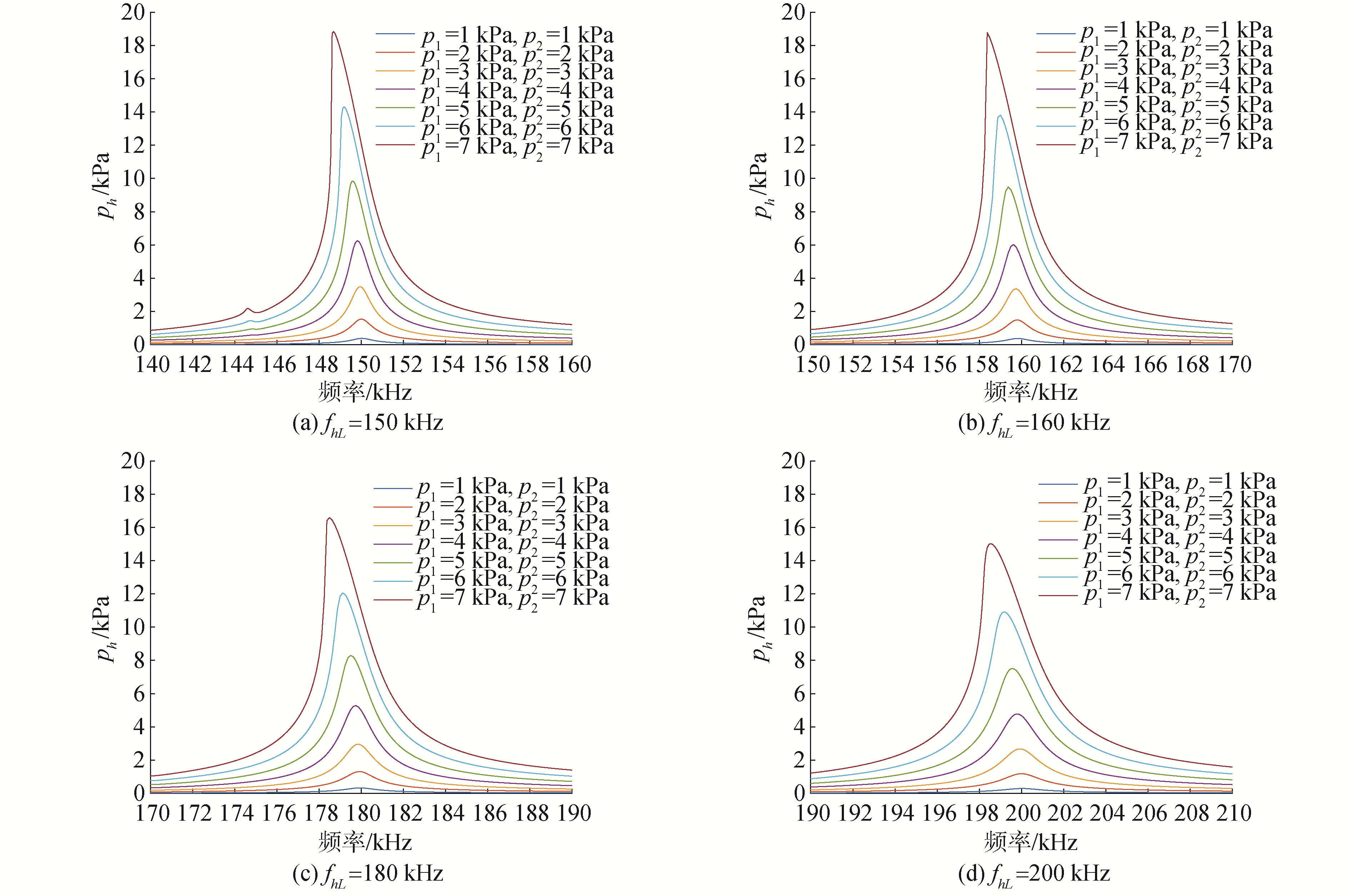
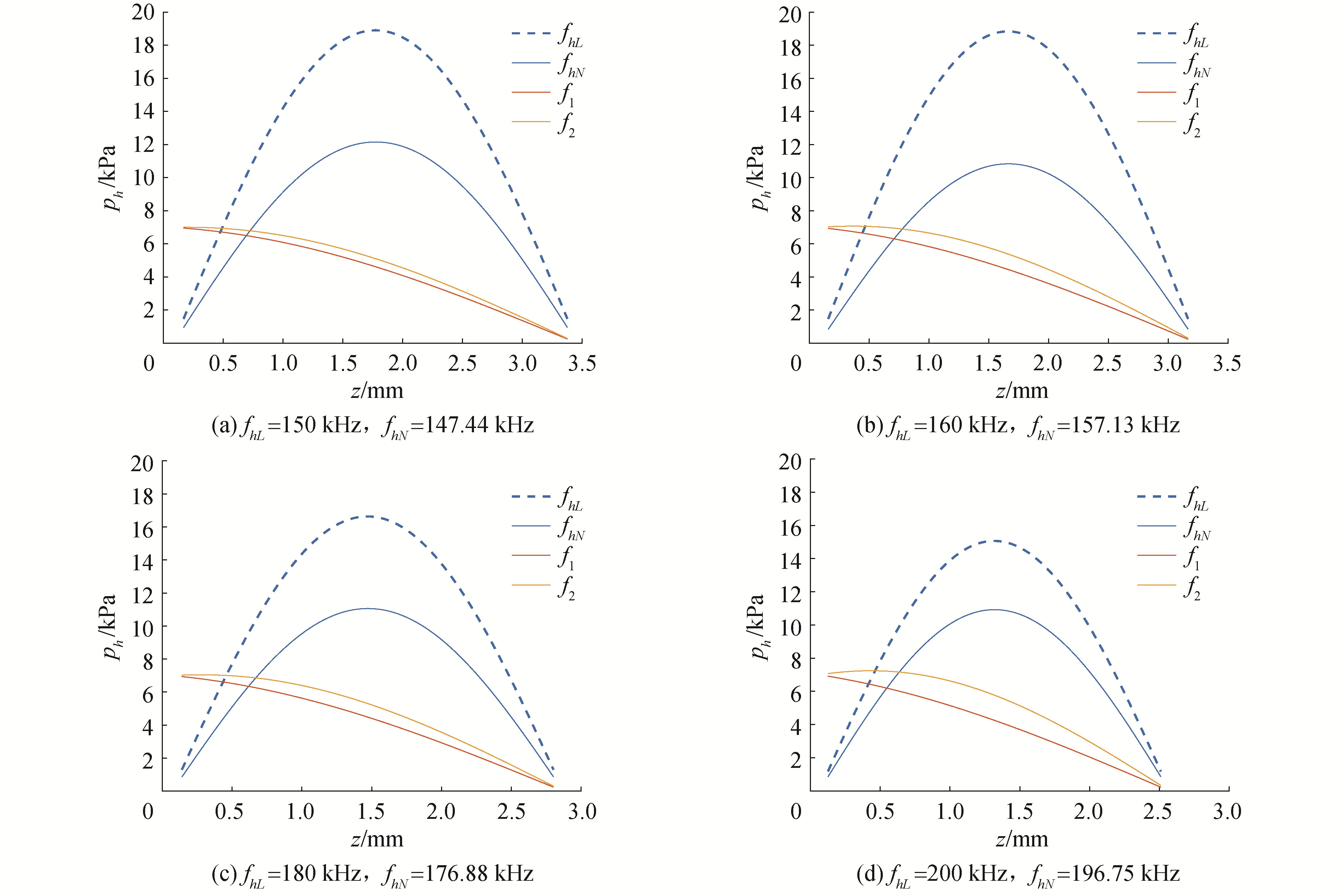
令双频声源的振幅从$p_{1}=p_{2}=1 \mathrm{kPa}$变化到$p_{1}=p_{2}=7 \mathrm{kPa}$, 记录$f_{h}$变化时和频声波的幅值, 记为$p_{h}$, 并绘制$p_{h}$随$f_{h}$的变化情况, 找到其中的最大值所对应的和频频率, 即为此时介质的非线性共振频率$f_{h N}$。
如图7所示，当介质受到双频声波激励时，含气泡水介质的共振频率降低，介质发生软化。与单频声波激励时相似，在低振幅时，介质的共振曲线具有对称性，且未出现共振频移现象。当振源振幅增加时，介质的共振频率逐渐降低，即存在非线性频移。
图 7 $N_{g}=2 \times 10^{11} / \mathrm{m}^{3}, R_{0 g}=4.5 \times 10^{-6} \mathrm{~m}^{3}$时双频声波激励下介质中的软化Fig. 7 Softening in the medium under dual-frequency acoustic excitation when $N_{g}=2 \times 10^{11} / \mathrm{m}^{3}, R_{0 g}=4.5 \times 10^{-6} \mathrm{~m}^{3}$下载:
全尺寸图片
综合图6和图7进行分析得知，在单频波和双频波激励下，介质中均可产生软化现象。并且与单频声波激励时相比，在双频声波激励时，想要介质发生软化，需要更高的振幅激励，且介质共振频率的偏移量较低，软化效应较弱。这是因为2列声波在通过非线性效应产生和频声波时能量有一部分损失，使和频声波获得的能量降低，对气泡的激励作用较弱。
此外，单频激励时，介质内的声压响应幅值比双频激励时的幅值高，是因为沿声波传播方向上的介质长度仅有半波长，双频激励时2列声波产生的和频声波传播的距离过短，能量没有得到积累。
3.3 气泡体积对介质软化的影响
由于含气泡水介质中的软化现象是基于多重散射理论时观察到的一种非线性效应, 所以气泡的体积和气泡密度是影响介质软化的一种重要因素。文献[19]仅在一维条件下指出了介质的声学软化源于气泡平均体积的变化, 但并未验证在相同激励条件下, 气泡初始体积不同的介质中软化效应的差异。本文将其扩展到三维情况, 并考虑了以下4个不同的气泡体积: $R_{0 g}=$ $4.5 \times 10^{-6} \mathrm{~m}^{3}, R_{0 g}=5 \times 10^{-6} \mathrm{~m}^{3}, R_{0 g}=8 \times 10^{-6} \mathrm{~m}^{3}$以及$R_{0 g}=10^{-5} \mathrm{~m}^{3}$。单位体积介质中气泡数目均为$2\times$ $10^{11} / \mathrm{m}^{3}$。令以上介质在线性条件下的共振频率$f_{L}$分别为$50 、60 、80$和$100 \mathrm{kHz}$, 采用3.2节中的方法, 对4种条件下介质中的非线性共振频率进行计算。
在某一振幅激励下介质中软化效应的强弱可以用表达式衡量：
$$ S=\Delta f / f_{L} $$ (14) 式中: $\Delta f=f_{L}-f_{N} ; f_{N}$为介质在该振幅激励下实际的非线性共振频率。
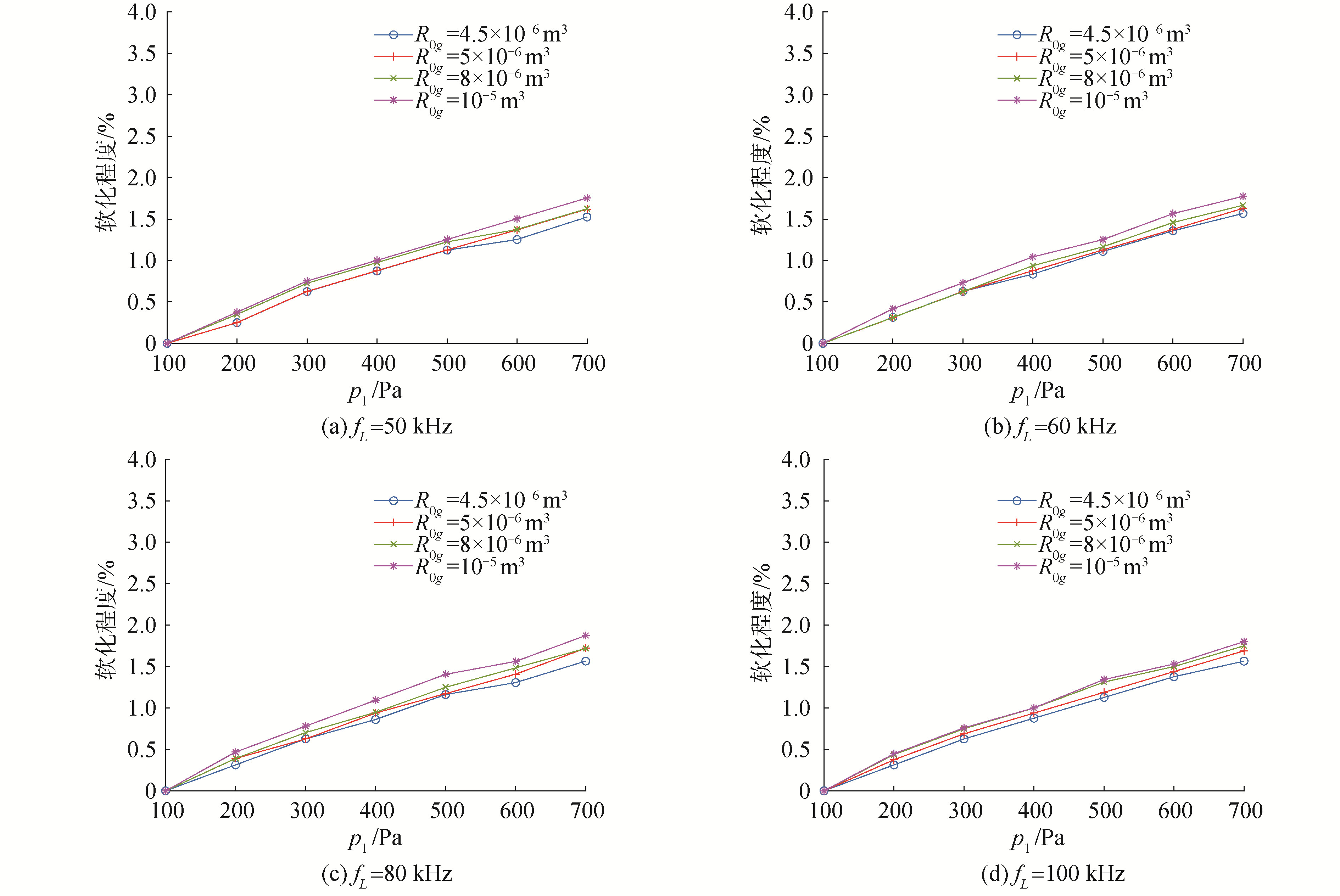
依据式(14)，对不同激励频率下介质的软化程度进行计算并绘制图像，如图8所示。
图 8 单频声波激励下不同气泡体积的介质中的软化程度Fig. 8 Degree of softening in media with different bubble volumes excited by single-frequency sound waves下载:
全尺寸图片
由图8可知，在单频声波激励下，气泡体积会影响介质的软化程度。在相同振幅的声波激励下，气泡体积较大的介质的软化程度更高。
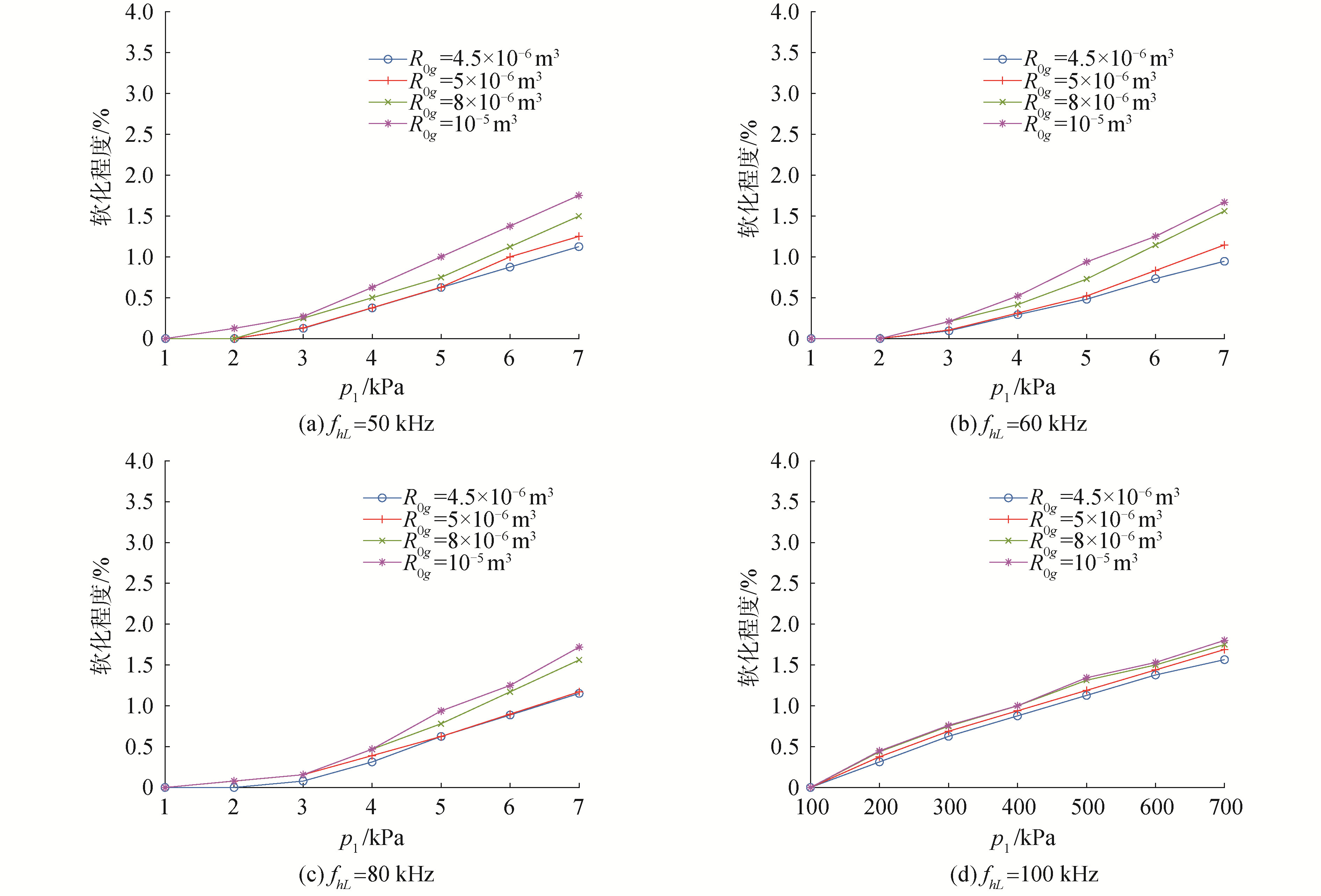
此外，与图8对比，图9中4条曲线的变化趋势存在较大差异，且随着激励振幅的增加，这种差异越来越明显，这说明在双频声波激励时，介质中的软化程度更容易受到气泡体积变化的影响。并且在双频声波激励时，曲线的斜率随振幅的增加而迅速增大，而单频声波激励时则与之相反，曲线的斜率随着振幅的增加而减小，这说明在双频声波激励时，介质的软化更依赖于振幅的变化。
图 9 双频声波激励下不同气泡体积的介质中的软化程度Fig. 9 Degree of softening in media with different bubble volumes excited by dual-frequency sound waves下载:
全尺寸图片
3.4 软化时介质中的声场
由3.2节可知，当受到声波激励时，含气泡水介质会发生软化。为了研究介质的软化对声波传播的影响，对含气泡水介质中的声场进行分析。
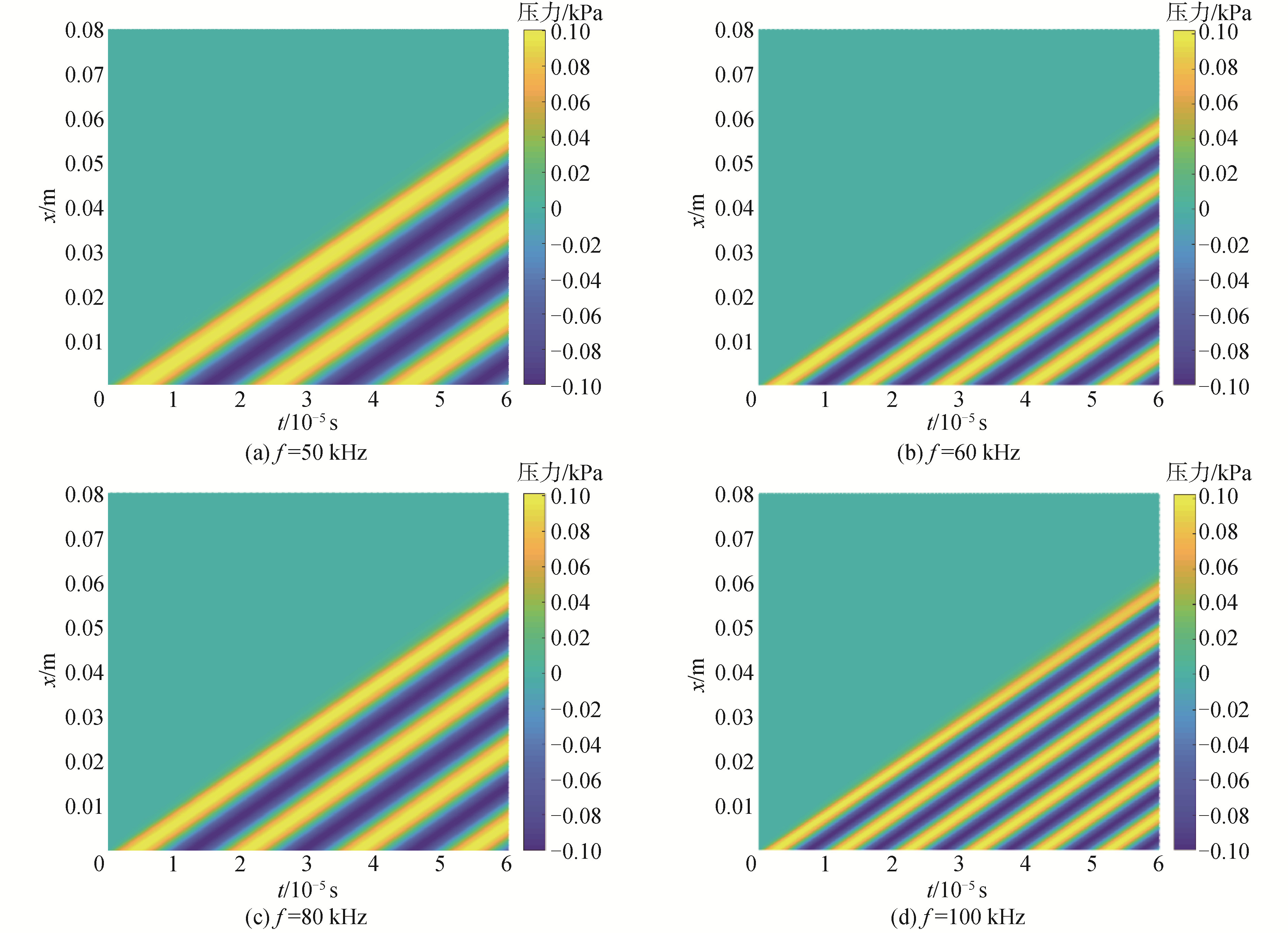
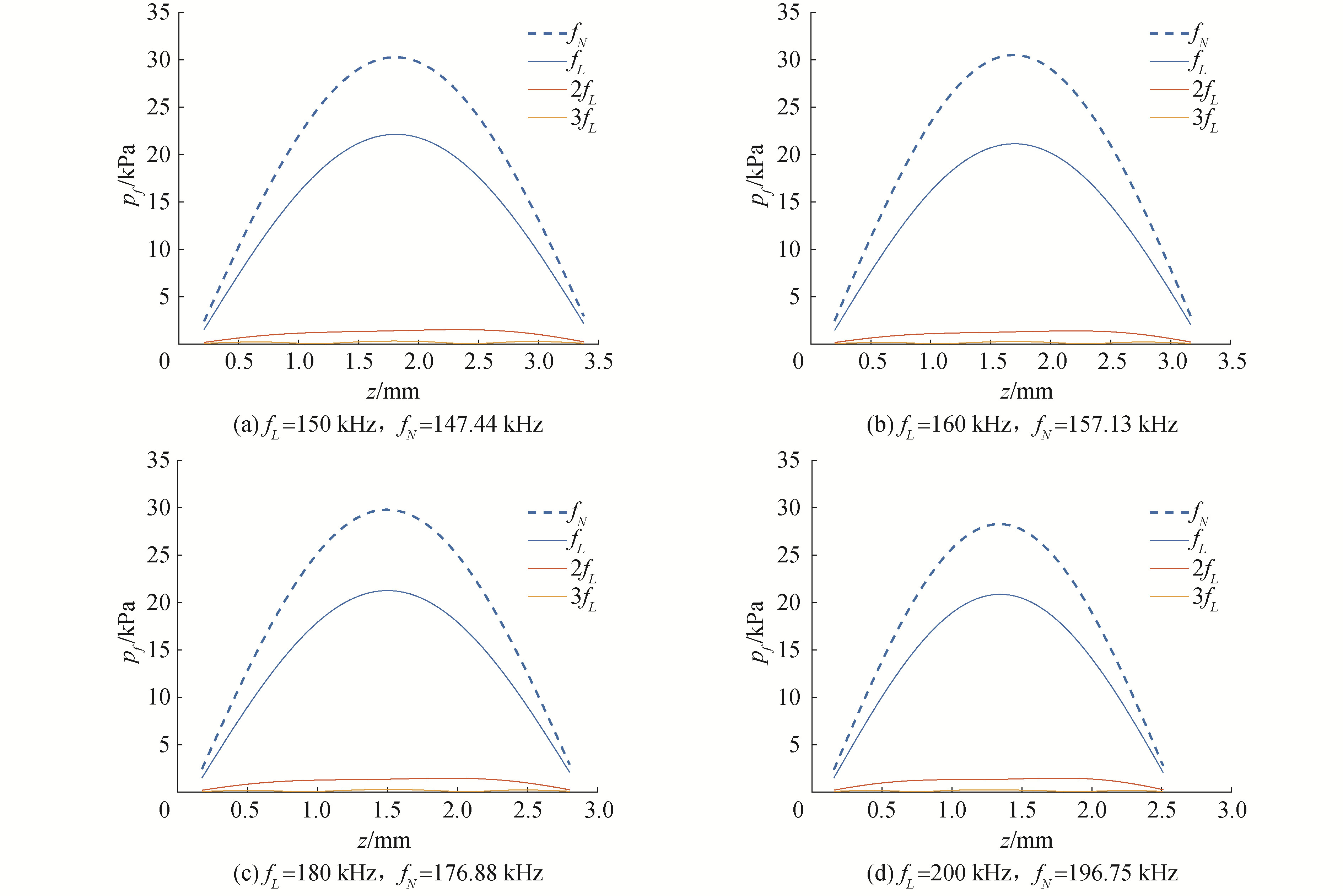
对于单频波激励, 令激励声波的振幅为$700 \mathrm{~Pa}$, 气泡体积$R_{0 g}=4.5 \times 10^{-6} \mathrm{~m}^{3}$, 单位体积介质中的气泡数目为$2 \times 10^{11} / \mathrm{m}^{3}$, 分别计算不同长度的介质中的声场, 如图10所示。其中$f_{L}$是线性假设时介质中的共振频率, $f_{N}$是软化条件下介质中实际的共振频率。图11为双频声波激励时介质中的声场。
图 10 单频声波激励时介质中的声场Fig. 10 Sound field in the medium when single-frequency wave excitation下载:
全尺寸图片
图 11 双频声波激励时介质中的声场Fig. 11 Sound field in the medium when dual-frequency wave excitation下载:
全尺寸图片
由图10可知，当单频声波激励时，介质发生声学软化，共振频率偏移，与线性条件下介质的共振频率相比，非线性共振频率在介质中的声压振幅响应有较大程度的增加，由此得到启发，可以考虑利用介质的非线性声学软化现象改变介质的声学特性，以提高介质中的振幅响应。
图11是双频声波激励下软化介质中的声场, 其中激励声波振幅为$p_{1}=p_{2}=7 \mathrm{kPa}$, 气泡体积$R_{0 g}=4.5 \times 10^{-6} \mathrm{~m}^{3}$, 单位体积介质中气泡数目为$2 \times 10^{11} / \mathrm{m}^{3}$。
由图11可知，当介质发生软化时，和频分量的幅值比2个声源的幅值高，说明在非线性条件下，可以获得比源信号幅度更高的和频分量。这一现象可以用作非线性频率混合，来获得更高振幅的信号。此外，和频分量在介质中处于共振状态，而源信号的幅值随着距离的增加逐渐减小，这表明在声波与气泡的非线性作用过程中，源信号的能量被转移到和频分量上，以使和频分量有较大的能量来激励气泡。可以将这种现象利用在参量接收阵中，将湮没在环境噪声中的低频声波的能量转移到高频信号上，增强接收信号的强度。
4. 结论
1) 当用单频声源和双频声源作为激励时，在声波传播方向上，长度为半波长的含气泡水介质中均会产生软化现象，声学特性发生改变，具体表现为介质的共振频率降低，且共振时声波的振幅均大于激励声波的振幅；
2) 含气泡水介质的非线性共振频移与振源的振幅有关，并且在一定范围内，随着振幅的增大，介质的软化效应增强，非线性频移现象也随之更加明显；
3) 介质软化效应的产生源于气泡平均体积的变化。随着激励振幅的增大，气泡振动处于非线性状态，气泡膨胀的体积大于气泡压缩的体积，因此达到新的平衡时气泡平均体积增大，介质的孔隙率和气泡的可压缩性增大，从而增强介质的非线性，使介质发生软化；
4) 在其他条件相同时，气泡体积越大，介质中的软化现象越明显；与单频声波激励时相比，在双频声波激励时，介质中的软化程度更容易受到气泡体积变化的影响，并更依赖于振幅的变化。
本文的研究结果表明，含气泡的水介质中具有与岩石砂砾等固体颗粒介质相似的软化现象，对该现象的研究有助于更好地理解声波与气泡的相互作用规律以及气泡在声场中的非线性动力学行为。可以考虑将这种性质应用到非线性超材料的设计中，以提高参量阵声发射和接收效率。
-
图 1 三维圆柱形空腔
Fig. 1 Three-dimensional cylindrical cavity
下载:
全尺寸图片
图 2 时间离散化
Fig. 2 Time discretization
下载:
全尺寸图片
图 3 空间离散化
Fig. 3 Spatial discretization
下载:
全尺寸图片
图 4 介质中的衰减
Fig. 4 Attenuation in the medium
下载:
全尺寸图片
图 5 $N_{g}=2 \times 10^{11} / \mathrm{m}^{3}, R_{0 g}=4.5 \times 10^{-6} \mathrm{~m}^{3}$时介质中的声速
Fig. 5 The speed of sound in the medium when $N_{g}=2 \times 10^{11} / \mathrm{m}^{3}, R_{0 g}=4.5 \times 10^{-6} \mathrm{~m}^{3}$
下载:
全尺寸图片
图 6 $N_{g}=2 \times 10^{11} / \mathrm{m}^{3}, R_{0 g}=4.5 \times 10^{-6} \mathrm{~m}^{3}$时单频声波激励下介质中的软化
Fig. 6 Softening in the medium under single-frequency acoustic excitation when $N_{g}=2 \times 10^{11} / \mathrm{m}^{3}, R_{0 g}=4.5 \times 10^{-6} \mathrm{~m}^{3}$
下载:
全尺寸图片
图 7 $N_{g}=2 \times 10^{11} / \mathrm{m}^{3}, R_{0 g}=4.5 \times 10^{-6} \mathrm{~m}^{3}$时双频声波激励下介质中的软化
Fig. 7 Softening in the medium under dual-frequency acoustic excitation when $N_{g}=2 \times 10^{11} / \mathrm{m}^{3}, R_{0 g}=4.5 \times 10^{-6} \mathrm{~m}^{3}$
下载:
全尺寸图片
图 8 单频声波激励下不同气泡体积的介质中的软化程度
Fig. 8 Degree of softening in media with different bubble volumes excited by single-frequency sound waves
下载:
全尺寸图片
图 9 双频声波激励下不同气泡体积的介质中的软化程度
Fig. 9 Degree of softening in media with different bubble volumes excited by dual-frequency sound waves
下载:
全尺寸图片
图 10 单频声波激励时介质中的声场
Fig. 10 Sound field in the medium when single-frequency wave excitation
下载:
全尺寸图片
图 11 双频声波激励时介质中的声场
Fig. 11 Sound field in the medium when dual-frequency wave excitation
下载:
全尺寸图片
表 1 双频激励时声源发射频率
Table 1 The emission frequency of the sound source when dual-frequency excitation
kHz 和频频率 声源发射频率 f1 f2 50 20 30 60 25 35 80 30 50 100 30 70 150 70 80 160 70 90 180 80 100 200 90 110 表 2 $N_{g}=2 \times 10^{11} / \bf{m}^{3}$时介质中的声速
Table 2 The speed of sound in the medium when $N_{g}=2 \times 10^{11} / \mathrm{m}^{3}$
激励频率/kHz 声速/(m/s) R0g=4.5×10-6 m3 R0g=5×10-6 m3 R0g=8×10-6 m3 R0g=10-5 m3 50 1 023.21 934.28 546.27 404.66 60 1 022.53 933.23 545.06 402.57 80 1 021.08 931.72 541.62 397.15 100 1 019.67 929.51 537.16 391.43 150 1 013.72 — — — 160 1 011.96 — — — 180 1 088.77 — — — 200 1 004.38 — — — 表 3 $N_{g}=2 \times 10^{11} / \bf{m}^{3}$时介质的长度
Table 3 The length of the medium when $N_{g}=2 \times 10^{11} / \mathrm{m}^{3}$
激励频率/kHz 介质长度/m R0g=4.5×10-6 m3 R0g=5×10-6 m3 R0g=8×10-6 m3 R0g=10-5 m3 50 0.010 23 0.009 34 0.005 47 0.004 04 60 0.008 52 0.007 78 0.004 54 0.003 35 80 0.006 38 0.005 82 0.003 38 0.002 48 100 0.005 09 0.004 65 0.002 69 0.001 96 150 0.003 38 — — — 160 0.003 17 — — — 180 0.002 80 — — — 200 0.002 51 — — — -
[1] 杨德森, 时洁, 时胜国, 等. 声波作用下的气泡非线性动力学特性影响因素及功率谱变化规律研究[J]. 声学学报, 2013, 38(2): 113-127. https://www.cnki.com.cn/Article/CJFDTOTAL-XIBA201302002.htm YANG Desen, SHI Jie, SHI Shengguo, et al. Investigation on bubble dynamics characteristics and power spectral variation in acoustic field[J]. Acta acustica, 2013, 38(2): 113-127. https://www.cnki.com.cn/Article/CJFDTOTAL-XIBA201302002.htm [2] 杨德森, 江薇, 时胜国, 等. 体积粘滞对气泡动力学特性及激励声波频谱能量的影响[J]. 哈尔滨工程大学学报, 2013, 34(6): 734-741. http://heuxb.hrbeu.edu.cn/#/digest?ArticleID=1453 YANG Desen, JIANG Wei, SHI Shengguo, et al. The effect of volume viscosity on dynamics characteristics of bubbles and spectral energy change of incentive sound wave[J]. Journal of Harbin Engineering University, 2013, 34(6): 734-741. http://heuxb.hrbeu.edu.cn/#/digest?ArticleID=1453 [3] 汪洋, 刘清宇, 鹿力成, 等. 海面风浪影响下的浅海声传播预报方法[J]. 哈尔滨工程大学学报, 2020, 41(8): 1163-1169. http://heuxb.hrbeu.edu.cn/#/digest?ArticleID=3396 WANG Yang, LIU Qingyu, LU Licheng, et al. A method of acoustic propagation prediction considering the impact of wind waves in shallow water[J]. Journal of Harbin Engineering University, 2020, 41(8): 1163-1169. http://heuxb.hrbeu.edu.cn/#/digest?ArticleID=3396 [4] AKULICHEV V A, BULANOV V A. Measurements of bubbles in sea water by nonstationary sound scattering[J]. The journal of the acoustical society of America, 2011, 130(5): 3438-3449. doi: 10.1121/1.3636371 [5] GAUNAURD G C, VBERALL H. Theory of resonant scattering from spherical cavities in elastic and viscoelastic media[J]. The journal of the acoustical society of America, 1978, 63(6): 1699-1712. doi: 10.1121/1.381908 [6] 秦波, 梁彬, 朱哲民, 等. 含气泡弱可压缩弹性材料的等效媒质法[J]. 声学学报, 2007, 32(2): 110-115. https://www.cnki.com.cn/Article/CJFDTOTAL-XIBA200702003.htm QIN Bo, LIANG Bin, ZHU Zhemin, et al. Effective medium method of slightly compressible elastic media permeated with air-filled bubbles[J]. Acta acustica, 2007, 32(2): 110-115. https://www.cnki.com.cn/Article/CJFDTOTAL-XIBA200702003.htm [7] 胡洁, 刘云飞. 含泡胶质体层的声透射特性研究[J]. 南京大学学报(自然科学版), 2013, 49(3): 394-401. doi: 10.13232/j.cnki.jnju.2013.03.007 HU Jie, LIU Yunfei. Acoustic transmission through a single layer of bubbly gel[J]. Journal of Nanjing University (natural sciences), 2013, 49(3): 394-401. doi: 10.13232/j.cnki.jnju.2013.03.007 [8] FOLDY L L. The multiple scattering of waves. I. general theory of isotropic scattering by randomly distributed scatterers[J]. Physical review, 1945, 67(3/4): 107-119. [9] KARGL S G. Effective medium approach to linear acoustics in bubbly liquids[J]. The journal of the acoustical society of America, 2002, 111(1): 168-173. [10] 范雨喆, 李海森, 徐超, 等. 气泡线性振动时近海面气泡群的声散射[J]. 声学学报, 2019, 44(3): 312-320. https://www.cnki.com.cn/Article/CJFDTOTAL-XIBA201903005.htm FAN Yuzhe, LI Haisen, XU Chao, et al. Acoustic scattering from bubble clouds near the sea surface based on linear oscillations[J]. Acta acustica, 2019, 44(3): 312-320. https://www.cnki.com.cn/Article/CJFDTOTAL-XIBA201903005.htm [11] CABARET J, TOURNAT V, BÉQUIN P. Amplitude-dependent phononic processes in a diatomic granular chain in the weakly nonlinear regime[J]. Physical review E, 2012, 86(4): 041305. [12] BONANOMI L, THEOCHARIS G, DARAIO C. Wave propagation in granular chains with local resonances[J]. Physical review E, 2015, 91(3): 033208. [13] LAUTERBORN W. Numerical investigation of nonlinear oscillations of gas bubbles in liquids[J]. The journal of the acoustical society of America, 1976, 59(2): 283-293. [14] OMTA R. Oscillations of a cloud of bubbles of small and not so small amplitude[J]. The journal of the acoustical society of america, 1987, 82(3): 1018-1033. [15] JAFARI SOJAHROOD A, LI Qian, BURGESS M, et al. Development of a nonlinear model for the pressure dependent attenuation and sound speed in a bubbly liquid and its experimental validation[J]. The journal of the acoustical society of America, 2016, 139(4): 2175. [16] MATSUMOTO Y, YOSHIZAWA S. Behaviour of a bubble cluster in an ultrasound field[J]. International journal for numerical methods in fluids, 2005, 47(6/7): 591-601. [17] DOC J B, CONOIR J M, MARCHIANO R, et al. Nonlinear acoustic propagation in bubbly liquids: multiple scattering, softening and hardening phenomena[J]. The journal of the acoustical society of America, 2016, 139(4): 1703-1712. [18] TEJEDOR SASTRE M T, VANHILLE C. A numerical model for the study of the difference frequency generated from nonlinear mixing of standing ultrasonic waves in bubbly liquids[J]. Ultrasonics sonochemistry, 2017, 34: 881-888. [19] TEJEDOR SASTRE M T, VANHILLE C. Nonlinear resonance of cavities filled with bubbly liquids: a numerical study with application to the enhancement of the frequency mixing effect[J]. Shock and vibration, 2018, 2018: 1-9. [20] HAMILTON M F, BLACKSTOCK D T. Nonlinear acoustics[M]. San Diego, CA: Academic Press, 1998. [21] TEJEDOR SASTRE M T, VANHILLE C. Numerical models for the study of the nonlinear frequency mixing in two and three-dimensional resonant cavities filled with a bubbly liquid[J]. Ultrasonics sonochemistry, 2017, 39: 597-610. [22] JOHNSON P A, ZINSZNER B, RASOLOFOSAON P N J. Resonance and elastic nonlinear phenomena in rock[J]. Journal of geophysical research: solid earth, 1996, 101(B5): 11553-11564. [23] YEE Kane. Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media[J]. IEEE transactions on antennas and propagation, 1966, 14(3): 302-307.
