Global navigation satellite system-acoustic combined observation model classification system
-
摘要: 本文回顾了海底大地测量全球导航卫星系统-声呐观测模型近二十年来的发展，以声速误差处理为主线给出了全球导航卫星系统-声呐观测模型的分类体系，按函数模型、随机模型和约束条件进行了归纳，探讨了未来发展方向。研究表明: 测距定位模型无需现场声速剖面测量，但需解决声速垂向梯度影响的有效参数化估计或改正问题；海底大地测量更为关注声速时空变化对观测值影响，为此推荐采用声速场误差加性补偿模型及其导出的声速场参数间接估计模型；海底局域网阵列存在类似共模环境误差，具有提升海洋环境参数估计及海底定位精度的能力。Abstract: This paper reviews the development of the global navigation satellite system (GNSS)-acoustic observation model in the seafloor geodesy over the past two decades. With a focus on the processing of sound speed errors, the classification system of the GNSS-acoustic observation models is presented, and these models are summarized according to the functional and stochastic models and constraint conditions. In addition, future development directions are discussed. It shows that the range-based positioning models do not need an in-field sound velocity profile measurement, but they must address effective parameterization estimation or correction of the vertical gradient effect of sound velocity. The seafloor geodesy is more concerned with the impact of spatiotemporal variations in the sound speed on observations. Thus, we recommend using an error compensation model for the sound speed field and an indirectly estimated model for sound speed field parameters. There are similar common-mode environmental error features in the seafloor local network arrays; thus, the seafloor arrays can enhance the estimation of ocean environmental parameters and further improve the seafloor positioning accuracy.
-
海底大地测量在研究地球动力学过程中具有重要的科学意义，包括地壳构造运动以及海洋、大气和固体地球层之间的耦合相互作用[1-2]。根据科学估计，人类只探索了大约5%的海洋，这使得海洋观测成为认识海洋的重要技术手段[3-4]。水下大地测量参考网是进行水下大地观测的重要基础设施，也是未来国家水下海洋观测和建立综合时空系统的重要组成部分。因此，海底大地测量是大地测量的重要新兴发展方向，也是未来地球科学重要支撑学科方向[5-6]。海底声学大地测量技术是基于声学手段实施海底大地测量的技术，自20世纪七八十年代提出至今，其发展大致经过了3个阶段[7]：1)海底声学直接测距技术阶段，海底测站间互测距定位因避免了声线穿越海表声速快速变化的温跃层，而具有较高的平面定位精度，成为海底水平扩张的有效监测手段[8-9]；2)海底声学间接测距技术阶段[10-11]，通过船载拖体中继换能器或海底锚系中继换能器，对海底多基站实施声学测量，进而形成海底的间接测距，有效扩大了海底大地测量实施空间范围；3)GNSS(global navigation satellite system)-声呐组合观测技术阶段，逐渐成为海底大地测量的主流观测技术，其在大尺度海底板块运动监测、地震活动监测等方面具有显著优势[12-16]。随着海底声学定位理论的不断发展和世界范围内区域海底控制网观测技术的不断进步，GNSS-声呐组合观测水平定位精度已达到2~3 cm，高程定位精度已达6~9 cm[17-18]。近年来，随着无人机、海面浮标/无人船、半潜式自主式水下航行器和波浪滑翔器等无人观测系统的发展，替代大型测量船的无人平台GNSS-声呐观测系统受到广泛关注，在经济、自主、连续观测方面具有显著优势[19-20]。整体上，经过近30年的发展，观测技术日趋成熟，但复杂海洋声速场时空变化仍然是制约深海海底精密定位的核心因素。在当前观测水平与精度下，要感知海底1 cm海底位移监测，GNSS-声呐组合观测技术至少需要2~3 a的复测资料[2]。
受海洋环境连续、动态变化影响，海洋声速场存在复杂的时空变化，而且这种变化相对于声速本身的数量级不容忽视[4, 21-22]，会导致海洋声线折射影响比电磁波折射影响更为严重[23-25]。受海洋环境观测成本和观测条件所限，实时获取测区高精度、高时空分辨率海洋声速场信息几无可能，通常只能以特定时间和空间分辨率获取参考声速剖面观测，甚至仅在特定地点和时间采集一条声速剖面[26]。因此，如何利用不完备的海洋声速观测信息，甚至无现场声速观测信息的条件下，实现水下精密定位就成为高精度海底大地测量的难点问题之一。目前，控制声速误差对海底大地测量定位影响的途径主要归纳为以下2类：
1) 控制网及观测方案设计。美国斯克利普斯海洋研究所(Scripps Institution of Oceanography)自提出海底大地测量之初，就推荐使用以水深为半径的圆上3个或3个以上点作为海底阵列，观测载体位于海面圆心处观测，以抵抗声速变化对定位的影响[12]，该方案迄今已被广泛采用，并通过实践证明该解决方案在提高平面定位精度方面是有效的[27-29]。近年来，不少学者也围绕海面测线或浮标构型优化设计以提高海洋控制网强度，从而削弱声速误差影响[11, 30-36]。
2) 声速场时空变化参数估计。在观测模型中对声速场时空变化予以补偿，即对声速时空变化进行参数估计，可简称声速场参数估计。可将声速场参数估计归纳为2类：一类为直接对声速场参数(如声速变化、水平梯度等)进行估计，可称为声速场参数直接估计法；另一类为对声速场时空变化对声呐观测的影响(如声信号传播时间等)进行参数化估计，可称为声速场参数间接估计法。
① 声速场参数直接估计法。针对声速时变影响，日本学者Fujita等采用二次或三次多项式函数对滑动时间窗口内声速误差进行表示，基于线性反演(分步迭代)的方式求解海底点坐标和声速系数[27, 37-38]；Ikuta等[39]将实际声速与参考声速之间的差异使用附有平滑约束的B样条函数进行拟合，用联合估计的方式求解海底点坐标和声速系数，获得了水平方向优于10 cm、垂直方向优于20 cm的重复观测精度；Yokota等[17, 40]深入分析了声速结构时空变化特点，提出基于短时窗口内的声速变化提取声速结构一阶梯度和二阶梯度的方法。Yasuda[13]基于B样条函数模型，按照惩罚最小二乘的估计准则，对海底基准位置以及声速时间变化和梯度特征进行联合估计。该类方法为反演声速场参数，存在不适定问题及其参数解释难题。在不测量声速剖面的情况下，有学者考虑声速结构随深度变化，采用线性/双线性模型近似声速场垂向结构，通过对该声速模型参数与海底站坐标进行估计，以提高海底定位的精度[41]。有学者提出了GNSS-声呐观测自构声速剖面替代现场声速剖面的定位模型[42]，但定位误差仍难以满足厘米级的海底大地测量需求。事实上，最近有学者通过构建更为合理的经验声速剖面模型，GNSS-声呐观测自构声速剖面可实现更高精度的海底大地测量定位[43]。事实上，由于无人GNSS-声呐观测系统很难获取现场声速剖面，在降低观测成本的同时，势必增加海底精密定位的难度。因此，无现场声速剖面观测将会涉及更为复杂的模型误差补偿问题，特别是声速场垂向梯度结构影响的参数化问题。
② 声速场参数间接估计法。Kido等[21]基于声速场时空变化对信号传播时间延迟影响分析，建立了垂直方向时延观测方程，提出了“天底总延迟”(nadir total delay, NTD)的基本概念[22]。Honsho等[44]在NTD概念基础上，提出使用B样条刻画垂直时延时间变化的建模方法，并从慢度场出发建立了顾及声速场水平梯度影响的天顶延迟模型[14]，随后Tomita[14]引入扩展卡尔曼滤波(extended kalman filter, EKF) 算法进行NTD参数和海底基站坐标参数联合求解。Watanabe等[18]将观测方向时延误差的时空变化项用样条函数刻画，将声速结构构建为关于三维空间和一维时间的四维模型，研发了GARPOS(GNSS-Acoustic ranging combined positioning solver)解算软件，并后续嵌入了马尔科夫链蒙特卡罗(markov chain monte carlo, MCMC)算法[45]。这类方法虽然回避了声速场反演问题，但声速场时空变化影响函数仍有待完善，特别存在参数化模型优化选取和超参数优化问题。Yang等[46]提出了校正距离观测值的水下弹性定位模型，该模型为统一海底大地测量定位模型和空间大地测量定位模型具有重要借鉴意义。
本文首先给出了GNSS-声呐观测模型的统一表达式，然后按照上述脉络梳理出了现有GNSS-声呐观测模型体系，最后提出了GNSS-声呐观测模型的可能研究方向。
1. GNSS-声呐观测模型统一表达及分类体系
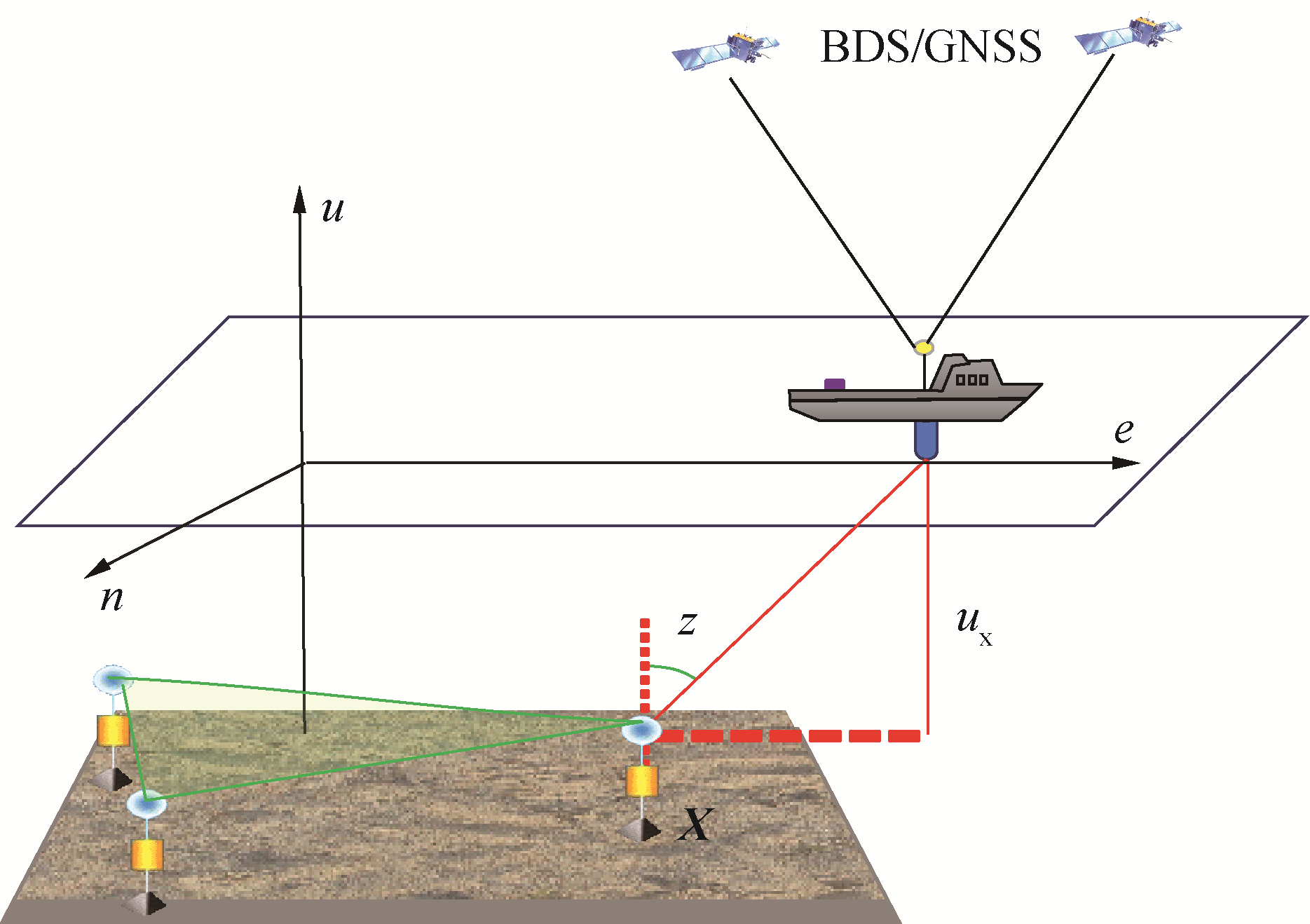
如图 1所示，不失一般性假设海底存在M个海底大地点(j=1, 2, …, M)，构建一个海底基准阵列，或称海底局域网，船载声学换能器向海底阵列发送声学测距信号，海底单元接收信号后返回声学应答信号后再次被海面换能器接收，据此进行声信号往返程传播时间测量，从而进行海底基准站或局域控制网定位[47]，可以建立GNSS-声呐组合观测模型：
$$ \left\{\begin{array}{l} \boldsymbol{L}=\boldsymbol{G}\left(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{p}_{\mathrm{c}}, \boldsymbol{p}_{\mathrm{a}}, \boldsymbol{p}_\mathtt{τ}\right)+\boldsymbol{\varepsilon}_{\mathrm{L}} \\ \mathbf{0}=\boldsymbol{C}\left(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{p}_{\mathrm{c}}, \boldsymbol{p}_{\mathrm{a}}, \boldsymbol{p}_\mathtt{τ}\right)+\boldsymbol{\varepsilon}_{\mathrm{c}} \end{array}\right. $$ (1) 
图 1 GNSS-声呐观测构型Fig. 1 GNSS-a positioning configuration
下载:
全尺寸图片
式中：第1个方程为GNSS-声呐观测方程，第2个方程为待估参数约束方程；L为观测向量，可分为时间观测值或距离观测值；G为非线性函数模型；x为海底控制点坐标或控制网阵列坐标；y为海面GNSS天线坐标(可视为已知值，或将海面定位结果作为先验信息与海底控制网坐标进行联合估计)；pc为声速时空变化参数；pa为臂长参数(可事先量测或后验估计)；pτ为海面换能器、海底应答器等硬件延迟参数；C为全部或部分模型参数的约束条件或先验信息相关的方程函数，例如，先验臂长先验信息[33, 48]、海面测线坐标先验信息[49-50]等；εL为观测模型随机误差向量；εc为约束方程随机误差向量。
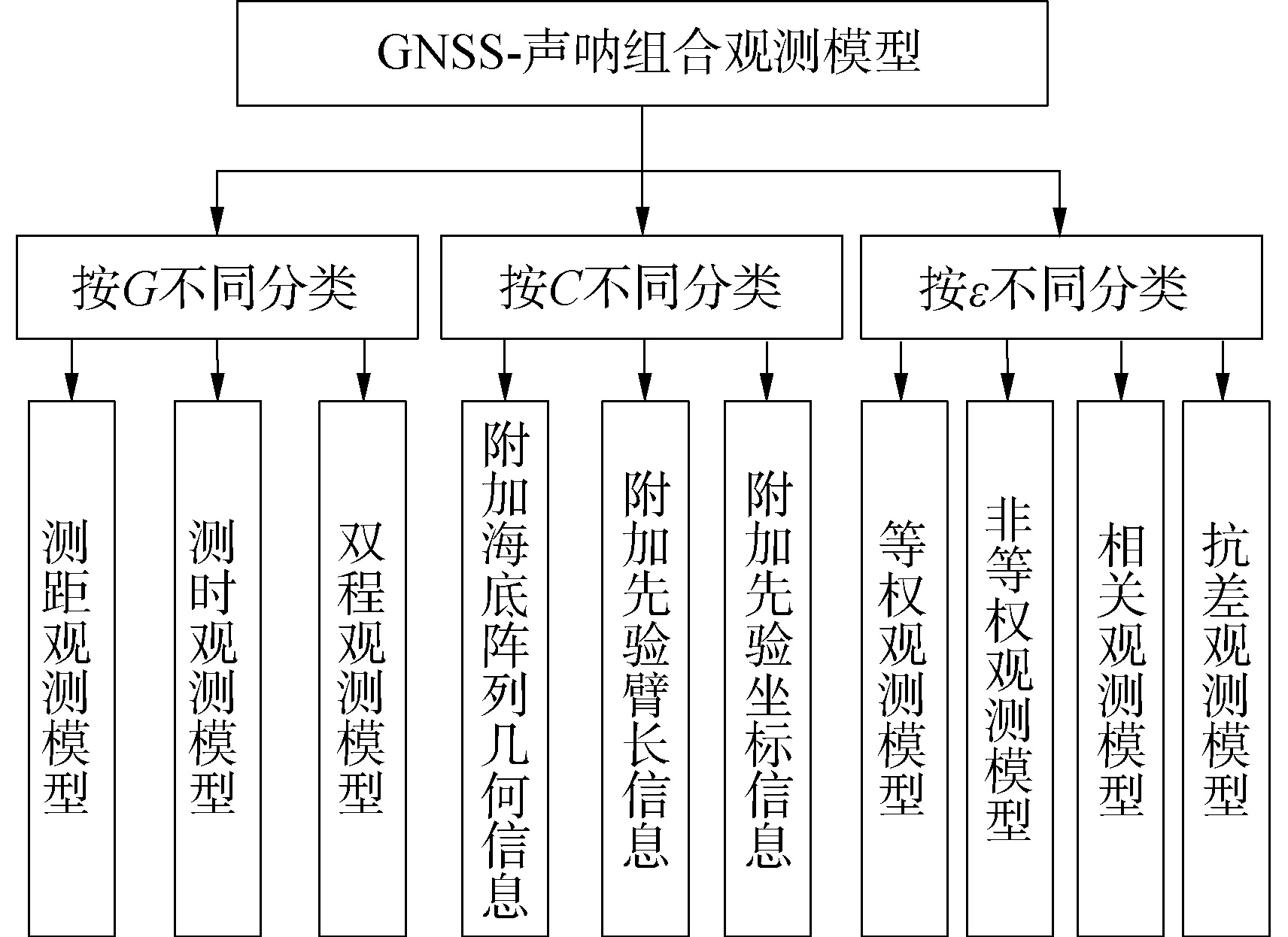
如图 2所示，GNSS-声呐观测模型可按函数模型(G)不同、附加约束条件(C)不同、随机模型(ε)不同予以分类，从而形成庞大的模型体系。按照更为细致的分类依据，上述模型分类体系可以进一步细分，例如，非等权观测模型中可进一步划分为先验非等权随机模型(包括声线入射角模型、声信号强度模型等)、后验随机模型(包括实时随机模型、方差分量估计模型等)[25, 50]；声线跟踪定位模型又分为二维声线跟踪和三维声线跟踪定位模型[52-53]。限于篇幅，后文仅对其中几类重要观测模型进行论述。
图 2 GNSS-声呐观测模型分类体系Fig. 2 Category systems of GNSS-A observation model下载:
全尺寸图片
1) 按函数模型分类。
按函数模型分类可分为测距定位模型和测时定位模型。测距定位模型可表示为：
$$ G_1=\left\|\boldsymbol{x}-\left(\boldsymbol{y}+\boldsymbol{R} \boldsymbol{p}_{\mathrm{a}}\right)\right\|_2+H\left(\boldsymbol{p}_{\mathrm{c}}\right)+K\left(\boldsymbol{p}_\mathtt{τ}\right) $$ (2) 式中：R为平台姿态参数构成的旋转阵；H为声速场时空变化对测距观测L=c0×T的影响(c0为常声速；T为信号传播时间；L为观测值)；K为硬件延迟对测距观测的影响。
基于声速剖面或声速场反演的测时观测模型可表示为：
$$ G_{2-1}=G_{2-1}^0\left(\boldsymbol{x}, \boldsymbol{p}_{\mathrm{c}}, t\right)+K^{\prime}\left(\boldsymbol{p}_\mathtt{τ}\right) $$ (3) 式中：$ G_{2-1}^0\left(\boldsymbol{x}, \boldsymbol{p}_{\mathrm{c}}\right)=\int_{u_x}^{u_y\left(\boldsymbol{p}_{\mathrm{a}}\right)}(\cos \beta(u))^{-1} c^{-1}\left(\boldsymbol{p}_{\mathrm{c}}, u\right) \mathrm{d} u $，K′为硬件延迟对时间观测T的影响；pc为基于参考声速剖面c0(u)描述声速场的参数。待定点水平坐标隐含于声线水平传播距离函数中。该模型即为基于测时模型的声速场参数直接估计模型，简记为G2-1。
基于声速误差影响补偿的测时观测模型可表示为：
$$ G_{2-2}=G_{2-2}^0(\boldsymbol{x})+H^{\prime}\left(\boldsymbol{p}_{\mathrm{c}}^{\prime}\right)+K^{\prime}\left(\boldsymbol{p}_\mathtt{τ}\right) $$ (4) 式中：$G_{2-2}^0(\boldsymbol{x})=\int_{u_x}^{u_y\left(\boldsymbol p_{\mathrm{a}}\right)}(\cos \beta(u))^{-1} c_0^{-1}(u) \mathrm{d} u $，c0(u)为参考声速剖面；H′为声速时空变化(相对于参考声速剖面)对时间观测T的影响；K′为硬件延迟对时间观测的影响；p′c为声速场参数的函数，例如，声速时变引起的声呐天顶延迟。该模型即为基于测时模型的声速场参数间接估计模型，简记为G2-2。
对于主动应答式声呐观测，需要考虑换能器收发时刻位置，构建以下双程观测模型：
$$ G_3=G_{\mathrm{s}}+G_{\mathrm{r}} $$ (5) 式中Gs、Gr分别表示往程和返程测距或测时函数模型。相比之下，Gs、Gr均为单程观测模型，适用广播式声呐观测。当采用单程观测近似双程观测时，需要考虑信号往返程期间载体的运动。由于GNSS-声呐采用应答观测模式，下文均推荐采用双程观测模型，但为了简化讨论，不再对单程和双程观测予以区分。
2) 按约束条件分类。
为了改善海洋声速误差抵御能力，可以在海底布设局域网，利用该局域网相对稳定的阵列几何或海底互测距信息，均可构建海底阵列约束。以阵列几何约束为例，可构造约束条件：
$$ \boldsymbol{x}_{j+1}(t)-\boldsymbol{x}_j(t)=\mathrm{const} \quad j=1, 2, \cdots $$ (6) 由于此时海底区域网一般限于数公里以内，其内部形变一般在数年甚至数十年尺度可忽略。该约束条件亦可通过函数模型G(x+Δ)实现，其中Δ为海底局域网相对于参考阵列 x的整体平移参数。
GNSS-声呐观测臂长通常在事先量测基础上再实施臂长参数估计，特别是垂向方向臂长参数往往存在不适定性。为此，可构建以下臂长先验信息约束：
$$ 0=\boldsymbol{p}_{\mathrm{a}}-\boldsymbol{p}_{\mathrm{a}}^0+\boldsymbol{\varepsilon}_{\mathrm{a}} $$ (7) 式中：pa0为臂长先验值；εa为先验臂长不确定度。海底换能器信号延迟往往通过实验室标定，亦可构建类似先验约束。
此外，可将海面控制点视为先验信息，与海底控制网坐标实施联合估计，即：
$$ \mathbf{0}=\boldsymbol{y}-\boldsymbol{y}^0+\boldsymbol{\varepsilon}_y $$ (8) 式中：y0为海面测线坐标先验值；εy为先验坐标不确定度。该模型可利用海面测线解的方差协方差，利于发现海面定位异常点。当海底控制网存在历史先验坐标信息或压力计观测时，可构造类似先验约束：
$$ \mathbf{0}=\boldsymbol{x}-\boldsymbol{x}^0+\boldsymbol{\varepsilon}_x $$ (9) 式中：x0为海底坐标先验值；εx为先验坐标不确定度。
3) 按随机模型分类。
最简单的随机模型即等权观测模型，即ΣεL=Iσ02，其中σ02为单位权方差。然而，研究表明，声呐观测权与高度角有关，此时可采用非等权观测模型，即：
$$ \boldsymbol{\varSigma}_{\varepsilon_{\mathrm{L}}}=\operatorname{diag}^{-1}\left(w_1, w_2, \cdots \cdots, w_n\right) {\sigma}_0^2 $$ (10) 式中：wi为第i个观测值的权，常用权函数为观测高度角或天顶角z的函数，即w=f(z)。亦有文献采用相对观测距离相关权函数[54]。
当仅考虑声呐观测随机误差时，理论上声呐观测值为独立观测。然而，当考虑观测模型存在未模型化时变系统误差时，需要考虑观测间的相关性，即采用相关观测模型：
$$ \boldsymbol{\varSigma}_{\varepsilon_{\mathrm{L}}}=\boldsymbol{P}^{-1} {\sigma}_0^2 $$ (11) 式中：P的非对角线元素$ q_{i, j}=\sqrt{w_i w_j} \exp \left(-\frac{\left|t_i-t_j\right|}{\mu_t}\right)$，ti、tj分别为第i和j次观测时间；μt为误差的特征相关时间[18, 55]。
任何观测都难免存在粗差观测，为此需从污染分布出发实施粗差探测或抗差估计，即采用以下抗差估计随机模型：
$$ \boldsymbol{\varSigma}_{\varepsilon_{\mathrm{L}}}=\overline{\boldsymbol{P}}^{-1} \boldsymbol{\sigma}_0^2 $$ (12) 在实际数据处理中，可对函数模型施加某种线性或非线性变化，例如差分变换消参、对数变换化积为和等，以达到简化观测模型的目的。值得注意的是，无论是差分变换还是对数变换，均需考虑变换后的观测值的随机模型变换问题[57-58]。需要指出，采用哪种观测模型，不仅取决于现实需要，也受限于系统观测条件，且很难一一枚举。
2. 测距观测模型
海洋信道是时变、空变、频变的复杂系统，声波在海水介质中传播中产生折射，导致声线弯曲和传播速度改变。声速随海水温度、盐度和压力变化而变化，具有明显的垂向梯度变化特征。当给定参考声速值，如平均/加权平均/调和平均声速值，声学测时数据可转换为距离信息，进而构建测距定位模型。由于测距定位模型采用与深度无关的常声速，忽略了海洋声速场的垂向梯度，难免引入较大的模型误差。即使如此，由于该模型继承了传统大地测量以及空间大地测量理论优势，本文认为该模型应作为大地测量学者的重要研究方向。需要注意的是，由于声波传播速度相对光速很慢，收发时刻载体位置差不容忽视，即需要采用双程观测模型[59-61]；同时，需要充分利用先验海洋环境观测信息，施加因声速场垂向梯度导致的声速误差改正，即：
$$ \boldsymbol{L}=\sum\limits_{J \in\{s, r\}}\left[\left\|\boldsymbol{x}-\boldsymbol{X}_J\right\|_2+\boldsymbol{H}_J\left(\boldsymbol{p}_{{\rm c}, J}\right)+\boldsymbol{\varepsilon}_J\right] $$ (13) 式中：J∈{s, r}为收发时刻相关参量索引；XJ=yJ+ RJpa为海面换能器坐标。在信号往返期间，声速场参数变化可忽略不计，亦属不可观参数，可估计期间平均意义的声速场参数。此外，硬件延迟可以认为在收发时刻是相同的。此时，上述观测模型可化为：
$$ \boldsymbol{L}=\sum\limits_{J \in\{s, r\}}\left\|\boldsymbol{x}-\left(\boldsymbol{y}_J+\boldsymbol{R}_J \boldsymbol{p}_{\mathrm{a}}\right)\right\|_2+2 \overline{\boldsymbol{H}}\left(\boldsymbol{p}_{\mathrm{c}}\right)+\boldsymbol{\varepsilon}_{\mathrm{L}}^{\prime} $$ (14) 式中：ε′L为信号往返程观测误差累积；H为当忽略声线双程差异时声速误差对测距的影响函数，表示为：
$$ \overline{\boldsymbol{H}}\left(\boldsymbol{p}_{\mathrm{c}}\right)=\overline{\boldsymbol{H}}_{\mathrm{u}}\left(k_{\mathrm{u}}\right)+\overline{\boldsymbol{H}}_{\mathrm{t}}\left(k_{\mathrm{t}}\right)+\overline{\boldsymbol{H}}_{\mathrm{e}}\left(k_{\mathrm{e}}\right)+\overline{\boldsymbol{H}}_n\left(k_n\right) $$ (15) 式中：ku、ke、kn分别为声速场的垂向梯度以及东向和北向的水平梯度，它们都是深度、水平坐标和时间的函数；kt为声速场的时变梯度。
若不强调待估参数的物理意义，可将H(pc)作为整体进行参数化。这种整体参数化的实质是利用系统误差在时间域内的延续性，即将其在时间域构建时变函数模型，例如[62]：
$$ \begin{gathered} \bar{H}\left(t_i\right)=b_0+b_1 t_i+b_2 \cos \left(2 \pi f t_i\right)+ \\ b_3 \sin \left(2 \pi f t_i\right) \end{gathered} $$ (16) 式中：ti为观测时刻；f为系统误差的周期项频率；pc= [b0 b1 b2 b3]为待估模型系数。值得注意的是，当存在不连续观测时段时，需要实施分时段参数化估计，否则将不满足系统误差的延续性理论假设。需要指出，这种延续性亦可采用随机模型描述，例如自回归模型[63]。
事实上，系统误差拟合模型(16)可视为有效声速拟合。有效声速不仅与时间有关，也与高度角有关，且当考虑声速场水平梯度时，有效声速还与方位角有关，即H=f(t, α, z)为时间t、方位角α和天顶角z的函数。为此，需要将上述单时间变量函数(16)予以扩展。一种可行的扩展即GNSS定位模型采用的天顶延迟估计模型，即：
$$ \begin{gathered} \bar{H}(t, z, \alpha)=m_{\mathrm{u}}(z) D_{\mathrm{u}}(t)+m_{\mathrm{e}}(z, \alpha) D_{\mathrm{e}}(t)+ \\ m_n(z, \alpha) D_n(t) \end{gathered} $$ (17) 式中：
$$ \left\{\begin{array}{l} m_{\mathrm{u}}(z)=(\cos z)^{-1} \\ m_{\mathrm{e}}(z, \alpha)=(\cos z)^{-1} \tan z \sin \alpha \\ m_{\mathrm{n}}(z, \alpha)=(\cos z)^{-1} \tan z \cos \alpha \end{array}\right. $$ (18) 为映射函数，即将天顶延迟映射为视线方向声呐延迟，其中，Du(t) 表示未对距离观测值施加声速场垂向梯度影响改正时的天顶声呐延迟(施加声速场垂向梯度改正后，与施加前数量级不同，但随时间变化应具有一定的相似性)；De(t)、Dn(t)为声速场e方向和n方向声速结构水平异质性引起的声呐信号延迟在垂向上的投影。
相比于模型(16)，模型(17)的实质是将H的时变性分解为观测几何变化部分和声速场参数变化部分，其中观测几何变化部分作为确定性信息纳入观测信息矩阵，而仅对声速场变化部分DK(t)予以参数化估计，其中下标K∈{n, e, u}。DK(t)的参数化问题，亦可借鉴模型(16)，即采用线性项加周期函数，也可采用B样条函数[64]，甚至直接采用GNSS天顶延迟常用的随机游走模型或分段线性估计模型[65]。
海底基站通常布设在没有显著起伏的海底区域，因而在同一个局域海底观测网内，各海底基准站具有相近的水深，因此，当缺少海洋垂向梯度变化模式约束时，难以对声速场垂向梯度参数实施参数估计。若要对式(15)中的Hu项实参数化估计，则需要引入关于声速在垂向的先验知识或信息，例如Chen采用的双线性声速剖面模型[41]，以及Xue采用指数衰减温度剖面模型以及经验声速公式构建的经验声速剖面模型。此外，也可利用海洋环境观测对Hu实加改正，但这需要更高时空分辨率的海洋环境观测[66]。
3. 测时观测模型
当存在先验声速场模型时，采用声线跟踪定位模型，即采用测时函数模型是一种先验声速场信息最有效的利用途径，其弊端主要源于复杂的声线跟踪计算成本。如引言所述，可将这类定位模型分为声速场参数直接估计模型和声速场参数间接估计模型，前者更适用于利用大地测量观测开展海洋环境科学研究，而后者更适用于大地测量定位应用，且前者可作为后者的理论基础。
3.1 声速场参数直接估计模型
略去臂长参数、硬件延迟参数，不考虑声速场水平梯度，对于给定的观测历元t，可将声信号测时观测模型表示为：
$$ T(t)=\underbrace{\int_{u_x}^{u_y}\left(\cos z^{\prime}(u)\right)^{-1} c^{-1}\left(\boldsymbol{p}_{\mathrm{c}}, u, t\right) \mathrm{d} u}_{G_{2-1}^0\left(\boldsymbol{x}, \boldsymbol{p}_{\mathrm{c}}\right)}+\varepsilon_{\mathrm{T}}(t) $$ (19) 式中：T(t)为声信号传播时间观测值；c(pc, u, t)为观测时刻的声速剖面；z′(u)为声线入射角，有别于后文中观测天顶角z。在实际中，c(pc, u, t)难以实时获取，而通常只能在参考声速剖面c0(u) 的基础上附加时变项[67]，即附加待估声速场时变参数 pc。
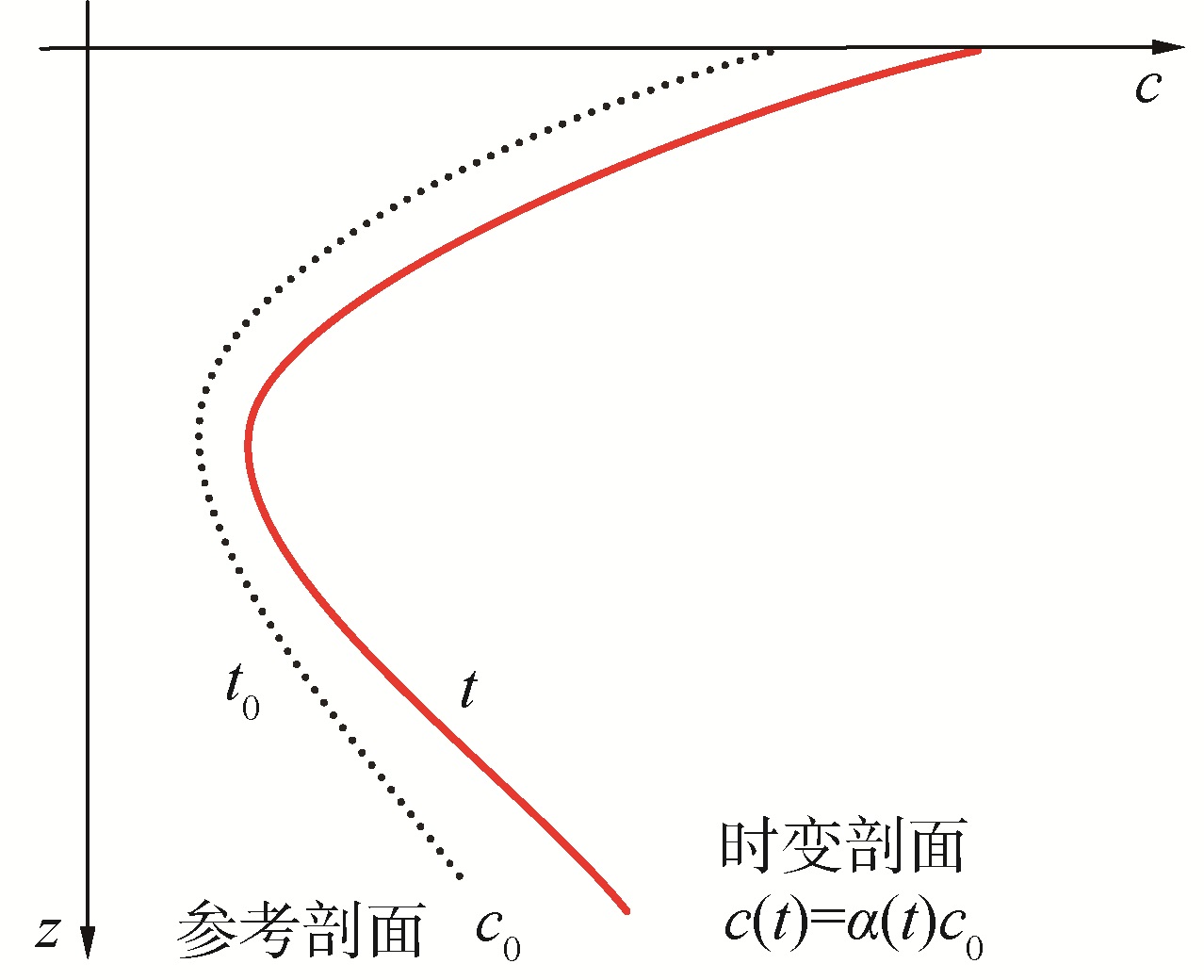
如图 3所示，当仅考虑声速场时变影响时，设参考剖面的测量时间为t0，记c0(u)=c(u, t0)，则参考剖面的时间代表性误差补偿可采用加性改正模型[37-38]：
$$ c\left(u, \boldsymbol{p}_{\mathrm{c}}, t\right)=c_0(u)+\delta_{\mathrm{t}}\left(t, \boldsymbol{p}_{\mathrm{c}}\right) $$ (20) 
图 3 参考声速剖面补偿示意Fig. 3 Reference sound velocity profile compensation下载:
全尺寸图片
式中pc为加性模型待估参数，或采用乘性改正模型[39]：
$$ c\left(u, \boldsymbol{p}_{\mathrm{c}}^{\prime}, t\right)=\varGamma_{\mathrm{t}}\left(t, \boldsymbol{p}_{\mathrm{c}}^{\prime}\right) c_0(u) $$ (21) 式中：$\varGamma_{\mathrm{t}}\left(t, \boldsymbol{p}_{\mathrm{c}}^{\prime}\right) $为随时间变化比例因子，用于刻画参考声速剖面随时间的变化；p′c为待估模型参数，通常采用多项式或B样条描述。
需要指出，$ \varGamma_{\mathrm{t}}\left(t, \boldsymbol{p}_{\mathrm{c}}^{\prime}\right) 、\delta_{\mathrm{t}}\left(t, \boldsymbol{p}_{\mathrm{c}}\right)$可视为参考声速剖面的补偿因子。加性补偿模型和乘性补偿模型存在转换关系：$\varGamma_{\mathrm{t}}\left(t, \boldsymbol{p}^{\prime}{ }_{\mathrm{c}}\right) c_0(u)=c_0(u)+[{\varGamma}_{\mathrm{t}}\left(t, \boldsymbol{p}^{\prime}{ }_{\mathrm{c}}\right)-1] c_0(u)=c_0(u)+\delta_{\mathrm{t}}\left(t, \boldsymbol{p}_{\mathrm{c}}\right) $，即：
$$ \delta_{\mathrm{t}}\left(t, \boldsymbol{p}_{\mathrm{c}}\right)=\left[\varGamma_{\mathrm{t}}\left(t, \boldsymbol{p}_{\mathrm{c}}^{\prime}\right)-1\right] c_0(u) $$ (22) 以加性改正模型为例，可选用二阶或三阶多项式模型，在一定的时间窗口内对声速剖面误差进行补偿，如二阶多项式补偿模型[37-38]：
$$ \delta_{\mathrm{t}}\left(t, \boldsymbol{p}_{\mathrm{c}}\right)=a_0+a_1\left(t-t_0\right)+a_2\left(t-t_0\right)^2 $$ (23) 式中：t0为参考时间；pc= [a0 a1 a2]T为待估模型系数。此外，B样条模型相对于多项式模型具备更强的柔性，具有很强的时变误差变化刻画能力[68-69]。因此，在进行声速估计时，可使用多项式模型在长时间窗提取偏差和趋势变化，使用B样条模型在短时间窗刻画声速场的不规则变化。
对于给定的声速场时变参数初值pc0，对非线性观测模型(19)进行线性化，可得：
$$ \mathrm{d} T=\left[\begin{array}{ll} \boldsymbol{a}(t) & \boldsymbol{b}(t) \end{array}\right]\left[\begin{array}{l} \mathrm{d} \boldsymbol{x} \\ \mathrm{d} \boldsymbol{p}_{\mathrm{c}} \end{array}\right]+\varepsilon_{\mathrm{T}}(t) $$ (24) 式中：$\mathrm{d} T=T(t)-G_2\left(\boldsymbol{x}^0, \boldsymbol{p}_{\mathrm{c}}^0\right) $为线性化模型观测值；
$$ \left\{\begin{array}{l} \boldsymbol{a}(t):=\left.\frac{\partial G_{2-1}\left(\boldsymbol{x}, \boldsymbol{p}_{\mathrm{c}}, t\right)}{\partial \boldsymbol{x}}\right|_{\boldsymbol{x}^0, p_{\mathrm{c}}^0} \\ \boldsymbol{b}(t):=\left.\frac{\partial G_{2-1}\left(\boldsymbol{x}, \boldsymbol{p}_{\mathrm{c}}, t\right)}{\partial \boldsymbol{p}_{\mathrm{c}}}\right|_{\boldsymbol{x}^0, p_{\mathrm{c}}^0} \end{array}\right. $$ (25) 为线性化设计矩阵，a(t)易于解析计算(声线在海底点处的切线方向余弦)，而 b(t)难以解析，可通过数值求偏导算法获得。基于线性化模型(24)，利用高斯-牛顿迭代法即获得观测模型(19)的非线性最小二乘估计。
顾及水下声速结构的水平异质性，进一步对海洋声速场水平梯度进行参数化，可建立更严密的声速场参数反演模型。本文推荐利用泰勒级数展开对声速场进行线性近似，即在很小的范围内，将声速场在时空原点(设于观测中间时刻和观测区域几何中心)处展开，忽略线性化残余项，则建立下述线性声速场模型，即：
$$ c(n, e, u, t)=c_0(u)+\underbrace{k_{\mathrm{t}}(t)}_{\delta_{\mathrm{t}}\left(t, \boldsymbol{p}_{\mathrm{c}}\right)} t+k_{\mathrm{n}}(t) n+k_{\mathrm{e}}(t) e $$ (26) 式中：kt(t)为声速场时间梯度，其与时间t的耦合项即为式(20)中的δt(t, pc)；kn(t)、ke(t)为声速场的水平梯度，是时间和深度的函数，其参数化表达式可抽象表示为：
$$ \left\{\begin{array}{l} k_{\mathrm{n}}(t)=\delta_{\mathrm{n}}\left(t, \boldsymbol{p}_{\mathrm{cn}}\right) \\ k_{\mathrm{e}}(t)=\delta_{\mathrm{e}}\left(t, \boldsymbol{p}_{\mathrm{ce}}\right) \end{array}\right. $$ (27) 类似地，结合声速场模型(26)和观测模型(19)，可将声速场模型参数与海底坐标参数进行联合反演。理论上，当考虑海洋水平梯度时，需要使用三维声线跟踪定位模型，但在实践中，由于海洋声速场水平梯度很小，二维声线和三维声线在水平方向的差异很小，亦可考虑采用二维声线跟踪近似[70]。
受限于目前海洋大地测量观测条件，上述声速场梯度是整个垂向水体平均意义下的概念。然而，海洋声速场存在显著的分层变化特征，随着深度的增大，其变化迅速衰减。因此，如何利用更多的声速场垂向甚至水平线性或非线性变化特征，实施声速场结构层析是未来海底大地测量的重要应用方向，该研究方向的难题主要还是声速场小尺度(几百米甚至数十米)变化模式的模型化刻画问题。
3.2 声速场参数间接估计模型
1) 乘性声速场补偿模型导出解。
日本学者很早就提出了采用乘性改正模型(21)对声速剖面进行补偿[37]。基于此，不难建立声速场参数直接补偿与间接补偿模型的关系：
$$ \begin{gathered} G_{2-1}\left(\boldsymbol{x}, \boldsymbol{p}_{\mathrm{c}}, t\right)=\int_{u_x}^{u_y}\left(\cos z^{\prime}(u)\right)^{-1} c^{-1}(u, t) \mathrm{d} u=\\ \int_{u_x}^{u_y}\left(\cos z^{\prime}(u)\right)^{-1} \varGamma^{-1}\left(t, \boldsymbol{p}_{\mathrm{c}}^{\prime}\right) c_0^{-1}(u) \mathrm{d} u= \\ \varGamma^{-1}\left(t, \boldsymbol{p}_{\mathrm{c}}^{\prime}\right) \int_{u_x}^{u_y}\left(\cos z^{\prime}(u)\right)^{-1} c_0^{-1}(u) \mathrm{d} u= \\ \varGamma^{-1}\left(t, \boldsymbol{p}_{\mathrm{c}}^{\prime}\right) G_{2-2}^0(\boldsymbol{x}) \end{gathered} $$ (28) 式中G2-20(x)为基于参考声速剖面计算得到的参考传播时间。对于给定的观测时间T，则可建立以下观测模型：
$$ T(t)=\varGamma^{-1}\left(t, \boldsymbol{p}_{\mathrm{c}}^{\prime}\right) G_{2-2}^0(\boldsymbol{x})+\varepsilon(t) $$ (29) 将误差项移到左侧，两边取对数可得：
$$ \underbrace{\ln T(t)}_{L^{\prime}(t)}=\underbrace{\ln G_{2-2}^0(\boldsymbol{x})}_{{G^{\prime}}_{2-2}[\boldsymbol{x}]}+\ln \varGamma^{-1}\left(t, \boldsymbol{p}_{\mathrm{c}}^{\prime}\right)+\varepsilon^{\prime}(t) $$ (30) 其中：
$$ \varepsilon^{\prime}(t)=-\ln \left(1-\frac{\varepsilon(t)}{T(t)}\right) \approx \frac{\varepsilon(t)}{T(t)} $$ (31) 显然，当假设测时精度与高度角无关时，即信号传播时间越长，则ε′(t)越小，即变换后的观测值ln T(t)的精度越高[18]，这与传统定位观测模型的误差性质正好相反[25]，在观测定权时需要予以考虑。
当采用指数模型描述声速剖面校正系数，设$ \varGamma^{-1}\left(t, \boldsymbol{p}_{\mathrm{c}}^{\prime}\right)=\mathrm{e}^{\gamma_0\left(t, \boldsymbol p_{\mathrm{ct}}^{\prime\prime}\right)}$，则可建立以下观测模型：
$$ L^{\prime}=G_{2-2}^{\prime}(\boldsymbol{x})+\gamma_0\left(t, \boldsymbol{p}_{\mathrm{ct}}^{\prime \prime}\right)+\varepsilon^{\prime}(t) $$ (32) 式中：$\gamma_0\left(t, \boldsymbol{p}_{\mathrm{ct}}^{\prime \prime}\right) $为声速场时变对观测值L′的影响。
进一步顾及声速场水平梯度影响，则可实现声速场时变和水平梯度的综合影响建模[18]：
$$ \gamma(t)=\gamma_0\left(t, \boldsymbol{p}_{\mathrm{ct}}^{\prime \prime}\right)+\gamma_1\left(t, \boldsymbol{p}_{\mathrm{ne}}^{\prime \prime}\right) \cdot \boldsymbol{X}^{\prime} $$ (33) 式中：X′表示海面换能器位置与海面图形中心位置的差值；$\gamma_0\left(t, \boldsymbol{p}_{\mathrm{ct}}^{\prime \prime}\right) $为声速场时变相关补偿因子，通常采用B样条拟合；$\gamma_1\left(t, \boldsymbol{p}_{\mathrm{ne}}^{\prime \prime}\right) $为声速空间变化相关补偿因子，通常采用B样条拟合。
需要指出，函数模型G均为基本观测模型，上述观测模型对基本观测模型进行了指数变换，导致变换后的模型具有一些新的统计性质。需要指出，差分变换是另一种模型变换[33, 71-72]，但因其变换为线性变化，当考虑差分观测相关性时，理论上差分观测模型与非差观测模型具有等价性[58]。然而，对于非线性模型变换，因其可能破坏观测误差的分布特征，例如，零均值随机量通过非线性变换可能不再具有零均值随机量[73-74]。因此，观测模型(30)的严密无偏最大似然估计仍有待研究。因此，本文建议尽量避免对观测模型进行非线性变换，而采用加性声速场补偿模型导出声速场参数间接估计解决方案。
2) 加性声速场补偿模型导出解。
声信号传播时间由沿射线路径上的声速剖面决定。由于声速场水平梯度非常小，沿射线路径上的声速可以近似为沿视线方向的声速。
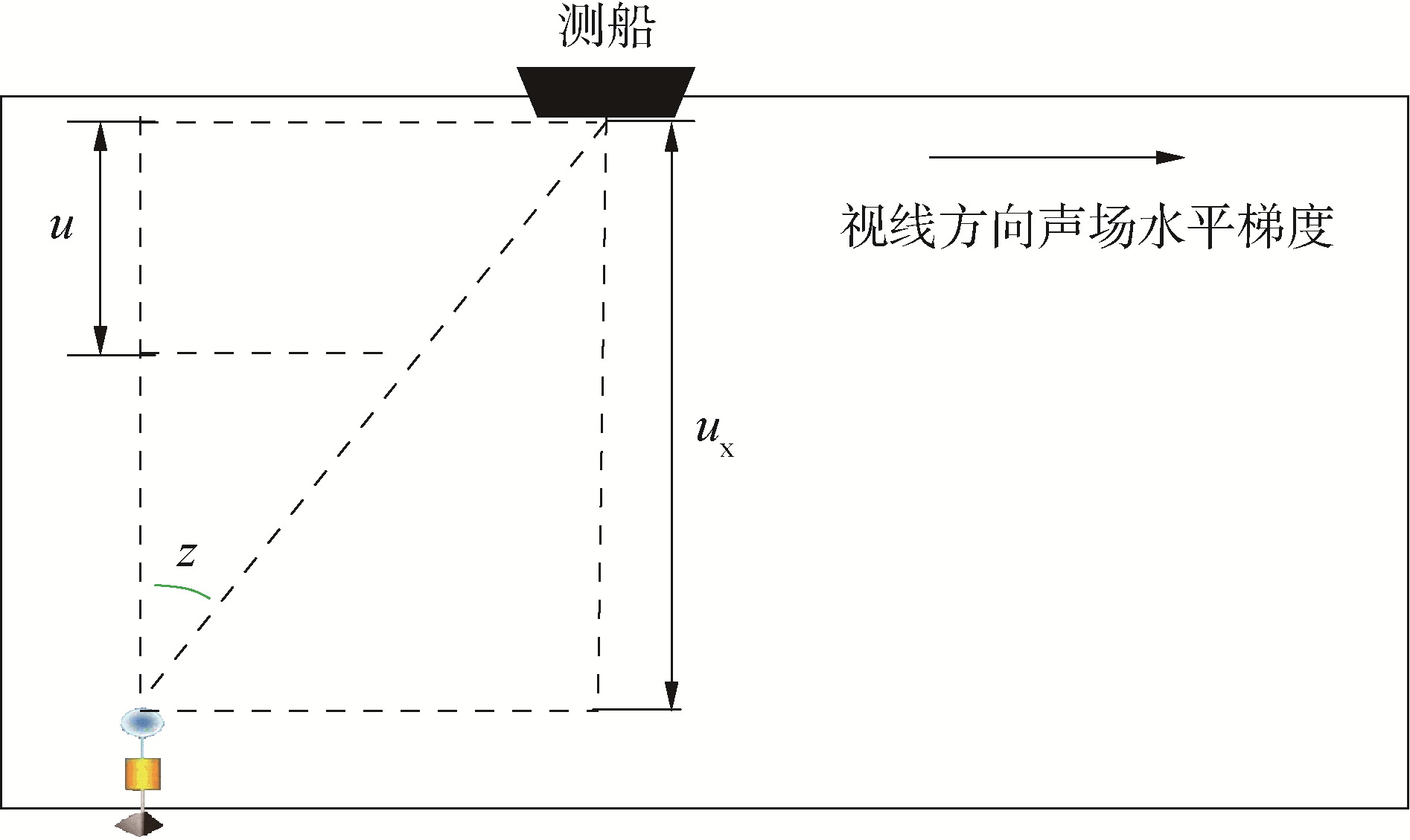
如图 4所示，设参考声速剖面位于海底控制点正上方，结合声速场的线性近似模型(26)，视线方向(line of sight, LOS)的声速剖面可表示为：
$$ \begin{gathered} c(\operatorname{LOS}, u)=c_0(u)+t k_{\mathrm{t}}(t)+ \\ \left(u_{\mathrm{X}}-u\right) \tan z k_{\mathrm{LOS}} \end{gathered} $$ (34) 
图 4 视线方向声速剖面示意Fig. 4 Schematic diagram of the velocity profile of the line of sight下载:
全尺寸图片
式中：u为视线上点的深度；kLOS=cos αkn(t)+sin αke(t) 为视线方向的声速水平梯度。结合线性化近似公式(x+dx)-1=x-1-x-2dx，信号传播时间函数可近似为：
$$ \begin{gathered} G_{2-1}\left(\boldsymbol{x}, \boldsymbol{p}_{\mathrm{c}}, t\right)=\int_{\mathrm{LOS}} c^{-1}(\operatorname{LOS}, u) \mathrm{d} s \approx \\ G_{2-2}^0(\boldsymbol{x})-D_{\mathrm{t}}(t)- \\ \tan z\left(\cos \alpha D_{\mathrm{n}}(t)+\sin \alpha D_{\mathrm{e}}(t)\right) \end{gathered} $$ (35) 式中：G2-20(x)为参考信号传播时间；
$$ \left\{\begin{array}{l} D_{\mathrm{t}}(t)=t k_{\mathrm{t}}(t) \int_{u_{\mathrm{X}}}^{u_{\mathrm{y}}}(\cos \beta(u))^{-1} c_0^{-2}(u) \mathrm{d} u \\ D_{\mathrm{n}}(t)=k_{\mathrm{n}}(t) \int_{u_{\mathrm{X}}}^{u_{\mathrm{y}}}(\cos \beta(u))^{-1} c_0^{-2}(u)\left(u_{\mathrm{X}}-u\right) \mathrm{d} u \\ D_{\mathrm{e}}(t)=k_{\mathrm{e}}(t) \int_{u_{\mathrm{X}}}^{u_{\mathrm{y}}}(\cos \beta(u))^{-1} c_0^{-2}(u)\left(u_{\mathrm{X}}-u\right) \mathrm{d} u \end{array}\right. $$ (36) 为视线方向声呐延迟。
为视线方向的声呐信号延迟。由于视线方向信号延迟与观测天顶角有关，不利于参数化估计，可将视线方向误差量投影到垂向进行分析，可引入(cos z)-1作为投影因子将式(35)转化为：
$$ G_{2-1} \approx G_{2-2}-m_{\mathrm{t}} Z_{\mathrm{t}}(t)-m_{\mathrm{n}} Z_{\mathrm{n}}(t)-m_{\mathrm{e}} Z_{\mathrm{e}}(t) $$ (37) 其中：
$$ \left\{\begin{array}{l} m_{\mathrm{t}}=(\cos z)^{-1} \\ m_{\mathrm{n}}=(\cos z)^{-1} \tan z \cos \alpha \\ m_{\mathrm{e}}=(\cos z)^{-1} \tan z \sin \alpha \end{array}\right. $$ (38) 可称为声呐天顶延迟映射函数；
$$ \left\{\begin{array}{l} Z_{\mathrm{t}}(t)=k_{\mathrm{t}}(t) t \int_{u_{\mathrm{x}}}^{u_{\mathrm{y}}} \lambda^{-1}(u) c_0^{-2}(u) \mathrm{d} u \\ Z_{\mathrm{n}}(t)=k_{\mathrm{n}}(t) \int_{u_{\mathrm{x}}}^{u_{\mathrm{y}}} \lambda^{-1}(u) c_0^{-2}(u)\left(u_{\mathrm{X}}-u\right) \mathrm{d} u \\ Z_{\mathrm{e}}(t)=k_{\mathrm{e}}(t) \int_{u_{\mathrm{x}}}^{u_{\mathrm{y}}} \lambda^{-1}(u) c_0^{-2}(u)\left(u_{\mathrm{X}}-u\right) \mathrm{d} u \end{array}\right. $$ (39) 称为声呐天顶延迟[58, 75]，λ(u)=(cos z)-1cos β(u)≈1为声线弯曲度量。可见，在海底单点观测条件下，只能提取声速场一级水平梯度信息，即假设声速场水平梯度与深度无关。
4. 海底网解观测模型
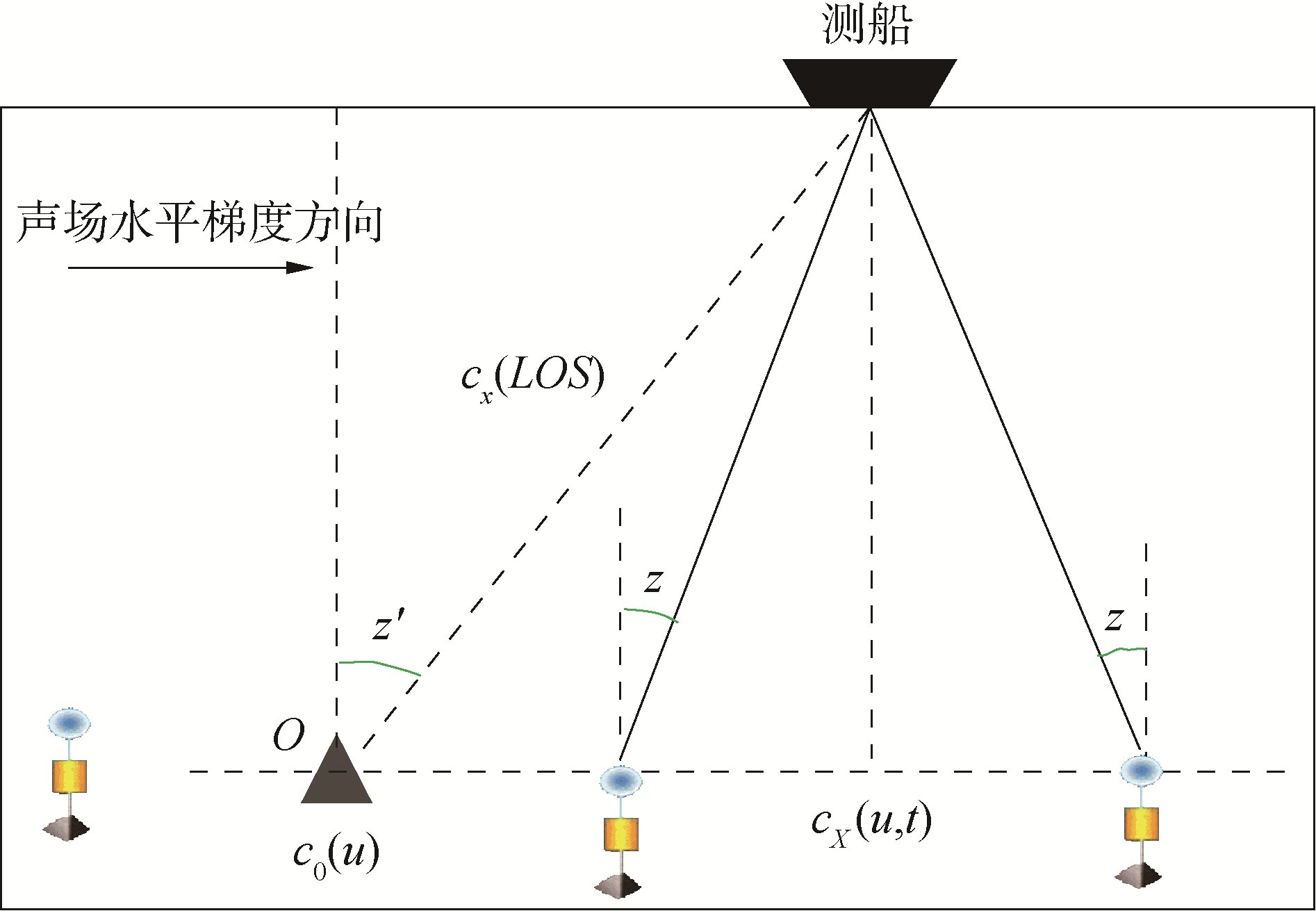
如图 5所示，当海底多个控制点构建局域网时，对于相同的观测天顶角z的2个海底基准站，由于声速场存在水平梯度的存在，会导致两者对同一测量船的测时存在一定差异，此为海底局域网感知海洋声速场梯度的基本原理。此时，无法在每个海底点处设定相同参考声速剖面，可将参考声速剖面设定在海底局域网的几何中心O(在实际现场测量中亦易于操作)，在测量船处的声速剖面为：
$$ \begin{aligned} c_{\mathrm{X}}^{\prime}(u, t)= & c_0(u)+k_{\mathrm{t}}(u, t) t+n_{\mathrm{x}} k_{\mathrm{n}}(u, t)+e_{\mathrm{x}} k_{\mathrm{e}}(u, t)= \\ & c_0(u)+k_{\mathrm{t}}(u, t) t+u_{\mathrm{X}} \tan z^{\prime} \cdot \\ & \left(\cos \alpha^{\prime} k_{\mathrm{n}}(u, t)+\sin \alpha^{\prime} k_{\mathrm{e}}(u, t)\right) \end{aligned} $$ (40) 
图 5 海底局域网感知深部声速场梯度示意Fig. 5 Deep-sea sound speed gradient identification by a local seafloor geodetic network下载:
全尺寸图片
式中：kt(u, t)、kn(u, t)、ke(u, t)表示声速场在深度u处的3个梯度分量；nX、eX为测量船的水平坐标；z′、α′分别为在原点o处观测海面船的天顶角和方位角。略去推导，对于海底点与海面船构成的视线方向剖面cx(LOS)可表示为[43]：
$$ \begin{gathered} c(\operatorname{LOS})=c^{\prime}{ }_{\mathrm{X}}(u, t)+u \tan z \cdot\\ \left(\cos \alpha k_{\mathrm{n}}(u, t)+\sin \alpha k_{\mathrm{e}}(u, t)\right) \end{gathered} $$ (41) 式中的第2项与式(34)中的最后一项几何意义相同，但参考剖面参考点不同，对应参数化形式略有不同。
基于视线方向声速剖面参数化模型(41)，类似于函数模型(37)的推导，可构建以下“五参数函数模型”：
$$ \begin{gathered} G_{2-1}\left(\boldsymbol{x}, \boldsymbol{p}_{\mathrm{c}}, t\right) \approx G_{2-2}^0(\boldsymbol{x})- \\ m_{\mathrm{t}} Z_{\mathrm{t}}(t)-m_{\mathrm{n}} Z_{\mathrm{n}}(t)-m_{\mathrm{e}} Z_{\mathrm{e}}(t)- \\ m_{\mathrm{n}^{\prime}} Z_{\mathrm{n}^{\prime}}(t)-m_{\mathrm{e}^{\prime}} Z_{\mathrm{e}^{\prime}}(t) \end{gathered} $$ (42) 其中：
$$ \left\{\begin{array}{l} m_{\mathrm{t}}=(\cos z)^{-1} \\ m_{\mathrm{n}}=(\cos z)^{-1} \tan z \cos \alpha \\ m_{\mathrm{e}}=(\cos z)^{-1} \tan z \sin \alpha \\ m_{\mathrm{n}^{\prime}}=(\cos z)^{-1} \tan z^{\prime} \cos \alpha^{\prime} \\ m_{\mathrm{e}^{\prime}}=(\cos z)^{-1} \tan z^{\prime} \sin \alpha^{\prime} \end{array}\right. $$ (43) 可称为声呐天顶延迟映射函数；
$$ \left\{\begin{array}{l} Z_{\mathrm{t}}(t)=\int_{u_{\mathrm{x}}}^{u_{\mathrm{y}}} \lambda^{-1}(u) c_0^{-2}(u) t k_{\mathrm{t}}(u, t) \mathrm{d} u \\ Z_{\mathrm{n}}(t)=\int_{u_{\mathrm{x}}}^{u_{\mathrm{y}}} \lambda^{-1}(u) c_0^{-2}(u) k_{\mathrm{n}}(u, t) u \mathrm{~d} u \\ Z_{\mathrm{e}}(t)=\int_{u_{\mathrm{x}}}^{u_{\mathrm{y}}} \lambda^{-1}(u) c_0^{-2}(u) k_{\mathrm{e}}(u, t) u \mathrm{~d} u \\ Z_{\mathrm{n}^{\prime}}(t)=\int_{u_{\mathrm{x}}}^{u_{\mathrm{y}}} \lambda^{-1}(u) c_0^{-2}(u) k_{\mathrm{n}}(u, t) u_{\mathrm{X}} \mathrm{d} u \\ Z_{\mathrm{e}^{\prime}}(t)=\int_{u_{\mathrm{x}}}^{u_{\mathrm{x}}} \lambda^{-1}(u) c_0^2(u) k_{\mathrm{e}}(u, t) u_{\mathrm{x}} \mathrm{d} u \end{array}\right. $$ (44) 称为声呐天顶延迟。
此时需要注意的是，当假设声速梯度与深度无关时，则可将上述后面4项合并为2项，但该退化形式显然是信息损失过程。Honsho等[14]构建了类似模型并称其为天底总延迟(NTD)估计模型，但该模型以慢度场为理论，映射函数采用了声线入射角变量。需要指出，海底位于水下，从海面俯视海底则成为“天底”有一定道理，但若从海底观测海面船，仍沿用传统地面观测卫星时天顶角、高度角等概念，则易于建立起与传统大地测量观测模型的联系。
因此，当海底存在多个海底点时，本文建议采用上述五参数天顶延迟模型。这也是海底采用阵列设计[27, 76]可以提高声速场时空误差抵御能力的重要原因所在，即采用海面走航和海底阵列的双层控制网设计[30, 33, 36, 77-78]，可以实现声速场双级水平梯度估计。此外，GARPOS软件亦考虑海底阵列解优势，采用GNSS-声呐观测模型：
$$ \begin{gathered} \gamma(t)=\gamma_0\left(t, \boldsymbol{p}_{\mathrm{ct}}^{\prime \prime}\right)+\gamma_1\left(t, \boldsymbol{p}_{\mathrm{ne}}^{\prime \prime}\right) \cdot \boldsymbol{X}^{\prime}+ \\ \gamma_2\left(t, \boldsymbol{p}_{\mathrm{n}^{\prime} \mathrm{e}^{\prime}}^{\prime \prime}\right) \cdot \boldsymbol{P}^{\prime} \end{gathered} $$ (45) 式中：X表示海面换能器位置与海面图形中心位置的差值；P表示海底应答器位置与海底多应答器构型中心位置的差值。相比于式(33)，$ \gamma_2\left(t, \boldsymbol{p}_{\mathrm{n}^{\prime} \mathrm{e}^{\prime}}^{\prime \prime}\right)$是在海底局域网观测条件下引入的二级声速空间变化补偿因子，亦可使用时间B样条模型实施参数估计。
需要强调的是，上述海底局域网网解模型(42)和(45)仅考虑单期观测，当存在海底基线观测或多期观测时，据此可发展出丰富的海底阵列约束解，进一步控制海洋环境误差影响，提高垂向定位精度。
5. 结束语
声速时空变化是制约水下高精度定位精度的重要因素之一，声速误差处理也就成为研究GNSS-声呐观测技术及其定位模型发展历程的一条重要线索。优化设计海面-海底控制网构型、反演声速场时空变化和参数化补偿声速时空变化对观测的影响，是控制声速误差对定位影响的3种途径。
1) 控制网的对称设计是控制系统误差的有效观测图形设计，且海底局域网阵列因具有类似共模环境误差而可提升海洋环境参数估计精度，同时海底局域网几何构型约束可进一步提高海底定位精度。从而构成高精度海底控制网定位的观测基础。未来，有望通过海面多载体无人观测系统，实现更高效、更高精度、更高时效性的海底大地测量观测。
2) 当海底控制网点位于相近深度时，不附加声速场时空变化的垂向结构信息，势必导致声速场层析模型存在不适定问题，此时，可在海底单点观测条件下采用一级声速梯度估计，亦可在海底局域网阵列观测条件下采用双级声速梯度估计。因此，未来引入更多的海洋声速场垂向变化模式结构信息，是实现GNSS-声呐观测层析声速场参数的关键所在。
3) 大地测量观测更关心声速场时空变化对观测值的影响，及其对水下定位影响，因此，声速场参数间接估计模型更为适用大地测量定位问题，而这些声速场相关参数与声速场参数的转换问题，也是有待深入研究，例如声呐天顶总延迟，与声速场时空变化梯度参数的转换关系问题。
4) 相比于日本的声速场误差乘性补偿模型，本文推荐采用声速场误差加性误差补偿模型及其导出的声速场参数间接估计模型。
基于参考声速剖面可构建高精度定位模型，且更符合传统大地测量习惯，建议作为重点研究方向，以顺应未来免现场声速剖面观测的无人GNSS-声呐系统发展趋势。然而，该模型的不足是因缺少关于声速场垂向梯度信息，从而影响定位精度，且导致声速场参数反演结果解释困难，因此，建议：首先利用GNSS-声呐观测反演声速场垂向梯度结构，然后反演声速场时变和空变特征参数；或利用海洋环境产品施加先验改正，但后续研究需要关注不同产品的时空分辨率及先验改正精度问题。
-
图 1 GNSS-声呐观测构型
Fig. 1 GNSS-a positioning configuration
下载:
全尺寸图片
图 2 GNSS-声呐观测模型分类体系
Fig. 2 Category systems of GNSS-A observation model
下载:
全尺寸图片
图 3 参考声速剖面补偿示意
Fig. 3 Reference sound velocity profile compensation
下载:
全尺寸图片
图 4 视线方向声速剖面示意
Fig. 4 Schematic diagram of the velocity profile of the line of sight
下载:
全尺寸图片
图 5 海底局域网感知深部声速场梯度示意
Fig. 5 Deep-sea sound speed gradient identification by a local seafloor geodetic network
下载:
全尺寸图片
-
[1] ALTAMIMI Z, BOUCHER C, WILLIS P. Terrestrial reference frame requirements within GGOS perspective[J]. Journal of geodynamics, 2005, 40(4-5): 363-374. doi: 10.1016/j.jog.2005.06.002 [2] BÜRGMANN R, CHADWELL D. Seafloor geodesy[J]. Annual review of earth and planetary sciences, 2014, 42: 509-534. doi: 10.1146/annurev-earth-060313-054953 [3] 吴立新, 陈朝晖, 林霄沛, 等. "透明海洋"立体观测网构建[J]. 科学通报, 2020, 65(25): 2654-2661. https://www.cnki.com.cn/Article/CJFDTOTAL-KXTB202025002.htm WU Lixin, CHEN Zhaohui, LIN Xiaopei, et al. Building the integrated observational network of "Transparent Ocean"[J]. Chinese science bulletin, 2020, 65(25): 2654-2661. https://www.cnki.com.cn/Article/CJFDTOTAL-KXTB202025002.htm [4] 吴立新, 荆钊, 陈显尧, 等. 我国海洋科学发展现状与未来展望[J]. 地学前缘, 2022, 29(5): 1-12. https://www.cnki.com.cn/Article/CJFDTOTAL-DXQY202205003.htm WU Lixin, JING Zhao, CHEN Xianyao, et al. Marine science in China: current status and future outlooks[J]. Earth science frontiers, 2022, 29(5): 1-12. https://www.cnki.com.cn/Article/CJFDTOTAL-DXQY202205003.htm [5] 杨元喜, 徐天河, 薛树强. 我国海洋大地测量基准与海洋导航技术研究进展与展望[J]. 测绘学报, 2017, 46(1): 1-8. https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201701002.htm YANG Yuanxi, XU Tianhe, XUE Shuqiang. Progresses and prospects in developing marine geodetic datum and marine navigation of China[J]. Acta geodaetica et cartographica sinica, 2017, 46(1): 1-8. https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201701002.htm [6] 杨元喜, 刘焱雄, 孙大军, 等. 海底大地基准网建设及其关键技术[J]. 中国科学: 地球科学, 2020, 50(7): 936-945. https://www.cnki.com.cn/Article/CJFDTOTAL-JDXK202007005.htm YANG Yuanxi, LIU Yanxiong, SUN Dajun, et al. Seafloor geodetic network establishment and key technologies[J]. Science China earth sciences, 2020, 5(7): 936-945. https://www.cnki.com.cn/Article/CJFDTOTAL-JDXK202007005.htm [7] NEWMAN A, BARTLOW N, SCHMIDT D, et al. Future directions in seafloor geodesy 2021 community workshop[C]//https://www.seafloorgeodesy.org/future-directions. 2021. [8] SPIESS F N, LOUGHRIDGE M S, MCGEHEE M S, et al. An acoustic transponder system[J]. Navigation, 1966, 13(2): 154-161. doi: 10.1002/j.2161-4296.1966.tb01818.x [9] SPIESS F N. Acoustic techniques for marine geodesy[J]. Marine geodesy, 1980, 4(1): 13-27. doi: 10.1080/15210608009379369 [10] SAKIC P, PIÉTÉ H, BALLU V, et al. No significant steady state surface creep along the North Anatolian Fault offshore Istanbul: results of 6 months of seafloor acoustic ranging[J]. Geophysical research letters, 2016, 43(13): 6817-6825. doi: 10.1002/2016GL069600 [11] QIN Xianping, YANG Yuanxi, SUN Bajiao. A robust method to estimate the coordinates of seafloor stations by direct-path ranging[J]. Marine geodesy, 2023, 46(1): 83-98. doi: 10.1080/01490419.2022.2113578 [12] SPIESS F N, CHADWELL C D, HILDEBRAND J A, et al. Precise GPS/Acoustic positioning of seafloor reference points for tectonic studies[J]. Physics of the earth and planetary interiors, 1998, 108(2): 101-112. doi: 10.1016/S0031-9201(98)00089-2 [13] YASUDA K, TADOKORO K, TANIGUCHI S, et al. Interplate locking condition derived from seafloor geodetic observation in the shallowest subduction segment at the Central Nankai Trough, Japan[J]. Geophysical research letters, 2017, 44(8): 3572-3579. doi: 10.1002/2017GL072918 [14] HONSHO C, KIDO M, TOMITA F, et al. Offshore postseismic deformation of the 2011 Tohoku earthquake revisited: application of an improved GPS-acoustic positioning method considering horizontal gradient of sound speed structure[J]. Journal of geophysical research: solid earth, 2019, 124(6): 5990-6009. doi: 10.1029/2018JB017135 [15] EVANS E L, MINSON S E, CHADWELL C D. Imaging the next Cascadia earthquake: optimal design for a seafloor GNSS-A network[J]. Geophysical journal international, 2022, 228(2): 944-957. [16] 杨元喜, 薛树强, 徐天河, 等. 海洋大地测量基准与水下导航[M]. 北京: 科学出版社. 2022. YANG Yuanxi, XUE Shuqiang, XU Tianhe, et al. Ocean geodetic datum and underwater navigation[M]. Chinese academy of sciences, Science press, 2022. [17] YOKOTA Y, ISHIKAWA T, WATANABE S I. Gradient field of undersea sound speed structure extracted from the GNSS-A oceanography: GNSS-A as a sensor for detecting sound speed gradient[J]. Marine geophysical research, 2019, 40(4): 493-504. doi: 10.1007/s11001-018-9362-7 [18] WATANABE S I, ISHIKAWA T, YOKOTA Y, et al. GARPOS: Analysis software for the GNSS-A seafloor positioning with simultaneous estimation of sound speed structure[J]. Frontiers in earth science, 2020, 8: 597532. doi: 10.3389/feart.2020.597532 [19] IINUMA T, KIDO M, OHTA Y, et al. GNSS-Acoustic observations of seafloor crustal deformation using a wave glider[J]. Frontiers in earth science, 2021, 9: 600946. doi: 10.3389/feart.2021.600946 [20] YOKOTA Y, KANEDA M, HASHIMOTO T, et al. Experimental verification of seafloor crustal deformation observations by UAV-based GNSS-A[J]. Scientific reports, 2023, 13(1): 4105. doi: 10.1038/s41598-023-31214-6 [21] KIDO M. Detecting horizontal gradient of sound speed in ocean[J]. Earth, planets and space, 2007, 59(8): e33-e36. doi: 10.1186/BF03352027 [22] KIDO M, OSADA Y, FUJIMOTO H. Temporal variation of sound speed in ocean: a comparison between GPS/acoustic and in situ measurements[J]. Earth, planets and space, 2008, 60(3): 229-234. doi: 10.1186/BF03352785 [23] 赵建虎, 梁文彪. 海底控制网测量和解算中的几个关键问题[J]. 测绘学报, 2019, 48(9): 1197-1202. https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201909014.htm ZHAO Jianhu, LIANG Wenbiao. Some key points of submarine control network measurement and calculation[J]. Acta geodaetica et cartographica sinica, 2019, 48(9): 1197-1202. https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB201909014.htm [24] SHAN Rui, LIU Huimin, ZHAO Shuang, et al. Investigation on vertical position and sound velocity variation for GNSS/Acoustic seafloor geodetic calibration based on moving survey data[J]. Remote sensing, 2022, 14(15): 3739. doi: 10.3390/rs14153739 [25] 王薪普, 薛树强, 曲国庆, 等. 水下定位声线扰动分析与分段指数权函数设计[J]. 测绘学报, 2021, 50(7): 982-989. https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB202107013.htm WANG Xinpu, XUE Shuqiang, QU Guoqing, et al. Disturbance analysis of underwater positioning acoustic ray and design of piecewise exponential weight function[J]. Acta geodaetica et cartographica sinica, 2021, 50(7): 982-989. https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB202107013.htm [26] 陈冠旭, 刘杨, 李梦昊, 等. GNSS-声学海底定位的声速误差处理方法综述[J]. 武汉大学学报(信息科学版), 2022, 47(9): 1349-1363. https://www.cnki.com.cn/Article/CJFDTOTAL-WHCH202209001.htm CHEN Guanxu, LIU Yang, LI Menghao, et al. Review on the processing methods of sound speed errors in GNSS-acoustic seafloor positioning[J]. Geomatics and Information Science of Wuhan University, 2022, 47(9): 1349-1363. https://www.cnki.com.cn/Article/CJFDTOTAL-WHCH202209001.htm [27] MATSUMOTO Y, FUJITA M, ISHIKAWA T. Development of multi-epoch method for determining seafloor station position[J]. Technical bulletin on hydrography and oceanography, 2008, 26: 16-22. [28] UJIHARA N, SATO M, ISHIKAWA T, et al. New analysis method for maintaining the observation continuity after replacement of seafloor stations[J]. Report of hydrographic and oceanographic researches, 2013, 50: 84-90. [29] 李林阳, 吕志平, 崔阳. 海底大地测量控制网研究进展综述[J]. 测绘通报, 2018(1): 8-13, 87. https://www.cnki.com.cn/Article/CJFDTOTAL-CHTB201801002.htm LI Linyang, LYU Zhiping CUI Yang. Summary of the research progress of seafloor geodetic control network[J]. Bulletin of surveying and mapping, 2018(1): 8-13, 87. https://www.cnki.com.cn/Article/CJFDTOTAL-CHTB201801002.htm [30] SATO M, FUJITA M, MATSUMOTO Y, et al. Improvement of GPS/acoustic seafloor positioning precision through controlling the ship's track line[J]. Journal of geodesy, 2013, 87(9): 825-842. doi: 10.1007/s00190-013-0649-9 [31] XUE Shuqiang, YANG Yuanxi. Positioning configurations with the lowest GDOP and their classification[J]. Journal of geodesy, 2015, 89(1): 49-71. doi: 10.1007/s00190-014-0760-6 [32] ZHAO Jianhu, ZOU Yajing, ZHANG Hongmei, et al. A new method for absolute datum transfer in seafloor control network measurement[J]. Journal of marine science and technology, 2015(21): 216-226. [33] CHEN Guanxu, LIU Yang, LIU Yanxiong, et al. Improving GNSS-acoustic positioning by optimizing the ship's track lines and observation combinations[J]. Journal of geodesy, 2020, 94(6): 61. doi: 10.1007/s00190-020-01389-1 [34] 曾安敏, 杨元喜, 明锋, 等. 海底大地基准点圆走航模式定位模型及分析[J]. 测绘学报, 2021, 50(7): 939-952. https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB202107010.htm ZENG Anmin, YANG Yuanxi, MING Feng, et al. Positioning model and analysis of the sailing circle mode of seafloor geodetic datum points[J]. Acta geodetica et cartographica sinica, 2021, 50(7): 939-952. https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB202107010.htm [35] LI Menghao, LIU Yang, LIU Yanxiong, et al. Simulative evaluation of the underwater geodetic network configuration on kinematic positioning performance[J]. Remote sensing, 2022, 14(8): 1939. doi: 10.3390/rs14081939 [36] 马越原, 杨元喜, 曾安敏. GNSS-A直线测量模式及航迹组合优化分析[J]. 地球物理学报, 2022, 65(10): 3797-3808. doi: 10.6038/cjg2022P0574 MA Yueyuan, YANG Yuanxi, ZENG Anmin. GNSS-A straight-line survey pattern and trajectory combination optimization analysis[J]. Chinese journal of geophysics. 2022, 65(10): 3797-3808. doi: 10.6038/cjg2022P0574 [37] FUJITA M, SATO M, YABUKI T. Development of seafloor positioning software using inverse method[J]. Report of hydrographic and oceanographic researches, 2004, 22: 50-56. [38] FUJITA M, ISHIKAWA T, MOCHIZUKI M, et al. GPS/Acoustic seafloor geodetic observation: method of data analysis and its application[J]. Earth, planets and space, 2006, 58(3): 265-275. doi: 10.1186/BF03351923 [39] IKUTA R, TADOKORO K, ANDO M, et al. A new GPS-acoustic method for measuring ocean floor crustal deformation: application to the Nankai Trough[J]. Journal of geophysical research: solid earth, 2008, 113: B02401. [40] YOKOTA Y, ISHIKAWA T. Gradient field of undersea sound speed structure extracted from the GNSS-A oceanography: GNSS-A as a sensor for detecting sound speed gradient[J]. SN applied sciences, 2019, 1: 693. doi: 10.1007/s42452-019-0699-6 [41] CHEN H H. Travel-time approximation of acoustic ranging in GPS/Acoustic seafloor geodesy[J]. Ocean engineering, 2014, 84: 133-144. doi: 10.1016/j.oceaneng.2014.04.015 [42] ZHAO Jianhua, LIANG Wenbiao, MA Jinye, et al. A self-constraint underwater positioning method without the assistance of measured sound velocity profile[J]. Marine geodesy, 2023, 46(1): 62-82. doi: 10.1080/01490419.2022.2079778 [43] XUE Shuqiang, LI Baojin, XIAO Zhen, et al. Centimeter-level-precision seafloor geodetic positioning model with self-structured empirical sound speed profile(accepted)[J]. Satellite navigation, 2023. [44] HONSHO C, KIDO M. Comprehensive analysis of traveltime data collected through GPS-Acoustic observation of Seafloor crustal movements[J]. Journal of geophysical research: solid earth, 2017, 122(10): 8583-8599. doi: 10.1002/2017JB014733 [45] WATANABE S I, ISHIKAWA T, NAKAMURA Y, et al. Full-Bayes GNSS-A solutions for precise seafloor positioning with single uniform sound speed gradient layer assumption[J]. Journal of geodesy, 2023, 97(10): 89. doi: 10.1007/s00190-023-01774-6 [46] YANG Yuanxi, QIN Xianping. Resilient observation models for seafloor geodetic positioning[J]. Journal of geodesy, 2021, 95(7): 79. doi: 10.1007/s00190-021-01531-7 [47] ASADA A, YABUKI T. Centimeter-level positioning on the seafloor[J]. Proceedings of the Japan academy, series B, 2001, 77(1): 7-12. doi: 10.2183/pjab.77.7 [48] 李景森, 薛树强, 肖圳, 等. GNSS/声呐组合观测臂长改正不确定度评估[J]. 武汉大学学报(信息科学版): 1-12. LI Jingsen, XUE Shuqiang, XIAO Zhen, et al. Uncertainty evaluation on the arm length correction of GNSS-A observation[J]. Geomatics and Information Science of Wuhan University, 2023, 1-12. [49] 邝英才, 吕志平, 王方超, 等. GNSS/声学联合定位的自适应滤波算法[J]. 测绘学报, 2020, 49(7): 854-864. https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB202007007.htm KUANG Yingcai, LYU Zhiping, WANG Fangchao, et al. The adaptive filtering algorithm of GNSS/acoustic joint positioning[J]. Acta geodaetica et cartographica sinica, 2020, 49(7): 854-864. https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB202007007.htm [50] ZHAO Shuang, WANG Zhenjie, NIE Zhixi, et al. Investigation on total adjustment of the transducer and seafloor transponder for GNSS/Acoustic precise underwater point positioning[J]. Ocean engineering, 2021, 221: 108533. doi: 10.1016/j.oceaneng.2020.108533 [51] WANG Zhenjie, ZHAO Shuang, JI Shengyue, et al. Real-time stochastic model for precise underwater positioning[J]. Applied acoustics, 2019, 150: 36-43. doi: 10.1016/j.apacoust.2019.01.021 [52] JENSEN F B, KUPERMAN W A, PORTER M B, et al. Computational ocean acoustics[M]. New York: Springer New York, 2011. [53] SAKIC P, BALLU V, CRAWFORD W C, et al. Acoustic ray tracing comparisons in the context of geodetic precise off-shore positioning experiments[J]. Marine geodesy, 2018, 41(4): 315-330. doi: 10.1080/01490419.2018.1438322 [54] 赵爽. 海底大地控制网高精度声学定位算法研究[D]. 青岛: 中国石油大学(华东), 2022. ZHAO Shuang, Research on algorithms of high precision acoustic positioning for seafloor geodetic networks[D]. Qingdao: Chinese University of Petroleum (East China), 2022. [55] FUKAHATA Y, WRIGHT T J. A non-linear geodetic data inversion using ABIC for slip distribution on a fault with an unknown dip angle[J]. Geophysical journal international, 2008, 173(2): 353-364. doi: 10.1111/j.1365-246X.2007.03713.x [56] YANG Y, SONG L, XU T. Robust estimator for correlated observations based on bifactor equivalent weights[J]. Journal of geodesy, 2002, 76(6): 353-358. [57] ZHAO Shuang, WANG Zhenjie, HE Kaifei, et al. investigation on stochastic model refinement for precise underwater positioning[J]. IEEE journal of oceanic engineering, 2020, 45(4): 1482-1496. doi: 10.1109/JOE.2019.2935481 [58] XUE Shuqiang, YANG Yuanxi, YANG Wenlong. Single-differenced models for GNSS-acoustic seafloor point positioning[J]. Journal of geodesy, 2022, 96(5): 38. doi: 10.1007/s00190-022-01613-0 [59] 辛明真, 葛茂荣, 阳凡林, 等. 顾及收发分置影响的海洋大地基准声线跟踪定位方法[J]. 地球物理学报, 2022, 65(10): 3809-3817. doi: 10.6038/cjg2022P0349 XIN Mingzhen, GE Maorong, YANG Fanlin, et al. A sound ray tracing positioning method for marine geodetic datum considering the effect of transceiver separation[J]. Chinese journal of geophysics, 2022, 65(10): 3809-3817. doi: 10.6038/cjg2022P0349 [60] 闫凤池, 王振杰, 赵爽, 等. 顾及双程声径的常梯度声线跟踪水下定位算法[J]. 测绘学报, 2022, 51(1): 31-40. https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB202201004.htm YAN Fengchi, WANG Zhenjie, ZHAO Shuang, et al. A layered constant gradient acoustic ray tracing underwater positioning algorithm considering round-trip acoustic path[J]. Acta geodaetica et cartographica sinica. 2022, 51(1);31-40. https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB202201004.htm [61] SUN Dajun, YU Miao, ZHENG Cuie, et al. Improved seafloor geodetic positioning via sound velocity correction based on the precise round-trip acoustic positioning model[J]. Marine geodesy, 2023, 46(1): 43-61. doi: 10.1080/01490419.2022.2054884 [62] YANG Yuanxi, QIN Xxianping. Resilient observation models for seafloor geodetic positioning[J]. Journal of geodesy, 2021, 95(7): 79. doi: 10.1007/s00190-021-01531-7 [63] 周江文. 系统误差的数学处理[J]. 测绘工程, 1999, 8(2): 1-4. doi: 10.3969/j.issn.1006-7949.1999.02.001 ZHOU Jiangwen. Mathematical processing of problems with systematic errors[J]. Engineering of surveying and mapping, 1999, 8(2): 1-4. doi: 10.3969/j.issn.1006-7949.1999.02.001 [64] CARL D B. A practical guide to splines[M]. New York: Springer-Verlag, 1978. [65] GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations[J]. Journal of geodesy, 2008, 82(7): 389-399. doi: 10.1007/s00190-007-0187-4 [66] WANG Junting, XU Tianhe, NIE Wenfeng, et al. The Construction of sound speed field based on back propagation neural network in the global ocean[J]. Marine geodesy, 2020, 43(6): 621-642. doi: 10.1080/01490419.2020.1815912 [67] YU Miao, CAI Kuijie, ZHENG Cuie, et al. Improvement of seafloor positioning through correction of sound Speed profile temporal variation[J]. IEEE/CAA Journal of automatica sinica, 2022, 10(4): 1099-1101. [68] YOKOTA Y, ISHIKAWA T, WATANABE S I. Seafloor crustal deformation data along the subduction zones around Japan obtained by GNSS-A observations[J]. Scientific data, 2018, 5: 180182. doi: 10.1038/sdata.2018.182 [69] 赵爽, 王振杰, 聂志喜, 等. 顾及声速结构时域变化的海底基准站高精度定位方法[J]. 测绘学报, 2023, 52(1): 41-50. https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB202301006.htm ZHAO Shuang, WANG Zhenjie, NIE Zhixi, et al. Precise positioning method for seafloor geodetic stations based on the temporal variation of sound speed structure[J]. Acta geodaetica et cartographica sinica, 2023, 52(1): 41-50. https://www.cnki.com.cn/Article/CJFDTOTAL-CHXB202301006.htm [70] YANG Wenlong, XUE Shuqiang, LIU Yixu. P-order secant method for rapidly solving the ray inverse problem of underwater acoustic positioning[J]. Marine geodesy, 2023, 46(1): 3-15. doi: 10.1080/01490419.2021.1992547 [71] XU Peiliang, ANDO M, TADOKORO K. Precise, three-dimensional seafloor geodetic deformation measurements using difference techniques[J]. Earth planets and space, 2005, 57(9): 795-808. doi: 10.1186/BF03351859 [72] 马越原, 曾安敏, 许扬胤. 圆走航模式下海底控制点对称差分定位模型及分析[J]. 武汉大学学报(信息科学版), 2021: 1-20. MA Yueyuan, ZENG Anmin, XU Yangyin. Symmetric difference positioning model and analysis of the sailing circle mode of seafloor control points[J]. Geomatics and Information Science of Wuhan University, 2021: 1-20. [73] XUE Shuqiang, DANG Yamin, LIU Jiping, et al. Bias estimation and correction for triangle-based surface area calculations[J]. International journal of geographical information science, 2016, 30(11): 2155-2170. doi: 10.1080/13658816.2016.1162795 [74] XUE Shuqiang, YANG Yuanxi. Unbiased nonlinear least squares estimations of short-distance equations[J]. Journal of navigation, 2017, 70(4): 19. [75] CHEN G, HERRING T A. Effects of atmospheric azimuthal asymmetry on the analysis of space geodetic data[J]. Journal of geophysical research: solid earth, 1997, 102(B9): 20489-20502. doi: 10.1029/97JB01739 [76] YOKOTA Y, OKUMURA M. Study for improving efficiency in seafloor geodetic observation by means of multi-acoustic ranging[J]. Report of hydrographic and oceanographic researches, 2015, 52: 79-87. [77] ZHAO Jianhu, ZOU Yajing, ZHANG Hongmei, et al. A new method for absolute datum transfer in seafloor control network measurement[J]. Journal of marine science and technology, 2016, 21(2): 216-226. doi: 10.1007/s00773-015-0344-z [78] NAKAMURA Y, YOKOTA Y, ISHIKAWA T, et al. Optimal transponder array and survey Line configurations for GNSS-A observation evaluated by numerical simulation[J]. Frontiers in earth science, 2021, 9: 600993. doi: 10.3389/feart.2021.600993
