半潜式平台纵摇运动高阶谱分析

王金光; 马山; 缪泉明

doi:10.11990/jheu.202107019

半潜式平台纵摇运动高阶谱分析

doi: 10.11990/jheu.202107019

王金光^{1, 2},
马山^1, ,,
缪泉明^{1, 2}

1.
哈尔滨工程大学船舶工程学院, 黑龙江哈尔滨 150001;
2.
招商局重工(江苏)有限公司, 江苏南通 226116

基金项目:

国家自然科学基金项目 51879058.

详细信息

作者简介:
王金光, 男, 高级工程师, 博士研究生;

马山, 男, 教授, 博士生导师.

通讯作者:
马山, E-mail: mashan01@hrbeu.edu.cn.

中图分类号: U674
出版历程
- 收稿日期: 2021-07-19
- 网络出版日期: 2022-10-31

High-order spectral analysis on the pitch motion of a semisubmersible

WANG Jinguang^{1, 2},
MA Shan^1, ,,
MIAO Quanming^{1, 2}

1.
College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China;
2.
China Merchants Heavy Industry (Jiangsu), Nantong 226116, China

摘要

摘要: 为了获取半潜式平台纵摇运动特征，系统地开展不同海况条件下的模型试验，并分析海况条件对纵摇运动的影响规律。本文在建立和完善高阶谱分析流程的基础上，通过对波高时历和纵摇时历进行互谱和交叉多谱分析来获得纵摇运动的线性传递函数和二次传递函数。结果表明：线性传递函数与海况关系不大，二次传递函数与海况密切相关；二阶传递函数主要集中于差频为固有频率附近，随着海况的增加，差频为谱峰频率附近的响应也逐渐凸显，据此推测，高海况条件下在波频范围内的纵摇运动具有一定的非线性。
- 半潜式平台 /
- 谱分析 /
- 传递函数 /
- 数据处理 /
- 耐波性 /
- 试验 /
- 傅里叶变换 /
- 统计方法
Abstract: The effects of wave conditions on the pitch motion were investigated on the basis of a series of wave basin tests under representative wave conditions to acquire the pitch motion characteristics of a semisubmersible. The high-order spectral analysis procedure is established and improved, deriving linear transfer functions and quadratic transfer functions (QTFs) via cross spectral and cross bi-spectral analyses, respectively. Results indicate that the former ones are unrelated to the encountered waves while the latter ones are highly dependent on the encountered waves. The distribution of significant QTFs is mainly concentrated on the off-diagonal line where the diff-frequency is equal to the natural frequency. Furthermore, with the increasingly rising wave conditions, the response gradually emerges on another off-diagonal line with diff-frequency equal to spectral peak frequency. Thus, the pitch motion in wave frequency would present certain nonlinearity in rough seas.
- semisubmersible /
- spectrum analysis /
- transfer function /
- data processing /
- seakeeping /
- experiment /
- Fourier transform /
- statistical method

HTML全文

半潜式平台因其优异的运动性能而被广泛应用于海上油气开发、海上吊装作业和海上风电开发等，该型浮体的低频运动特征受到广泛关注。挪威船级社DNV^[1]和美国船级社ABS^[2]针对半潜式平台发布技术指南中特别论述了低频横摇和纵摇运动对气隙以及波浪砰击分析重要性。Ma等^[3]运用统计方法研究半潜式钻井平台的Morison单元对低频纵荡运动的影响，并指出水线面以下部分在粘性阻尼中占主导成分，而水线面以上部分是粘性慢漂力的主要诱因。Li等^[4]分析半潜式生产平台在极限海况下运动响应谱，并且发现水池试验和数值模拟结果在波频范围内吻合较好，但在低频范围内存在较大偏差，纵摇响应的差异尤为明显并且其低频部分占主导地位。Matos等^[5]以半潜式生产平台实际遭遇的海况条件和运动响应为研究对象，揭示了横摇和纵摇的低频共振特性，并指出了二阶运动分析时考虑方向谱的重要性。孙刘璐等^[6]同样基于实测数据对半潜式平台开展了运动响应分析和极值预报，并且验证了平台横摇和纵摇运动满足设计指标。白雪平等^[7]通过模型试验和数值模拟来研究阻尼特性对浮式平台运动响应的影响，并且发现不同边缘型式的垂荡板对二阶阻尼产生较大影响。如上所述，半潜式平台非线性运动研究的主流做法还是以运动响应统计特征和响应谱作为判断依据。多阶谱分析方法是在声学和光学领域发展起来的，并已经应用于海洋工程领域。Kim等^[8]通过多阶谱分析获得固定驳船纵向波浪力的二阶传递函数，并将重构的二阶力与试验结果对比来验证其有效性。Kim等^[9]开展模型试验研究船体的弹振响应，借助多阶谱分析获得垂向弯矩的二阶传递函数，进而发现高频和波频能量在同一量级，并且高频部分的占比随着波高增加而增大。高阶谱分析方法的分析流程较为繁琐，关于浮体应用案例较少，并且分析结果受到采样间隔、采样时长和窗函数等多种因素影响，该方法可以得出二阶和频或差频项的量化结果，这对研究半潜式平台的非线性运动具有重要价值。

本文基于不同海况下的水池试验结果，在频域和时域范围内开展数据对比，以此确定海况对纵摇运动的影响以及波频和低频成分的变化趋势。

1. 理论基础

半潜式平台纵摇运动的固有周期通常大于30 s，除了在波频力作用下的一阶纵摇响应外，在差频力作用下还会呈现低频纵摇共振现象。为了实现频域范围内的量化分析，通过自谱分析、互谱分析和交叉多谱分析来获取平台纵摇运动的线性传递函数和二阶传递函数。忽略三阶以上响应，半潜式平台的时域非线性运动可表示为二阶沃尔特拉方程^[8]：

$$ \begin{array}{c} y(n) = \sum\limits_{k = 0}^\infty h (k)x(n - k) + \\ \sum\limits_{k = 0}^\infty {\sum\limits_{l = 0}^\infty q } (k, l)x(n - k)x(n - l) \end{array} $$

(1)

式中：x为波面升高时历；y为半潜式平台的响应；h(k)为线性脉冲响应函数；q(k, l)为二阶脉冲响应函数。对式(1)两端进行直接傅里叶变换可获得频域方程^[8]：

$$ Y(f) = H(f)X(f) + \sum\limits_{{f_1} + {f_2} = f} Q \left( {{f_1}, {f_2}} \right)X\left( {{f_1}} \right)X\left( {{f_2}} \right) $$

(2)

式中：X(f)和Y(f)分别为x和y的傅里叶变换；H(f)为线性传递函数；Q(f₁, f₂)为二阶传递函数。对比式(1)和式(2)可以看出，时域范围内的相乘项x(n-k)x(n-l)通过傅里叶变换转化为频域范围内卷积积分，并以f₁+f₂=f的形式呈现。

假设波浪可视为平稳随机过程，其均值为零且符合高斯分布，那么波面起伏及其三重乘积的期望值都为零：

$$ {\rm{E}}[x(t - \tau )] = 0 $$

(3)

$$ {\rm{E}}\left[ {x\left( {t - {t_1}} \right)x\left( {t - {t_2}} \right)x(t - \tau )} \right] = 0 $$

(4)

上述条件成立时，平台响应与波面升高之间的互谱S_yx(f)和交叉多谱S_yxx(f₁, f₂)可分别表示为：

$$ \begin{array}{c} {S_{yx}}(f) = {\rm{E}}\left[ {Y(f){X^*}(f)} \right] = \\ H(f){\rm{E}}\left[ {X(f){X^*}(f)} \right] = H(f){S_{xx}}(f) \end{array} $$

(5)

$$ \begin{array}{c} {S_{yxx}}\left( {{f_1}, {f_2}} \right) = 2Q\left( {{f_1}, {f_2}} \right){S_{xx}}\left( {{f_1}} \right){S_{xx}}\left( {{f_2}} \right) + \\ {S_{xx}}\left( {{f_2}} \right)\delta \left( {{f_1} + {f_2}} \right){\rm{E}}[y(n)] \end{array} $$

(6)

式中：δ(f₁+f₂)为Dirac-Delta函数; f₁+f₂=0时值为1，否则值为0；S_xx(f)为自谱；S_yx(f)为互谱；S_yxx(f₁, f₂)交叉多谱，它们可通过傅里叶变换得到：

$$ {S_{xx}}(f) = {\rm{E}}\left[ {X(f){X^*}(f)} \right] $$

(7)

$$ {S_{yx}}(f) = {\rm{E}}\left[ {X(f){Y^*}(f)} \right] $$

(8)

$$ {S_{yxx}}\left( {{f_1}, {f_2}} \right) = {\rm{E}}\left[ {X\left( {{f_1}} \right)X\left( {{f_2}} \right){Y^*}\left( {{f_1} + {f_2}} \right)} \right] $$

(9)

因此通过互谱分析和交叉多谱分析，可以求得平台运动的线性传递函数H(f)和二阶传递函数Q(f₁, f₂)。

$$ H(f) = \frac{{{S_{yx}}(f)}}{{{S_{xx}}(f)}} $$

(10)

$$ Q\left( {{f_1}, {f_2}} \right) = \frac{{{S_{yxx}}\left( {{f_1}, {f_2}} \right) - {S_{xx}}\left( {{f_2}} \right)\delta \left( {{f_1} + {f_2}} \right){\rm{E}}[y(n)]}}{{2{S_{xx}}\left( {{f_1}} \right){S_{xx}}\left( {{f_2}} \right)}} $$

(11)

2. 试验设置

半潜式平台的浮体由4个纵向浮筒，4个垂向立柱以及2根连接立柱的横撑组成，其几何构型见图 1，主尺度和重量信息见表 1。模型试验在挪威Sintef海洋研究院水池完成，缩尺比为1 ∶50，试验测量内容包括平台六自由度运动，系泊缆张力和选定位置的波面升高等^[10]。

图 1 浮体构型

Fig. 1 Hull configuration

下载: 全尺寸图片

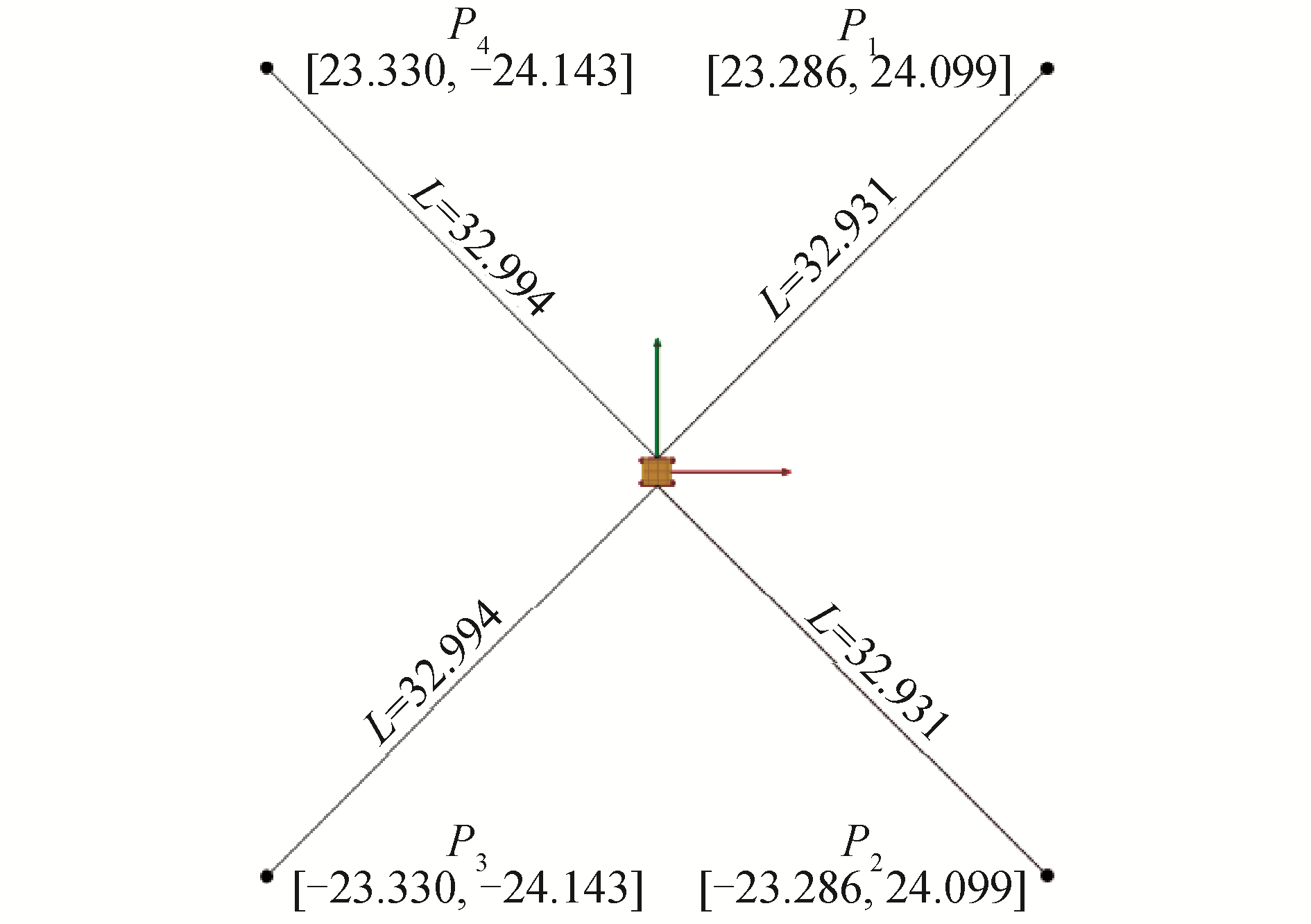
表 1 半潜式平台主要参数

Table 1 Main particulars of the semi-submersible

名称	数值
浮筒：(长, 宽, 高)(L_p, B_p, H_p)/m	(107.5, 14.3, 9.5)
立柱：(长, 宽)(L_c, B_c)/m	(12.5, 12.5)
横撑：直径d/m	5.0
吃水D/m	23.0
排水量Δ/t	39 206
重心垂向高度Z_G/m	23.7
绕x轴回转半径R_xx/m	36.1
绕y轴回转半径R_yy/m	35.8
绕z轴回转半径R_zz/m	42.3

试验平台由4条弹性缆组成的水平系泊系统来实现定位，系泊布置方式见图 2。系泊缆在水平面内间隔90°，各缆在浮体端连接点位于平台舯部且靠近水线面，这可以降低纵荡与纵摇之间的耦合作用，如图 3所示。平台在水面内的回复力随位移呈线性变化，选用系泊缆刚度保证平台纵荡和横荡固有周期大于100 s，从而避开波浪能量范围，通过自由衰减试验测得的固有周期及其对应的固有频率见表 2。

图 2 系泊布置方式

Fig. 2 Mooring system arrangement

下载: 全尺寸图片

图 3 系泊缆连接

Fig. 3 Mooring line connection

下载: 全尺寸图片

表 2 固有周期和固有频率

Table 2 Natural periods and natural frequencies

运动名称	固有周期T_n/s	固有频率ω_n/(rad·s^-1)
纵荡ξ_x	117.0	0.053 7
横荡ξ_y	136.0	0.046 2
横摇α	52.1	0.120 6
纵摇β	56.5	0.111 2

3. 波浪生成与校核

根据平台的目标作业海域，波浪谱使用Torsethaugen^[11]谱简化形式。该型谱中风浪或者涌浪的主导地位由谱峰周期T_P与T_f=a_fH_s^1/3之间关系决定，式中a_f为风区长度系数。当T_P < T_f时风浪占主导，当T_P≥T_f时涌浪占主导。根据平台设计海况，试验方案选用的一系列不规则波条件见表 3。

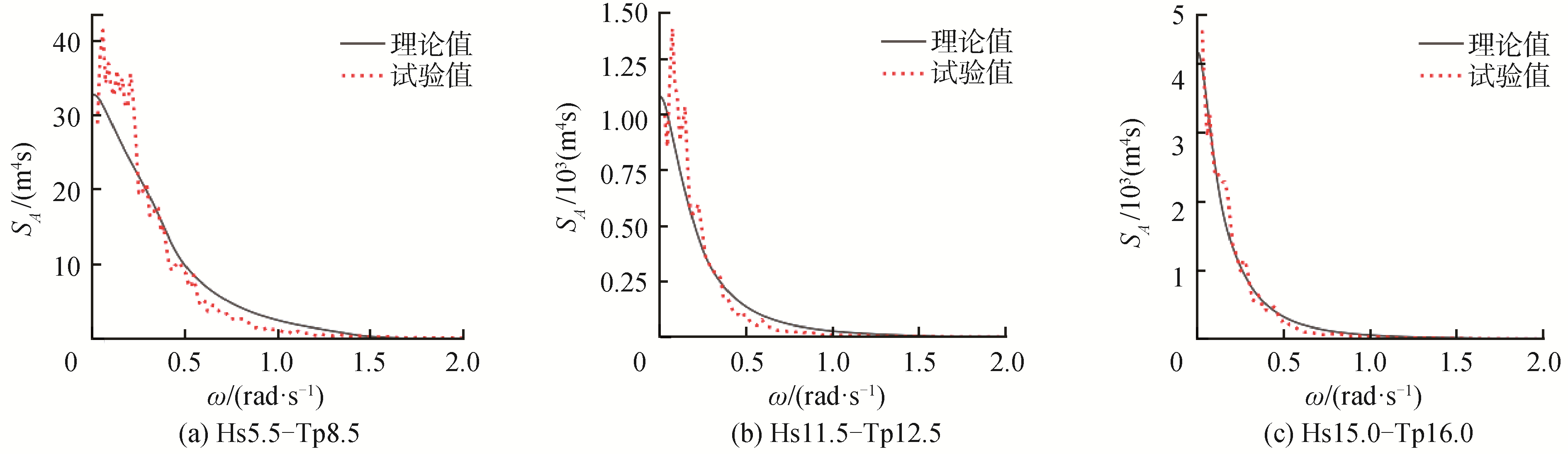
表 3 不规则波条件

Table 3 Irregular wave conditions

试验名称	波高H_s/m	谱峰周期T_p/s
Hs5.5-Tp8.5	5.5	8.5
Hs11.5-Tp12.5	11.5	12.5
Hs15.0-Tp16.0	15.0	16.0

波浪调试完成后，浪高仪测得目标位置的波高时历见图 4。对稳定段数据进行傅里叶变换可以获得试验波浪的谱密度。实际数据处理时，为获得光顺结果将波高时历切分为多段，每段重复率为50%，计算各段谱密度之后再加权平均。试验采样频率为200 Hz，据此选取每段数据长度为2¹³。波浪谱的理论值与试验值的对比见图 5，不同海况条件下生成的波浪与目标值都非常吻合。波浪谱的各项参数对比见表 4，波高和谱峰周期与目标值差异小于5%。

图 4 波高和波包时历

Fig. 4 Wave elevation and wave envelope time series

下载: 全尺寸图片

图 5 波浪谱对比

Fig. 5 Comparison of wave spectrum

下载: 全尺寸图片

表 4 波浪谱参数对比

Table 4 Comparison of wave spectrum parameters

名称	Hs5.5-Tp8.5		Hs11.5-Tp12.5		Hs15.0-Tp16.0
名称	理论值	试验值	理论值	试验值	理论值	试验值
波高H_s/m	5.50	5.27	11.50	11.31	15.00	14.82
谱峰周期T_p/s	8.50	8.49	12.50	12.86	16.00	16.32
平均跨零周期T_z/s	7.50	7.55	9.61	10.33	11.38	11.99
零阶谱矩M₀/m²	1.81	1.73	8.30	8.00	14.34	13.72
一阶谱矩M₁/(m²·s^-1)	1.44	1.35	5.09	4.57	7.34	6.68
二阶谱矩M₂/(m²·s^-2)	1.27	1.20	3.55	2.96	4.37	3.77

半潜式平台差频响应与波群分布密切相关，因此在保证波浪谱一致的前提下，进一步对波群特性进行分析。波群能量可由波包谱来表征，对目标波浪谱进行自卷积分可以获得波包谱的理论值；利用Hilbert变换可计算波包时历，如图 4所示，对其进行傅里叶变换可以获得波包谱的试验值。图 6显示波包谱理论值与试验值的对比，两者在整体趋势上保持一致，但差频值较小时存在较大差异，Hs5.5-Tp8.5和Hs11.5-Tp11.5海况下的偏差可达25%。波包谱与生成波浪的随机种子数密切相关，这种随机性会增加试验分析的难度。

图 6 波包谱对比

Fig. 6 Comparison of wave envelope spectrum

下载: 全尺寸图片

4. 纵摇结果与分析

本文研究对象为半潜式平台纵摇运动。在低频范围内，平台的惯性力和阻尼力较小，它们引起的不同运动之间的耦合作用也较小，同时系泊系统中缆绳的连接方式也可降低的纵荡与纵摇之间相互作用。在波频范围内，由于平台采用双对称构型，所以运动之间的耦合项对纵摇的影响并不明显。综上分析，本文并未考虑纵摇与其他运动之间的耦合效应。

4.1 响应谱

模型试验测得平台在选定典型海况条件下的纵摇响应，对其滤波处理可获得波频和低频成分，截止频率选为0.25 rad/s，各成分的时历曲线见图 7。

图 7 滤波后的纵摇时历结果

Fig. 7 Filtered pitch motion time series

下载: 全尺寸图片

表 5显示滤波前后纵摇时历的统计结果，包括平均值、标准差、最大值和最小值。对比不同海况下的结果可知，Hs5.5-Tp8.5低频成分的极值(最大值或最小值的绝对值)与其他2种海况比较接近；波频成分的极值明显小于其他2种海况。关于每个海况下的结果特点，Hs5.5-Tp8.5低频纵摇贡献占主导；Hs15.0-Tp16.0波频纵摇贡献占主导。通过结果对比可以看出，随着海况的增加，波频纵摇贡献不断增大，低频纵摇贡献反而略有减小。为了从频率角度评估平台的纵摇响应，通过快速傅里叶变换来计算纵摇谱密度，计算方法与波浪谱相同。从图 8的纵摇响应谱可以看出，在不同海况条件下，平台纵摇响应的最大值都发生在低频范围内，并与表 2中自由衰减试验得到的纵摇固有频率重合，这说明平台低频纵摇是由差频波浪激励的共振运动引起的。随着波浪谱峰频率减小，平台在波频范围内的响应逐渐增大，在Hs11.5-Tp12.5和Hs15.0-Tp16.0海况下，波频响应最大值所在频率与波浪的谱峰频率基本一致，这表明波频纵摇主要是由一阶波浪激励引起的。

表 5 纵摇统计结果

Table 5 Statistical results of pitch

名称	符号/单位	Hs5.5-Tp8.5			Hs11.5-Tp12.5			Hs15.0-Tp16.0
名称	符号/单位	总值	低频	波频	总值	低频	波频	总值	低频	波频
平均值	β_mean/(°)	0.37	0.37	0.00	0.75	0.75	0.00	0.73	0.73	0.00
标准差	β_std/(°)	1.50	1.44	0.41	1.91	1.49	1.17	1.97	1.30	1.46
最小值	β_min/(°)	-4.24	-4.01	-1.95	-6.64	-3.63	-4.91	-6.61	-3.91	-5.59
最大值	β_max/(°)	5.66	4.88	1.70	8.35	5.43	4.80	8.34	4.63	5.19

图 8 纵摇响应谱

Fig. 8 Pitch response spectrum

下载: 全尺寸图片

基于二阶频域分析理论，频域内纵摇响应谱计算公式^[9]：

$$ \begin{array}{c} {S_\beta }(\omega ) = |H(\omega ){|^2}{S_\zeta }(\omega ) + \\ \frac{1}{\pi }\int\limits_{ - \infty }^\infty {|Q(\omega - \theta , \theta ){|^2}{S_\zeta }(\omega - \theta ){S_\zeta }(\theta ){\rm{d}}\theta } \end{array} $$

(12)

由于纵摇固有频率ω_n附近的波浪谱密度S_ζ(ω_n)很小，低频纵摇响应取决于公式右端的第2项。从波包谱不难判断，卷积积分项S_ζ(ω-θ)S_ζ(θ)随着海况的增加而增大，按照二阶势流理论假设，二阶传递函数Q(ω-θ, θ)与海况无关，那么低频响应也必然增大。而从图 8中试验获得的纵摇响应谱可以看出，海况增加后低频响应反而有所减小，该物理现象值得进一步深入研究。

4.2 纵摇运动的线性和二阶传递函数分析

通过互谱分析和交叉多谱分析可计算得到平台运动的线性传递函数H(ω)和二阶传递函数Q(ω₁, ω₂)。由于各个海况的波能范围有限，因此无法得到整个频率范围内的结果。交叉多谱分析时，为保证数据低频特性，选取每段数据长度取为2¹³。实际计算时采用窗函数来获得能量谱的相合结果，其中自谱和互谱分析采用Hanning型窗函数W₁(n)，交叉多谱分析采用二维优化型窗函数W₂(m, n)，后者表达式为：

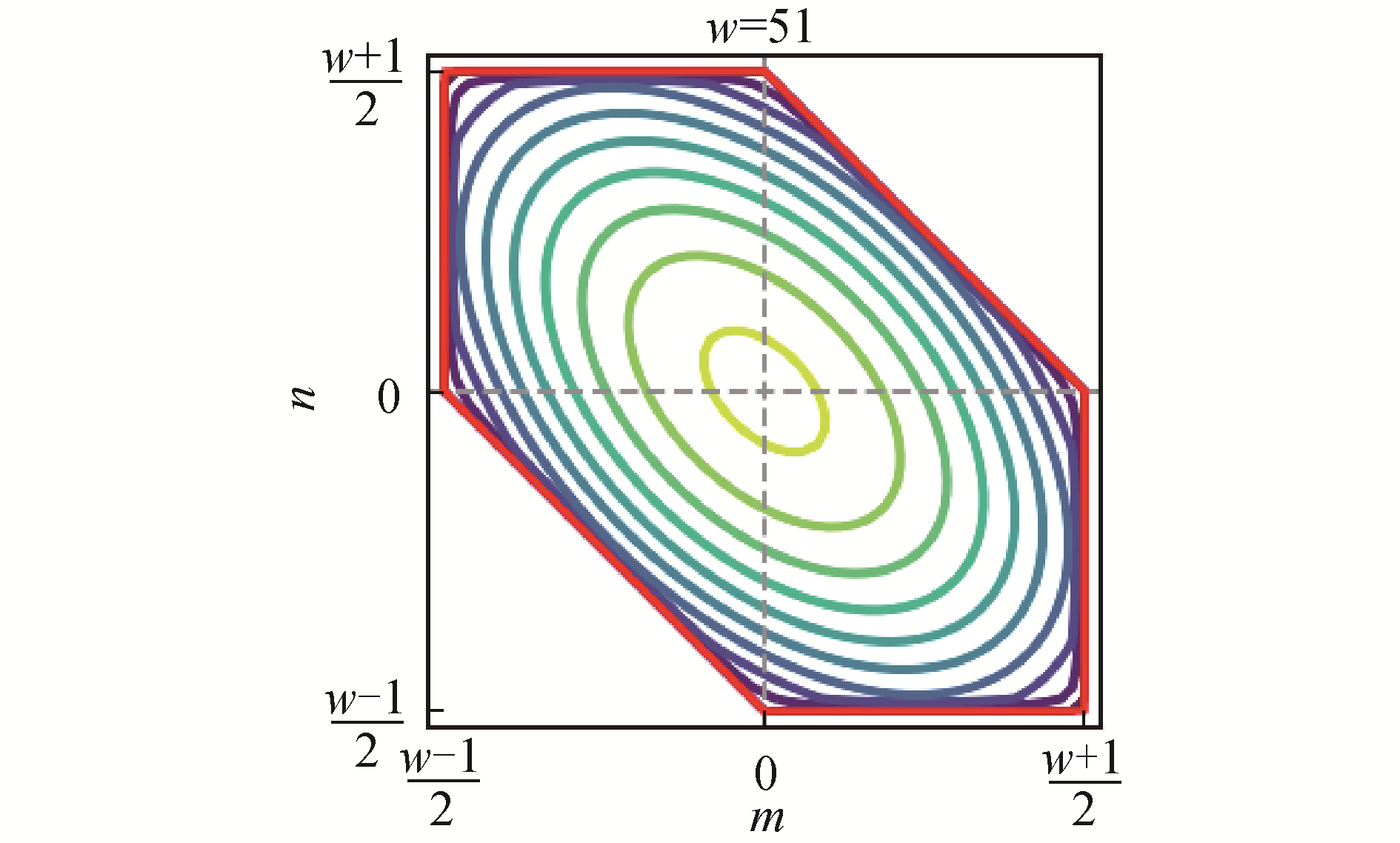
$$ \begin{array}{c} {W_2}(m, n) = \frac{4}{{7{M^2}}}\left[ {1 - \frac{{{m^2} + {n^2} + mn}}{{{M^2}}}} \right]\\ (m, n) \in G \end{array} $$

(13)

式中：w为窗口尺寸，其值为大于1的奇数；M为比例因子，M=(w-1)/2；G的范围定义为|m| + |n| + |m+n| ≤2M。图 9给出W₂(m, n)分布的实例。

图 9 二维优化型窗函数W₂(m, n)

Fig. 9 2-D optimal window function W₂(m, n)

下载: 全尺寸图片

纵摇线性传递函数在波浪能量范围0.3~ 0.8 rad/s的对比见图 10。不难看出，不同海况条件下线性传递函数的结果基本相同，据此可以判断波频范围的纵摇运动传递函数对海况条件并不敏感。

图 10 纵摇线性传递函数对比

Fig. 10 Comparison of pitch linear transfer functions

下载: 全尺寸图片

二阶传递函数的计算公式(11)中，波浪自谱平方作为除数，如果该数值很小，其微小扰动都会引起极大误差。为保证计算结果的可靠性，对波浪和纵摇响应的频谱进行截断处理。不同海况条件均选用0.4~1.0 rad/s频率范围，以便于对比。

图 11显示纵摇交叉多谱的在第4象限结果(ω₁为正，ω₂为负)，图中反斜线ω₁+ω₂=ω_n代表差频值等于固有频率，ω₁+ω₂=ω_p代表差频值等于谱峰频率，纵线ω₁=ω_p和横线ω₂=ω_p表示了谱峰频率所在位置。Hs11.5-Tp12.5和Hs15.0-Tp16.0 2个高海况下的峰值更大，其值约为低海况Hs5.5-Tp8.5的8倍。在反对角线上，各海况条件下纵摇交叉多谱的能量都主要集中差频为纵摇固有频率附近，并且低海况时，在选定频率范围内的分布较为均匀；而高海况时，在差频为谱峰频率附近的分布逐渐凸显。

图 11 纵摇交叉多谱

Fig. 11 Cross bi-spectrum of pitch

下载: 全尺寸图片

图 12显示纵摇二阶传递函数，坐标轴以及各线意义同上，可以看出不同海况条件下的峰值非常接近。在反对角线上，二阶传递函数主要分布在差频为纵摇固有频率附近，但高海况时差频接近谱峰频率时的纵摇响应也非常明显，这与交叉多谱相似。沿横轴和纵轴方向，低海况Hs5.5-Tp8.5的二阶传递函数的分布比较均匀，高海况时则是向高频方向集中，这与交叉多谱的趋势相反。为便于观察，图 13进一步给出了差频为固有频率时纵摇二阶传递函数的对比。从图 12中不难看出，不同海况下二阶传递函数存在较大差异。Hs11.5-Tp12.5和Hs15.0-Tp16.0海况下的二阶传递函数随着波浪频率的增加而增大，它们在0.4-0.8 rad/s频率范围内的数值明显小于Hs5.5-Tp8.5。

图 12 纵摇二阶传递函数

Fig. 12 Quadratic transfer functions of pitch

下载: 全尺寸图片

图 13 差频为固有频率的纵摇二阶传递函数对比

Fig. 13 Comparison of pitch quadratic transfer functions with diff-frequency equal to natural frequency

下载: 全尺寸图片

通过交叉多谱和二阶传递函数可以看出，高海况下纵摇二阶响应的分范围更广，除差频为固有频率外，差频为谱峰频率附近的响应也非常明显。据此可以判断，极端海况条件下平台在波频范围的纵摇具有一定非线性。同时在高海况下，当波浪频率ω₁或ω₂接近谱峰频率时，差频为固有频率附近的纵摇二阶传递函数急剧减小，这与一阶运动正好相反，据此推测平台一阶运动在某种机理下对二阶纵摇响应产生一定的抑制作用。

导致上述结果的原因是多重的，这里根据低频纵摇运动方程来分析一些成因。忽略平台各个自由度之间的耦合效应，低频纵摇为：

$$ \begin{array}{c} \left[ {\left( {{I_{yy}} + {A_{yy}}} \right)\beta _t^{(2)} + \left( {B + {B^E}} \right)\beta _t^{(2)} + } \right.\\ \left. {\left( {C + {C^E}} \right){\beta ^{(2)}}} \right] = M_{yy}^{(2)} \end{array} $$

(14)

式中：β⁽²⁾、β_t⁽²⁾和β_tt⁽²⁾分别为低频纵摇运动、速度和加速度；I_yy和A_yy分别为转动惯量和附加转动惯量；B和B^E分别为势流阻尼和附加阻尼；C和C^E分别为静水力刚度和附加刚度；M_yy⁽²⁾为波浪二阶激励。

首先，在纵摇固有频率附近，阻尼项(B+B^E)主要取决于粘性阻尼，半潜式平台的浮体部分由浮筒、立柱和横撑组成，这些细长杆的粘性效应随着海况以及一阶运动的增加而增大，因此低频纵摇幅值会相应减小。更重要的是，试验平台横撑顶部距离静水面仅为5.0 m，高海况下平台的一阶垂荡和纵摇会导致横撑出水，从而纵摇方向发生非线性刚度和回复力矩，这既会引发波频纵摇的非线性，也会限制低频纵摇的进一步增加。通过以上分析可以判断，由于半潜式平台自身的几何特性，其一阶运动可能影响二阶响应，而一阶运动极值又跟海况条件密切相关，因此数值模拟时有必要根据海况条件对二阶纵摇运动传递函数进行修正。

5. 结论

1) 通过模型试验研究了半潜式平台的纵摇运动，统计及结果表明随着海况的增加，波频响应不断增大而低频响应略有减小。

2) 对纵摇试验结果开展高阶谱分析来获取二阶传递函数。二阶传递函数主要集中于差频等于固有频率附近，海况增加后，靠近谱峰频率的响应急剧降低；差频等于谱峰频率的响应逐渐凸显。

3) 根据二阶传递函数的分布特征推断，在高海况下波频纵摇具有一定的非线性，并且对二阶响应产生抑制作用。

本文研究表明，互谱分析和交叉多谱相结合的方法是获取半潜式平台纵摇特征及其影响因素的有效手段，也可为数值模型的改进提供重要参考。

图 1 浮体构型

Fig. 1 Hull configuration

下载: 全尺寸图片

图 2 系泊布置方式

Fig. 2 Mooring system arrangement

下载: 全尺寸图片

图 3 系泊缆连接

Fig. 3 Mooring line connection

下载: 全尺寸图片

图 4 波高和波包时历

Fig. 4 Wave elevation and wave envelope time series

下载: 全尺寸图片

图 5 波浪谱对比

Fig. 5 Comparison of wave spectrum

下载: 全尺寸图片

图 6 波包谱对比

Fig. 6 Comparison of wave envelope spectrum

下载: 全尺寸图片

图 7 滤波后的纵摇时历结果

Fig. 7 Filtered pitch motion time series

下载: 全尺寸图片

图 8 纵摇响应谱

Fig. 8 Pitch response spectrum

下载: 全尺寸图片

图 9 二维优化型窗函数W₂(m, n)

Fig. 9 2-D optimal window function W₂(m, n)

下载: 全尺寸图片

图 10 纵摇线性传递函数对比

Fig. 10 Comparison of pitch linear transfer functions

下载: 全尺寸图片

图 11 纵摇交叉多谱

Fig. 11 Cross bi-spectrum of pitch

下载: 全尺寸图片

图 12 纵摇二阶传递函数

Fig. 12 Quadratic transfer functions of pitch

下载: 全尺寸图片

图 13 差频为固有频率的纵摇二阶传递函数对比

Fig. 13 Comparison of pitch quadratic transfer functions with diff-frequency equal to natural frequency

下载: 全尺寸图片

表 1 半潜式平台主要参数

Table 1 Main particulars of the semi-submersible

名称	数值
浮筒：(长, 宽, 高)(L_p, B_p, H_p)/m	(107.5, 14.3, 9.5)
立柱：(长, 宽)(L_c, B_c)/m	(12.5, 12.5)
横撑：直径d/m	5.0
吃水D/m	23.0
排水量Δ/t	39 206
重心垂向高度Z_G/m	23.7
绕x轴回转半径R_xx/m	36.1
绕y轴回转半径R_yy/m	35.8
绕z轴回转半径R_zz/m	42.3

表 2 固有周期和固有频率

Table 2 Natural periods and natural frequencies

运动名称	固有周期T_n/s	固有频率ω_n/(rad·s^-1)
纵荡ξ_x	117.0	0.053 7
横荡ξ_y	136.0	0.046 2
横摇α	52.1	0.120 6
纵摇β	56.5	0.111 2

表 3 不规则波条件

Table 3 Irregular wave conditions

试验名称	波高H_s/m	谱峰周期T_p/s
Hs5.5-Tp8.5	5.5	8.5
Hs11.5-Tp12.5	11.5	12.5
Hs15.0-Tp16.0	15.0	16.0

表 4 波浪谱参数对比

Table 4 Comparison of wave spectrum parameters

名称	Hs5.5-Tp8.5		Hs11.5-Tp12.5		Hs15.0-Tp16.0
名称	理论值	试验值	理论值	试验值	理论值	试验值
波高H_s/m	5.50	5.27	11.50	11.31	15.00	14.82
谱峰周期T_p/s	8.50	8.49	12.50	12.86	16.00	16.32
平均跨零周期T_z/s	7.50	7.55	9.61	10.33	11.38	11.99
零阶谱矩M₀/m²	1.81	1.73	8.30	8.00	14.34	13.72
一阶谱矩M₁/(m²·s^-1)	1.44	1.35	5.09	4.57	7.34	6.68
二阶谱矩M₂/(m²·s^-2)	1.27	1.20	3.55	2.96	4.37	3.77

表 5 纵摇统计结果

Table 5 Statistical results of pitch

名称	符号/单位	Hs5.5-Tp8.5			Hs11.5-Tp12.5			Hs15.0-Tp16.0
名称	符号/单位	总值	低频	波频	总值	低频	波频	总值	低频	波频
平均值	β_mean/(°)	0.37	0.37	0.00	0.75	0.75	0.00	0.73	0.73	0.00
标准差	β_std/(°)	1.50	1.44	0.41	1.91	1.49	1.17	1.97	1.30	1.46
最小值	β_min/(°)	-4.24	-4.01	-1.95	-6.64	-3.63	-4.91	-6.61	-3.91	-5.59
最大值	β_max/(°)	5.66	4.88	1.70	8.35	5.43	4.80	8.34	4.63	5.19

参考文献(11)

[1]	DNVGL. OTG-13, Prediction of air gap for column-stabilized units[S], 2019.
[2]	ABS. Guidance notes on air gap and wave impact analysis for semisubmersibles[S], 2020.
[3]	MA Shan, XU Dekang, DUAN Wenyang, et al. The numerical study of viscous drag force influence on low-frequency surge motion of a semi-submersible in storm sea states[J]. Ocean engineering, 2020, 213: 107511. doi: 10.1016/j.oceaneng.2020.107511
[4]	LI Da, LU Wenyue, LI Xin, et al. Second-order resonant motions of a deep-draft semi-submersible under extreme irregular wave excitation[J]. Ocean engineering, 2020, 209: 107496. doi: 10.1016/j.oceaneng.2020.107496
[5]	MATOS V L F, RIBEIRO E O, SIMOS A N, et al. Full scale measurements and theoretical predictions of 2nd order pitch and roll slow motions of a semisubmersible platform[J]. Journal of offshore mechanics and arctic engineering, 2013, 135(3): 1-10.
[6]	孙刘璐, 于思源, 武文华, 等. 基于现场实测数据的半潜式平台运动响应分析和极值预测研究[J]. 海洋工程, 2022, 40(1): 57-64. https://www.cnki.com.cn/Article/CJFDTOTAL-HYGC202201007.htm SUN Liulu, YU Siyuan, WU Wenhua, et al. Motion analysis and extreme value prediction of semi-submersible platform based on prototype monitoring data[J]. The ocean engineering, 2022, 40(1): 57-64. https://www.cnki.com.cn/Article/CJFDTOTAL-HYGC202201007.htm
[7]	白雪平, 宋春辉, 张建宏, 等. 浮式平台阻尼特性对运动响应的影响[J]. 船舶工程, 2022, 44(S1): 597-602. https://www.cnki.com.cn/Article/CJFDTOTAL-CANB2022S1108.htm Bai Xueping, SONG Chunhui, LU Wenyue, et al. Effect of damping characteristics of floating platform on motion response[J]. Ship engineering, 2022, 44(S1): 597-602. https://www.cnki.com.cn/Article/CJFDTOTAL-CANB2022S1108.htm
[8]	KIM N, KIM C H. Cross-bi-spectral estimation of nonlinear force on fixed structure in nonlinear waves[C]//Proceedings of 12th International Offshore and Polar Engineering Conference. Kitakyushu, Japan, 2002.
[9]	KIM Y, PARK S G. On the second order effect of the springing response of large blunt ship[J]. International journal of naval architecture and ocean engineering, 2015, 7(5): 873-887. doi: 10.1515/ijnaoe-2015-0061
[10]	NUNO F. EXWAVE Semi-submersible model tests[R], 2016.
[11]	TORSETHAUGEN K, HAVER S. Simplified double peak spectral model for ocean waves[C]//Proceedings of the International Offshore and Polar Engineering Conference, 2004: 76-84.

点击查看大图

图(13) / 表(5)

摘要

半潜式平台纵摇运动高阶谱分析

doi: 10.11990/jheu.202107019

作者简介: 王金光, 男, 高级工程师, 博士研究生; 马山, 男, 教授, 博士生导师.

通讯作者: 马山, E-mail: mashan01@hrbeu.edu.cn.

出版历程

High-order spectral analysis on the pitch motion of a semisubmersible

1. 理论基础

2. 试验设置

3. 波浪生成与校核

4. 纵摇结果与分析

4.1 响应谱

4.2 纵摇运动的线性和二阶传递函数分析

5. 结论

出版历程

目录

作者简介:
王金光, 男, 高级工程师, 博士研究生;

马山, 男, 教授, 博士生导师.

通讯作者:
马山, E-mail: mashan01@hrbeu.edu.cn.