New strategy for interconversion of positive, negative, and zero Poisson's ratios
-
摘要: 针对正、负和零泊松比值难以调节的问题，本文基于曲杆/板组成的内凹式十边形多孔结构，提出了一种转换策略。采用数值模拟和实验相结合的方法验证了在不同胞壁曲率下，结构的泊松比不同(范围包括正、负和零)。研究发现: 结构的泊松比绝对值随着有效真实应变的增大而逐渐减小，随后出现了相反的泊松比值。对这种现象进行了分析，并提出了曲率效应影响机制。Abstract: To address the problem that the positive, negative and zero Poisson's ratios are difficult to adjust, a new conversion strategy is proposed based on re-entrant decagonal cellular structures composed of curved rods/plates. A combination of experiments and numerical simulations are performed to verify that the Poisson's ratios of the structures are different (the range includes positive, negative, and zero) under various rod curvatures. The absolute value of the Poisson's ratios of such structure is found to decrease gradually with the increasing effective true strain, followed by the appearance of reversed Poisson's ratios. Theoretical analysis is conducted to explain such phenomena, and a curvature effect is proposed.
-
泊松比(Poisson′s ratio，PR)目前广泛用于表征材料的力学性能[1]。自然界中材料的泊松比大多介于0.2~0.5，泊松比为负值或为零的材料在自然界中较少，需要通过人为设计得到。
负泊松比(negative Poisson′s ratio, NPR)材料在拉伸时呈横向扩张，在压缩时呈横向收缩，故又被称为拉胀材料[2]。与具有正泊松比的传统材料相比，负泊松比材料具有优异的力学性能，如抗剪切性[3-4]、抗压痕性[5]、能量吸收和断裂韧性[6-7]等可以显著提高，这使其在各个领域具有广阔的应用前景[8-9]，特别是在航空航天、生物医疗、国防以及智能系统等领域。并已代表性地用于飞机涡轮发动机的叶片中。
自然界中的负泊松比材料确实存在，如奶牛乳头部分皮肤和猫的皮肤[10]。Ting等[11]的工作表明，对于各向异性材料，只要应变能密度函数是正定的，泊松比可以有任意正负值。因此，泊松比的负值不仅是假设的，而且可以在人造材料中实现。Lakes[3]首次人为造出具有负泊松比的聚氨酯泡沫。在后续研究中根据材料内部胞元的变形机制，负泊松比材料可分为内凹型[8]、手性型[12]、旋转型[13]和穿孔型[14]。
Gibson等[15]提出了内凹型蜂窝结构。Master等[16]发现了二维内凹结构的负泊松比行为。当在任一方向施加载荷时，对角肋的移动方式会导致另一个方向的负泊松比效应。另一种由于内凹性而表现出负泊松比效应的多胞结构是双箭头[17-18]和星形[19]。这些结构中的负泊松比机制类似于内凹结构。在拉伸过程中，双箭头和星形单元打开，导致拉胀效应。
Prall等[20]提出手性蜂窝结构的概念。手性是指镜像上不能重叠，手性结构由等半径的圆形元素通过与节点相切的直韧带(壁)连接而成。这种配置通过节点的旋转和相关韧带的弯曲提供了平面内的负泊松比效应，以及允许在组成材料的弹性范围内产生高应变的变形机制。这些结构的泊松比约为-1[12]。
Grima等[13]提出了带有旋转单元的负泊松比结构。在此类结构中，负泊松比行为是由通过铰链相互连接的刚性多边形的旋转获得的，如旋转正方形[13]、旋转矩形[21]、旋转平行四边形和菱形[22]、旋转三角形[23-25]和旋转四面体[26]。基于旋转刚性单元模型的灵感，负泊松比行为也在具有菱形或星形开孔[14]的片材中得到验证。
零泊松比(zero Poisson′s ratio, ZPR)材料在受单向拉压时，不会出现横向收缩和扩张。自然界中软木等材料所呈现的泊松比被观察到等于或接近于零[27-28]。零泊松比材料因其不同寻常的特性和在医学[29]、组织工程[30]和航空[31]等不同领域的潜在应用而备受关注。在航空领域，变形机翼中使用的柔性蒙皮需要提供足够的协同变形以承受空气载荷。此外，根据光滑度的要求，需要对柔性蒙皮的不变形方向进行限制。在这些方案中，泊松比为零的材料更为可取[32]。目前针对零泊松比材料的设计主要有2种思路：1)通过材料胞元的设计实现零泊松比效应；2)混合正、负泊松比胞元获得重组后的具有零泊松比效应的新型胞元。
程文杰等[32]提出一种新型十字型混合零泊松比蜂窝结构并进行了理论验证。何玉龙等[33]通过折纸结构设计出新型零泊松比结构，并对其进行了几何分析及其耗能性能研究。Huang等[34]提出了一种由六边形部分和薄板部分组成的新颖的平面内零泊松比蜂窝结构。六边形结构用于承受面外压缩并产生面内柔性，而薄板用于产生面外柔性。这2个部分对有效力学性能有不同的贡献，需要分别设计平面内和平面外的性能。
针对正、负泊松比胞元混合构型的设计也有广泛的研究。Olympio[35]提出的构型可以实现整体微元的零泊松比效应。当周期微元受到一个方向的载荷时，微元中的正、负泊松比胞元分别收缩(膨胀)和膨胀(收缩)相同的横向变形量，整个周期微元的等效横向变形为零，即表现出零泊松比效应。Gong等[36]设计了一种零泊松比蜂窝，可以实现沿2个正交方向的变形，并通过抑制非变形方向的泊松变形，避免了变形方向的有效刚度大幅增加。
本文基于曲杆/板组成的内凹式十边形多孔结构提出了一种正、负和零泊松比相互转换的新策略。即通过改变杆的曲率，结构的泊松比可实现为正、负和零。
1. 结构的设计与制备
1.1 几何构型设计
本文提出的内凹式十边形蜂窝结构如图 1(a)所示，由4×10个胞元组成。其内凹十边形胞元如图 1(b)所示。胞元的每条边均由如图 1(c)所示的正弦梁组成。当竖向力作用于蜂窝结构时，曲梁会偏转和弯曲，导致整体结构的大变形行为。通过改变曲梁的曲率参数可以在整个蜂窝结构中实现不同的泊松比效应。余弦梁的几何形状可以表示为:
$$ t(s)=\frac{k}{L}\left(1-\cos \left(\frac{2 \pi s}{L}\right)\right) $$ (1) 
图 1 内凹式十边形蜂窝结构的几何构型设计Fig. 1 Geometric configuration design of re-entrant decagonal honeycomb structure
下载:
全尺寸图片
式中：t为余弦梁的函数形式；L为余弦梁的长度；k为余弦梁的曲率。2个胞元之间均由横向直梁连接。横向直梁的存在可以联动整个结构的横向变形。
1.2 样品制备
制备样品的材料体系选用热塑性聚氨酯。热塑性聚氨酯是增材制造技术中最常用的聚合物之一，在世界上应用广泛。具有来源广、韧性好、强度高、成本低、耐高温等优点。且热塑性聚氨酯是一种成熟的环保材料，具有优良的耐磨性、耐老化性和安全性等优点。采用熔融沉积(FDM)3-D打印技术(HORI Z500，北京汇天威科技有限公司)对样品进行制备。图 2(a)为样品的3-D打印示意图。制备的样品实物如图 2(b)所示。这种增材制造技术有许多优点：可以制造不同材料和尺寸的复杂实体或腔体结构；结构的打印精度极高(可达0.05 mm)，制造成本较低。根据ASTM D638-14拉伸实验测试标准，获得了原材料热塑性聚氨酯的拉伸应力-应变曲线，如图 3所示，其材料基本力学性能如表 1所示。
图 2 样品的制备过程示意Fig. 2 Schematic diagram of the preparation process of the sample下载:
全尺寸图片
图 3 原材料热塑性聚氨酯的拉伸应力-应变曲线Fig. 3 The stress-strain curve of the base material TPU下载:
全尺寸图片
表 1 热塑性聚氨酯的弹性属性Table 1 The elastic properties of thermoplastic polyurethane属性 量值 密度/(kg·m-3) 1 150 泊松比 0.3 杨氏模量/MPa 52 2. 研究方法
2.1 有限元方法
为了研究和探索结构在竖向荷载作用下的变形特征及力学性能，采用商用有限元(FE)计算软件ABAQUS/Explicit求解器进行了数值模拟。首先通过建模软件SOILDWORKS建立了结构的三维CAD模型，并导入到ABAQUS中。在有限元模型中，由于结构的瞬变特性，考虑了几何非线性。采用适用于求解大应变问题的八节点线性减缩积分六面体单元(C3D8R)对蜂窝结构进行网格划分。采用线性减缩积分单元的优点是：当网格发生畸变时，分析精度不会受到很大影响[37-38]。在每个模型中，结构横截面上都有3个以上的单元，以满足网格收敛性要求。表 1中列出的热塑性聚氨酯(TPU)材料的力学参数应用到有限元模型中。拉伸试验的有限元模型如图 4所示。蜂窝上下表面用卡具固定，并采用体积中心有参考点的离散刚体对拉伸卡具进行模拟。在模拟过程中，卡具与试样之间进行绑定。同时，顶部参考点受竖向位移载荷作用，其他5个自由度均固定。同时，限制底部卡具基准点的所有自由度。为了消除边界效应，在结构中间设置4个参考点作为测量点，用于监测结构的横向变形和竖向变形。
图 4 蜂窝结构有限元模型Fig. 4 The FE model of the honeycomb structure下载:
全尺寸图片
2.2 实验方法
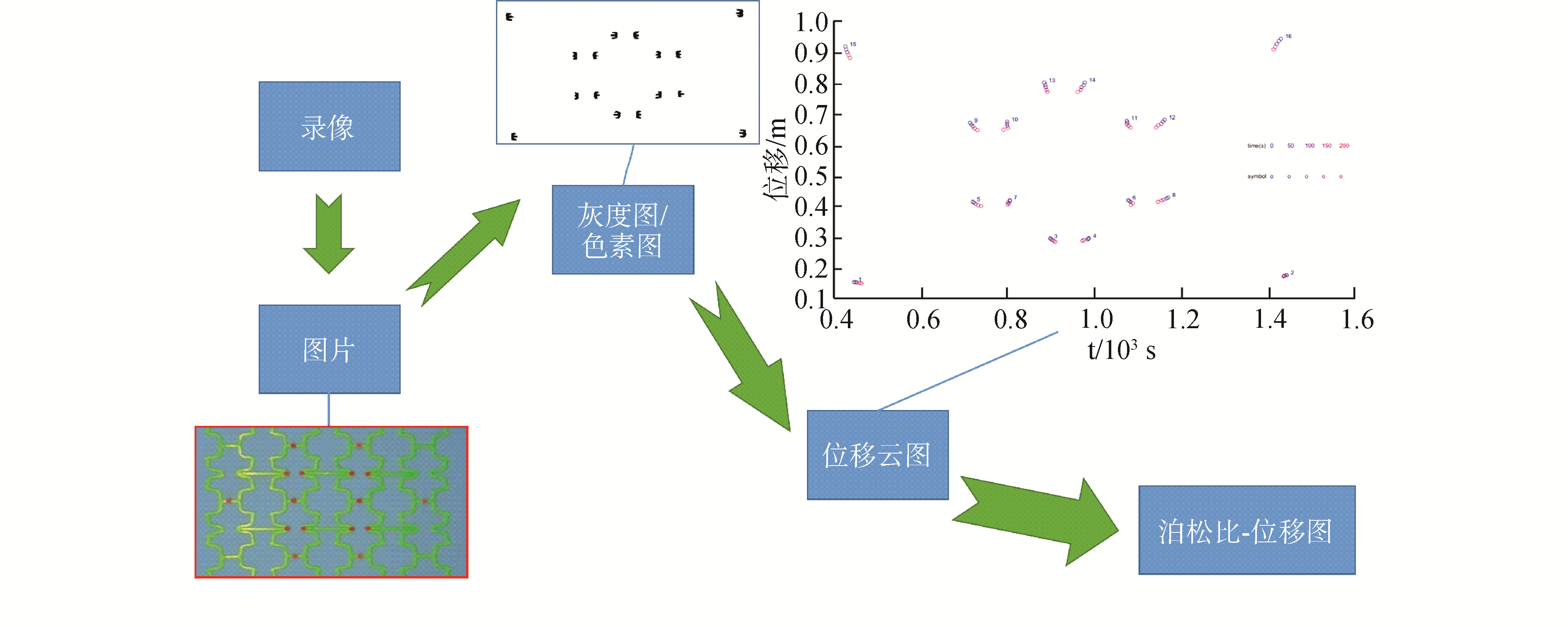
为了验证有限元结果的有效性，采用INSTRON 5569试验机对结构沿垂直方向进行了准静态拉伸试验。准静态拉伸试样的实验装置如图 5(a)所示，试样上下两端通过特制夹具进行固定，以便和试验机夹头进行连接。实验过程采用位移加载控制，恒定位移速率设置为1 mm/min，避免了动态影响。在试验过程中，监测试样的横向变形和纵向变形。为了准确测量试样的泊松比值，提出一种简易的DIC技术方法。拉伸试验前，在样品中心标记点，如图 5(b)所示。在拉伸过程中，使用高分辨率数码相机对拉伸试样进行视频记录，如图 5(a)所示。然后将视频裁剪成反映整个拉伸过程的一系列连续图片，利用图像处理技术得到每个标记点中心的运动轨迹，通过轨迹的计算即可得到试样的纵向应变-横向应变图，继而得到结构泊松比值，其整个方法过程如图 6所示。实验测试结果也用于验证有限元结果。
图 5 实验技术方法Fig. 5 Experimental techniques and methods下载:
全尺寸图片
图 6 简易的DIC技术方法Fig. 6 Simple DIC technology method下载:
全尺寸图片
3. 结果分析与讨论
3.1 胞元构型的确定
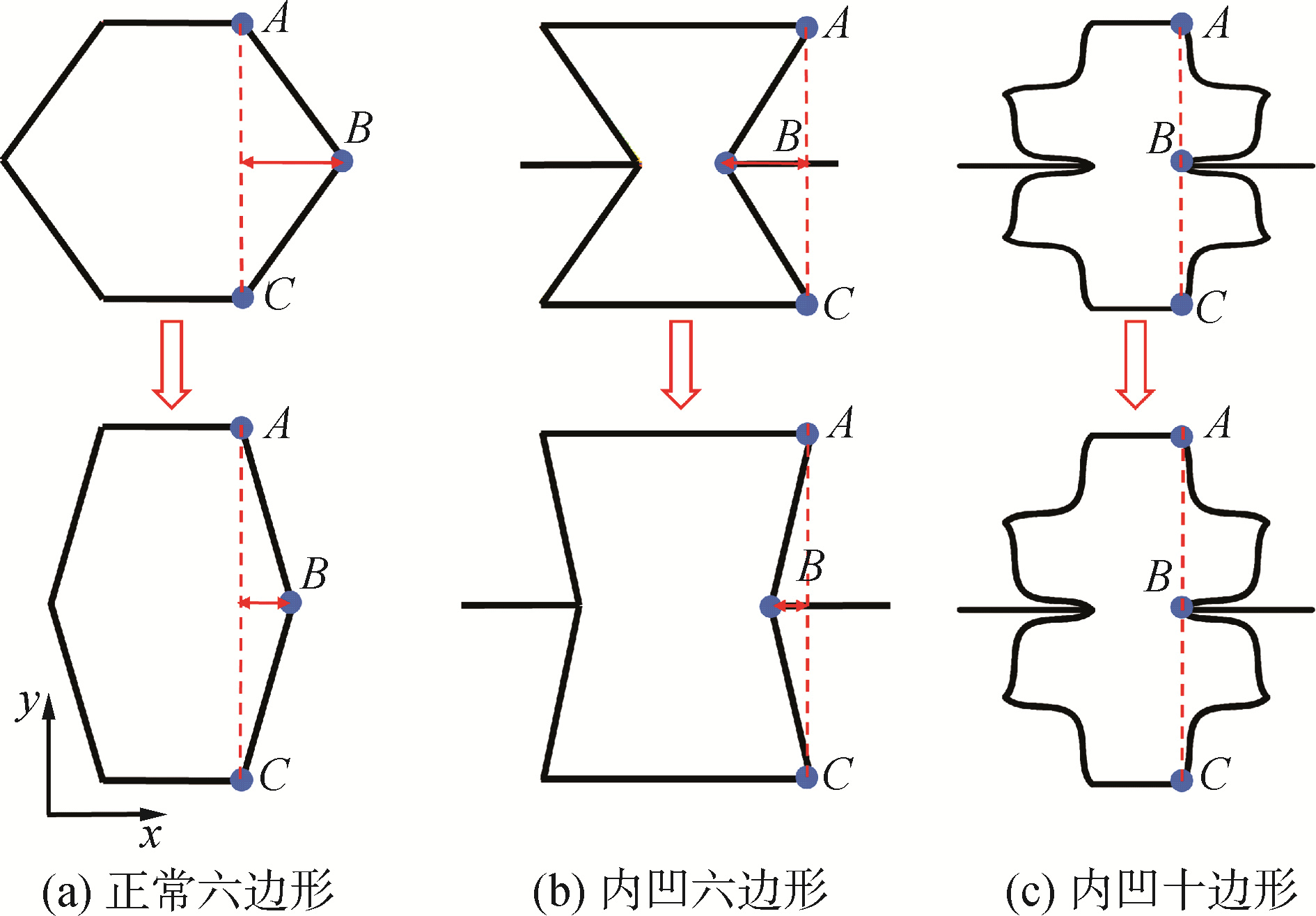
图 7对比了正常凸式六边形胞元、内凹式六边形胞元和内凹式十边形胞元的几何特征。可以看出结构的泊松比效应是由A、B和C 3个节点的移动方向共同决定的。对于正常凸式六边形和内凹式六边形胞元，3个节点坐标在x方向的位置满足: xA=xC≠xB。在y向拉伸载荷下，节点B在x方向的坐标xB总是朝向xA和xc坐标方向移动。这种外凸(或内凹)的机制使正常六边形胞元和内凹式六边形胞元呈现相反的泊松比效应，分别表现出正泊松比效应和负泊松比效应。在内凹式十边形胞元中，3个节点的坐标在x方向的位置满足: xA=xC=xB。因为这种胞元同时存在内凹和外凸的机制，如果杆是直的，在y向拉伸载荷下节点B的坐标xB依然和节点A和C的坐标一致，即xA=xC=xB，此种情况下胞元的泊松比表现为零。但是，如果杆具有特殊的曲率，则在y方向拉伸情况下节点B的坐标xB将远离节点A和C的坐标(xA和xc)，即表现出正或负泊松比效应，其具体分析见下节。因此，本文选用具有不同曲率的内凹十边形胞元组成具有不同泊松比效应的蜂窝结构。
图 7 胞元构型的对比Fig. 7 Comparison of cell configurations下载:
全尺寸图片
3.2 曲率的影响
本文考虑了3种杆曲率内凹十边形胞元，如图 8所示。在局部坐标系(s, t)中杆的曲率函数被表达为式(1)。为简化分析，把L视为一个常数。3种胞元杆的曲率k分别取为2、0和-2。限定t′(s)s=0=t′(s)s=L=0，所以对于不同的曲率k，杆的末端总是具有相同的方向。
图 8 曲率的影响Fig. 8 The effect of curvature下载:
全尺寸图片
为了拓展工程应用，曲板也常作为内凹十边形多孔结构的胞元壁，且为说明胞元在拉伸载荷和压缩载荷下表现出同种性质的泊松比效应，本节中3种具有不同曲率k的胞元结构均由曲板组成，且受到压缩载荷作用，其变形情况如图 8所示。可以看出，当k>0时, 胞元结构呈现正的泊松比；当k=0时，胞元结构呈现零泊松比；当k < 0时，胞元结构呈现负的泊松比。很明显，对于不同的k，胞元可以实现正、负和零泊松比的转换。
3.3 实验结果与仿真结果的对比
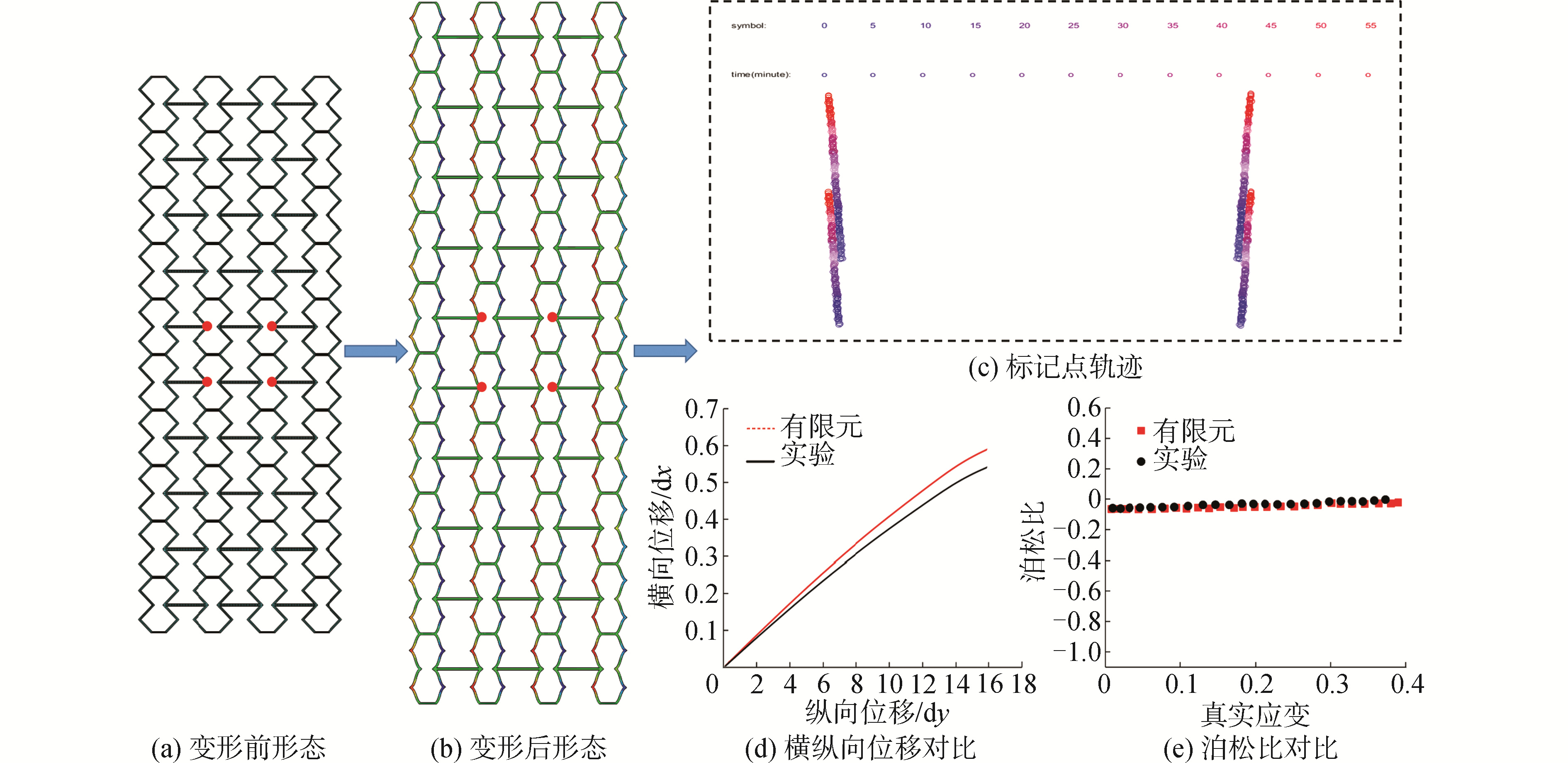
本节在3.2节单胞研究的基础上进行了蜂窝结构的研究。蜂窝样品的结构参数为：曲梁长度L=10 mm，曲梁面内厚度T=1 mm，所有试样的面外厚度均为b=1.6 mm。图 9展示了k=2情况下蜂窝结构在拉伸载荷下的响应分析。将实验得到的蜂窝结构纵向位移(dy)和横向位移(dx)响应与仿真结果进行了对比，如图 9(d)所示。蜂窝结构在拉伸载荷下呈现出的变形形态如图 9(a)、(b)所示。图 9(e)为蜂窝结构在变形过程中表现出的泊松比值。从图 9中可以看出，实验结果与有限元预测在泊松比量值和变形形态方面表现出定量一致性。其结果略区别于单胞结构，即当k>0时，蜂窝结构呈现正的泊松比，随着真实应变的增大，结构的泊松比呈现减小趋势，随后出现负的泊松比。结构的泊松比从正到零，再到负，是一条近乎线性的曲线。这是因为在小变形时，结构节点位置大致满足xA=xC=xB，非零泊松比是由杆的曲率效应造成的。变形较大时，杆件的曲率减小, xB偏离xA和xC，即出现位错。随着位错的增加和曲率的减小，内凹(或凸)机制将取代曲率效应成为影响泊松比的主要因素。在小变形条件下，有限元分析结果与实验结果吻合较好。在较大的变形量下，虽然泊松比的变化趋势相似，但有限元计算结果与实验结果有较大偏差。其偏差主要由以下2个原因造成的：1)熔融沉积(FDM)3-D打印技术在结构尺寸过大的情况下，打印质量存在一定缺陷；2)在有限元计算中把材料假设成了理想弹性，而结构在大变形情况下会有部分塑性变形发生，这也是造成结果偏差的原因之一。
图 9 k=2情况下蜂窝结构在拉伸载荷下的响应分析Fig. 9 Response analysis of honeycomb structure under tensile load when k=2下载:
全尺寸图片
图 10展示了k=0情况下蜂窝结构在拉伸载荷下的响应分析。图 10(d)为实验得到的蜂窝结构纵向位移(dy)和横向位移(dx)响应与仿真的对比结果。蜂窝结构在拉伸载荷下呈现出的变形形态如图 10(a)、(b)所示。图 10(e)为蜂窝结构在变形过程中表现出的泊松比值。从图 10中可以看出，实验结果与有限元预测在泊松比量值和变形形态方面表现出定量一致性。即当k=0时，蜂窝结构随着真实应变的增大始终呈现近乎零的泊松比。这是因为在结构变形时，节点位置坐标大致始终满足xA=xC=xB。
图 10 k=0情况下蜂窝结构在拉伸载荷下的响应分析Fig. 10 Response analysis of honeycomb structure under tensile load when k=0下载:
全尺寸图片
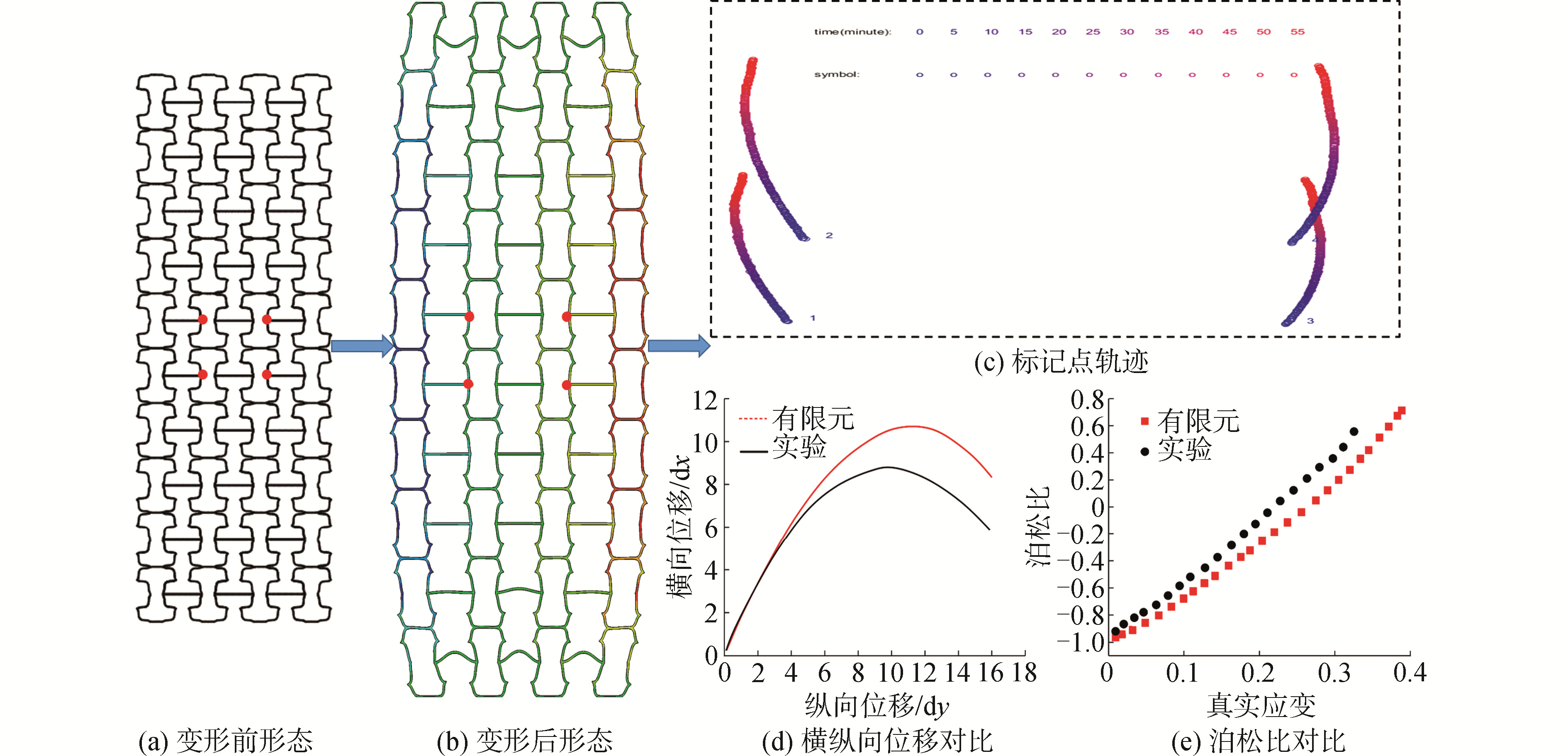
图 11展示了k=-2情况下蜂窝结构在拉伸载荷下的响应分析。图 11(d)为实验得到的蜂窝结构纵向位移(dy)和横向位移(dx)响应与仿真的对比结果。蜂窝结构在拉伸载荷下呈现出的变形形态如图 11(a)(b)所示。图 11(e)为蜂窝结构在变形过程中表现出的泊松比值。从图 11中可以看出，实验结果与有限元预测在泊松比量值和变形形态方面表现出定量一致性。即当k < 0时，结构的泊松比从负到零，再到正。其原因同样是：在小变形时，结构节点位置大致满足xA=xC=xB，非零泊松比是由杆的曲率效应造成的；大变形时，内凹(或凸)机制将取代曲率效应成为影响泊松比的主要因素。
图 11 k=-2情况下蜂窝结构在拉伸载荷下的响应分析Fig. 11 Response analysis of honeycomb structure under tensile load when k=-2下载:
全尺寸图片
4. 结论
1) 当曲率k>0时，结构呈现正的泊松比，随着真实应变的增大，结构的泊松比呈现减小趋势，随后出现负的泊松比。结构的泊松比从正到零，再到负，是一条近乎线性的曲线。
2) 当曲率k=0时，结构在整个变形中始终表现为近乎零的泊松比。
3) 当曲率k < 0时，结构呈现负的泊松比，随着真实应变的增大，结构的泊松比转变为正。即结构的泊松比从负到零，再到正。
不同曲率下内凹十边形蜂窝结构的泊松比绝对值随着有效真实应变的增大，逐渐减小，而后出现了相反的泊松比。对这种现象进行了分析，并提出了一种曲率效应。结果表明，在小变形条件下，杆件的非零泊松比是由杆件的曲率效应引起的。而在大变形条件下，泊松比的转换是由结构内凹(或凸)的机制取代曲率效应成为主导机制引起的。
-
图 1 内凹式十边形蜂窝结构的几何构型设计
Fig. 1 Geometric configuration design of re-entrant decagonal honeycomb structure
下载:
全尺寸图片
图 2 样品的制备过程示意
Fig. 2 Schematic diagram of the preparation process of the sample
下载:
全尺寸图片
图 3 原材料热塑性聚氨酯的拉伸应力-应变曲线
Fig. 3 The stress-strain curve of the base material TPU
下载:
全尺寸图片
图 4 蜂窝结构有限元模型
Fig. 4 The FE model of the honeycomb structure
下载:
全尺寸图片
图 5 实验技术方法
Fig. 5 Experimental techniques and methods
下载:
全尺寸图片
图 6 简易的DIC技术方法
Fig. 6 Simple DIC technology method
下载:
全尺寸图片
图 7 胞元构型的对比
Fig. 7 Comparison of cell configurations
下载:
全尺寸图片
图 8 曲率的影响
Fig. 8 The effect of curvature
下载:
全尺寸图片
图 9 k=2情况下蜂窝结构在拉伸载荷下的响应分析
Fig. 9 Response analysis of honeycomb structure under tensile load when k=2
下载:
全尺寸图片
图 10 k=0情况下蜂窝结构在拉伸载荷下的响应分析
Fig. 10 Response analysis of honeycomb structure under tensile load when k=0
下载:
全尺寸图片
图 11 k=-2情况下蜂窝结构在拉伸载荷下的响应分析
Fig. 11 Response analysis of honeycomb structure under tensile load when k=-2
下载:
全尺寸图片
表 1 热塑性聚氨酯的弹性属性
Table 1 The elastic properties of thermoplastic polyurethane
属性 量值 密度/(kg·m-3) 1 150 泊松比 0.3 杨氏模量/MPa 52 -
[1] GREAVES G N. Poisson's ratio over two centuries: challenging hypotheses[J]. Notes and records: the royal society journal of the history of science, 2013, 67(1): 37-58. doi: 10.1098/rsnr.2012.0021 [2] EVANS K E, NKANSAH M A, HUTCHINSON I J, et al. Molecular network design[J]. Nature, 1991, 353(6340): 124. doi: 10.1038/353124a0 [3] LAKES R. Foam structures with a negative poisson's ratio[J]. Science, 1987, 235(4792): 1038-1040. doi: 10.1126/science.235.4792.1038 [4] CHOI J B, LAKES R S. Non-linear properties of polymer cellular materials with a negative Poisson's ratio[J]. Journal of materials science, 1992, 27(17): 4678-4684. doi: 10.1007/BF01166005 [5] ALLEN T, SHEPHERD J, HEWAGE T A M, et al. Low-kinetic energy impact response of auxetic and conventional open-cell polyurethane foams[J]. Physica status solidi (b), 2015, 252(7): 1631-1639. doi: 10.1002/pssb.201451715 [6] LAKES R S, ELMS K. Indentability of conventional and negative poisson's ratio foams[J]. Journal of composite materials, 1993, 27(12): 1193-1202. doi: 10.1177/002199839302701203 [7] SCARPA F, CIFFO L G, YATES J R. Dynamic properties of high structural integrity auxetic open cell foam[J]. Smart materials and structures, 2004, 13(1): 49-56. doi: 10.1088/0964-1726/13/1/006 [8] SAXENA K K, DAS R, CALIUS E P. Three decades of auxetics research-materials with negative poisson's ratio: a review[J]. Advanced engineering materials, 2016, 18(11): 1847-1870. doi: 10.1002/adem.201600053 [9] MILTON G W. Composite materials with poisson's ratios close to-1[J]. Journal of the mechanics and physics of solids, 1992, 40(5): 1105-1137. doi: 10.1016/0022-5096(92)90063-8 [10] LEES C, VINCENT J F, HILLERTON J E. Poisson's ratio in skin[J]. Bio-medical materials and engineering, 1991, 1(1): 19-23. doi: 10.3233/BME-1991-1104 [11] TING T C T, CHEN T. Poisson's ratio for anisotropic elastic materials can have no bounds[J]. The quarterly journal of mechanics and applied mathematics, 2005, 58(1): 73-82. doi: 10.1093/qjmamj/hbh021 [12] PRALL D, LAKES R S. Properties of a chiral honeycomb with a poisson's ratio of-1[J]. International journal of mechanical sciences, 1997, 39(3): 305-314. doi: 10.1016/S0020-7403(96)00025-2 [13] GRIMA J N, EVANS K E. Auxetic behavior from rotating squares[J]. Journal of materials science letters, 2000, 19(17): 1563-1565. doi: 10.1023/A:1006781224002 [14] GRIMA J N, GATT R. Perforated sheets exhibiting negative poisson's ratios[J]. Advanced engineering materials, 2010, 12(6): 460-464. doi: 10.1002/adem.201000005 [15] LORNA J M, GIBSON F G, ASHBY S C, et al. The mechanics of two-dimensional cellular materials[J]. Proceedings of the royal society of London A mathematical and physical sciences, 1982, 382(1782): 25-42. doi: 10.1098/rspa.1982.0087 [16] MASTERS I G, EVANS K E. Models for the elastic deformation of honeycombs[J]. Composite structures, 1996, 35(4): 403-422. doi: 10.1016/S0263-8223(96)00054-2 [17] LARSEN U D, SIGNUND O, BOUWSTA S. Design and fabrication of compliant micromechanisms and structures with negative Poisson's ratio[J]. Journal of microelectromechanical systems, 1997, 6(2): 99-106. doi: 10.1109/84.585787 [18] MA Z D. Three-dimensional auxetic structures and applications thereof, in, US, 2011. [19] GRIMA J N, GATT R, ALDERSON A, et al. On the potential of connected stars as auxetic systems[J]. Molecular simulation, 2005, 31(13): 925-935. doi: 10.1080/08927020500401139 [20] EVANS K E. The design of doubly curved sandwich panels with honeycomb cores[J]. Composite structures, 1991, 17(2): 95-111. doi: 10.1016/0263-8223(91)90064-6 [21] GRIMA J N, ALDERSON A, EVANS K E. Negative poisson's ratios from rotating rectangles[J]. Computational methods in science and technology, 2004, 10(2): 137-145. doi: 10.12921/cmst.2004.10.02.137-145 [22] GRIMA J N, FARRUGIA P S, GATT R, et al. On the auxetic properties of rotating rhombi and parallelograms: a preliminary investigation[J]. Physica status solidi (b), 2008, 245(3): 521-529. doi: 10.1002/pssb.200777705 [23] GRIMA J N, EVANS K E. Auxetic behavior from rotating triangles[J]. Journal of materials science, 2006, 41(10): 3193-3196. doi: 10.1007/s10853-006-6339-8 [24] GRIMA J N, CHETCUTI E, MANICARO E, et al. On the auxetic properties of generic rotating rigid triangles[J]. Proceedings of the royal society A: mathematical, physical and engineering sciences, 2012, 468(2139): 810-830. doi: 10.1098/rspa.2011.0273 [25] GRIMA J N, GATT R, ELLUL B, et al. Auxetic behaviour in non-crystalline materials having star or triangular shaped perforations[J]. Journal of non-crystalline solids, 2010, 356(37/38/39/40): 1980-1987. [26] ALDERSON A, EVANS K E. Rotation and dilation deformation mechanisms for auxetic behaviour in the α-cristobalite tetrahedral framework structure[J]. Physics and chemistry of minerals, 2001, 28(10): 711-718. doi: 10.1007/s002690100209 [27] GREAVES G N. Poisson's ratio over two centuries: challenging hypotheses[J]. Notes and records of the royal society of london, 2013, 67(1): 37-58. doi: 10.1098/rsnr.2012.0021 [28] FORTES M A, TERESA NOGUEIRA M. The poison effect in cork[J]. Materials science and engineering: a, 1989, 122(2): 227-232. doi: 10.1016/0921-5093(89)90634-5 [29] SOMAN P, FOZDAR D Y, LEE J W, et al. A three-dimensional polymer scaffolding material exhibiting a zero Poisson's ratio[J]. Soft matter, 2012, 8(18): 4946-4951. doi: 10.1039/c2sm07354d [30] ENGELMAYR G C Jr, CHENG Mingyu, BETTINGER C J, et al. Accordion-like honeycombs for tissue engineering of cardiac anisotropy[J]. Nature materials, 2008, 7(12): 1003-1010. doi: 10.1038/nmat2316 [31] CHEN Jinjin, SHEN Xing, LI Jiefeng. Zero Poisson's ratio flexible skin for potential two-dimensional wing morphing[J]. Aerospace science and technology, 2015, 45: 228-241. doi: 10.1016/j.ast.2015.05.011 [32] 程文杰, 周丽, 张平, 等. 零泊松比十字形混合蜂窝设计分析及其在柔性蒙皮中的应用[J]. 航空学报, 2015, 36(2): 680-690. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201502029.htm CHENG Wenjie, ZHOU Li, ZHANG Ping, et al. Design and analysis of a zero Poisson's ratio mixed cruciform honeycomb and its application in flexible skin[J]. Acta aeronautica et astronautica sinica, 2015, 36(2): 680-690. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201502029.htm [33] 何玉龙, 王志华, 树学峰, 等. 新型折纸结构的运动特征及力学响应[C]//2018年全国固体力学学术会议. [S. l. ], 2018. HE Yulong, WANG Zhihua, SHU Xuefeng, et al. Motion characteristics and mechanical response of a novel origami structure[C]//2018 National Conference on solid mechanics. [S. l. ], 2018. [34] HUANG Jian, GONG Xiaobo, ZHANG Qiuhua, et al. In-plane mechanics of a novel zero Poisson's ratio honeycomb core[J]. Composites part B: engineering, 2016, 89: 67-76. doi: 10.1016/j.compositesb.2015.11.032 [35] OLYMPIO K R, GANDHI F. Zero poisson's ratio cellular honeycombs for flex skins undergoing one-dimensional morphing[J]. Journal of intelligent material systems and structures, 2010, 21(17): 1737-1753. doi: 10.1177/1045389X09355664 [36] GONG Xiaobo, HUANG Jian, SCARPA F, et al. Zero Poisson's ratio cellular structure for two-dimensional morphing applications[J]. Composite structures, 2015, 134: 384-392. doi: 10.1016/j.compstruct.2015.08.048 [37] FLANAGAN D P, BELYTSCHKO T. A uniform strain hexahedron and quadrilateral with orthogonal hourglass control[J]. International journal for numerical methods in engineering, 1981, 17(5): 679-706. doi: 10.1002/nme.1620170504 [38] BURSI O S, JASPART J P. Calibration of a finite element model for isolated bolted end-plate steel connections[J]. Journal of constructional steel research, 1997, 44(3): 225-262. doi: 10.1016/S0143-974X(97)00056-4
