Characteristics of the wave group of parametric rolling for the C11 container ship amid head random waves
-
摘要: 针对迎浪随机波中集装箱船的参数激励横摇问题，本文主要研究船舶遭遇到的波浪条件与船舶参数激励横摇状态的相关性。基于C11集装箱船迎浪不规则波参数激励横摇实验，通过横摇幅值定义船舶发生显著参数激励横摇的时间段，然后通过波群方法分析船舶在横摇筛选段附近遭遇特征波群的特性。研究结果表明: 船舶遭遇特征波群参数与船舶参数激励横摇的剧烈程度有较强的相关性, 船舶遭遇特征波群数量和连长个数是船舶参数横摇剧烈程度的重要影响因素。Abstract: This study investigates the correlation between ship-encountered wave groups and the status of ship parametric rolling while focusing on the parametric rolling of a container ship in random waves. The rolling amplitude is used to define the time segment of significant parametric rolling based on the parametric excitation rolling test of the C11 container ship in irregular waves. The wave group method then analyzes the ship's characteristics when it encounters characteristic wave groups during the selected parametric rolling segments. Results show a strong correlation between the ship-encountered characteristic wave groups and the intensity of ship parametric rolling. The number and length of the runs of characteristic wave groups have a significant impact on the severity of ship parametric rolling in random seas.
-
Keywords:
- head wave /
- random wave /
- wave group /
- container ship /
- parametric rolling /
- statistical theory of run /
- dangerous sea state /
- model test
-
集装箱船由于其运载量大、装卸效率高等特点，一直是大宗货物运输和远洋贸易中的主要力量。因此，集装箱船的航行性能和安全性一直备受关注。船舶参数激励横摇是船舶在波浪中的失稳形式之一，通常会在迎浪或随浪航行时发生。集装箱船由于需要装载大量的货物、保持较高航速，通常具有较大的艏艉外飘。因此集装箱船相对于其他船舶，在海浪中航行时初稳性变化更加剧烈，更容易发生参数激励横摇，更容易发生船舶失稳事故[1]。
随机波浪中的船舶参数激励横摇受海洋环境因素影响较大，是一个复杂的非线性力学问题，有较强的非各态历经性。Bulian等[2]在拖曳水池针对部分约束的集装箱船开展迎浪长峰不规则波参数横摇实验，发现参数横摇有显著的非各态历经性，不同随机种子数下横摇峰值累积概率密度曲线有明显差别，横摇摇幅不服从瑞利分布。
Park[3]等对2条集装箱船在不规则波中进行数值模拟，发现在不规则波数值模拟中，特别是集中在横摇固有频率1/2附近的海浪谱离散频率，其离散数量和离散方法对船舶参数激励横摇有明显影响。许文浩[4]分析了模型实验和数值模拟中船舶遭遇随机波浪引起的横摇和纵摇运动幅值概率的不确定性，其分析结果表明在相同海况不同子波序列中，船舶参数激励横摇幅值概率密度函数具有很强的离散性, 验证了船舶参数激励横摇运动幅值具有显著的非各态历经特征。
随机波中船舶参数激励横摇的发生具有很强的随机性，其剧烈程度与船舶遭遇的波浪特性密切相关。Belenky等[5]通过与海洋波群的比较，定义了一个临界波群并分析了波群中的不同顺序波的波幅、周期、波陡等参数的概率统计规律。Anastopoulos等[6]提出了一种基于马尔可夫链、含有多个子波的单个波群构建方法，并且将衍生波群用于船舶稳性评估。Kennedy[7]提出了一种基于贝叶斯假说检验的单侧或双侧算法来预测船舶参数激励横摇的概率，数值分析结果表明使用纵摇运动构建的贝叶斯概率模型比升沉运动构建的模型可以更好地识别船舶参数激励横摇运动的发生。马小剑[8]利用2种模拟群性波浪方法，即采用谱峰因子和频谱与波包谱相结合的方法对系泊船舶进行横摇运动响应分析。Wang等[9]利用单自由度方程对船舶参数激励横摇运动进行数值模拟，采用波包谱模拟不规则波波群。通过对船舶横摇运动模拟结果分析，发现群长因子对船舶参数激励横摇有明显的影响。
当前基于波群的参数激励横摇研究中主要是通过设定理论波群模型来研究波群参数的影响，缺乏对随机波中船舶发生参数激励横摇摇幅与波群相关性的分析。为研究随机波中船舶参数激励横摇运动的作用机理，本文以C11集装箱船为研究对象，对迎浪随机波中参数激励横摇实验数据进行分析，通过横摇幅值定义船舶发生参数激励横摇的危险时段，研究船舶发生参数激励横摇过程中遭遇特征波群的波群参数，分析给出了船舶参数激励横摇与船舶遭遇波浪波群特性的相关性。
1. 船型参数和实验条件
1.1 C11集装箱船参数
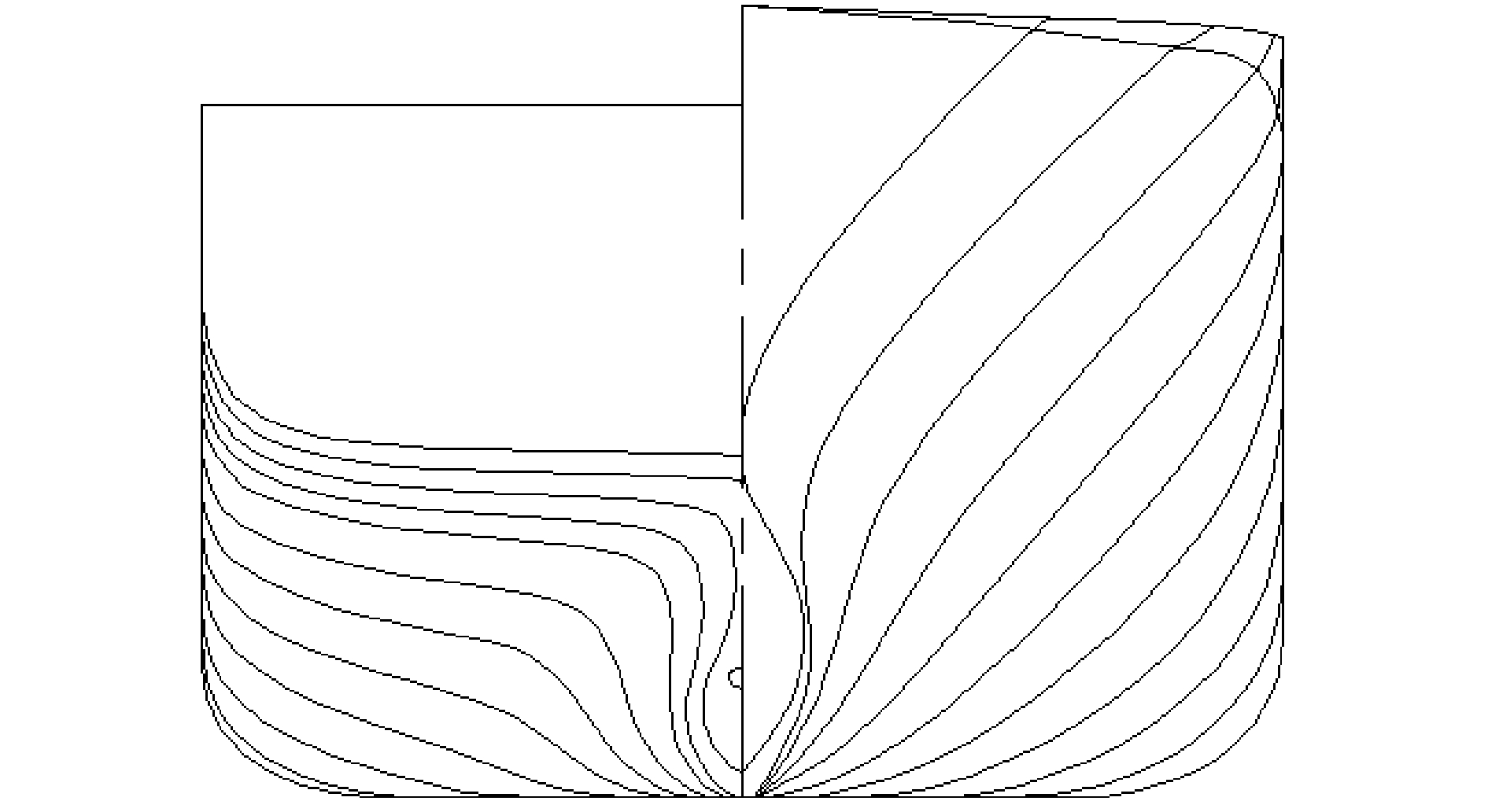
本文研究船型为巴拿马型C11集装箱船，其船艏艉均有明显的外飘，船舯则是渐近直壁。船舶模型满足和实船的几何相似和运动相似条件。船舶主尺度如表 1所示，船舶型线图如图 1所示。模型与实船的缩尺比为1∶65.5。
表 1 C11集装箱船主要参数Table 1 Principal dimensions of C11 container ship参数 实船尺度 模型尺度 垂线间长Lpp/m 262.00 4.000 型宽B/m 40.00 0.611 型深/m 24.45 0.373 平均吃水/m 11.80 0.180 方形系数 0.566 0.566 排水体积/m3 69 957.96 0.249 重心垂向位置(距基线)/m 18.44 0.281 重心纵向位置(距船舯)/m -5.77 -0.088 横摇初稳性高/m 1.90 0.029 横摇惯性半径/m 0.38B 0.38B 纵摇惯性半径/m 0.24Lpp 0.24Lpp 横摇固有周期/s 24.50 3.027 
图 1 C11集装箱船型线图Fig. 1 Offset lines of C11 container ship
下载:
全尺寸图片
1.2 波浪参数和实验工况
本文分析的模型实验数据来自于中船重工702所。实验是在中船重工702所拖曳水池进行，实验船模采用自航方式，船模上装备有舵、桨和电子推进方式。模型实验中螺旋桨转速可通过手动调整来维持目标航速，而舵角通过自动调整维持船舶迎浪浪向不变。在模型实验时，船艏前大约1.5 m的右侧前方布置浪高仪。
本次实验海况选定为7级海况，海浪谱类型为ITTC双参数谱，实船有义波高为7.5 m，谱峰周期为14.4 s。分别开展了傅氏数为0、0.05和0.10等3个航速下迎浪180°的随机波中船舶参数激励横摇实验，每个航速下进行了10组随机种子数相同海浪谱下的实验，每组随机种子数下测试时间不小于10 min。下文中所有横摇运动和波浪数据的统计分析都是按傅氏数相似转换成实船尺度进行。本文重点讨论零航速和傅氏数为0.05工况。实验中典型场景如图 2所示。
图 2 模型实验中发生的典型参数激励横摇过程Fig. 2 Typical parametric rolling phenomena in model test下载:
全尺寸图片
2. 参数激励横摇发生时段识别和波群分析方法
为了研究参数激励横摇与船舶遭遇波浪特性的相关性，分析随机波群作用的影响规律。本文首先针对物理模型实验测量结果中的横摇运动数据进行筛选，找出较为明显的参数激励横摇运动时段，给出船舶参数激励横摇显著时间信号的筛选方法。然后介绍船舶参数激励横摇对应波浪的波群分析方法。
2.1 参数激励横摇发生筛选段的定义
船舶参数激励横摇主要指船舶迎浪或随浪航行时，当船舶遭遇波浪频率接近横摇固有频率2倍时，因船舶在波浪中复原力矩随时间周期性变化，在短时间产生很大的横摇角的非线性共振现象。
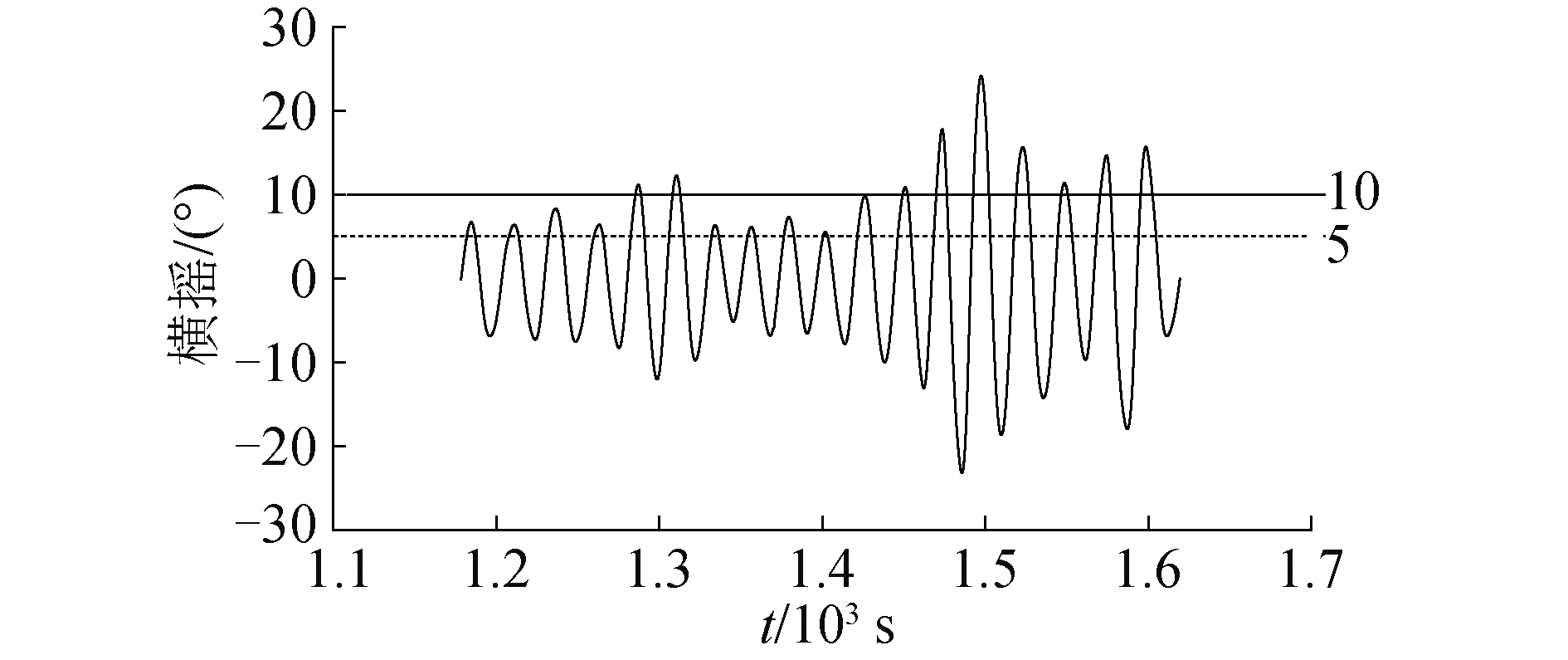
船舶横摇幅值是描述船舶横摇状态最直观和最易测量的参数。大量的实验和数值模拟研究都以船舶横摇幅值为标准，判断船舶参数激励横摇的剧烈程度。本文以702所迎浪不规则波参数激励横摇实验数据为基础，对其中的横摇运动时历进行分析。首先针对横摇幅值时间序列进行统计，将最小幅值超过5°，最大幅值超过一定横摇角的横摇时历片段定义为船舶参数激励横摇筛选段(结合横摇摇幅随航速统计变化规律和个人主观经验，最大幅值在零航速时取为10°，傅氏数为0.05时取为7°)，即迎浪中船舶发生参数激励横摇的危险时段。在本文中统一使用横摇筛选段简称船舶发生参数激励横摇的危险时段，零航速时选取的横摇筛选段示意如图 3所示。
图 3 船舶参数激励横摇筛选段示意Fig. 3 Selected ship parametric rolling segments下载:
全尺寸图片
图 3(a)为零航速第1组随机种子数波浪时历下的参数激励横摇完整时历，图 3(b)为横摇筛选段对应的横摇时历，是通过本节定义的横摇筛选段处理方法分析得到的较为危险的横摇运动时历。统计结果中有5组横摇筛选段，说明在零航速第1组随机种子数波浪激励作用下的实验中，船舶共发生5次较为显著的参数激励横摇过程。图 4为横摇筛选段1对应的横摇运动时历示意图，清晰展示了随机波中船舶参数激励横摇运动的一次发生过程，横摇幅值由小到大再变小，呈现包络状，持续变化。
图 4 横摇筛选段1示意Fig. 4 Selected parametric rolling segment 1下载:
全尺寸图片
2.2 波群分析方法
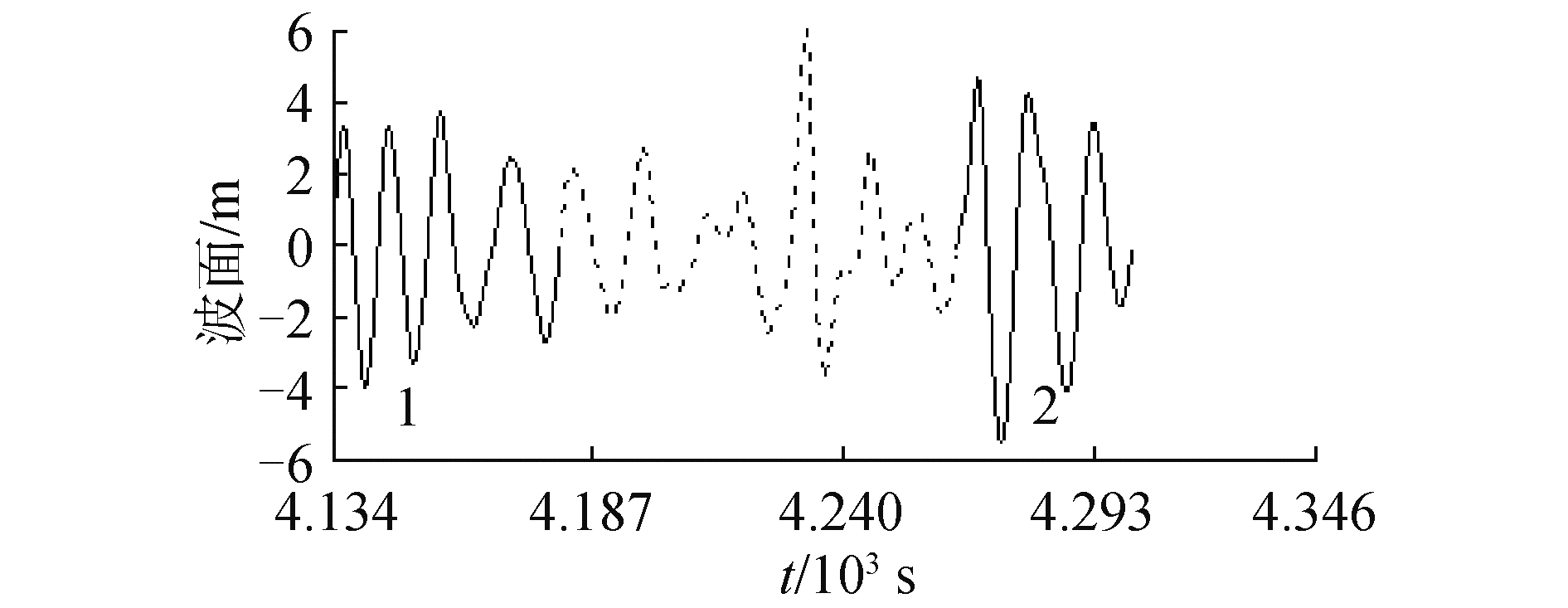
Masson等[10]将波群看作为一连续出现的大波组成的波列，波群中每个单独波浪的波高都超过了某个预设阀值，同时每个波浪的周期值在一个小范围内变化。俞聿修等[11]介绍了波包线方法、波能过程线方法和连的统计理论等波群分析方法。本文利用连的统计理论直接对实验测试的波浪数据进行时域统计，其中波群的波高门槛值设定为0.4 Hs，其中Hs表示波浪有义波高。波群连长即连续出现的各波高超过波高门槛值的子波个数，在统计时单个波群连长下限设定为3。波群示意图如图 5所示。在图 5的波浪片段中有2组波群，波群连长分别为4和3。本文在分析出横摇筛选段后，将其对应时间范围内的波群定义为与船舶参数激励横摇相关的特征波群，同时考虑对应的波浪特性和横摇特性，分析二者的相关性。
图 5 波群示意Fig. 5 Definition of wave group下载:
全尺寸图片
在统计横摇筛选段对应的特征波群时历时，波浪中波群出现的时间范围与横摇筛选段所在时间范围并非完全重复，有些波群只有部分波浪在横摇筛选段对应范围内。本文将与横摇筛选段起始时刻有重复时间段的波群也纳入横摇筛选段中对应的特征波群(横摇筛选段终止时刻后仍连续出现的波群不计入横摇筛选段对应特征波群)，统计横摇筛选段对应特征波群数量、波群连长、每个横摇筛选段中特征波群所有波浪的平均周期和平均波高等参数。波浪参数和横摇参数均是采用上跨零点法统计。图 6和图 7为零航速随机波浪种子数1对应的横摇筛选段横摇时历, 与其对应的特征波群波浪时历总体和局部示意图。
图 6 横摇筛选段横摇与对应特征波群波面时历示意Fig. 6 Selected ship parametric rolling segments and related characteristic wave groups下载:
全尺寸图片
图 7 横摇筛选段1对应的特征波群时历示意Fig. 7 Selected ship parametric rolling segment 1 and the encountered characteristic wave groups下载:
全尺寸图片
图 6展示了5个横摇筛选段范围内的全部实验特征波群时历。图 7为横摇筛选段1与其对应的特征波群，可以看出第1个波群有部分波浪在横摇筛选段前方，将此波群也看作横摇筛选段对应波群，因此在横摇筛选段1中共对应4个波群。
3. 不同航速下横摇筛选段和特征波群统计结果
3.1 不同航速下的横摇筛选段统计结果
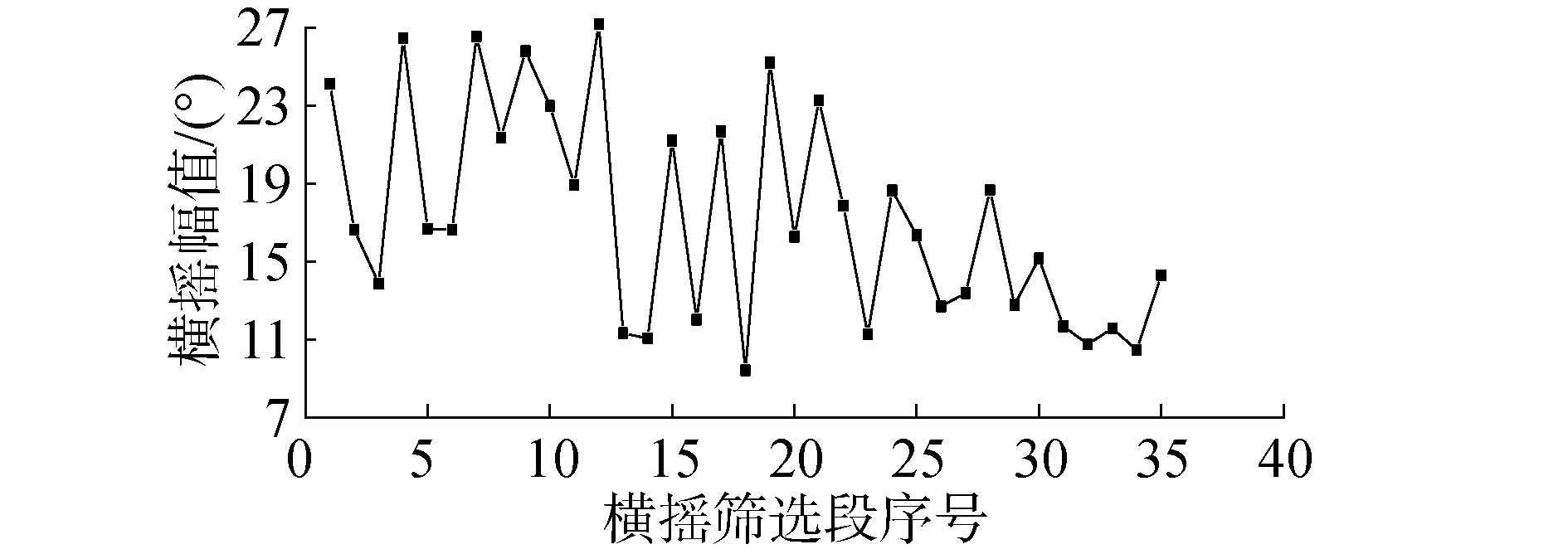
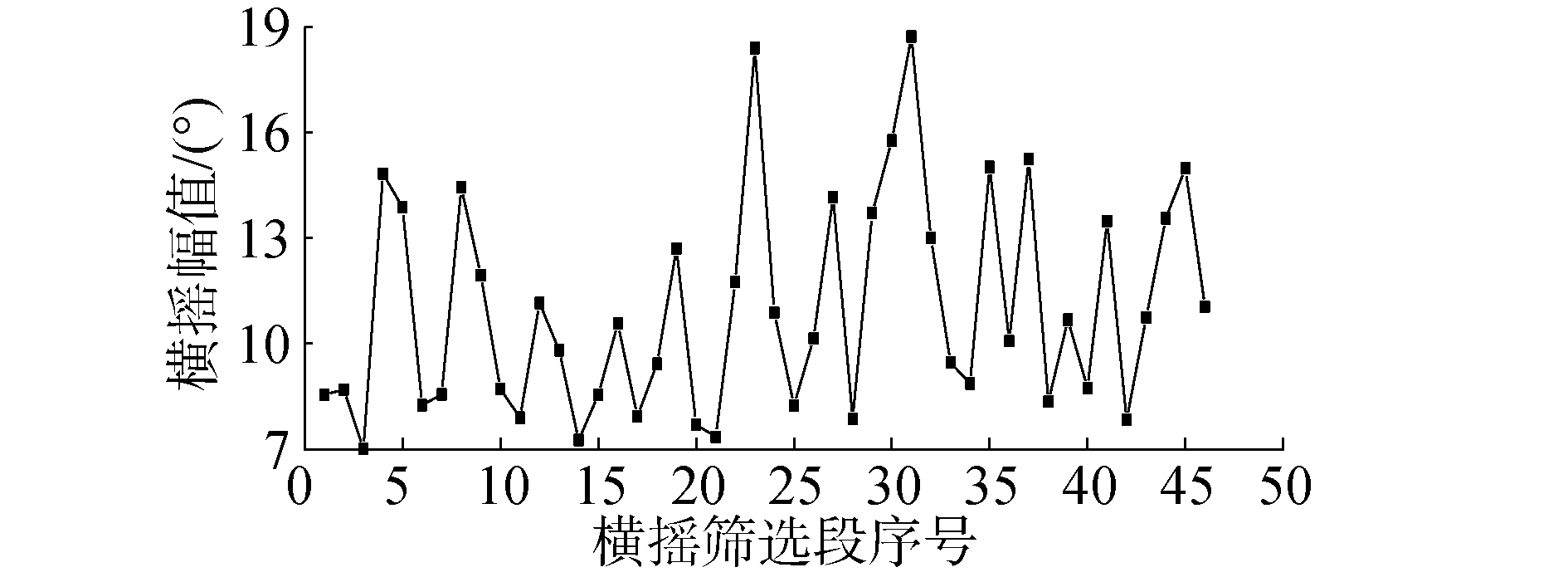
如前文所述，模型实验中针对零航速，傅氏数为0.05、0.1共3个航速都进行了10个随机种子数不规则波中的船舶参数激励横摇测试，其中傅氏数0.05、0.1每个随机种子数下进行了2次波浪截断。在0.1傅氏数下横摇运动幅值相对较小，因此本文没有进行统计。在零航速和0.05傅氏数下，分别有35组和46组横摇筛选段，每个横摇筛选段中横摇最大值的统计结果如图 8和图 9所示。
图 8 Fn=0时各个横摇筛选段中最大摇幅排列结果Fig. 8 Maximum parametric roll amplitude in each selected segment under Fn=0下载:
全尺寸图片
图 9 Fn=0.05时各个横摇筛选段中最大摇幅排列结果Fig. 9 Maximum parametric roll amplitude in each selected segment under Fn=0.05下载:
全尺寸图片
通过图 8和图 9可以看出，不同横摇筛选段下船舶参数激励横摇最大值变化明显，参数激励横摇的剧烈程度明显差异；零航速时船舶参数激励横摇剧烈程度总体上大于傅氏数为0.05的情况。
3.2 不同横摇筛选段对应特征波群统计结果
通过3.1节中对横摇筛选段中横摇最大值的分析，可看出不同筛选段下船舶参数激励横摇运动的剧烈程度明显不同。本节为了分析参数激励横摇产生与遭遇到的波浪之间的相关性，利用波群方法对实验波浪时历进行统计，计算横摇筛选段对应特征波群的相关统计参数。波群统计参数包括横摇筛选段特征波群波浪平均周期、平均波高和每个横摇筛选段中的特征波群数量、每个横摇筛选段对应所有特征波群的波群连长和。其中，横摇筛选段特征波群平均周期、平均波高是指在一个横摇筛选段中，对应横摇筛选段下所有特征波群中波浪的平均周期、平均波高；波群数量和波群连长和均指单个横摇筛选段中特征波群结果的累加。统计结果如图 10~17所示。
图 10 Fn=0时不同横摇筛选段中特征波群平均周期Fig. 10 Mean encountered wave period of characteristic wave groups in different parametric rolling segments under Fn=0下载:
全尺寸图片
图 11 Fn=0时不同横摇筛选段中特征波群平均波高Fig. 11 Mean encountered wave height of characteristic wave groups in different parametric rolling segments under Fn=0下载:
全尺寸图片
图 12 Fn=0时不同横摇筛选段中特征波群数量Fig. 12 Total number of characteristic wave groups in different parametric rolling segments under Fn=0下载:
全尺寸图片
图 13 Fn=0时不同横摇筛选段中特征波群连长和Fig. 13 Total length of runs of characteristic wave groups in different parametric rolling segments under Fn=0下载:
全尺寸图片
图 14 Fn=0.05时不同横摇筛选段中特征波群平均遭遇周期Fig. 14 Mean encountered wave period of characteristic wave groups in different parametric rolling segments under Fn=0.05下载:
全尺寸图片
图 15 Fn=0.05时不同横摇筛选段中特征波群平均遭遇波高Fig. 15 Mean encountered wave height of characteristic wave groups in different parametric rolling segments under Fn=0.05下载:
全尺寸图片
图 16 Fn=0.05时不同横摇筛选段中特征波群数量Fig. 16 Total number of characteristic wave groups in different parametric rolling segments under Fn=0.05下载:
全尺寸图片
图 17 Fn=0.05时不同横摇筛选段中特征波群连长特性Fig. 17 Total length of runs of characteristic wave groups in different parametric rolling segments under Fn=0.05下载:
全尺寸图片
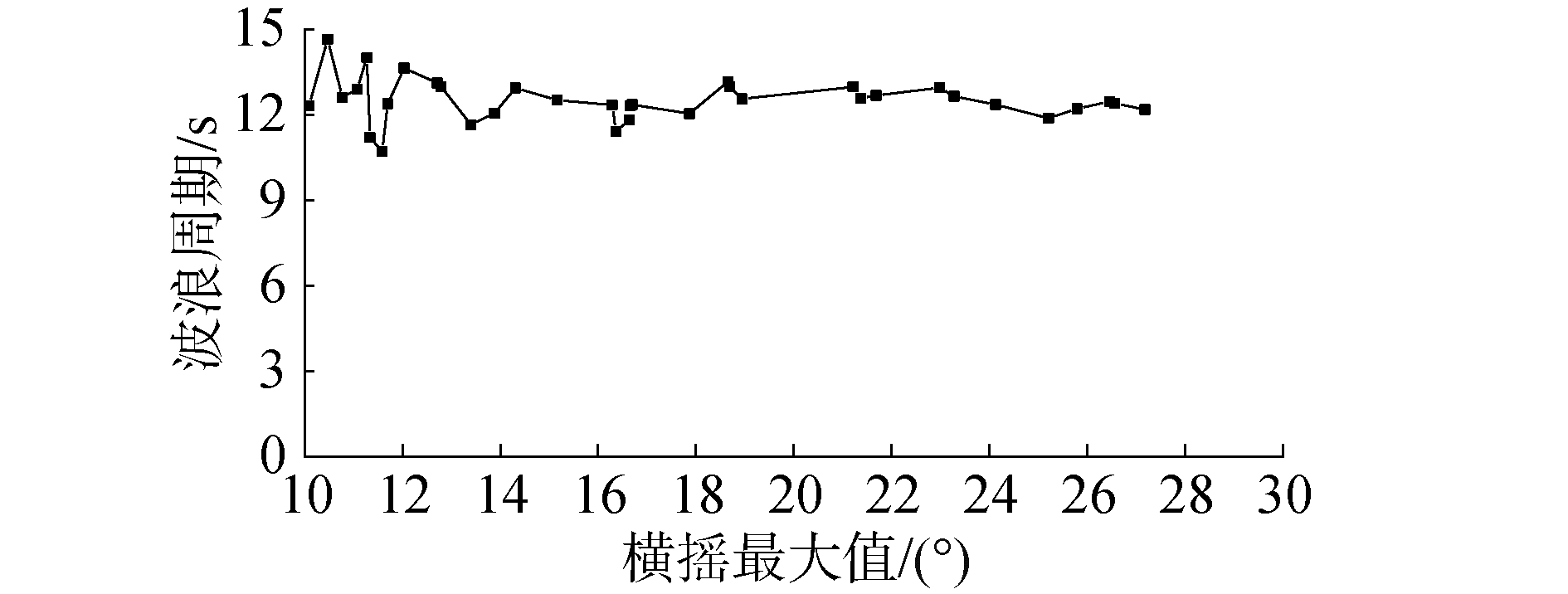
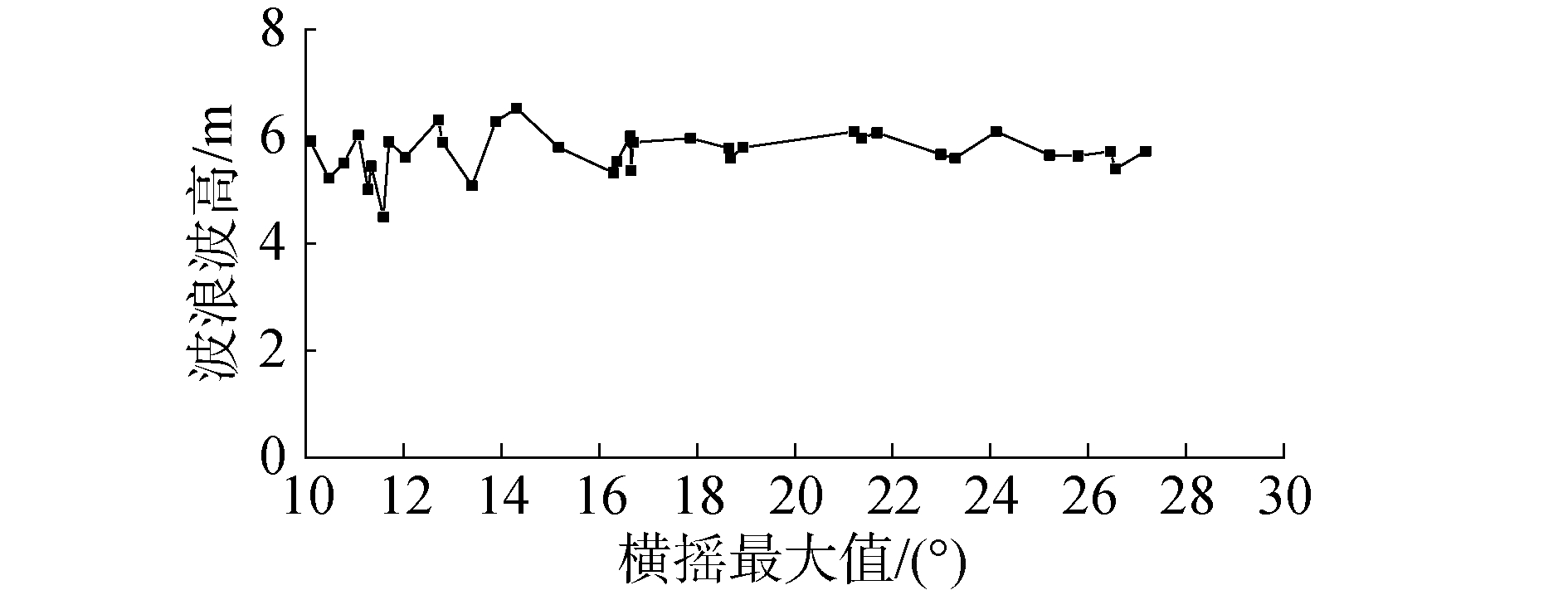
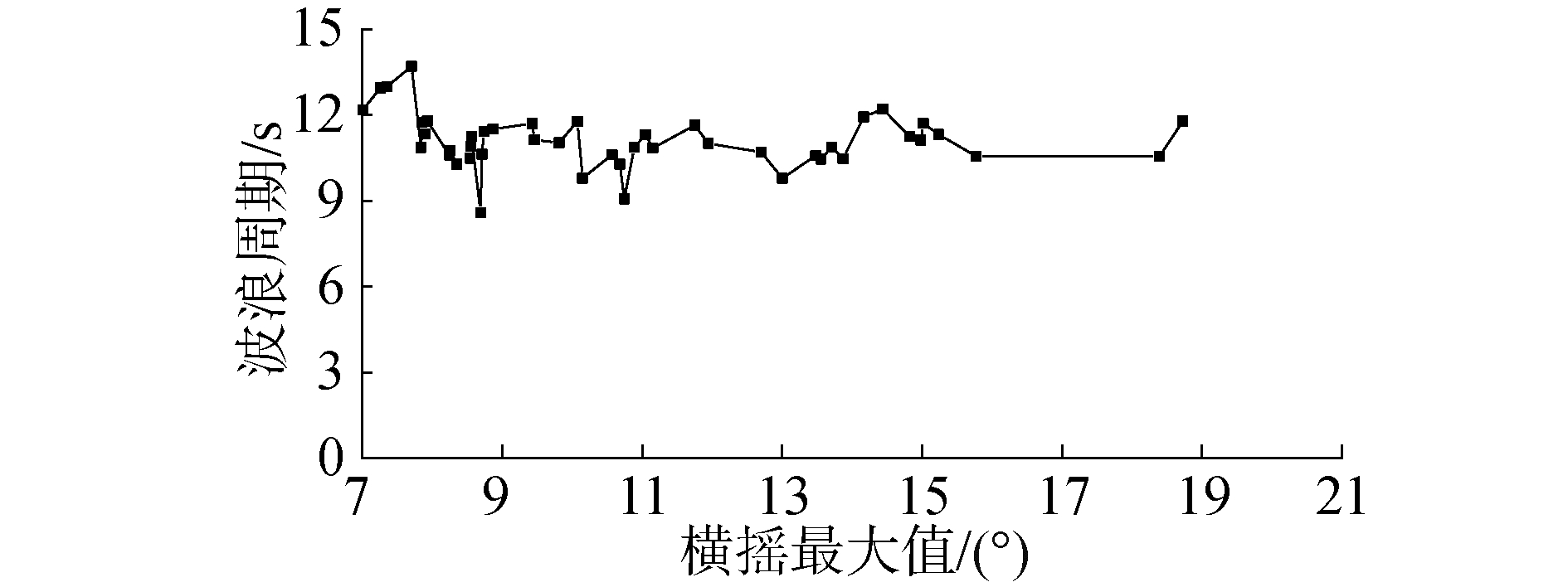
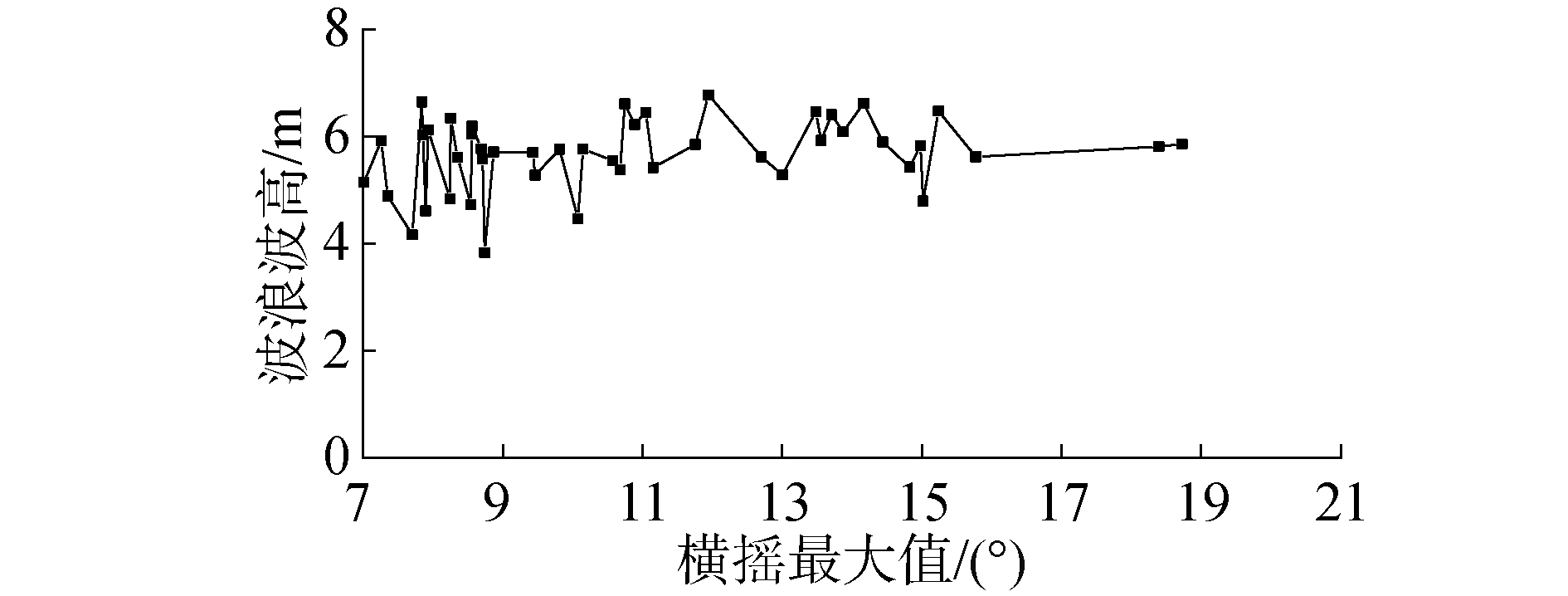
图 10~15分别展示了2个航速下横摇筛选段对应的波群参数。通过图 10~11、图 14~15可以看出横摇筛选段对应的波群参数中，波群波浪的平均周期和平均波高随着最大摇幅变化有一定波动，但基本保持平稳。图 10中给出的零航速下船舶参数激励横摇遭遇波群平均周期在12.5 s左右; 图 14给出的傅氏数0.05情况下遭遇的波群平均周期为11 s左右。该船舶横摇固有周期为24.5 s，在零航速时遭遇的波群周期更为接近横摇固有周期的一半，因此相对于傅氏数0.05情况下船舶参数横摇摇幅总体上要更大，如图 8~9的对比所示。
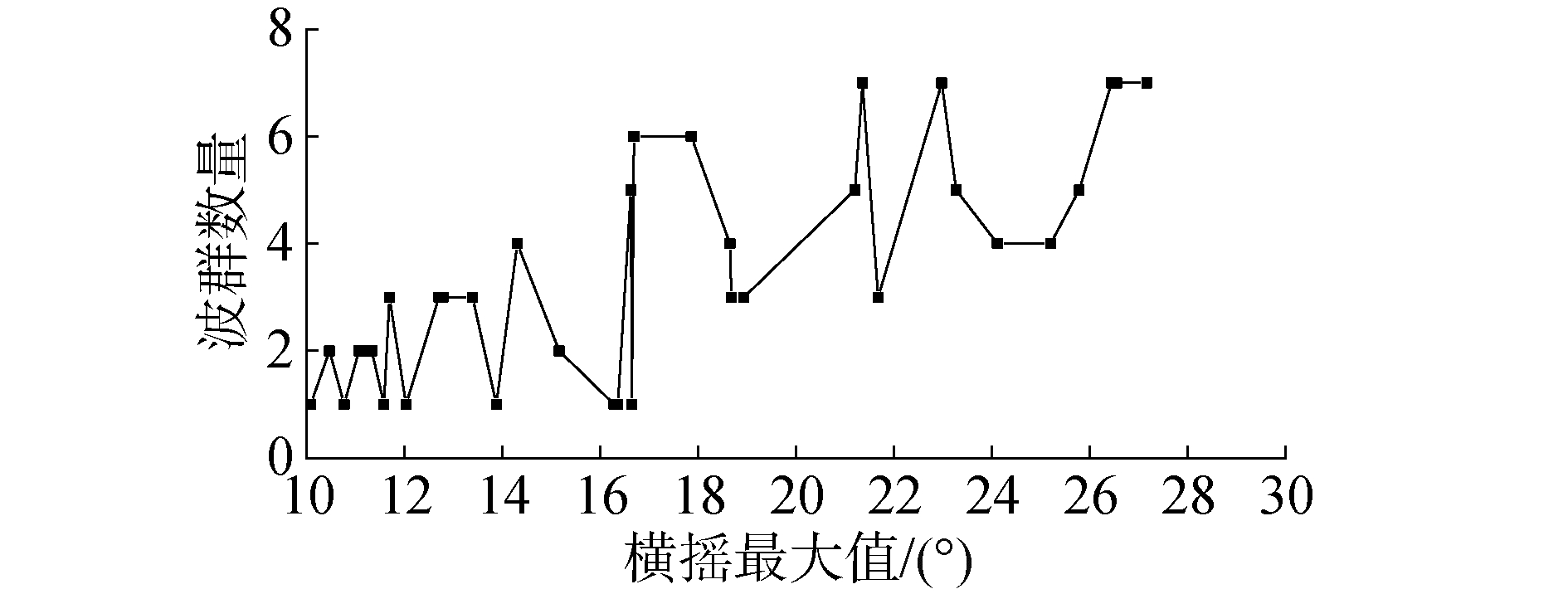
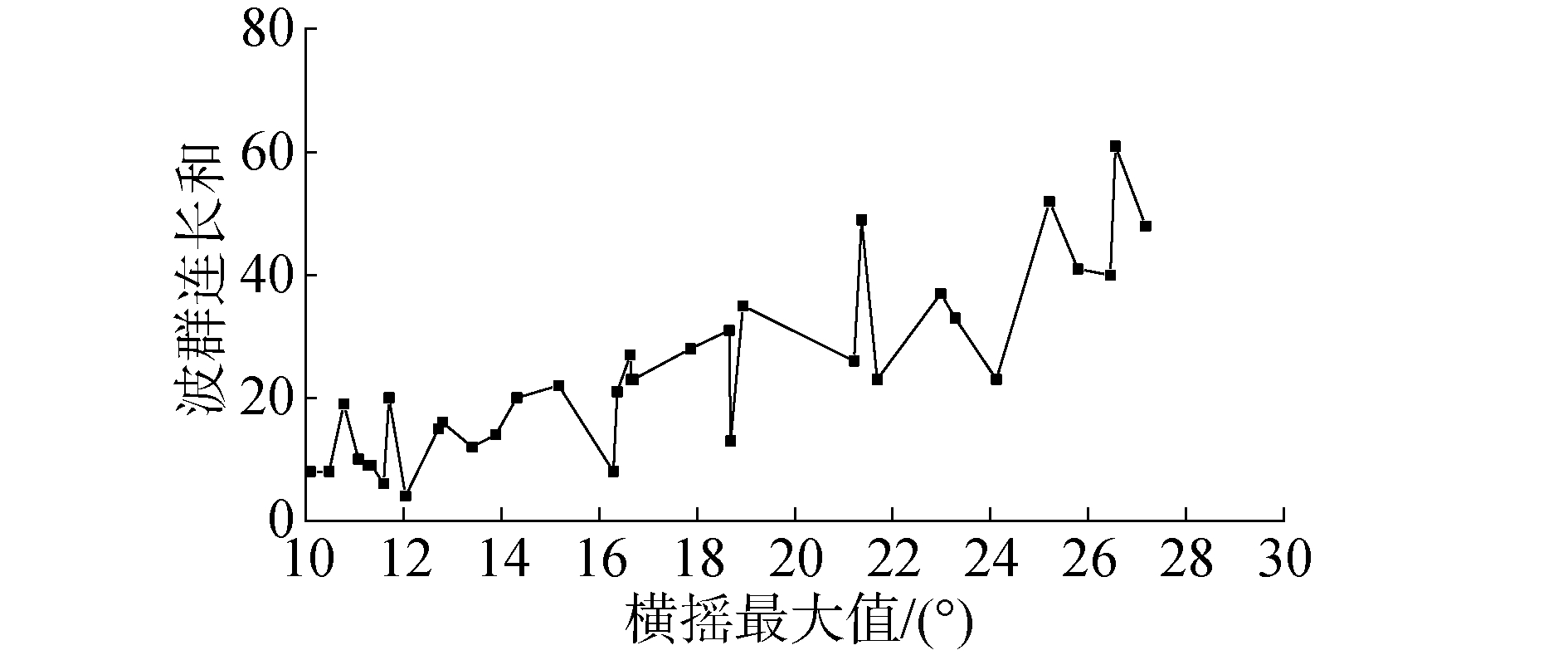
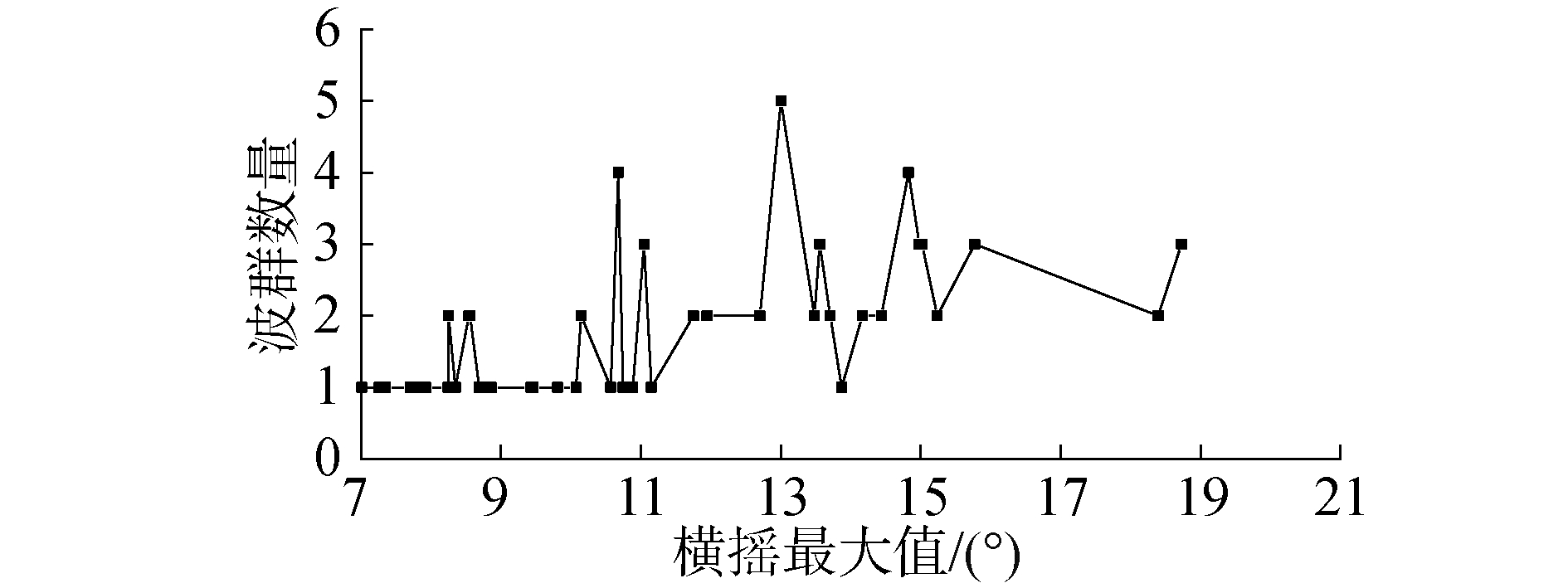
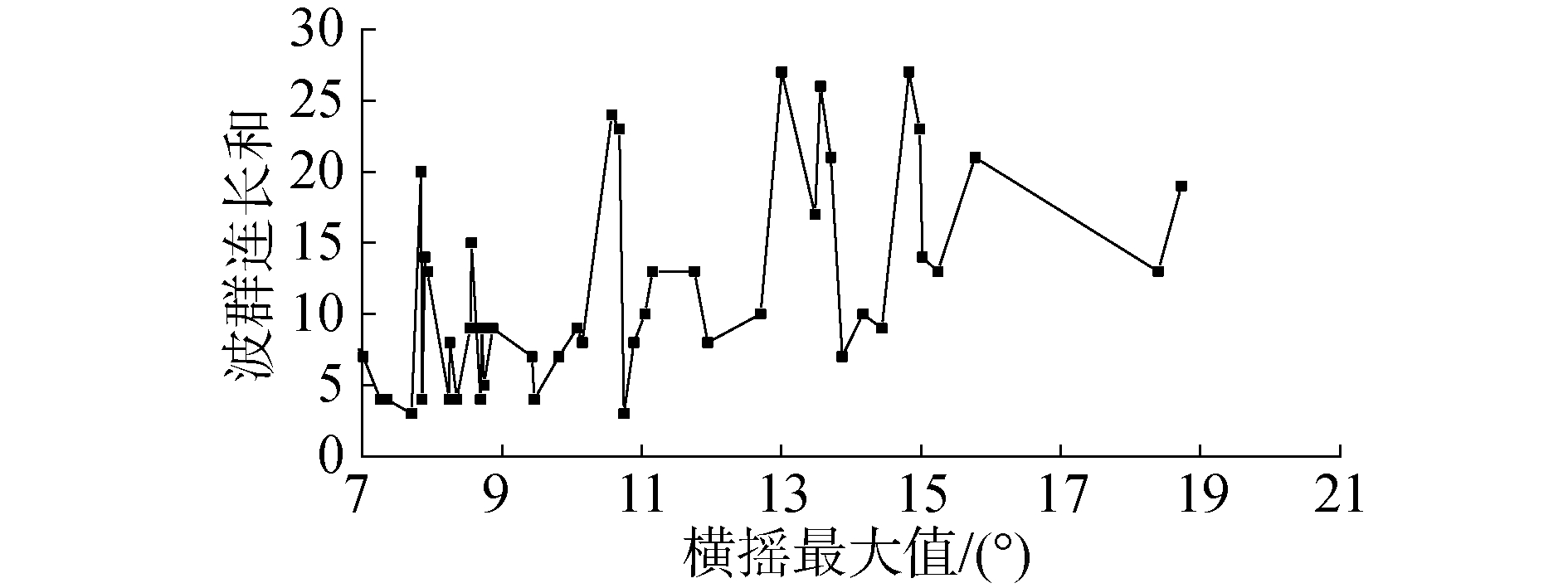
图 12~13显示在零航速情况下不同筛选段中的特征波群数量和特征波群连长和随横摇筛选段中横摇最大值增加而上升的趋势明显，即随着横摇摇幅的增加，船舶遭遇到的波群数量和子波总和都增加。而在傅氏数为0.05情况下，图 16~17显示某个筛选段中的特征波群数量和特征波群连长和随着摇幅最大值增加而呈现振荡变化的特性，就单个横摇筛选段而言，船舶发生参数激励横摇的波群数量和子波个数随机性较强，后续可以结合数值模拟统计更多横摇时历下的数据以克服随机性，使得规律更为明显。总体上来看随着摇幅增加，船舶遭遇的波群数量和子波总和也呈现增加的趋势。
4. 横摇筛选段中特征波群参数分段统计结果
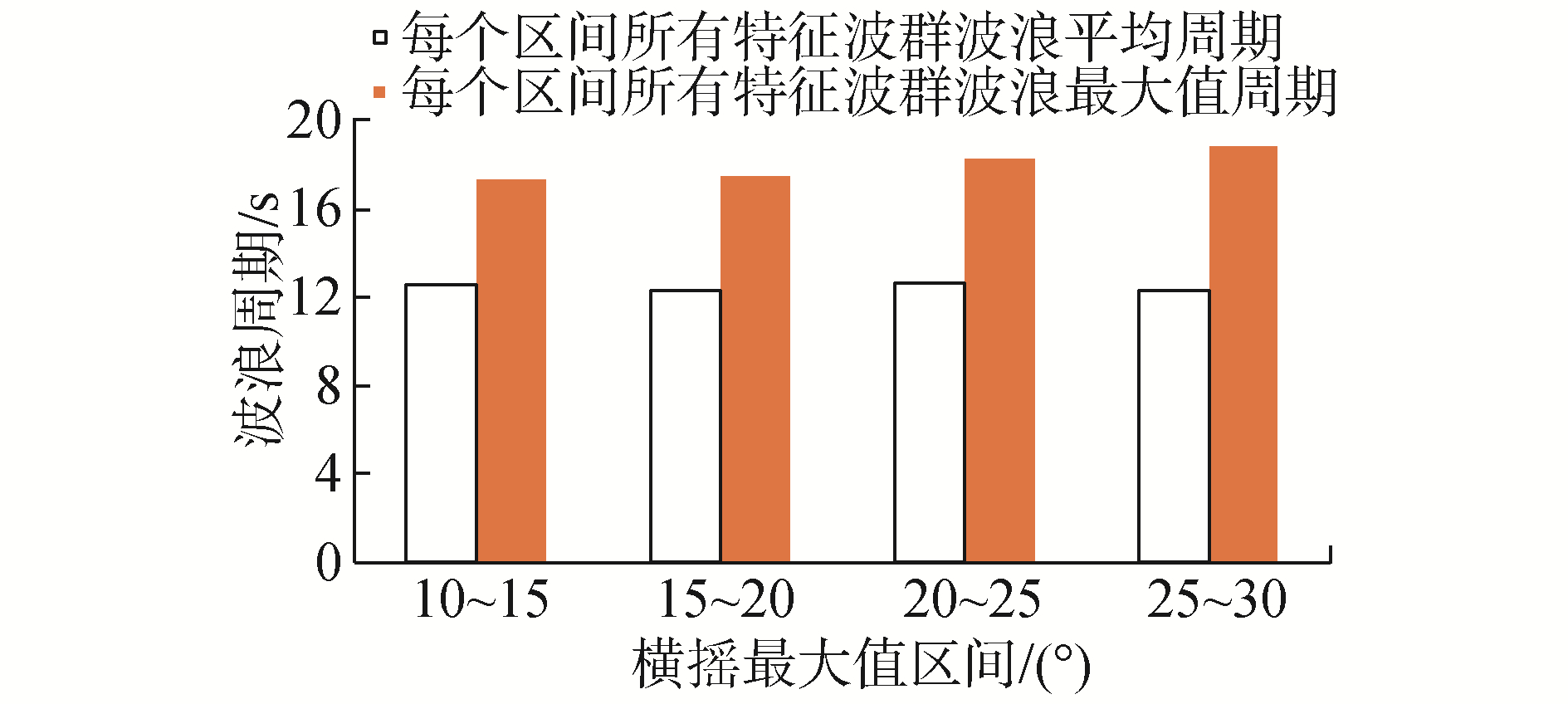
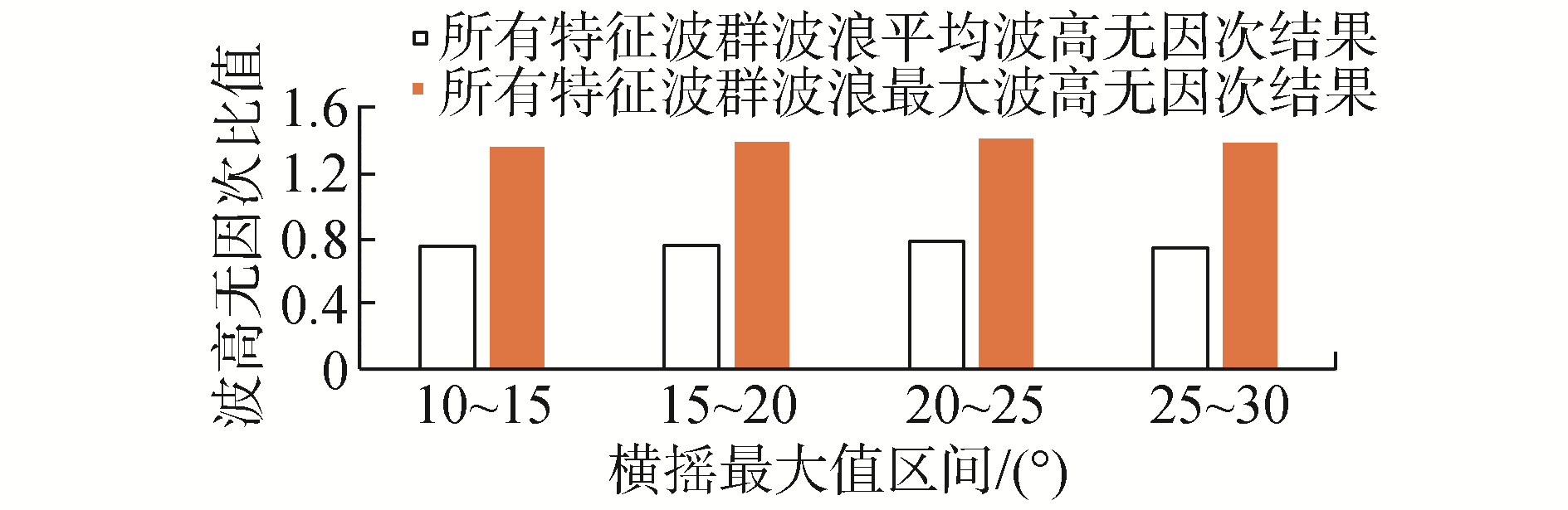
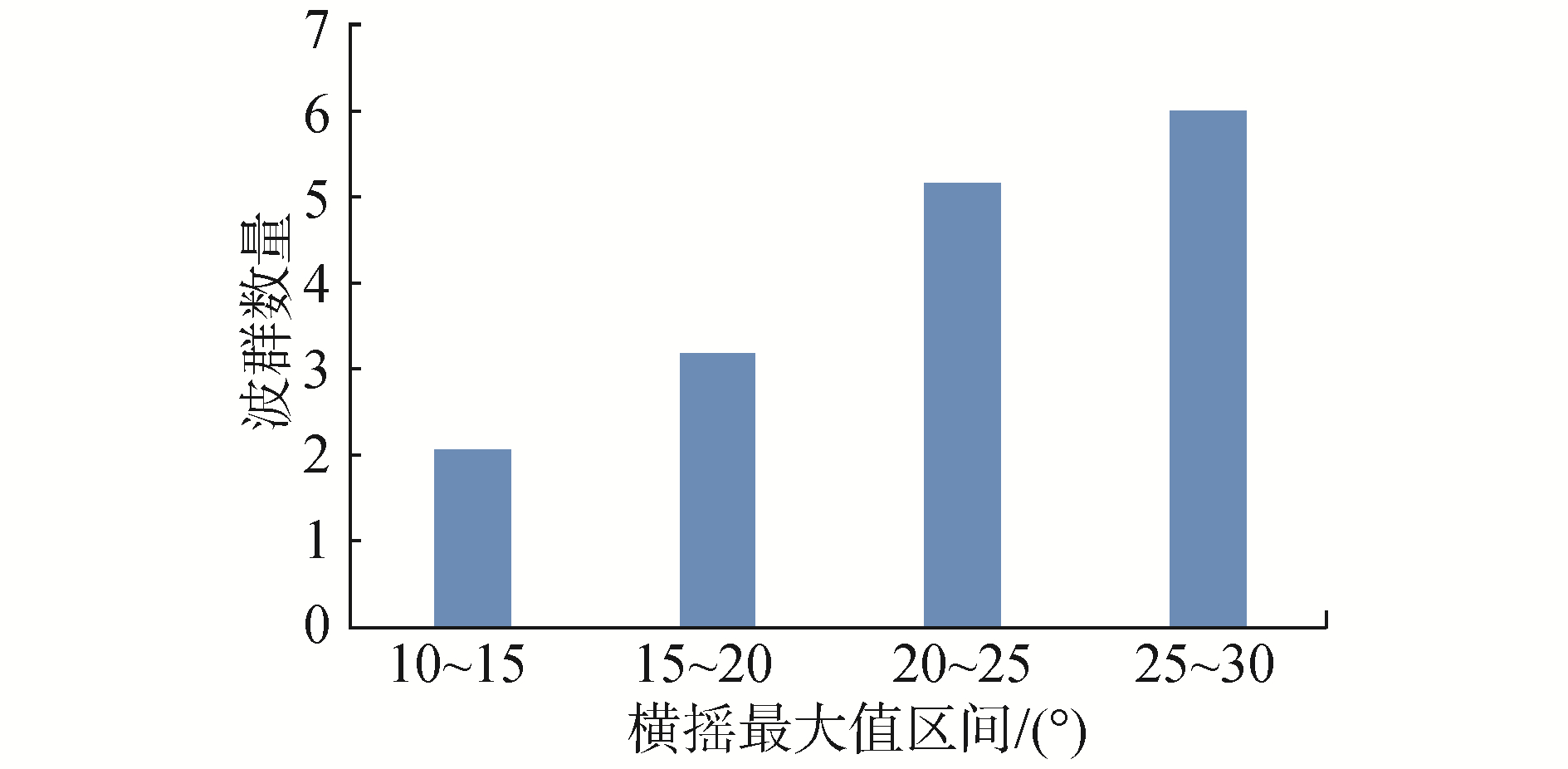
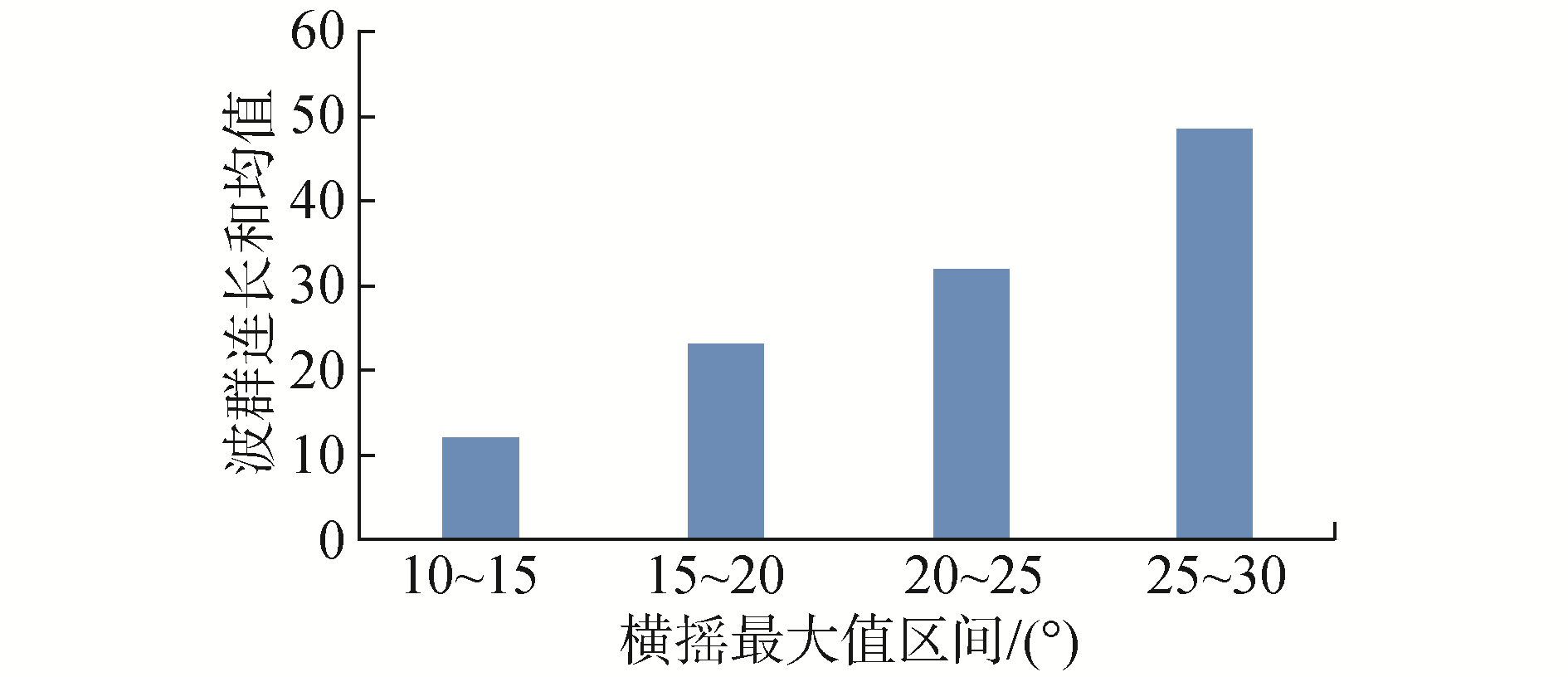
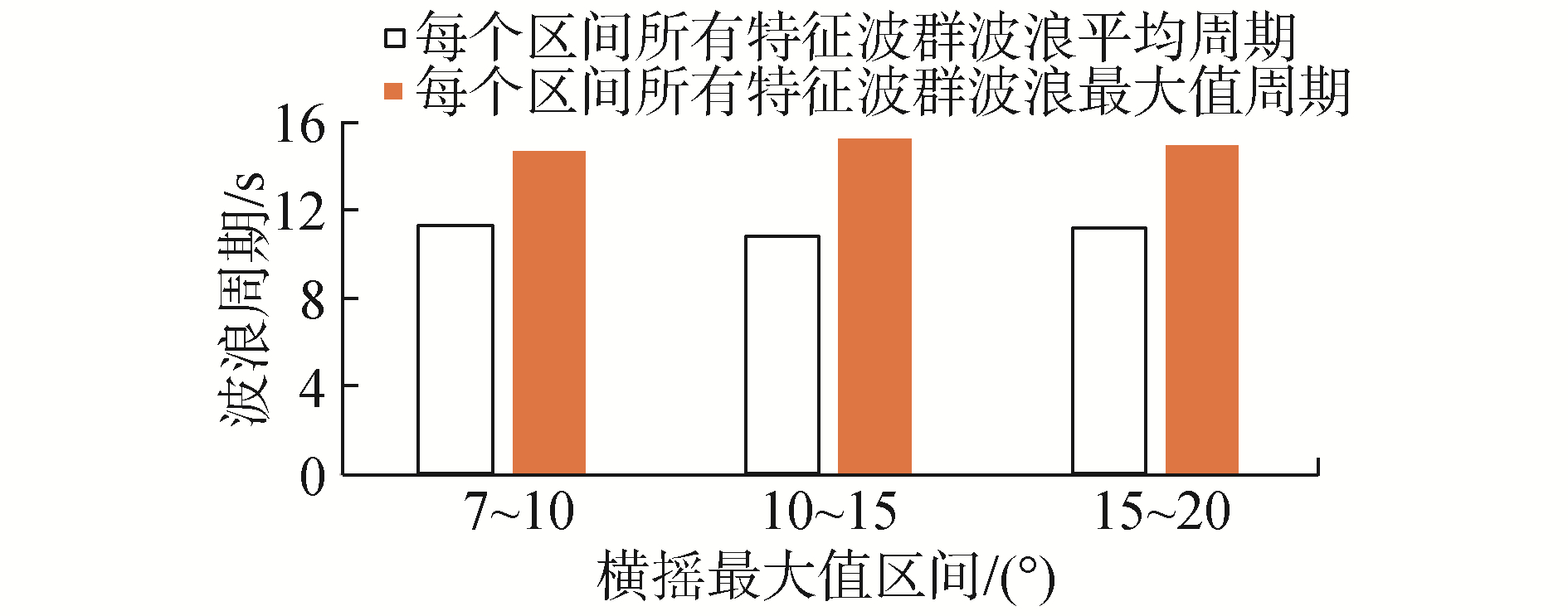
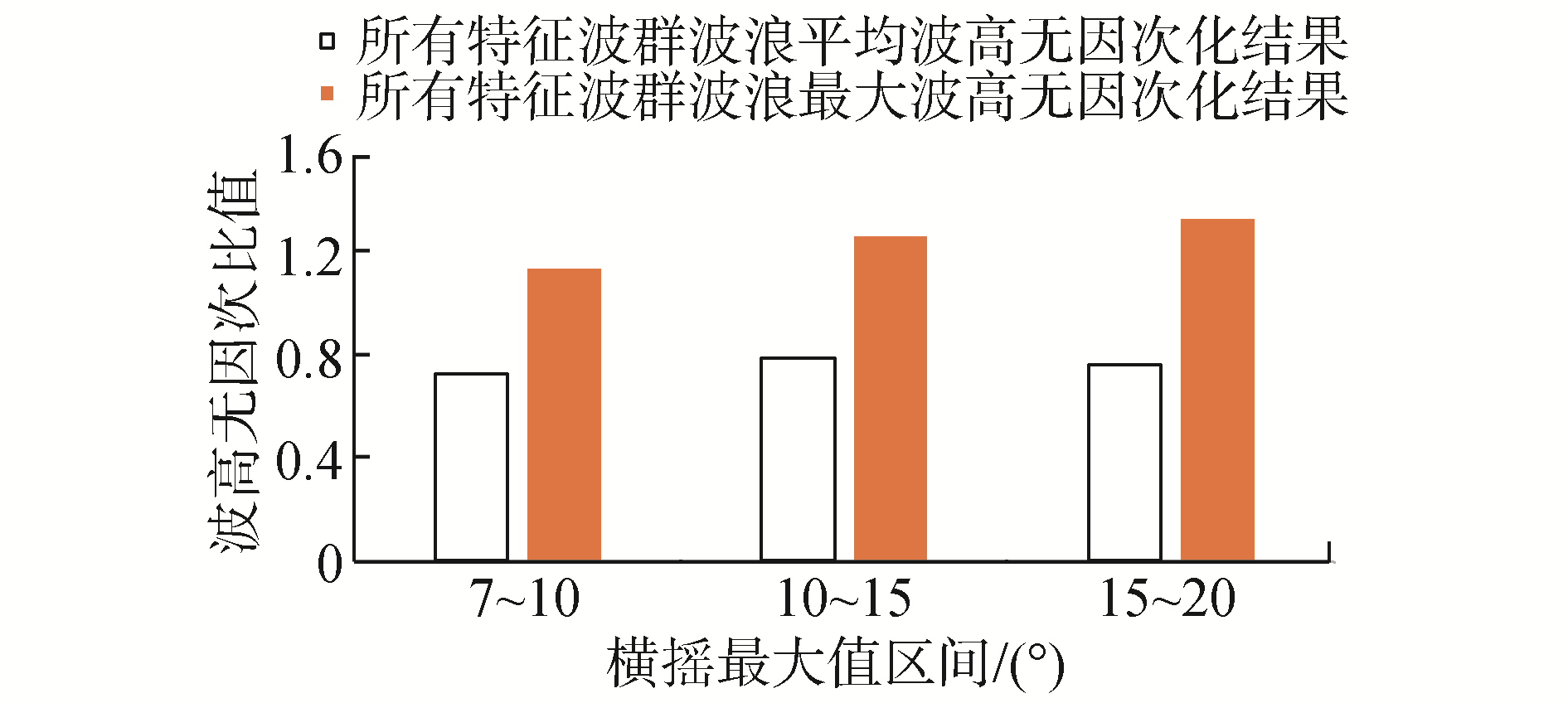
本节针对第3节中的统计结果，对横摇筛选段中横摇最大值及其对应特征波群的相关参数按照单个横摇筛选段最大横摇摇幅划分区间，进行分段统计。分析每个区间中不同横摇筛选段遭遇的平均波群数量、波群平均连长和、波群子波平均周期和波高的均值。在统计时，0航速时横摇摇幅从10°开始，每隔5°横摇范围定义为船舶发生参数激励横摇的一个区间，共划分为4个区间。在Fn=0.05时，单个筛选段的最大摇幅从7°开始，7°~10°为一个区间，然后每5°为一个区间，共有3个区间，分析不同区间中特征波群参数的变化趋势。同时将特征波群波高统计结果除以实验波浪的有义波高，将波高参数无因次化，方便与前文中波群门槛值设定比例进行比较。图 18~25分别为零航速和傅氏数为0.05下的分段统计结果。
图 18 Fn=0时不同横摇摇幅特征波群波浪平均周期、最大周期Fig. 18 Mean and maximum wave period of all wave groups in different rolling amplitude under Fn=0下载:
全尺寸图片
图 19 Fn=0时不同横摇摇幅特征波群波浪平均波高、最大波高无因次化结果Fig. 19 Dimensionless mean and maximum wave height of all wave groups in different rolling amplitude under Fn=0下载:
全尺寸图片
图 20 Fn=0时不同横摇摇幅所有特征波群数量均值Fig. 20 Mean characteristic wave group numbers in different rolling amplitude under Fn=0下载:
全尺寸图片
图 21 Fn=0时不同横摇摇幅所有特征波群连长和均值Fig. 21 Mean length of runs of encountered wave groups in different rolling amplitude under Fn=0下载:
全尺寸图片
图 22 Fn=0.05时不同横摇摇幅特征波群波浪平均周期、最大周期Fig. 22 Mean and maximum wave period of all encountered wave groups in different rolling amplitude under Fn=0.05下载:
全尺寸图片
图 23 Fn=0.05时不同横摇摇幅所有特征波群波浪平均波高、最大波高无因次化结果Fig. 23 Dimensionless mean and maximum wave height of all encountered wave groups in different rolling amplitude under Fn=0.05下载:
全尺寸图片
图 24 Fn=0.05时不同横摇摇幅所有特征波群数量均值Fig. 24 Mean wave group numbers in different rolling amplitude ranges under Fn=0.05下载:
全尺寸图片
图 25 Fn=0.05时不同横摇摇幅所有特征波群连长和均值Fig. 25 Mean length of runs of encounter wave groups in different rolling amplitude range under Fn=0.05下载:
全尺寸图片
图 18和图 22统计结果表明，在零航速下，每个区间中特征波群波浪平均周期为12.23~12.66 s；在傅氏数为0.05时，每个区间中特征波群波浪平均周期为11.02~11.19 s；不同航速下每个区间内的特征波群的平均波浪周期、最大波浪周期随不同横摇筛选段横摇最大值变化不大。图 19和图 23结果表明，不同航速下每个区间内的特征波群的平均波高都近似为0.75 Hs，零航速下的最大波高接近1.4 Hs，Fn=0.05时，7~10°的最大波高要小于其他部分的最大波高，剩余2个区间的最大波高接近1.3 Hs。傅氏数为0.05情况下特征波群中的最大波高要略小于零航速时的结果。
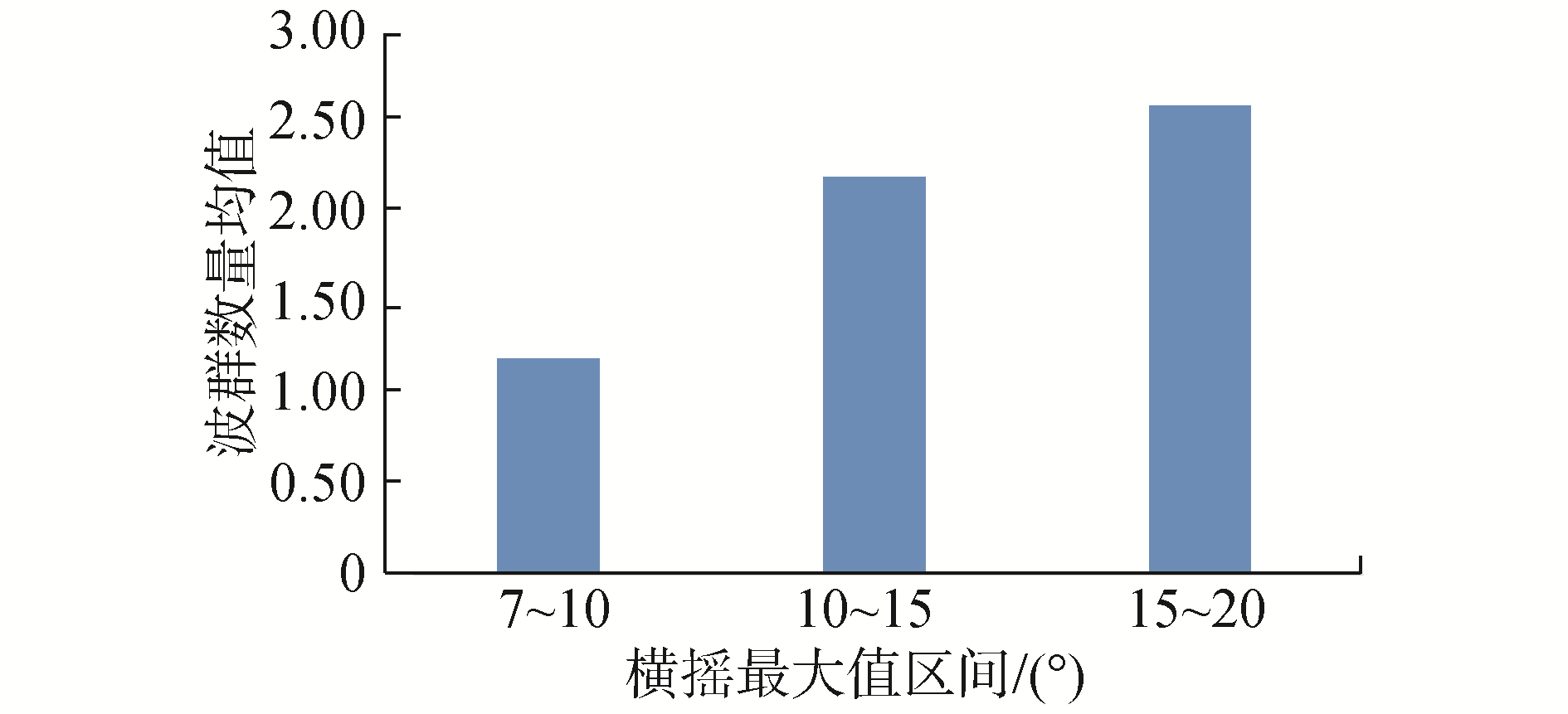
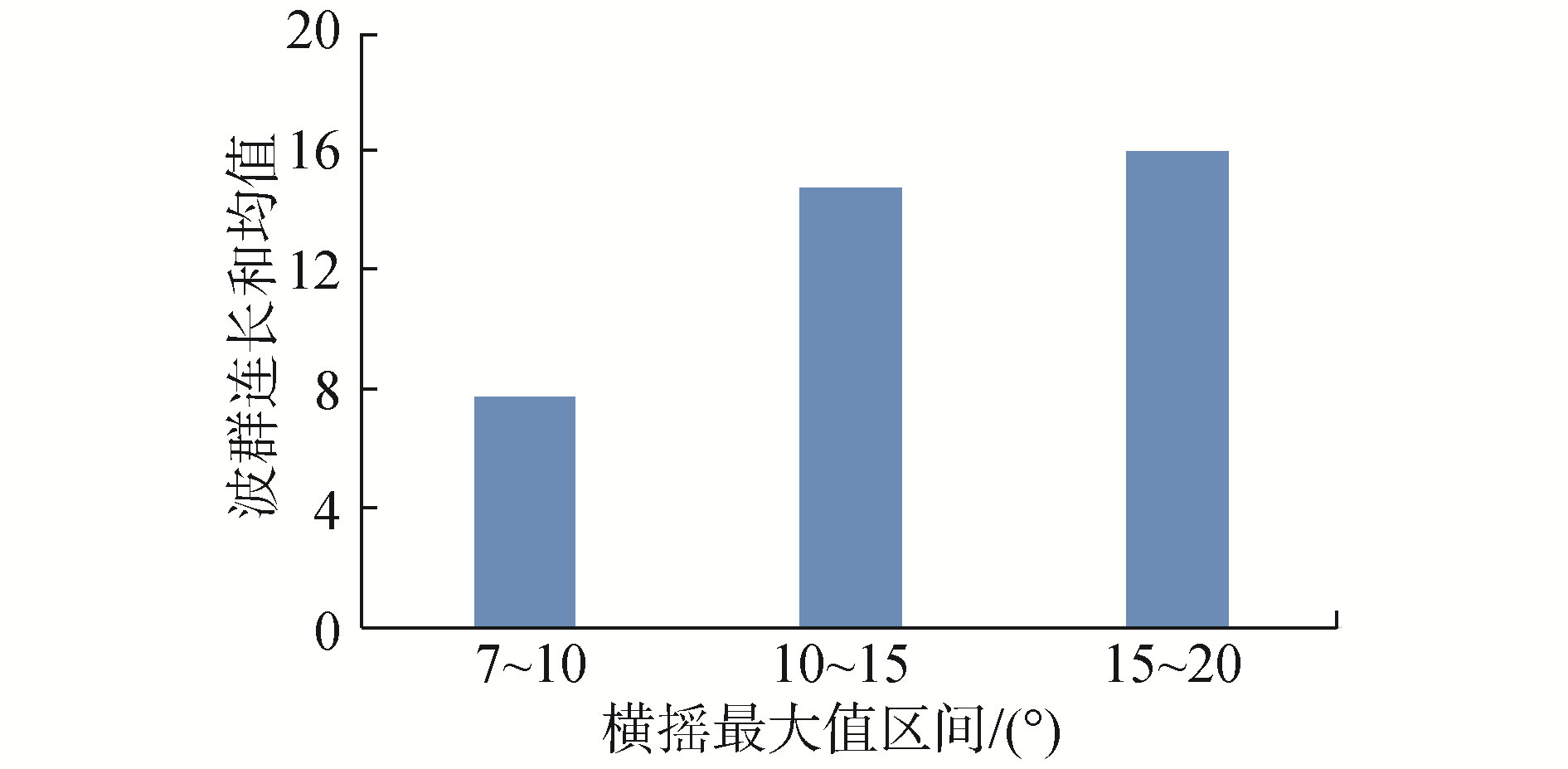
图 20~21和图 24~25的分析结果表明，不同航速下，每个区间中横摇筛选段中船舶遭遇的特征波群数量均值和波群连长和均值都是随着横摇摇幅的增大而增大，趋势变化明显。相对于图 12~13与图 16~17中的统计结果，区间统计结果减弱了实验的不确定性对统计规律的影响，其结果表明船舶遭遇的波群特性是影响船舶参数激励横摇的重要因素。在整体上，船舶发生参数激励横摇摇幅的剧烈程度与遭遇到的波群数量和子波个数是正相关的。随着参数激励横摇摇幅的增加，所遭遇到的平均波群数量和连长和增加。如在10°~15°横摇摇幅区间，零航速下遭遇到的平均波群数量是2个，傅氏数为0.05时是2.2个。而在15°~20°横摇摇幅区间，对应航速下遭遇到的平均波群数量分别为3.2和2.6个。
5. 结论
1) 通过横摇筛选段对应特征波群的波浪周期分析，在特定航速、不同参数激励横摇摇幅下遭遇波群的平均波浪周期变化不大，就本文所研究的C11集装箱船，零航速时船舶遭遇的平均波浪周期与横摇固有周期的比值更接近1/2，参数激励横摇的摇幅相对于傅氏数0.05要更大，表明船舶参数激励横摇的剧烈程度与船舶遭遇到的平均波浪周期大小密切相关。
2) 通过横摇筛选段遭遇波群的无因次子波波高分析，在特定海况下船舶遭遇到波群的平均波高、最大波高随参数激励横摇摇幅均变化不大，不同航速下每个摇幅区间内的特征波群的平均波高都近似为0.75 Hs(Hs表示有义波高)。对于参数激励横摇发生过程中所遭遇波群的最大波高，在傅氏数为0.05时相对于零航速时要略小一些。
3) 在研究波群数量与随机波中船舶参数激励横摇相关性时，就某具体的船舶参数激励横摇过程而言，所遭遇到的波群数量和子波个数随摇幅变化有一定的随机性。但是就统计意义上来看，通过横摇筛选段的最大摇幅区间与所遭遇到的平均波群数量和连长和的统计分析，随着参数激励横摇摇幅的增加，所遭遇到的平均波群数量和连长和增加。表明船舶发生参数激励横摇时遭遇波群数量和连长个数是重要的影响因素。
-
图 1 C11集装箱船型线图
Fig. 1 Offset lines of C11 container ship
下载:
全尺寸图片
图 2 模型实验中发生的典型参数激励横摇过程
Fig. 2 Typical parametric rolling phenomena in model test
下载:
全尺寸图片
图 3 船舶参数激励横摇筛选段示意
Fig. 3 Selected ship parametric rolling segments
下载:
全尺寸图片
图 4 横摇筛选段1示意
Fig. 4 Selected parametric rolling segment 1
下载:
全尺寸图片
图 5 波群示意
Fig. 5 Definition of wave group
下载:
全尺寸图片
图 6 横摇筛选段横摇与对应特征波群波面时历示意
Fig. 6 Selected ship parametric rolling segments and related characteristic wave groups
下载:
全尺寸图片
图 7 横摇筛选段1对应的特征波群时历示意
Fig. 7 Selected ship parametric rolling segment 1 and the encountered characteristic wave groups
下载:
全尺寸图片
图 8 Fn=0时各个横摇筛选段中最大摇幅排列结果
Fig. 8 Maximum parametric roll amplitude in each selected segment under Fn=0
下载:
全尺寸图片
图 9 Fn=0.05时各个横摇筛选段中最大摇幅排列结果
Fig. 9 Maximum parametric roll amplitude in each selected segment under Fn=0.05
下载:
全尺寸图片
图 10 Fn=0时不同横摇筛选段中特征波群平均周期
Fig. 10 Mean encountered wave period of characteristic wave groups in different parametric rolling segments under Fn=0
下载:
全尺寸图片
图 11 Fn=0时不同横摇筛选段中特征波群平均波高
Fig. 11 Mean encountered wave height of characteristic wave groups in different parametric rolling segments under Fn=0
下载:
全尺寸图片
图 12 Fn=0时不同横摇筛选段中特征波群数量
Fig. 12 Total number of characteristic wave groups in different parametric rolling segments under Fn=0
下载:
全尺寸图片
图 13 Fn=0时不同横摇筛选段中特征波群连长和
Fig. 13 Total length of runs of characteristic wave groups in different parametric rolling segments under Fn=0
下载:
全尺寸图片
图 14 Fn=0.05时不同横摇筛选段中特征波群平均遭遇周期
Fig. 14 Mean encountered wave period of characteristic wave groups in different parametric rolling segments under Fn=0.05
下载:
全尺寸图片
图 15 Fn=0.05时不同横摇筛选段中特征波群平均遭遇波高
Fig. 15 Mean encountered wave height of characteristic wave groups in different parametric rolling segments under Fn=0.05
下载:
全尺寸图片
图 16 Fn=0.05时不同横摇筛选段中特征波群数量
Fig. 16 Total number of characteristic wave groups in different parametric rolling segments under Fn=0.05
下载:
全尺寸图片
图 17 Fn=0.05时不同横摇筛选段中特征波群连长特性
Fig. 17 Total length of runs of characteristic wave groups in different parametric rolling segments under Fn=0.05
下载:
全尺寸图片
图 18 Fn=0时不同横摇摇幅特征波群波浪平均周期、最大周期
Fig. 18 Mean and maximum wave period of all wave groups in different rolling amplitude under Fn=0
下载:
全尺寸图片
图 19 Fn=0时不同横摇摇幅特征波群波浪平均波高、最大波高无因次化结果
Fig. 19 Dimensionless mean and maximum wave height of all wave groups in different rolling amplitude under Fn=0
下载:
全尺寸图片
图 20 Fn=0时不同横摇摇幅所有特征波群数量均值
Fig. 20 Mean characteristic wave group numbers in different rolling amplitude under Fn=0
下载:
全尺寸图片
图 21 Fn=0时不同横摇摇幅所有特征波群连长和均值
Fig. 21 Mean length of runs of encountered wave groups in different rolling amplitude under Fn=0
下载:
全尺寸图片
图 22 Fn=0.05时不同横摇摇幅特征波群波浪平均周期、最大周期
Fig. 22 Mean and maximum wave period of all encountered wave groups in different rolling amplitude under Fn=0.05
下载:
全尺寸图片
图 23 Fn=0.05时不同横摇摇幅所有特征波群波浪平均波高、最大波高无因次化结果
Fig. 23 Dimensionless mean and maximum wave height of all encountered wave groups in different rolling amplitude under Fn=0.05
下载:
全尺寸图片
图 24 Fn=0.05时不同横摇摇幅所有特征波群数量均值
Fig. 24 Mean wave group numbers in different rolling amplitude ranges under Fn=0.05
下载:
全尺寸图片
图 25 Fn=0.05时不同横摇摇幅所有特征波群连长和均值
Fig. 25 Mean length of runs of encounter wave groups in different rolling amplitude range under Fn=0.05
下载:
全尺寸图片
表 1 C11集装箱船主要参数
Table 1 Principal dimensions of C11 container ship
参数 实船尺度 模型尺度 垂线间长Lpp/m 262.00 4.000 型宽B/m 40.00 0.611 型深/m 24.45 0.373 平均吃水/m 11.80 0.180 方形系数 0.566 0.566 排水体积/m3 69 957.96 0.249 重心垂向位置(距基线)/m 18.44 0.281 重心纵向位置(距船舯)/m -5.77 -0.088 横摇初稳性高/m 1.90 0.029 横摇惯性半径/m 0.38B 0.38B 纵摇惯性半径/m 0.24Lpp 0.24Lpp 横摇固有周期/s 24.50 3.027 -
[1] FRANCE W N, LEVADOU M, TREAKLE T W, et al. An investigation of head-sea parametric rolling and its influence on container lashing systems[J]. Marine technology and SNAME news, 2003, 40(1): 1-19. doi: 10.5957/mt1.2003.40.1.1 [2] BULIAN G, FRANCESCUTTO A, UMEDA N, et al. Qualitative and quantitative characteristics of parametric ship rolling in random waves in the light of physical model experiments[J]. Ocean engineering, 2008, 35(17/18): 1661-1675. [3] PARK D M, KIM Y, SONG K H. Sensitivity in numerical analysis of parametric roll[J]. Ocean engineering, 2013, 67: 1-12. doi: 10.1016/j.oceaneng.2013.04.008 [4] 许文浩. 集装箱船随机海浪中参数激励横摇数值模拟及统计特征分析[D]. 哈尔滨: 哈尔滨工程大学. 2018. XU Wenhao. Numerical simulation of container ship parametric rolling and statistical characteristics analysis in irregular waves[D]. Harbin: Harbin Engineering University, 2018. [5] BASSLER C C, BELENKY V, DIPPER M J. Characteristics of wave groups for the evaluation of ship response in irregular seas[C]//Proceedings of ASME 2010 29th international conference on ocean, offshore and Arctic engineering, Shanghai, China. 2010: 227-237. [6] ANASTOPOULOS P A, SPYROU K J. Ship dynamic stability assessment based on realistic wave group excitations[J]. Ocean engineering, 2016, 120: 256-263. doi: 10.1016/j.oceaneng.2016.04.018 [7] KENNEDY J M, FORD J J, PEREZ T, et al. Detection of parametric roll resonance using Bayesian discrete-frequency model selection[J]. IFAC-PapersOnLine, 2018, 51(29): 444-449. doi: 10.1016/j.ifacol.2018.09.447 [8] 马小剑, 刘珍, 嵇春艳, 等. 波浪群性作用下系泊船运动响应和统计特征值分析[J]. 水动力学研究与进展(A辑), 2016, 31(6): 760-768. https://www.cnki.com.cn/Article/CJFDTOTAL-SDLJ201606014.htm MA Xiaojian, LIU Zhen, JI Chunyan, et al. The analysis of moored ship motion response and the statistic characteristics under the wave group action[J]. Chinese journal of hydrodynamics, 2016, 31(6): 760-768. https://www.cnki.com.cn/Article/CJFDTOTAL-SDLJ201606014.htm [9] WANG Liyuan, TANG Yougang, ZHANG Xiaorui, et al. Studies on parametric roll motion of ship under wave group by numerical simulation[J]. Ocean engineering, 2018, 163: 391-399. doi: 10.1016/j.oceaneng.2018.05.066 [10] MASSON D, CHANDLER P. Wave groups: a closer look at spectral methods[J]. Coastal engineering, 1993, 20(3/4): 249-275. [11] 俞聿修, 柳淑学. 随机波浪及其工程应用[M]. 4版. 大连: 大连理工大学出版社, 2011. Yu Yuxiu. Random wave and its applications to engineering[M]. 4th edition. Dalian University of Technology Press, 2011.
