Investigation of motion response and force characteristics of twin-barge floatover installation in the continuous load transfer process
-
摘要: 针对传统分阶段模拟方法不能准确描述浮托安装荷载连续转移过程中驳船运动及缓冲装置受力特征的问题，本文利用具有时变特性的质量点对驳船连续压载过程进行等效表征，提出了一种计及荷载连续转移效应的双船浮托安装数值模拟方法，对荷载连续转移过程中驳船的运动响应特性、桩腿耦合缓冲装置和甲板支撑缓冲装置的受力特征进行了研究。结果表明：双船浮托安装荷载连续转移数值模拟方法可准确地模拟上部组块与导管架桩腿对接全过程，荷载转移过程中驳船纵倾可导致6个缓冲装置受力不均衡，进而引发荷载转移速率的差异。而在上部组块与导管架接触及上部组块与驳船脱离的瞬间，浮托安装系统的动力特征及受力特性发生突变，该特殊现象未在分阶段数值模拟或模型试验中出现。Abstract: The numerical simulation method with individual stages cannot accurately describe the mechanical characteristics of barge movement and buffer device in a continuous mating procedure of twin-barge floatover installation. In this paper, a novel method with time-varying mass points has been adopted to simulate the ballasting process of barge installation. A numerical simulation method, which is capable of considering the effect of continuous load transfer, has also been proposed. With this numerical simulation method, the motion response of barges, impact load on leg mating unit (LMU), and deck support unit (DSU) have been investigated. The proposed continuous load transfer numerical simulation method can accurately simulate the complete mating stage between the topside and jacket platform. Furthermore, the trim of the barge in the continuous ballasting process can lead to inconsistent impact loads on different LMUs, which may result in different load transfer rates. Additionally, the motion response of the barge and impact loads on DSU change suddenly when the topside makes contact with the jacket platform or is separated from the barges. This special phenomenon did not appear in staged numerical simulations or model tests.
-
目前常用的超大型上部组块一体化安装方法主要浮吊安装和浮托安装。浮吊安装法海上作业时间较长，且受限于浮吊起重船的作业能力和租用工期，总体安装费用较高。浮托安装法则借助于潮汐变化或快速调载设备使超大型上部组块从浮托驳船逐渐转移至基础结构上，无需借助大型浮吊设备，可在短时间内完成安装，总体安装费用较低。相较于浮吊安装法，浮托安装法在超大型海洋平台上部组块的安装方面具有显著优势。
根据作业过程中驳船的数量可将浮托安装方法分为单船浮托安装和双船浮托安装。其中单船浮托安装方法的承载重量有限，且对基础结构的构造具有特殊的要求，多用于浅水和中等水深开口式导管架平台上部组块的安装。而双船浮托安装方法采用双驳船进行承载，故可以承载的重量更大，且对基础结构无特殊要求，可用于超浅水或超深水大型导管架平台和Spar平台上部组块的安装。相对于单船浮托安装，双船浮托安装涉及多船协同作业及2次荷载转移过程，其耦合作用过程更加复杂而且安装过程易受系统本身及外界因素的影响，施工作业难度较大，因此有必要对双船浮托安装过程中的驳船运动响应及系统受力特征进行深入研究。
双船浮托安装过程中上部组块的荷载转移是一个连续的过程，以往的研究中常将此连续过程按照荷载转移比例划分为若干独立阶段进行分析[1]，如Khaled等[2]采用分阶段方法对双船浮托安装过程进行了模拟，并对双船浮托安装关键阶段的结构强度进行了校核。Sun等[3]、阮志豪等[4]对双船浮托安装过程中多体水动力特性及耦合作用机理进行了研究，建立了双船浮托安装分阶段时域耦合分析模型。许鑫等[5]开展了双船浮托安装典型荷载转移状态模型试验研究，验证了数值模型的准确性。Bai等[6]、Kim等[7]和Koo等[8]分别对导管架平台、半潜式平台和Spar平台的上部组块浮托安装不同荷载转移阶段进行了试验研究，充分验证了浮托安装超大型上部组块的可行性。
然而，在荷载连续转移过程中驳船的排水量、惯性矩、浮心重心等关键参数均会发生显著的变化，传统的分阶段模拟方法无法准确的描述荷载连续转移过程中浮托安装系统的动力特性及受力特征。许鑫[9]利用变平均湿表面方法对浮托安装过程中驳船受到的波浪荷载进行了研究，研究表明当驳船吃水变化较大时，3个水平方向的力和力矩将显著增大。Bai等[10]、Tao等[11]设计了驳船自动压载系统，通过模型试验研究了上部组块荷载连续转移过程中浮托安装系统的结构响应特征，发现荷载连续转移过程中浮托驳船会发生纵倾，进而对浮托安装系统的运动及缓冲装置的碰撞力产生显著影响。但受限于试验条件，未能对荷载连续转移过程中浮托安装系统的运动和受力特性进行系统的研究。
本文研究采用随时间变化的质量点近似模拟驳船连续压载过程，建立了计及荷载连续转移效应的双船浮托安装模拟方法，对荷载转移全过程(包括预对接过程、对接过程和退船过程)中驳船和组块的垂向重心、缓冲装置的垂向及侧向受力以及不同海况下结构的运动和受力特征进行了研究。
1. 双船浮托安装过程及分析理论
1.1 双船浮托安装过程
双船浮托安装过程大体分为如下几个阶段，如图 1所示。
图 1 双船浮托安装过程示意Fig. 1 Diagram of the twin-barge installation
下载:
全尺寸图片
1) 滑移装船、单船运输：如图 1(a)所示，上部组块在相关装备辅助下滑移至运输驳船上，随后整体由拖轮拖航至安装地点附近并进行系泊定位。
2) 驳船就位、单船转双船：如图 1(b)所示，2艘浮托驳船向运输驳船靠拢，通过协同控制卷锚机和纵荡护舷使组块支撑点与驳船甲板缓冲装置(deck support unit，DSU)对齐。增大运输驳船吃水、降低组块高度，组块重量逐渐转移至浮托驳船。重量完全转移后组块与运输驳船分离，运输驳船撤离。
3) 双船进入、荷载转移：如图 1(c)所示，浮托驳船与上部组块整体靠近导管架，调整交叉系缆使组块插尖与导管架桩腿缓冲装置(leg mating unit, LMU)对齐。通过增加浮托驳船吃水、降低组块高度，组块重量通过插尖和LMU逐渐转移至导管架结构上。
4) 双船撤离、安装完成：如图 1(d)所示，组块重量完全转移至导管架结构后，进一步增加浮托驳船吃水使组块支撑点与浮托驳船DSU分离。当两者间距足够大时浮托驳船撤离，安装完成。
双船浮托安装涉及2次荷载转移，由于组块支撑点与浮托驳船DSU、组块插尖与导管架LMU的间距非常小，环境荷载作用下3艘驳船及上部组块发生复杂耦合作用，而组块、驳船及导管架之间将发生剧烈的碰撞，故荷载转移过程对浮托安装作业的成败具有决定性的作用，本文将对上部组块由浮托驳船转移至导管架结构这一连续过程进行研究。
1.2 双船浮托安装耦合动力分析理论
1.2.1 单浮体运动控制方程
在刚体假设条件下，根据牛顿第二定律可得环境荷载作用下浮托驳船重心位置处的六自由度运动控制方程[12]：
$$ (\mathit{\boldsymbol{M}} + \mathit{\boldsymbol{A}})\left[ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}\mathit{\boldsymbol{v}}}}{{{\rm{d}}t}}}\\ {\frac{{{\rm{d}}\mathit{\boldsymbol{\omega }}}}{{{\rm{d}}t}}} \end{array}} \right] + \mathit{\boldsymbol{D}}\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{v}}\\ \mathit{\boldsymbol{\omega }} \end{array}} \right] + \mathit{\boldsymbol{K}}\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{x}}\\ \mathit{\boldsymbol{\theta }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{f}}\\ {\mathit{\boldsymbol{m}} - \mathit{\boldsymbol{\omega }} \times (\mathit{\boldsymbol{I\omega }})} \end{array}} \right] $$ (1) 式中：M和I分别为驳船的质量和转动惯量矩阵；A为驳船的附加质量矩阵；υ和ω分别是驳船水平速度和转动速度向量；x和θ分别是驳船水平位移和转动角度向量；t为时间变量；K为驳船静水回复力刚度矩阵；f和m分别是驳船受到的力和力矩，f的表达式为：
$$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{f}} = \mathit{\boldsymbol{f}}_{{\rm{wave }}}^{(1)} + \mathit{\boldsymbol{f}}_{{\rm{wave }}}^{(2)} + {\mathit{\boldsymbol{f}}_{{\rm{wind }}}} + {\mathit{\boldsymbol{f}}_{{\rm{current }}}} + }\\ {{\mathit{\boldsymbol{f}}_{{\rm{mooring }}}} + {\mathit{\boldsymbol{f}}_{{\rm{coupled }}}} + {\mathit{\boldsymbol{f}}_{{\rm{ex }}}}} \end{array} $$ (2) 式中：fwave(1)和fwave(2)分别为作用在驳船上的一阶和二阶波浪力；fwind和fcurrent分别为风、流荷载；fmooring为系缆的回复力；fcoupled为驳船与其他结构之间的作用力，包括结构之间的碰撞力、系缆约束力等；fex为其他荷载，如拖轮的作用力等。此外，作用在浮体上的力矩m同样包含以上成分。
根据驳船频域运动方程和时域运动方程的对应关系，可将单驳船运动控制方程进一步表示为：
$$ \begin{array}{*{20}{c}} {[\mathit{\boldsymbol{M}} + \mathit{\boldsymbol{A}}(\infty )]\left[ {\begin{array}{*{20}{c}} {\frac{{{\rm{d}}\mathit{\boldsymbol{v}}}}{{{\rm{d}}t}}}\\ {\frac{{{\rm{d}}\mathit{\boldsymbol{\omega }}}}{{{\rm{d}}t}}} \end{array}} \right] + \int\limits_{ - \infty }^t \mathit{\boldsymbol{R}} (t - \tau ){\rm{d}}\tau + \mathit{\boldsymbol{K}}\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{x}}\\ \mathit{\boldsymbol{\theta }} \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{f}}\\ {\mathit{\boldsymbol{m}} - \mathit{\boldsymbol{\omega }} \times (\mathit{\boldsymbol{I\omega }})} \end{array}} \right]} \end{array} $$ (3) 式中：A(∞)为驳船强迫运动频率为无穷时对应的附加质量矩阵；R(t-τ)浮体的延迟函数，可通过下式计算得到：
$$ \mathit{\boldsymbol{R}}(t) = \frac{2}{\pi }\int\limits_0^\infty \mathit{\boldsymbol{B}} (\omega )\cos (\omega t){\rm{d}}\omega $$ (4) 式中B(ω)为驳船势流阻尼矩阵。
1.2.2 多浮体运动控制方程
双船浮托安装涉及浮托驳船、上部组块以及导管架基础等多个结构，多个结构相互耦合、相互干涉。考虑多体结构之间的耦合效应，浮托驳船及上部组块的运动方程可表示为:
$$ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{M}}_a} + {{\boldsymbol{A}}_a}(\infty )}&{{{\boldsymbol{A}}_{ab}}(\infty )}\\ {{{\boldsymbol{A}}_{ba}}(\infty )}&{{{\boldsymbol{M}}_b} + {{\boldsymbol{A}}_b}(\infty )} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\mathop {\boldsymbol{\xi }}\limits^{..} }_1}}\\ {{{\mathop {\boldsymbol{\xi }}\limits^{..} }_2}} \end{array}} \right] + }\\ {\int\limits_{ - \infty }^\tau {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{R}}_a}(t - \tau )}&{{{\boldsymbol{R}}_{ab}}(t - \tau )}\\ {{{\boldsymbol{R}}_{ba}}(t - \tau )}&{{{\boldsymbol{R}}_b}(t - \tau )} \end{array}} \right]} \left[ {\begin{array}{*{20}{c}} {{{\mathop {\boldsymbol{\xi }}\limits^. }_1}}\\ {{{\mathop {\boldsymbol{\xi }}\limits^. }_2}} \end{array}} \right]d\tau + }\\ {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{K}}_a}}&0\\ 0&{{{\boldsymbol{K}}_b}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{{\boldsymbol{\xi }}_1}}\\ {{{\boldsymbol{\xi }}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{{\boldsymbol{F}}_1}}\\ {{{\boldsymbol{F}}_2}} \end{array}} \right]} \end{array} $$ (5) $$ {{\boldsymbol{M}}_T}{{\boldsymbol{\ddot \xi }}_3} + {{\boldsymbol{D}}_T}{{\boldsymbol{\dot \xi }}_3} + {{\boldsymbol{K}}_T}{{\boldsymbol{\xi }}_3} = {{\boldsymbol{F}}_3} $$ (6) 式中：Ma和Mb分别为浮托驳船A和浮托驳船B的质量矩阵；Aa(∞)和Ab(∞)分别为浮托驳船A和浮托驳船B频率无穷大时强迫运动时的附加质量矩阵；Aab(∞)和Aba(∞)为两艘浮托驳船毗邻布置而引起的附加质量矩阵；ξ1和ξ2分别为两艘浮托驳船的位移向量；Ra(t-τ)、Rb(t-τ)、Rab(t-τ)和Rba(t-τ)分别为浮托驳船A和浮托驳船B对应的延迟函数矩阵，以及驳船相互干涉产生的延迟函数矩阵；Ka和Kb分别为浮托驳船A和浮托驳船B的静水回复力刚度矩阵；F1和F2分别为浮托驳船A和浮托驳船B对应荷载向量；MT为上部组块的质量矩阵；DT为上部组块的阻尼矩阵；KT为上部组块的回复力刚度矩阵，与约束条件有关；ξ3为上部组块的位移；F3为上部组块受到的外荷载，包括自身重力、浮托驳船的支撑力、上部组块与浮托驳船之间的碰撞力以及上部组块所受的风荷载等。
2. 环境条件及数值模型
2.1 环境条件
为探究随机波浪作用下双船浮托安装荷载连续转移过程中驳船的响应特性，根据目标安装海域的水文资料，选取了6组不同海况进行研究，并采用JONSWAP谱表征随机波浪的能量分布，所选海况的波浪参数如表 1所示。
表 1 随机海况的波浪参数Table 1 Wave parameters of the selected sea states工况 有效波高Hs/m 跨零周期TZ/s 谱峰升高因子γ 浪向/(°) C1 0.50 4.00 1.80 180 C2 0.75 5.00 1.80 180 C3 1.00 6.00 1.80 180 C4 0.50 4.00 1.80 135 C5 0.75 5.00 1.80 135 C6 0.50 4.00 1.80 90 2.2 导管架结构
目标导管架平台为六桩腿平台，工作水深为25.00 m，长32.00 m，宽30.20 m，高33.40 m。上部组块长81.00 m，宽50.00 m，高21.25 m，重10 000 t。上部组块底层甲板下方设有6个插尖与导管架桩腿LMU对接，插尖的外侧设有6个支撑点与浮托驳船DSU对接。上部组块主要参数如表 2所示。
表 2 上部组块主要参数Table 2 Main particulars of the topsidem 参数 数值 参数 数值 长 81.00 横摇回转半径 22.56 宽 50.00 纵摇回转半径 15.19 高 21.35 艏摇回转半径 26.31 2.3 浮托驳船结构
浮托驳船系统为2艘完全相同的半潜式驳船，驳船总长153.20 m，型宽为38.00 m，型深为9.00 m，主要参数如表 3所示。
表 3 浮托驳船的主要参数Table 3 Main particulars of the barge参数 数值 参数 数值 吃水/m 5.00 垂向COG/m 5.58 排水量/kg 1.88×107 横摇回转半径/m 9.11 纵向COG/m 80.73 纵摇回转半径/m 44.64 横向COG/m 0 艏摇回转半径/m 44.62 2.4 DSU/LMU
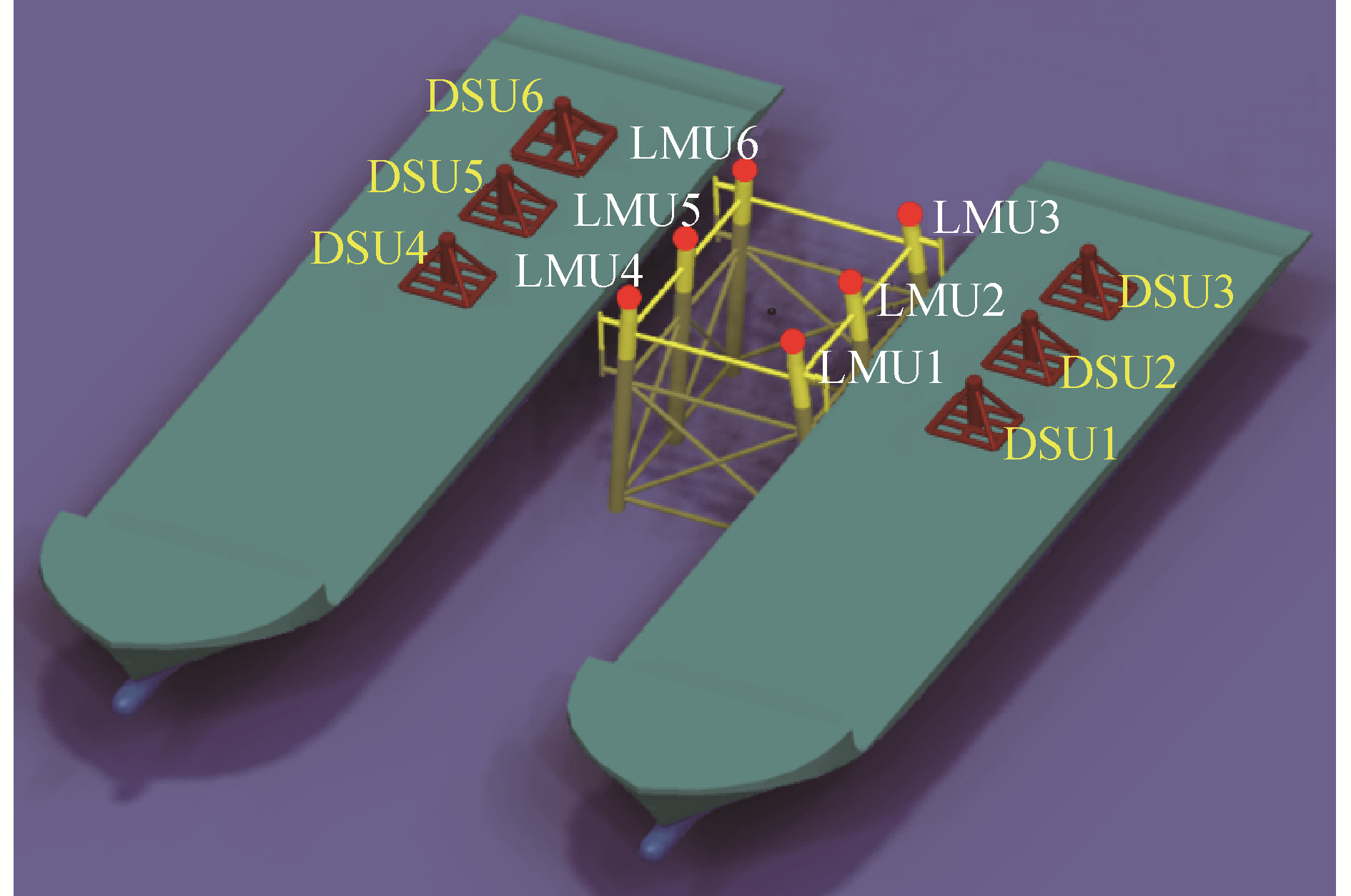
DSU和LMU是海洋平台安装中常见的机械缓冲装置，如图 2所示，其内部的垂向和横向橡胶构件可有效吸收碰撞产生的冲击能量，底部的沙箱可避免缓冲过程中的刚性碰撞。在数值模拟中，DSU与LMU的垂向及横向橡胶材质构件可简化为弹簧阻尼模型。
图 2 缓冲装置示意Fig. 2 Diagram of the buffers下载:
全尺寸图片
数值模型共有6个LMU和DSU，其中LMU安装于导管架桩腿顶端，DSU安装于2艘浮托驳船的甲板上，LMU和DSU的位置关系如图 3所示。
图 3 DSU和LMU位置关系示意Fig. 3 Diagram of the positions between DSUs and LMUs下载:
全尺寸图片
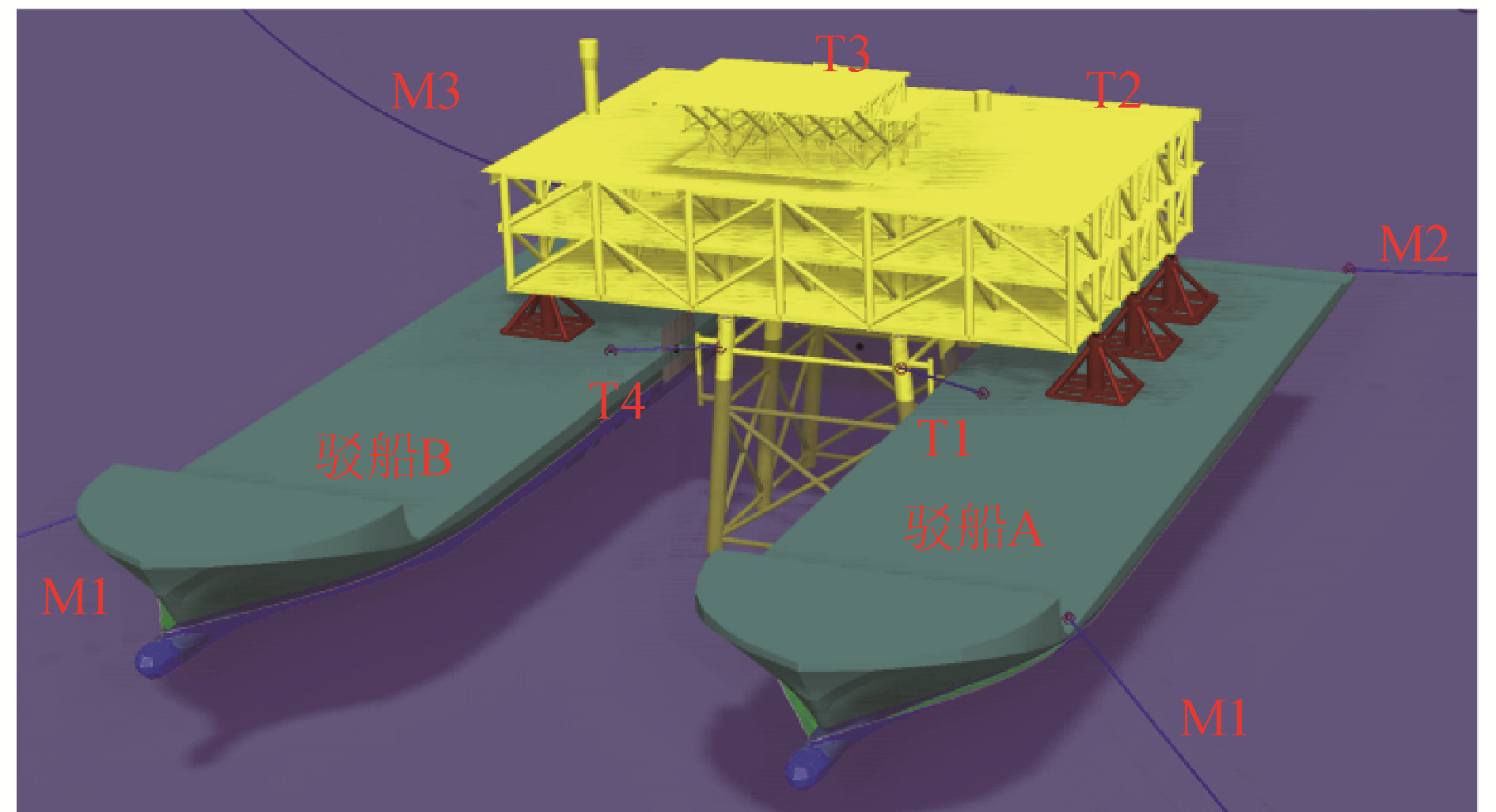
2.5 双船浮托安装荷载连续转移耦合动力分析模型
为探究双船浮托安装荷载连续转移下浮托安装系统的动力响应特性及受力特征，利用随时间变化的质量点近似模拟浮托驳船的连续压载过程，建立了双船浮托安装荷载连续转移耦合动力分析模型，如图 4所示。导管架结构固定于海底，组块通过DSU支撑在驳船甲板上，驳船外侧以系泊缆与海底相连，内侧以缆绳与导管架相连，浮托驳船系泊系统的布置如图 4所示，系泊系统参数见表 4。
图 4 双船浮托安装荷载连续转移耦合动力分析模型Fig. 4 Coupled dynamic analysis model of twin-barge float-over installation considering continuous loads transfer effect下载:
全尺寸图片
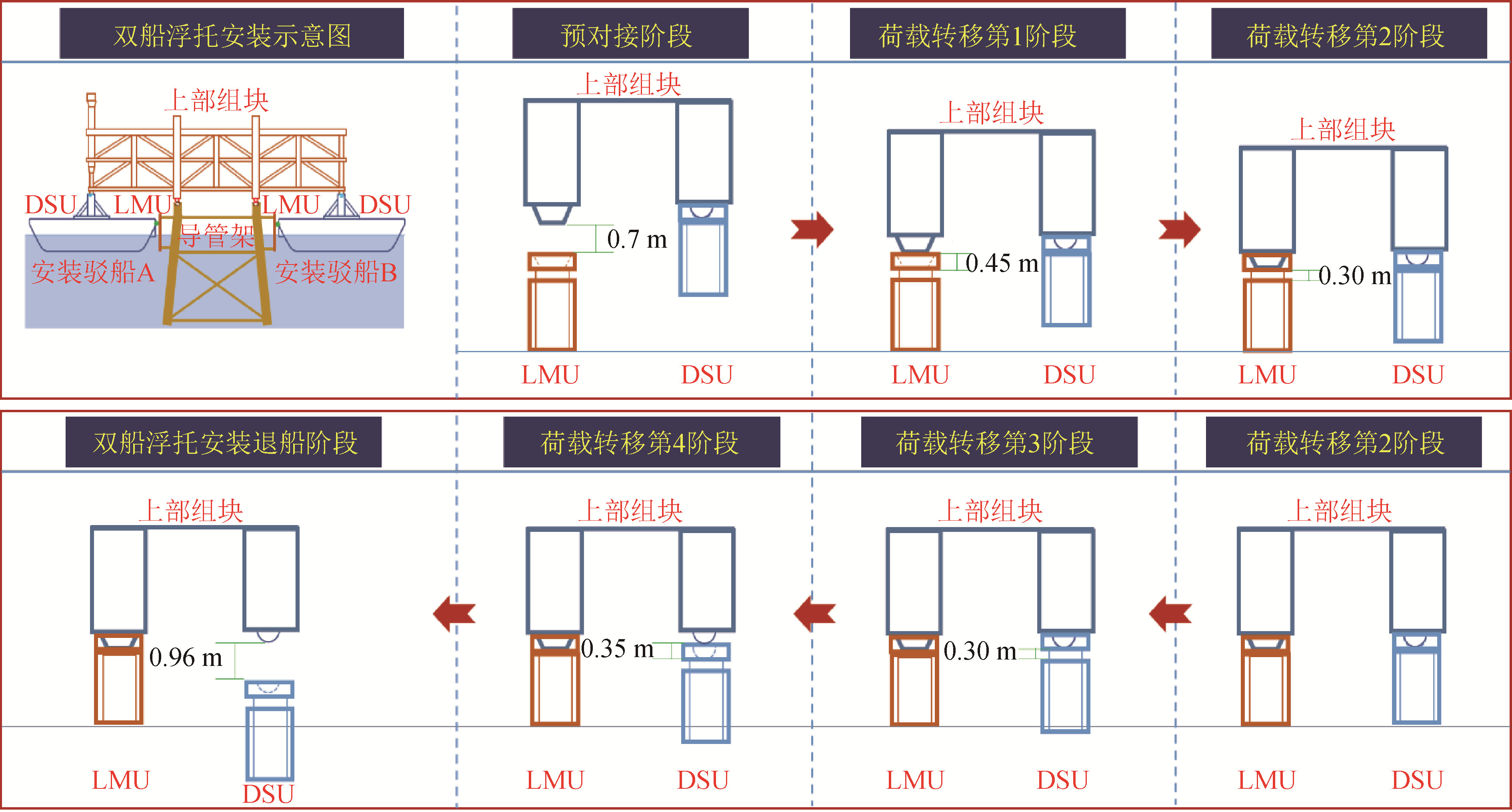
表 4 系泊系统的主要参数Table 4 Main parameters of the mooring system类别 长度/m 轴向刚度/(N·m-1) 单位长度重量/(kg·m-1) 预张力/N M1/M4 650.00 4.00×105 24.17 392 000 M2/M3 650.00 4.00×105 24.17 392 000 T1/T4 14.20 2.07×106 4.80 441 000 T2/T3 40.10 7.33×105 4.80 392 000 为清晰地描述荷载连续转移过程，根据上部组块与DSU和LMU的相对位置关系，将荷载连续转移过程划分成6个密切相关的阶段，不同阶段上部组块与DSU和LMU的相对关系如图 5所示。
图 5 LMU和DSU对接示意Fig. 5 Diagram of mating process on LMUs and DSUs下载:
全尺寸图片
1) 预对接阶段：上部组块插尖与LMU接收器顶端间距逐渐减小至两者平齐的过程，此过程中上部组块的重量完全由DSU承载，浮托驳船吃水由5 m增加至5.7 m，排水量增加2 647 t。
2) 荷载转移第1阶段：上部组块插尖从LMU接收器顶端逐渐下移至LMU接收器底端的过程，此过程中上部组块的重量开始转移至导管架桩腿上，浮托驳船吃水增加0.45 m，排水量增加1 715 t。
3) 荷载转移第2阶段：LMU冲程未压缩至LMU冲程完全压缩的过程，此过程中上部组块的重量由LMU和DSU共同承担，驳船吃水增加0.30 m，排水量增加1 965 t。
4) 荷载转移第3阶段：DSU冲程由完全压缩至完全放开的过程，此过程中上部组块位置基本保持不变，其重量主要由LMU承担，驳船吃水增加0.30 m，排水量增加2 234 t。
5) 荷载转移第4阶段：上部组块支撑点与DSU接收器由完全接触至两者平齐的过程，此过程上部组块位置基本保持不变，其重量主要由LMU承担，驳船吃水增加0.35 m，排水量增加2 489 t。
6) 退船阶段：上部组块支撑点与DSU接收器顶端平齐至间隔一定距离的过程，此过程上部组块位置基本不变，其重量主要由LMU承担，驳船吃水增加0.96 m，最终吃水为8.06 m，排水量增加4 430 t，最终排水量为34 280 t。
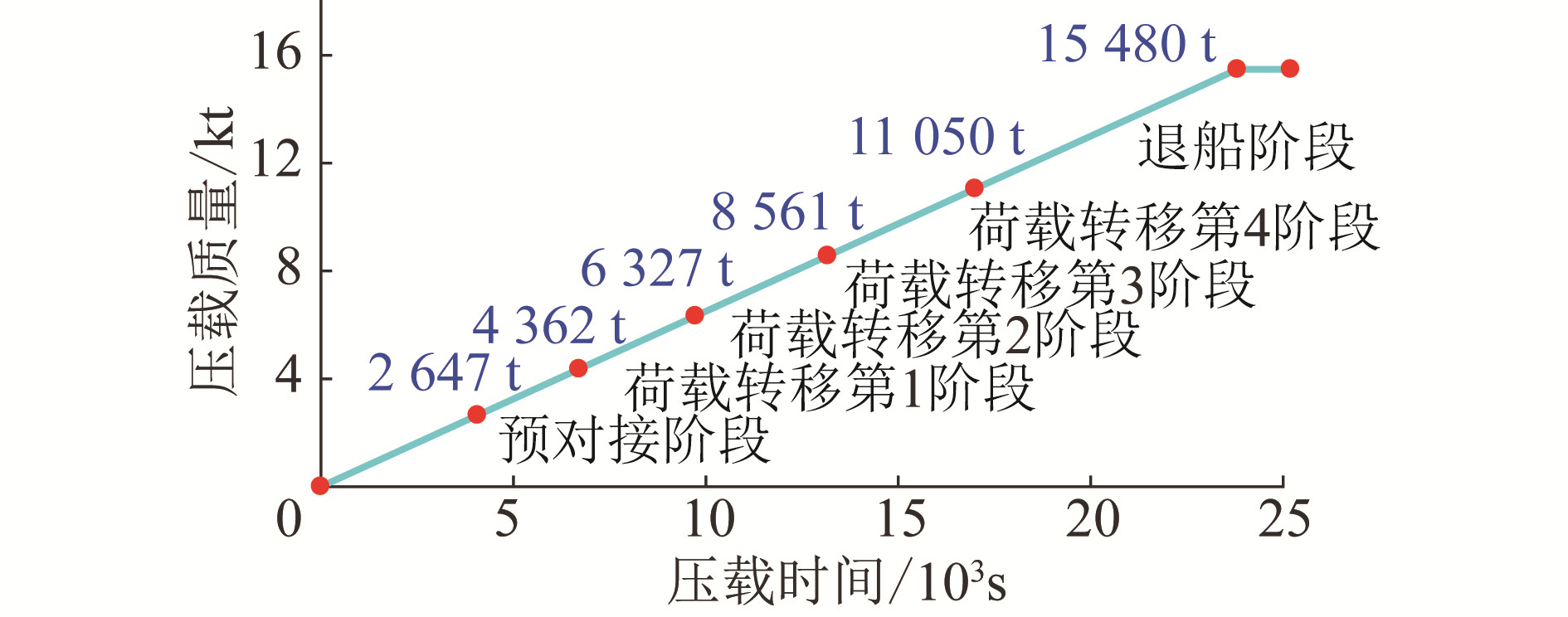
实际浮托安装荷载转移过程大约持续6 h，合理考虑退船时间，整个荷载连续转移过程约为7 h(25 200 s)，模拟时间步长为0.02 s，在每个时间步内对模型的重量、重心、惯性矩等参数进行更新。荷载连续转移过程中不同阶段驳船压载水量的增加按照随时间均匀变化的方式进行模拟，压载水质量变化规律如图 6所示。
图 6 压载水质量随时间变化的曲线Fig. 6 Curve of ballast water with time下载:
全尺寸图片
3. 荷载连续转移过程浮托安装系统的运动及受力特性
3.1 上部组块和驳船重心垂向位置连续变化特性
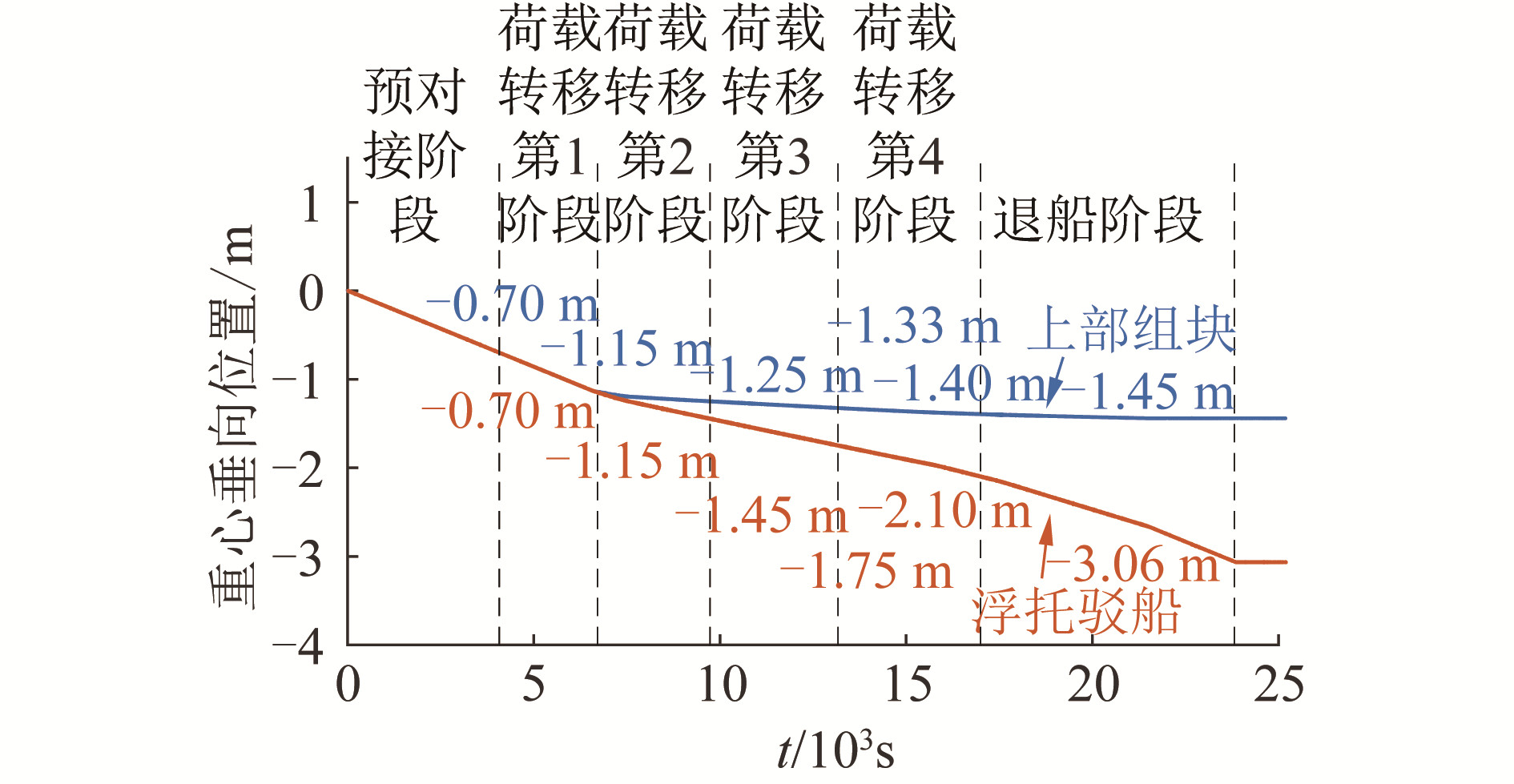
为验证建立的荷载连续转移模拟方法的有效性，首先对静水条件下上部组块和浮托驳船重心垂向位置变化规律进行研究，结果如图 7所示。
图 7 驳船及上部组块垂向位置变化曲线Fig. 7 Curves of the vertical positions of the barge and topside下载:
全尺寸图片
由图 7可知，预对接阶段持续4 070 s，此阶段驳船与上部组块的垂向重心均下降了0.70 m，与预设值相符；荷载转移第1阶段持续2 640 s，驳船和上部组块垂向重心下降了0.45 m，与预设值相符，表明在此之前组块重量完全由驳船承载；荷载转移第2阶段持续3 020 s，驳船垂向重心下降了0.30 m，与预设值相符，但由于上部组块插尖与导管架LMU接收器发生接触，受LMU垂向弹簧作用，上部组块垂向重心仅下降了0.10 m；荷载转移第3阶段持续3 440 s，驳船垂向重心下降0.30 m，而组块垂向重心下降0.08 m，此时组块重量开始向导管架转移；荷载转移第4阶段持续时间为3 830 s，驳船垂向重心下降0.35 m，组块垂向重心下降0.07 m，组块重量逐步由驳船转移至导管架上；退船阶段持续8 200 s，分为2部分，第1部分持续6 800 s，驳船垂向重心下降0.96 m，而组块垂向重心下降0.05 m，第2部分持续时间为1 400 s，驳船和上部组块垂向重心均不再变化，上部组块安装完成。
由驳船和上部组块垂向重心位置变化规律可知，本文建立的双船浮托安装荷载连续转移模拟方法可准确地模拟上部组块荷载连续转移过程，数值模拟结果与预设结果非常接近。
3.2 LMU及DSU垂向受力特性
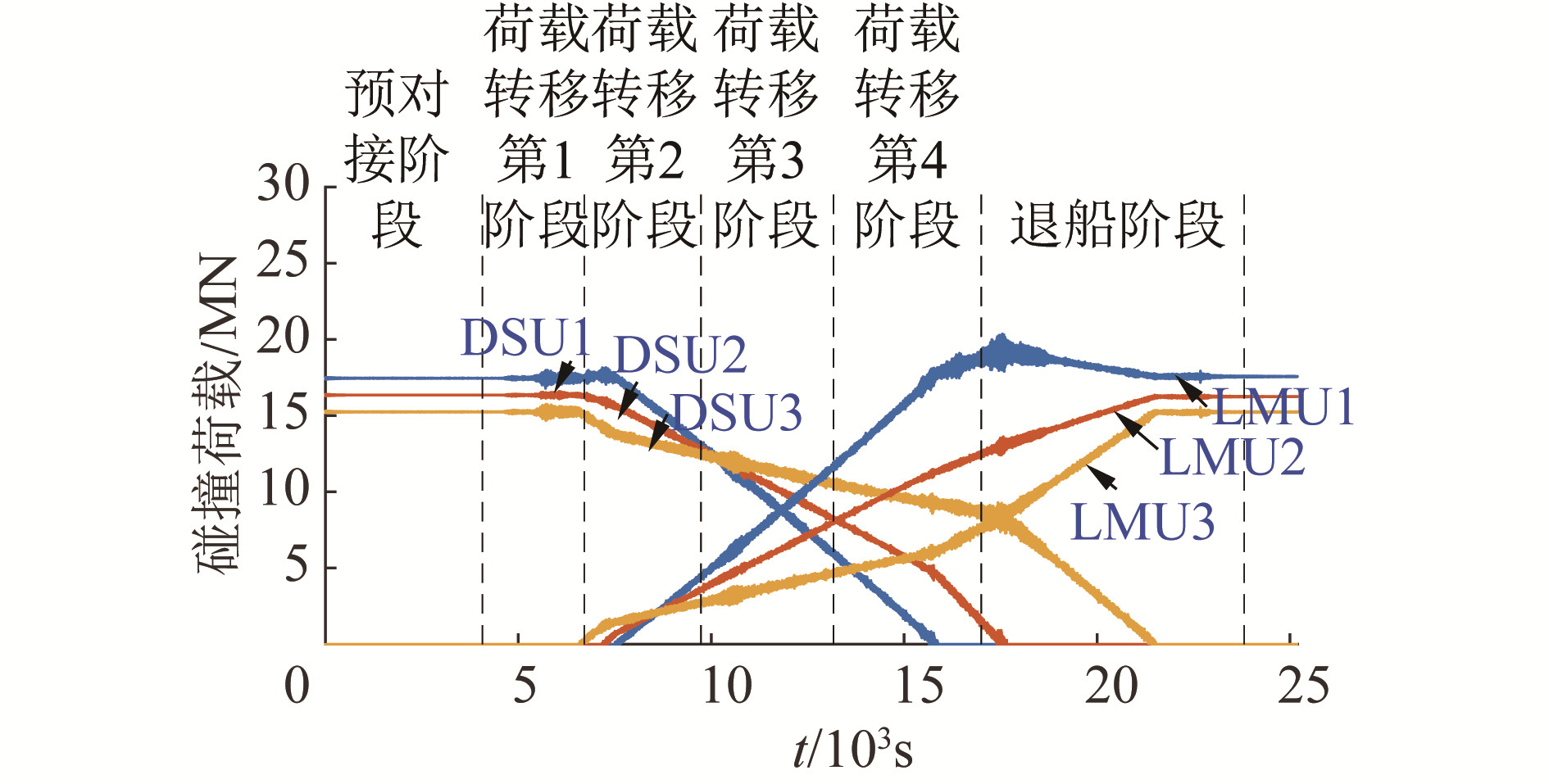
在有效波高0.5 m、跨零周期4.0 s、顺向波浪作用下，缓冲装置的垂向受力如图 8所示。
图 8 LMU和DSU垂向受力变化Fig. 8 Curves of the vertical forces of the LMUs and DSUs下载:
全尺寸图片
图中有5个现象需要特别注意。1)作用在不同DSU和LMU上的垂向荷载具有差异性，其中作用在DSU1/LMU1上的垂向荷载大于DSU2/LMU2上的垂向荷载，两者均大于DSU3/LMU3上的垂向荷载，这是因为上部组块位于浮托驳船的中后部，浮托驳船在浮力和重力的共同作用下将产生一定的纵倾，导致靠近驳船重心处的DSU1和LMU1受到的垂向荷载大于远离驳船重心处DSU3和LMU3受到的垂向荷载；2)在预对接和荷载转移第1阶段，DSU受到的垂向荷载保持恒定，而LMU受到的垂向荷载基本为零，表明组块重量完全由驳船承载，组块插尖与导管架LMU接收器之间无明显作用，荷载未转移；3)在荷载转移第2、3、4阶段，不同DSU受到的垂向荷载逐渐减小，与之对应的LMU垂向荷载逐渐增大，两者之和恒定，表明组块重量由浮托驳船逐渐转移至导管架结构，组块重量由DSU和LMU共同承载；4)由于驳船纵倾，不同DSU和LMU之间荷载转移开始的时间及转移速率具有差异性，其中DSU1荷载转移开始时间晚于DSU2，且两者均晚于DSU3。但DSU1荷载转移速度最快，其垂向荷载最先减小为零，DSU2次之，DSU3最慢。DSU1率先与上部组块支撑点发生分离，DSU2随后，DSU3最后分离；5)退船初始阶段，DSU和LMU的动态垂向荷载幅值明显增大，因为部分DSU与组块脱离导致驳船运动幅值增大，引发DSU/LMU与组块碰撞。随着驳船吃水进一步增加，DSU垂向荷载逐渐减小为零，LMU垂向荷载逐渐稳定，浮托安装完成。值得注意的是，这一特殊现象在常规分阶段方法从未观测到。
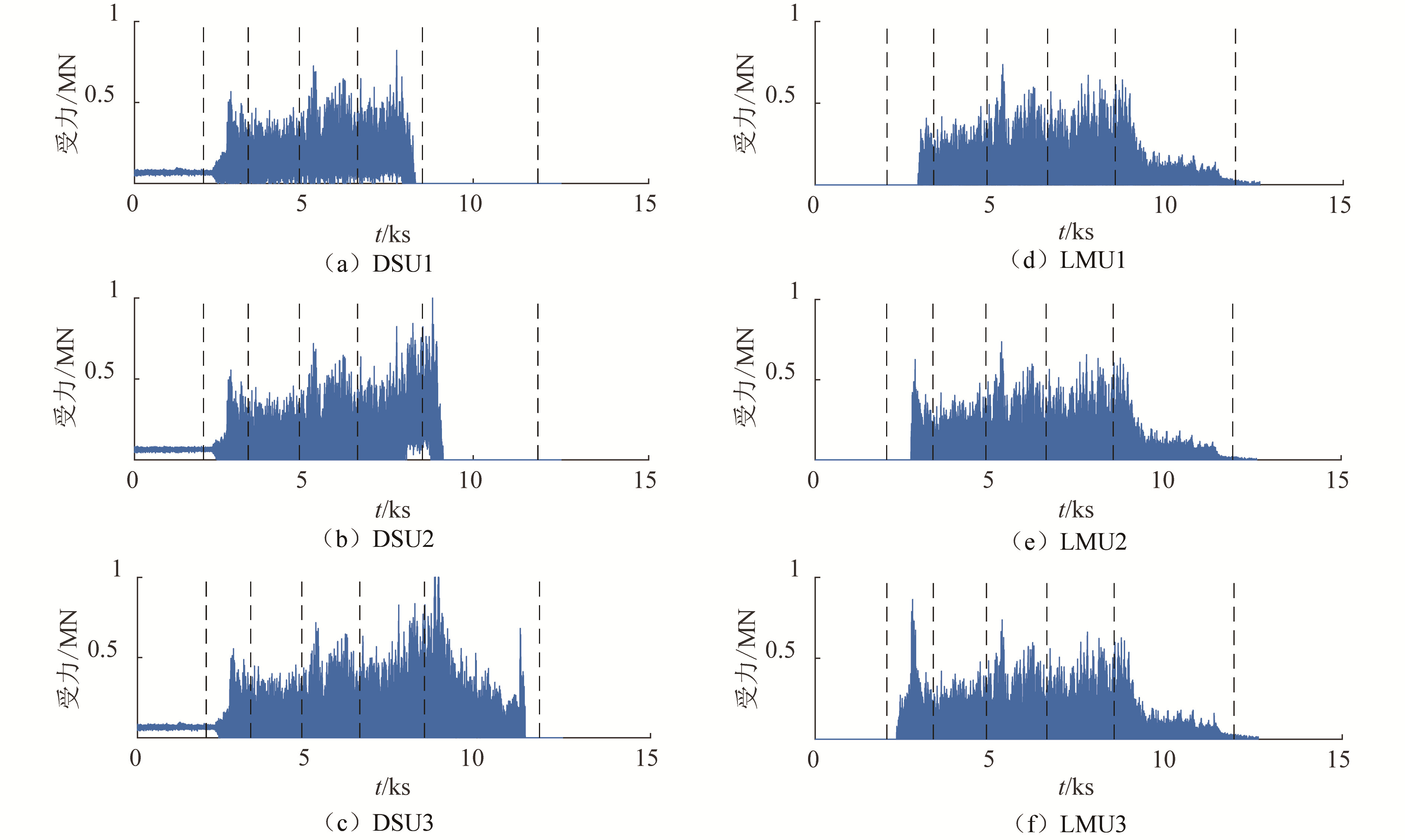
3.3 LMU及DSU侧向受力特性
通过设置沿环向布置的弹簧模拟DSU和LMU的侧向约束作用，在有效波高0.5 m、跨领周期4.0 s、顺向波浪作用下，缓冲装置的侧向受力如图 9所示。由图 9可知，在预对接阶段，驳船的运动导致上部组块支撑点和DSU之间发生相对运动，DSU受到侧向冲击荷载的作用，但上部组块插尖与LMU无接触，故LMU未受到侧向碰撞荷载；在荷载转移第1阶段，上部组块的插尖开始进入LMU接收范围，驳船运动使组块插尖与LMU发生侧向碰撞，而两者的碰撞将加剧组块支撑点与DSU的碰撞，故此时DSU和LMU均受到较大的侧向碰撞力；在荷载转移第2~4阶段，组块支撑点一直处在DSU接收器内，且插尖位于LMU接收器内，驳船运动将引发DSU和LMU的侧向碰撞；在退船阶段，组块支撑点与DSU接收器逐渐分离，驳船运动对组块运动的影响逐渐减弱，故DSU和LMU的侧向碰撞力将逐渐减小为零。由于驳船纵倾，不同DSU所受侧向碰撞力的变化规律有所不同，其中DSU1受到的侧向荷载最先减小为零，其次是DSU2，最后是DSU3，而LMU侧向荷载变化规律基本相同。
图 9 DSU和LMU侧向受力曲线Fig. 9 Curves of the lateral forces on DSUs and LMUs下载:
全尺寸图片
由分析结果可知，在荷载转移过程中DSU和LMU将会受到显著的横向碰撞荷载，尤其是在上部组块插尖进入LMU接收器或上部组块支撑点脱离DSU接收器的瞬间，两者受到的冲击荷载均会发生显著的变化，在实际施工作业过程中需要特别注意，同时这也是常规分阶段模拟中无法捕捉到的现象。
3.4 不同海况下双船浮托安装系统运动及受力特性
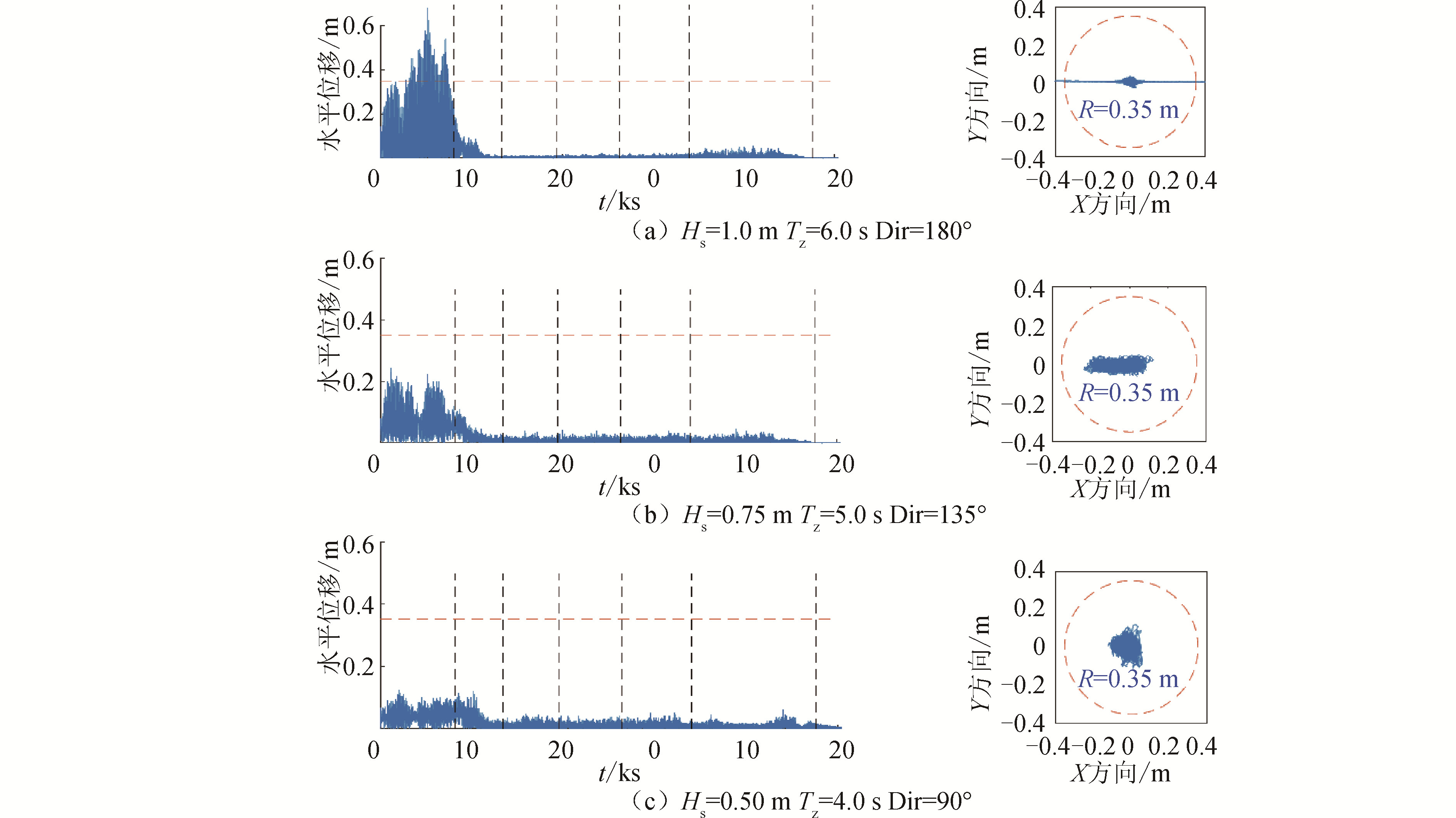
基于双船浮托安装荷载连续转移数值模型，对不同海况下浮托安装系统的运动及受力特性进行了系统的研究。不同海况下上部组块插尖与导管架LMU接收器之间的水平相对运动如图 10所示，由于篇幅有限，仅选取LMU1处的数据进行分析。
图 10 不同海况下组块插尖与LMU接收器的水平相对运动LMU半径(R=0.35 m)Fig. 10 Horizontal relative motion of the topside tip to the LMU receiver under different sea states LMU半径(R=0.35 m)下载:
全尺寸图片
由图 10可知，顺向波浪下组块插尖与LMU接收器之间的水平相对运动具有相似规律。在预对接阶段，插尖与LMU接收器间距较大，LMU侧向刚度对组块的运动无约束作用，两者的水平相对运动较大；在荷载转移阶段，随着组块插尖逐渐进入LMU接收器，LMU侧向刚度将对组块运动产生约束作用，两者的水平相对运动迅速减小。此外，随着波高和周期增加，插尖与LMU接收器的水平相对运动急剧增大，且顺浪向的相对运动明显大于横浪向的相对运动，表明安装环境对浮托安装作业具有显著影响。大多数海况下组块插尖与LMU接收器的水平相对运动最大值均小于LMU接收器的半径，即上部组块插尖可顺利进入LMU接收器完成荷载转移过程。而在波高1.0 m，周期6.0 s顺向波浪的作用下，组块插尖与LMU接收器在预对接阶段的水平相对运动最大值大于LMU接收器的半径，但在预对接的后期，由于上部组块的插尖与导管架基础LMU之间的间距非常小，浮托驳船和上部组块的运动将会导致插尖与LMU之间的短暂接触，两者发生接触后，2艘浮托驳船、上部组块、导管架基础结构可以看成一个整体，由于导管架基础结构的约束作用，整个浮托安装系统抵抗波浪荷载的能力显著提升，驳船的动力特性发生显著变化，运动响应将明显降低，与之对应的组块插尖与LMU接收器的水平相对运动显著减小，满足对接要求，而这一特殊现象在传统分阶段模拟中未出现。
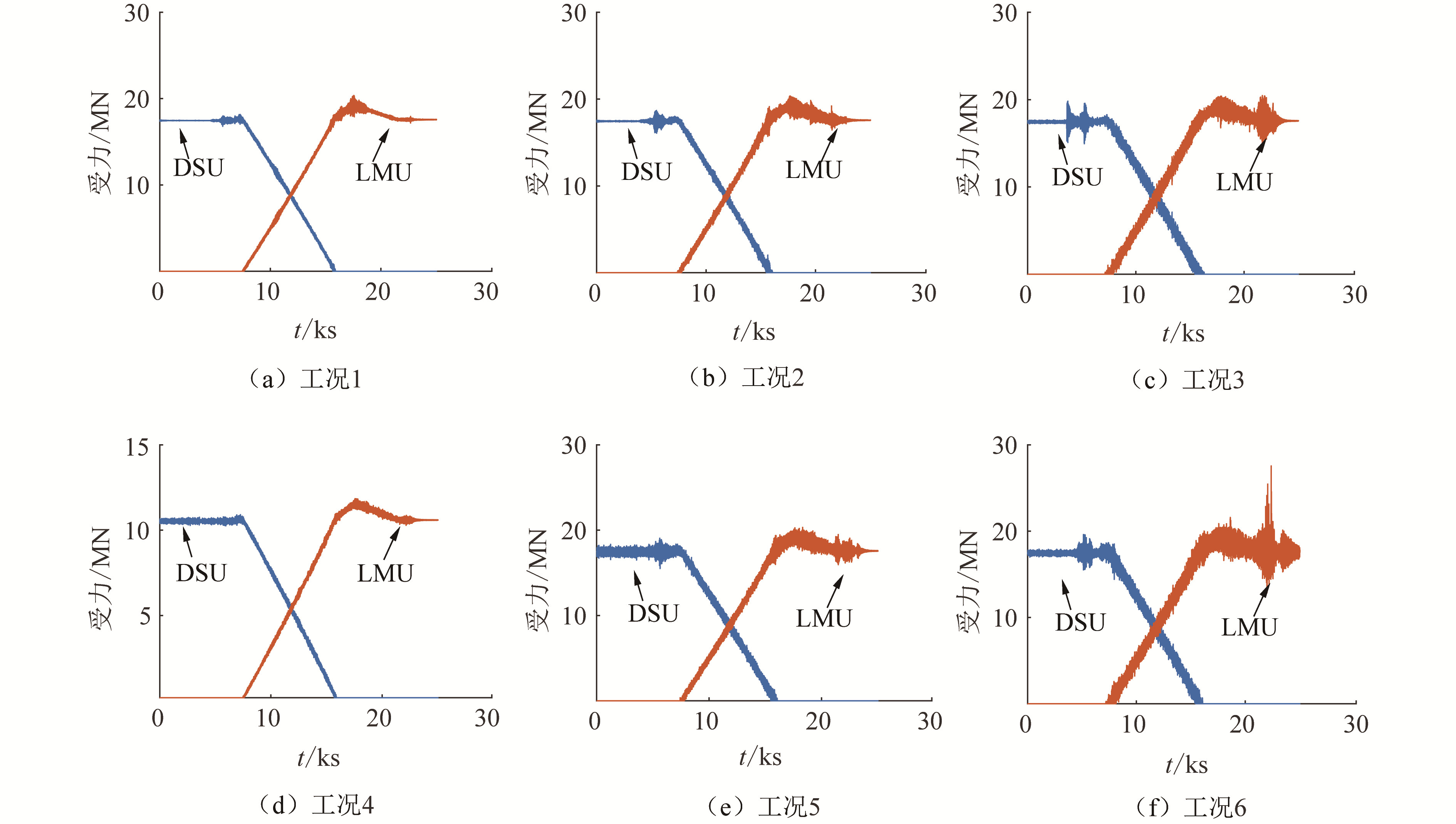
以DSU1和LMU1的垂向荷载数据为例，不同海况下DSU和LMU受到的垂向荷载如图 11所示。由图可知，不同海况下DSU和LMU垂向受力的整体变化规律相似，但有4点不同：1)在相同浪向下，随着输入波浪参数的增大，DSU和LMU垂向受力幅值的变化范围显著增加，这是因为波浪增大导致驳船运动响应加剧，使上部组块与驳船之间的相对运动增大，产生更大的垂向动态荷载，此现象可由组块插尖与LMU的水平相对运动规律证实；2)当DSU的垂向荷载减小为零时，LMU的垂向荷载呈先增大后减小最后稳定的变化趋势，是因为上部组块支撑点与驳船DSU的分离不同步，在某些支撑点与DSU分离的瞬间，驳船的约束力骤变，运动响应随之剧增，此运动通过未分离的DSU传递至上部组块，导致LMU垂向荷载增大。当组块所有支撑点均与DSU分离后，上部组块逐渐趋于稳定，LMU的垂向荷载也逐渐趋近于常数，这一特殊现象在传统分阶段模拟中未出现；3)横向波浪作用下DSU和LMU的垂向动态荷载大于斜向波浪，两者均大于顺向波浪作用下DSU和LMU的垂向动态荷载，且在退船阶段横向波浪作用下组块插尖与LMU之间存在显著冲击荷载。这是因为斜向波浪和横向波浪均有横向波浪荷载分量，在横向波浪荷载作用下驳船的横摇运动响应较大，导致组块与DSU和LMU之间的碰撞较大，因此在浮托安装作业过程中需要特别注意波浪方向的影响。
图 11 不同海况下DSU和LMU受到的垂向冲击荷载Fig. 11 Vertical impact loads of LMU and DSU under different sea states下载:
全尺寸图片
4. 结论
1) 随着驳船压载水的增加，驳船和上部组块的垂向位置连续下降，且降幅与预设值基本相符，表明本文提出的方法可以准确描述双船浮托安装的荷载连续转移过程。
2) 随着驳船的压载，DSU的垂向荷载逐渐减小，与之对应的LMU垂向荷载增加，两者之和基本保持恒定。由于驳船的纵倾效应，不同DSU和LMU受到的垂向荷载大小、荷载转移开始及结束的时刻和转移速率存在显著差异，此现象为荷载连续转移过程的特有现象。
3) 在预对接阶段上部组块插尖与LMU接收器之间的水平相对运动明显大于其他阶段的水平相对运动，且这种相对运动会随着波浪环境的恶劣程度显著增加，但均能顺利完成对接。
4) 横向波浪作用下缓冲装置所受垂向动态荷载明显大于其他方向，且垂向动态荷载会随输入波浪环境的恶劣程度而显著增加。
-
图 1 双船浮托安装过程示意
Fig. 1 Diagram of the twin-barge installation
下载:
全尺寸图片
图 2 缓冲装置示意
Fig. 2 Diagram of the buffers
下载:
全尺寸图片
图 3 DSU和LMU位置关系示意
Fig. 3 Diagram of the positions between DSUs and LMUs
下载:
全尺寸图片
图 4 双船浮托安装荷载连续转移耦合动力分析模型
Fig. 4 Coupled dynamic analysis model of twin-barge float-over installation considering continuous loads transfer effect
下载:
全尺寸图片
图 5 LMU和DSU对接示意
Fig. 5 Diagram of mating process on LMUs and DSUs
下载:
全尺寸图片
图 6 压载水质量随时间变化的曲线
Fig. 6 Curve of ballast water with time
下载:
全尺寸图片
图 7 驳船及上部组块垂向位置变化曲线
Fig. 7 Curves of the vertical positions of the barge and topside
下载:
全尺寸图片
图 8 LMU和DSU垂向受力变化
Fig. 8 Curves of the vertical forces of the LMUs and DSUs
下载:
全尺寸图片
图 9 DSU和LMU侧向受力曲线
Fig. 9 Curves of the lateral forces on DSUs and LMUs
下载:
全尺寸图片
图 10 不同海况下组块插尖与LMU接收器的水平相对运动LMU半径(R=0.35 m)
Fig. 10 Horizontal relative motion of the topside tip to the LMU receiver under different sea states LMU半径(R=0.35 m)
下载:
全尺寸图片
图 11 不同海况下DSU和LMU受到的垂向冲击荷载
Fig. 11 Vertical impact loads of LMU and DSU under different sea states
下载:
全尺寸图片
表 1 随机海况的波浪参数
Table 1 Wave parameters of the selected sea states
工况 有效波高Hs/m 跨零周期TZ/s 谱峰升高因子γ 浪向/(°) C1 0.50 4.00 1.80 180 C2 0.75 5.00 1.80 180 C3 1.00 6.00 1.80 180 C4 0.50 4.00 1.80 135 C5 0.75 5.00 1.80 135 C6 0.50 4.00 1.80 90 表 2 上部组块主要参数
Table 2 Main particulars of the topside
m 参数 数值 参数 数值 长 81.00 横摇回转半径 22.56 宽 50.00 纵摇回转半径 15.19 高 21.35 艏摇回转半径 26.31 表 3 浮托驳船的主要参数
Table 3 Main particulars of the barge
参数 数值 参数 数值 吃水/m 5.00 垂向COG/m 5.58 排水量/kg 1.88×107 横摇回转半径/m 9.11 纵向COG/m 80.73 纵摇回转半径/m 44.64 横向COG/m 0 艏摇回转半径/m 44.62 表 4 系泊系统的主要参数
Table 4 Main parameters of the mooring system
类别 长度/m 轴向刚度/(N·m-1) 单位长度重量/(kg·m-1) 预张力/N M1/M4 650.00 4.00×105 24.17 392 000 M2/M3 650.00 4.00×105 24.17 392 000 T1/T4 14.20 2.07×106 4.80 441 000 T2/T3 40.10 7.33×105 4.80 392 000 -
[1] TAHAR A, HALKYARD J, STEEN A, et al. Float over installation method—comprehensive comparison between numerical and model test results[J]. Journal of offshore mechanics and Arctic engineering, 2006, 128(3): 256-262. doi: 10.1115/1.2199556 [2] GEBA K A, WELAYA Y M A, LEHETA H W, et al. The hydrodynamic performance of a novel float-over installation[J]. Ocean engineering, 2017, 133: 116-132. doi: 10.1016/j.oceaneng.2017.01.034 [3] SUN L, TAYLOR R E, CHOO Y S. Multi-body dynamic analysis of float-over installations[J]. Ocean engineering, 2012, 51: 1-15. doi: 10.1016/j.oceaneng.2012.05.017 [4] 阮志豪, 张万里, 李怀亮. 双船浮托法数值模拟[J]. 中国海洋平台, 2018, 33(1): 40-50. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGHY201801008.htm RUAN Zhihao, ZHANG Wanli, LI Huailiang. Numerical simulation of two barge floatover method[J]. China offshore platform, 2018, 33(1): 40-50. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGHY201801008.htm [5] XU Xin, YANG Jianmin, LI Xin, et al. Time-domain simulation for coupled motions of three barges moored side-by-side in floatover operation[J]. China Ocean engineering, 2015, 29(2): 155-168. doi: 10.1007/s13344-015-0012-4 [6] BAI Xiaodong, LUO Hanbing, XIE Peng. Experimental analysis of dynamic response of floatover installation using rapid transfer technique in continuous load transfer process[J]. Journal of marine science and technology, 2020, 25(4): 1182-1198. doi: 10.1007/s00773-020-00708-7 [7] KIM N W, NAM B W, KWON Y J, et al. An experimental study on the float-over installation of a semi- submersible[C]//Proceedings of the 29th International Ocean and Polar Engineering Conference. Hawaii, 2019: 335-340. [8] KOO B, MAGEE A, LAMBRAKOS K, et al. Model tests for floatover installation of spar topsides[C]//Proceedings of ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering. Shanghai, 2010: 363-371. [9] 许鑫. 浮托安装系统耦合动力响应研究[D]. 上海: 上海交通大学, 2014. XU Xin. Investigation on couplng dynamic response of the floatover system[D]. Shanghai: Shanghai Jiao Tong University, 2014. [10] BAI Xiaodong, LUO Hanbing, XIE Peng. Experimental investigation on hydrodynamic performance of side-by-side three barges in topsides floatover installation in beam seas[J]. Ocean engineering, 2021, 236: 109516. doi: 10.1016/j.oceaneng.2021.109516 [11] TAO W, WANG S, SONG X, et al. A continuous simulation method of load transfer process during twin-barge float-over installation[C]//Proceedings of the 30th International Ocean and Polar Engineering Conference. Shanghai, 2020: 938-943.
