1/4 cell-based two-level coarse-mesh finite difference acceleration method
-
摘要: 为了进一步降低采用栅元尺度的粗网有限差分方法加速高保真中子输运计算的外迭代步以获得更大的加速收益，本文依据傅里叶分析结果提出并实施了一种1/4栅元尺度的两级栅元尺度的粗网有限差分加速方法，同时实现了基于构造实体几何的以1/4栅元为单位的几何构建方法。本文采用C5G7 RA和VERA Problem #4三维基准题验证方法的正确性和加速效果，并基于秦山一期压水堆1/4模型进行不同工况下的实堆高保真稳态临界计算。结果表明: 在保证精度的前提下，本文提出的基于1/4栅元的两级栅元尺度的粗网有限差分加速方法能够针对真实的1/4几何模型将外迭代次数进一步降低1/3左右。秦山一期压水堆临界硼浓度最大误差为-21×10-6，1/4模型高保真中子物理计算时间为88.3核时。从降低迭代次数和减少计算规模2方面有效降低高保真输运计算的计算负担。Abstract: To further reduce the number of iterations of high-fidelity neutron transport calculations using the cell-based coarse-mesh finite difference (CMFD) method to obtain great acceleration benefits, this paper proposes and implements a 1/4 cell-based two-level CMFD acceleration method based on Fourier analysis and implements the geometric modeling method based on constructive solid geometry with 1/4 cells. C5G7 RA and VERA benchmark #4 3D problems were used to verify the correctness and acceleration effect of the method, and high-fidelity steady-state critical calculations were performed under different operating conditions based on the 1/4 cell-based model of Qinshan Phase I PWR. The results show that the application of the 1/4 cell-based two-level CMFD acceleration method can further reduce the number of outer iterations by about 1/3 with guaranteed accuracy. The maximum error of the critical boron concentration of Qinshan Phase I PWR is -21×10-6, and the high-fidelity neutron physics calculation time is 88.3 core hours for the 1/4 cell-based model. The method effectively reduces the computational burden of high-fidelity transport calculation in terms of reducing the iteration number and computational scale.
-
粗网有限差分方法(coarse mesh finite difference，CMFD)[1]因其便于实施、加速效果好，得以在全堆芯输运计算中广泛研究和应用。但是，用于加速的低阶系统求解往往引入额外的计算负担，尤其瞬态模拟，CMFD求解时间与特征线方法(method of characteristics, MOC)中子输运求解时间相当[2]，且存在数值不稳定性的天然缺陷。为解决上述问题，学者们提出了多种更加稳定有效的CMFD方法[3-7]。同时为有效降低CMFD自身的计算量，提出针对能量或空间的多级加速方法[8-9]。对于高保真中子输运计算，无论采用何种类型的CMFD，仅采用基于栅元尺度的CMFD加速，都存在加速效果的瓶颈。以外迭代为MOC为例，无论CMFD怎样收敛，外迭代次数会保持在一个特定的数值[10]。而对于高保真中子输运计算来说，迭代次数是决定耗时的关键因素，如何打破这个瓶颈，在等价的前提下进一步减少迭代次数，成为限制高保真中子输运方法发展的新挑战。为研究有限差分法渐近收敛速度，傅里叶分析是一种广泛应用的标准方法[11]，研究结果表明对于传统CMFD方法，当适当减小光学厚度时可获得更好的收敛性。
本文针对基于广义平衡理论的粗网有限差分(gCMFD)方法[3]进行了傅里叶分析，依据傅里叶分析的结果基于全三维一步法精细化输运求解程序HNET[12-13]重新构建以1/4栅元为单位的几何建模模块，并以此为基础实现1/4栅元尺度gCMFD两级加速，从而能够从降低迭代次数和减少计算规模2个方面有效降低高保真输运计算的计算负担。采用C5G7 RA和VERA Problem #4三维基准题验证方法的正确性和加速效果，并基于秦山一期压水堆不同稳态运行工况开展1/4模型稳态临界计算，综合验证程序的计算能力和加速效果。
1. 傅里叶分析与两级gCMFD加速
在HNET中，目前采用栅元尺度的两级gCMFD方法加速2D/1D精细化中子输运计算：二维采用MOC计算为一维NEM和三维多群gCMFD提供粗网均匀化宏观截面、局部径向节块不连续因子(nodal discontinuity factor，NDF)和扩散系数修正因子(modified diffusion coefficient factor，MDF)，一维采用NEM计算为三维gCMFD提供局部轴向NDF和MDF，通过这些参数构建基于栅元均匀化网格的三维多群CMFD线性系统。再次求解全局三维多群gCMFD，为径向二维MOC计算提供栅元的平均中子通量密度、轴向泄漏项、边界偏中子流和特征值，同时，为轴向一维NEM计算提供节块的平均通量和径向泄漏项。然而，多群gCMFD线性系统自身条件数大，同样面临求解耗时严重的问题。基于同样的思路，应用gCMFD方法建立与多群gCMFD完全等价的单群gCMFD线性系统，以加速多群gCMFD的迭代求解过程，能够实现在能量方面对多群gCMFD求解的有效加速，进而减少其计算负担。相比于多群gCMFD，单群gCMFD线性系统自身条件数很低，计算代价也很低。因此，不会增加过多的额外计算负担。
1.1 gCMFD傅里叶分析
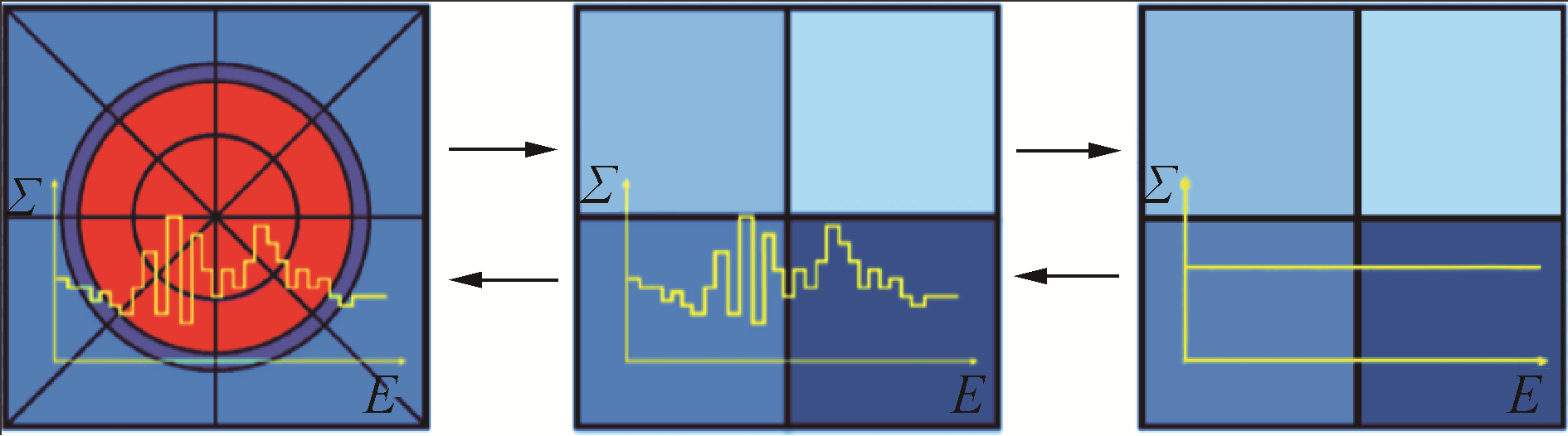
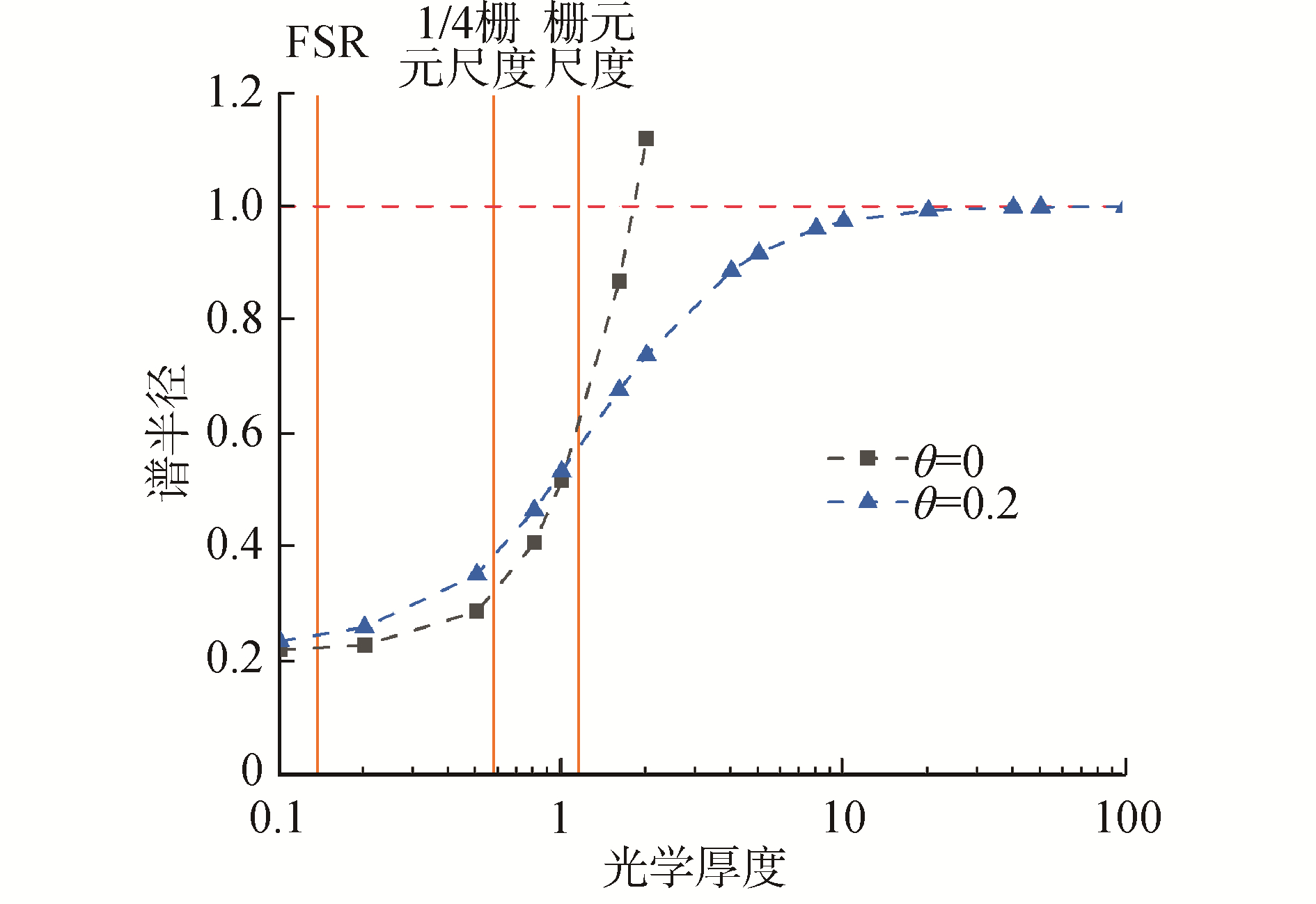
傅里叶分析是研究有限差分法渐近收敛速度的一种广泛应用的标准方法，已被广泛应用于CMFD加速方法的分析。图 1为按照文献[11]中的方法绘制的gCMFD谱半径随着光学厚度的变化曲线，并以C5G7基准题提供的宏观截面和栅元尺寸数据，针对较难收敛的慢化剂材料标注平源区、1/4栅元以及栅元尺度对应的位置。其中，光学厚度ΣtΔ为分群总截面与栅元尺寸大小的乘积，θ为计算修正扩散系数时人为定义的系数，而使用修正扩散系数可以使CMFD的收更加平滑，谱半径ρ的意义为衰减系数矩阵的特征值的绝对值的最大值：
$$ \rho^l=\frac{\left|\mathit{\pmb{\Phi}}^{l+2}-\mathit{\pmb{\Phi}}^{l+1}\right|}{\left|\mathit{\pmb{\Phi}}^{l+1}-\mathit{\pmb{\Phi}}^l\right|} $$ (1) $$ \mathit{\pmb{\Phi}}^l=\left[\phi_1^l, \cdots, \phi_k^l, \cdots, \phi_K^l\right] $$ (2) 
图 1 gCMFD在不同光学厚度下的谱半径Fig. 1 Spectral radius of gCMFD at different optical thicknesses
下载:
全尺寸图片
式中：ϕkl的上标l表示gCMFD迭代次数编号；下标k表示细网编号；Φl为l迭代步下全局通量矩阵; Φkl必为l迭代步下细网k内的通量值。
若谱半径小于1，则说明收敛；若大于1则说明会发散；且谱半径越小说明加速效果越好。通过图 1可以看到，随着粗网光学厚度减小，gCMFD谱半径也在变小，意味着粗网格尺寸越小，收敛性越好，但当粗网格尺寸继续减小时，收敛性变化趋于平缓，而实现难度和计算负担会成倍增加。综合考虑加速收益与实现复杂度，1/4栅元尺度的gCMFD为最值得尝试的选择。傅里叶分析的结果为通过建立基于1/4栅元的gCMFD加速系统来进一步改善收敛性能提供了重要的理论依据。
1.2 1/4栅元尺度的两级gCMFD加速方法
1/4栅元尺度的多群gCMFD方法的推导从多群稳态中子输运方程的形式开始：
$$ \begin{array}{c} \left(\mathit{\Omega}_x \frac{\partial}{\partial x}+\mathit{\Omega}_y \frac{\partial}{\partial y}+\mathit{\Omega}_z \frac{\partial}{\partial z}\right) \psi_g(\boldsymbol{r}, \mathit{\pmb{\Omega}})+ \\ \Sigma_{t, g}(\boldsymbol{r}) \psi_g(\boldsymbol{r}, \mathit{\pmb{\Omega}})=Q_g(\boldsymbol{r}, \mathit{\pmb{\Omega}}) \end{array} $$ (3) 式中：ψ、Σt、Q分别是中子角通量密度、总截面和源项；下标g为能群编号。
将式(3)在空间和1/4栅元内积分即可得到1/4栅元尺度的3D多群离散扩散方程：
$$ \begin{array}{c} \sum\limits_{n \in \text { neighbors }} \bar{J}_{g, c}^{\oplus} A_{\text {cn }}^{\oplus}+V_c^{\oplus} \Sigma_{t, g, c}^{\oplus} \bar{\phi}_{g, c}^{\oplus}= \\ V_c^{\oplus}\left(\frac{\chi_{g, c}^{\oplus}}{k_{\text {eff }}^{\oplus}} \sum\limits_{g^{\prime}=1}^G \nu \Sigma_{f, g^{\prime}, c}^{\oplus} \bar{\phi}_{g^{\prime}, c}^{\oplus}+\sum\limits_{g^{\prime}=1}^G \Sigma_{s, g^{\prime} \rightarrow g, c}^{\oplus} \bar{\phi}_{g^{\prime}, c}^{\oplus}\right) \\ \end{array} $$ (4) 式中：上标⊕表示为1/4栅元的参数；c和n为中心节块和邻近节块的编号；cn为中心节块和邻近节块的交界面；J、ϕ、Σs、νΣf、χ、keff分别是节块中子流密度、节块平均中子通量密度、散射截面、裂变截面、裂变谱和有效增殖因子；Vc⊕为中心节块的体积；Acn⊕为交界面的面积。
交界面处从中心节块c流向邻近节块n的中子流为：
$$ \bar{J}_{g, c n}^{\oplus}=\tilde{D}_{g, c n}^{\oplus} \bar{\phi}_{g, c}^{\oplus}-\tilde{D}_{g, n c}^{\oplus} \bar{\phi}_{g, n}^{\oplus} $$ (5) 式中$\tilde{D} $为节块扩散系数。
在传统CMFD方法中，若任何一个$\tilde{D} $为负值，则会出现当中心节块的通量上升时，中子流依然从邻近节块流入中心节块这一不符合物理规律的现象。为了解决这个问题，在基于广义平衡理论的CMFD方法(gCMFD)中定义了节块不连续因子(NDF)fg, cndis, ⊕和扩散系数修正因子(MDF)fg, cndif, ⊕，通过NDF和MDF建立与精细中子输运计算的严格等价，使得gCMFD的粗网计算结果与精细输运计算保持一致，同时也保证了线性系统的稳定性，实现了高效加速。$\tilde{D} $的定义改写为：
$$ \left\{ {\begin{array}{*{20}{l}} {\tilde{D}_{g, c n}^{\oplus}=\frac{2 f_{g, c n}^{\mathrm{dis}, \oplus}}{\frac{f_{g, c n}^{\mathrm{dis}, \oplus} h_{c n}^{\oplus}}{f_{g, c n}^{\mathrm{dif}, \oplus} D_{g, c}^{\oplus}}+\frac{f_{g, n c}^{\mathrm{dis}, \oplus} h_{n c}^{\oplus}}{f_{g, n c}^{\mathrm{dif}, \oplus} D_{g, n}^{\oplus}}}}\\ {\tilde{D}_{g, n c}^{\oplus}=\frac{2 f_{g, n c}^{\mathrm{dis}, \oplus}}{\frac{f_{g, c n}^{\mathrm{dis}, \oplus} h_{c n}^{\oplus}}{f_{g, c n}^{\mathrm{dif}, \oplus} D_{g, c}^{\oplus}}+\frac{f_{g, n c}^{\text {dis, } \oplus} h_{n c}^{\oplus}}{f_{g, n c}^{\text {dif }, \oplus} D_{g, n}^{\oplus}}}} \end{array}} \right. $$ (6) 对于在边界处的节点，$\tilde{D} $为：
$$ \tilde{D}_{g, c n}^{\text {boundary }, \oplus}=\frac{2 f_{g, c n}^{\mathrm{dis}, \oplus}}{\frac{f_{g, c n}^{\text {dis,}\oplus} h_{c n}^{\oplus}}{f_{g, c n}^{\mathrm{dif},\oplus} D_{g, c}^{\oplus}}+\frac{2}{\alpha}} $$ (7) 式中：α为反照率，其值随着边界条件的改变而改变；hcn⊕为中心节块到邻近节块方向上的厚度。
MDF和NDF的求解可以通过使用来自径向MOC和轴向NEM计算得到的1/4栅元的表面中子流、通量和网格平均通量信息来表征，具体计算过程可以参考文献[3]，在此不再赘述。
对于1/4栅元尺度的多群gCMFD方法中使用的均匀化参数，可以根据高阶输运计算的与区域相关的宏观截面和通量信息来量化：
$$ \bar{\phi}_{g, c}^{\oplus}=\frac{\sum\limits_{k \in 1 / 4 \text {Cell}} V_k \phi_{g, k}^{\mathrm{MOC}}}{\sum\limits_{k \in 1 / 4 \text {Cell}} V_k} $$ (8) $$ \mathit{\Sigma}_{t, g, c}^{\oplus}=\frac{\sum\limits_{k \in 1 / 4 \text {Cell}} V_k \mathit{\Sigma}_{t, g, k} \phi_{g, k}^{\mathrm{MOC}}}{\sum\limits_{k \in 1 / 4 \text {Cell}} V_k \phi_{g, k}^{\mathrm{MOC}}} $$ (9) $$ \mathit{\Sigma}_{s, g^{\prime} \rightarrow g, c}^{\oplus}=\frac{\sum\limits_{k \in 1 / 4 \text {Cell}} V_k \mathit{\Sigma}_{s, g^{\prime} \rightarrow g, k} \phi_{g^{\prime}, k}^{\mathrm{MOC}}}{\sum\limits_{k \in 1 / 4 \text {Cell}} V_k \phi_{g^{\prime}, k}^{\mathrm{MOC}}} $$ (10) $$ \nu \mathit{\Sigma}_{f, g, c}^{\oplus}=\frac{\sum\limits_{k \in 1 / 4 \text {Cell}} V_k \nu \mathit{\Sigma}_{f, g, k} \phi_{g, k}^{\mathrm{MOC}}}{\sum\limits_{k \in 1 / 4 \text {Cell}} V_k \phi_{g, k}^{\mathrm{MOC}}} $$ (11) $$ \chi_{g, c}^{\oplus}=\frac{\sum\limits_{k \in 1 / 4 \text {Cell}} V_k \chi_{g, k} \nu \mathit{\Sigma}_{f, g, k} \phi_{g, k}^{\mathrm{MOC}}}{\sum\limits_{k \in 1 / 4 \text {Cell}} V_k \nu \mathit{\Sigma}_{f, g, k} \phi_{g, k}^{\mathrm{MOC}}} $$ (12) $$ D_{g, c}^{\oplus}=\frac{1}{3\mathit{\Sigma}_{t, g, c}^{\oplus}} $$ (13) 式中下标k是平源区的编号。如此，便可以建立1/4栅元尺度的多群gCMFD的线性系统：
$$ \begin{array}{c} V_c^{\oplus}\left(-\sum\limits_{g^{\prime}} \mathit{\Sigma}_{s, g g^{\prime}, c}^{k, \oplus} \bar{\phi}_{g^{\prime}, c}^{k, \oplus}+\mathit{\Sigma}_{t, g}^{k, \oplus} \bar{\phi}_{g, c}^{k, \oplus}\right)+ \\ \left(\tilde{D}_{g, c W}^{k, \oplus}+\tilde{D}_{g, c N}^{k, \oplus}+\tilde{D}_{g, c E}^{k, \oplus}+\right. \\ \left.\tilde{D}_{g, c S}^{k, \oplus}+\tilde{D}_{g, c T}^{k, \oplus}+\tilde{D}_{g, c B}^{k, \oplus}\right) \bar{\phi}_{g, c}^{k, \oplus}- \\ \left(\tilde{D}_{g, W c}^{k, \oplus} \bar{\phi}_{g, , W}^{k, \oplus}+\tilde{D}_{g, N c}^{k, \oplus} \bar{\phi}_{g, N}^{k, \oplus}+\tilde{D}_{g, E c}^{k, \oplus} \bar{\phi}_{g,E}^{k, \oplus}+\right. \\ \left.\tilde{D}_{g, S c}^{k, \oplus} \bar{\phi}_{g, S}^{k, \oplus}+\tilde{D}_{g, T c}^{k, \oplus} \bar{\phi}_{g, T}^{k, \oplus}+\tilde{D}_{g, B c}^{k, \oplus} \bar{\phi}_{g, B}^{k, \oplus}\right)= \\ V_c^{\oplus}\left(\bar{S} k-1, \oplus_{g, c}+\frac{\chi_g^{\oplus}}{k_{\mathrm{eff}}^{\oplus}} \sum\limits_{g^{\prime}} \nu \mathit{\Sigma}_{f, g^{\prime}, c}^{k, \oplus} \bar{\phi}_{g^{\prime}, c}^{k, \oplus}\right) \end{array} $$ (14) 由于多群gCMFD本身的条件数较大，如果利用Wielandt Shift加速逆幂迭代，则条件数会变得更大，导致一级多群gCMFD线性系统的收敛速度仍然较慢，而单群gCMFD线性系统的求解成本要低得多。因此基于同样的思路，在1/4栅元尺度的多群gCMFD线性系统下通过在能群上归并来自多群gCMFD的截面、通量和中子流信息来建立1/4栅元尺度的单群gCMFD线性系统，实现加速收敛：
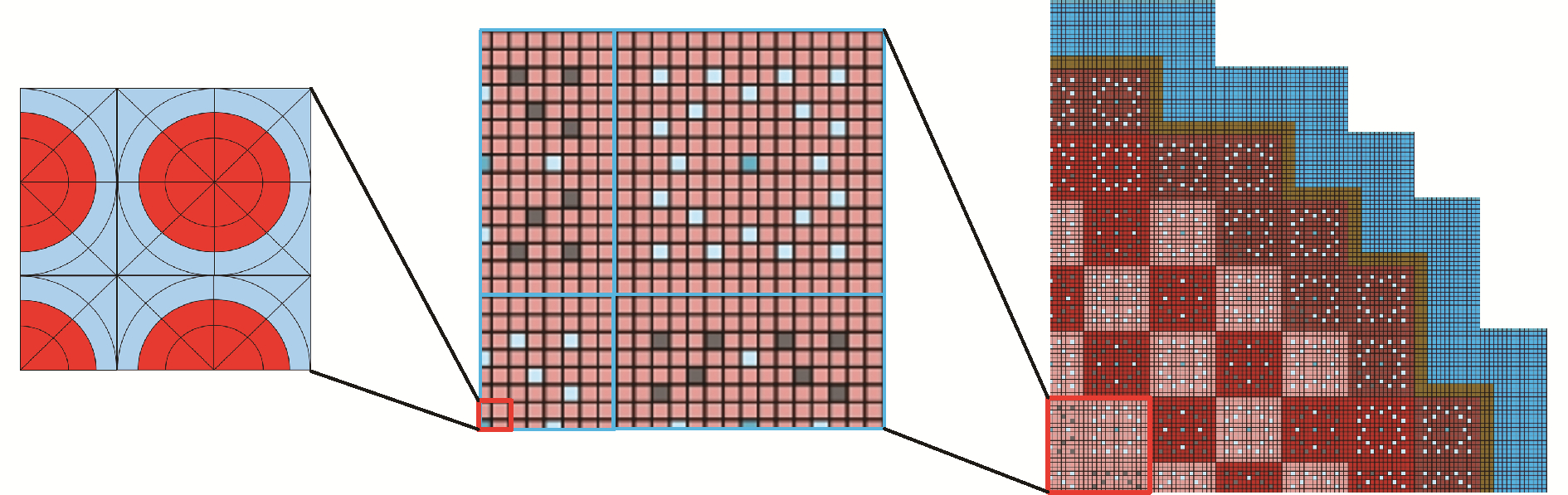
$$ \begin{array}{c} V_c^{\oplus} \mathit{\Sigma}_a^{k, \oplus} \bar{\phi}_c^{k, \oplus}+\left(\tilde{D}_{c W}^{k, \oplus}+\tilde{D}_{c N}^{k, \oplus}+\tilde{D}_{c E}^{k, \oplus}+\right. \\ \left.\tilde{D}_{c S}^{k, \oplus}+\tilde{D}_{c T}^{k, \oplus}+\tilde{D}_{c B}^{k, \oplus}\right) \bar{\phi}_c^{k, \oplus}- \\ \left(\tilde{D}_{W c}^{k, \oplus} \bar{\phi}_W^{k, \oplus}+\tilde{D}_{N c}^{k, \oplus} \bar{\phi}_N^{k, \oplus}+\tilde{D}_{E c}^{k, \oplus} \bar{\phi}_E^{k, \oplus}+\right. \\ \left.\tilde{D}_{S c}^{k, \oplus} \bar{\phi}_S^{k, \oplus}+\tilde{D}_{Tc}^{k, \oplus} \bar{\phi}_T^{k, \oplus}+\tilde{D}_{B c}^{k, \oplus} \bar{\phi}_B^{k, \oplus}\right)= \\ V_c^{\oplus}\left(\bar{S}_c^{k-1, \oplus}+\frac{1}{k_{\text {eff }}^{\oplus}} \nu \mathit{\Sigma}_f^{k-1, \oplus} \bar{\phi}_c^{k-1, \oplus}\right) \end{array} $$ (15) 1/4栅元尺度的多群gCMFD方法的建立流程与栅元尺度的多群gCMFD基本相同，只不过前者是基于1/4栅元为粗网大小进行求解，而不是基于完整的栅元，如图 2所示。
图 2 1/4栅元尺度的两级CMFD加速方法Fig. 2 1/4 cell based multi-level CMFD acceleration method下载:
全尺寸图片
即便是如此微小的处理，获得的收益也是显著的。在粗网尺寸变为1/4栅元后，MOC与gCMFD中传递的标通量信息增多，也更加精细，减小了其间的映射误差，从而实现良好的加速性能，但gCMFD本身的计算负担也同时增加。
2. 基于1/4栅元的几何建模及特征线布置
构造实体几何(constructive solid geometry，CSG)方法是许多高级建模软件(如CAD)的首选方法，利用不同结构化几何间简单的布尔运算就能很方便地得到不同的几何体。因具有建模灵活，能够降低几何信息的存储的特性，非常适合高度结构化且重复度很高的反应堆模型的建模。
2.1 1/4栅元为单位的几何建模
HNET原有的几何模块是以栅元为单位的，只能构建完整的组件，无法适应当沿x或y方向的组件数为奇数，如17×17的布置时1/4堆芯的建模和计算。在这种情况下，在堆芯切割面处中存在1/2组件和1/4组件，而当组件内栅元的布置也是奇数，如15×15时，切割面处便存在1/2栅元和1/4栅元。为实现以1/4栅元为单位来逐层组装呈堆芯，利用CSG的思想，可通过定义栅元中慢化剂的边界面、燃料组件的圆柱面即可构建一个栅元的模型，再将栅元的模型的中心创建2个互相垂直的面，将其划分成为1/4栅元模型，并按照象限号进行区分和存储，1/4栅元按照象限编号索引排列即可还原为完整的栅元，进而构成二维的组件，二维组件再通过轴向上的堆叠即可组成三维组件的模型，进而完成全堆芯或1/4堆芯的建模，结构层次如图 3所示。值得注意的是，当以1/4栅元为单位建模后，轴向的NEM计算也基于1/4栅元进行。
图 3 1/4堆芯结构层次图Fig. 3 Hierarchical diagram of the 1/4 reactor core structure下载:
全尺寸图片
2.2 1/4栅元模块化特征线布置
模块化特征线可以大幅减少MOC的计算量内存消耗，同时还可以精确地处理反射边界条件。在栅元模块化特征线模式中，只有外形尺寸和网格划分完全相同的栅元，共用同一套特征线的几何信息，如何保证特征线在相邻的模块间精准连接是模块化特征线布置的重点和难点。针对对称切割模型的特征线布置，合理地布置射线仍然可以使特征线精确连接，具体可参考文献[14]。假设离散的方位角数量为N、初始射线间距为t、模块宽度为w、高度为h。将整个方位角区域[0, 2π]进行等分，若取n∈{1, 2, ⋯, N}，则方位角αn为：
$$ \alpha_n=\frac{2 \pi}{N}(n-0.5) $$ (16) 得到方位角αn后，为保证整栅元和1/4栅元特征线布置方式相同，应保证在整栅元中沿x方向和y方向的特征线数目nx和ny为偶数，整栅元的nx和ny为：
$$ n_x=\operatorname{Ceiling}\left(\frac{w}{t}\left|\sin \alpha_n\right|\right) $$ (17) $$ n_y=\operatorname{Ceiling}\left(\frac{w}{t}\left|\cos \alpha_n\right|\right) $$ (18) 对应的1/4栅元的nx和ny分别为：
$$ n_x=2\operatorname{Ceiling}\left(\frac{w}{2 t}\left|\sin \alpha_n\right|\right) $$ (19) $$ n_y=2\operatorname{Ceiling}\left(\frac{w}{2 t}\left|\cos \alpha_n\right|\right) $$ (20) 得知nx和ny后，为了保证射线的均匀和对称，需要对方位角αn进行修正，得到修正后的有效方位角αn, eff为：
$$ \alpha_{n, \text { eff }}=\arctan \left(\frac{h n_x}{w n_y}\right) $$ (21) 同样，修正后的射线间距teff为：
$$ t_{\text {eff }}=\frac{w}{n_x} \sin \alpha_{n, \text { eff }} $$ (22) 3. 三维基准题数值验证
本文首先基于C5G7-RA、VERA Problem #4三维基准题验证建模和加速方法的正确性和效果。
3.1 C5G7-RA三维基准题验证
C5G7三维基准题是OECD/NEA发布的用于验证输运求解器非均匀堆芯计算能力的的基准题。该基准题根据控制棒插入位置和深度，定义了3种堆芯布置，分别为提棒(UR)、插棒A(RA)和插棒B(RB)，3种堆芯布置的非均匀性和计算难度依次增大。本文选取RA来进行加速效果的验证和分析。其1/4堆芯布置可参考文献[15]。
图 4 模块间特征线连接示意Fig. 4 Connection of characteristic rays among different modules下载:
全尺寸图片
计算过程中，轴向燃料区域划分为18层，反射层区域划分为18层；燃料、控制棒及裂变室3种栅元，径向共划分为5环(其中燃料区域3环)、辐向划分为8个扇形分区；反射层区域内采用矩形网格划分；截面来源于基准题报告提供的7群宏观截面；射线间距选择0.01 cm，一个卦限内选取18方位角和3极角，采用Tabuchi-Yamamoto极角求积组，收敛准则为keff和裂变源均小于1×10-5，核数布置为径向1个核，轴向18个核，每层由1个核进行计算，总共18核。
为验证1/4栅元尺度的多群gCMFD与栅元尺度的多群gCMFD2种方法的加速效果，同时探究1/4栅元尺度的单群gCMFD对1/4栅元尺度的多群gCMFD的加速效果，分别构建了栅元尺度的多群gCMFD(Cell-MG-gCMFD)、1/4栅元尺度的多群gCMFD(1/4Cell-MG-gCMFD)以及1/4栅元尺度的两级gCMFD(1/4Cell-TL-gCMFD)3个算例进行计算，在每种计算条件下按恰好到达最小外迭代次数设定多群和单群的最大迭代次数，统计MOC和gCMFD的迭代次数与计算时间以及有效增殖因子，并以Cell-MG-gCMFD方案的总计算时间为基准，比较和统计了其他方案的总计算时间相较基准改进的倍数，定义为加速比，如表 1中所示。
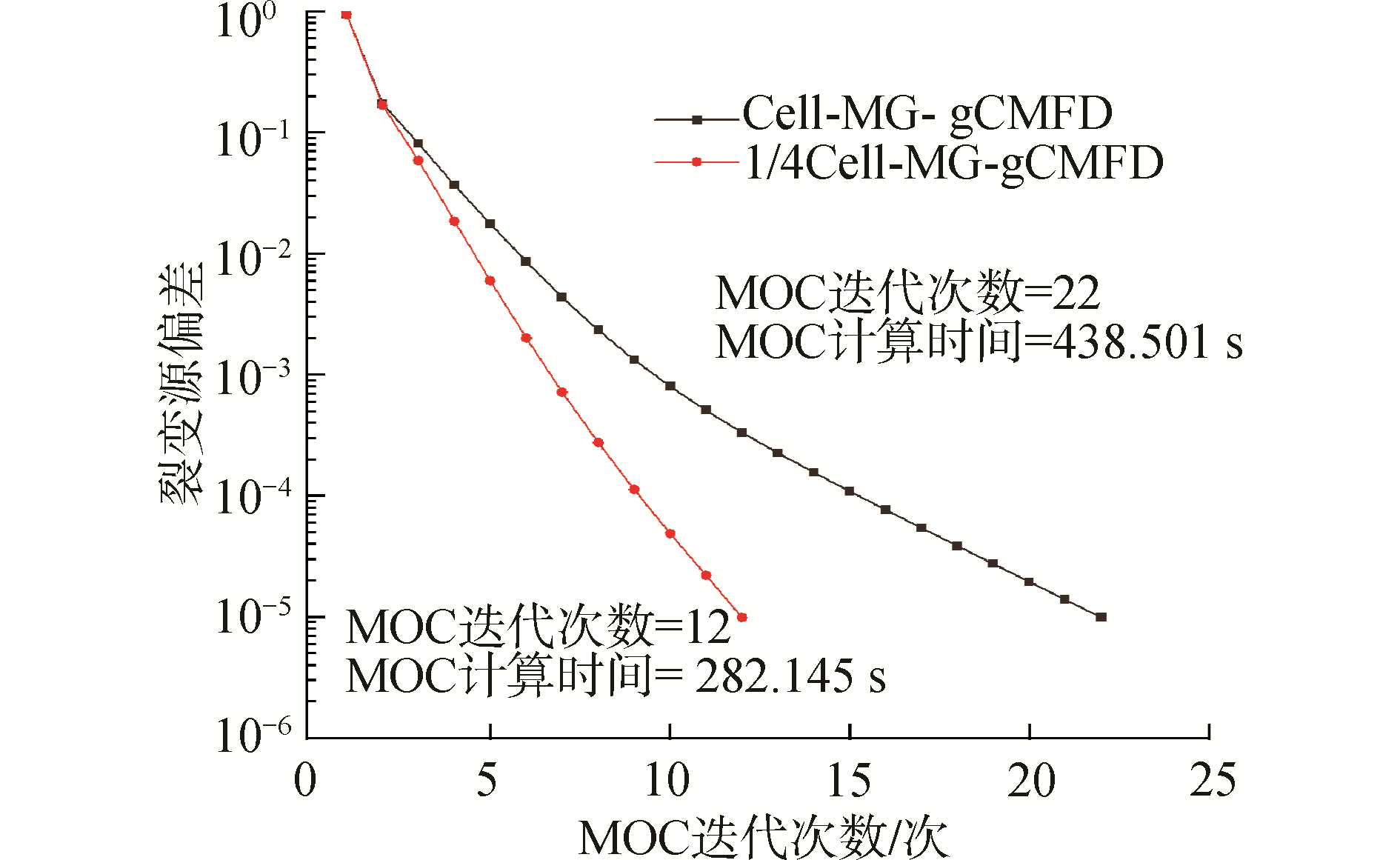
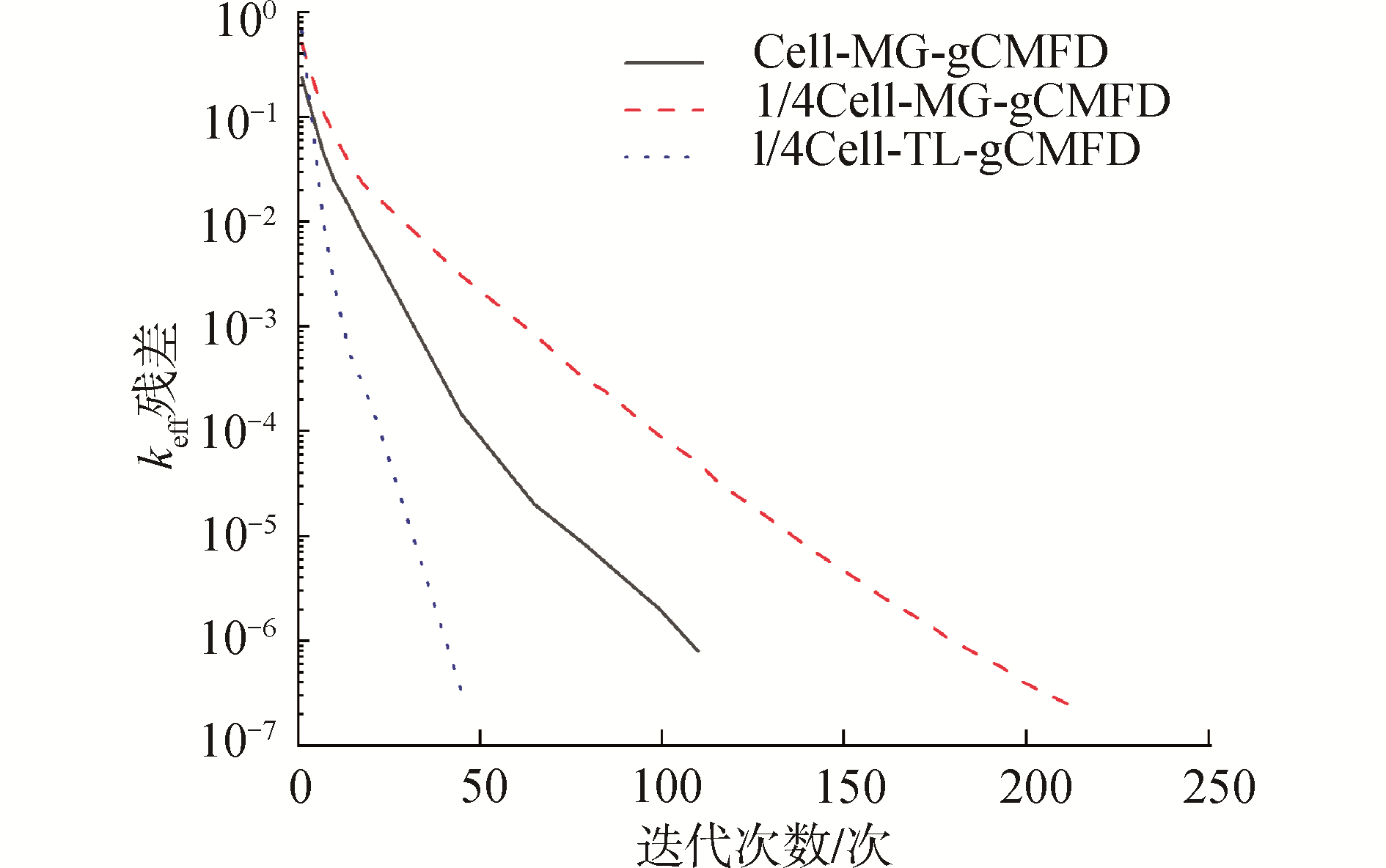
表 1 C5G7 RA三维基准题计算结果Table 1 The computed result for the iterations and computational time for 3D C5G7 RA case参数 MOC MG gCMFD CG gCMFD MG+CG MOC+ gCMFD keff 误差/10-5 加速比 迭代次数 计算时间/s 最大迭代次数 总迭代次数 计算时间/s 最大迭代次数 总迭代次数 计算时间/s 总计算时间/s 总计算时间/s 计算值 参考值 Cell-MG-gCMFD 22 438.5 5 110 2.2 — — — 2.2 440.7 1.127 55 1.128 06 -50 — 1/4Cell-MG-gCMFD 12 282.1 18 214 25.1 — — — 25.1 307.3 1.127 51 — -54 1.434 1/4Cell-TL-gCMFD 12 280.3 4 47 6.0 20 599 4.074 10.1 290.3 1.127 51 — -54 1.518 由表 1可知，使用1/4Cell-MG-gCMFD方法，MOC的最少迭代次数从22次减为12次，成功打破了Cell-MG-gCMFD方法的加速瓶颈，加速比为1.434。然而，由于MG gCMFD的计算规模和迭代次数增加，其计算时间也变为原来的12倍，但是这种耗时的增加又可以通过代价很小的1/4Cell-CG-gCMFD方法进一步限制下来，这样两级gCMFD加速方法构成的1/4Cell-TL-gCMFD加速系统的加速比进一步提升至1.518，且计算精度与单级相同。图 5展示了在栅元尺度和1/4栅元尺度下当令MG gCMFD完全收敛时MOC迭代次数变化，可以清晰观察到1/4Cell-MG-gCMFD对MOC收敛显著的加速效果。图 6展示了每一个外迭代内最后一步MG gCMFD对应迭代次数与其收敛残差的变化趋势，进一步说明了1/4Cell-MG-gCMFD虽然可以加速外迭代的收敛，但自身收敛难度增加，而加入1/4栅元尺度的单群CMFD构成两级CMFD加速方法后，其迭代次数和收敛效果都得到了明显的改善。
图 5 不同加速方案MOC迭代收敛曲线Fig. 5 The iteration history of MOC accelerated by different method下载:
全尺寸图片
图 6 MG-gCMFD迭代收敛历史Fig. 6 The convergence history of MG-CMFD下载:
全尺寸图片
3.2 VERA Problem #4三维基准题验证
为进一步探究1/4栅元尺度的单群gCMFD对1/4栅元尺度的多群gCMFD计算代价的缩减效果，同时验证本文实现的1/4建模方法的正确性，本文采用基于HELIOS-47能群的VERA Problem #4基准题进行测试。此问题组件的轴向结构和径向布置可参考文献[16]。
计算时，特征线间距为0.03 cm，每卦限内采用16个方位角和3个极角，特征值的收敛标准为1.0×10－5，裂变源采用无穷范数误差，其收敛标准为1.0×10-5。MG gCMFD和CG gCMFD的特征值收敛标准为1.0×10－8。径向为反射边界，轴向为真空边界。每层分配一个核，共使用58核进行计算。
针对此基准题，本文基于HNET程序构建全模型下基于栅元的两级gCMFD(Cell-TL-gCMFD-全模型)、全模型下基于1/4栅元的两级gCMFD加速(1/4Cell-TL-gCMFD-全模型)以及1/4模型下基于1/4栅元的两级gCMFD加速(1/4Cell-TL-gCMFD-1/4模型)3个算例进行计算，其中全模型指计算完整的3×3组件模型，而1/4模型为3×3模组件型的1/4模型。在每种算例下按单群CMFD充分收敛(最大迭代次数设为1 000)的情况下恰好到达最小外迭代次数来设定多群CMFD最大迭代次数，统计MOC和CMFD的迭代次数与计算时间以及有效增殖因子，并计算了加速比，如表 2中所示。Cell-TL-gCMFD-全模型与1/4Cell-TL-gCMFD-全模型2个算例的有效增殖因子与参考值的偏差均为15×10-5，表明本文构建的1/4模型与原有几何构建方法计算精度相同。同时，由于应用基于1/4栅元的两级CMFD加速，MOC的迭代次数从11次减少到8次，但由于CMFD的计算量大幅增加，两级CMFD的计算时间变为原来的4倍，然而在增加了特征线交点信息与CMFD的计算量的情况下加速比仍达到了1.651，较7群有了明显的提高。而在1/4模型下，由于MOC的计算量变为全模型的1/4，相较基于栅元的两级CMFD加速计算，平均每个迭代步下MOC的计算时间从81.83 s减少为19.875 s，减少了3/4，同时总迭代次数减少了3次，CMFD的计算量相差无几，但在1/4栅元尺度上收敛性能提升，整体计算加速比达到4.294。
表 2 VERA Problem #4三维基准题计算结果Table 2 The computed result for the iterations and computational time for VERA Problem #4 case参数 MOC MG gCMFD CG gCMFD MG+CG MOC+ gCMFD keff 加速比 迭代次数 计算时间/s 最大迭代次数 总迭代次数 计算时间/s 总迭代次数 计算时间/s 总计算时间/s 总计算时间/s 计算值 参考值 Cell-TL-gCMFD-全模型 11 900.1 3 13 60.6 1 591 9.8 70.4 970.5 0.999 13 0.998 98 — 1/4Cell-TL-gCMFD-全模型 8 545.3 5 40 186.3 2 451 67.7 254.0 799.3 0.999 13 — 1.651 1/4Cell-TL-gCMFD-1/4模型 8 159.0 5 40 56.1 2 662 10.9 67.0 226.0 0.999 13 — 4.294 在C5G7基准题中，Cell-MG-gCMFD方案平均每个迭代步下MOC计算时间为19.93 s，1/4Cell-MG-gCMFD方案为23.51 s，时间稍有所提升，而在VERA基准题中，时间分别为81.83 s和68.16 s，时间明显下降。实际上，在以1/4栅元为单位构建几何模型后，模块化特征线的单位也变为1/4栅元，MOC的总计算量和信息存储量没有发生改变，但是索引的序列变为原来的4倍，导致在特征线连接时时间稍有所增加，但不会增加很多。而在VERA基准题中，单次外迭代的计算更为困难，但基于1/4栅元的多级CMFD加速可以为其提供更好的迭代初值，能够显著的加速其收敛计算，总体的收益远大于由于索引序列增加带来的计算时间增加。
4. 实堆验证
为进一步表明基于1/4栅元的多级CMFD加速方法计算1/4模型的优越性，本文针对秦山一期核电厂首炉堆芯在寿期初、热态零功率工况下，展开了1/4堆芯的稳态计算。
4.1 秦山1/4堆芯模型
秦山一期核电厂由313个组件组成，其中每个组件均由15×15的栅元组成，栅元间距为1.33 cm，活性区轴向高度为290 cm。本文构建的秦山1/4堆芯模型，完整包含了燃料棒、毒物棒、控制棒、导向管、定位格架、围板和反射层等结构。同时考虑到上下反射层区域等，在轴向上划分为62层。堆芯内燃料组件按秦山一期核电厂首炉堆芯燃料装载方案布置，模型的径向几何示意图如图 7所示。
图 7 秦山1/4堆芯径向几何示意Fig. 7 Radial geometry configurtion for Qinshan 1/4 core下载:
全尺寸图片
计算时，特征线间距为0.05 cm，每卦限内采用10个方位角和3个极角的组合，特征值的收敛标准为1.0×10－6，裂变源采用无穷范数误差，其收敛标准为1.0×10－4。MG gCMFD的特征值收敛标准为1.0×10－10，最大迭代次数为4；CG gCMFD的特征值收敛标准为1.0×10－10，最大迭代次数为50。径向对称轴处为反射边界，其余均为真空边界。在山河超算平台使用62个节点进行计算，每个节点使用16核计算一层堆芯模型，共使用992核进行计算。
4.2 数值结果
本文分别针对ARO工况和4种控制棒束插入工况进行了稳态临界计算，其中4根控制棒分别命名为T1、T2、T3、T4，初始状态为未插入，插入状态为in。在令有效增殖因子为1(误差为10-7×10-5)时，得到了各工况下的末端硼浓度。对比《数字化反应堆30万千瓦核电厂基准问题模拟计算报告》中的参考值，各工况下的末端硼浓度如表 3所示，最大偏差在-21×10-6，低于通用的设计准则50×10-6及设计院针对程序验证准则30×10-6，满足精度要求。
表 3 秦山1/4三维堆芯模型末端硼浓度计算结果Table 3 Calculation results of critical boron concentration of Qinshan 1/4 3D core model10-6 工况 参考值 计算值 偏差 ARO 1 301.0 1 292.88 -8.12 T4in 1 209.0 1 197.00 -12.00 T4+T3in 1 168.8 1 154.50 -14.30 T4+T3+T2in 1 064.6 1 048.50 -16.10 T4+T3+T2+T1in 794.0 773.00 -21.00 同时针对ARO工况采用报告中给出的硼浓度数据进行高保真稳态临界计算，得到特征值和归一化栅元功率分布。为了表明本文提出并实施的方法在实堆应用中的效果，分别统计了原有的栅元尺度下全模型以及1/4栅元尺度下1/4模型的总计算时间。临界偏差为-191×10-5，特征值为0.998 09。如表 4所示，2种计算方案得到的特征值均为0.998 09，与临界值1的偏差为-191×10-5, 低于通用的设计准则500×10-5，满足精度要求。同时，基于1/4栅元多级CMFD加速方法的1/4模型高保真全堆芯输运计算外迭代次数从12次减少为9次，总时间为88.3核时，加速比为2.637。
表 4 秦山核电站三维堆芯模型ARO工况临界计算结果Table 4 Critical calculation results of Qinshan 3D core model under ARO condition参数 MOC迭代次数 计算总时间/s 计算核时 加速比 全模型-Cell 12 845.1 232.9 — 1/4模型-1/4 Cell 9 320.5 88.3 2.637 计算得到的ARO工况下的归一化栅元功率分布如图 8所示，功率在轴向呈现出明显的中心高，两侧低的趋势；而在径向上，由于燃料分区布置和毒物棒对功率分布的影响，呈现出功率峰的交替分布。
图 8 不同工况下归一化栅元功率的三维分布Fig. 8 distribution of normalized pin power under different conditions下载:
全尺寸图片
5. 结论
1) 针对基于1/4栅元的多群CMFD方法计算成本升高，进一步提出并实施基于1/4栅元的单群CMFD方法加速多群CMFD的收敛构成两级CMFD加速，以小代价获取大的时间收益。
2) 采用三维基准题验证方法的正确性和加速效果，计算结果表明，本文提出的1/4栅元尺度多级CMFD加速方法成功突破原有加速瓶颈，加速效果显著。同时基于秦山一期压水堆模型不同稳态运行工况开展1/4模型高保真稳态临界计算，验证了HNET的实堆计算能力，具有较好的计算精度和计算效率。然而1/4栅元尺度的单群CMFD计算代价仍然巨大，未来可进一步基于1/4栅元几何建模功能开发基于整栅元的单群CMFD加速1/4栅元多群CMFD实现空间-能量混合加速，进一步提升加速效果。
-
图 1 gCMFD在不同光学厚度下的谱半径
Fig. 1 Spectral radius of gCMFD at different optical thicknesses
下载:
全尺寸图片
图 2 1/4栅元尺度的两级CMFD加速方法
Fig. 2 1/4 cell based multi-level CMFD acceleration method
下载:
全尺寸图片
图 3 1/4堆芯结构层次图
Fig. 3 Hierarchical diagram of the 1/4 reactor core structure
下载:
全尺寸图片
图 4 模块间特征线连接示意
Fig. 4 Connection of characteristic rays among different modules
下载:
全尺寸图片
图 5 不同加速方案MOC迭代收敛曲线
Fig. 5 The iteration history of MOC accelerated by different method
下载:
全尺寸图片
图 6 MG-gCMFD迭代收敛历史
Fig. 6 The convergence history of MG-CMFD
下载:
全尺寸图片
图 7 秦山1/4堆芯径向几何示意
Fig. 7 Radial geometry configurtion for Qinshan 1/4 core
下载:
全尺寸图片
图 8 不同工况下归一化栅元功率的三维分布
Fig. 8 distribution of normalized pin power under different conditions
下载:
全尺寸图片
表 1 C5G7 RA三维基准题计算结果
Table 1 The computed result for the iterations and computational time for 3D C5G7 RA case
参数 MOC MG gCMFD CG gCMFD MG+CG MOC+ gCMFD keff 误差/10-5 加速比 迭代次数 计算时间/s 最大迭代次数 总迭代次数 计算时间/s 最大迭代次数 总迭代次数 计算时间/s 总计算时间/s 总计算时间/s 计算值 参考值 Cell-MG-gCMFD 22 438.5 5 110 2.2 — — — 2.2 440.7 1.127 55 1.128 06 -50 — 1/4Cell-MG-gCMFD 12 282.1 18 214 25.1 — — — 25.1 307.3 1.127 51 — -54 1.434 1/4Cell-TL-gCMFD 12 280.3 4 47 6.0 20 599 4.074 10.1 290.3 1.127 51 — -54 1.518 表 2 VERA Problem #4三维基准题计算结果
Table 2 The computed result for the iterations and computational time for VERA Problem #4 case
参数 MOC MG gCMFD CG gCMFD MG+CG MOC+ gCMFD keff 加速比 迭代次数 计算时间/s 最大迭代次数 总迭代次数 计算时间/s 总迭代次数 计算时间/s 总计算时间/s 总计算时间/s 计算值 参考值 Cell-TL-gCMFD-全模型 11 900.1 3 13 60.6 1 591 9.8 70.4 970.5 0.999 13 0.998 98 — 1/4Cell-TL-gCMFD-全模型 8 545.3 5 40 186.3 2 451 67.7 254.0 799.3 0.999 13 — 1.651 1/4Cell-TL-gCMFD-1/4模型 8 159.0 5 40 56.1 2 662 10.9 67.0 226.0 0.999 13 — 4.294 表 3 秦山1/4三维堆芯模型末端硼浓度计算结果
Table 3 Calculation results of critical boron concentration of Qinshan 1/4 3D core model
10-6 工况 参考值 计算值 偏差 ARO 1 301.0 1 292.88 -8.12 T4in 1 209.0 1 197.00 -12.00 T4+T3in 1 168.8 1 154.50 -14.30 T4+T3+T2in 1 064.6 1 048.50 -16.10 T4+T3+T2+T1in 794.0 773.00 -21.00 表 4 秦山核电站三维堆芯模型ARO工况临界计算结果
Table 4 Critical calculation results of Qinshan 3D core model under ARO condition
参数 MOC迭代次数 计算总时间/s 计算核时 加速比 全模型-Cell 12 845.1 232.9 — 1/4模型-1/4 Cell 9 320.5 88.3 2.637 -
[1] SMITH K S. Spatial homogenization methods for light water reactor analysis[D]. Cambridge: Massachusetts Institute of Technology, 1980. [2] ZHU A. Transient methods for pin-resolved whole core transport[D]. Ann Aibor: University of Michigan, 2016. [3] HAO Chen, KANG Le, XU Yunlin, et al. 3D whole-core neutron transport simulation using 2D/1D method via multi-level generalized equivalence theory based CMFD acceleration[J]. Annals of nuclear energy, 2018, 122: 79-90. doi: 10.1016/j.anucene.2018.08.014 [4] XU Y, DOWNAR T. Convergence analysis of a CMFD method based on generalized equivalence theory[J]. Physor, 2012, 4: 15-20. [5] ZHU Ang, JARRETT M, XU Yunlin, et al. An optimally diffusive Coarse Mesh Finite Difference method to accelerate neutron transport calculations[J]. Annals of nuclear energy, 2016, 95: 116-124. doi: 10.1016/j.anucene.2016.05.004 [6] HONG S G, CHO N Z. CRX: a code for rectangular and hexagonal lattices based on the method of characteristics[J]. Annals of nuclear energy, 1998, 25(8): 547-565. doi: 10.1016/S0306-4549(97)00113-8 [7] LI Jin, XU Yunlin, WANG Dean, et al. Demonstration of a linear prolongation cmfd method on moc[J]. EPJ web of conferences, 2021, 247: 03006. doi: 10.1051/epjconf/202124703006 [8] HAO Chen, XU Yunlin, DOWNAR T J. Multi-level coarse mesh finite difference acceleration with local two-node nodal expansion method[J]. Annals of nuclear energy, 2018, 116: 105-113. doi: 10.1016/j.anucene.2018.02.002 [9] LIU Zhouyu, ZHOU Xinyu, CAO Liangzhi, et al. A new three-level CMFD method based on the loosely coupled parallel strategy[J]. Annals of nuclear energy, 2020, 145: 107529. doi: 10.1016/j.anucene.2020.107529 [10] LI Jin, XU Yunlin, WANG Dean, et al. Demonstration of a linear prolongation cmfd method on moc[J]. EPJ web of conferences, 2021, 247: 03006. doi: 10.1051/epjconf/202124703006 [11] ZHU Kaijie, HAO Chen, KONG Boran, et al. Fine mesh finite difference acceleration method based on the Generalized Equivalence Theory for the 2-D MOC transport calculation[J]. Annals of nuclear energy, 2021, 161: 108450. doi: 10.1016/j.anucene.2021.108450 [12] 康乐. 精细化瞬态中子输运计算的多级加速理论研究[D]. 哈尔滨: 哈尔滨工程大学, 2022. KANG Le. Study on the multilevel acceleration theory for high-fidelity time-dependent neutron transport calculation[D]. Harbin: Harbin Engineering University, 2022. [13] 郝琛, 朱雁凌, 康乐, 等. 高保真中子输运计算的多级加速理论及应用[J]. 原子能科学技术, 2022, 56(2): 296-307. https://www.cnki.com.cn/Article/CJFDTOTAL-YZJS202202009.htm HAO Chen, ZHU Yanling, KANG Le, et al. Study and application of multi-level acceleration theory for high-fidelity neutron transport calculation[J]. Atomic energy science and technology, 2022, 56(2): 296-307. https://www.cnki.com.cn/Article/CJFDTOTAL-YZJS202202009.htm [14] 吴文斌. 基于并行技术的2D/1D耦合三维全堆输运方法研究[D]. 北京: 清华大学, 2014. WU Wenbin. Research on 2D/1D coupling three-dimensional full-stack transportation method based on parallel technology[D]. Beijing: Tsinghua University, 2014. [15] 宋佩涛. MOC三维全堆芯中子输运CPUs/GPUs异构并行算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2021. SONG Peitao. Research on the CPUs/GPUs heterogeneous parallel algorithm for method of characteristics solution of 3-d whole-core neutron transport calculation[D]. Harbin: Harbin Engineering University, 2021. [16] TURNER J A, CLARNO K, SIEGER M, et al. The Virtual environment for reactor applications (vera): design and architecture[J]. Computational physics, 2016, 326: 544-568. doi: 10.1016/j.jcp.2016.09.003
