An analysis of the radionuclide diffusion rule at a radioactive site
-
摘要: 为了掌握某放射性操作场所核事故情形下的放射性核素微场扩散规律，本文采用计算流体力学建模方法，建立了2种典型通排风条件下核素扩散模型。结果表明: 不同放射性核素、不同通排风方式等对微场放射性核素迁移扩散方向和大气弥散因子的变化范围影响较大，应急处置人员应采取不同的防护措施以有效降低个人有效剂量。计算流体力学建模方法可有效模拟微场环境放射性核素迁移扩散。Abstract: To master the microfield transmission and diffusion law of radionuclides in a nuclear accident in a radioactive operating place, two typical diffusion models of radionuclides under ventilation and exhaust conditions are established by using the computational fluid dynamics (CFD) modeling method. The simulation results show that the directions of transmission and diffusion, as well as the range of atmospheric dispersion factors, are greatly influenced by various radionuclides and different ventilation and exhaust conditions in a microfield environment. The emergency response personnel should take various protective measures to effectively reduce the personal effective dose. The CFD modeling method could effectively simulate the transmission and diffusion of the radionuclides in a microfield environment.
-
Keywords:
- radioactive /
- nuclide /
- CFD /
- diffusion /
- model /
- microfield
-
核事故发生后，放射性核素将弥散开并形成不同强度分布的辐射场，对现场工作人员和应急处置人员产生一定的辐射影响，对放射性核素在场所内的迁移扩散开展精细化计算是做好工作人员辐射防护的前提。同时，它也是客观评价核事故状态下辐射后果的一项重要内容，对于事故情形下的人员受照剂量及后果评估具有重要的现实意义[1-2]。目前，对于微场放射性核素扩散规律的研究，主要有现场测量与物理风洞实验测量相结合获取，基于蒙特卡罗、计算流体力学(CFD)等专用计算软件理论计算等方法。前者得到的结果最为可靠，但也受到风洞模拟分析技术难以准确描述自然风过程、模拟微场条件多变性的实验周期较长、过程耗费大等诸多客观条件限制；后者是目前应用最为广泛的方法，克服了前者方法的诸多缺点，可在有限的实验技术条件下开展多工况、多技术状态的模拟分析[3-4]。
某放射性操作场所日常作为234U等锕系核素、3H等放射源的操作场所，为准确掌握场所内典型放射源操作期间不同通排风条件下的放射性核素迁移扩散规律，评估典型事故场景下人员的受照剂量，本文采用CFD建模方法构建了建筑物内部微场扩散模型，计算了微场扩散大气弥散因子，为事故情形下的应急决策和防护提供了技术支持[5]。
1. CFD基本理论及建模
1.1 CFD基本理论
CFD主要遵循：质量守恒定律、动量守恒定律以及能量守恒定律[6]。有学者还建议补充加入动量矩守恒定律和热力学第二定律。此外，在实际的计算分析中，为了对不同的流体状态进行详细计算，考虑流体的形态，例如层流或者湍流，以及加入特定的方程进行修正[7-8]。
1.2 CFD建模
本文在进行建模时，主要考虑了基于CFD的三大定律方程。
1) 质量守恒方程。
质量守恒方程(mass conservation equation)也被称为连续性方程，其基本表达式为：
$$ \frac{{\partial \left( {\rho {v_x}} \right)}}{{\partial x}} + \frac{{\partial \left( {\rho {v_y}} \right)}}{{\partial y}} + \frac{{\partial \left( {\rho {v_z}} \right)}}{{\partial z}} + \frac{{\partial (\rho )}}{{\partial t}} = 0 $$ (1) 式中：ρ代表流体的密度，为常数；vx、vy和vz分别代表流体在x、y、z方向上的速度矢量分量；t代表时间。
在连续不可压缩的流体中，流体的密度被当做常数：
$$ \nabla \cdot (\mathit{\boldsymbol{v}}) = 0\;\;\;\;({\mathop{\rm div}\nolimits} (\mathit{\boldsymbol{v}}) = 0) $$ (2) 2) 动量守恒方程。
动量守恒方程(momentum conservation equation)也被称为运动方程或Navier-Stokes(N-S)方程，其基本公式为：
$$ \begin{array}{c} \rho \left( {\frac{{\partial {v_x}}}{{\partial t}} + {v_x}\frac{{\partial {v_x}}}{{\partial x}} + {v_y}\frac{{\partial {v_y}}}{{\partial y}} + {v_z}\frac{{\partial {v_z}}}{{\partial z}}} \right) = \\ {f_x}\rho \left( {\frac{{\partial {\tau _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{yx}}}}{{\partial y}} + \frac{{\partial {\tau _{zx}}}}{{\partial z}}} \right) \end{array} $$ (3) $$ \begin{array}{c} \rho \left( {\frac{{\partial {v_y}}}{{\partial t}} + {v_x}\frac{{\partial y}}{{\partial x}} + {v_y}\frac{{\partial {v_y}}}{{\partial y}} + {v_z}\frac{{\partial {v_z}}}{{\partial z}}} \right) = \\ {f_y}\rho \left( {\frac{{\partial {\tau _{xy}}}}{{\partial x}} + \frac{{\partial {\tau _{yy}}}}{{\partial y}} + \frac{{\partial {\tau _{zy}}}}{{\partial z}}} \right) \end{array} $$ (4) $$ \begin{array}{c} \rho \left( {\frac{{\partial {v_z}}}{{\partial t}} + {v_x}\frac{{\partial z}}{{\partial x}} + {v_y}\frac{{\partial {v_y}}}{{\partial y}} + {v_z}\frac{{\partial {v_z}}}{{\partial z}}} \right) = \\ {f_z}\rho \left( {\frac{{\partial {\tau _{xz}}}}{{\partial x}} + \frac{{\partial {\tau _{yz}}}}{{\partial y}} + \frac{{\partial {\tau _{zz}}}}{{\partial z}}} \right) \end{array} $$ (5) 式中：τx、τy和τz分别代表流体在x、y、z方向上的分子粘性应力分量。将牛顿剪切定律引入到式(3)~(5)中，并将方程组中的应力项消除，则可推导出粘度为常数的不可压缩N-S方程：
$$ \frac{{{D_v}}}{{Dt}} = f - \frac{1}{\rho }\nabla \rho + v\nabla _v^2 $$ (6) 3) 能量守恒方程。
能量守恒方程(energy conservation equation)计算公式为：
$$ \frac{{{\rm{D}}T}}{{{\rm{D}}t}} = \frac{\lambda }{{\rho {c_\rho }}}\nabla ({\mathop{\rm grad}\nolimits} T) + \frac{{{S_T}}}{\rho } $$ (7) 式中：λ代表流体导热系数项；ST代表流体的热源修正项；ρ代表流体的密度，为常数。
4) 组分质量守恒方程。
此外，为了计算污染物在控制体积内的浓度，还需要在上述方程的基础上引入组分的概念，加入组分质量方程，计算公式为：
$$ \frac{{\partial \left( {\rho {c_s}} \right)}}{{\partial t}} + {\mathop{\rm div}\nolimits} \left( {{\rho _u}{c_s}} \right) = {\mathop{\rm div}\nolimits} \left[ {{D_s}{\mathop{\rm grad}\nolimits} \left( {\rho {c_s}} \right)} \right] + {S_s} $$ (8) 式中：cS代表组分S的体积浓度；ρcS代表组分S的质量浓度；DS代表组分S的散系数；SS代表组分的质量生产率，也就是大气扩散的释放速率。
基于上述理论模型，本文采用计算流体力学数值模拟通用软件Cradle CFD2020中的标准k-ε湍流模型模拟气载放射性核素扩散的流场和浓度场[9-10]。由于房间尺寸有限，因此在模拟过程中仅考虑房间内的湍流扩散过程，不考虑层流扩散行为。
2. 模拟事故情景分析
事故情景1：在1个密闭的房间1中央，放置234U放射源，房间内设置有专用的通风设置，气流走向为上进下排，234U放射源由于事故出现1 mm的小破口，产生的234U气溶胶以0.1 m/s的速率进行缓慢释放，释放时间一直持续到人员手动干预为止。
事故情景2：在1个密闭的房间2中央，放置3H高压气瓶，房间内设置有专用的通风设置，气流走向为下进上排，3H高压气瓶由于事故出现爆炸，大量的3H气瞬间释放，释放的持续时间不超过0.5 s，最大释放速率达到840 m/s。
3. 边界条件确定
3.1 案例选定
某场所的放射源操作主要集中在2个房间：房间1用于234U放射源操作的房间，其通排风设置为上进下排；房间2用于高压气瓶贮存的3H放射源操作房间，其通排风设置为下进上排。因此，选取该2个典型的放射源操作间作为放射性事故发生场所，释放源位置固定在日常操作位置。基于此，给出2个典型操作间的建模边界条件。
3.2 房间1
房间1为234U放射性源操作房间，计算过程中的相关边界条件设置如下。
通风布局：上进下排。
源项释放：气溶胶，缓慢均匀连续释放，为点源释放，释放速率为0.1 m/s，考虑均一化设置释放源强1 Bq/m3。
释放点位置：房间中心点，距离地面高度为1.5 m。
扩散模式：随气流流场扩散，不考虑气溶胶粒径影响。
进风：进风口尺寸为0.3 m×0.3 m，进风速率为1.4 m/s，速率均匀。
排风：排风口尺寸为0.3 m×0.3 m，排风速率为1.4 m/s，速率均匀。
壁面条件：将上部进风口设置为速度入口边界(velocity inlet)、侧面的排风口设置为压力出口边界(pressure outlet)、源项释放设置为速度入口边界(velocity inlet)，具体见图 1中的箭头指示。
图 1 房间1网格划分Fig. 1 Grid division diagram of room 1
下载:
全尺寸图片
热源：无热源，因此不考虑温度对扩散的影响。
计算区域网格分辨率：0.1 m。
释放点周围0.5 m网格分辨率：0.001 m。
建模确定的房间1的网格划分如图 1所示。
3.3 房间2
房间2为3H放射源操作房间，计算过程中的相关边界条件设置如下。
通风布局：下进上排。
源项释放：气体，瞬时释放，为点源释放，释放初始速率8 m/s，考虑均一化设置释放源强1 Bq/m3。
释放点位置：房间中心点，距离地面1.5 m高度。
扩散模式：初始为气流喷放，随后随气流流场扩散。
进风：进风口尺寸为0.3 m×0.3 m，进风速率为0.3 m/s，速率均匀。
排风：进风口尺寸为0.3 m×0.3 m，排风速率为0.3 m/s，速率均匀。
壁面条件：将侧面进风口设置为速度入口边界(velocity inlet)、顶部的排风口设置为压力出口边界(pressure outlet)、源项释放设置为速度入口边界(velocity inlet)，具体见图 2中的箭头指示。
图 2 房间2网格划分Fig. 2 Grid division diagram of room 2下载:
全尺寸图片
热源：无热源，因此不考虑温度对扩散的影响。
计算区域网格分辨率：0.1 m。
释放点周围0.5 m网格分辨率：0.001 m。
建模确定的房间2的网格划分如图 2所示。
4. 结果与分析
4.1 房间1
考虑到计算获取的扩散因子作为人员受照剂量评价的输入，放射性物质泄漏场景一般发生在近地面状态，234U气溶胶粒径较重等客观条件，计算结果重点对距离0.1 m和1 m这2个高度的污染物浓度分布进行分析。
4.1.1 计算结果
采用归一化的大气弥散因子DF(diffusion factor)来对计算得到的核素空气浓度进行处理：
$$ {\rm{DF}} = Q/A $$ (9) 式中：Q代表计算得到的空气浓度，Bq/m3；A释放的核素源项，Bq/s。
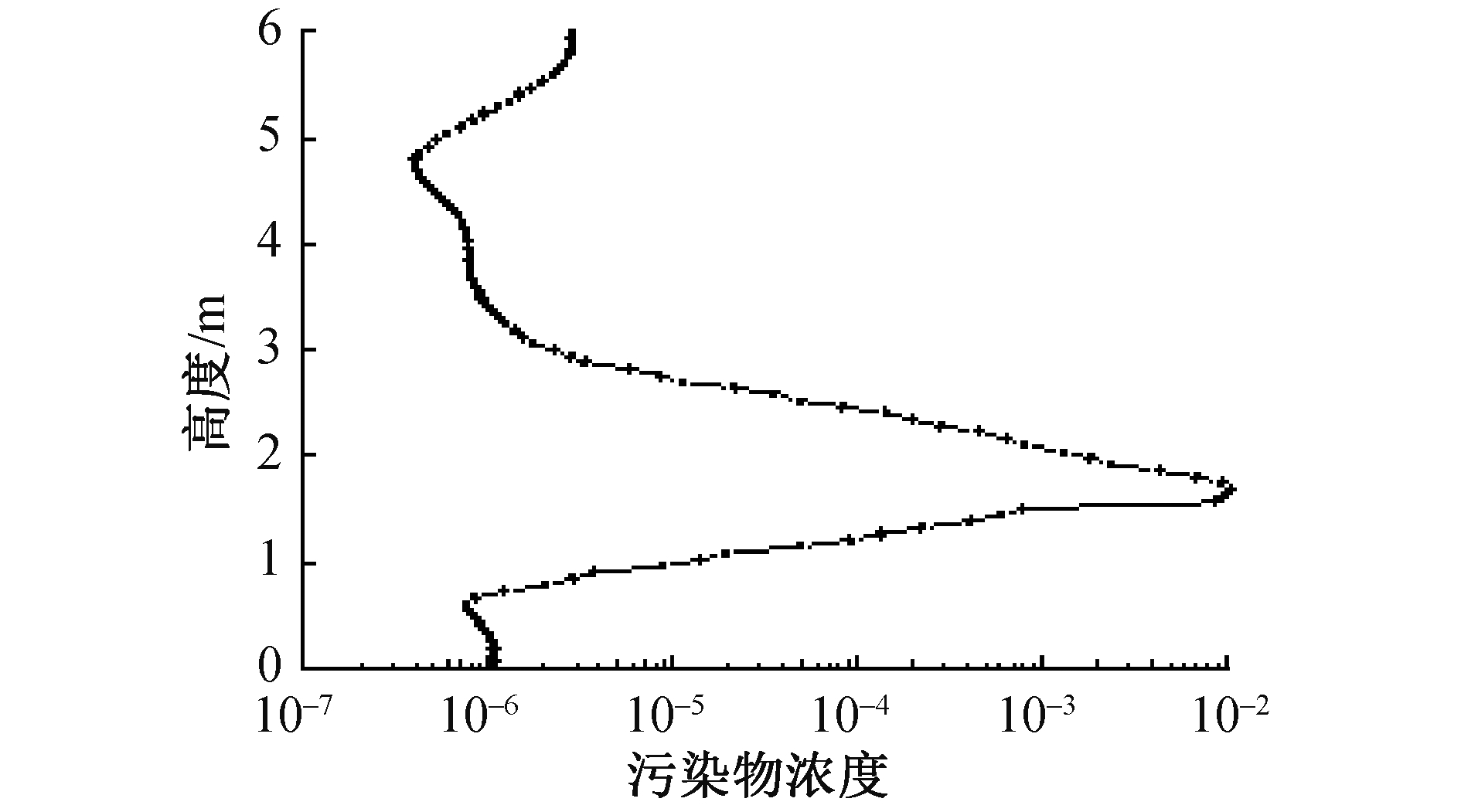
图 3给出了释放点30 cm处垂直高度污染物浓度的变化曲线，可以看出在高度1.68 m处浓度达到最大值，最大为1.07×10-2，然后浓度随高度增加降低，在高度4.8 m时出现一个拐点，污染物的浓度随高度增加而增加，拐点处的浓度为3.95×10-7。
图 3 房间1释放点处垂直高度浓度分布曲线Fig. 3 Distribution curve of vertical concentration at the release point in room one下载:
全尺寸图片
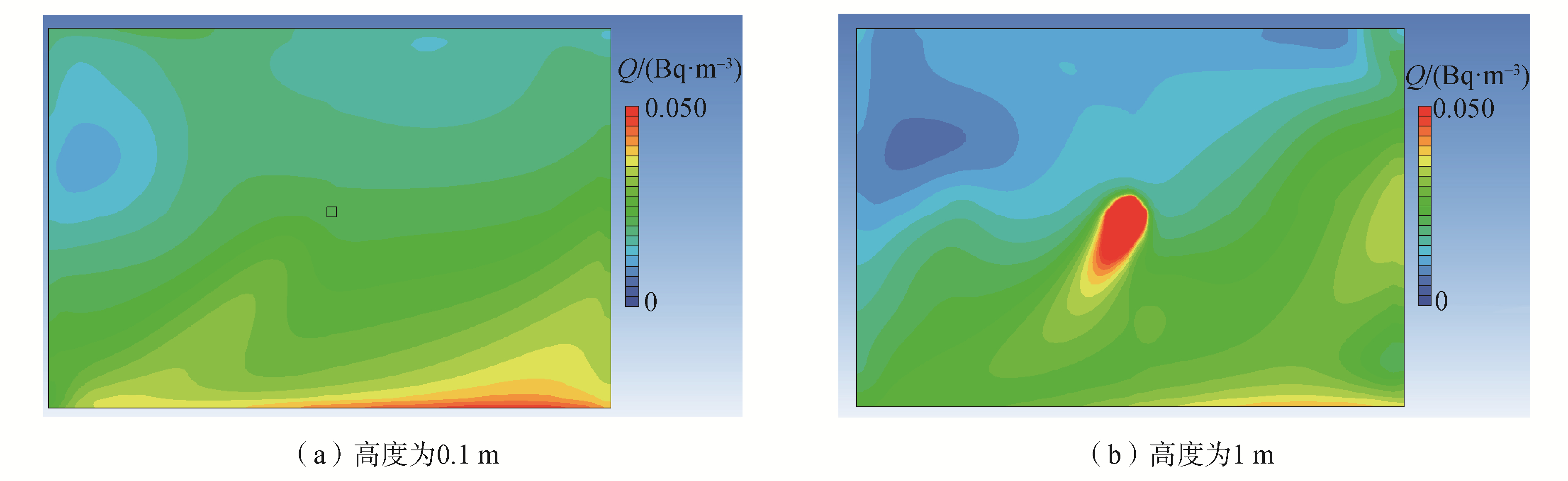
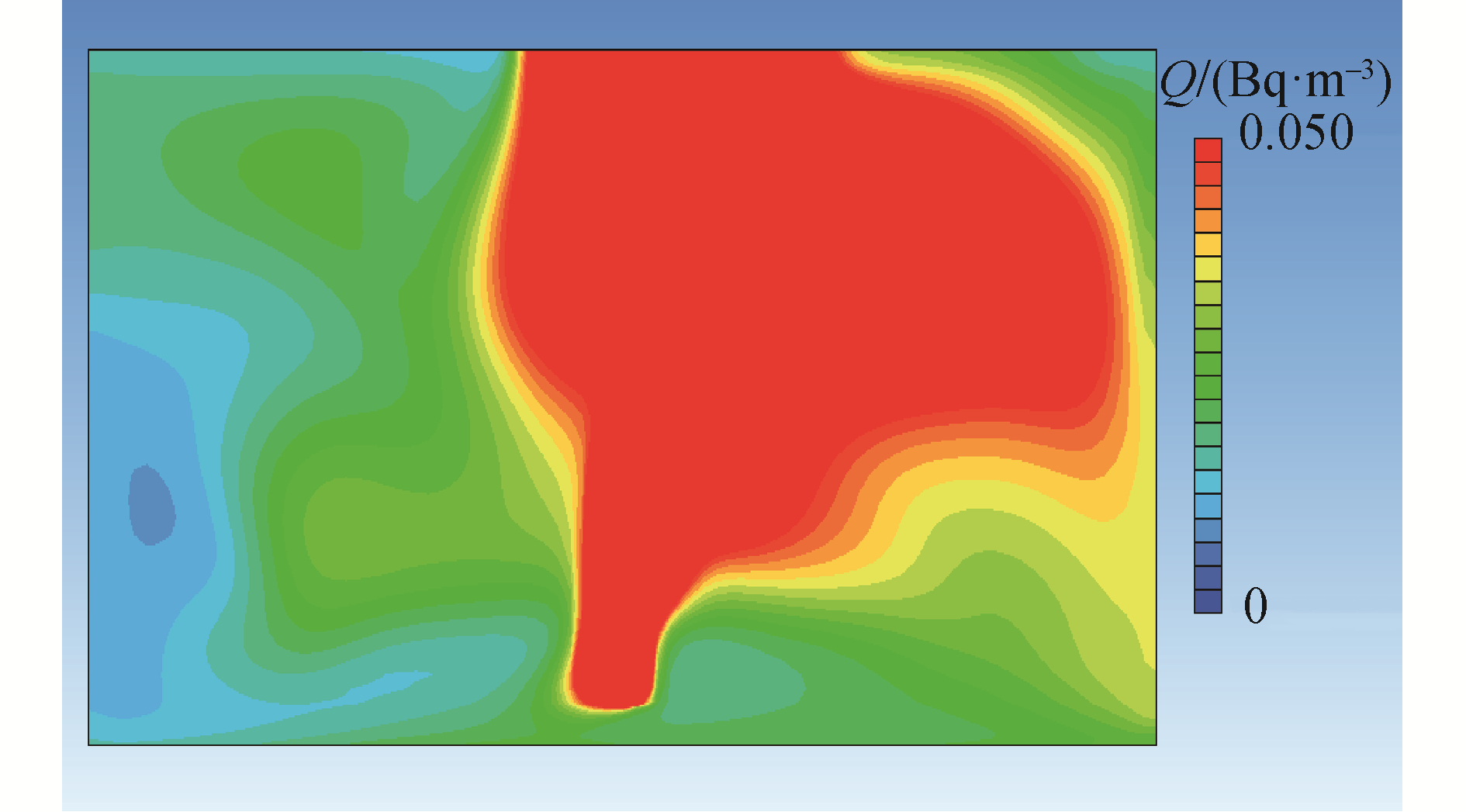
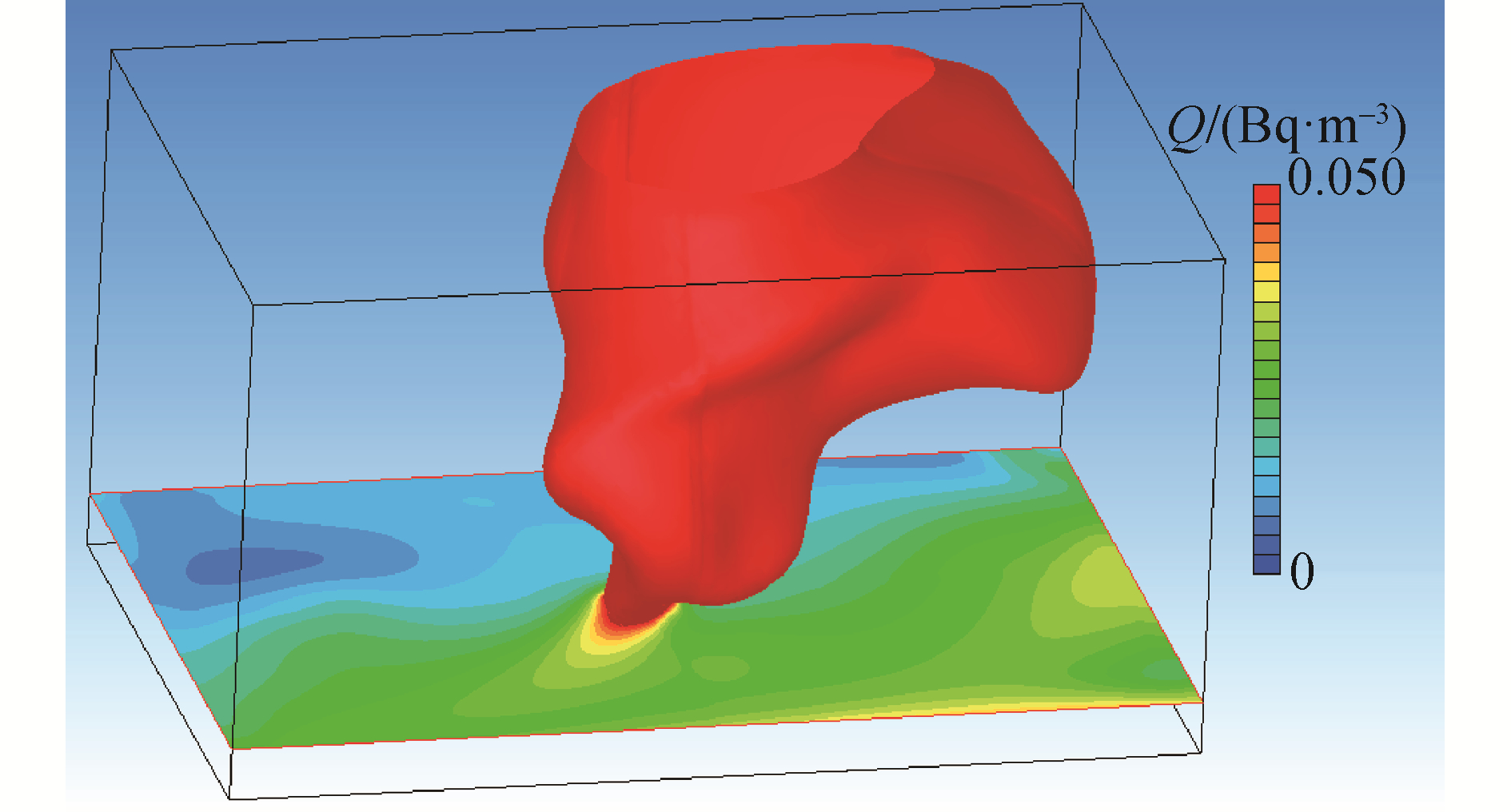
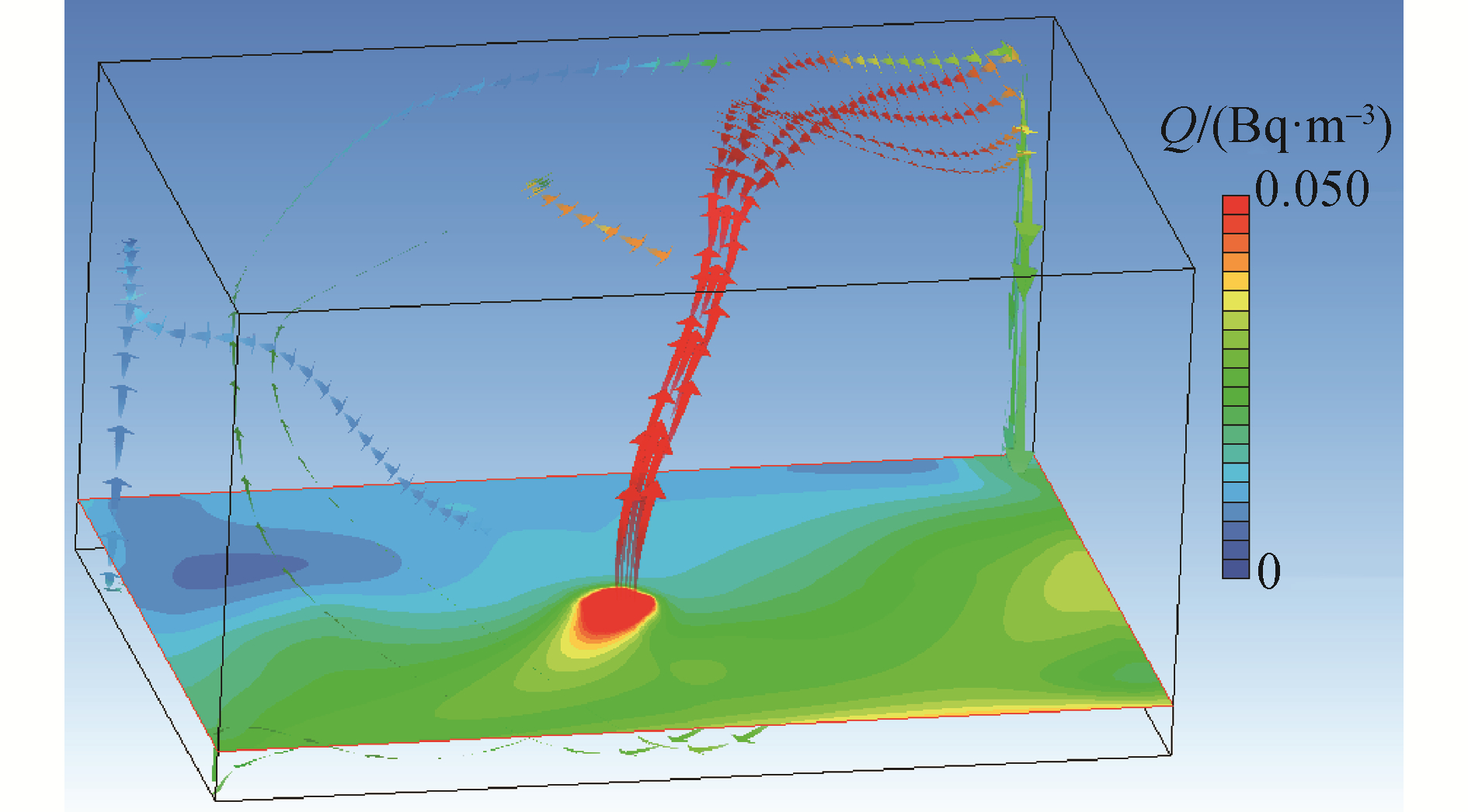
图 4给出了释放10 min后距离地面0.1 m和1 m这2种高度处的污染物浓度分布。图 5给出了释放10 min后，放射性物质在垂直方向的浓度分布图，图 6给出了0.05 s/m3污染物弥散因子等值面三维分布图；图 7给出了整个房间内污染物的浓度流线分布图。
图 4 不同高度污染物浓度分布Fig. 4 Concentration distribution of pollutants at different heights下载:
全尺寸图片
图 5 放射性物质垂向分布Fig. 5 Vertical distribution of radioactive material下载:
全尺寸图片
图 6 0.05 s/m3等值面三维分布Fig. 6 Isosurface three dimensional distribution diagram下载:
全尺寸图片
图 7 房间1污染物浓度流线分布Fig. 7 Distribution diagram of pollutant concentration streamline in room 1下载:
全尺寸图片
4.1.2 结果分析
由计算结果可知：
1) 由图 5和图 7可以看出，由于房间的通风作用，在进风口处，放射性气溶胶由于气流流场作用形成了一定的下沉聚集。
2) 由图 5和图 6可以看出，放射性气溶胶主要聚集释放到排风口的区域，从图 5垂向分布图可以看出，放射性气溶胶在一定高度处形成了空间三维聚集区。
3) 由图 3可以看出，放射性气溶胶聚集区域集中在离地面1.8 m高度的空间范围，短时间内地面或近地面的气溶胶浓度并不是高浓度区域。
4) 假定出现放射性物质释放事故时，工作人员所处的位置距离释放点为0.3 m，则依据建模获取的大气弥散因子值0.145 s/m3，计算得到该工作人员停留10 min的受照剂量约为2.34 mSv[11]，关键照射途径为吸入内照射，其中内照射剂量占比近似100%。因此，针对房间1的发生的放射性物质释放事故，做好人员吸入内照射的防护可大大降低个人受照剂量。
5) 从放射性核素的空间分布可以看出，房间1的进风口与出风口的逆风向侧的放射性核素浓度最低。因此，如有外部支援的应急人员进入房间进行应急处置时，可选在从该区域作为进出路线或短暂停留区域，以减少人员受照剂量。
4.2 房间2
考虑到房间2内放射性泄漏为短期瞬时释放，且放射性核素为3H，质量较轻，在释放后以气体形式传输和扩散。因此，在进行房间2污染物扩散模拟时，重点考虑不同时间段污染物的等值面分布情况。
4.2.1 计算结果
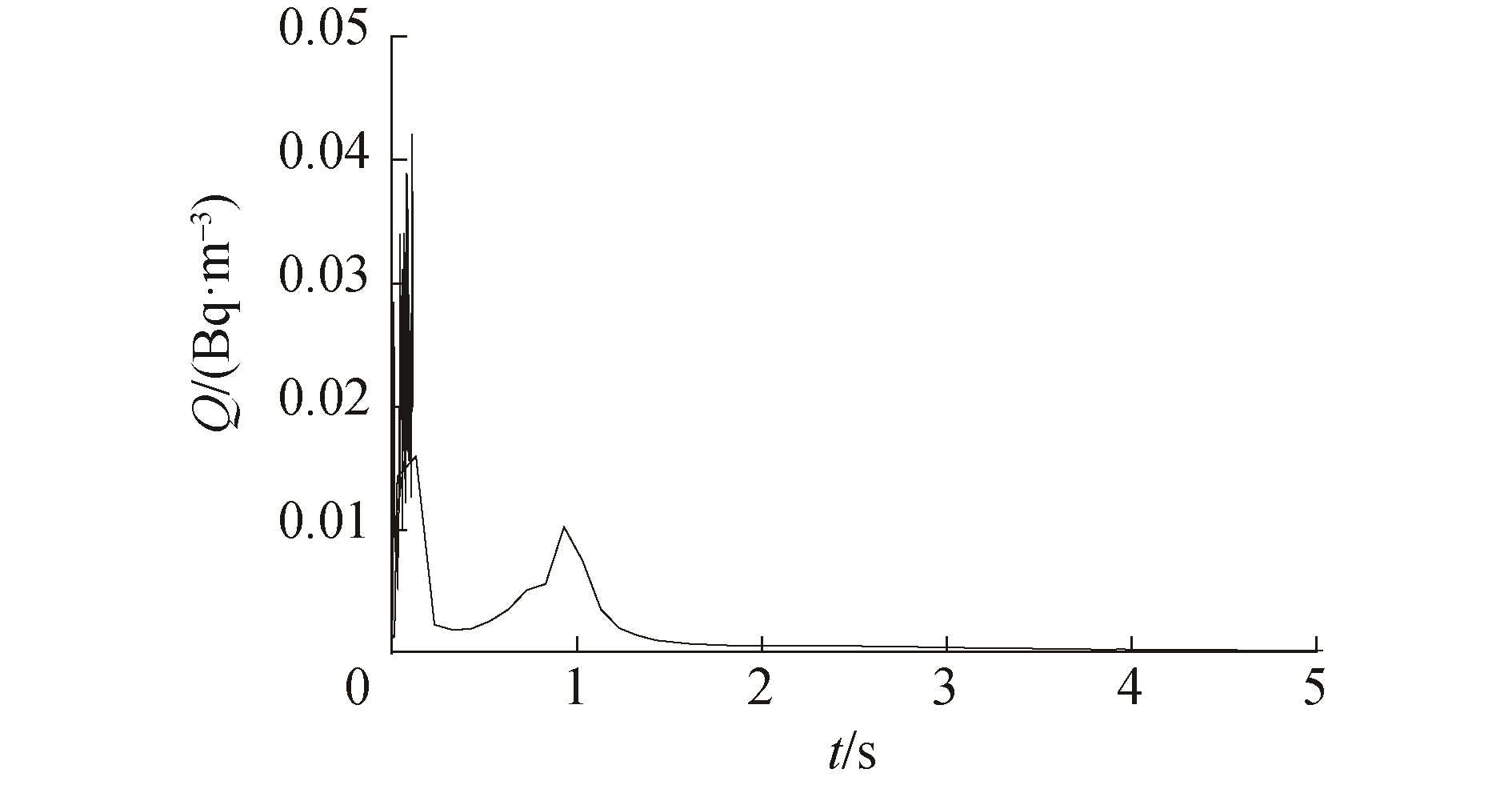
图 8给出了释放点处(本文设置其为5号监测点)3H的浓度随时间的变化曲线。
图 8 房间2释放点处3H的浓度变化Fig. 8 Concentration change of 3H at the release point of room 2下载:
全尺寸图片
可以看出其浓度变化非常剧烈，基本在释放开始(0.109 s)，浓度迅速升高到4.21×10-2，然后又迅速降低，在1 s的时候还出现一个小的峰值，主要是由于房间内的通风过程造成3H的扩散波动引起的。
图 9给出释放1 min内1、2、4、6、24、40、50、60 s等不同时间点房间2内0.05 s/m3污染物浓度等值面三维分布图。
图 9 不同时间点0.05 s/m3等值面三维分布Fig. 9 Three dimensional distribution diagram of isosurface at different time(DF=0.05 s/m3)下载:
全尺寸图片
4.2.2 结果分析
由上述结果可以看出：
1) 瞬态释放的3H在短时间内可迅速喷射到操作间的顶部，然后随着通风系统的作用在顶部分散，地面处的污染物浓度相对较低，同时主要分布在释放点周围的区域。
2) 假定工作人员距离释放点的最近距离为0.3 m(工作人员位于释放点的正上方位置)，经计算释放后该处的大气弥散因子为0.45 s/m3。利用该计算结果，假定工作人员在该处停留10 min且无任何防护措施，计算得到人员在10 min内的受照剂量为1.31 mSv[12]，其中内照射剂量贡献约占100%。因此，在该情形下做好人员的3H的吸入内照射和皮肤渗透内照射防护可大大降低个人的受照剂量[13]。
3) 在发生事故后，3H会迅速弥散开，考虑到对于放射性氚的防护手段有限，经评估在事故源项对外环境释放后影响不大的情况下，可采取开启应急排风一段时间后再行进入房间进行应急处置[14-15]。
4) 由于在放射性释放事故发生的数秒内，房间贴近地面部位的3H放射性浓度较低，其污染的空气多聚集在房间顶部。因此，现场人员可采取迅速下蹲的姿势离开事故现场，可达到有效降低个人受照剂量的效果[16-17]。
5. 结论
1) 不同的放射性核素、不同通排风方式等对放射源操作间的核素迁移扩散影响较大，应结合房间的实际情况以及实际操作放射源的特点分别制定针对性强的辐射防护措施。
2) 基于CFD建模的方法可有效实现污染物在房间内微场环境迁移扩散模拟。
目前，多个研究实践表明，CFD模型在模拟微场环境下的放射性核素迁移扩散规律上具有一定的优势，特别对于微场环境的模拟，结果的合理性和科学性均得到较好的验证。本项目针对某放射性操作场所的实际特点开展的污染扩散模拟工作仅停留在初步假定条件预估，在实际应用时，应结合房间内构筑物布局、人员实际岗位特点等设置更为合理的边界条件，以更为逼真的模拟泄漏事故发生后的初始场景，为事故应急处置提供科学的依据。因此，下阶段的研究工作重点是场景的实景化模拟。
-
图 1 房间1网格划分
Fig. 1 Grid division diagram of room 1
下载:
全尺寸图片
图 2 房间2网格划分
Fig. 2 Grid division diagram of room 2
下载:
全尺寸图片
图 3 房间1释放点处垂直高度浓度分布曲线
Fig. 3 Distribution curve of vertical concentration at the release point in room one
下载:
全尺寸图片
图 4 不同高度污染物浓度分布
Fig. 4 Concentration distribution of pollutants at different heights
下载:
全尺寸图片
图 5 放射性物质垂向分布
Fig. 5 Vertical distribution of radioactive material
下载:
全尺寸图片
图 6 0.05 s/m3等值面三维分布
Fig. 6 Isosurface three dimensional distribution diagram
下载:
全尺寸图片
图 7 房间1污染物浓度流线分布
Fig. 7 Distribution diagram of pollutant concentration streamline in room 1
下载:
全尺寸图片
图 8 房间2释放点处3H的浓度变化
Fig. 8 Concentration change of 3H at the release point of room 2
下载:
全尺寸图片
图 9 不同时间点0.05 s/m3等值面三维分布
Fig. 9 Three dimensional distribution diagram of isosurface at different time(DF=0.05 s/m3)
下载:
全尺寸图片
-
[1] 商照荣, 吴浩, 刘华. 辐射环境质量评价模式的建立[J]. 国外医学(放射医学核医学分册), 2003(6): 281-284. https://www.cnki.com.cn/Article/CJFDTOTAL-GWYF200306011.htm SHANG Zhaorong, WU Hao, LIU Hua. Development of model for assessment of radiation discharge to the environment[J]. Foreign medical science section of radiation medicine and nuclear medicine, 2003(6): 281-284. https://www.cnki.com.cn/Article/CJFDTOTAL-GWYF200306011.htm [2] 陈迎锋, 王建龙, 林晓玲, 等. 反应堆堆厅放射性核素泄漏率试验[J]. 清华大学学报(自然科学版), 2013, 53(9): 1300-1304. https://www.cnki.com.cn/Article/CJFDTOTAL-QHXB201309016.htm CHEN Yingfeng, WANG Jianlong, LIN Xiaoling, et al. Leakage rates of radioactive nuclides in a reactor hall[J]. Journal of Tsinghua University (science and technology), 2013, 53(9): 1300-1304. https://www.cnki.com.cn/Article/CJFDTOTAL-QHXB201309016.htm [3] SIMON H, NAHAS G, COULON N. Air-steam leakage through cracks in concrete walls[J]. Nuclear engineering and design, 2007, 237(15/16/17): 1786-1794. [4] OLSHER R. A practical look at Monte Carlo variance reduction methods in radiation shielding[J]. Nuclear engineering and technology, 2006, 38(3): 225-230. [5] 岳会国. 核事故应急准备与响应手册[M]. 北京: 中国环境科学出版社, 2012. YUE Huiguo. Nuclear accident emergency preparedness and response manual[M]. Beijing: China environmental science press, 2012. [6] SHAHID MAHMOOD. A research on the ship hull form optimization using viscous CFD and genetic algorithm[D]. 哈尔滨: 哈尔滨工程大学, 2012: 4-8. [7] 韩波. 面向对象计算流体力学显示系统研究与应用[D]. 南京: 南京理工大学, 2004. HAN Bo. Research and application of object-oriented computational fluid dynamics display system[D]. Nanjing: Nanjing University of Science and Technology, 2004. [8] SUGIYAMA G, NASSTROM J, POBANZ B, et al. Atmospheric dispersion modeling[J]. Health physics, 2012, 102(5): 493-508. doi: 10.1097/HP.0b013e31824c7bc9 [9] 乔清党, 李冰, 岳会国, 等. 核事故应急气载放射性物质扩散的精细化模拟方法研究[J]. 核安全, 2014, 13(1): 28-33. https://www.cnki.com.cn/Article/CJFDTOTAL-HAQY201401006.htm QIAO Qingdang, LI Bing, YUE Huiguo, et al. Refined analogy method research of diffusion of airborne radioactive substance released of nuclear accident[J]. Nuclear safety, 2014, 13(1): 28-33. https://www.cnki.com.cn/Article/CJFDTOTAL-HAQY201401006.htm [10] 王志鹏. 氨气泄漏数值模拟及应急响应措施研究[D]. 北京: 中国地质大学(北京), 2013: 6-9. WANG Zhipeng. Numerical simulation and emergency response measures for ammonia leakage[D]. Beijing: China University of Geosciences, 2013: 6-9. [11] 陈天豪, 傅力凯. 核辐射剂量估算在核事故应急中的应用[J]. 武警学院学报, 2019, 35(6): 11-16. https://www.cnki.com.cn/Article/CJFDTOTAL-WUJI201906002.htm CHEN Tianhao, FU Likai. Application of nuclear radiation dose estimation in nuclear accident emergency[J]. Journal of the armed police academy, 2019, 35(6): 11-16. https://www.cnki.com.cn/Article/CJFDTOTAL-WUJI201906002.htm [12] 蒋国强, 罗德礼, 陆光达. 氚和氚的工程技术[M]. 北京: 国防工业出版社, 2007. JIANG Guoqiang, LUO Deli, LU Guangda. Tritium and industry technology of tritium[M]. Beijing: National defense industry press, 2007. [13] 王天运, 王世琦, 高缨. 环境污染事故放射性气溶胶扩散的应急控制及消除方法[J]. 核安全, 2021, 20(3): 17-24. https://www.cnki.com.cn/Article/CJFDTOTAL-HAQY202103004.htm WANG Tianyun, WANG Shiqi, GAO Ying. Emergency control and elimination of radioactive aerosol diffusion in environmental pollution accidents[J]. Nuclear safety, 2021, 20(3): 17-24. https://www.cnki.com.cn/Article/CJFDTOTAL-HAQY202103004.htm [14] 葛宝珠, 陆芊芊, 陈学舜, 等. 放射性核素大气扩散数值模拟研究综述[J]. 环境科学学报, 2021, 41(5): 1599-1609. https://www.cnki.com.cn/Article/CJFDTOTAL-HJXX202105002.htm GE Baozhu, LU Qianqian, CHEN Xueshun, et al. A review of the numerical simulations of the atmospheric dispersion of radionuclides[J]. Acta scientiae circumstantiae, 2021, 41(6): 1599-1609. https://www.cnki.com.cn/Article/CJFDTOTAL-HJXX202105002.htm [15] 黄燕. 海洋小型压水堆核事故核素扩散模型研究[J]. 产业与科技论坛, 2021, 20(8): 48-50. https://www.cnki.com.cn/Article/CJFDTOTAL-CYYT202108023.htm HUANG Yan. Research on radionuclide diffusion model of marine small pressurized water reactor nuclear accident[J]. Industrial & science tribune, 2021, 20(8): 48-50. https://www.cnki.com.cn/Article/CJFDTOTAL-CYYT202108023.htm [16] 陈天豪, 傅力凯. 核辐射剂量估算在核事故应急中的应用[J]. 武警学院学报, 2019, 35(6): 11-16. https://www.cnki.com.cn/Article/CJFDTOTAL-WUJI201906002.htm CHEN Tianhao, FU Likai. Application of nuclear radiation dose estimation in nuclear accident emergency[J]. Journal of the armed police academy, 2019, 35(6): 11-16. https://www.cnki.com.cn/Article/CJFDTOTAL-WUJI201906002.htm [17] 林韩清, 陈春花, 郑晓磊, 等. 基于计算流体力学的近岸海域放射性核素弥散模型研究[J]. 辐射研究与辐射工艺学报, 2018, 36(3): 60-66. https://www.cnki.com.cn/Article/CJFDTOTAL-FYFG201803008.htm LIN Hanqing, CHEN Chunhua, ZHENG Xiaolei, et al. Study on offshore dispersion of radionuclides using computational fluid dynamic model[J]. Journal of radiation research and radiation processing, 2018, 36(3): 60-66. https://www.cnki.com.cn/Article/CJFDTOTAL-FYFG201803008.htm
